Bi-Objective Optimization and Emergy Analysis of Multi-Distributed Energy System Considering Shared Energy Storage
Abstract
:1. Introduction
2. System Architecture and Models
2.1. Architecture of Shared Energy Storage System
2.1.1. SESO Model
2.1.2. Power Interaction Model between DESs
2.2. MDES Model and Cost Model
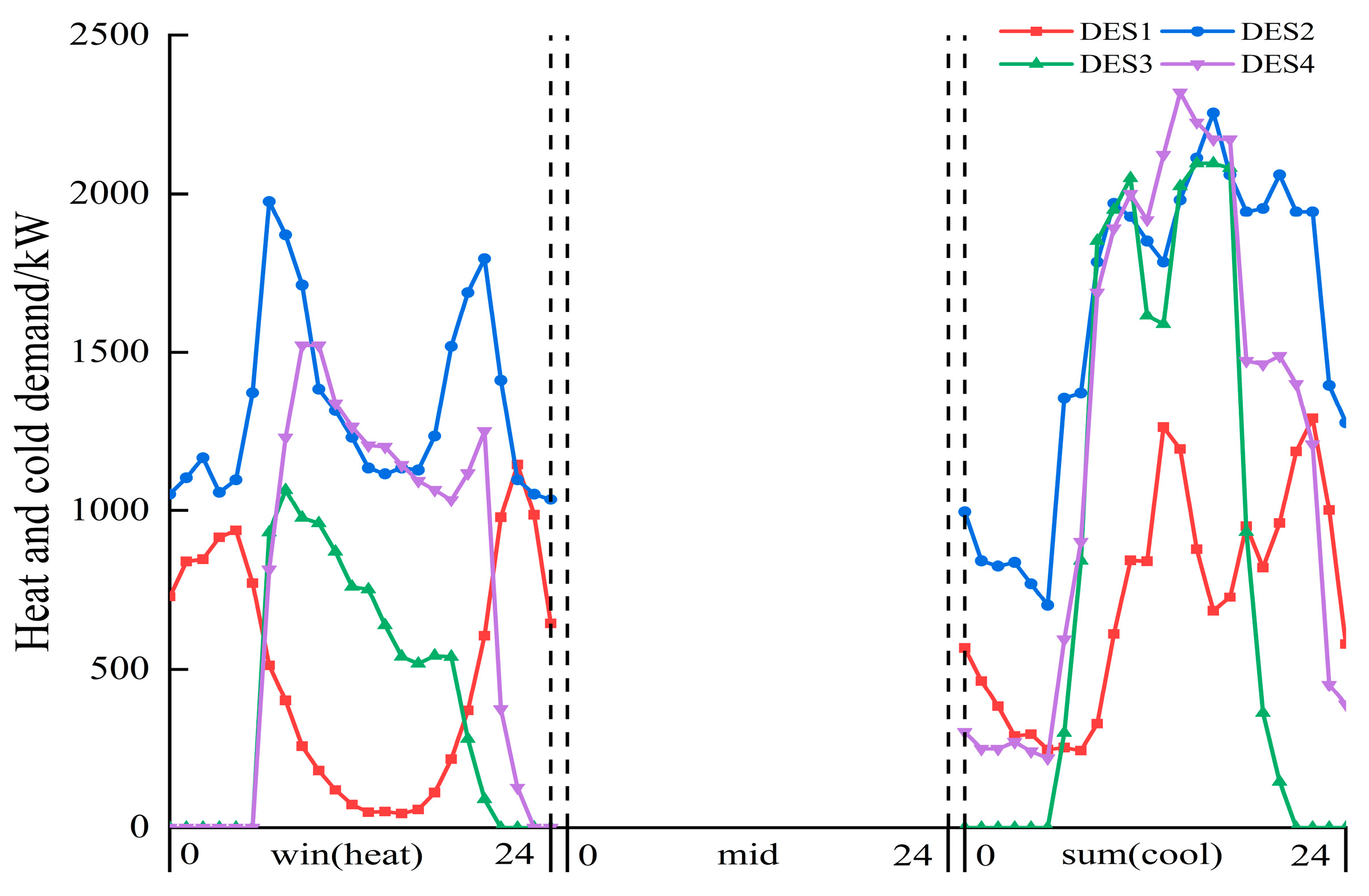
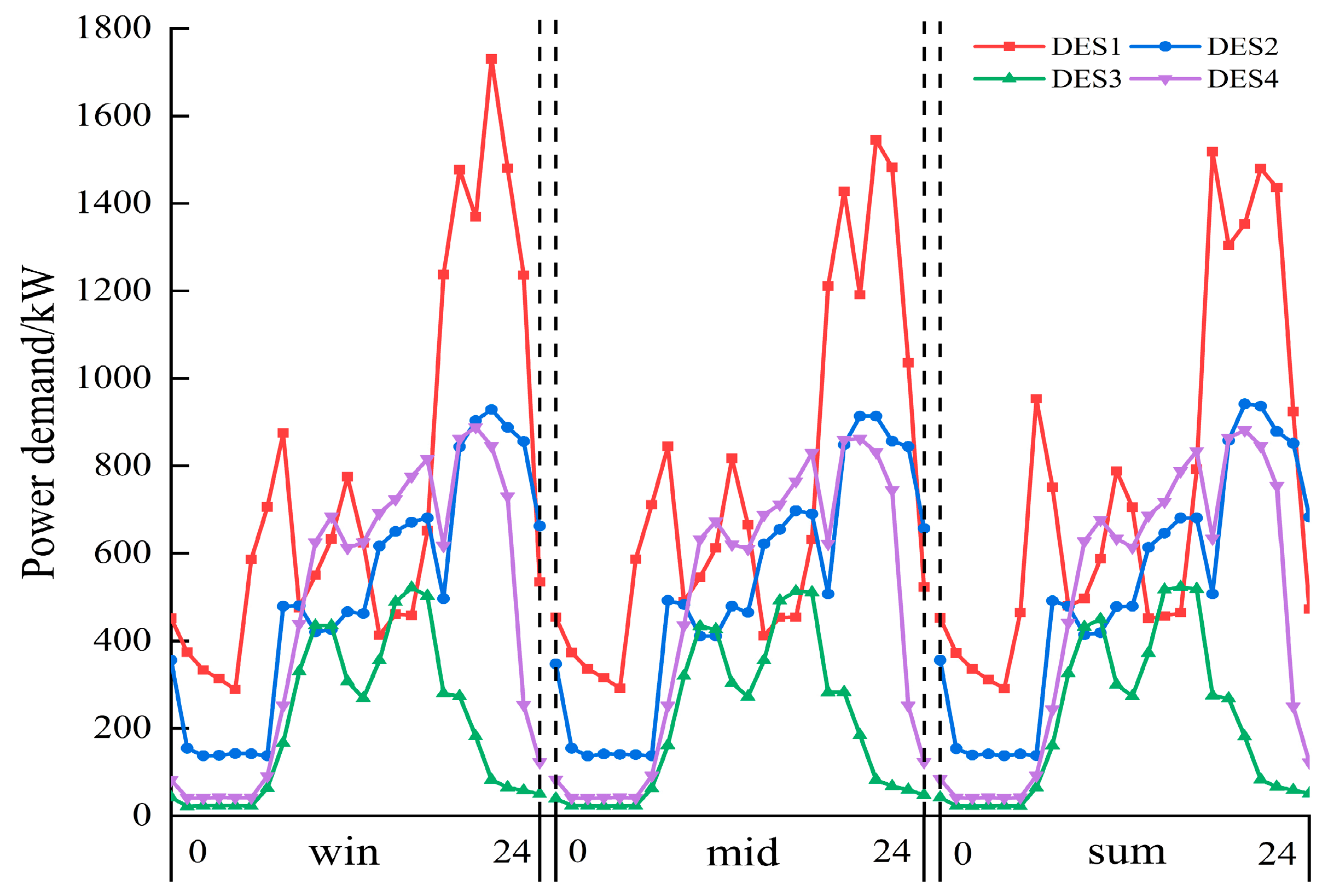
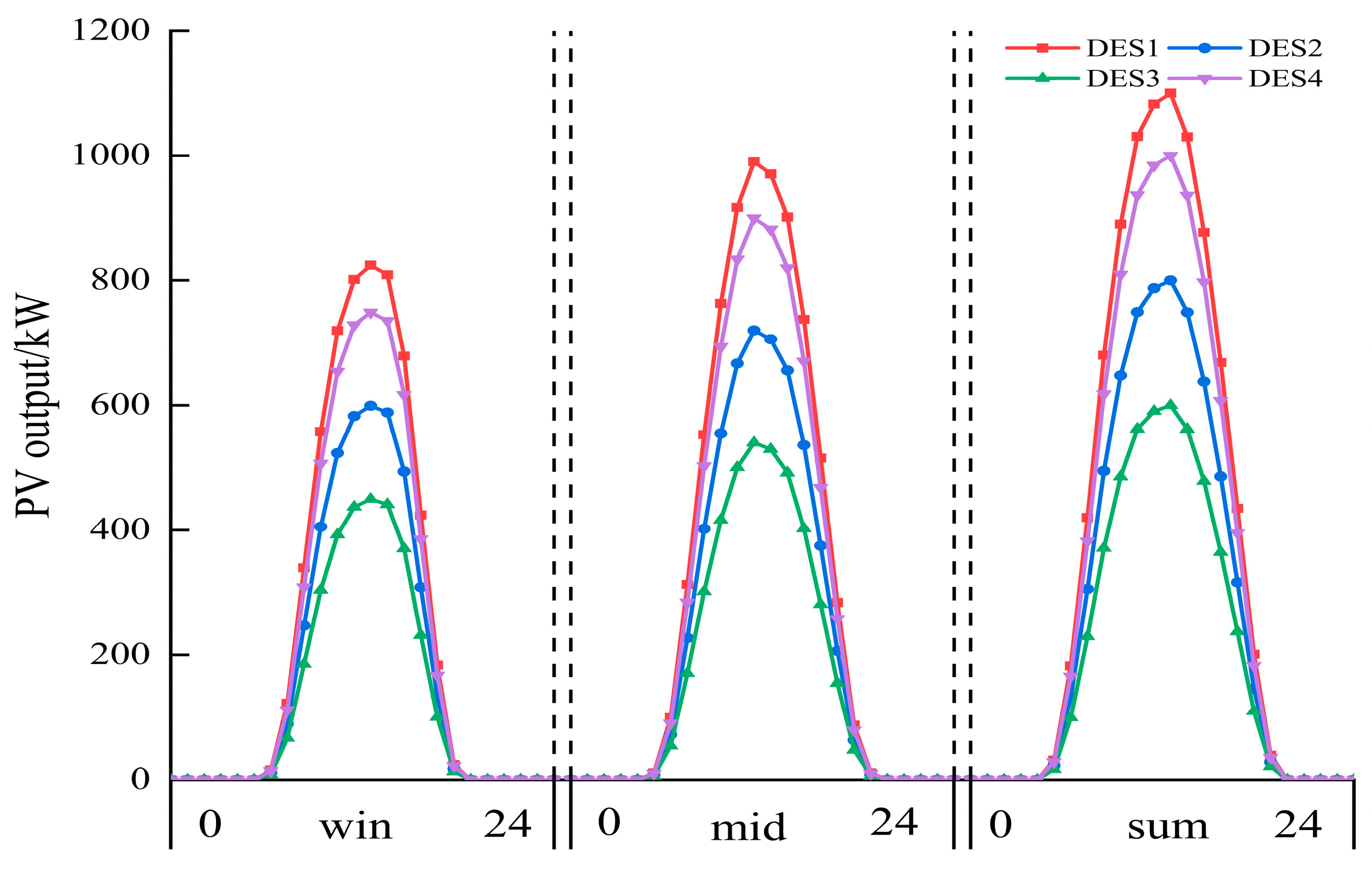
2.2.1. DES Energy Model
2.2.2. DES Cost Model
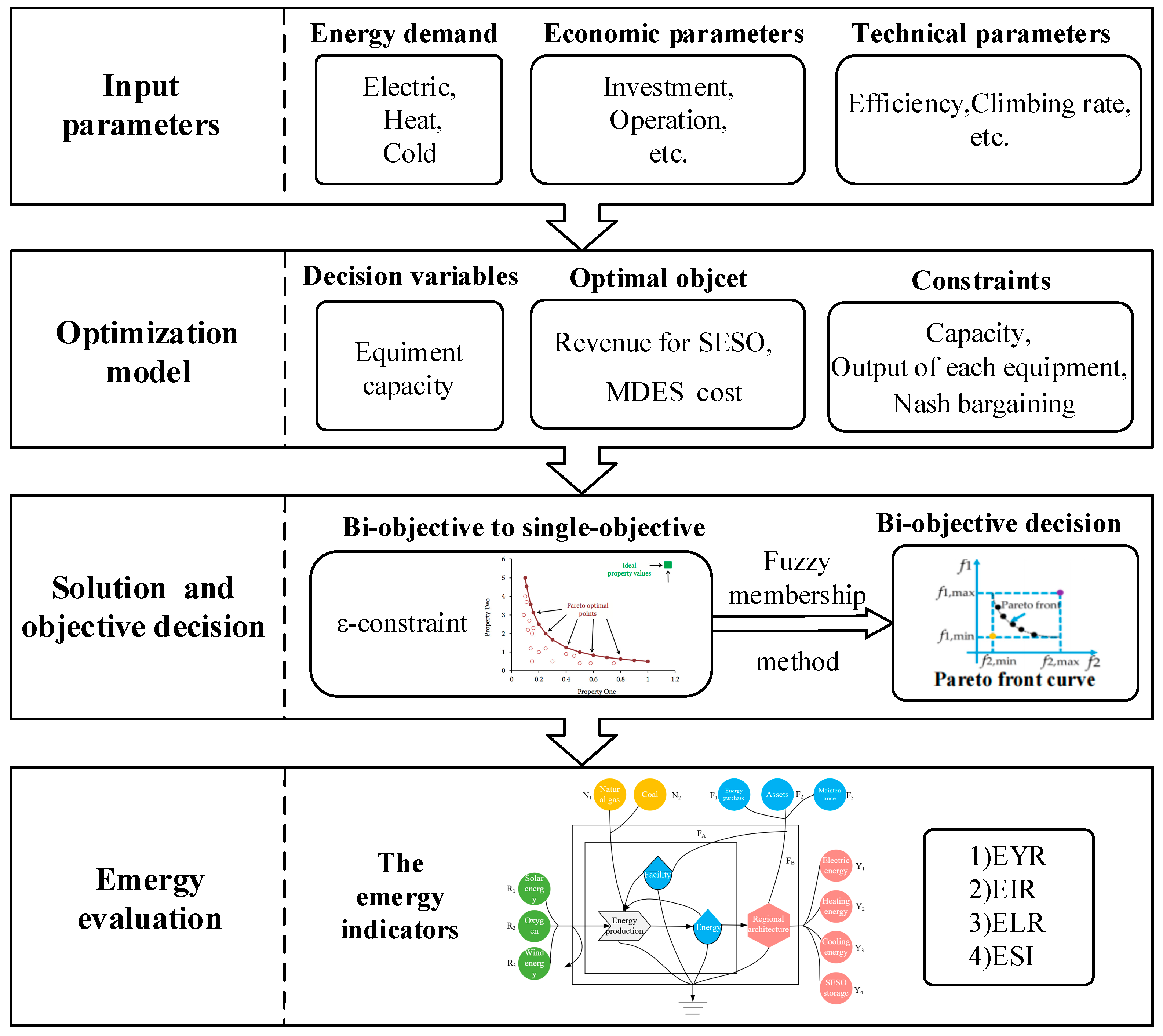
3. Solution Process and Evaluation Method
3.1. System Pareto Solutions
3.2. Nash Bargaining of DESs
3.3. Bi-Objective Solution Process
3.4. System Sustainability Analysis Based on Emergy Theory
4. Results and Discussion
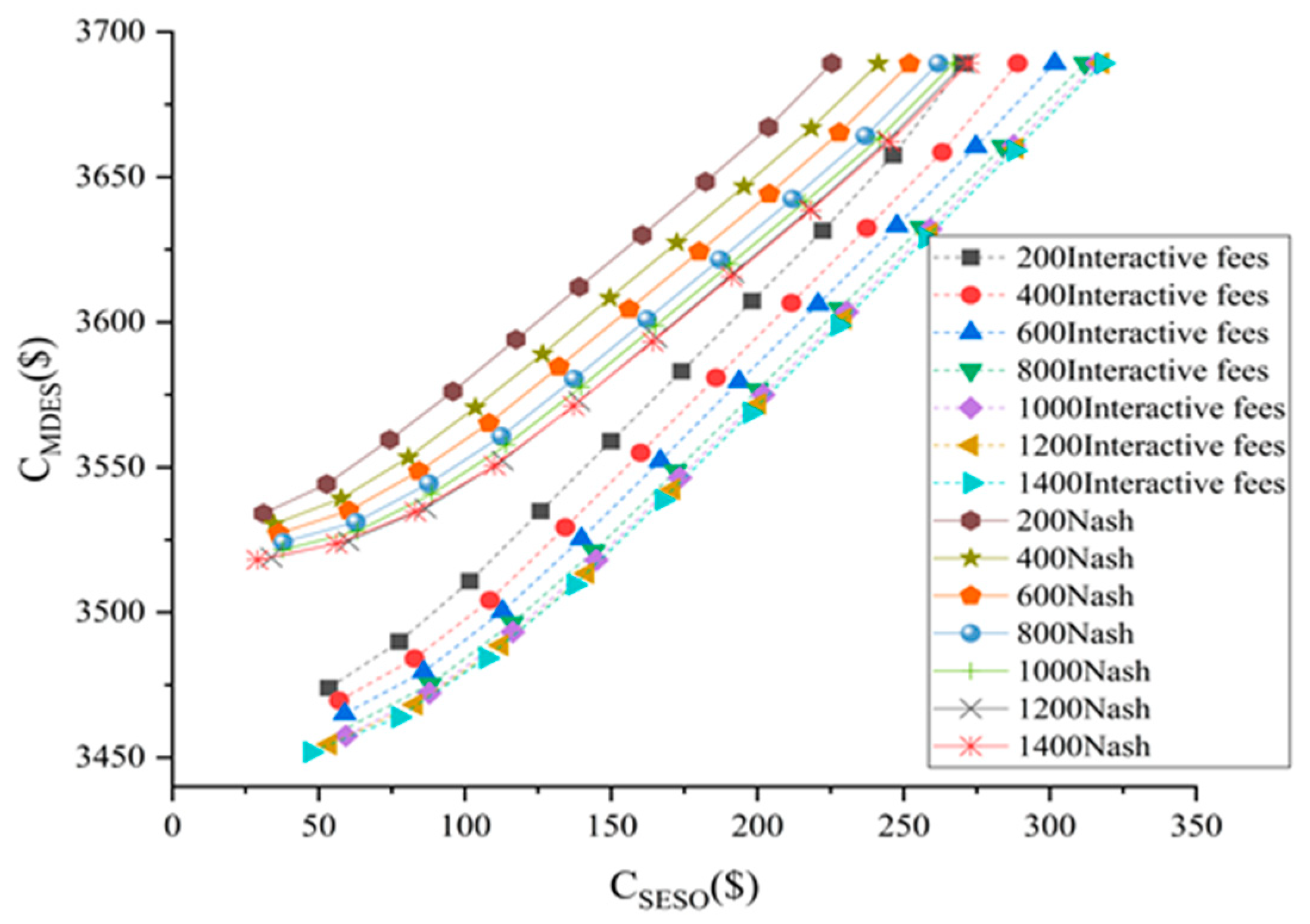
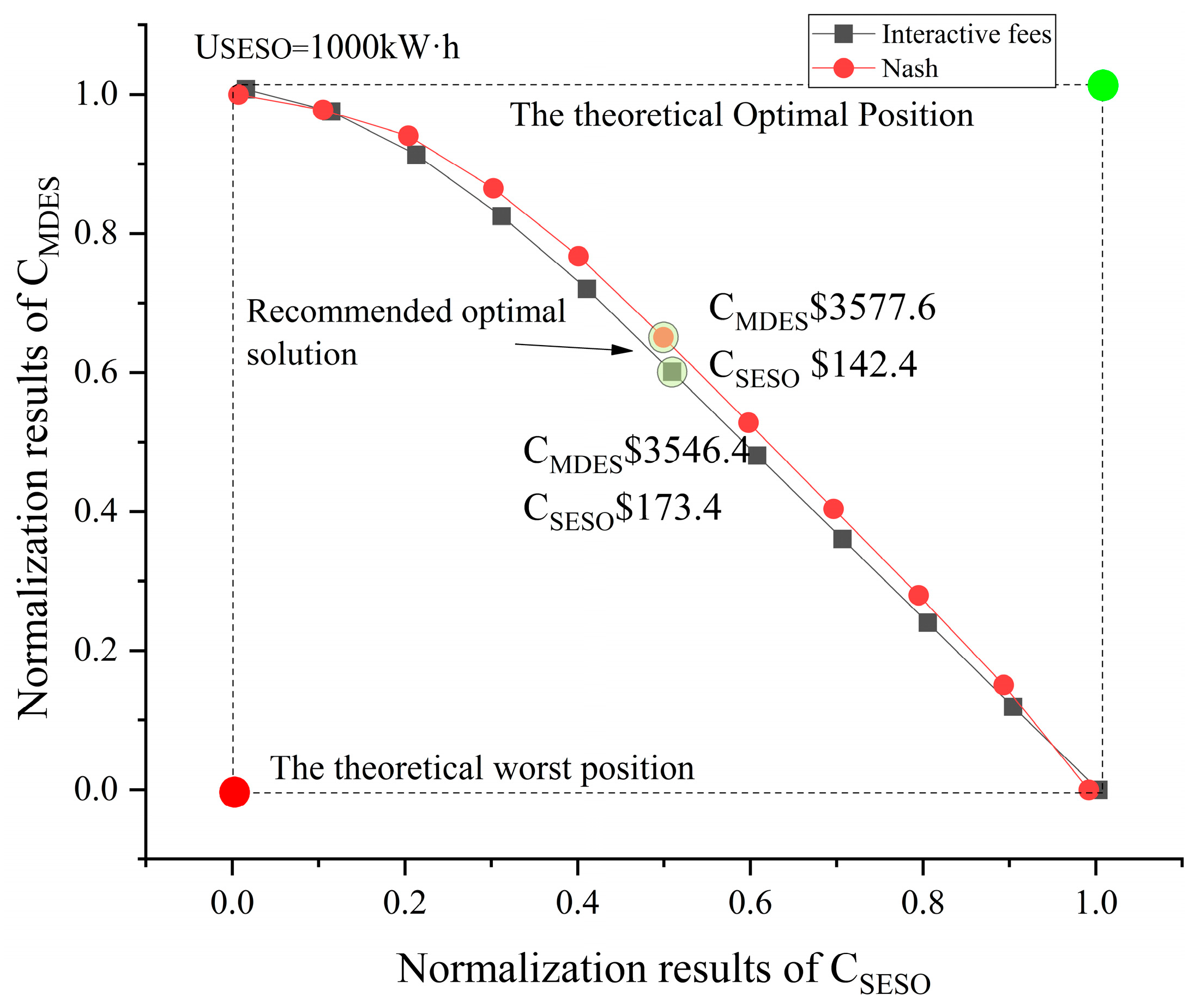
4.1. The Impact of SESO on MDES
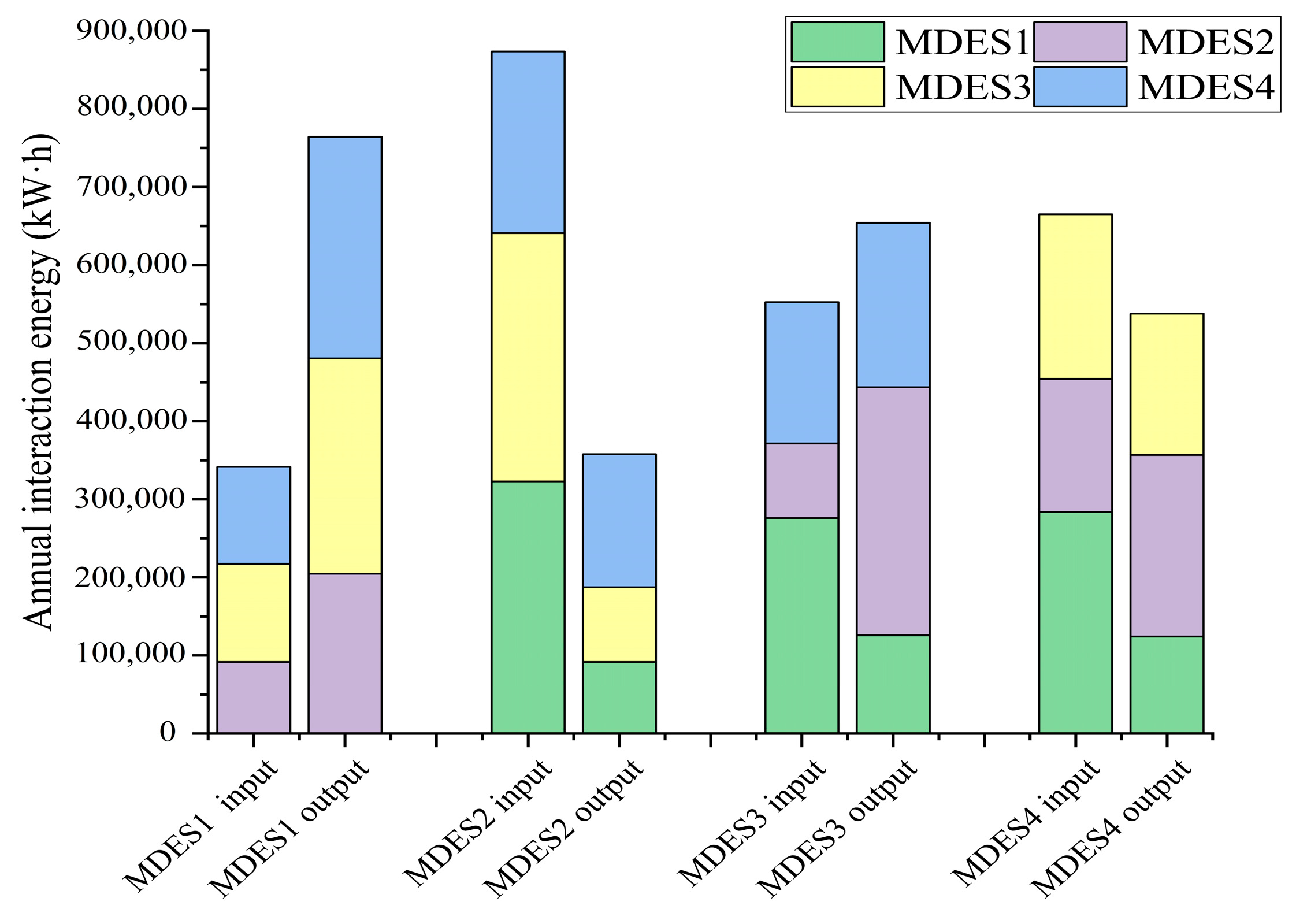
4.2. System Emergy Analysis
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Absorption refrigeration |
| CHP | Combined heat and power generation |
| DES | Distributed energy system |
| EB | Electric boiler |
| EC | Electric compression refrigeration |
| EISS | Energy information scheduling system |
| GN | Gas network |
| MDES | Multi distributed energy system |
| PG | Power grid |
| PV | Photovoltaic panel |
| SES | Shared energy storage |
| SESO | Shared Energy Storage Operator |
| Cbi | Equipment construction cost ($) |
| Cb, Xi | Construction cost of equipment X (CHP, EB, AC, EC, PV) in the i DES ($) |
| CDES_all | Total cost of DES |
| CEGi | Electricity purchasing cost ($) |
| Cg | Gas purchase costs ($) |
| Ci | The operation cost of the ith DES after participating in Nash bargaining of communicating energy storage and interacting with no charge in a cycle |
| C*I | Operation cost of the ith DES after optimization |
| CI | Interaction cost with other DESs ($) |
| COPACi | Coefficient of performance of AC |
| CMDES_avg | The average daily operating cost of MDES |
| CSESO | Revenue for SESO ($) |
| CSESO_avg | The average daily revenue of SESO |
| CSESO1 | Operating income of SESO ($) |
| CSESO2 | Construction cost of SESO ($) |
| CSESO3 | Maintenance cost of SESO ($) |
| CSESOi | Interaction cost with SESO ($) |
| Cmi | Cost of equipment maintenance ($) |
| Cm_Xi | Maintenance cost of equipment X ($) |
| CMDES_all | Total cost of DES ($) |
| CMDESi | The operation cost of the ith DES consdering SESO ($) |
| CMDESi_iso | Operation cost of the ith DES without shared energy storage ($) |
| CtMi | Interaction cost of MDESi ($/kW) |
| EIR | Emergy investment ratio |
| ELR | Environmental load ratio |
| Em | The total solar emergy (sej) |
| ESI | Emergy sustainability index |
| EYR | Emergy yield ratio |
| EtSESO | Capacity of SESO at time t (kW·h) |
| F | Emergy values of purchased energy and services (sej) |
| fm | Proportion coefficient of maintenance cost and construction cost |
| N | Emergy values of non-renewable energy (sej) |
| pgas | Natural gas unit price ($/m3) |
| Pmaxi,j | The upper limit of interaction power between MDES (kW) |
| PMAXSESO | Maximum power of SESO (kW) |
| pSESO | Operation cycle of SESO (year) |
| PtACci | Cold output of AC (kW) |
| PtAChi | Heat consumption power of AC (kW) |
| PtCHPei | Electric output of CHP (kW) |
| PtCHPhi | Heat output of CHP (kW) |
| PtECi | Cold output of EC (kW) |
| PtECei | Power consumption of EC (kW) |
| ptEG | t Timing of power grid electricity price |
| PtEBei | Power consumption of EB (kW) |
| PtEBhi | Thermal power of EB (kW) |
| PtEGi | Electric network power (kW) |
| Pti,j | Interaction power between DESi and DESj (kW) |
| Ptload,ci | Cooling load (kW) |
| Ptload,ei | Electric load (kW) |
| Ptload,hi | Thermal load (kW) |
| PtPVi | Electric power of PV (kW) |
| PtSESO,c/d | Power of MDESi charging/discharging with SESO (kW) |
| PtSESOi,c/d | Charge/discharge power at t time in SESO (kW) |
| PtSESO,d | Total discharge power at time t of SESO (kW) |
| pXi | Operation cycle of equipment X ($) |
| QLHV | Low heating value of natural gas |
| R | Emergy values of local renewable energy (sej) |
| r | Interest rate |
| TXi | Operation cycle of equipment X |
| USESO | Maximum capacity of SESO (kW·h) |
| UXi | Equipment X installation scale ($/kW) |
| Y | Emergy values of output energy products (sej) |
| Ym | The output of emergy products |
| Zi | The bargaining income transfer of the ith DES |
| α | Proportional coefficient between maximum power and a maximum capacity of SESO |
| ηc/d | Charging/discharging efficiency of SESO (kW) |
| ηCHP,ei | Power Generation Efficiency of CHP |
| ηCHP,hi | CHP thermal efficiency |
| ηEB | Coefficient of performance of EB |
| ηEC | Refrigeration efficiency of EC |
| λmaxCHPei | Upper limit of CHP climbing rate (kW) |
| λSESO | Unit power rental cost ($/kW) |
| λSESO,P | Unit power cost of SESO ($/kW) |
| λSESO,U | Unit capacity cost of SESO ($/kW·h) |
| λtEG | t Timing of power grid electricity price ($/kW·h) |
| λtM | Unit interactive power costs between DESs ($/kW) |
| λXi | Equipment X (CHP, EB, AC, EC, PV) unit construction cost ($/kW) |
References
- Li, C.; Shi, H.; Cao, Y.; Wang, J.; Kuang, Y.; Tan, Y.; Wei, J. Comprehensive Review of Renewable Energy Curtailment and Avoidance: A Specific Example in China. Renew. Sustain. Energy Rev. 2015, 41, 1067–1079. [Google Scholar] [CrossRef]
- Shang, B.; Jiang, T.; Bao, Z. A Study on Inter-Regional Cooperation Patterns and Evolution Mechanism of Traditional and Renewable Energy Sources. Sustainability 2022, 14, 16022. [Google Scholar] [CrossRef]
- Vahid-Pakdel, M.; Nojavan, S.; Mohammadi-Ivatloo, B.; Zare, K. Stochastic Optimization of Energy Hub Operation with Consideration of Thermal Energy Market and Demand Response. Energy Convers. Manag. 2017, 145, 117–128. [Google Scholar] [CrossRef]
- Yu, H.; Yang, X.; Chen, H.; Lou, S.; Lin, Y. Energy Storage Capacity Planning Method for Improving Offshore Wind Power Consumption. Sustainability 2022, 14, 14589. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Huang, Y.; Yu, H.; Du, R.; Zhang, F.; Zhang, F.; Zhu, J. Optimal Scheduling of the Regional Integrated Energy System Considering Economy and Environment. IEEE Trans. Sustain. Energy 2019, 10, 1939–1949. [Google Scholar] [CrossRef]
- Zhao, N.; You, F. Can Renewable Generation, Energy Storage and Energy Efficient Technologies Enable Carbon Neutral Energy Transition? Appl. Energy 2020, 279, 15889. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Ekonomou, L. Economic Analysis of Energy Storage System Integration with a Grid Connected Intermittent Power Plant, for Power Quality Purposes. Technology 2016, 11, 65–71. [Google Scholar]
- Walker, A.; Kwon, S. Design of Structured Control Policy for Shared Energy Storage in Residential Community: A Stochastic Optimization Approach. Appl. Energy 2021, 298, 117182. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer Energy Trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Li, J.L.; Jiang, Y.R.; Zhang, L.J. Policy Recommendations and Business Model Exploration of Electrochemical Energy Storage in Qinghai Province. Energy Sci. Technol. 2021, 19, 7–12. (In Chinese) [Google Scholar]
- Lombardi, P.; Schwabe, F. Sharing Economy as a New Business Model for Energy Storage Systems. Appl. Energy 2017, 188, 485–496. [Google Scholar] [CrossRef]
- Mignoni, N.; Scarabaggio, P.; Carli, R.; Dotoli, M. Control Frameworks for Transactive Energy Storage Services in Energy Communities. Control Eng. Pract. 2023, 130, 105364. [Google Scholar] [CrossRef]
- Fathi, M.; Bevrani, H. Adaptive Energy Consumption Scheduling for Connected Microgrids Under Demand Uncertainty. IEEE Trans. Power Deliv. 2013, 28, 1576–1583. [Google Scholar] [CrossRef]
- Fathi, M.; Bevrani, H. Statistical Cooperative Power Dispatching in Interconnected Microgrids. IEEE Trans. Sustain. Energy 2013, 4, 586–593. [Google Scholar] [CrossRef]
- Dimitrov, P.; Piroddi, L.; Prandini, M. Distributed Allocation of a Shared Energy Storage System in a Microgrid. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Venkatesan, K.; Govindarajan, U. Optimal Power Flow Control of Hybrid Renewable Energy System with Energy Storage: A WOANN Strategy. J. Renew. Sustain. Energy 2019, 11, 015501. [Google Scholar] [CrossRef]
- Scarabaggio, P.; Carli, R.; Dotoli, M. Noncooperative Equilibrium-Seeking in Distributed Energy Systems Under AC Power Flow Nonlinear Constraints. IEEE Trans. Control. Netw. Syst. 2022, 9, 1731–1742. [Google Scholar] [CrossRef]
- Adewumi, O.B.; Fotis, G.; Vita, V.; Nankoo, D.; Ekonomou, L. The Impact of Distributed Energy Storage on Distribution and Transmission Networks’ Power Quality. Appl. Sci. 2022, 12, 6466. [Google Scholar] [CrossRef]
- Zheng, S.; Jin, X.; Huang, G.; Lai, A.C. Coordination of Commercial Prosumers with Distributed Demand-Side Flexibility in Energy Sharing and Management System. Energy 2022, 248, 123634. [Google Scholar] [CrossRef]
- Choudhury, S. Review of Energy Storage System Technologies Integration to Microgrid: Types, Control Strategies, Issues, and Future Prospects. J. Energy Storage 2022, 48, 103966. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, W.; Chen, L.; Zheng, B.; Mei, S. Service Pricing and Load Dispatch of Residential Shared Energy Storage Unit. Energy 2020, 202, 117543. [Google Scholar] [CrossRef]
- Shuai, X.Y.; Wang, X.L.; Huang, J. Optimal Configuration of Shared Energy Storage Capacity Under Multiple Regional Integrated Energy Systems Interconnection. J. Glob. Energy Interconnect. 2021, 4, 382–392. (In Chinese) [Google Scholar] [CrossRef]
- Szabó, D.Z.; Duck, P.; Johnson, P. Optimal Trading of Imbalance Options for Power Systems Using an Energy Storage Device. Eur. J. Oper. Res. 2018, 285, 3–22. [Google Scholar] [CrossRef]
- Guelpa, E.; Sciacovelli, A.; Verda, V. Entropy Generation Analysis for the Design Improvement of a Latent Heat Storage System. Energy 2013, 53, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Jing, R.; Na Xie, M.; Wang, F.X.; Chen, L.X. Fair P2P Energy Trading between Residential and Commercial Multi-Energy Systems Enabling Integrated Demand-Side Management. Appl. Energy 2020, 262, 114551. [Google Scholar] [CrossRef]
- Xu, Y.-P.; Liu, R.-H.; Tang, L.-Y.; Wu, H.; She, C. Risk-Averse Multi-Objective Optimization of Multi-Energy Microgrids Integrated with Power-to-Hydrogen Technology, Electric Vehicles and Data Center under a Hybrid Robust-Stochastic Technique. Sustain. Cities Soc. 2022, 79, 103699. [Google Scholar] [CrossRef]
- Nehra, A.; Caplan, A.J. Nash Bargaining in a General Equilibrium Framework: The Case of a Shared Surface Water Supply. Water Resour. Econ. 2022, 39, 100206. [Google Scholar] [CrossRef]
- Liu, N.; Cheng, M.; Yu, X.; Zhong, J.; Lei, J. Energy-Sharing Provider for PV Prosumer Clusters: A Hybrid Approach Using Stochastic Programming and Stackelberg Game. IEEE Trans. Ind. Electron. 2018, 65, 6740–6750. [Google Scholar] [CrossRef]
- Odum, H.T. Environmental Accounting. In The Economics of the Environment and Natural Resources; Wiley-Blackwell: Hoboken, NJ, USA, 1996. [Google Scholar]
- Wang, J.; Wang, J.; Yang, X.; Xie, K.; Wang, D. A Novel Emergy-Based Optimization Model of a Building Cooling, Heating and Power System. Energy Convers. Manag. 2022, 268, 115987. [Google Scholar] [CrossRef]
- Liu, J.Y.; Yang, Z.F.; Jiang, D.N. Emergy Theory and Practice: Ecological Environmental Accounting and Urban Green Management; Science Press: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Pan, H.; Zhang, X.; Wu, J.; Zhang, Y.; Lin, L.; Yang, G.; Deng, S.; Li, L.; Yu, X.; Qi, H.; et al. Sustainability Evaluation of a Steel Production System in China Based on Emergy. J. Clean. Prod. 2015, 112, 1498–1509. [Google Scholar] [CrossRef]
- Peng, T.; Lu, H.F.; Wu, W.L.; Campbell, D.E.; Zhao, G.S.; Zou, J.H.; Chen, J. Should a Small Combined Heat and Power Plant (CHP) Open to Its Regional Power and Heat Networks? Integrated Economic, Energy, and Emergy Evaluation of Optimization Plans for Jiufa CHP. Energy 2008, 33, 437–445. [Google Scholar] [CrossRef]
- Tian, L.T.; Cheng, L.; Guo, J.B.; Sun, S.M.; Cheng, Y.; Wei, D.J. Multi-energy System Valuation Method Based on Emergy Analysis. Power Syst. Technol. 2019, 43, 2925–2934. (In Chinese) [Google Scholar] [CrossRef]
- Li, L.; Cao, X.; Zhang, S. Shared Energy Storage System for Prosumers in a Community: Investment Decision, Economic Operation, and Benefits Allocation under a Cost-Effective Way. J. Energy Storage 2022, 50, 104710. [Google Scholar] [CrossRef]
- Chen, T.; Wu, G.X.; Zhou, N.C.; Lv, X.H.; Liu, W.; Wu, X.H. Optimal configuration of integrated energy system on user side in Southwest China. Renew. Energy Resour. 2021, 39, 8. (In Chinese) [Google Scholar]
- Walker, A.; Kwon, S. Analysis on Impact of Shared Energy Storage in Residential Community: Individual versus Shared Energy Storage. Appl. Energy 2021, 282, 116172. [Google Scholar] [CrossRef]
- Zhou, C.; Zheng, J.; Jing, Z.; Wu, Q.; Zhou, X. Multi-Objective Optimal Design of Integrated Energy System for Park-Level Microgrid. Power Syst. Technol. 2018, 42, 1687–1697. (In Chinese) [Google Scholar]
- Ma, M.; Huang, H.; Song, X.; Peña-Mora, F.; Zhang, Z.; Chen, J. Optimal Sizing and Operations of Shared Energy Storage Systems in Distribution Networks: A Bi-Level Programming Approach. Appl. Energy 2022, 307, 118170. [Google Scholar] [CrossRef]









| Name | Constraints | Remark |
|---|---|---|
| CHP | PtCHP,ei: Electric output of CHP (kW) PtCHP,ei: Heat output of CHP (kW) ηCHP,ei: Power Generation Efficiency of CHP ηCHP,hi: CHP thermal efficiency λmaxCHP,ei: Upper limit of CHP climbing rate (kW) | |
| EB | PtEB,hi: Thermal power of EB (kW) ηEB: Coefficient of performance of EB PtEB,ei: Power consumption of EB (kW) | |
| AC | PtAC,ci: Cold output of AC (kW) PtAC,hi: Heat consumption power of AC (kW) COPAC,i: coefficient of performance of AC | |
| EC | PtEC,i: Cold output of EC (kW) PtEC,ei: Power consumption of EC (kW) ηEC: Refrigeration efficiency of EC | |
| Electric heat and cold balance | PtPVi: electric power of PV (kW) PtEGi: electric network power (kW) Pteload,ei: electric load (kW) Ptload,hi: thermal load (kW) Ptload,ci: cooling load (kW) | |
| Electric balance considering SESO | Ptload,hi: thermal load (kW) Ptload,ci: cooling load (kW) |
| Parameter | Transform Rate of Emergy | Unit |
|---|---|---|
| Solar energy | 1.000 × 106 [31] | sej/MJ |
| Oxygen | 5.160 × 1010 [32] | sej/kg |
| Wind energy | 7.900 × 108 [31] | sej/MJ |
| Natural gas | 1.460 × 1011 [31] | sej/MJ |
| Coal | 1.110 × 1012 [31] | sej/kg |
| Investment cost | 3.460 × 1012 [33] | sej/$ |
| Electrical load demand | 2.210 × 1011 [31] | sej/MJ |
| Cool load demand | 6.070 × 1010 [34] | sej/MJ |
| Head load demand | 6.070 × 1010 [34] | sej/MJ |
| Parameters | Title |
|---|---|
| SESO unit power rental Cost/($/kW) | 0.04 |
| SESO unit power cost/($/kW) | 142.8 |
| SESO unit capacity cost/($/kW·h) | 157.1 |
| SESO operation cycle/a | 8 |
| The proportional coefficient between the upper limit of SESO power and the upper limit of capacity | 0.20 |
| Power generation efficiency of CHP unit | 0.35 |
| EB heat efficiency | 0.95 |
| Coefficient of performance of AC | 1.50 |
| EC refrigeration efficiency | 2.50 |
| Natural gas unit price/($/m3) | 0.36 |
| Unit scale construction cost of CHP/($/kW) | 457.1 |
| EB unit scale construction cost/($/kW) | 171.4 |
| AC unit scale construction cost/($/kW) | 171.4 |
| EC unit scale construction cost/($/kW) | 154.3 |
| PV unit construction cost/($/kW) | 342.9 |
| Equipment operating cycle/year | 20 |
| Interest rate | 0.05 |
| Ratio of maintenance cost to construction cost | 0.02 |
| NO. | Parameter | Total Emergy Value without SESO | MDES Emergy Value of Interactive Charge Considering MDES | MDES Emergy Value of Nash Bargaining Considering MDES |
|---|---|---|---|---|
| R1 | Solar energy | 1.516 × 1014 | 1.648 × 1014 | 1.640 × 1014 |
| R2 | Oxygen | 2.714 × 1018 | 2.532 × 1018 | 2.511 × 1018 |
| R3 | Wind energy | 1.857 × 1015 | 2.211 × 1015 | 2.096 × 1015 |
| R | Renewable | 2.72 × 1018 | 2.53 × 1018 | 2.513 × 1018 |
| N1 | Natural gas | 1.717 × 1019 | 1.538 × 1019 | 1.545 × 1019 |
| N2 | Coal | 5.875 × 1017 | 6.996 × 1017 | 6.632 × 1017 |
| N | Non-renewable | 1.78 × 1019 | 1.61 × 1019 | 1.611 × 1019 |
| F1 | PV assets | 2.331 × 1018 | 2.331 × 1018 | 2.331 × 1018 |
| F2 | CHP assets | 3.729 × 1018 | 3.729 × 1018 | 3.729 × 1018 |
| F3 | CHP assets | 3.729 × 1018 | 3.729 × 1018 | 3.729 × 1018 |
| F4 | EC assets | 8.691 × 1017 | 8.691 × 1017 | 8.691 × 1017 |
| F5 | EB assets | 9.657 × 1017 | 9.657 × 1017 | 9.657 × 1017 |
| F6 | Operating cost | 1.939 × 1017 | 1.939 × 1017 | 1.939 × 1017 |
| F | Purchased emergy | 9.89 × 1018 | 9.89 × 1018 | 9.887 × 1018 |
| Y1 | Electrical load demand | 1.244 × 1019 | 1.244 × 1019 | 1.244 × 1019 |
| Y2 | SESS storage | 0.000 | 7.358 × 1017 | 7.376 × 1017 |
| Y3 | Cool load demand | 5.810 × 1017 | 5.810 × 1017 | 5.810 × 1017 |
| Y4 | Heat load demand | 3.836 × 1017 | 3.836 × 1017 | 3.836 × 1017 |
| Y | Emergy yield | 1.34 × 1019 | 1.41 × 1019 | 1.414 × 1019 |
| NO. | Without SESO | SESO and Interactive Fees | Rate of Change | SESO and Nash Bargaining | Rate of Change |
|---|---|---|---|---|---|
| ELR | 10.18 | 10.24 | 0.62% | 10.35 | 1.67% |
| EYR | 1.36 | 1.43 | 5.49% | 1.43 | 5.15% |
| ESI | 0.1331 | 0.1396 | 4.84% | 0.1382 | 3.83% |
| EIR | 0.4828 | 0.5312 | 10.02% | 0.5308 | 9.94% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Wang, Y.; Han, K.; Zhao, C.; Han, J.; Zhu, Y. Bi-Objective Optimization and Emergy Analysis of Multi-Distributed Energy System Considering Shared Energy Storage. Sustainability 2023, 15, 1011. https://doi.org/10.3390/su15021011
Ye Z, Wang Y, Han K, Zhao C, Han J, Zhu Y. Bi-Objective Optimization and Emergy Analysis of Multi-Distributed Energy System Considering Shared Energy Storage. Sustainability. 2023; 15(2):1011. https://doi.org/10.3390/su15021011
Chicago/Turabian StyleYe, Zhaonian, Yongzhen Wang, Kai Han, Changlu Zhao, Juntao Han, and Yilin Zhu. 2023. "Bi-Objective Optimization and Emergy Analysis of Multi-Distributed Energy System Considering Shared Energy Storage" Sustainability 15, no. 2: 1011. https://doi.org/10.3390/su15021011
APA StyleYe, Z., Wang, Y., Han, K., Zhao, C., Han, J., & Zhu, Y. (2023). Bi-Objective Optimization and Emergy Analysis of Multi-Distributed Energy System Considering Shared Energy Storage. Sustainability, 15(2), 1011. https://doi.org/10.3390/su15021011








