Influence of Pipe-Jacking Reaction on Earth Pressure of Back Wall of Pilot Tunnel of Subway Station
Abstract
1. Introduction
2. Engineering Background
3. Numerical Simulation
3.1. Finite Element Model
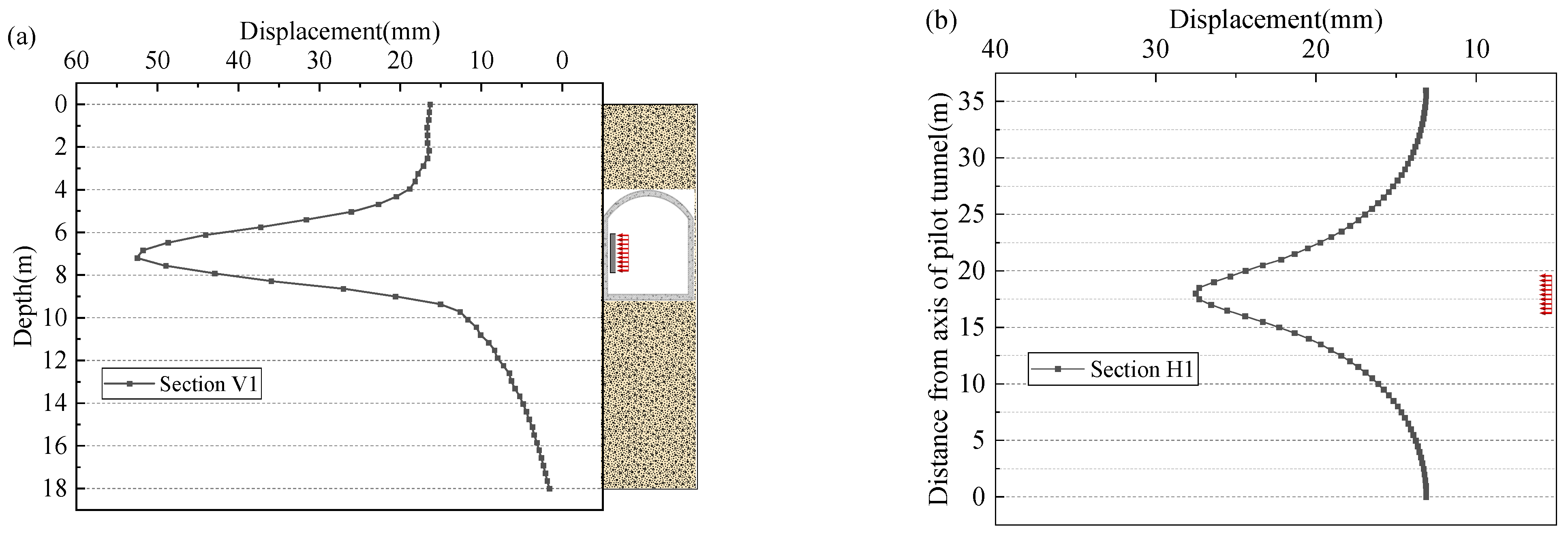
3.2. Loading Area of Jacking Reaction and Monitoring Section Layout
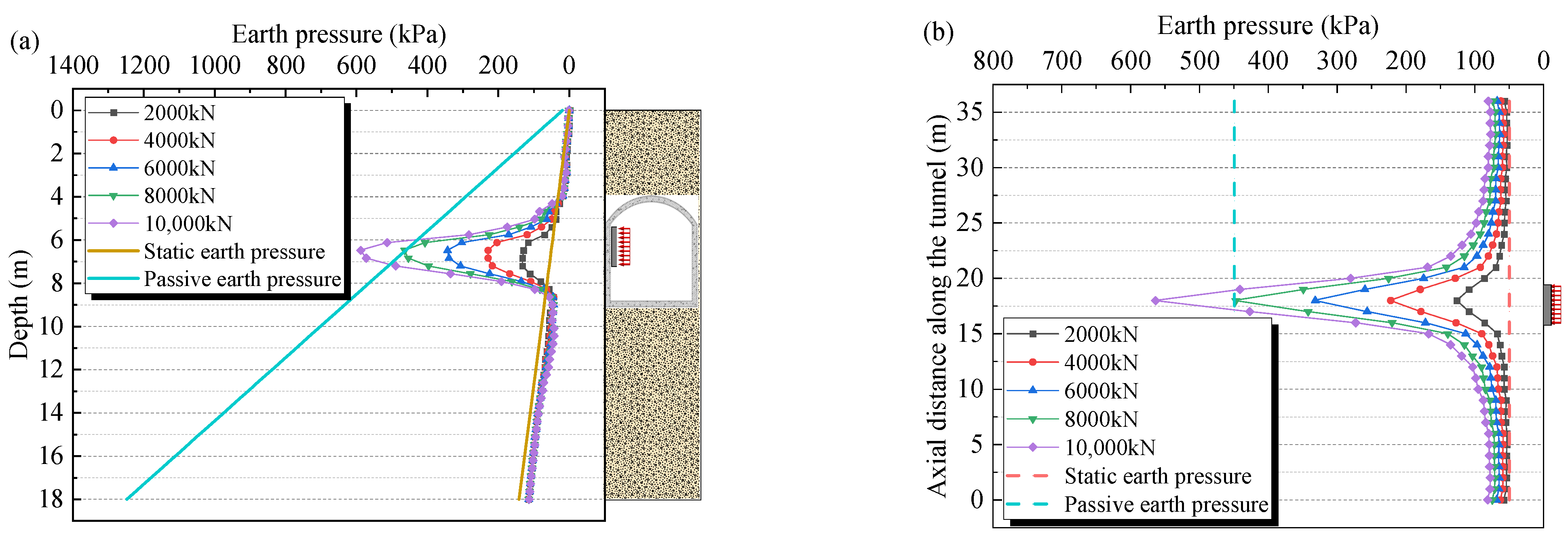
3.3. Distribution of Earth Pressure on the Back Wall of Pilot Tunnel
4. Effect of Jacking Reaction Parameters on the Back Wall
4.1. Loading Intensity
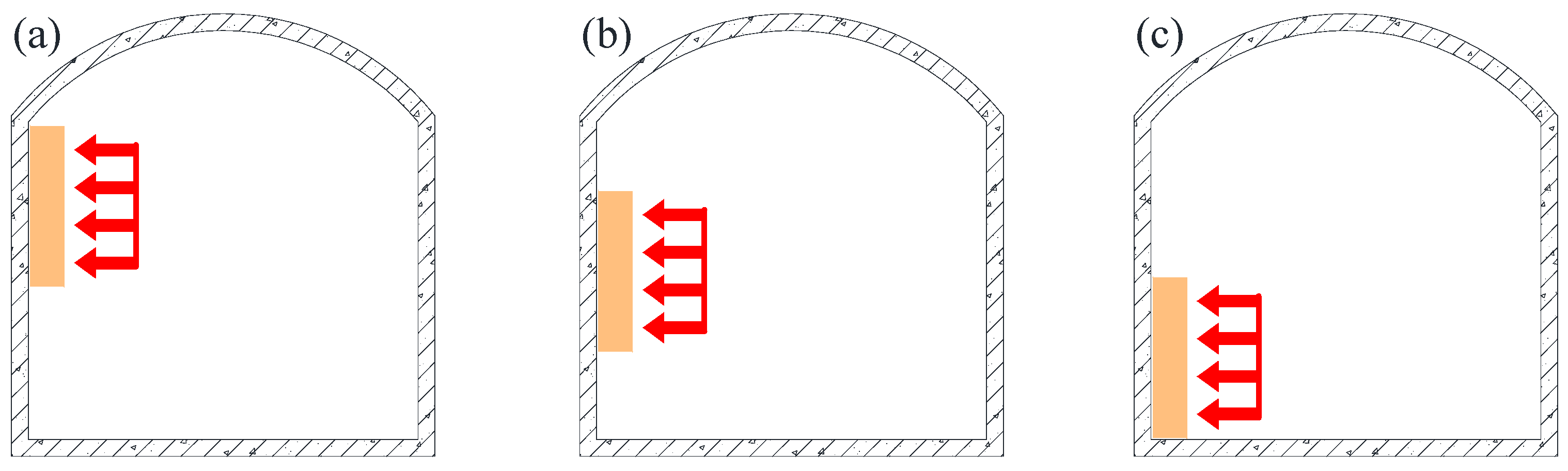
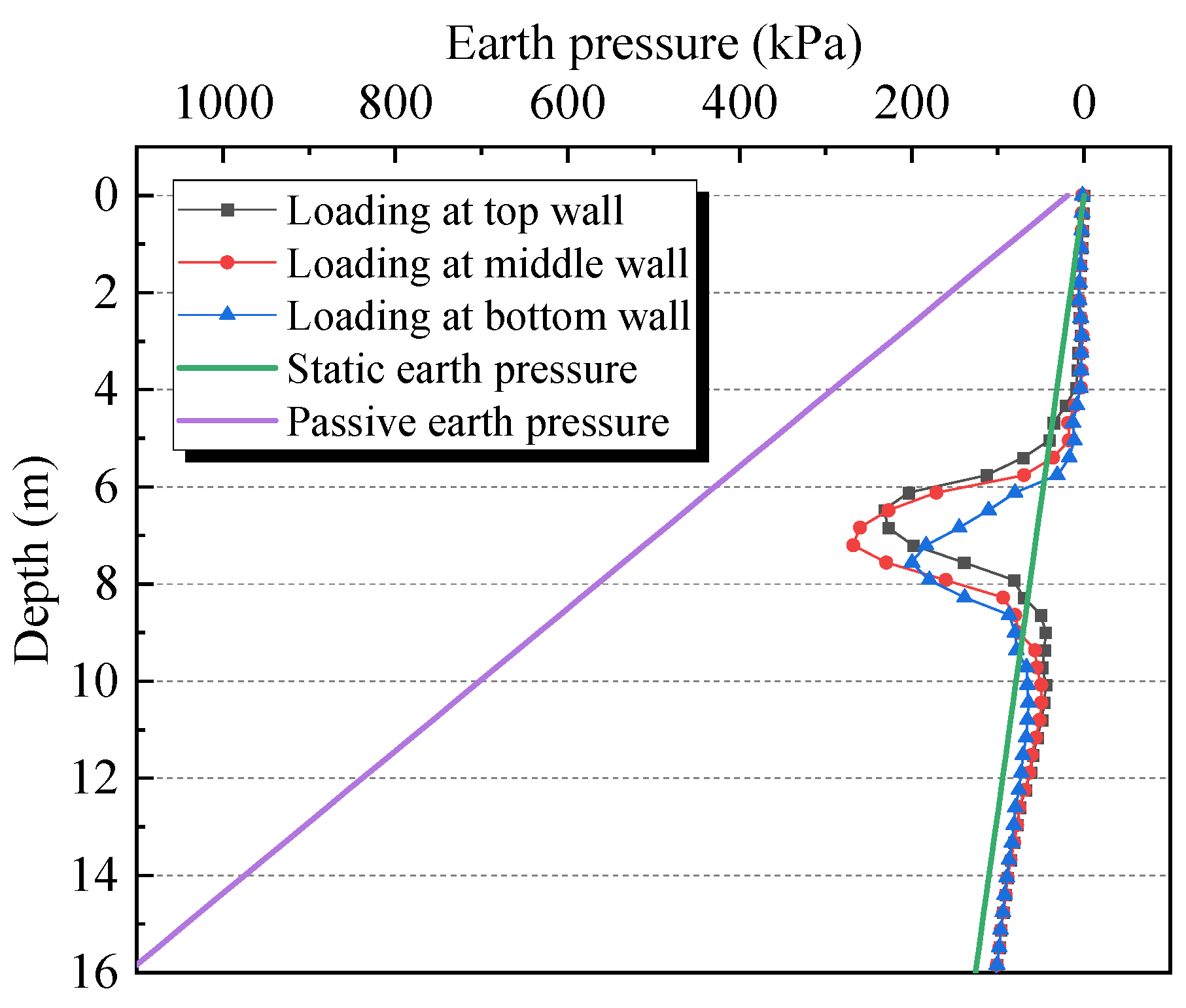
4.2. Loading Position
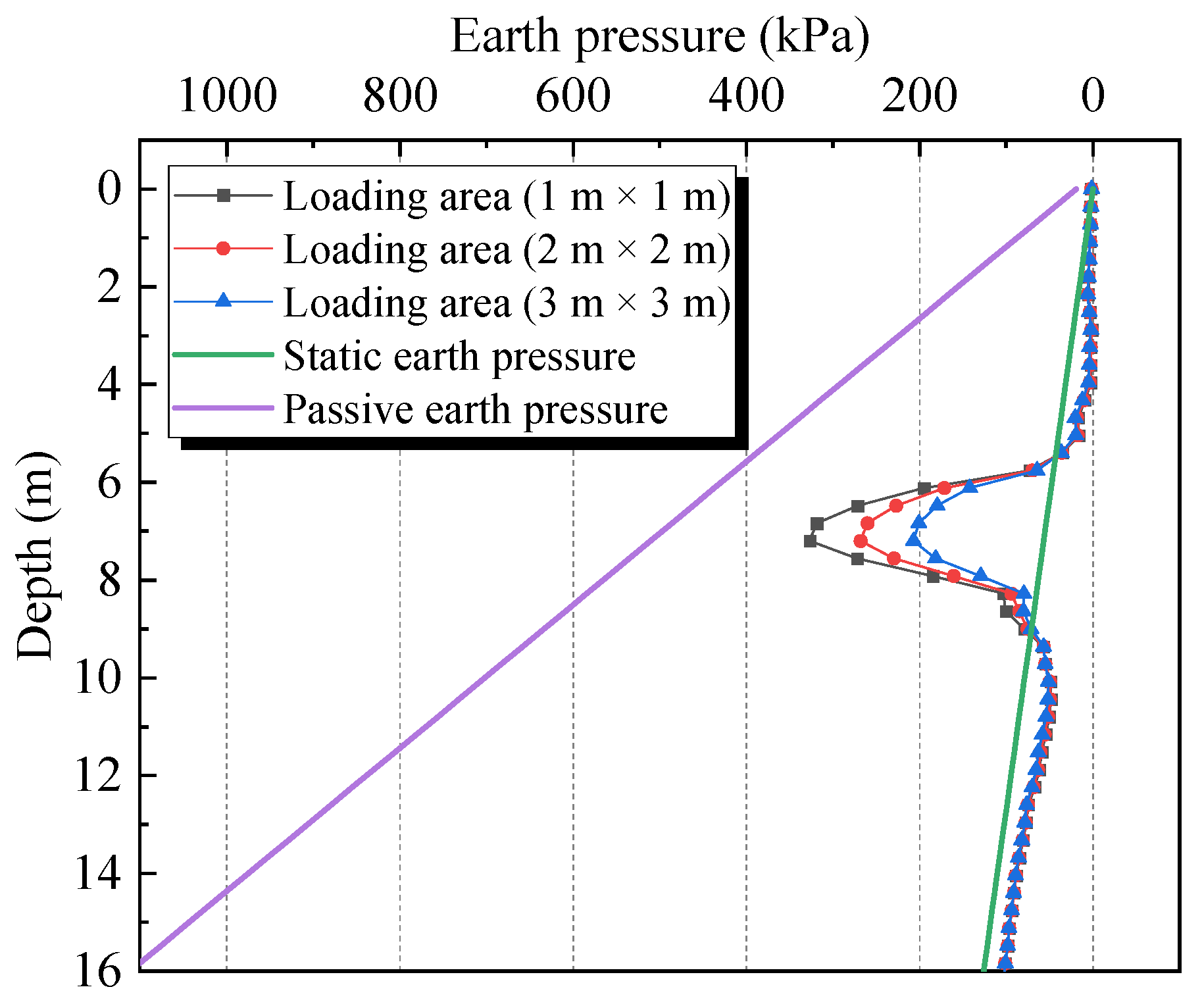
4.3. Loading Area
5. Calculation of Soil Reaction on the Back Wall
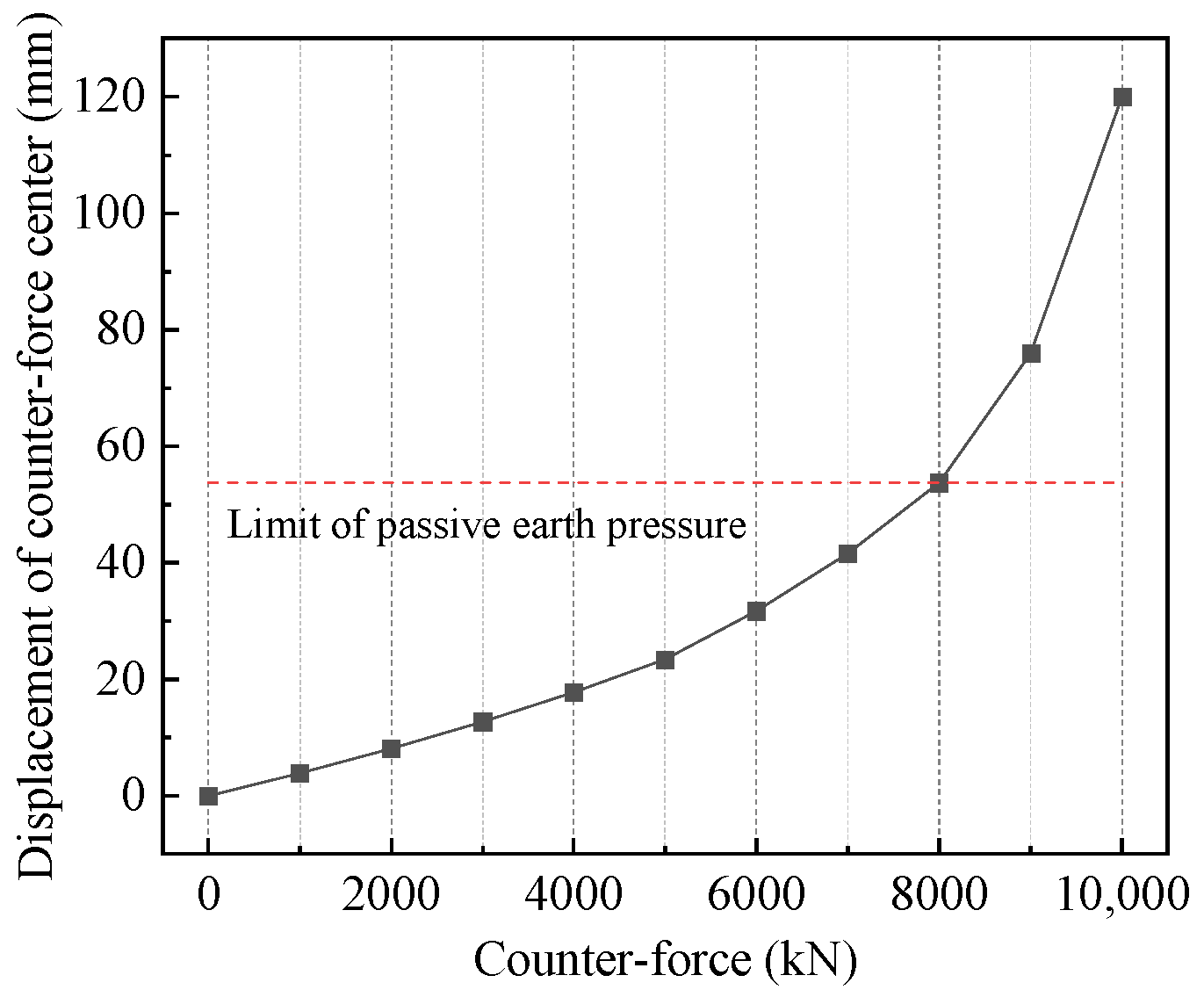
5.1. Relationship between Earth Pressure and Displacement in Limit State
5.2. Calculation of Soil Reaction
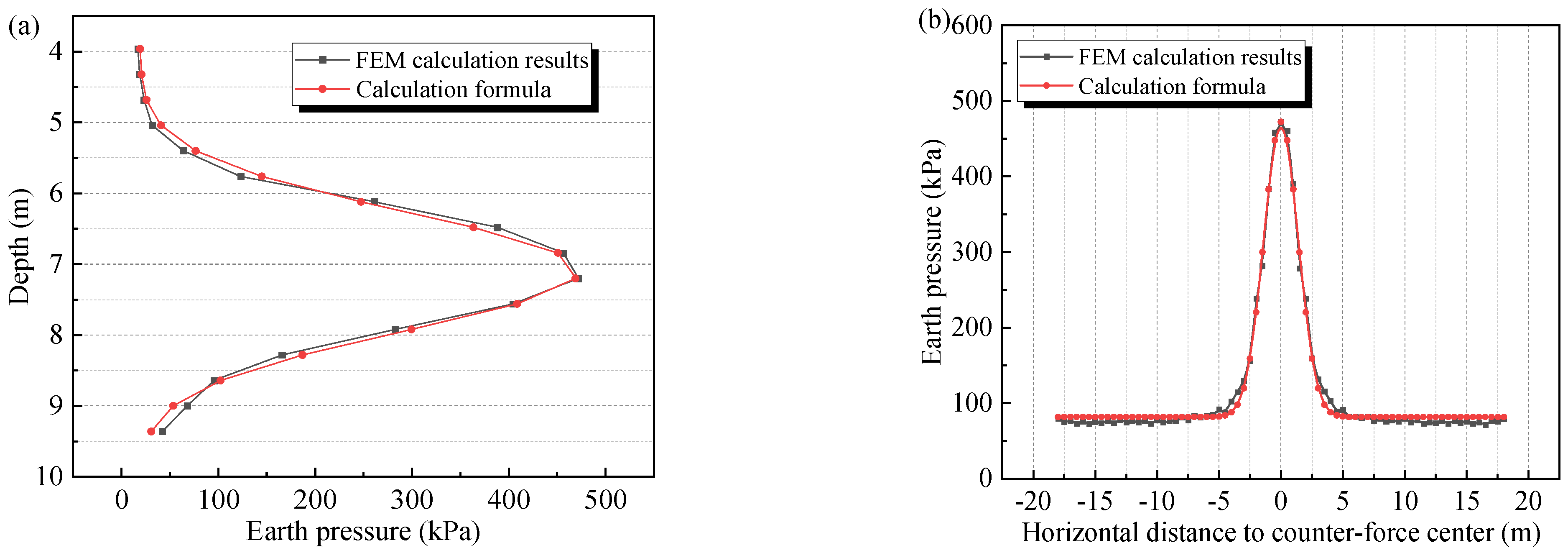
5.3. Compared with FEA Results
6. Conclusions
- (1)
- Under the action of the jacking reaction, the earth pressure at section V1 shows a large distribution in the middle part and small distribution in other parts, with a distribution pattern between “U” and “V” shapes, similar to the normal distribution curve.
- (2)
- With the increase in the load, the horizontal displacement and earth pressure of the back wall increases, and the rate of the horizontal displacement increases with the increase in the load. The maximum horizontal displacement of the back wall is greatest when the load is applied to the middle wall, followed by the top wall and then, the bottom wall. In particular, when the loading position is changed from the middle to the bottom, the maximum horizontal displacement is reduced by approximately 24.25%.
- (3)
- As the loading area increases, the maximum horizontal displacement of the back wall decreases, in the order of 11.8% and 14.45% relative to the previous level. The earth pressure of the back wall also decreases, in the order of 17.92% and 22.76% relative to the previous level.
- (4)
- Based on the function relation between the earth pressure and horizontal displacement, a calculation method of the soil reaction considering the displacement is presented. The accuracy of the formula is verified by comparing it with the FEA results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, P.J.; Nie, Y.T.; Shi, P.X.; Jiang, X.; Lu, B.; Zhao, W. Flexural performance of a novel pipe-roof structure and optimization of key parameters. J. Constr. Steel Res. 2022, 199, 107594. [Google Scholar] [CrossRef]
- Lu, B.; Dong, J.C.; Zhao, W.; Du, X.; Cheng, C.; Bai, Q.; Wang, Z.G.; Zhao, M.C.; Han, J.Y. Novel pipe-roof method for a super shallow buried and large-span metro underground station. Undergr. Space 2022, 7, 134–150. [Google Scholar] [CrossRef]
- Bai, Q.; Zhao, W.; Cao, W.X.; Jia, P.J.; Cheng, C.; Lu, B. Test and numerical simulation of excavation of subway stations using the small pipe-roof-beam method. Int. J. Geomech. 2022. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.S. Research of surface settlement for a single arch long-span subway station using the Pipe-roof Pre-construction Method. Tunn. Undergr. Space Technol. 2018, 72, 210–217. [Google Scholar] [CrossRef]
- Jia, P.J.; Zhao, W.; Chen, Y.; Li, S.G.; Han, J.Y.; Dong, J.C. A case study on the application of the steel tube slab structure in construction of a subway station. Appl. Sci. 2018, 8, 1437. [Google Scholar] [CrossRef]
- Jia, P.J.; Zhao, W.; Du, X.; Chen, Y.; Zhang, C.Z.; Bai, Q.; Wang, Z.G. Study on ground settlement and structural deformation for large span subway station using a new pre-supporting system. R. Soc. Open Sci. 2019, 6, 181035. [Google Scholar] [CrossRef]
- Jia, P.J.; Zhao, W.; Guan, Y.P.; Dong, J.C.; Wang, Q.H.; Cheng, C. Experimental study on the flexural behavior of steel tube slab composite beams and key parameters optimization. Adv. Struct. Eng. 2019, 22, 2476–2489. [Google Scholar] [CrossRef]
- Jia, P.J.; Zhao, W.; Khoshghalb, A.; Ni, P.P.; Jiang, B.F.; Chen, Y.; Li, S.G. A new model to predict ground surface settlement induced by jacked pipes with flanges. Tunn. Undergr. Space Technol. 2020, 98, 103330. [Google Scholar] [CrossRef]
- Wang, Z.G.; Zhao, W.; Wang, H.; Chen, Y.; Bai, Q.; Li, S.G. Analysis of the influence of geometrical parameters of circular steel pipe with flange plate on the jacking force. Undergr. Space 2022, 7, 324–336. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, K.N.; Huang, C.B.; Li, Z.; Deng, M.L. Analysis of surface subsidence of tunnel built by pipe-roof pre-construction method. Rock Soil Mech. 2011, 32, 3701–3707. [Google Scholar]
- Zhang, Y.; Tao, L.J.; Dong, L.P.; Zhao, X.; Bian, J.; An, S.; Chen, X.H. Theoretical analysis and research on the tight row horizontal pipe curtain. Chin. J. Geotech. Eng. 2021, 43, 365–374. [Google Scholar]
- Sofianos, A.I.; Loukas, P.; Chantzakos, C. Pipe jacking a sewer under Athens. Tunn. Undergr. Space Technol. 2004, 19, 193–203. [Google Scholar] [CrossRef]
- Milligan, G.W.E.; Norris, P. Site-based research in pipe jacking-objectives, procedures and a case history. Tunn. Undergr. Space Technol. 1996, 11, 3–24. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, S.L.; Xu, Z.L.; Xia, X.H. Prediction of lateral displacement of soil behind the reaction wall caused by pipe jacking operation. Tunn. Undergr. Space Technol. 2014, 40, 210–217. [Google Scholar] [CrossRef]
- Sun, Y.; Su, J.B.; Xia, X.H.; Xu, Z.L. Numerical analysis of soil deformation behind the reaction wall of an open caisson induced by horizontal parallel pipe-jacking construction. Can. Geotech. J. 2015, 52, 2008–2016. [Google Scholar] [CrossRef]
- Gong, C.; Wei, G.; Xu, R.Q. Permissible counterforce calculation in rectangular open caisson working well during pipe jacking. Rock Soil Mech. 2005, 7, 1127–1131. [Google Scholar]
- Yan, Z.G.; Zhu, H.H.; Li, X.Y.; Liu, X.Z.; Xu, Z.H. 3D-FEM analysis on stability of shaft with conduit jacked synchronously in two directions. Chin. J. Geotech. Eng. 2005, 8, 891–896. [Google Scholar]
- Chen, C.L.; Wei, G.; Chen, H.H. Study on calculating methods of earth counterforce in rectangular working shaft by SMW methods. Rock Soil Mech. 2007, 28, 769–773. [Google Scholar]
- Wei, G.; Xu, R.Q.; Song, J.L. Researches on earth counterforce calculation in circular working shaft by SMW methods. J. Zhejiang Univ. Eng. Sci. 2005, 39, 99–103. [Google Scholar]
- Zhao, C.X.; Li, Y.M.; Liu, G.; Meng, X.R. Mechanism analysis and control technology of surrounding rock failure in deep soft rock roadway. Eng. Fail. Anal. 2020, 115, 104611. [Google Scholar] [CrossRef]
- Huang, Z.K.; Zhang, D.M.; Pitilakis, K.; Tsinidis, G.; Huang, H.W.; Zhang, D.M.; Argyroudis, S. Resilience assessment of tunnels: Framework and application for tunnels in alluvial deposits exposed to seismic hazard. Soil Dyn. Earthq. Eng. 2022, 162, 107456. [Google Scholar] [CrossRef]
- Yang, S.Q.; Chen, M.; Jing, H.W.; Chen, K.F.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Guo, X.Y.; Wang, Z.Z.; Geng, P.; Chen, C.J.; Zhang, J. Ground surface settlement response to subway station construction activities using pile–beam–arch method. Tunn. Undergr. Space Technol. 2021, 108, 103729. [Google Scholar] [CrossRef]
- Xu, R.Q. Methods of earth pressure calculation for excavation. J. Zhejiang Univ. Eng. Sci. 2000, 4, 22–27. [Google Scholar]
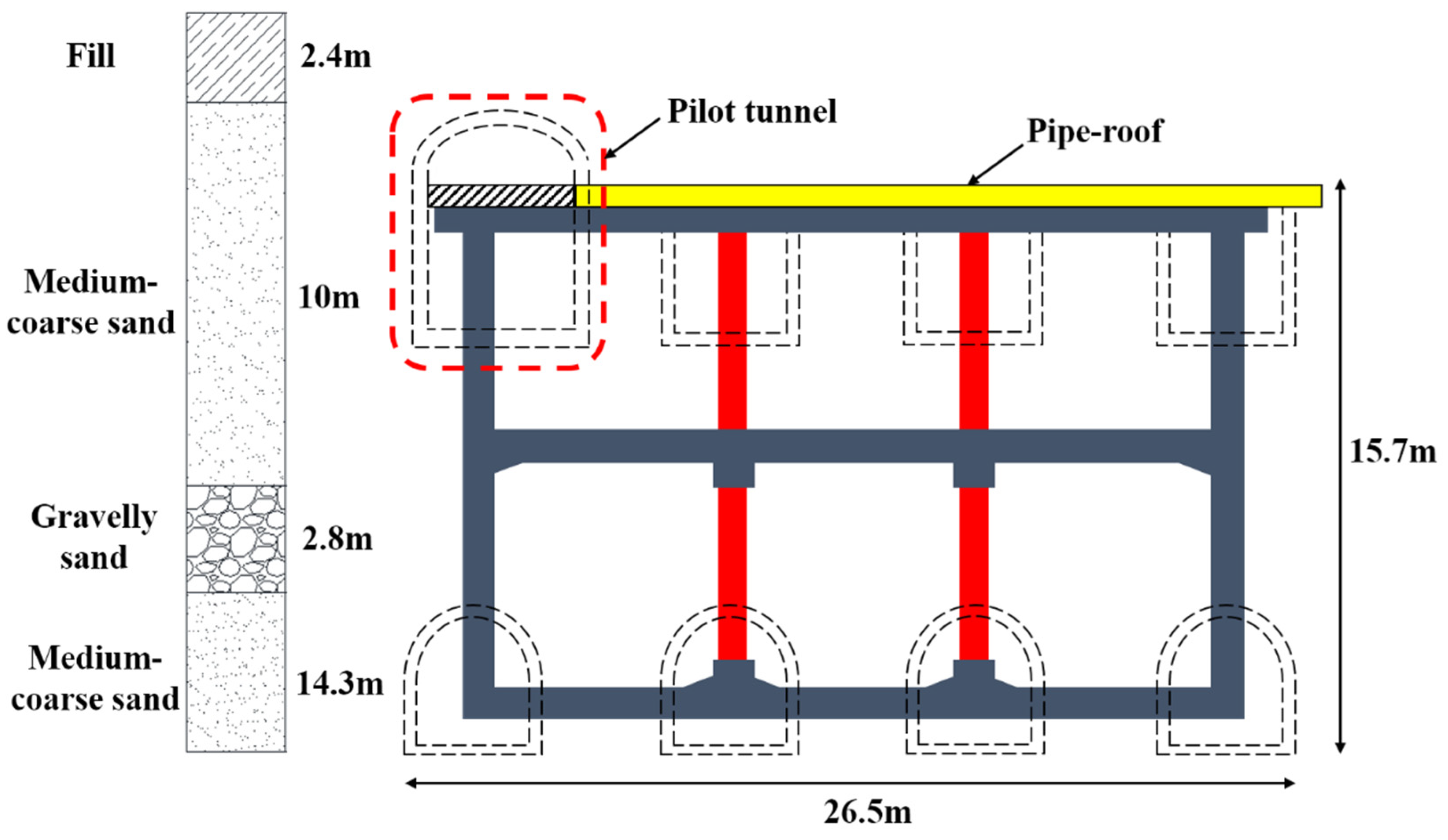
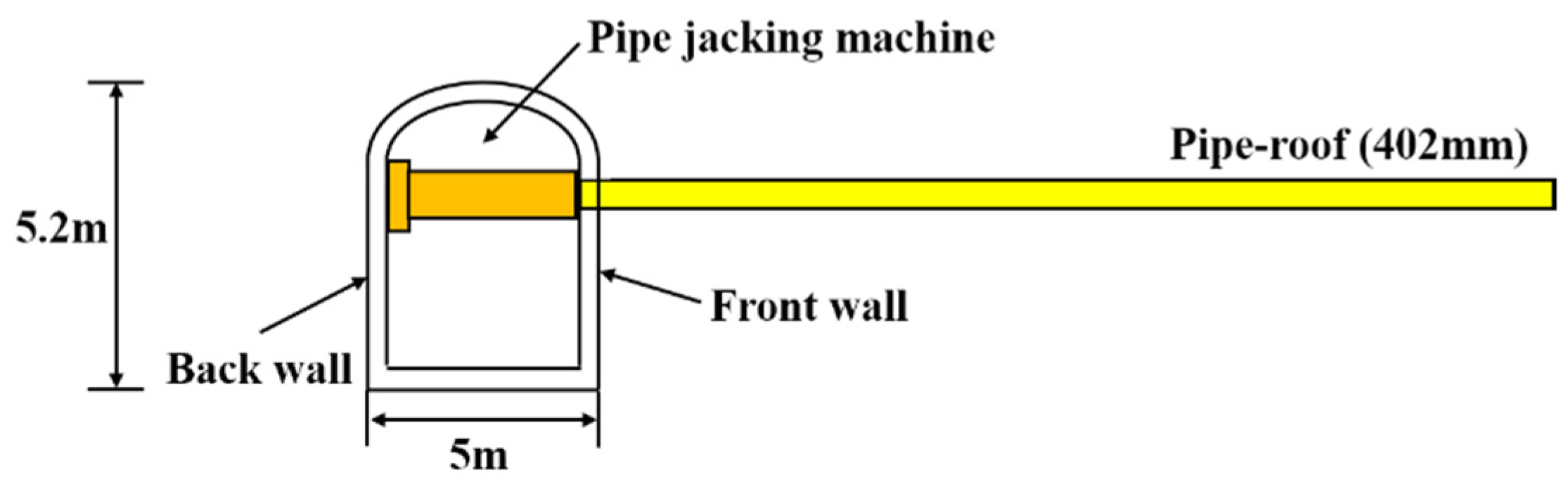
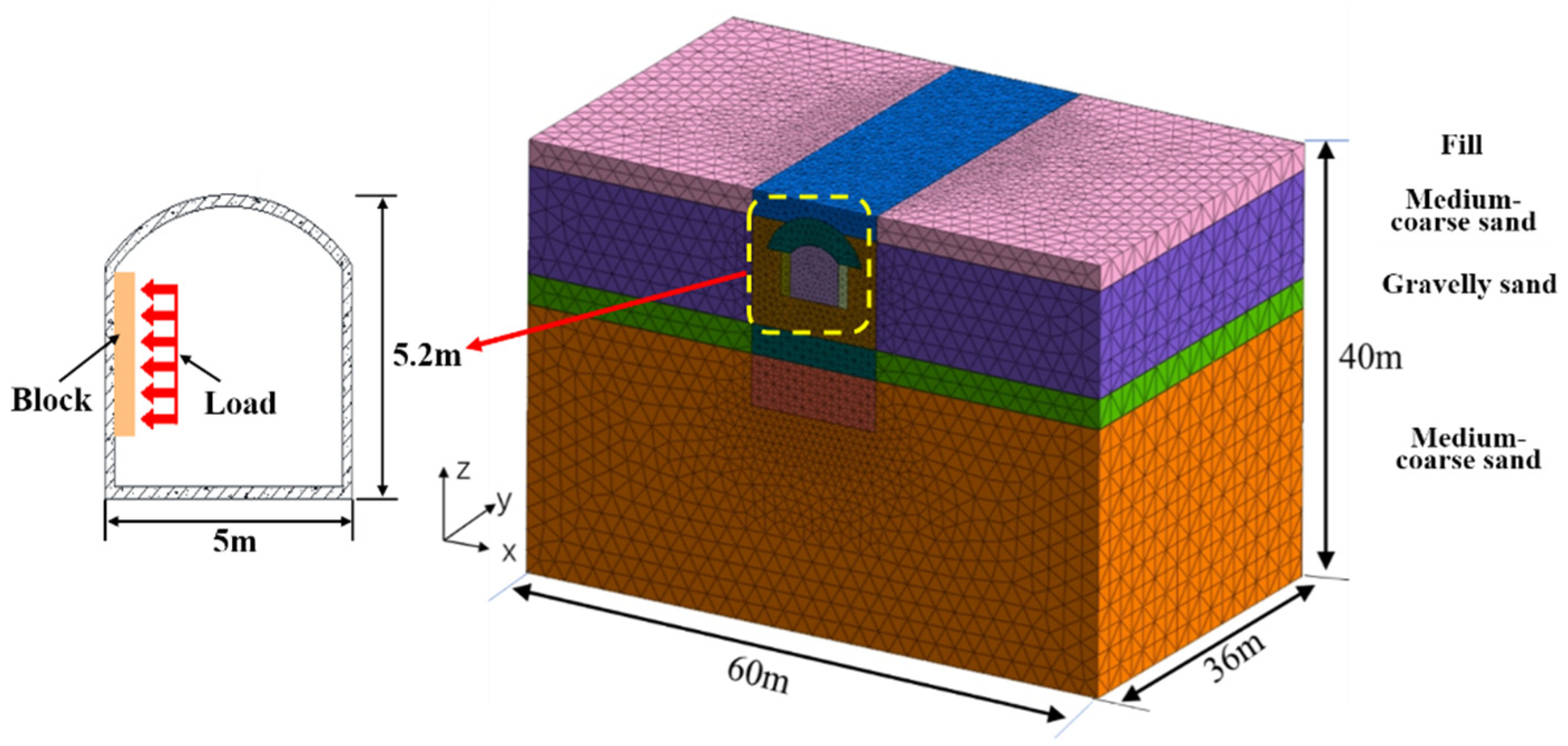







| Name | Thickness H/m | Friction Angle | Cohesion c/kPa | Poisson’s Ratio μ | Deformation Modulus E/MPa | Weight γ/kN·m−3 |
|---|---|---|---|---|---|---|
| Miscellaneous fill | 2.4 | 30 | 5 | 0.28 | 14.2 | 18.0 |
| Medium coarse sand | 10 | 35 | 2 | 0.28 | 15.5 | 19.3 |
| Gravel sand | 2.8 | 35.9 | 2 | 0.29 | 26.9 | 19.5 |
| Medium coarse sand | 14.3 | 35.9 | 2 | 0.28 | 26.9 | 19.4 |
| Reinforcement zone | 2.5 | 38 | 40 | 0.35 | 25 | 21.0 |
| Initial support | 0.3 | - | - | 0.3 | 31,500 | 25.0 |
| Name | Vertical Direction | Horizontal Direction |
|---|---|---|
| Theoretical values | 63.92 | 72.51 |
| Simulated values | 76.60 | 81.76 |
| Relative errors | 16.54% | 11.31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Q.; Zhao, W.; Wang, X.; Ma, H.; Zhao, Z. Influence of Pipe-Jacking Reaction on Earth Pressure of Back Wall of Pilot Tunnel of Subway Station. Sustainability 2023, 15, 1033. https://doi.org/10.3390/su15021033
Bai Q, Zhao W, Wang X, Ma H, Zhao Z. Influence of Pipe-Jacking Reaction on Earth Pressure of Back Wall of Pilot Tunnel of Subway Station. Sustainability. 2023; 15(2):1033. https://doi.org/10.3390/su15021033
Chicago/Turabian StyleBai, Qian, Wen Zhao, Xin Wang, Huili Ma, and Zhen Zhao. 2023. "Influence of Pipe-Jacking Reaction on Earth Pressure of Back Wall of Pilot Tunnel of Subway Station" Sustainability 15, no. 2: 1033. https://doi.org/10.3390/su15021033
APA StyleBai, Q., Zhao, W., Wang, X., Ma, H., & Zhao, Z. (2023). Influence of Pipe-Jacking Reaction on Earth Pressure of Back Wall of Pilot Tunnel of Subway Station. Sustainability, 15(2), 1033. https://doi.org/10.3390/su15021033






