The Impact of Environmental Regulation on Urban Green Efficiency—Evidence from Carbon Pilot
Abstract
:1. Introduction
2. Literature Review
2.1. Research on Effectiveness of Market-Based Environmental Regulations
2.2. Research on the Mechanism of Environmental Regulations
2.3. Research on Spatial Spillover Effects of Environmental Regulations
3. Theoretical Foundations and Research Hypotheses
3.1. Effectiveness of Carbon Trading
3.2. Market and Government Synergies
3.3. The Transmission Mechanism of Carbon Emissions Trading
3.4. Spatial Spillover Effects of Carbon Emissions Trading
4. Study Design and Data Selection
4.1. Model Construction
4.2. Description of Variables
4.2.1. Explained and Core Explanatory Variables
4.2.2. Control Variables
4.2.3. Proxy Variables for Market Mechanisms and Administrative Intervention
4.2.4. Intermediate Variables
4.2.5. Substitution of Variables
4.3. Data Sources
5. Empirical Results
5.1. Baseline Regression
5.2. Market and Government Synergies
5.3. Analysis of Conduction Mechanisms
6. Robustness Analysis
6.1. Parallel Trends and Analysis of Dynamic Effects
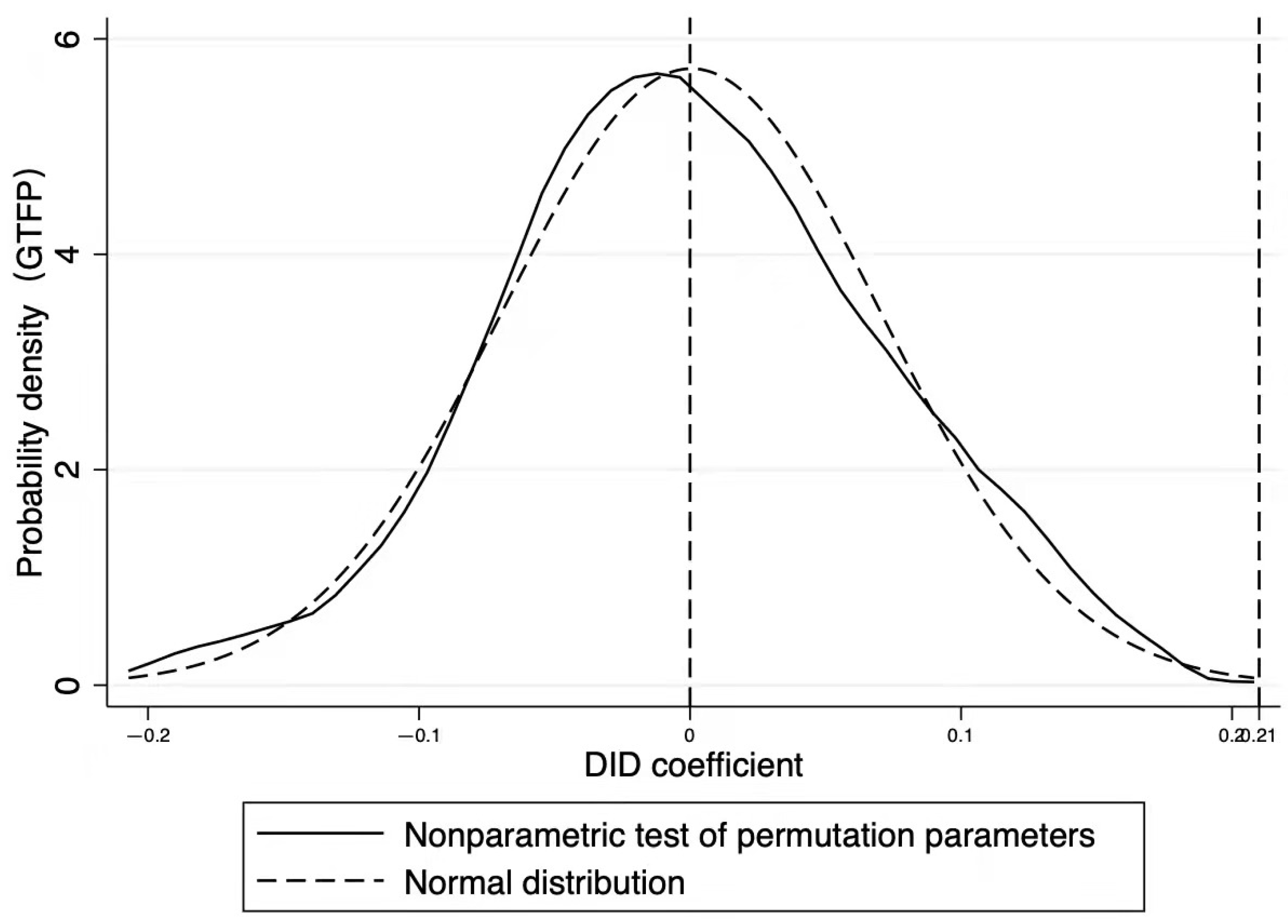
6.2. Placebo Test
6.3. PSM-DID Test
6.4. Changing the Window Period Test
6.5. Substitution of Explanatory Variables
7. Spatial Spillover Effects
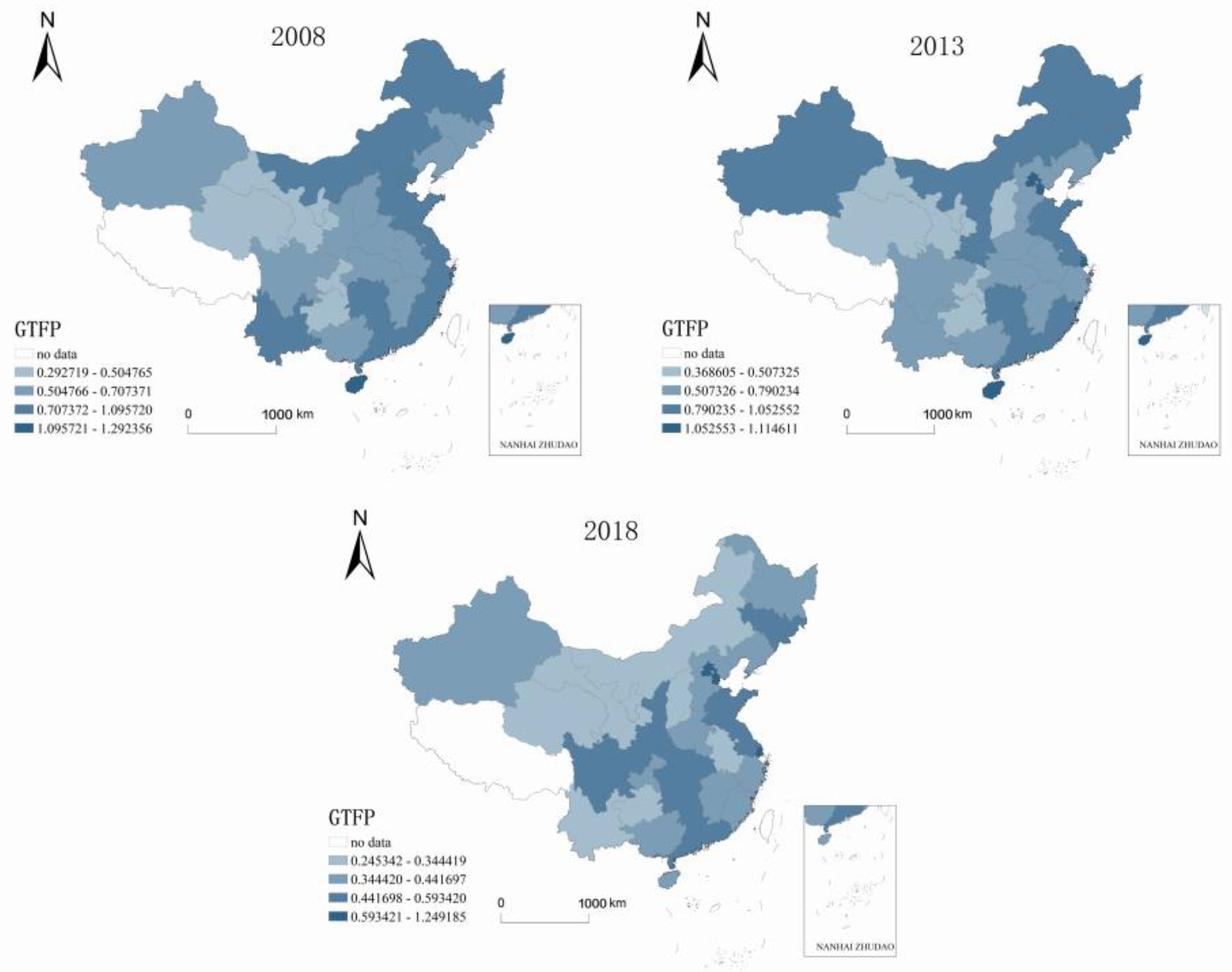
7.1. Analysis of Spatial and Temporal Patterns
7.2. Spatial Panel Model
7.2.1. Model Construction
7.2.2. Selection of the Space Matrix
7.2.3. Spatial Autocorrelation Test
7.3. Point Estimation Results
7.4. Decomposition of Partial Differential Effects
8. Conclusions and Policy Implications
8.1. Research Conclusions
8.2. Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tong, Y.; Liu, H.; Ma, Y. The impact of China’s tourism economy on urban green development and spatial spillover effects. J. Geogr. 2021, 76, 2504–2521. [Google Scholar]
- Wu, Y.Y.; Qi, J.; Xian, Q.; Chen, J.D. A study on the carbon emission reduction effect of China’s carbon market: A synergistic perspective of market mechanism and administrative intervention. China Ind. Econ. 2021, 8, 114–132. [Google Scholar]
- Fu, J.; SZ, X.; Cao, X. The impact of emission right trading mechanism on green development. China Popul.-Resour. Environ. 2018, 28, 12–21. [Google Scholar]
- Blackman, A.; Kildegaard, A. Clean technological change in developing-country industrial clusters: Mexican leather tanning. Environ. Econ. Policy Stud. 2010, 12, 115–132. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Zhu, X.; Li, H. How does carbon emissions trading scheme affect steel enterprises’ pollution control performance? A quasi natural experiment from China. Sci. Total Environ. 2023, 858, 159871. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Chen, D. Haze pollution, government governance and high-quality economic development. Econ. Res. 2018, 53, 20–34. [Google Scholar]
- Tian, G.; Yu, S.; Wu, Z.; Xia, Q. Study on the Emission Reduction Effect and Spatial Difference of Carbon Emission Trading Policy in China. Energies 2022, 15, 1921. [Google Scholar] [CrossRef]
- Hu, Y.F.; Ding, Y. Can a carbon trading mechanism balance corporate effectiveness and green efficiency? China Popul. Resour. Environ. 2020, 30, 56–64. [Google Scholar]
- Dechezleprêtre, A.; Koźluk, T.; Kruse, T.; Nachtigall, D.; De Serres, A. Do environmental and economic performance go together? a review of micro-level empirical evidence from the past decade or so. Int. Rev. Environ. Resour. Econ. 2019, 13, 1–18. [Google Scholar] [CrossRef]
- Conrad, K.; Wastl, D. The impact of environmental regulation on productivity in German industries. Empir. Econ. 1996, 20, 615–633. [Google Scholar] [CrossRef]
- Greenstone, M.; List, A.J.; Syverson, C. The Effects of Environmental Regulation on the Competitiveness of U.S. Manufacturing. NBER Work. Pap. 2012, 93, 431–435. [Google Scholar]
- Popp, D. International innovation and diffusion of air pollution control technologies: The effects of NOX and SO2 regulation in the US, Japan, and Germany. J. Environ. Econ. Manag. 2006, 51, 46–71. [Google Scholar] [CrossRef] [Green Version]
- Feng, T.; Yu, Z.J.; Hao, Z. Has environmental regulation achieved “increased quantity and quality” of green technology innovation: Evidence from the environmental protection target responsibility system. China Ind. Econ. 2021, 2, 136–154. [Google Scholar]
- Wan, P.; Yang, G.; Chen, L. How environmental technology standards affect the green transformation of China’s manufacturing industry—A perspective based on technological transformation. China Ind. Econ. 2021, 9, 118–136. [Google Scholar]
- Zhu, S.N.; Li, W.X. Does environmental regulation drive factor mismatch correction in the industrial sector—Empirical evidence from micro data of Chinese industrial firms. Macroecon. Res. 2021, 2, 149–161. [Google Scholar]
- Deng, C.; Zhao, H.; Xie, B. The impact of land resource mismatch on green total factor productivity of urban industries in China. J. Geogr. 2021, 76, 1865–1881. [Google Scholar]
- Cheng, J.; Yi, J.; Dai, S.; Xiong, Y. Can low-carbon city construction facilitate green growth? Evidence from China’s pilot low-carbon city initiative. J. Clean. Prod. 2019, 231, 1158–1170. [Google Scholar] [CrossRef]
- Li, X.; Yu, D.; Yu, J. Spatial spillover effects of heterogeneous environmental regulations on carbon productivity—Based on a spatial Durbin model. China Soft Sci. 2020, 4, 82–96. [Google Scholar]
- Zhang, B.; Zhou, J.; Yan, Z. Low carbon city pilot policies and total factor energy efficiency improvement—A quasi-natural experiment from three batches of pilot policy implementation. Econ. Rev. 2021, 42, 32–49. [Google Scholar]
- Tian, L.; Liu, C. “Peer” institutional pressure and corporate green innovation—The spillover effect of environmental pilot policies. Econ. Manag. 2021, 43, 156–172. [Google Scholar]
- Dong, Z.; Wang, H. An examination of the effectiveness of market-based environmental regulation policies—Empirical evidence from the perspective of carbon emissions trading policies. Stat. Res. 2021, 38, 48–61. [Google Scholar]
- Jiang, H.; Sun, M. Carbon emissions trading, industrial structure and regional emission reduction. Mod. Econ. Inq. 2021, 11, 65–73. [Google Scholar]
- Choi, J.; Kim, I. Regional total factor productivity and local employment growth: Evidence from Korea. Asia-Pac. J. Reg. Sci. 2017, 1, 511–518. [Google Scholar] [CrossRef]
- Walter, I.; Ugelow, J. Environment policies in developing countries. Amhio 1979, 8, 102–109. [Google Scholar]
- Eskelan, G.; Harrison, A.E. Moving to greener pastures? multinationals and the pollution haven hypothesis. J. Dev. Econ. 2003, 70, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H. A study on the strategic interaction of inter-regional environmental regulation—An explanation of the non-fully enforced universality of environmental regulation. China Ind. Econ. 2016, 7, 74–90. [Google Scholar]
- Shan, H. Re-estimation of capital stock K in China:1952–2006. Res. Quant. Econ. Technol. Econ. 2008, 25, 17–31. [Google Scholar]
- Tone, K.; Tsutsui, M. Dynamic DEA with network structure: A slacks-based measure approach. Omega 2014, 42, 124–131. [Google Scholar] [CrossRef]
- Yu, Y.; Zheng, X.; Zhang, L. Economic development level, industrial structure and carbon emission intensity: A provincial panel data analysis in China. Econ. Theory Econ. Manag. 2011, 31, 72–81. [Google Scholar]
- Xing, H.; Gu, J.; Zhang, J. The impact of synergistic agglomeration of two industries on total factor productivity of urban manufacturing industry—Based on endowment difference perspective. East China Econ. Manag. 2021, 35, 72–79. [Google Scholar]
- Chen, Y.W.; Hu, W.M. Price distortions, factor mismatches and efficiency losses: Theory and applications. Economics 2011, 10, 1401–1422. [Google Scholar]
- Huang, D. Financial development and urban total factor productivity growth—An example of 26 cities in the Yangtze River Delta urban agglomeration. Econ. Geogr. 2021, 41, 77–86. [Google Scholar]
- Liu, J.Y.; Woodward, R.T.; Zhang, Y.J. Has carbon emissions trading reduced PM2.5 in China? Environ. Sci. Technol. 2021, 55, 6631–6643. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Zanehale, D. The impact of heterogeneous environmental regulations on urban environmental pollution—A study based on static and dynamic spatial Durbin models. East China Econ. Manag. 2021, 35, 75–82. [Google Scholar]
| GTFP | GTFP | |
|---|---|---|
| x | 0.229 *** | 0.210 *** |
| (3.60) | (4.14) | |
| Controls | NO | YES |
| Time fixed effects | YES | YES |
| Individual fixed effects | YES | YES |
| Provincial and regional interaction effects | YES | YES |
| N | 341 | 341 |
| R2 | 0.780 | 0.801 |
| F | 12.94 | 12.27 |
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Variables | GTFP | GTFP | GTFP | GTFP |
| X | 0.130 | 0.167 *** | −0.096 | −0.003 |
| (1.64) | (3.53) | (−0.63) | (−0.02) | |
| c.x#c.price | 0.003 ** | |||
| (2.14) | ||||
| c.x#c.percent | 0.728 ** | |||
| (2.15) | ||||
| c.x#c.finance | 2.248 ** | |||
| (2.50) | ||||
| finance | −1.120 | |||
| (−1.27) | ||||
| c.x#c.income | 0.979 * | |||
| (1.78) | ||||
| income | −0.172 | |||
| (−0.25) | ||||
| Control variables | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES |
| Provincial and regional interaction effects | YES | YES | YES | YES |
| N | 341 | 341 | 341 | 341 |
| R2 | 0.803 | 0.791 | 0.804 | 0.803 |
| F | 21.63 | 17.06 | 25.85 | 12.55 |
| Variables | GTFP | lneg | Score | z1 | Score | le | Score |
|---|---|---|---|---|---|---|---|
| x | 0.210 *** | −0.168 *** | 0.170 *** | 0.980 ** | 0.197 *** | −0.178 *** | 0.166 *** |
| (4.14) | (−2.99) | (3.14) | (2.12) | (3.97) | (−3.73) | (2.97) | |
| lneg | −0.233 ** | ||||||
| (−2.47) | |||||||
| z1 | 0.012 * | ||||||
| (1.72) | |||||||
| le | −0.245 * | ||||||
| (−1.99) | |||||||
| Control variables | YES | YES | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES | YES | YES |
| Provincial and regional interaction effects | YES | YES | YES | YES | YES | YES | YES |
| R2 | 0.801 | 0.967 | 0.806 | 0.692 | 0.802 | 0.965 | 0.803 |
| F | 12.27 | 3.438 | 14.25 | 2.091 | 12.29 | 3.965 | 11.23 |
| (1) | |
|---|---|
| Variables | GTFP |
| pre3 | −0.067 * |
| (−1.97) | |
| pre2 | −0.018 |
| (−0.35) | |
| pre1 | 0.062 |
| (1.06) | |
| current | 0.105 ** |
| (2.21) | |
| post1 | 0.136 ** |
| (2.11) | |
| post2 | 0.192 *** |
| (3.13) | |
| post3 | 0.237 *** |
| (2.93) | |
| post4 | 0.324 *** |
| (3.05) | |
| post5 | 0.456 ** |
| (2.51) | |
| Controls | YES |
| Time fixed effects | YES |
| Individual fixed effects | YES |
| Provincial and regional interaction effects | YES |
| N | 341 |
| R2 | 0.810 |
| F | 9.402 |
| Variables | tfp | tfp | ||
|---|---|---|---|---|
| x | 0.070 *** | 0.100 *** | −0.167 ** | −0.120 ** |
| (2.82) | (3.04) | (−2.26) | (−2.34) | |
| Control variables | NO | YES | NO | YES |
| Time fixed effects | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES |
| Provincial and regional interaction effects | YES | YES | YES | YES |
| R2 | 0.596 | 0.612 | 0.988 | 0.988 |
| F | 7.957 | 3.579 | 5.097 | 2.469 |
| W1 | W2 | |||
|---|---|---|---|---|
| Moran’s I | p | Moran’s I | p | |
| 2008 | 0.279 *** | 0.005 | 0.231 *** | 0.006 |
| 2009 | 0.269 *** | 0.007 | 0.204 ** | 0.012 |
| 2010 | 0.214 ** | 0.022 | 0.276 *** | 0.002 |
| 2011 | 0.182 ** | 0.040 | 0.345 *** | 0.000 |
| 2012 | −0.047 | 0.460 | 0.269 *** | 0.002 |
| 2013 | 0.054 | 0.238 | 0.318 *** | 0.000 |
| 2014 | 0.131 * | 0.089 | 0.304 *** | 0.001 |
| 2015 | 0.022 | 0.324 | 0.143 ** | 0.048 |
| 2016 | 0.089 | 0.159 | 0.182 * | 0.021 |
| 2017 | 0.340 *** | 0.001 | 0.395 *** | 0.000 |
| 2018 | 0.294 *** | 0.003 | 0.571 *** | 0.000 |
| W1 | W2 | |||
|---|---|---|---|---|
| Type of Test | Statistical Values | p | Statistical Values | p |
| LR_spatial_lag | 39.11 | 0.0000 | 12.58 | 0.0501 |
| LR_spatial_error | 42.63 | 0.0000 | 32.08 | 0.0000 |
| Wald_spatial_lag | 38.36 | 0.0000 | 11.10 | 0.0494 |
| Wald_spatial_error | 38.88 | 0.0000 | 23.31 | 0.0007 |
| Hausman Test | 35.37 | 0.0007 | 17.99 | 0.1578 |
| Static Doberman | Dynamic Doberman | |||
|---|---|---|---|---|
| W1 | W2 | W1 | W2 | |
| L.lnsco | 0.346 *** | 0.390 *** | ||
| (6.33) | (7.12) | |||
| x | 0.260 *** | 0.164 ** | 0.190 *** | 0.136 * |
| (5.49) | (2.28) | (3.87) | (1.85) | |
| Wx | −0.026 | 0.210 | −0.044 | 0.102 |
| (−0.30) | (1.36) | (−0.50) | (0.66) | |
| Controls | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES |
| 0.275 *** | 0.283 *** | 0.229 *** | 0.212 ** | |
| (4.01) | (3.53) | (3.16) | (2.53) | |
| sigma2_e | 0.024 *** | 0.026 *** | 0.024 *** | 0.025 *** |
| (12.74) | (12.74) | (13.42) | (13.43) | |
| Log-L | −80.3019 | −80.3019 | 69.9237 | −80.3019 |
| R2 | 0.2811 | 0.0313 | 0.4687 | 0.0243 |
| Observations | 330 | 330 | 330 | 330 |
| W1 | W2 | |||||
|---|---|---|---|---|---|---|
| Direct Effects | Indirect Effects | Total Effect | Direct Effects | Indirect Effects | Total Effect | |
| x | 0.265 *** | 0.060 | 0.325 ** | 0.183 *** | 0.345 * | 0.528 *** |
| (5.34) | (0.50) | (2.33) | (2.65) | (1.81) | (3.20) | |
| lnk | 0.141 * | 0.051 * | 0.192 ** | 0.188 *** | 0.205 | 0.393 * |
| (2.41) | (1.91) | (2.39) | (3.16) | (1.04) | (1.82) | |
| lns | 0.767 *** | 0.277 *** | 1.044 *** | 0.729 *** | 0.292 ** | 1.021 *** |
| (4.90) | (2.65) | (4.70) | (4.55) | (2.18) | (3.92) | |
| lne | 0.187 *** | −0.206 ** | −0.020 | 0.098 * | 0.038 | 0.136 * |
| (3.73) | (−2.19) | (−0.20) | (1.85) | (1.50) | (1.82) | |
| lnp | 0.020 | 0.007 | 0.027 | 0.022 | 0.009 | 0.031 |
| (1.40) | (1.23) | (1.39) | (1.46) | (1.17) | (1.42) | |
| lnt | 0.087 * | −0.396 *** | −0.309 ** | 0.088 * | 0.035 | 0.123 |
| (1.75) | (−3.57) | (−2.42) | (1.66) | (1.36) | (1.63) | |
| Short-Term | Long-Term | ||||||
|---|---|---|---|---|---|---|---|
| Direct Effects | Indirect Effects | Total Effect | Direct Effects | Indirect Effects | Total Effect | ||
| W1 | x | 0.188 *** | −0.005 | 0.183 | 0.291 *** | 0.044 | 0.334 |
| (3.90) | (−0.05) | (1.50) | (3.87) | (0.22) | (1.46) | ||
| W2 | x | 0.139 ** | 0.164 | 0.303 ** | 0.239 ** | 0.383 | 0.622 * |
| (2.06) | (0.93) | (2.07) | (2.20) | (1.06) | (1.87) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, A.; Xu, N. The Impact of Environmental Regulation on Urban Green Efficiency—Evidence from Carbon Pilot. Sustainability 2023, 15, 1136. https://doi.org/10.3390/su15021136
Tang A, Xu N. The Impact of Environmental Regulation on Urban Green Efficiency—Evidence from Carbon Pilot. Sustainability. 2023; 15(2):1136. https://doi.org/10.3390/su15021136
Chicago/Turabian StyleTang, Anbao, and Ning Xu. 2023. "The Impact of Environmental Regulation on Urban Green Efficiency—Evidence from Carbon Pilot" Sustainability 15, no. 2: 1136. https://doi.org/10.3390/su15021136
APA StyleTang, A., & Xu, N. (2023). The Impact of Environmental Regulation on Urban Green Efficiency—Evidence from Carbon Pilot. Sustainability, 15(2), 1136. https://doi.org/10.3390/su15021136








