Evaluation of the Performance of Polycrystalline and Monocrystalline PV Technologies in a Hot and Arid Region: An Experimental Analysis
Abstract
:1. Introduction
- Determine the performance of polycrystalline and monocrystalline solar modules in an arid region characterized by a large potential of solar irradiation and high temperatures.
- Study the influence of environmental parameters on the output power of solar modules with different technologies (monocrystalline and polycrystalline).
- Investigate the effects of temperature and dust on the performance of PV modules of type monocrystalline and polycrystalline.
- Apply a meta-heuristic optimization algorithm for the extraction of parameters from monocrystalline and polycrystalline solar modules.
2. Experimental Data Collection
- -
- Measuring accuracy for the I-V characteristic is less than 1%, and for the peak power measurements, the accuracy is ±5%.
- -
- It utilizes an irradiation reference sensor (Phox) with an integrated Pt100/Pt1000 temperature sensor.
- -
- The measuring ranges supported by the PVPM 2540C are as follows:
- Voltage DC: 25/50/100/250 V;
- Current DC: 2/5/10/40 A;
- Temperature: −40 °C to +120 °C with Pt1000;
- Irradiance: 0–1300 W/m2 (Standard sensor).
3. Experimental Results
3.1. Characterization of Polycrystalline and Monocrystalline Solar Modules Operate under Different Solar Irradiation
3.2. Comparison between Poly-Si and Mono-Si for Different Solar Irradiation
3.3. Effect of Dust on Monocrystalline Solar Module for Different Solar Irradiation
3.4. Effect of Dust on Polycrystalline Solar Module for Different Solar Irradiation
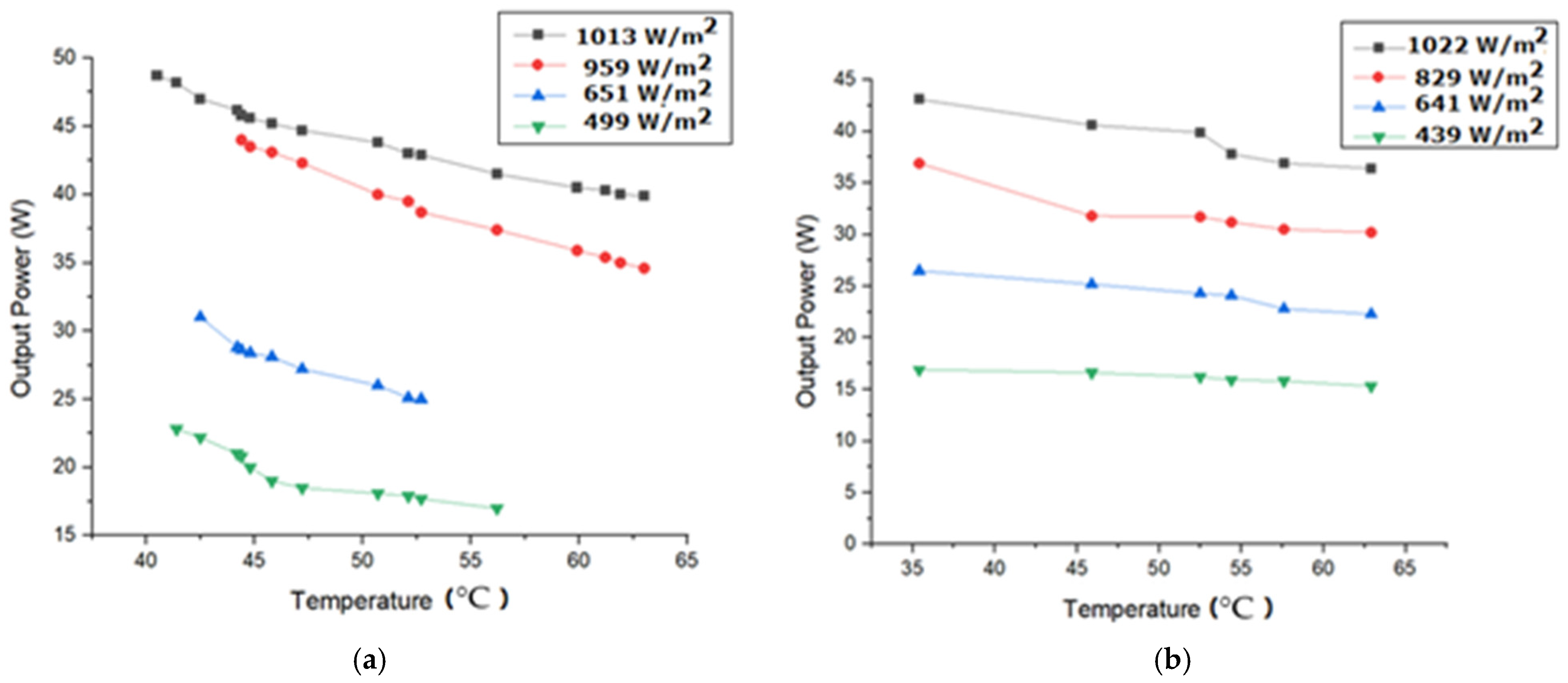
3.5. Effect of Temperature on Polycrystalline and Monocrystalline Solar Modules for Different Incident Solar Irradiation
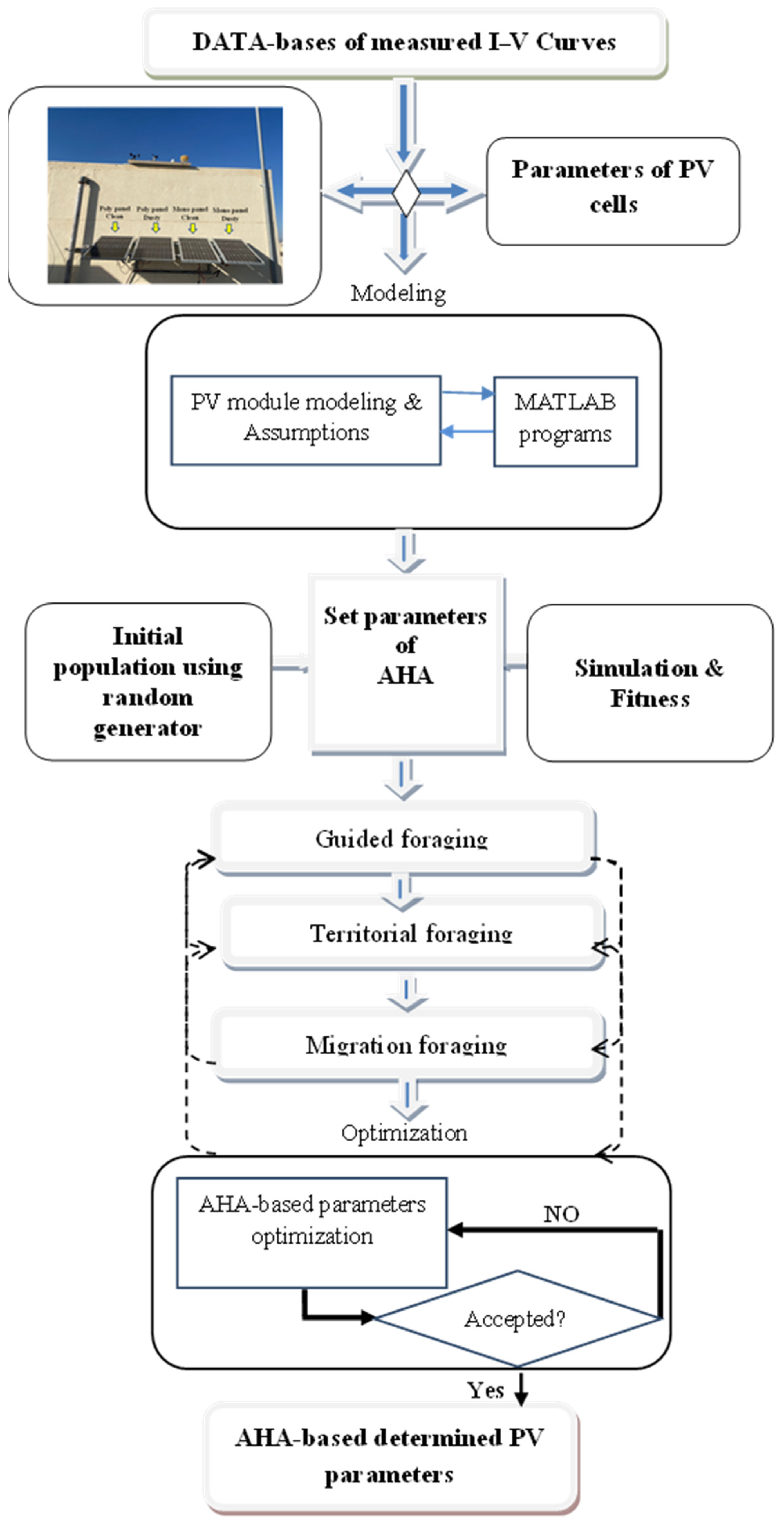
4. Numerical Results Using AHA
4.1. Problem Definition
- PV data acquisition under different conditions.
- Preprocess data and set objectives.
- Determine the initial configuration of the AHA.
- Generate the initial population.
- State the fitness function.
- Identify the AHA operators, i.e., guided, territorial and migration foraging.
4.2. AHA Mathematical Model
4.2.1. Initialization
4.2.2. Guided Foraging
4.2.3. Territorial Foraging
4.2.4. Migration Foraging
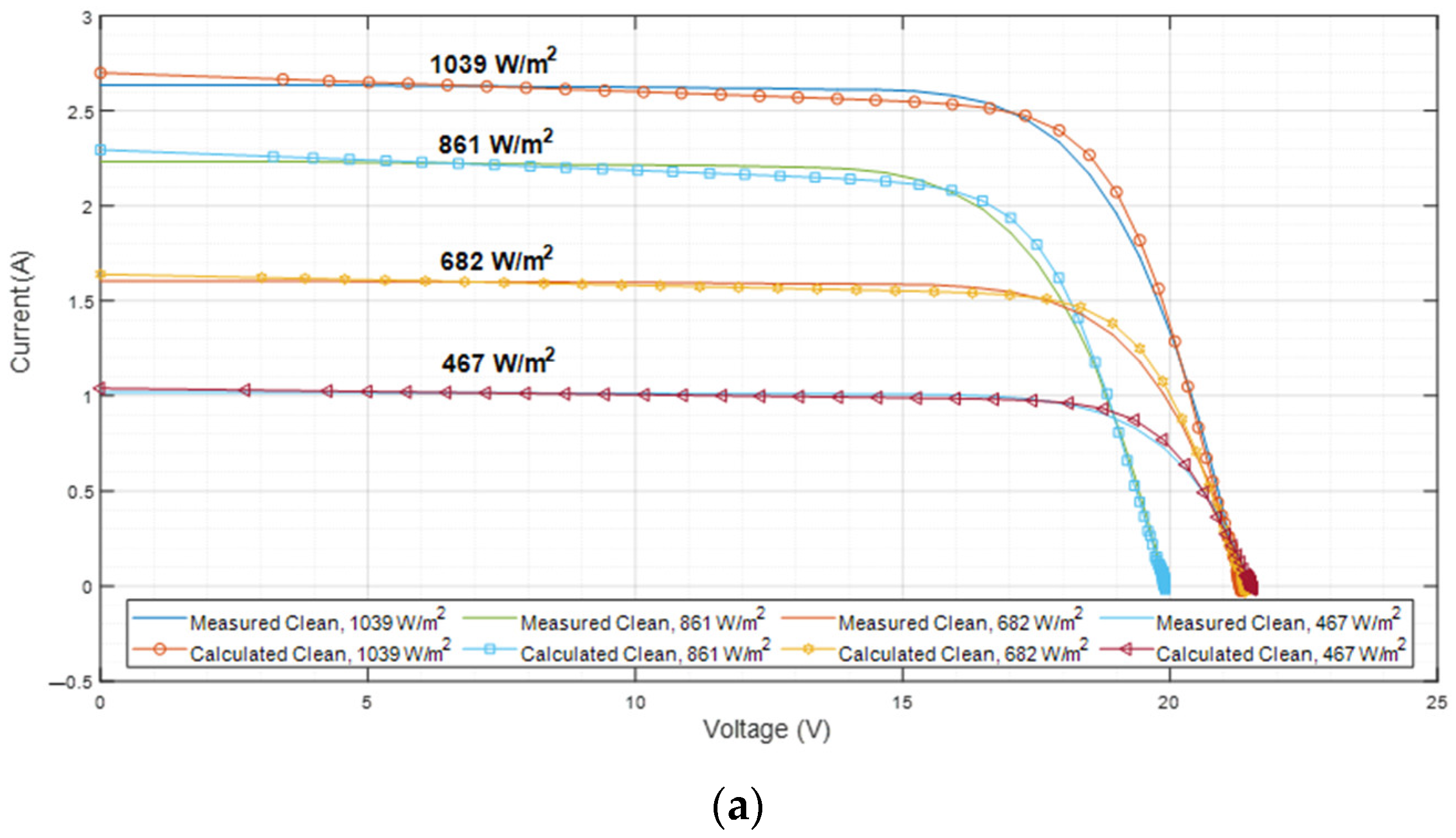
4.3. Extraction of Parameters Using AHA for Mono and Poly Solar Module
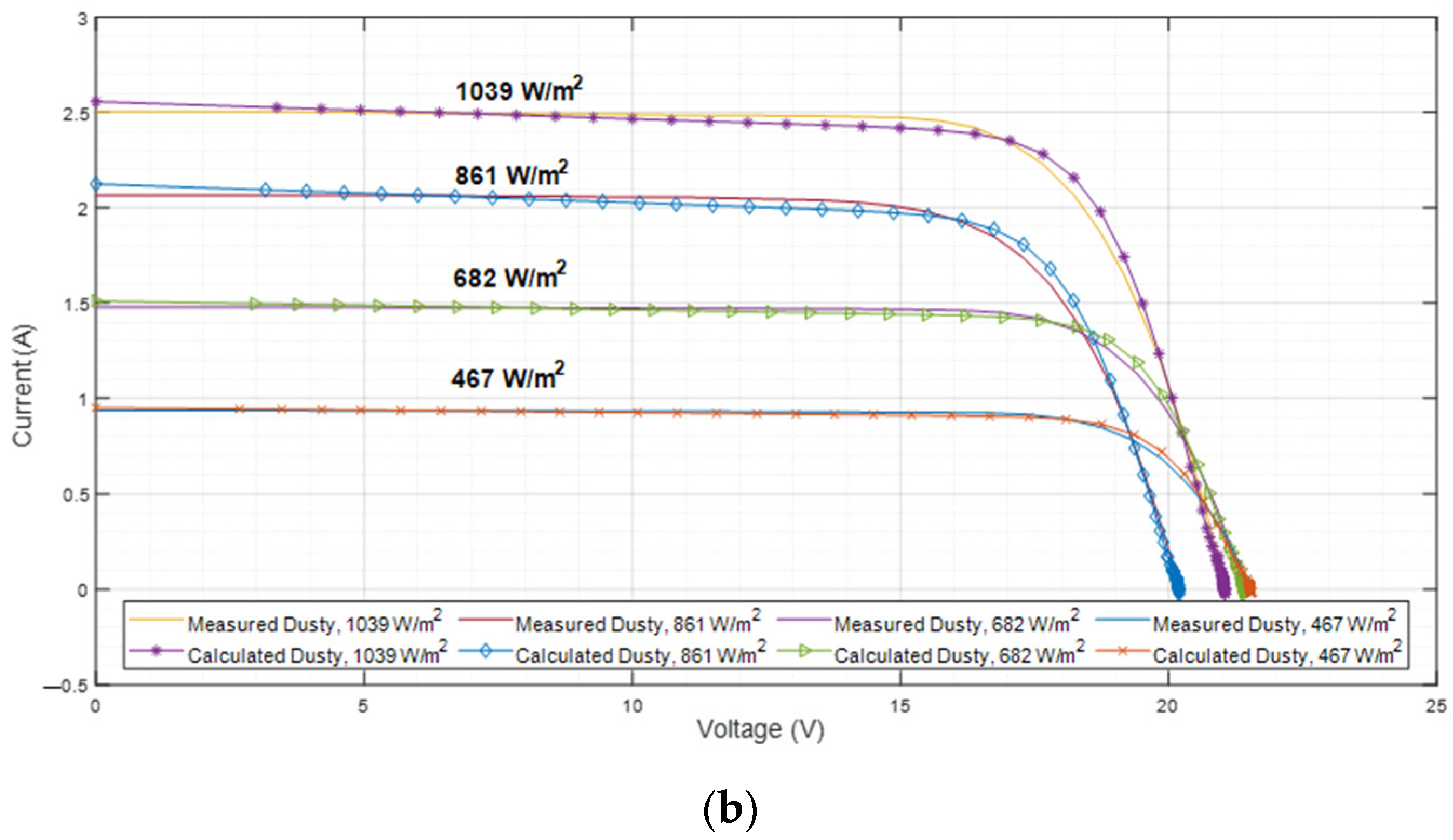
4.4. Effect of Dust on Monocrystalline and Polycrystalline Solar Module
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Ideality factor. |
| AHA | Artificial Hummingbirds Algorithm. |
| CPV | concentrated PV. |
| HG | Daily solar irradiation (Wh/m2). |
| Icalc | Calculated currents (A). |
| Impp | Maximum current power point (A). |
| Imeas | Measured currents (A). |
| IPh | Photocurrent (A) |
| IS | Saturation current (A). |
| ISC | Short circuit current (A). |
| Mono-Si (m-Si) | Monocrystalline silicon solar module. |
| N | Number of measured points. |
| Pmpp | Maximum power point (W). |
| Poly-Si (p-Si) | Polycrystalline silicon solar module. |
| Pout | Output power (W). |
| PV | Photovoltaic. |
| RMSE | Root mean square error. |
| RS | Series resistance. |
| RSh | Shunt resistance. |
| SC | Solar cells. |
| SDM | Single diode model. |
| StD | Standard deviation |
| T | Ambient temperature (°C). |
| TM | Thermoelectric module. |
| Vmpp | Maximum voltage power point (V). |
| VOC | Open circuit voltage (V) |
| VT | Visit table of food sources in the AHA |
References
- Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable Energy in the Sustainable Development of Electrical Power Sector: A Review. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Available online: https://www.worldbank.org/en/topic/energy/publication/solar-photovoltaic-power-potential-by-country (accessed on 20 March 2023).
- Solanki, C.S. Solar Photovoltaic Fundamentals, Technologies and Applications; PHI Learning Pvt. Ltd.: Delhi, India, 2016. [Google Scholar]
- Moller, H.J. Semiconductors for Solar Cells; Artech House Publishers: Norwood, MA, USA, 1993. [Google Scholar]
- Garg, H.P.; Prakash, J. Solar Energy: Fundamentals and Applications; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Kymakis, E.; Kalykakis, S.; Papazoglou, T.M. Performance analysis of a grid connected photovoltaic park on the island of Crete. Energy Convers. Manag. 2009, 50, 433–438. [Google Scholar] [CrossRef]
- Chokmaviroj, S.; Wattanapong, R.; Suchart, Y. Performance of a 500 kWP grid connected photovoltaic system at Mae Hong Son Province, Thailand. Renew. Energy 2006, 31, 19–28. [Google Scholar] [CrossRef]
- Sharma, V.; Chandel, S. Performance analysis of a 190 kWp grid interactive solar photovoltaic power plant in India. Energy 2013, 55, 476–485. [Google Scholar] [CrossRef]
- Mpholo, M.; Nchaba, T.; Monese, M. Yield and performance analysis of the first grid-connected solar farm at Moshoe shoe I International Airport, Lesotho. Renew. Energy 2018, 81, 845–852. [Google Scholar] [CrossRef]
- Ghiani, E.; Pilo, F.; Cossu, S. Evaluation of photovoltaic installations performances in Sardinia. Energy Convers. Manag. 2013, 76, 1134–1142. [Google Scholar] [CrossRef]
- Abu Hussein, L.; Ayadi, O.; Fathi, M. Performance comparison for sun-tracking mechanism photovoltaic (PV) and concentrated photovoltaic (CPV) solar panels with fixed system PV panels in Jordan. In Proceedings of the 12th international renewable engineering conference, (IREC), Amman, Jordan, 14–15 April 2021; pp. 1–8. [Google Scholar]
- Başoğlu, M.E.; Kazdaloğlu, A.; Erfidan, T.; Bilgin, M.Z.; Cąkir, B. Performance analyzes of different photovoltaic module technologies under izmit, Kocaeli climatic conditions. Renew. Sustain. Energy Rev. 2015, 52, 357–365. [Google Scholar] [CrossRef]
- Martín-Martínez, S.; Cañas-Carretón, M.; Honrubia-Escribano, A.; Gómez- Lázaro, E. Performance evaluation of large solar photovoltaic power plants in Spain. Energy Convers. Manag. 2019, 183, 515–528. [Google Scholar] [CrossRef]
- Ayadi, O.; Jamra, M.; Jaber, A.; Ahmad, L.; Alnaqep, M. An experimental comparison of bifacial and monofacial PV modules. In Proceedings of the 12th international renewable engineering conference (IREC), Amman, Jordan, 14–15 April 2021; pp. 1–8. [Google Scholar]
- Beskirli, A.; Dag, I. Parameter extraction for photovoltaic models with tree seed algorithm. Energy Rep. 2023, 9, 174–185. [Google Scholar] [CrossRef]
- Farayola, A.M.; Sun, Y.; Ali, A. Global maximum power point tracking and cell parameter extraction in Photovoltaic systems using improved frefly Algorithm. Energy Rep. 2022, 8, 162–186. [Google Scholar] [CrossRef]
- Abd El-Mageed, A.A.; Abohany, A.A.; Saad, H.M.H.; Sallam, K.M. Parameter extraction of solar photovoltaic models using queuing search optimization and differential evolution. Appl. Soft Comput. 2023, 134, 110032. [Google Scholar] [CrossRef]
- Ali, F.; Sarwar, A.; Bakhsh, F.I.; Ahmad, S.; Shah, A.A.; Ahmed, H. Parameter extraction of photovoltaic models using atomic orbital search algorithm on a decent basis for novel accurate RMSE calculation. Energy Convers. Manag. 2023, 277, 116613. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Badawy, M.; Mirjalili, S.; Elhosseini, M.A. Photovoltaic parameter estimation using improved moth flame algorithms with local escape operators. Comput. Elect. Eng. 2023, 106, 108603. [Google Scholar] [CrossRef]
- Benhmamou, D.; Elyaqouti, M.; Arjdal, E.H.; Saadaoui, D.; Lidaighbi, S.; Chaouf, J.; Ibrahim, A.; Aqel, R.; El fatmi, D.D.; Obukhov, S. A novel hybrid numerical with analytical approach for parameter extraction of photovoltaic modules. Energy Convers. Manag. 2022, 14, 100219. [Google Scholar]
- Xu, J.; Zhou, C.; Wei Li, W. Photovoltaic single diode model parameter extraction by dI/dV-assisted deterministic method. Solar Energy 2023, 251, 30–38. [Google Scholar] [CrossRef]
- Haddad, S.; Lekouaghet, B.; Benghanem, M.; Soukkou, A. Parameter Estimation of Solar Modules Operating Under Outdoor Operational Conditions Using Artificial Hummingbird Algorithm. IEEE Access 2022, 10, 1109. [Google Scholar] [CrossRef]
- Zorrilla-Casanova, J.; Piliougine, M.; Carretero, J.; Bernaola, P.; Carpena, P.; Mora-López, L.; Sidrach-de-Car Dona, M. Analysis of dust losses in photovoltaic Modules. In Proceedings of the World Renewable Energy Congress 2011, Linköping, Sweden, 8–13 May 2011. [Google Scholar]
- Colvin, D.J.; Iqbal, N.; Yerger, J.H.; Li, F.; Sinha, A.; Vicnansky, G.; Brummer, G.; Zheng, N.; Schneller, E.J.; Barkaszi, J.; et al. Degradation of Monocrystalline Silicon Photovoltaic Modules From a 10-Year-Old Roof top System in Florida. IEEE J. Photovolt. 2023, 13, 275–282. [Google Scholar] [CrossRef]
- Benghanem, M.; Almohammedi, A.; Al-Mashraqi, A.; Mellit, A. Dust Effect of Solar Cell Characteristic Using Matlab/Simulink: Case Study at Madinah City, KSA. Int. J. Energy Environ. Econ. 2018, 26, 59–76. [Google Scholar]
- Abdellatif, S.O.; Amr, L.; Kirah, K.; Ghali, H.A. Experimental Studies for Glass Light Transmission Degradation in Solar Cells Due to Dust Accumulation Using Effective Optical Scattering Parameters and Machine Learning Algorithm. IEEE J. Photovolt. 2023, 13, 158–164. [Google Scholar] [CrossRef]
- Boubaker, S.; Benghanem, M.; Mellit, A.; Kahouli, O.; Kolsi, L. Deep Neural Networks for Predicting Solar Radiation at Hail Region, Saudi Arabia. IEEE Access 2021, 9, 36719–36729. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bioinspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Benghanem, M.; Al-Mashraqi, A.A.; Daffallah, K.O. Performance of solar cells using thermoelectric module in hot sites. Renew. Energy 2016, 89, 51–59. [Google Scholar] [CrossRef]
- Phinikarides, A.; Kindyni, N.; Makrides, G.; Georghiou, G.E. Review of photovoltaic degradation rate methodologies. Renew. Sustain Energy Rev. 2014, 40, 143–152. [Google Scholar] [CrossRef]
- Congedo, P.; Malvoni, M.; Mele, M.; Giorgi, M.D. Performance measurements of monocrystalline silicon PV modules in South-eastern Italy. Energy Convers. Manag. 2013, 68, 1–10. [Google Scholar] [CrossRef]
- Malvoni, M.; Leggieri, A.; Maggiotto, G.; Congedo, P.; Giorgi, M.D. Long term performance, losses and efficiency analysis of a 960 kWp photovoltaic system in the Mediterranean climate. Energy Convers. Manag. 2017, 145, 169–181. [Google Scholar] [CrossRef]


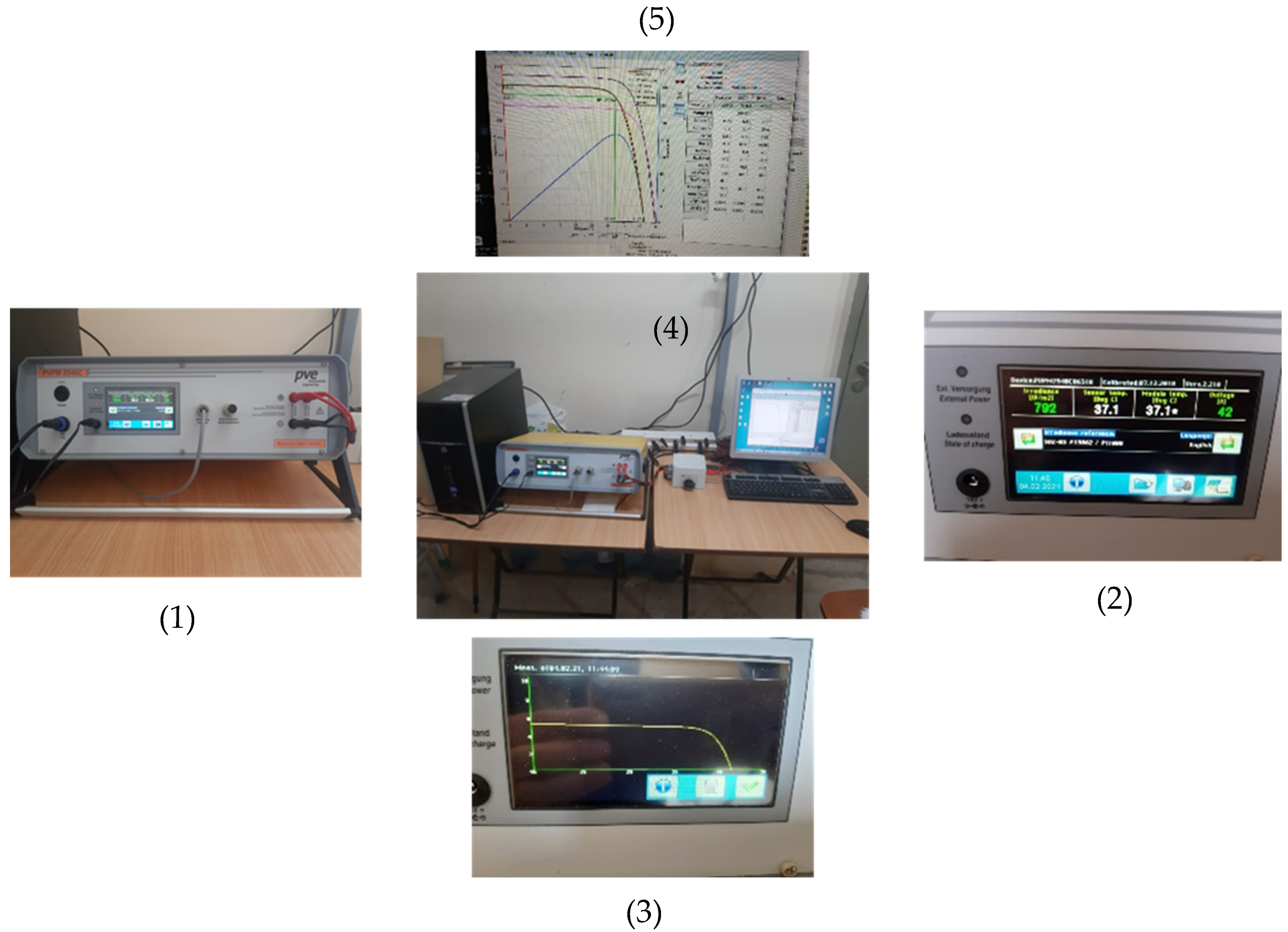
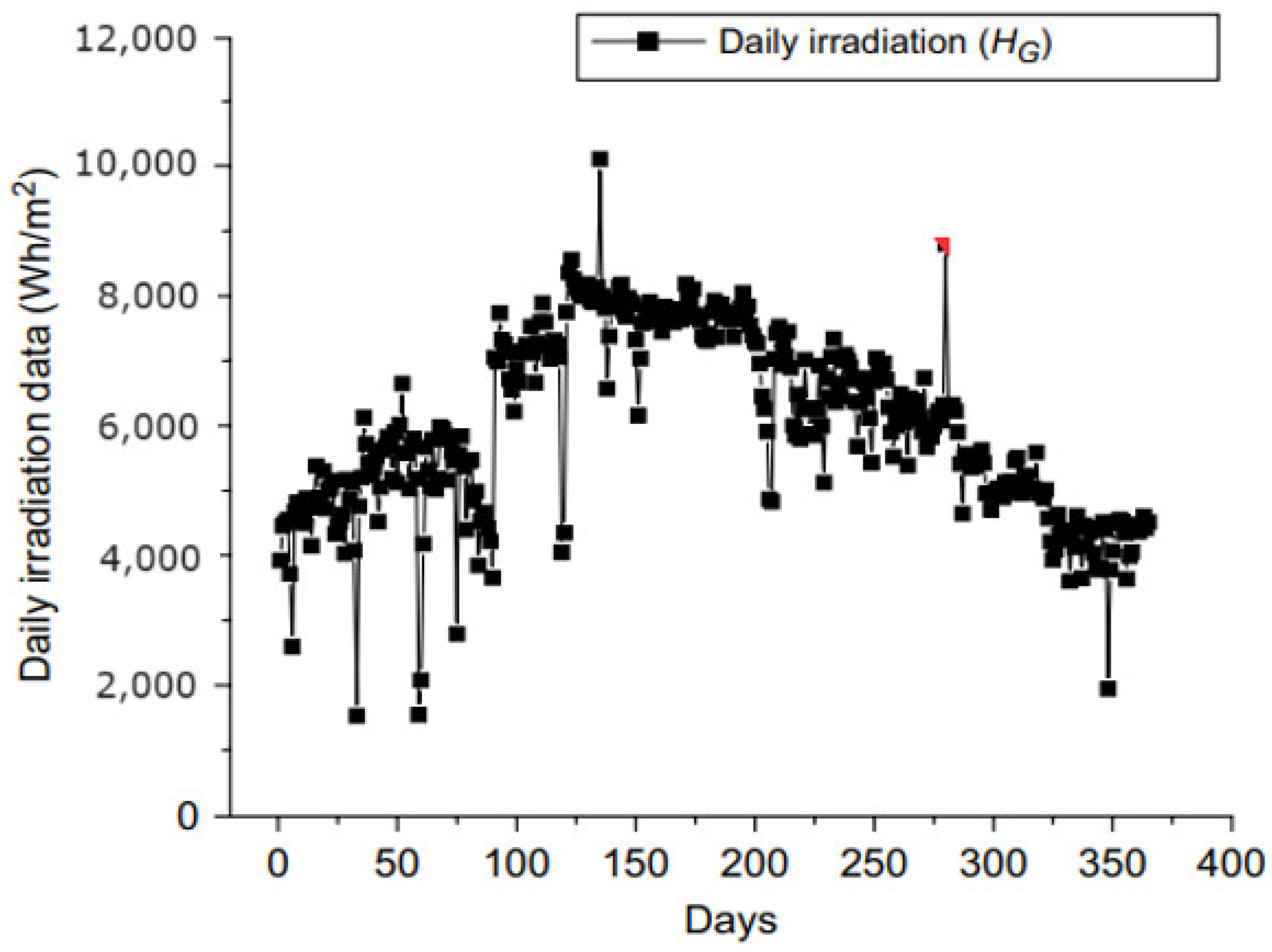


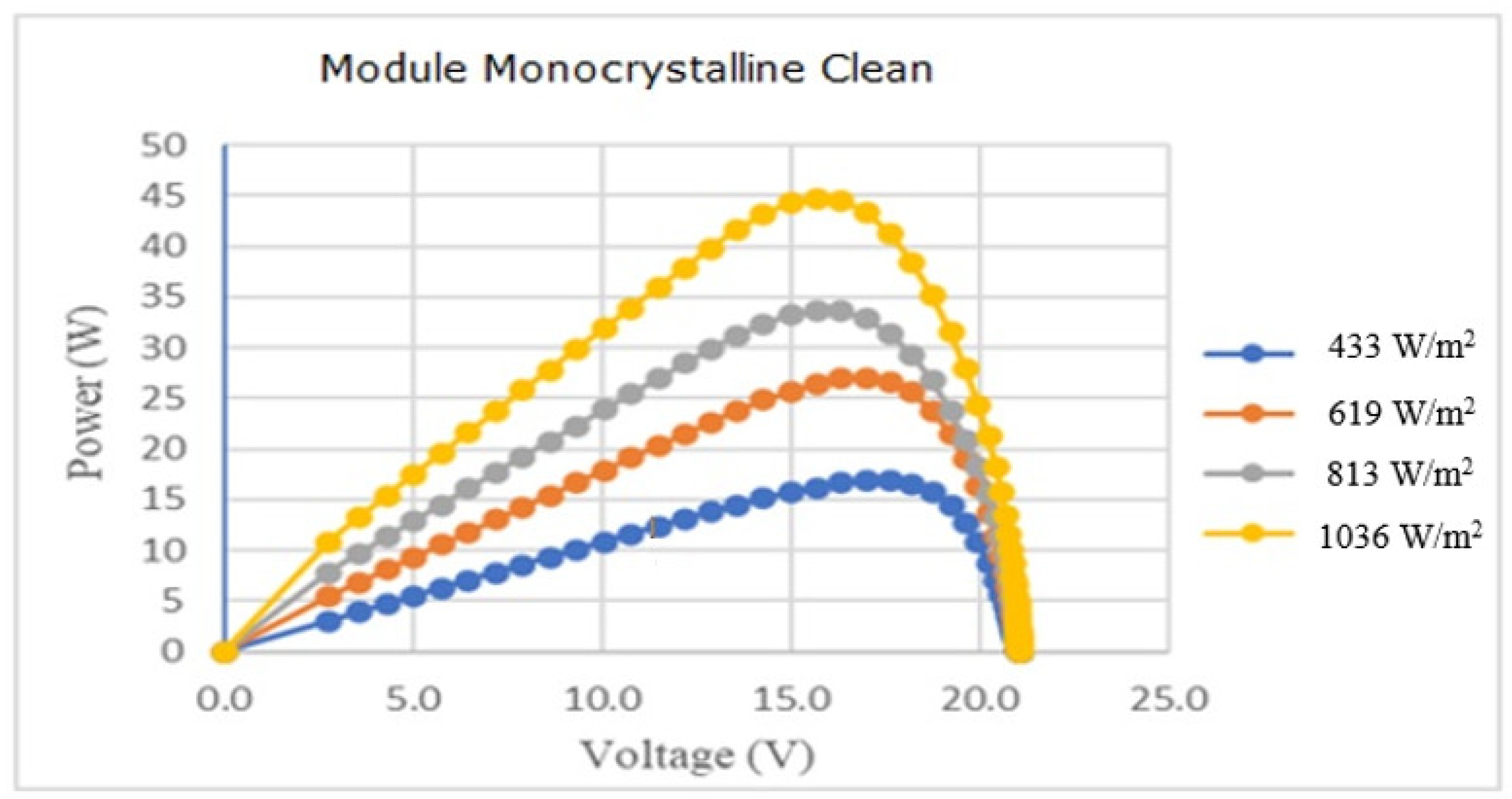



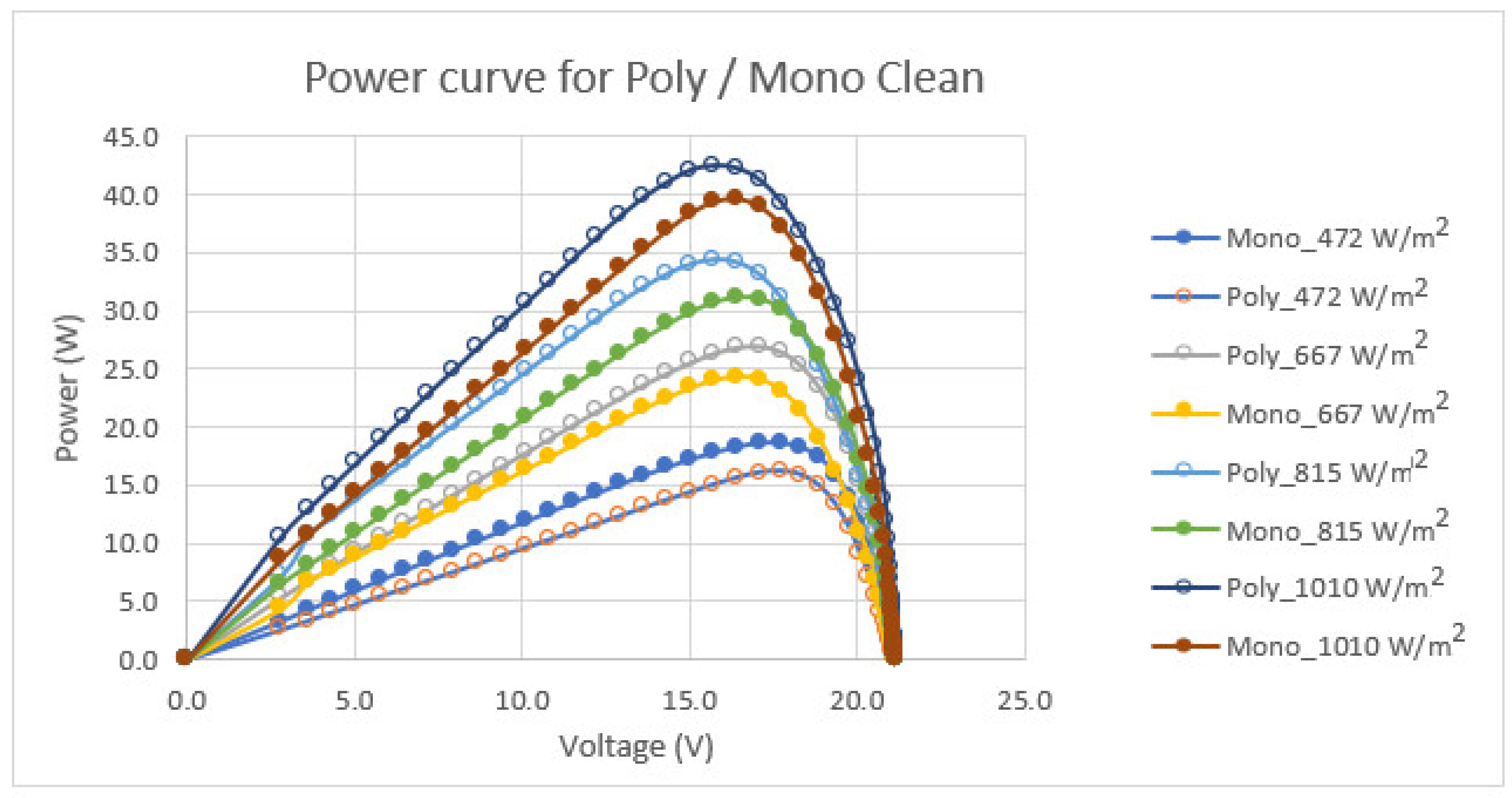
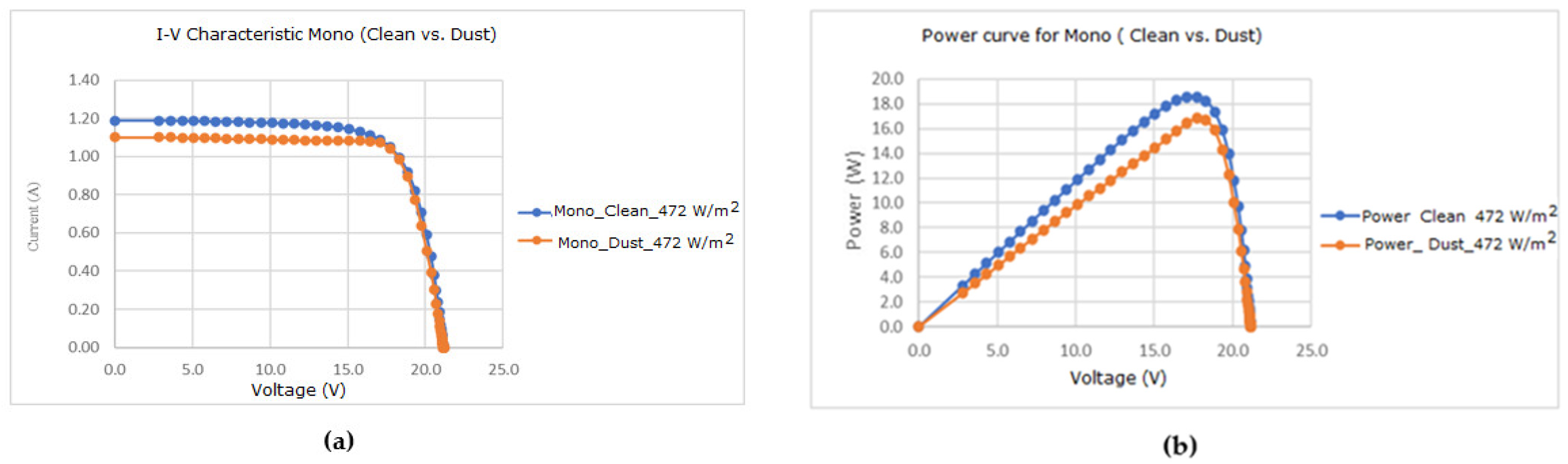
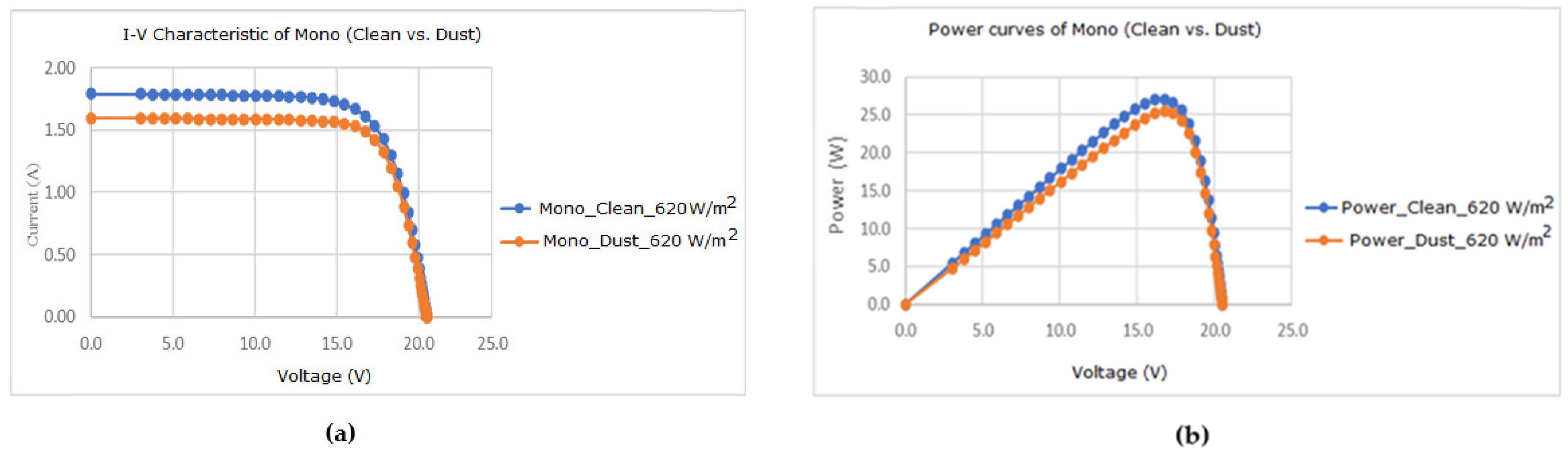
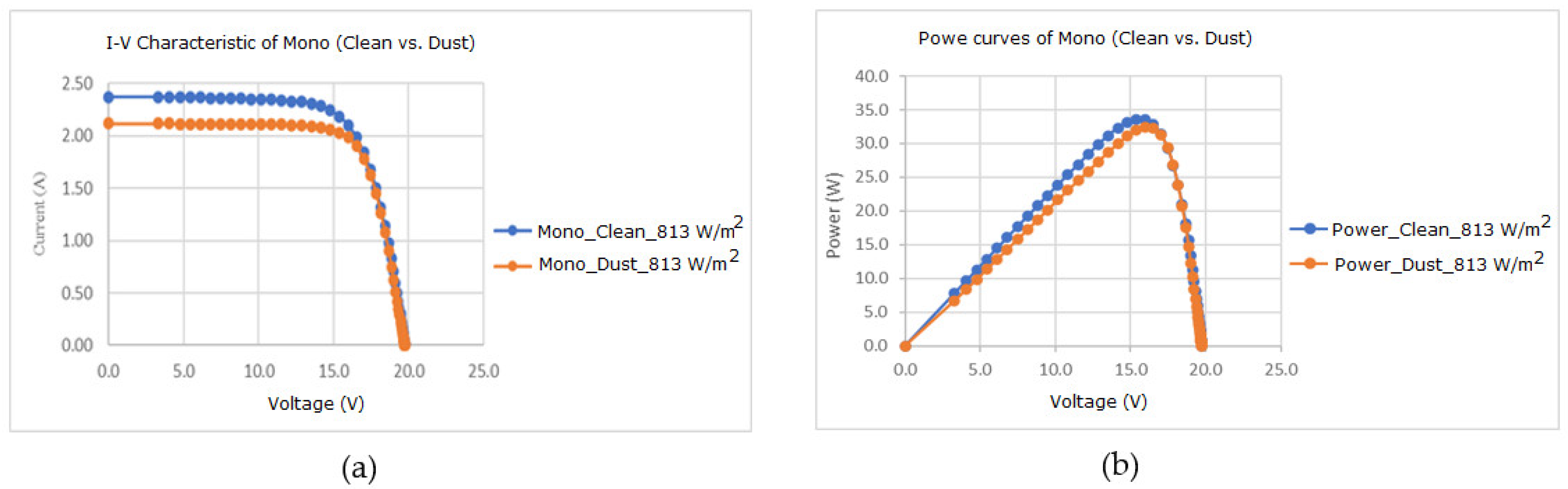
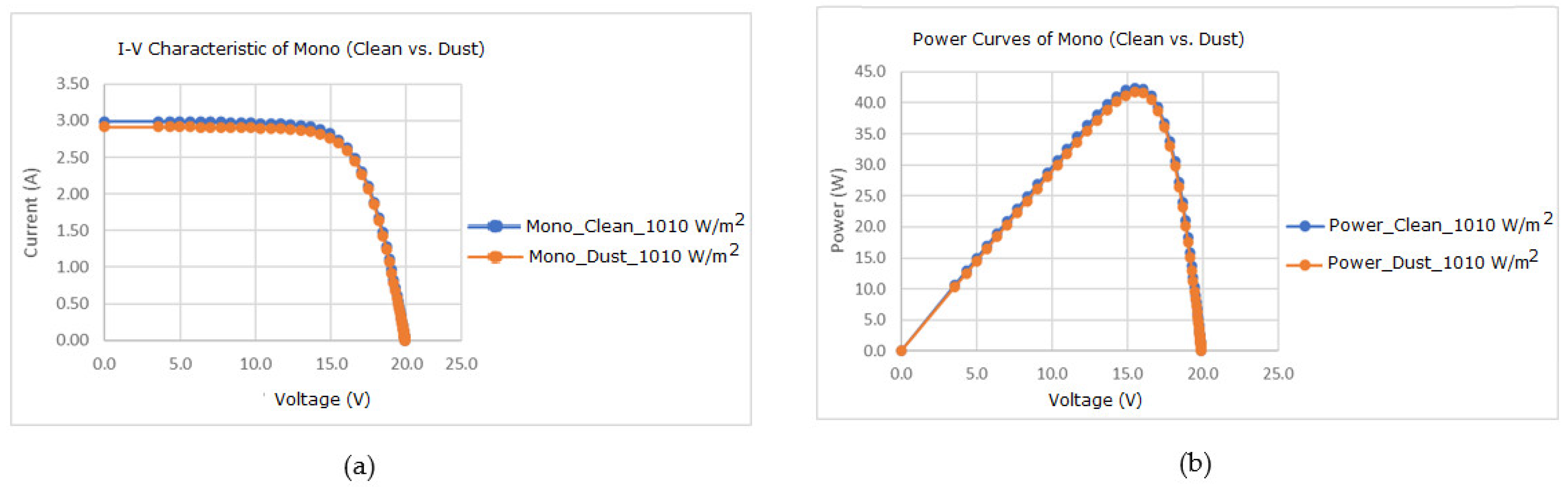

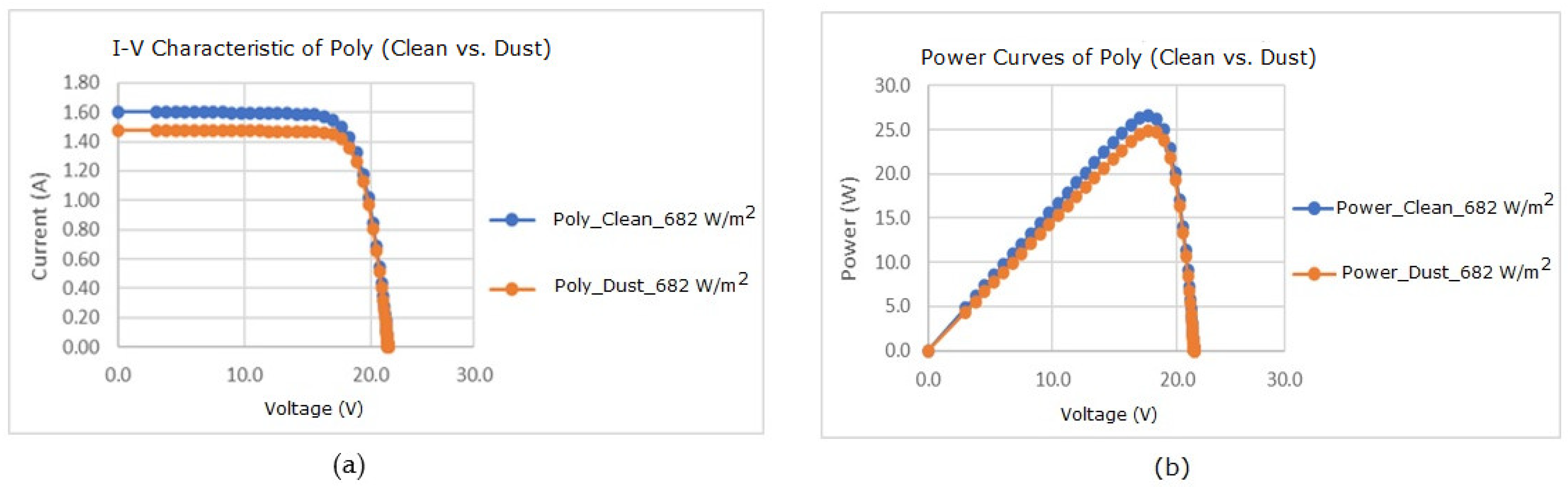
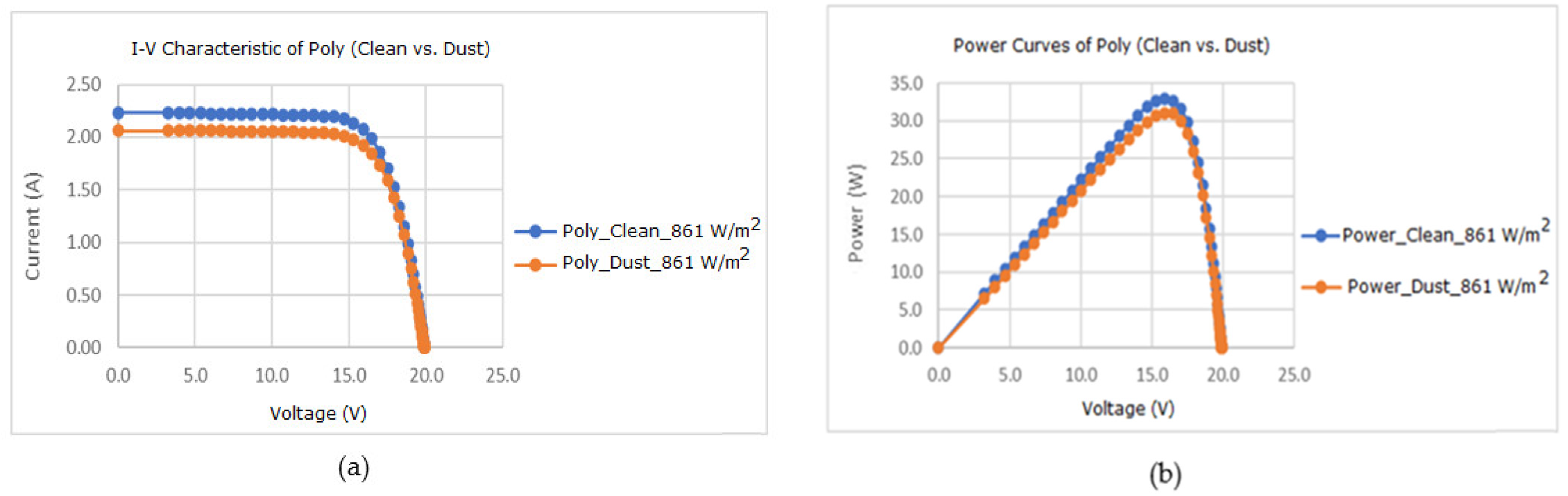
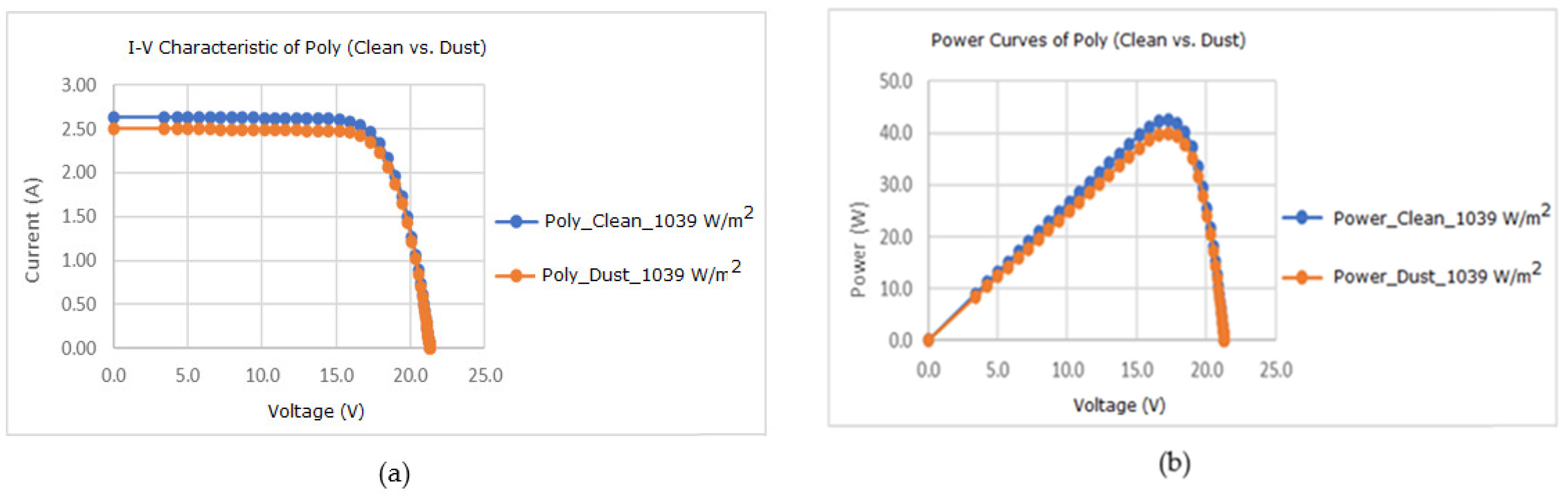


| Solar Irradiation (W/m2) | 467–472 | 620–682 | 813–861 | 1010–1039 | |
|---|---|---|---|---|---|
| Polycrystalline | Drop in Isc (%) | 7.56 | 10.61 | 10.54 | 2.34 |
| Drop in Pout (%) | 10.21 | 5.90 | 3.57 | 1.65 | |
| Monocrystalline | Drop in Isc (%) | 9.80 | 7.50 | 7.62 | 4.94 |
| Drop in Pout (%) | 8.09 | 6.39 | 6.36 | 6.11 | |
| Solar Radiation (W/m2) | 1013–1022 | 829–959 | 641–651 | 439–499 | |
|---|---|---|---|---|---|
| Drop in output power (%) | Temperature coefficient of monocrystalline solar module (−0.45%/°C) | 15.5 | 20.6 | 19.24 | 9 |
| Temperature coefficient of polycrystalline solar module (−0.5%/°C) | 14.37 | 17.47 | 27.75 | 21 | |
| Irradiance/ Temperature | Clean/ Dusty | Iph [A] | I0 [µA] | A | Rs [Ω] | Rsh [×100 Ω] | RMSE | StD |
|---|---|---|---|---|---|---|---|---|
| 1039 W/m2 T = 52.3 °C | Clean | 2.71498795 | 4.3389067 × 10−14 | 1.9943433 | 0.04958563 | 8.42730791 | 3.570402 × 10−2 | 2.344988 × 10−4 |
| Dusty | 2.56957483 | 6.7138523 × 10−14 | 1.9988951 | 0.05060903 | 9.24463587 | 3.486062 × 10−2 | 9.034900 × 10−4 | |
| 861 W/m2 T = 54.3 °C | Clean | 2.31570534 | 3.4162075 × 10−13 | 1.9971951 | 0.05482136 | 7.40724899 | 3.147642 × 10−2 | 9.700919 × 10−4 |
| Dusty | 2.13760170 | 2.1855790 × 10−13 | 1.9999998 | 0.05601773 | 8.51343056 | 2.941896 × 10−2 | 2.673247 × 10−4 | |
| 682 W/m2 T = 41.1 °C | Clean | 1.64562215 | 7.6568296 × 10−15 | 1.9999934 | 0.06092164 | 14.3884834 | 2.466798 × 10−2 | 1.619375 × 10−3 |
| Dusty | 1.51510937 | 6.6665514 × 10−15 | 1.9976565 | 0.06123857 | 18.1167955 | 2.017081 × 10−2 | 3.065316 × 10−4 | |
| 467 W/m2 T = 33.6 °C | Clean | 1.04145997 | 1.7017386 × 10−15 | 1.9981190 | 0.07720321 | 25.3188248 | 1.431206 × 10−2 | 6.552128 × 10−5 |
| Dusty | 0.95337204 | 1.6362433 × 10−15 | 1.9999456 | 0.07784661 | 32.5428040 | 1.442506 × 10−2 | 2.600168 × 10−4 |
| Irradiance/ Temperature | Clean/ Dusty | Iph [A] | I0 [µA] | A | Rs [Ω] | Rsh [×100 Ω] | RMSE | StD |
|---|---|---|---|---|---|---|---|---|
| 1010 W/m2 T = 63.1 °C | Clean | 3.1173 | 8.3440 × 10−13 | 1.9879246 | 0.05422757 | 4.8638443 | 4.1560 × 10−2 | 1.5170 × 10−3 |
| Dusty | 3.0432 | 1.0752 × 10−12 | 1.9999080 | 0.05178131 | 5.1247748 | 4.2884 × 10−2 | 1.1612 × 10−3 | |
| 813 W/m2 T = 61.7 °C | Clean | 2.4770 | 8.8809 × 10−13 | 1.9999979 | 0.05894576 | 5.7179067 | 3.4723 × 10−2 | 1.4762 × 10−3 |
| Dusty | 2.1825 | 2.2399 × 10−13 | 1.9781553 | 0.05572144 | 9.3905214 | 3.0486 × 10−2 | 4.2035 × 10−4 | |
| 620 W/m2 T = 43.9 °C | Clean | 1.8657 | 4.2106 × 10−14 | 1.9998346 | 0.06494558 | 8.0546604 | 2.8451 × 10−2 | 5.4287 × 10−4 |
| Dusty | 1.6375 | 1.7559 × 10−14 | 1.9853981 | 0.06389599 | 13.989217 | 2.1341 × 10−2 | 5.8067 × 10−4 | |
| 472 W/m2 T = 36.1 °C | Clean | 1.2410 | 4.5245 × 10−15 | 1.9999995 | 0.08065016 | 10.813073 | 2.1447 × 10−2 | 5.9408 × 10−5 |
| Dusty | 1.0166 | 2.4274 × 10−15 | 1.9803798 | 0.07498811 | 23.634772 | 1.2835 × 10−2 | 4.4790 × 10−4 |
| Irradiance/Temperature | m-Si Module | Impp [A] | Vmpp [V] | Pmpp [W] | Power Drop [%] |
|---|---|---|---|---|---|
| 1010 Wm−2/63.1 °C | Clean | 2.4577 | 17.2915 | 42.4974 | 6.0643 |
| Dusty | 2.3427 | 17.0404 | 39.9202 | ||
| 813 Wm−2/61.7 °C | Clean | 2.0704 | 15.9196 | 32.9607 | 5.7285 |
| Dusty | 1.9247 | 16.1438 | 31.0725 | ||
| 620 Wm−2/43.9 °C | Clean | 1.5022 | 17.6949 | 26.5817 | 6.1832 |
| Dusty | 1.4165 | 17.6053 | 24.9381 | ||
| 472 Wm−2/36.1 °C | Clean | 0.9540 | 18.1163 | 17.2838 | 6.6893 |
| Dusty | 0.8916 | 18.0894 | 16.1277 |
| Irradiance/Temperature | p-Si module | Impp [A] | Vmpp [V] | Pmpp [W] | Power Drop [%] |
|---|---|---|---|---|---|
| 1039 Wm−2/52.3 °C | Clean | 2.7376 | 15.4982 | 42.4283 | 1.6546 |
| Dusty | 2.6954 | 15.4803 | 41.7263 | ||
| 861 Wm−2/54.3 °C | Clean | 2.1011 | 15.9914 | 33.5997 | 3.4885 |
| Dusty | 1.9823 | 16.3590 | 32.4276 | ||
| 682 Wm−2/41.1 °C | Clean | 1.6147 | 16.7625 | 27.0665 | 5.8797 |
| Dusty | 1.4879 | 17.1211 | 25.4751 | ||
| 467 Wm−2/33.6 °C | Clean | 1.0487 | 17.7218 | 18.5846 | 9.1689 |
| Dusty | 0.9487 | 17.7936 | 16.8806 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benghanem, M.; Haddad, S.; Alzahrani, A.; Mellit, A.; Almohamadi, H.; Khushaim, M.; Aida, M.S. Evaluation of the Performance of Polycrystalline and Monocrystalline PV Technologies in a Hot and Arid Region: An Experimental Analysis. Sustainability 2023, 15, 14831. https://doi.org/10.3390/su152014831
Benghanem M, Haddad S, Alzahrani A, Mellit A, Almohamadi H, Khushaim M, Aida MS. Evaluation of the Performance of Polycrystalline and Monocrystalline PV Technologies in a Hot and Arid Region: An Experimental Analysis. Sustainability. 2023; 15(20):14831. https://doi.org/10.3390/su152014831
Chicago/Turabian StyleBenghanem, Mohamed, Sofiane Haddad, Ahmed Alzahrani, Adel Mellit, Hamad Almohamadi, Muna Khushaim, and Mohamed Salah Aida. 2023. "Evaluation of the Performance of Polycrystalline and Monocrystalline PV Technologies in a Hot and Arid Region: An Experimental Analysis" Sustainability 15, no. 20: 14831. https://doi.org/10.3390/su152014831
APA StyleBenghanem, M., Haddad, S., Alzahrani, A., Mellit, A., Almohamadi, H., Khushaim, M., & Aida, M. S. (2023). Evaluation of the Performance of Polycrystalline and Monocrystalline PV Technologies in a Hot and Arid Region: An Experimental Analysis. Sustainability, 15(20), 14831. https://doi.org/10.3390/su152014831






