Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event
Abstract
:1. Introduction
2. Unsaturated Slope Stability
2.1. Unsaturated Flow in Porous Medium
2.2. Soil-Atmosphere Interaction
2.3. Unsaturated Shear Strength
3. Failure Probability
3.1. First-Order Second-Moment Method
3.2. Transient Failure Probability
4. Case Study
4.1. Assessment of the Transient and Unsaturated Deterministic Stability
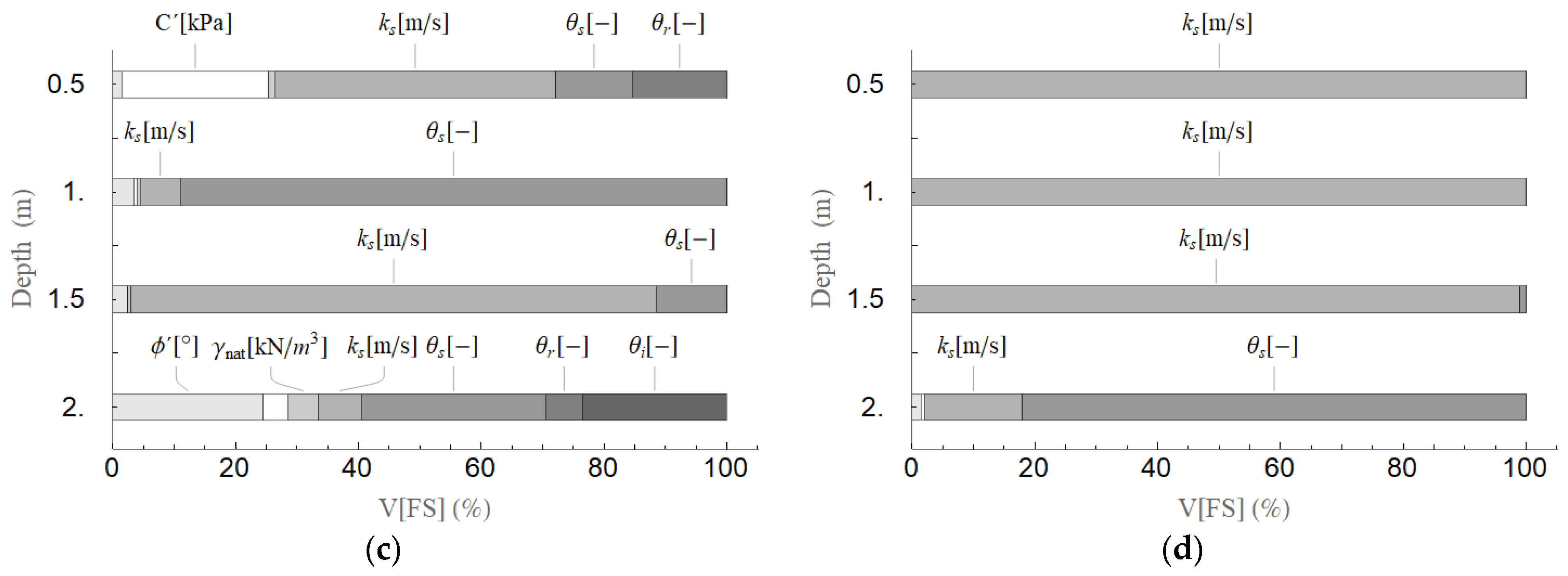
4.2. Parametric Analysis of Stochastic Variables
4.3. Assessment of the Probability of Transient Unsaturated Failure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walker, L.R.; Shiels, A.B. Physical Causes and Consequences for Landslide Ecology. Landslide Ecol. 2013, 46–82. [Google Scholar]
- Cho, S.E. Stability Analysis of Unsaturated Soil Slopes Considering Water-Air Flow Caused by Rainfall Infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Tsai, T.L.; Chen, H.E.; Yang, J.C. Numerical Modeling of Rainstorm-Induced Shallow Landslides in Saturated and Unsaturated Soils. Environ. Geol. 2008, 55, 1269–1277. [Google Scholar] [CrossRef]
- Song, Y.S.; Chae, B.G.; Lee, J. A Method for Evaluating the Stability of an Unsaturated Slope in Natural Terrain during Rainfall. Eng. Geol. 2016, 210, 84–92. [Google Scholar] [CrossRef]
- Yang, K.H.; Uzuoka, R.; Thuo, J.N.; Lin, G.L.; Nakai, Y. Coupled Hydro-Mechanical Analysis of Two Unstable Unsaturated Slopes Subject to Rainfall Infiltration. Eng. Geol. 2017, 216, 13–30. [Google Scholar] [CrossRef]
- Cao, W.; Wan, Z.; Li, W. Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty. Sustainability 2023, 15, 717. [Google Scholar] [CrossRef]
- Li, S.; Qiu, C.; Huang, J.; Guo, X.; Hu, Y.; Mugahed, A.S.Q.; Tan, J. Stability Analysis of a High-Steep Dump Slope under Different Rainfall Conditions. Sustainability 2022, 14, 11148. [Google Scholar] [CrossRef]
- Mburu, J.W.; Li, A.J.; Lin, H.-D.; Lu, C.W. Investigations of Unsaturated Slopes Subjected to Rainfall Infiltration Using Numerical Approaches—A Parametric Study and Comparative Review. Sustainability 2022, 14, 14465. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, K.; Kim, J.; Kim, Y. Analysis of Rainfall-Induced Landslide on Unsaturated Soil Slopes. Sustainability 2017, 9, 1280. [Google Scholar] [CrossRef]
- Chowdhury, R.; Flentje, P.; Bhattacharya, G. Geotechnical Slope Analysis; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9780415469746. [Google Scholar]
- Rojas, K.R.C. Estudo Dos Deslizamentos Superficiais Deflagrados por Chuvas Implementando a Análise Não Saturada e Transiente em Escala Regional. Master’s Dissertation, University of Brasília, Faculty of Technology, Department of Civil and Environmental Engineering, Brasília, Brazil, 2017. [Google Scholar]
- Cavalcante, A.L.B.; Zornberg, J.G. Efficient Approach to Solving Transient Unsaturated Flow Problems. I: Analytical Solutions. Int. J. Geomech. 2017, 17, 04017013. [Google Scholar] [CrossRef]
- Cavalcante, A.L.B.; Camapum de Carvalho, J. Probabilidade de Ruptura Transiente de Taludes Não Saturados Em Bordas de Reservatórios; Federal University of Goiás: Goiânia, Brazil, 2017. [Google Scholar]
- Cavalcante, A.L.B.; Mascarenhas, P.V.S. Efficient Approach in Modeling the Shear Strength of Unsaturated Soil Using Soil Water Retention Curve. Acta Geotech. 2021, 16, 3177–3186. [Google Scholar] [CrossRef]
- Taha, M.R.; Hossain, M.K.; Mofiz, S.A. Effect of Suction on the Strength of Unsaturated Soils. In Proceedings of the Geo-Denver 2000, Denver, CO, USA, 5–8 August 2000; pp. 521–587. [Google Scholar]
- Nishimura, T.; Fredlund, D.G. Relationship between Shear Strength and Matric Suction in an Unsaturated Silty Soil. In Unsaturated Soils for Asia; CRC Press: Boca Raton, FL, USA, 2000; pp. 563–568. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils. Soil Dyn. Earthq. Eng. 1993, 12, 449–450. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1943. [Google Scholar]
- Buckingham, E. Studies on the Movement of Soil Moisture. Bur. Soils Bull. 1907, 38, 61. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media. Hydrol. Pap. 1964, 3, 27. [Google Scholar]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the Soil-Water Characteristic Curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Yeh, T.C.J.; Chen, L.; Wang, Z.; Duan, L.; An, K.; Gong, C. Finite Analytic Method Based on Mixed-Form Richards’ Equation for Simulating Water Flow in Vadose Zone. J. Hydrol. 2016, 537, 146–156. [Google Scholar] [CrossRef]
- Cavalcante, A.L.B.; Zornberg, J.G. Efficient Approach to Solving Transient Unsaturated Flow Problems. II: Numerical Solutions. Int. J. Geomech. 2017, 17, 04017014. [Google Scholar] [CrossRef]
- Costa, M.B.A.; Cavalcante, A.L.B. Novel Approach to Determine Soil-Water Retention Surface. Int. J. Geomech. 2020, 20, 04020054. [Google Scholar] [CrossRef]
- Costa, M.B.A.; Cavalcante, A.L.B. Bimodal Soil–Water Retention Curve and k -Function Model Using Linear Superposition. Int. J. Geomech. 2021, 21, 04021116. [Google Scholar] [CrossRef]
- Bordoloi, S.; Ng, C.W.W. The Effects of Vegetation Traits and Their Stability Functions in Bio-Engineered Slopes: A Perspective Review. Eng. Geol. 2020, 275, 105742. [Google Scholar] [CrossRef]
- Chirico, G.B.; Borga, M.; Tarolli, P.; Rigon, R.; Preti, F. Role of Vegetation on Slope Stability under Transient Unsaturated Conditions. Procedia Environ. Sci. 2013, 19, 932–941. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a Changing Climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Silva, A.P.N. Probabilidade de Ruptura Transiente de Encostas Medida Durante Eventos Significativos de Precipitação. Master’s Dissertation, University of Brasília, Faculty of Technology, Department of Civil and Environmental Engineering, Brasília, Brazil, 2018. [Google Scholar]
- Terry, J.P.; Wotling, G. Rain-Shadow Hydrology: Influences on River Flows and Flood Magnitudes across the Central Massif Divide of La Grande Terre Island, New Caledonia. J. Hydrol. 2011, 404, 77–86. [Google Scholar] [CrossRef]
- Croney, D.; Coleman, J.D.; Black, W.P. Studies of the Movement and Distribution of Water in Soil in Relation to Highway Design and Performance. Highw. Res. Board Spec. Rep. 1958, 40, 226–252. [Google Scholar]
- Bishop, A.W. The Principle of Effective Stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The Shear Strength of Unsaturated Soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Vanapalli, S.K. Shear Strength of Unsaturated Soils and Its Applications in Geotechnical Engineering Practice. In Keynote Address, Proceedings of the 4th Asia-Pacific Conference Unsaturated Soils, Newcastle, Australia, 23–25 November 2009; pp. 579–598.
- Lu, N.; Godt, J.W.; Wu, D.T. A Closed-Form Equation for Effective Stress in Unsaturated Soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Travis, Q.B.; Houston, S.L.; Marinho, F.M.; Schmeeckle, M. Unsaturated Infinite Slope Stability Considering Surface Flux Conditions. J. Geotech. Geoenviron. Eng. 2010, 136, 963–974. [Google Scholar] [CrossRef]
- Gitirana, G.D.F.N., Jr. Weather-Related Geo-Hazard Assessment Model for Railway Embankment Stability. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Azevedo, G.F. Sistema de Análise Quantitativa de Risco Por Escorregamentos Rasos Deflagrados por Chuvas em Regiões Tropicais. Ph.D. Thesis, University of Brasília, Faculty of Technology, Department of Civil and Environmental Engineering, Brasília, Brazil, 2015. [Google Scholar]
- Silva Júnior, A.C. Abordagem Rítmica Probabilística Aplicada em Análises de Fluxo e Estabilidade de Taludes. Ph.D. Thesis, University of Brasília, Faculty of Technology, Department of Civil and Environmental Engineering, Brasília, Brazil, 2015. [Google Scholar]
- Lee, J.H.; Park, H.J. Assessment of Shallow Landslide Susceptibility Using the Transient Infiltration Flow Model and GIS-Based Probabilistic Approach. Landslides 2016, 13, 885–903. [Google Scholar] [CrossRef]
- Lemos, M.A.C.; Dias, A.D.; Cavalcante, A.L.B. Deterministic and Probabilistic Approach in Slope Stability of a Tropical Soil. Int. J. Geol. Earth Sci. 2020, 6, 9–14. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y. Probabilistic Simulation of Entire Process of Rainfall-Induced Landslides Using Random Finite Element and Material Point Methods with Hydro-Mechanical Coupling. Comput. Geotech. 2021, 132, 103989. [Google Scholar] [CrossRef]
- Albuquerque, E.A.C.; de Faria Borges, L.P.; Cavalcante, A.L.B.; Machado, S.L. Prediction of Soil Water Retention Curve Based on Physical Characterization Parameters Using Machine Learning. Soils Rocks 2022, 45, 1–13. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Hong, L.; Han, L.; Wang, L. Comprehensive Review of Machine Learning in Geotechnical Reliability Analysis: Algorithms, Applications and Further Challenges. Appl. Soft Comput. 2023, 136, 110066. [Google Scholar] [CrossRef]
- Aminpour, M.; Alaie, R.; Khosravi, S.; Kardani, N.; Moridpour, S.; Nazem, M. Slope Stability Machine Learning Predictions on Spatially Variable Random Fields with and without Factor of Safety Calculations. Comput. Geotech. 2023, 153, 105094. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Li, X. Adaptive Ensemble Learning of Radial Basis Functions for Efficient Geotechnical Reliability Analysis. Comput. Geotech. 2022, 146, 104753. [Google Scholar] [CrossRef]
- Karir, D.; Ray, A.; Kumar Bharati, A.; Chaturvedi, U.; Rai, R.; Khandelwal, M. Stability Prediction of a Natural and Man-Made Slope Using Various Machine Learning Algorithms. Transp. Geotech. 2022, 34, 100745. [Google Scholar] [CrossRef]
- Wong, F.S. First-Order, Second-Moment Methods. Comput. Struct. 1985, 20, 779–791. [Google Scholar] [CrossRef]
- Ering, P.; Babu, G.S. Probabilistic Back Analysis of Rainfall Induced Landslide—A Case Study of Malin Landslide, India. Eng. Geol. 2016, 208, 154–164. [Google Scholar] [CrossRef]
- Marin, R.J.; Velásquez, M.F.; Sánchez, O. Applicability and Performance of Deterministic and Probabilistic Physically Based Landslide Modeling in a Data-Scarce Environment of the Colombian Andes. J. S. Am. Earth Sci. 2021, 108, 103175. [Google Scholar] [CrossRef]
- Cooke, R.A.; Mostaghimi, S.; Woeste, F. Effect of Hydraulic Conductivity Probability Distribution Function on Simulated Solute Leaching. Water Environ. Res. 1995, 67, 159–168. [Google Scholar] [CrossRef]
- Mesquita, M.D.G.B.D.F.; Moraes, S.O.; Corrente, J.E. More Adequate Probability Distributions to Represent the Saturated Soil Hydraulic Conductivity. Sci. Agric. 2002, 59, 789–793. [Google Scholar] [CrossRef]
- Mesquita, M.D.G.B.D.F. Caracterização Estatística da Condutividade Hidráulica Saturada do Solo. Ph.D. Thesis, School of Agriculture Luíz de Queiroz, São Paulo, Brazil, 2001. [Google Scholar]
- Bong, T.; Son, Y. Impact of Probability Distribution of Hydraulic Conductivity on Groundwater Contaminant Transport. KSCE J. Civ. Eng. 2019, 23, 1963–1973. [Google Scholar] [CrossRef]
- Malkawi, A.I.H.; Hassan, W.F.; Abdulla, F.A. Uncertainty and Reliability Analysis Applied to Slope Stability. Struct. Saf. 2000, 22, 161–187. [Google Scholar] [CrossRef]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A Distributed Conceptual and Physically Based Model to Forecast the Temporal and Spatial Occurrence of Shallow Landslides Triggered by Rainfall in Tropical and Mountainous Basins. Landslides 2015, 13, 497–517. [Google Scholar] [CrossRef]
- Campos, T.M.P.; Motta, M.F.B. Resistência Ao Cisalhamento de Solos Não Saturados; Brazilian Association of Soil Mechanics and Geotechnical Engineering: São Paulo, Brazil, 2015; ISBN 9788578110796. [Google Scholar]
- USACE. Risk-Based Analysis in Geotechnical Engineering for Support of Planning Studies; USACE: Washington, DC, USA, 1999.




| Parameter Type | Parameter | Mean | CoV |
|---|---|---|---|
| Deterministic Parameters | β (°) | 62 | – |
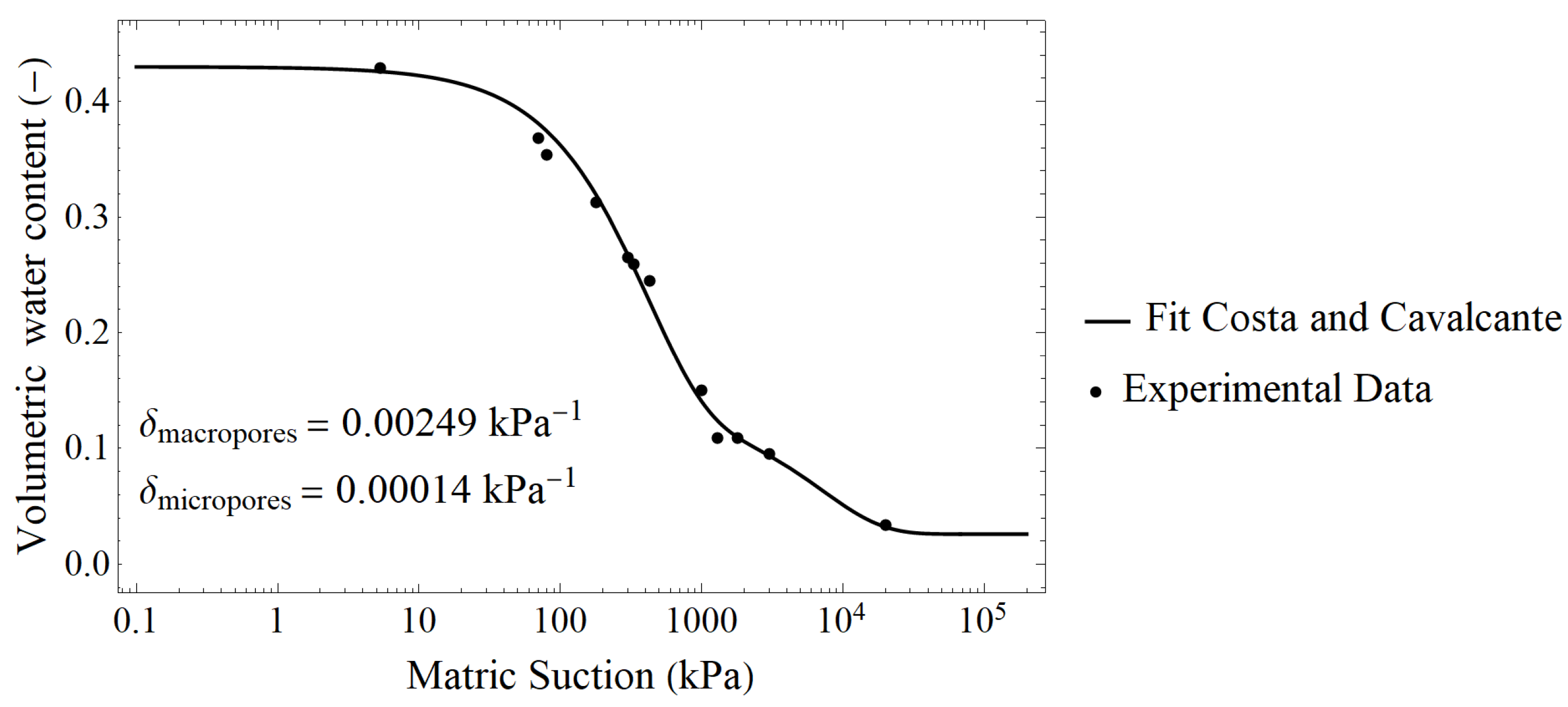
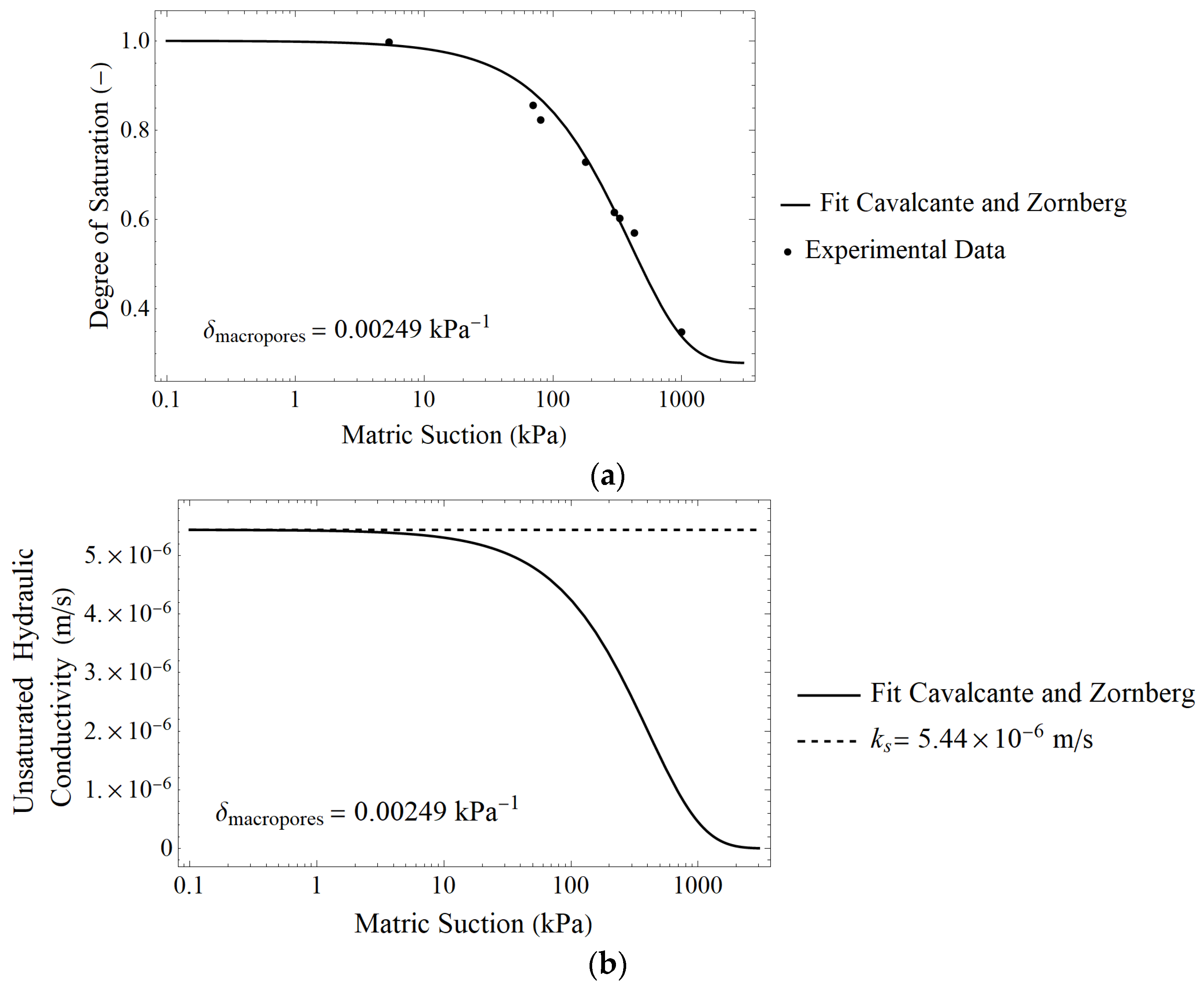
| δ (kPa−1) | 0.00249 | – | |
| vi (ms−1) | 5.73 × 10−6 | – | |
| c (-) | 0.375 | ||
| Probabilistic Parameters | ϕ′ (°) | 24 | 9 |
| C’ (kPa) | 5 | 30 | |
| γd (kNm−3) | 18 | 5 | |
| Log [ks] (ms−1) | Log [5.4 × 10−6] | 80 | |
| θr (m3m−3) | 0.026 | 10 | |
| θs (m3m−3) | 0.43 | 13 | |
| θi (m3m−3) | 0.05 | 10 |
| Expected Performance Level | P (FS ≤ FSc) |
|---|---|
| High | 3.0 × 10−7 |
| Good | 3.0 × 10−5 |
| Above average | 3.0 × 10−3 |
| Below average | 6.0 × 10−3 |
| Poor | 2.5 × 10−2 |
| Unsatisfactory | 7.0 × 10−2 |
| Dangerous | 1.6 × 10−1 |
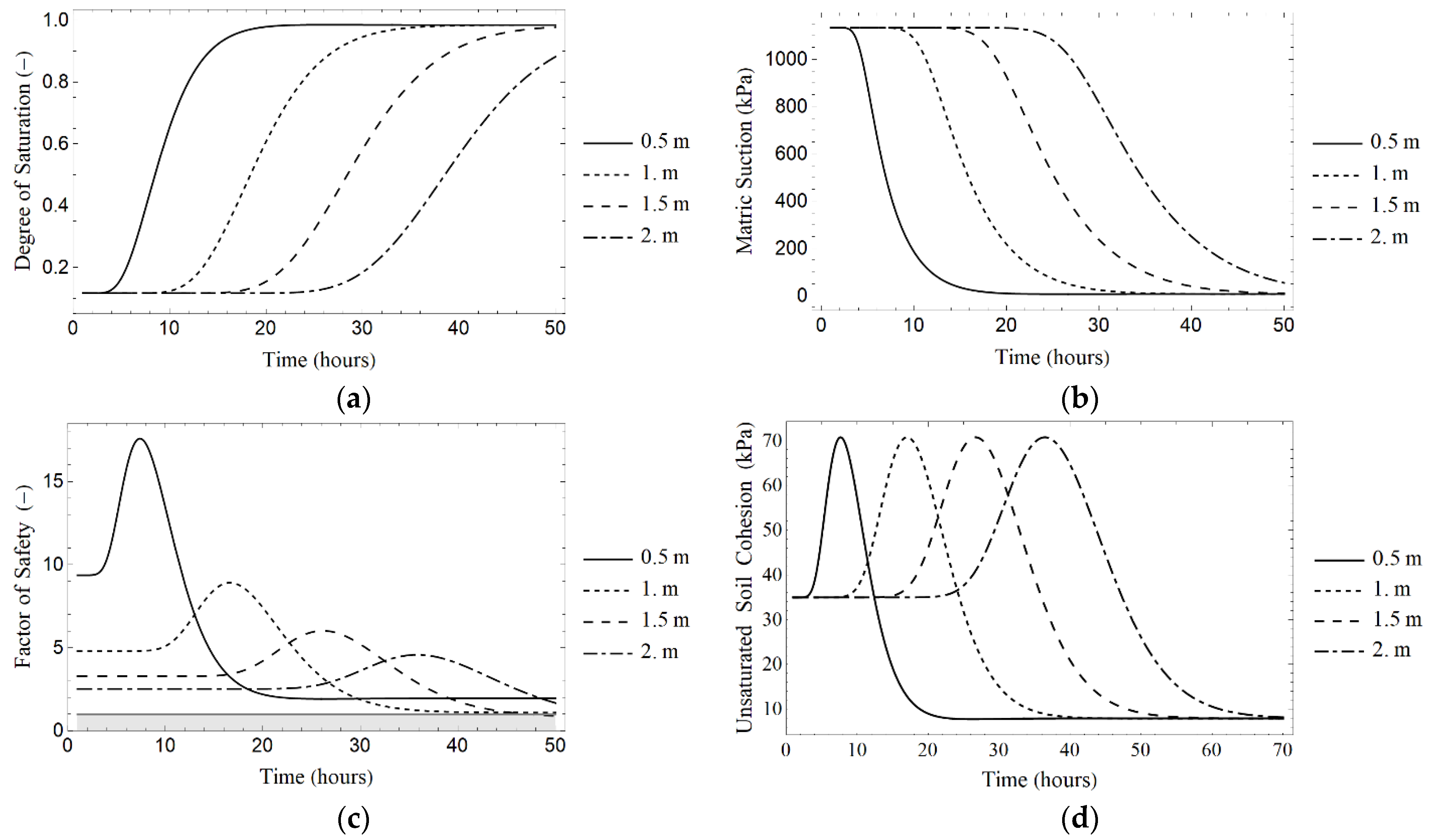
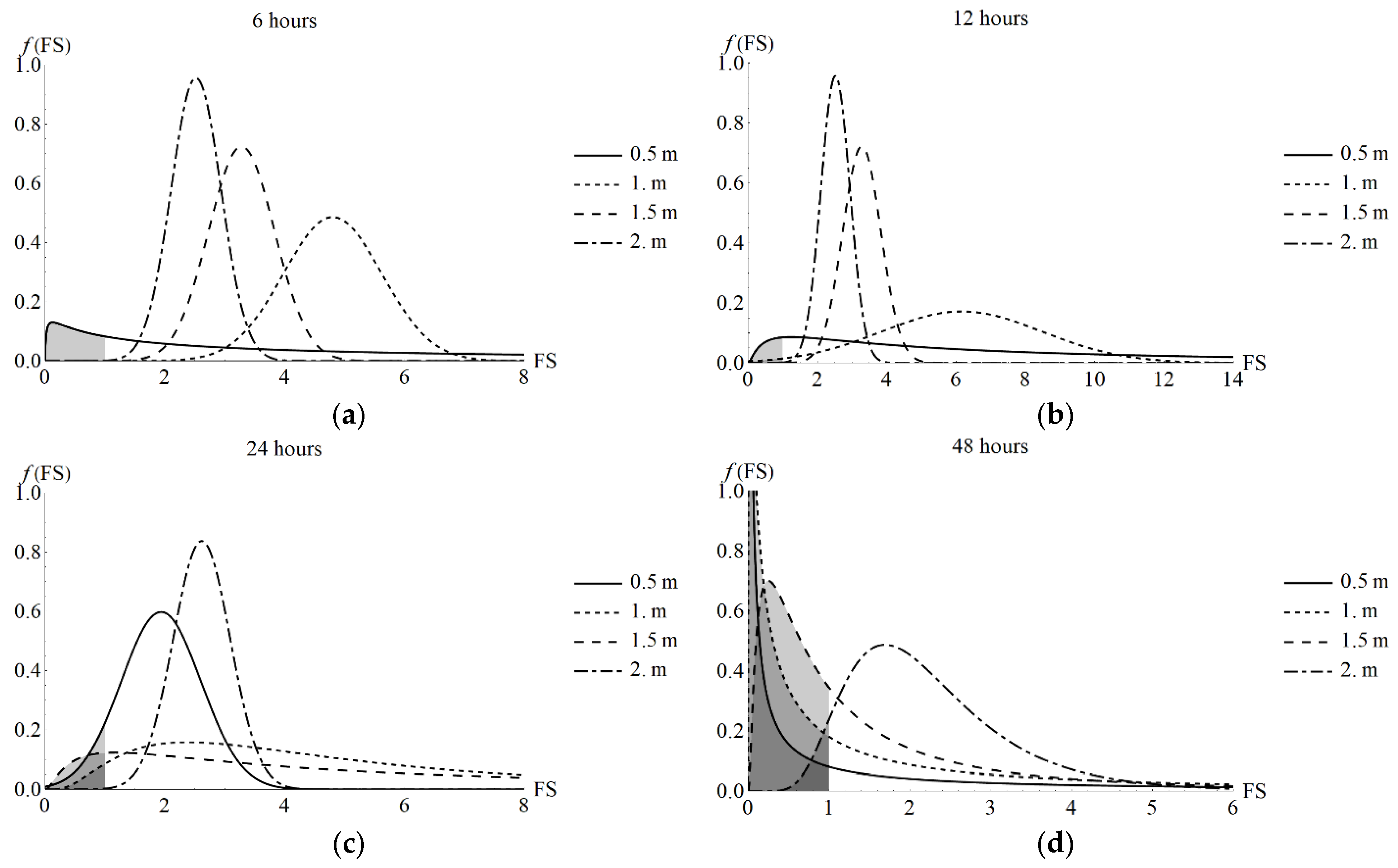
| Analysis Time (h) | z (m) | θ (m3m−3) | Sr (–) | Ψ (kPa) | FS (–) | σ [FS] (–) | p (FS ≤ 1) (%) |
|---|---|---|---|---|---|---|---|
| 6 | 0.5 | 0.10 | 0.24 | −672.56 | 15.74 | 9.03 | 1.06 × 100 |
| 1.0 | 0.05 | 0.12 | −1133.86 | 4.80 | 0.82 | 1.85 × 10−4 | |
| 1.5 | 0.05 | 0.12 | −1133.86 | 3.28 | 0.55 | 1.81 × 10−3 | |
| 2.0 | 0.05 | 0.12 | −1133.86 | 2.52 | 0.42 | 1.36 × 10−2 | |
| 12 | 0.5 | 0.35 | 0.80 | −94.66 | 8.85 | 4.06 | 1.20 × 100 |
| 1.0 | 0.07 | 0.15 | −930.23 | 6.16 | 2.32 | 9.12 × 10−1 | |
| 1.5 | 0.05 | 0.12 | −1133.74 | 3.28 | 0.55 | 1.82 × 10−3 | |
| 2.0 | 0.05 | 0.12 | −1133.88 | 2.52 | 0.42 | 1.36 × 10−2 | |
| 24 | 0.5 | 0.42 | 0.98 | −6.45 | 1.93 | 0.67 | 7.89 × 100 |
| 1.0 | 0.35 | 0.81 | −90.08 | 4.39 | 2.19 | 3.81 × 100 | |
| 1.5 | 0.12 | 0.28 | −590.39 | 5.72 | 3.52 | 3.79 × 100 | |
| 2.0 | 0.05 | 0.12 | −1103.43 | 2.61 | 0.48 | 3.59 × 10−2 | |
| 48 | 0.5 | 0.42 | 0.98 | −6.70 | 1.96 | 134.90 | 2.96 × 10−1 |
| 1.0 | 0.42 | 0.98 | −6.70 | 1.10 | 9.04 | 4.40 × 100 | |
| 1.5 | 0.42 | 0.97 | −11.56 | 0.96 | 3.18 | 12.35 × 100 | |
| 2.0 | 0.36 | 0.84 | −74.46 | 2.05 | 1.55 | 15.58 × 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, K.R.C.B.d.; Dantas, A.P.d.N.; Cavalcante, A.L.B.; Assis, A.P.d. Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event. Sustainability 2023, 15, 15260. https://doi.org/10.3390/su152115260
Costa KRCBd, Dantas APdN, Cavalcante ALB, Assis APd. Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event. Sustainability. 2023; 15(21):15260. https://doi.org/10.3390/su152115260
Chicago/Turabian StyleCosta, Katherin Rocio Cano Bezerra da, Ana Paola do Nascimento Dantas, André Luís Brasil Cavalcante, and André Pacheco de Assis. 2023. "Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event" Sustainability 15, no. 21: 15260. https://doi.org/10.3390/su152115260
APA StyleCosta, K. R. C. B. d., Dantas, A. P. d. N., Cavalcante, A. L. B., & Assis, A. P. d. (2023). Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event. Sustainability, 15(21), 15260. https://doi.org/10.3390/su152115260







