Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability
Abstract
:1. Introduction
2. Literature Review
2.1. System Dynamics Modeling and Its Applications in Supply Chain Management
2.2. System Dynamics Modeling for Sustainable Supply Chain Management
2.3. Sustainable Supply Chain Management in Apparel Manufacturing
2.4. System Dynamics Modeling for Supply Chain Management in Apparel Manufacturing
2.5. Identified Research Gap and the Study’s Proposed Contribution
3. Hypothesis and Research Questions
4. Materials and Methods
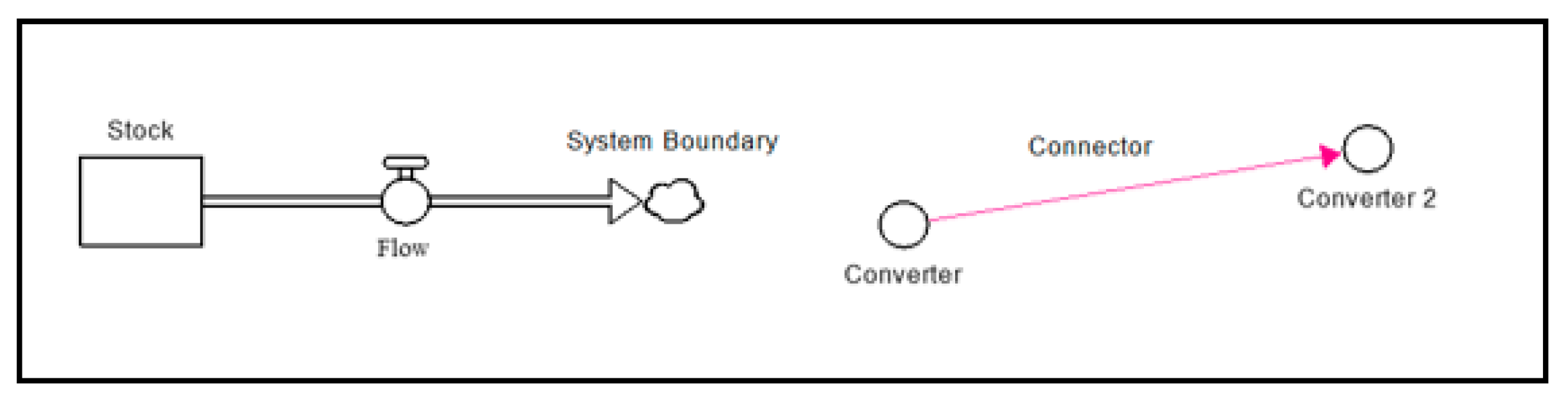
4.1. SDM Software
- Define the objective of the product’s supply chain.
- Establish the project scope by identifying its boundaries, inputs, and outputs.
- Define the functional unit as a specific number of goods produced per day.
- Create the STELLA® model using all four building blocks.
- Add equations with conditional statements to the flow, such as “if_then_else”.
- Create and add initial conditions for each stock and converter.
- Run the model and monitor the stocks and flows for the inputs given (i.e., a given scenario).
- Change the inputs and rerun the model for different scenarios until the material flows and waste are minimized.
4.2. Elements of SDM
- Appropriate units of measurement must be specified for each model variable to prevent formulation errors.
- Model equations must have self-consistent units. In other words, the left and right sides of each equation should reduce to the same units.
- All stocks within a flow chain must have the same units of measurement.
- Stocks must be defined with an initial value at time equals zero.
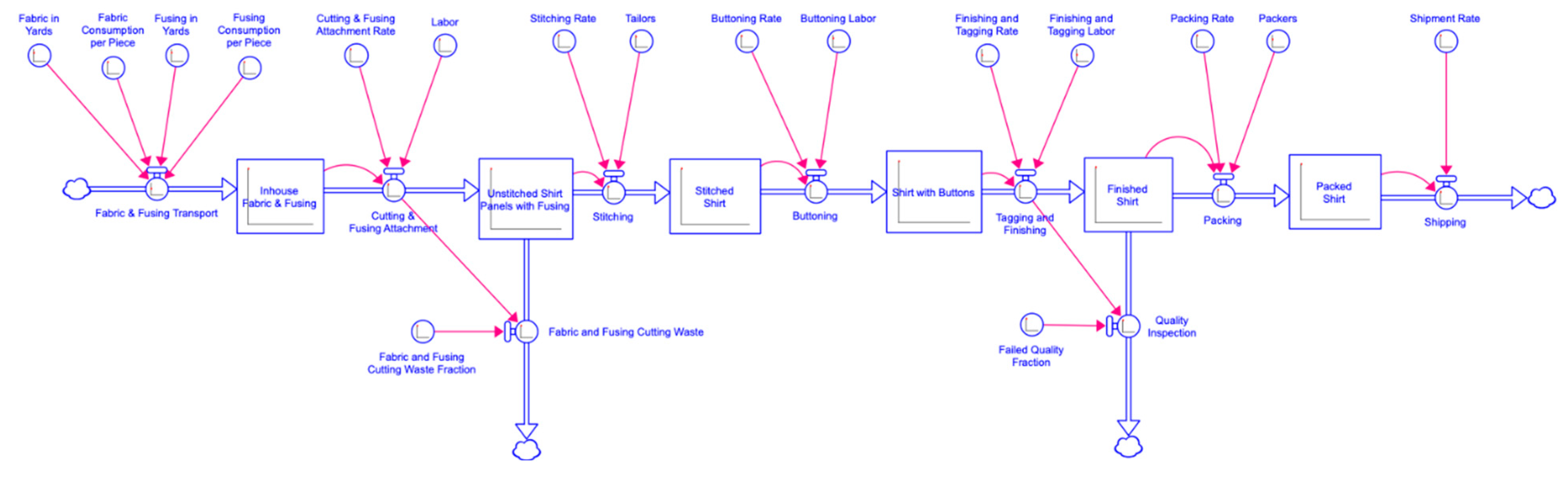
4.3. Supply Chain Model of the Manufacturing Process for Shirts
4.4. Development of SDM Converters, Flow Equations, and Stock Equations for This Model
4.4.1. SDM Converters in Figure 3
4.4.2. SDM Flow Equations in Figure 3
4.4.3. SDM Stock Equation in Figure 3
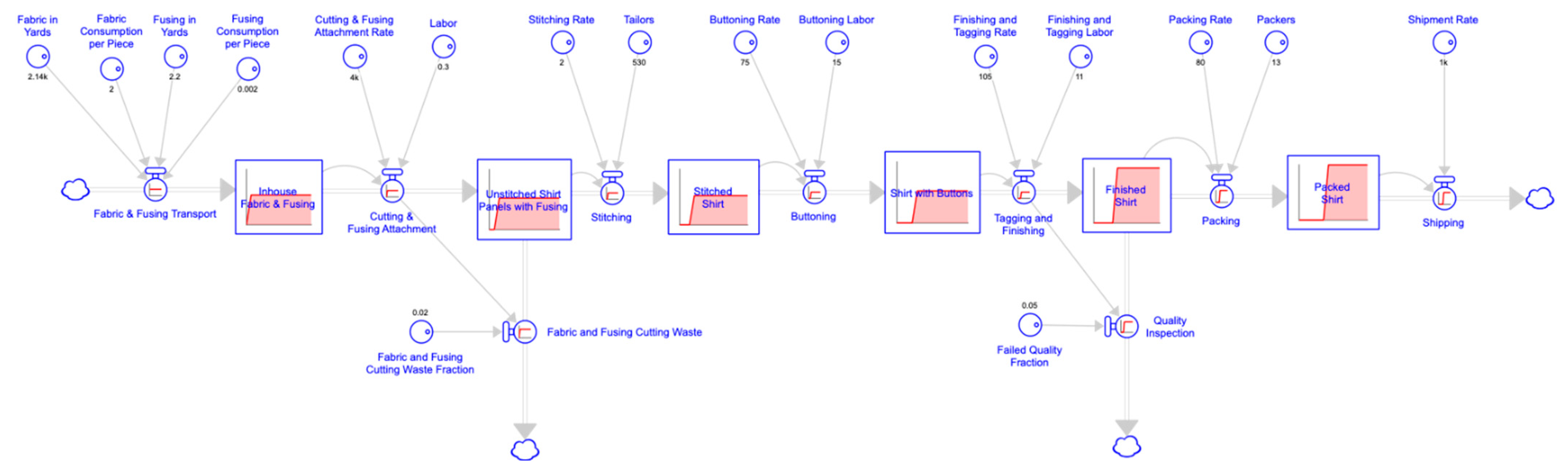
5. Simulation Results
5.1. Initial Simulation
5.2. Optimized Simulation
- Starting with the final stock in the supply chain, determine if the stock is increasing or decreasing with time.
- Adjust the converters that impact the input flow to that stock and re-run the simulation.
- Repeat step 2 until the stock value remains unchanged with time.
- Move to the next upstream stock in the supply chain and repeat steps 1 through to 3 for that stock.
- Repeat this process until the initial flow at the beginning of the supply chain model is reached.
5.3. Analysis of Optimized Supply Chain for Sustainability
6. Discussion on Simulation Results and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Serial Nos. | Name of the Flow | Equations | Unit |
|---|---|---|---|
| 1. | Fabric and Fusing Transport | (Fabric_in_Yards + Fusing_in_Yards)/(Fabric_Consumption_per_Piece+Fusing_Consumption_per_Piece) | Pieces/day |
| 2. | Cutting and Fusing Attachment | IF (Inhouse_Fabric_&_Fusing/DT) < (Cutting_&_Fusing_Attachment_Rate*Labor) THEN (Inhouse_Fabric_&_Fusing/DT) ELSE (Cutting_&_Fusing_Attachment_Rate*Labor) | Pieces/day |
| 3. | Fabric and Fusing Cutting Waste Fraction | (Cutting_&_Fusing_Attachment*Fabric_and_Fusing_Cutting_Waste_Fraction) | Pieces/day |
| 4. | Stitching | IF (Unstitched_Shirt_Panels_with_Fusing/DT) < (Stitching_Rate*Tailors) THEN (Unstitched_Shirt_Panels_with_Fusing/DT) ELSE (Stitching_Rate*Tailors) | Pieces/day |
| 5. | Buttoning | IF (Stitched_Shirt/DT) < (Buttoning_Rate*Buttoning_Labor) THEN (Stitched_Shirt/DT) ELSE (Buttoning_Rate*Buttoning_Labor) | Pieces/day |
| 6. | Tagging and Finishing | IF (Shirt_with_Buttons/DT) < (Finishing_and_Tagging_Rate*Finishing_and_Tagging_Labor) THEN (Shirt_with_Buttons/DT) ELSE (Finishing_and_Tagging_Rate*Finishing_and_Tagging_Labor) | Pieces/day |
| 7. | Quality Inspection | (Failed_Quality_Fraction*Tagging_and_Finishing) | Pieces/day |
| 8. | Packing | IF (Finished_Shirt/DT) < (Packing_Rate*Packers) THEN Finished_Shirt/DT ELSE (Packing_Rate*Packers) | Pieces/day |
| 9. | Shipping | IF (Packed_Shirt/DT) < (Shipment_Rate) THEN (Packed_Shirt/DT) ELSE (Shipment_Rate) | Pieces/day |
| Serial Nos. | Stock | Stock’s Variable Name | Equation of Stock | Unit |
|---|---|---|---|---|
| 1. | In-house Fabric and Fusing | In-house_Fabric_&_Fusing | Inhouse Fabric & Fusing (t) = Inhouse Fabric & Fusing (t − dt) + Fabric and Fus ing Transport (t) − Cutting and Fusing Attachment (t) | Pieces/day |
| 2. | Unstitched Shirt Panels with Fusing | Unstitched_Shirt_Panels_with_Fusing | Unstitched Shirt Panels with Fusing (t) = Unstitched Shirt Panels with Fusing (t − dt) + Cutting and Fusing Attachment (t) − Stitching (t) − Fabric and Cutting Fus- ing Waste (t) | Pieces/day |
| 3. | Stitched Shirt | Stitched_Shirt | Stitched Shirt (t) = Stitched Shirt (t − dt) + Stitching (t) − Buttoning (t) | Pieces/day |
| 4. | Shirt with Buttons | Shirt_with_Buttons | Shirt with Buttons (t) = Shirt with But tons (t − dt) + Buttoning (t) − Tagging and Finishing (t) | Pieces/day |
| 5. | Finished Shirt | Finished_Shirt | Finished Shirt (t) = Finished Shirt (t-dt) + Tagging and Finishing (t) − Packing (t) − Quality Inspection (t) | Pieces/day |
| 6. | Packed Shirt | Packed_Shirt | Packed Shirt (t) = Packed Shirt (dt − t) + Packing (t) − Shipping (t) | Pieces/day |
| Serial Nos. | Converter | Converter’s Variable Name | Unit |
|---|---|---|---|
| 1. | Fabric in Yards | Fabric_in_Yards | Yards/day |
| 2. | Fabric Consumption per Piece | Fabric_Consumption_per_Piece | Yards/pieces |
| 3. | Fusing in Yards | Fusing_in_Yards | Yards/day |
| 4. | Fusing Consumption per Piece | Fusing_Consumption_per_Piece | Yards/pieces |
| 5. | Cutting and Fusing Attachment Rate | Cutting_&_Fusing_Attachment_Rate | Pieces/day |
| 6. | Labor | Labor | Unitless |
| 7. | Fabric and Fusing Cutting Waste Fraction | Fabric_and_Fusing_Cutting_Waste Fraction | Unitless |
| 8. | Stitching Rate | Stitching_Rate | Pieces/day |
| 9. | Tailors | Tailors | Unitless |
| 10. | Buttoning Rate | Buttoning_Rate | Pieces/day |
| 11. | Buttoning Labor | Buttoning_Labor | Unitless |
| 12. | Finishing and Tagging Rate | Finishing_and_Tagging_Rate | Pieces/day |
| 13. | Finishing and Tagging Labor | Finishing_and_Tagging_Labor | Unitless |
| 14. | Failed Quality Fraction | Failed_Quality_Fraction | Unitless |
| 15. | Packing Rate | Packing_Rate | Pieces/day |
| 16. | Packers | Packers | Unitless |
| 17. | Shipment Rate | Shipment_Rate | Pieces/day |
Appendix B
| Serial Nos. | Fabric and Fusing Transport | Cutting and Fusing Attachment | Fabric and Fusing Cutting Waste | Stitching | Buttoning | Tagging and Finishing | Quality Inspection | Packing | Shipping |
|---|---|---|---|---|---|---|---|---|---|
| 1. | 1.25 K | 1 | 0.02 | 1 | 1 | 1 | 0.05 | 1 | 1 |
| 2. | 1.25 K | 1.2 K | 24 | 0.98 | 1 | 1 | 0.05 | 0.95 | 1 |
| 3. | 1.25 K | 1.2 K | 24 | 1.18 K | 0.98 | 1 | 0.05 | 0.95 | 0.95 |
| 4. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 0.98 | 0.049 | 0.95 | 0.95 |
| 5. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 0.931 | 0.95 |
| 6. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 0.931 |
| 7. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 8. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 9. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 10. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 11. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 12. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 13. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| 14. | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| Final | 1.25 K | 1.2 K | 24 | 1.18 K | 1.13 K | 1.13 K | 56.3 | 800 | 800 |
| Serial Nos. | In-House Fabric and Fusing | Unstitched Shirt Panels with Fusing | Stitched Shirt | Shirt with Buttons | Finished Shirt | Packed Shirt |
|---|---|---|---|---|---|---|
| 1. | 1 | 1 | 1 | 1 | 1 | 1 |
| 2. | 1.25 K | 0.98 | 1 | 1 | 0.95 | 1 |
| 3. | 1.3 K | 1.18 K | 0.98 | 1 | 0.95 | 0.95 |
| 4. | 1.35 K | 1.18 K | 1.18 K | 0.98 | 0.95 | 0.95 |
| 5. | 1.4 K | 1.18 K | 1.23 K | 1.13 K | 0.931 | 0.95 |
| 6. | 1.45 K | 1.18 K | 1.28 K | 1.13 K | 1.07 K | 0.931 |
| 7. | 1.5 K | 1.18 K | 1.33 K | 1.13 K | 1.34 K | 800 |
| 8. | 1.55 K | 1.18 K | 1.38 K | 1.13 K | 1.61 K | 800 |
| 9. | 1.6 K | 1.18 K | 1.43 K | 1.13 K | 1.88 K | 800 |
| 10. | 1.65 K | 1.18 K | 1.48 K | 1.13 K | 2.14 K | 800 |
| 11. | 1.7 K | 1.18 K | 1.53 K | 1.13 K | 2.41 K | 800 |
| 12. | 1.75 K | 1.18 K | 1.58 K | 1.13 K | 2.68 K | 800 |
| 13. | 1.8 K | 1.18 K | 1.64 K | 1.13 K | 2.95 K | 800 |
| 14. | 1.85 K | 1.18 K | 1.69 K | 1.13 K | 3.22 K | 800 |
| Final | 1.9 K | 1.18 K | 1.74 K | 1.13 K | 3.49 K | 800 |
Appendix C
| Serial Nos. | Fabric and Fusing Transport | Cutting and Fusing Attachment | Fabric and Fusing Cutting Waste Fraction | Stitching | Buttoning | Tagging and Finishing | Quality Inspection | Packing | Shipping |
|---|---|---|---|---|---|---|---|---|---|
| 1. | 1072 | 1072 | 0.02 | 1 | 1 | 1 | 0.05 | 1 | 1 |
| 2. | 1072 | 1072 | 21 | 0.98 | 1 | 1 | 0.05 | 0.95 | 1 |
| 3. | 1072 | 1072 | 21 | 1051 | 0.98 | 1 | 0.05 | 0.95 | 0.95 |
| 4. | 1072 | 1072 | 21 | 1051 | 1051 | 0.98 | 0.049 | 0.95 | 0.95 |
| 5. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 0.0931 | 0.95 |
| 6. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 0.931 |
| 7. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 8. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 9. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 10. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 11. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 12. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 13. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| 14. | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| Final | 1072 | 1072 | 21 | 1051 | 1051 | 1051 | 53 | 998 | 998 |
| Serial Nos. | In-House Fabric and Fusing | Unstitched Shirt Panels with Fusing | Stitched Shirt | Shirt with Buttons | Finished Shirt | Packed Shirt |
|---|---|---|---|---|---|---|
| 1. | 1 | 1 | 1 | 1 | 1 | 1 |
| 2. | 1072 | 0.98 | 1 | 1 | 0.95 | 1 |
| 3. | 1072 | 1051 | 0.98 | 1 | 0.95 | 0.95 |
| 4. | 1072 | 1051 | 1051 | 0.98 | 0.95 | 0.95 |
| 5. | 1072 | 1051 | 1051 | 1051 | 998 | 0.95 |
| 6. | 1072 | 1051 | 1051 | 1051 | 998 | 0.931 |
| 7. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 8. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 9. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 10. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 11. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 12. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 13. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| 14. | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
| Final | 1072 | 1051 | 1051 | 1051 | 998 | 998 |
- Fabric and Fusing Transport (flow): Transporting the fabric and fusing into the factory is the first step in our simulated model for manufacturing shirts. In our simulated model, this flow is called Fabric and Fusing Transport. It refers to the rate that fabric and fusing are transported to the factory. To calculate this flow, four converters were used: Fabric in Yards, Fabric Consumption per Piece, Fusing in Yards, and Fusing Consumption per Piece. Fabric in Yards refers to the total fabric yardage required to manufacture up to 1000 shirts per day. Its value is 2144 yards/day. Fabric Consumption per Piece refers to the amount of fabric consumed to manufacture one shirt. Its value is two yards/piece. Fusing in Yards is the total fusing yardage required to manufacture up to 1000 shirts per day. Its value is 2.2 yards/day. Fusing Consumption per Piece is the amount of fusing consumed to manufacture one shirt. Its value is 0.002 yards/piece. The equation used for this flow is (Fabric_in_Yards+Fusing_in_Yards)/(Fabric_Consumption_per_Piece+Fusing_Consumption_per_Piece). (2144 + 2.2)/(2 + 0.002). The value of Fabric and Fusing Transport flow at its equilibrium is 1072 pieces/day.
- In-house Fabric and Fusing (stock): After transporting the fabric and fusing into the factory, the next step is inventory of the in-house fabric and fusing. In the model, this inventory is called In-house Fabric and Fusing. To calculate this stock, one stock, one inflow, and one outflow were used: In-house Fabric and Fusing, Fabric and Fusing Transport, and Cutting and Fusing Attachment, respectively. The equation for this stock is In-house Fabric and Fusing (t) = Inhouse Fabric and Fusing (t-dt) + Fabric and Fusing Transport (t) − Cutting and Fusing Attachment (t). In-house Fabric and Fusing = 1072 + 1072 − 1072. The value of Inhouse Fabric and Fusing stock at its equilibrium is 1072 pieces.
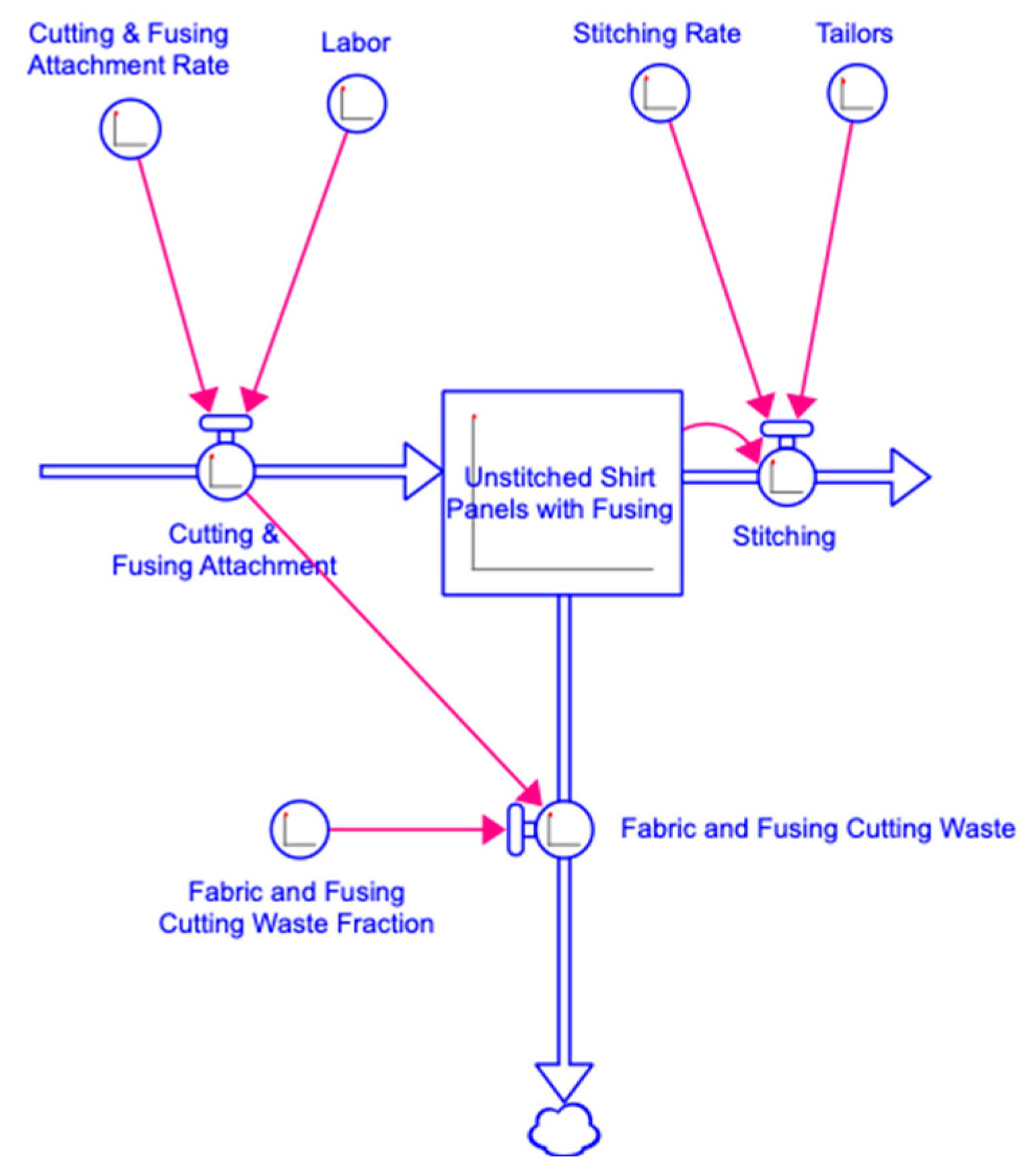
- Cutting and Fusing Attachment (flow): Once the fabric and fusing are in-house, the labor cuts the fabric into shirt panels using a cutting machine. Once the shirt panels are ready, fusing is cut and attached to the shirt. In the model, this process is called Cutting and Fusing Attachment. To calculate this flow, two converters and one previous stock were used, Cutting and Fusing Attachment Rate and Labor and Inhouse Fabric and Fusing, respectively. Cutting and Fusing Attachment Rate refers to the number of shirt panels cut and fused each day. Its value is 4000 pieces/day. Labor equals the amount of labor (in full-time equivalent employees) needed to cut and fuse up to 1000 shirt panels, valued at 0.3. The equation for this flow is IF (Inhouse_Fabric_&_Fusing/DT) < (Cutting_&_Fusing_Attachment_Rate*Labor) THEN (Inhouse_Fabric_&_Fusing/DT) ELSE (Cutting_&_Fusing_Attachment_Rate*Labor). IF (1072/1) < (4000*0.3) THEN (1072/1) ELSE (4000*3). IF (1072) < (1200) THEN (1072) ELSE (1200). The value of Cutting and Fusing Attachment flow at its equilibrium is 1072 pieces/day.
- Fabric and Cutting Fusing Waste (Flow): The process of cutting fabric into shirt panels produces fabric waste. The process of fusing cutting also produces fusing waste. To calculate Unstitched Shirt Panels with Fusing, the waste that occurred during the fabric and fusing attachment process must be considered. In the model, this process is called Fabric and Fusing Cutting Waste. To calculate this flow, one converter and a previous flow were used, Fabric and Fusing Cutting Waste Fraction and Cutting and Fusing Attachment, respectively. Fabric and Fusing Cutting Waste Fraction is the fraction of fabric and fusing waste generated from cutting, valued at 0.02. The equation of this flow is Cutting_&_Fusing_Attachment * Fabric_&_Fusing_Cutting_Waste_Fraction. (1072*0.02). The value of Fabric and Cutting Fusing Waste flow at its equilibrium is 21 pieces/day.
- Unstitched Shirt Panels with Fusing (stock): Unstitched shirt panels with fusing are now in inventory following the cutting and fusing attachment process and fabric and fusing cutting waste process. In the model, this stock is called Unstitched Shirt Panels with Fusing. To calculate this stock, one stock, one inflow, and two outflows were used. The equation for this stock is Unstitched Shirt Panels with Fusing (t) = Unstitched Shirt Panels with Fusing (t-dt) + Cutting & Fusing Attachment (t) − Stitching (t) − Fabric & Cutting Fusing Waste (t). 1051 + 1072 − 1051 − 21. The value of Unstitched Shirt Panels with Fusing stock at its equilibrium is 1051 pieces.
- Stitching (flow): Following cutting and fusing, shirt panels are sewn by in-house tailors. In the model, this process is called Stitching, which refers to the rate that shirts are sewn. This flow is calculated using two converters, Stitching Rate and Tailors, and one previous stock, Unstitched Shirt Panels with Fusing. The Stitching Rate is the number of shirts sewn by a tailor using a sewing machine per day, valued at 2 pieces/day. Tailors refer to the number of tailors required to sew shirts per day, valued at 530. Unstitched Shirt Panels with Fusing is the quantity of unstitched, cut shirt panels attached with fusing, valued at 1051 pieces. The equation of this flow is IF (Unstitched_Shirt_Panels_with_Fusing/DT) < (Stitching_Rate*Tailors) THEN (Unstitched_Shirt_Panels_with_Fusing/DT) ELSE (Stitching_Rate*Tailors). IF (1051/1) < (2*530) THEN (1051/1) ELSE (2*530) = IF (1051) < (1060) THEN (1051) ELSE (1060). The value of Stitching flow at its equilibrium is 1051 pieces/day.
- Stitched Shirt (stock): Once the shirts are stitched, an inventory of stitched shirts is the next step. In the model, this stock is called Stitched Shirt. It is a stock that refers to the number of shirts stitched by tailors. To calculate this stock, one stock, one inflow, and one outflow were used: Stitched Shirt, Stitching, and Buttoning, respectively. The equation for this stock is Stitched Shirt (t) = Stitched Shirt (t − dt) + Stitching (t) − Buttoning (t). 1051 + 1051 − 1051. The value of Stitched Shirt stock at its equilibrium is 1051 pieces.
- Buttoning (flow): The labor attaches buttons to shirts after they have been stitched. In the model, this process is called Buttoning, which refers to the rate at which shirts are buttoned. This flow is calculated using two converters, Buttoning Rate and Buttoning Labor, and one previous stock, Stitched Shirt. Buttoning Rate is the number of shirts buttoned per day by one laborer, valued at 75 pieces/day. Buttoning Labor is the amount of labor needed to attach buttons to shirts per day, valued at 15. The value of Stitched Shirt is 1051 pieces. The equation for this flow is IF (Stitched_Shirt/DT) < (Buttoning_Rate*Buttoning_Labor) THEN (Stitched_Shirt/DT) ELSE (Buttoning_Rate*Buttoning_Labor). IF (1051/1) < (75*15) THEN (1051/1) ELSE (75*15). IF (1051) < (1125) THEN (1051) ELSE (1125). The value of Buttoning flow at its equilibrium is 1051 pieces/day.
- Shirt with Buttons (stock): An inventory of buttoned shirts is created after the buttoning process. In the model, this stock is called Shirt with Buttons, which refers to the number of shirts with buttons attached. To calculate this stock, one stock, one inflow, and one outflow were used: Shirt with Buttons, Buttoning, and Tagging and Finishing, respectively. The equation for this stock is Shirt with Buttons (t) = Shirt with Buttons (t − dt) + Buttoning (t) − Tagging and Finishing (t). 1051 + 1051 − 1051. The value of Shirt with Buttons stock at its equilibrium is 1051 pieces.
- Tagging and Finishing (flow): Shirts are then tagged and finished by the laborers. In the model, this flow is called Tagging and Finishing, which refers to the rate that shirts are tagged and finished. This flow is calculated using two converters, Finishing and Tagging Rate and Labor, and one previous stock, Shirt with Buttons. Finishing and Tagging Rate is the number of shirts finished and tagged by one laborer per day. Brand tags are attached to the shirts as part of the tagging process. The finishing process includes uncut thread tails trimmed, stains removed, defective shirts altered and pressed, etc., valued at 105 pieces/day. Finishing and Tagging Labor is the amount of labor required to finish the shirts and add hand tags per day, valued at 11. The equation for this flow is IF (Shirt_with_Buttons/DT) < (Finishing_&_Tagging_Rate*Finishing_&_Tagging_Labor) THEN (Shirt_with_Buttons/DT) ELSE (Finishing_&_Tagging_Rate*Finishing_&_Tagging_Labor). IF (1051/1) < (105*11) THEN (1051/1) ELSE (105*11). IF (1051) < (1155) THEN (1051) ELSE (1151). The value of Tagging and Finishing flow at its equilibrium is 1051 pieces/day.
- Quality Inspection (flow): All tagged and finished shirts are put through a quality inspection process, wherein shirts that fail the quality test are rejected. In the model, this flow is called Quality Inspection. It refers to the rate at which shirts pass quality inspection. This flow is calculated using one converter, Failed Quality Fraction, and one flow, Tagging and Finishing. It describes the fraction of shirts rejected during inspection due to poor quality, valued at 0.05. The equation for this flow is Failed_Quality_Fraction * Tagging_and_Finishing. (0.05*1051). The value of Quality Inspection flow at its equilibrium is 53 pieces/day.
- Finished Shirt (stock): Finished shirts are in inventory after tagging, finishing, and quality inspection. In the model, this stock is called Finished Shirt. It refers to the number of shirts finished after they are tagged, finished, and passed through a quality inspection process. To calculate this stock, one stock, one inflow, and two outflows are used: Finished Shirt, Tagging and Finishing, Packing, and Quality Inspection, respectively. The equation for this stock is Finished Shirt (t) = Finished Shirt (t-dt) + Tagging and Finishing (t) − Packing (t) − Quality Inspection (t). 998 + 1051 − 998 − 53. The value of Finished Shirt stock at its equilibrium is 998 pieces.
- Packing (flow): Shirts are packed after they have been finished. In the model, this flow is called Packing. It refers to the rate that shirts are packed for shipping. This flow is calculated using two converters, Packing Rate and Packers, and one stock, Finished Shirt. Packing Rate indicates the number of shirts packed for shipping by one laborer per day, valued at 80 pieces/day. Packers indicates the amount of labor required to pack shirts per day, valued at 13. The equation for this flow is IF (Finished_Shirt/DT) < (Packing_Rate*Packers) THEN (Finished_Shirt/DT) ELSE (Packing_Rate*Packers). IF (998/1) < (80*13) THEN (998/1) ELSE (80*13). (998) < (1040) THEN (998) ELSE (1040). The value of Packing flow at its equilibrium is 998 pieces/day.
- Packed Shirt (stock): The next step is an inventory of packed shirts. In the model, this stock is called Packed Shirt. To calculate this stock, one stock, one inflow, and two outflows were used: Finished Shirt, Tagging and Finishing, Packing, and Quality Inspection, respectively. The equation for this stock is Packed Shirt (t) = Packed Shirt (dt − t) + Packing (t) − Shipping (t). 998 + 998 − 998. The value of Packed Shirt stock at its equilibrium is 998 pieces.
- Shipping (flow): The shirts are now ready for shipment. In the model, this flow is called Shipping. It refers to the rate that shirts are shipped. It is calculated by using one converter, Shipment Rate, and one stock, Packed Shirt. Shipment Rate is the number of shirts shipped per day, valued at 1000 pieces. The equation for this flow is IF (Packed_Shirt/DT) < (Shipment_Rate) THEN (Packed_Shirt/DT) ELSE (Shipment_Rate). IF (998/1) < (1000) THEN (998/1) ELSE (1000). IF (998) < (1000) THEN (998) ELSE (1000). The value of Shipping flow at its equilibrium is 998 pieces/day.
References
- Radzicki, M.J.; Taylor, R.A. Introduction to System Dynamics; US Department of Energy: Washington, DC, USA, 1997. Available online: http://www.systemdynamics.org/DL-IntroSysDyn/inside.htm (accessed on 20 June 2023).
- Zhang, H.; Calvo-Amodio, J.; Haapala, K.R. A conceptual model for assisting sustainable manufacturing through system dynamics. J. Manuf. Syst. 2013, 32, 543–549. [Google Scholar] [CrossRef]
- Forrester, J.W. Industrial dynamics. J. Oper. Res. Soc. 1997, 48, 1037–1041. [Google Scholar] [CrossRef]
- Radzicki, M.J.; Taylor, R.A. Origin of system dynamics: Jay W. Forrester and the history of system dynamics. In US Department of Energy’s Introduction to System Dynamics; US Department of Energy: Washington, DC, USA, 2008. [Google Scholar]
- Angerhofer, B.J.; Angelides, M.C. System dynamics modelling in supply chain management: Research review. In Proceedings of the 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165), Orlando, FL, USA, 10–13 December 2000; pp. 342–351. [Google Scholar]
- Pérez-Pérez, J.F.; Parra, J.F.; Serrano-Garcia, J. A system dynamics model: Transition to sustainable processes. Technol. Soc. 2021, 65, 101579. [Google Scholar] [CrossRef]
- Richardson, G.P. Core of System Dynamics. In System Dynamics: Theory and Applications; Springer: New York, NY, USA, 2020; pp. 11–20. [Google Scholar]
- Dyllick, T.; Hockerts, K. Beyond the business case for corporate sustainability. Bus. Strategy Environ. 2002, 11, 130–141. [Google Scholar] [CrossRef]
- Elkington, J.; Rowlands, I.H. Cannibals with forks: The triple bottom line of 21st century business. Altern. J. 1999, 25, 42. [Google Scholar]
- Hill, T.; Hill, T. Manufacturing Strategy: Text and Cases; Springer: Berlin/Heidelberg, Germany, 2000; Volume 2. [Google Scholar]
- World Commission on Environment and Development. Our Common Future; Peterson’s: Colorado Springs, CO, USA, 1987. [Google Scholar]
- Carter, C.R.; Rogers, D.S. A framework of sustainable supply chain management: Moving toward new theory. Int. J. Phys. Distrib. Logist. Manag. 2008, 38, 360–387. [Google Scholar] [CrossRef]
- Ghufran, M.; Khan, K.I.A.; Thaheem, M.J.; Nasir, A.R.; Ullah, F. Adoption of Sustainable Supply Chain Management for Performance Improvement in the Construction Industry: A System Dynamics Approach. Architecture 2021, 1, 161–182. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Schunk, D.; Plott, B. Using simulation to analyze supply chains. In Proceedings of the 2000 Winter Simulation Conference Proceedings (Cat. No. 00CH37165), Orlando, FL, USA, 10–13 December 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 1095–1100. [Google Scholar]
- Dicken, P. Global Shift: Reshaping the Global Economic Map in the 21st Century; Sage: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Nayak, R.; Padhye, R. Introduction: The apparel industry. In Garment Manufacturing Technology; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–17. [Google Scholar]
- Bheda, R.; Narag, A.; Singla, M. Apparel manufacturing: A strategy for productivity improvement. J. Fash. Mark. Manag. Int. J. 2003, 7, 12–22. [Google Scholar] [CrossRef]
- Muthu, S.S. Handbook of Sustainable Apparel Production; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Chowdhury, N.R.; Chowdhury, P.; Paul, S.K. Sustainable practices and their antecedents in the apparel industry: A review. Curr. Opin. Green Sustain. Chem. 2022, 37, 100674. [Google Scholar] [CrossRef]
- Chowdhury, M.M.H.; Rahman, S.; Quaddus, M.A.; Shi, Y. Strategies to mitigate barriers to supply chain sustainability: An apparel manufacturing case study. J. Bus. Ind. Mark. 2023, 38, 869–885. [Google Scholar] [CrossRef]
- Shen, B.; Li, Q.; Dong, C.; Perry, P. Sustainability issues in textile and apparel supply chains. Sustainability 2017, 9, 1592. [Google Scholar] [CrossRef]
- Bubicz, M.E.; Barbosa-Póvoa, A.P.F.D.; Carvalho, A. Social sustainability management in the apparel supply chains. J. Clean. Prod. 2021, 280, 124214. [Google Scholar] [CrossRef]
- Köksal, D.; Strähle, J.; Müller, M.; Freise, M. Social sustainable supply chain management in the textile and apparel industry—A literature review. Sustainability 2017, 9, 100. [Google Scholar] [CrossRef]
- Rathore, B. Future of textile: Sustainable manufacturing & prediction via chatgpt. Eduzone Int. Peer Rev./Ref. Multidiscip. J. 2023, 12, 52–62. [Google Scholar]
- Jiang, L.; Folmer, H.; Bu, M. Interaction between output efficiency and environmental efficiency: Evidence from the textile industry in Jiangsu Province, China. J. Clean. Prod. 2016, 113, 123–132. [Google Scholar] [CrossRef]
- Fatima, A.; Tufail, M. Improving Efficiency of Apparel Manufacturing Through the Principles of Resource Management. Cloth. Text. Res. J. 2023, 41, 225–235. [Google Scholar] [CrossRef]
- Mukherjee, K. Energy use efficiency in the Indian manufacturing sector: An interstate analysis. Energy Policy 2008, 36, 662–672. [Google Scholar] [CrossRef]
- Oelze, N. Sustainable supply chain management implementation—Enablers and barriers in the textile industry. Sustainability 2017, 9, 1435. [Google Scholar] [CrossRef]
- Freise, M.; Seuring, S. Social and environmental risk management in supply chains: A survey in the clothing industry. Logist. Res. 2015, 8, 2. [Google Scholar] [CrossRef]
- Awudu, I.; Zhang, J. Uncertainties and sustainability concepts in biofuel supply chain management: A review. Renew. Sustain. Energy Rev. 2012, 16, 1359–1368. [Google Scholar] [CrossRef]
- Sreedevi, R.; Saranga, H. Uncertainty and supply chain risk: The moderating role of supply chain flexibility in risk mitigation. Int. J. Prod. Econ. 2017, 193, 332–342. [Google Scholar] [CrossRef]
- Barnett, V.; O’Hagan, A. Setting Environmental Standards: The Statistical Approach to Handling Uncertainty and Variation; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Merschmann, U.; Thonemann, U.W. Supply chain flexibility, uncertainty and firm performance: An empirical analysis of German manufacturing firms. Int. J. Prod. Econ. 2011, 130, 43–53. [Google Scholar] [CrossRef]
- Shen, B. Sustainable fashion supply chain: Lessons from H&M. Sustainability 2014, 6, 6236–6249. [Google Scholar]
- Zimon, D.; Domingues, P. Proposal of a concept for improving the sustainable management of supply chains in the textile industry. Fibres Text. East. Eur. 2018, 26, 8–12. [Google Scholar] [CrossRef]
- Herrmann, F.F.; Barbosa-Povoa, A.P.; Butturi, M.A.; Marinelli, S.; Sellitto, M.A. Green supply chain management: Conceptual framework and models for analysis. Sustainability 2021, 13, 8127. [Google Scholar] [CrossRef]
- Hillier, F.S. Introduction to Operations Research; McGrawHill: New York, NY, USA, 2001. [Google Scholar]
- Shamsuddoha, M. Integrated supply chain model for sustainable manufacturing: A system dynamics approach. In Sustaining Competitive Advantage via Business Intelligence, Knowledge Management, and System Dynamics; Emerald Group Publishing Limited: Bingley, UK, 2015; pp. 155–399. [Google Scholar]
- Forrester, J.W. System dynamics, systems thinking, and soft OR. Syst. Dyn. Rev. 1994, 10, 245–256. [Google Scholar] [CrossRef]
- Wee Kwan Tan, A.; Kumar, A. A decision-making model for reverse logistics in the computer industry. Int. J. Logist. Manag. 2006, 17, 331–354. [Google Scholar] [CrossRef]
- Poles, R. System Dynamics modelling of a production and inventory system for remanufacturing to evaluate system improvement strategies. Int. J. Prod. Econ. 2013, 144, 189–199. [Google Scholar] [CrossRef]
- Ghisellini, P.; Cialani, C.; Ulgiati, S. A review on circular economy: The expected transition to a balanced interplay of environmental and economic systems. J. Clean. Prod. 2016, 114, 11–32. [Google Scholar] [CrossRef]
- Genovese, A.; Acquaye, A.A.; Figueroa, A.; Koh, S.L. Sustainable supply chain management and the transition towards a circular economy: Evidence and some applications. Omega 2017, 66, 344–357. [Google Scholar] [CrossRef]
- Santos, M.J. Theoretical contributions towards rethinking corporate social responsibility. Manag. Res. J. Iberoam. Acad. Manag. 2014, 12, 288–307. [Google Scholar]
- Fontes, C.H.d.O.; Freires, F.G.M. Sustainable and renewable energy supply chain: A system dynamics overview. Renew. Sustain. Energy Rev. 2018, 82, 247–259. [Google Scholar]
- Rebs, T.; Brandenburg, M.; Seuring, S. System dynamics modeling for sustainable supply chain management: A literature review and systems thinking approach. J. Clean. Prod. 2019, 208, 1265–1280. [Google Scholar] [CrossRef]
- Kaveh, A.; Vazirinia, Y. Optimization of tower crane location and material quantity between supply and demand points: A comparative study. Period. Polytech. Civ. Eng. 2018, 62, 732–745. [Google Scholar] [CrossRef]
- Andersen, M.; Skjoett-Larsen, T. Corporate social responsibility in global supply chains. Supply Chain Manag. Int. J. 2009, 14, 75–86. [Google Scholar] [CrossRef]
- Saberi, S.; Kouhizadeh, M.; Sarkis, J.; Shen, L. Blockchain technology and its relationships to sustainable supply chain management. Int. J. Prod. Res. 2019, 57, 2117–2135. [Google Scholar] [CrossRef]
- Abdelkafi, N.; Täuscher, K. Business models for sustainability from a system dynamics perspective. Organ. Environ. 2016, 29, 74–96. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Triantaphyllou, E. Multi-Criteria Decision Making Methods; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Majumder, M.; Majumder, M. Multi criteria decision making. In Impact of Urbanization on Water Shortage in Face of Climatic Aberrations; Springer: Singapore, 2015; pp. 35–47. [Google Scholar]
- Wang, J.-J.; Jing, Y.-Y.; Zhang, C.-F.; Zhao, J.-H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-criteria decision making (MCDM) methods and concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Karloff, H. Linear Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gass, S.I. Linear Programming: Methods and Applications; Courier Corporation: North Chelmsford, MA, USA, 2003. [Google Scholar]
- Kibira, D.; Jain, S.; McLean, C. A system dynamics modeling framework for sustainable manufacturing. In Proceedings of the 27th Annual System Dynamics Society Conference, Albuquerque, NM, USA, 26–30 July 2009; Volume 301, pp. 1–22. [Google Scholar]
- Jain, S.; Kibira, D. A framework for multi-resolution modeling of sustainable manufacturing. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3423–3434. [Google Scholar]
- Jain, S.; Lindskog, E.; Johansson, B. Supply chain carbon footprint tradeoffs using simulation. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–12. [Google Scholar]
- Jain, S.; Lindskog, E.; Andersson, J.; Johansson, B. A hierarchical approach for evaluating energy trade-offs in supply chains. Int. J. Prod. Econ. 2013, 146, 411–422. [Google Scholar] [CrossRef]
- Jain, S.; Sigurðardóttir, S.; Lindskog, E.; Andersson, J.; Skoogh, A.; Johansson, B. Multi-resolution modeling for supply chain sustainability analysis. In Proceedings of the 2013 Winter Simulations Conference (WSC), Washington, DC, USA, 8–11 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1996–2007. [Google Scholar]
- Wofuru-Nyenke, O.K.; Briggs, T.A.; Aikhuele, D.O. Advancements in sustainable manufacturing supply chain modelling: A review. Process Integr. Optim. Sustain. 2023, 7, 3–27. [Google Scholar] [CrossRef]
- Bentahar, O.; Benzidia, S. Sustainable supply chain management: Trends and challenges. HAL Post-Print 2018, hal-02511038. [Google Scholar] [CrossRef]
- Choi, T.-M.; Cai, Y.-J. Impacts of lead time reduction on fabric sourcing in apparel production with yield and environmental considerations. Ann. Oper. Res. 2020, 290, 521–542. [Google Scholar] [CrossRef]
- Choi, T.-M.; Cai, Y.-J.; Shen, B. Sustainable fashion supply chain management: A system of systems analysis. IEEE Trans. Eng. Manag. 2018, 66, 730–745. [Google Scholar] [CrossRef]
- Asif, A. An overview of sustainability on apparel manufacturing industry in Bangladesh. Sci. J. Energy Eng. 2017, 5, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Shi, D.; Li, X. Governance of sustainable supply chains in the fast fashion industry. Eur. Manag. J. 2014, 32, 823–836. [Google Scholar] [CrossRef]
- Morana, R.; Seuring, S. A three level framework for closed-loop supply chain management—Linking society, chain and actor level. Sustainability 2011, 3, 678–691. [Google Scholar] [CrossRef]
- Amatulli, C.; De Angelis, M.; Korschun, D.; Romani, S. Consumers’ perceptions of luxury brands’ CSR initiatives: An investigation of the role of status and conspicuous consumption. J. Clean. Prod. 2018, 194, 277–287. [Google Scholar] [CrossRef]
- Perry, P.; Towers, N. Determining the antecedents for a strategy of corporate social responsibility by small-and medium-sized enterprises in the UK fashion apparel industry. J. Retail. Consum. Serv. 2009, 16, 377–385. [Google Scholar] [CrossRef]
- Perry, P.; Towers, N. Conceptual framework development: CSR implementation in fashion supply chains. Int. J. Phys. Distrib. Logist. Manag. 2013, 43, 478–501. [Google Scholar] [CrossRef]
- Mair, S.; Druckman, A.; Jackson, T. Investigating fairness in global supply chains: Applying an extension of the living wage to the Western European clothing supply chain. Int. J. Life Cycle Assess. 2018, 23, 1862–1873. [Google Scholar] [CrossRef] [PubMed]
- Mair, S.; Druckman, A.; Jackson, T. Higher wages for sustainable development? Employment and carbon effects of paying a living wage in global apparel supply chains. Ecol. Econ. 2019, 159, 11–23. [Google Scholar] [CrossRef]
- Clarke-Sather, A.; Cobb, K. Onshoring fashion: Worker sustainability impacts of global and local apparel production. J. Clean. Prod. 2019, 208, 1206–1218. [Google Scholar] [CrossRef]
- Morgan, E.; Foxon, T.J.; Tallontire, A. ‘I prefer 30°’?: Business strategies for influencing consumer laundry practices to reduce carbon emissions. J. Clean. Prod. 2018, 190, 234–250. [Google Scholar] [CrossRef]
- Ma, K.; Wang, L.; Chen, Y. A collaborative cloud service platform for realizing sustainable make-to-order apparel supply chain. Sustainability 2017, 10, 11. [Google Scholar] [CrossRef]
- Garcia, S.; Cordeiro, A.; de Alencar Nääs, I.; Neto, P.L.d.O.C. The sustainability awareness of Brazilian consumers of cotton clothing. J. Clean. Prod. 2019, 215, 1490–1502. [Google Scholar] [CrossRef]
- Choi, T.-M. Incorporating social media observations and bounded rationality into fashion quick response supply chains in the big data era. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 386–397. [Google Scholar] [CrossRef]
- Na, Y.; Na, D.K. Investigating the sustainability of the Korean textile and fashion industry. Int. J. Cloth. Sci. Technol. 2015, 27, 23–33. [Google Scholar] [CrossRef]
- Atilgan, T. Eco-labelling applications in the textile & apparel sector in Turkey. Fibres Text. East. Eur. 2007, 15, 14. [Google Scholar]
- Yang, Y.; Han, H.; Lee, P.K. An exploratory study of the mechanism of sustainable value creation in the luxury fashion industry. Sustainability 2017, 9, 483. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y.; Wang, Y.; Wang, L.; Shen, M. Decomposing the decoupling of water consumption and economic growth in China’s textile industry. Sustainability 2017, 9, 412. [Google Scholar] [CrossRef]
- Li, B.; Wu, K. Environmental management system adoption and the operational performance of firm in the textile and apparel industry of China. Sustainability 2017, 9, 992. [Google Scholar] [CrossRef]
- Chi, T. Building a sustainable supply chain: An analysis of corporate social responsibility (CSR) practices in the Chinese textile and apparel industry. J. Text. Inst. 2011, 102, 837–848. [Google Scholar] [CrossRef]
- Dabija, D.-C.; Pop, N.A.; Postelnicu, C. Ethics of the garment retail within the context of globalization and sustainable development. Ind. Textilă 2016, 67, 270–279. [Google Scholar]
- Shi, X.; Qian, Y.; Dong, C. Economic and environmental performance of fashion supply chain: The joint effect of power structure and sustainable investment. Sustainability 2017, 9, 961. [Google Scholar] [CrossRef]
- Nagurney, A.; Yu, M. Sustainable fashion supply chain management under oligopolistic competition and brand differentiation. Int. J. Prod. Econ. 2012, 135, 532–540. [Google Scholar] [CrossRef]
- Pineda-Henson, R.; Culaba, A.B. A diagnostic model for green productivity assessment of manufacturing processes. Int. J. Life Cycle Assess. 2004, 9, 379–386. [Google Scholar] [CrossRef]
- Ghazinoory, S. Cleaner production in Iran: Necessities and priorities. J. Clean. Prod. 2005, 13, 755–762. [Google Scholar] [CrossRef]
- Jin Gam, H.; Cao, H.; Farr, C.; Heine, L. C2CAD: A sustainable apparel design and production model. Int. J. Cloth. Sci. Technol. 2009, 21, 166–179. [Google Scholar] [CrossRef]
- Jordeva, S.; Tomovska, E.; Trajković, D. Current state of pre-consumer apparel waste management in Macedonia. Fibres Text. East. Eur. 2015, 23, 13–16. [Google Scholar]
- Wickramasinghe, G.; Perera, A. Effect of total productive maintenance practices on manufacturing performance: Investigation of textile and apparel manufacturing firms. J. Manuf. Technol. Manag. 2016, 27, 713–729. [Google Scholar] [CrossRef]
- Pinheiro, E.; Francisco, A. Management and characterization of textile solid waste in a local productive arrangement. Fibres Text. East. Eur. 2016, 4, 8–13. [Google Scholar] [CrossRef]
- Van der Velden, N.M.; Vogtländer, J.G. Monetisation of external socio-economic costs of industrial production: A social-LCA-based case of clothing production. J. Clean. Prod. 2017, 153, 320–330. [Google Scholar] [CrossRef]
- Hirscher, A.-L.; Niinimäki, K.; Armstrong, C.M.J. Social manufacturing in the fashion sector: New value creation through alternative design strategies? J. Clean. Prod. 2018, 172, 4544–4554. [Google Scholar] [CrossRef]
- Bala, B.; Islam, M.; Ghosh, S.; Hossain, M.; Hoque, A.; Saha, S. Modelling of supply chain of ready-made garments in Bangladesh. Syst. Res. Behav. Sci. 2020, 37, 38–55. [Google Scholar] [CrossRef]
- Issa, M.; Elgholmy, S.; Shetab, A.; Fors, M.N. A system dynamics model of apparel supply chain under mass customization. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Toronto, ON, Canada, 23–25 October 2019. [Google Scholar]
- Wilson, S. Building apparel manufacturing competitiveness through policy—A system dynamics approach. J. Fash. Mark. Manag. Int. J. 2020, 24, 277–302. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Pasek, Z.J. Risk assessment for the supply chain of fast fashion apparel industry: A system dynamics framework. Int. J. Prod. Res. 2016, 54, 28–48. [Google Scholar] [CrossRef]
- Lidia, M.W.; Arai, T.; Ishigaki, A.; Yudoko, G. Applying system dynamics approach to the fast fashion supply chain: Case study of an SME in Indonesia. Asian J. Technol. Manag. 2012, 5, 42–52. [Google Scholar]
- Corinna Cagliano, A.; DeMarco, A.; Rafele, C.; Volpe, S. Using system dynamics in warehouse management: A fast-fashion case study. J. Manuf. Technol. Manag. 2011, 22, 171–188. [Google Scholar] [CrossRef]
- Haddad, M.; Otayek, R. Assessing the Sustainment of a Lean Implementation Using System Dynamics Modeling: A Case Study of Apparel Manufacturing in Lebanon. Int. J. Syst. Dyn. Appl. (IJSDA) 2019, 8, 14–29. [Google Scholar] [CrossRef]
- Domina, T.; Koch, K. The textile waste lifecycle. Cloth. Text. Res. J. 1997, 15, 96–102. [Google Scholar] [CrossRef]
- Rathinamoorthy, R. Sustainable apparel production from recycled fabric waste. In Sustainable Innovations in Recycled Textiles; Springer: Singapore, 2018; pp. 19–52. [Google Scholar]
- Core System Dynamics Modeling Software. Available online: https://systemdynamics.org/tools/core-software/ (accessed on 21 June 2023).

| Serial Nos. | Stocks (All Numbers Are per Day) | Description |
|---|---|---|
| 1. | Inhouse Fabric and Fusing | In-house quantity of fabric and fusing required to make up to 1000 shirts. |
| 2. | Unstitched Shirt Panels with Fusing | Quantity of unstitched, cut shirt panels attached with fusing. |
| 3. | Stitched Shirt | The number of shirts stitched. |
| 4. | Shirts with Buttons | The number of shirts with buttons attached. |
| 5. | Finished Shirt | The number of shirts finished after completing the tagging, finishing, and quality inspection. |
| 6. | Packed Shirt | The number of shirts packed for shipping. |
| Serial Nos. | Converters | Description |
|---|---|---|
| 1. | Fabric Consumption per Piece | The amount of fabric consumed to manufacture one shirt. |
| 2. | Fabric in Yards | The fabric yardage required to manufacture up to 1000 shirts per day. |
| 3. | Fusing in Yards | The fusing yardage required to manufacture up to 1000 shirts per day. |
| 4. | Fusing Consumption per Piece | The amount of fusing consumed to manufacture one shirt. |
| 5. | Cutting and Fusing Attachment Rate | The number of shirt panels cut and fused per day. |
| 6. | Labor | The amount of labor (in full-time equivalent employees) required to cut shirt panels and attach fusing to the panels per day. |
| 7. | Cutting and Fusing | Waste fraction: the fraction of fabric and fusing waste generated from cutting. |
| 8. | Stitching Rate | The number of shirts sewn by a tailor using a sewing machine per day. |
| 9. | Tailors | The number of tailors required to sew up to 1000 shirts per day. |
| 10. | Buttoning Rate | The number of shirts buttoned per day by one laborer. |
| 11. | Buttoning Labor | The amount of labor needed to attach buttons to shirts per day. |
| 12. | Finishing and Tagging Rate | The number of shirts finished and tagged by one laborer per day. |
| 13. | Finishing and Tagging Labor | The amount of labor required to finish the shirts and add hand tags per day. |
| 14. | Failed Quality Fraction | The fraction of shirts rejected during inspection due to poor quality. |
| 15. | Packing Rate | The number of shirts packed for shipping by one laborer per day. |
| 16. | Packers | The amount of labor required to pack up to 1000 shirts per day. |
| 17. | Shipment Rate | The number of shirts shipped per day. |
| Serial Nos. | Flows | Description |
|---|---|---|
| 1. | Fabric and Fusing Transport | The rate at which fabric and fusing are transported to the factory. |
| 2. | Cutting and Fusing Attachment | The rate at which shirt panels are cut and attached to the fusing. |
| 3. | Cutting and Fusing Waste | The rate of waste generation by cutting and fusing. |
| 4. | Stitching | The rate at which shirts are sewn. |
| 5. | Buttoning | The rate at which shirts are buttoned. |
| 6. | Tagging and Finishing | The rate at which shirts are finished and tagged. |
| 7. | Quality Inspection | The rate at which shirts pass quality inspection. |
| 8. | Packing | The rate at which shirts are packed for shipping. |
| 9. | Shipping | The rate at which shirts are shipped. |
| Serial Nos. | Converter | Converter’s Variable Name | Unit |
|---|---|---|---|
| 1. | Cutting and Fusing Attachment Rate | Cutting_&_Fusing_Attachment_Rate | Pieces/day |
| 2. | Labor | Labor | Unitless |
| 3. | Cutting and Fusing Waste Fraction | Cutting_&_Fusing_ Waste_Fraction | Unitless |
| 4. | Stitching Rate | Stitching_Rate | Pieces/day |
| 5. | Tailors | Tailor | Unitless |
| Serial Nos. | Name of the Flow | Equation | Unit |
|---|---|---|---|
| 1. | Cutting and Fusing Attachment | IF (Inhouse_Fabric_&_Fusing/DT) < (Cutting_&_Fusing_Attachment_Rate*Labor) THEN (Inhouse_Fabric_&_Fusing/DT) ELSE (Cutting_&_Fusing_Attachment_Rate*Labor) | Pieces/day |
| 2. | Fabric and Fusing Cutting Waste | (Cutting_&_Fusing_Attachment*Fabric_and_Fusing_Cutting_Waste_Fraction) | Pieces/day |
| 3. | Stitching | IF (Unstitched_Shirt_Panels_with_Fusing/DT) < (Stitching_Rate*Tailors) THEN (Unstitched_Shirt_Panels_with_Fusing/DT) ELSE (Stitching_Rate*Tailors) | Pieces/day |
| Serial Nos. | Name of the Stock | Equation of Stock | Unit |
|---|---|---|---|
| 1. | Unstitched Shirt Panels with Fusing (t) | Unstitched Shirt Panels with Fusing (t − dt) + Cutting and Fusing Attachment (t) − Stitching (t) − Fabric and Cutting Fusing Waste (t) | Pieces per day |
| Serial Nos. | Converters | Initial Simulation’s Input Values |
|---|---|---|
| 1. | Fabric in Yards | 2500 |
| 2. | Fabric Consumption per Piece | 2 |
| 3. | Fusing in Yards | 2.2 |
| 4. | Fusing Consumption per Piece | 0.002 |
| 5. | Cutting and Fusing Attachment Rate | 4000 |
| 6. | Labor | 0.3 |
| 7. | Fabric and Fusing Cutting Waste Fraction | 0.02 |
| 8. | Stitching Rate | 3 |
| 9. | Tailors | 530 |
| 10. | Buttoning Rate | 75 |
| 11. | Buttoning Labor | 15 |
| 12. | Finishing and Tagging Rate | 105 |
| 13. | Finishing and Tagging Labor | 11 |
| 14. | Failed Quality Fraction | 0.05 |
| 15. | Packing Rate | 80 |
| 16. | Packers | 10 |
| 17. | Shipment Rate | 1000 |
| Serial Nos. | Converters | Optimized Simulation Input Values |
|---|---|---|
| 1. | Fabric in Yards | 2144 |
| 2. | Fabric Consumption per Piece | 2 |
| 3. | Fusing in Yards | 2.2 |
| 4. | Fusing Consumption per Piece | 0.002 |
| 5. | Cutting and Fusing Attachment Rate | 4000 |
| 6. | Labor | 0.3 |
| 7. | Fabric and Fusing Cutting Waste Fraction | 0.02 |
| 8. | Stitching Rate | 2 |
| 9. | Tailors | 530 |
| 10. | Buttoning Rate | 75 |
| 11. | Buttoning Labor | 15 |
| 12. | Finishing and Tagging Rate | 105 |
| 13. | Finishing and Tagging Labor | 11 |
| 14. | Failed Quality Fraction | 0.05 |
| 15. | Packing Rate | 80 |
| 16. | Packers | 13 |
| 17. | Shipment Rate | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaur, G.; Kander, R. Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability. Sustainability 2023, 15, 15353. https://doi.org/10.3390/su152115353
Kaur G, Kander R. Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability. Sustainability. 2023; 15(21):15353. https://doi.org/10.3390/su152115353
Chicago/Turabian StyleKaur, Gurinder, and Ronald Kander. 2023. "Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability" Sustainability 15, no. 21: 15353. https://doi.org/10.3390/su152115353
APA StyleKaur, G., & Kander, R. (2023). Supply Chain Simulation of Manufacturing Shirts Using System Dynamics for Sustainability. Sustainability, 15(21), 15353. https://doi.org/10.3390/su152115353






