Study on the Stability and Seepage Characteristics of Underwater Shield Tunnels under High Water Pressure Seepage
Abstract
:1. Introduction
2. Theoretical Method and Numerical Models
2.1. Basic Principles of Fluid–Solid Coupling
2.1.1. Stress Balance Equation
2.1.2. Seepage Continuity Equation
2.1.3. Theoretical Derivation of an Anisotropic Permeability Coefficient Expression
2.2. Numerical Modeling
2.2.1. Modeling Assumptions
- (1)
- The solid units of the model follow the Mohr–Coulomb yield criterion;
- (2)
- The properties of the soil and structural units do not change during excavation, and the soil particles and fluids are incompressible;
- (3)
- The geotechnical body is regarded as a porous medium, and the flow of fluid in the pores conforms to Darcy’s law;
- (4)
- The shield shell and lining units are considered to be perfectly elastic, and both are impermeable.
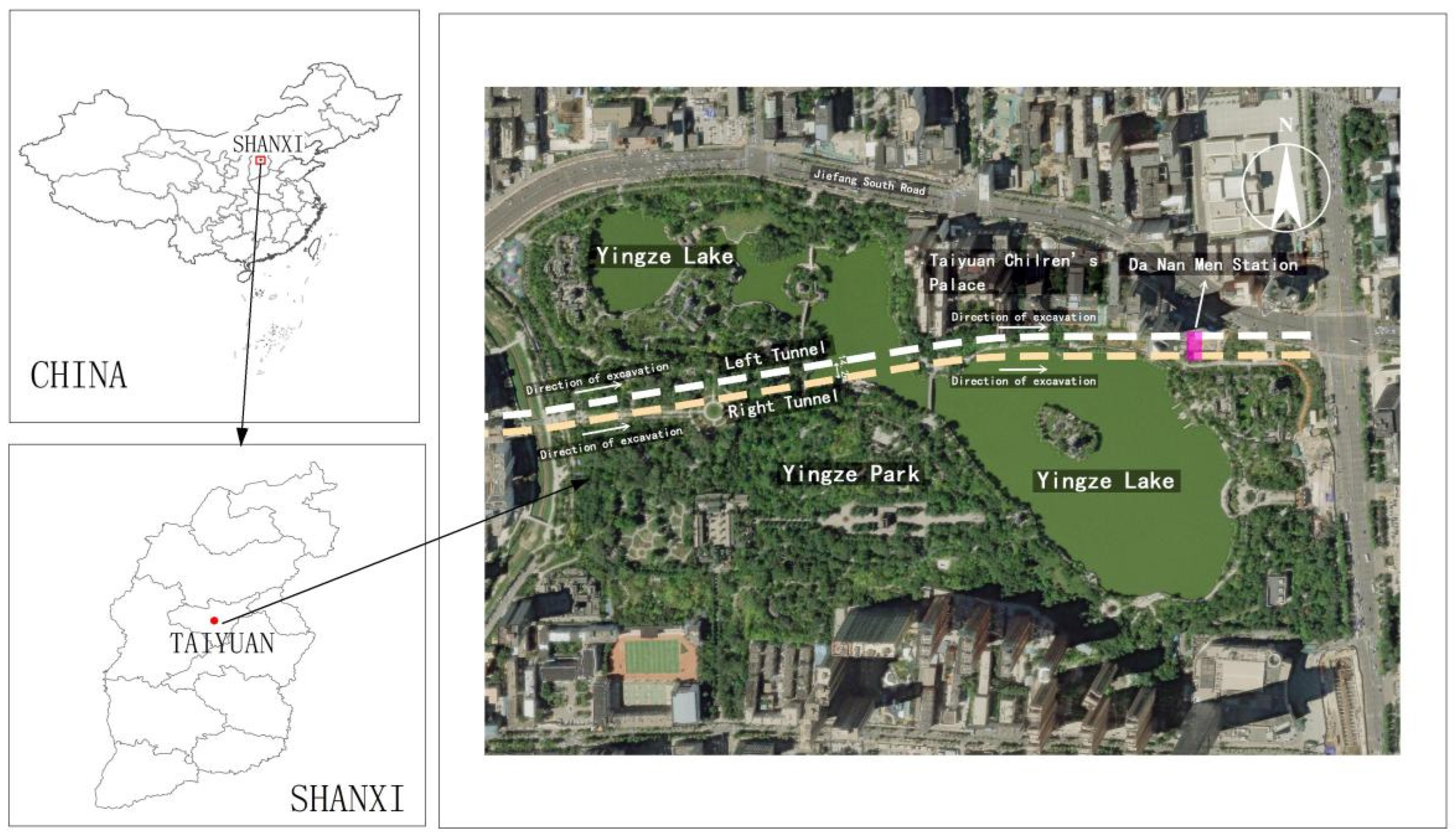
2.2.2. Engineering Background
2.2.3. Modeling
2.2.4. Calculation Parameters
2.2.5. Simulation Process
2.3. Boundary Conditions and Initial Conditions
3. Results and Discussions
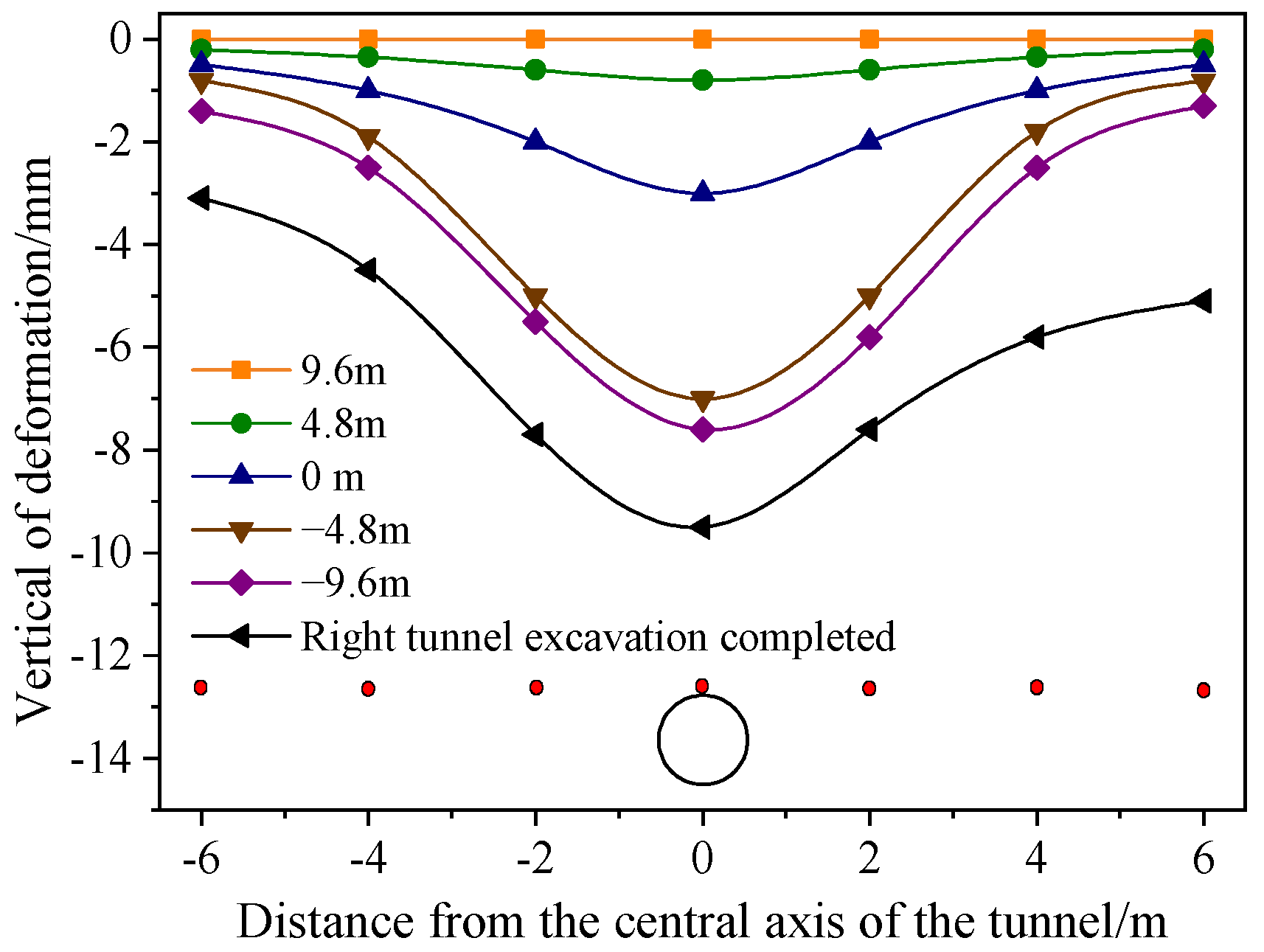
3.1. Analysis of Displacement Field
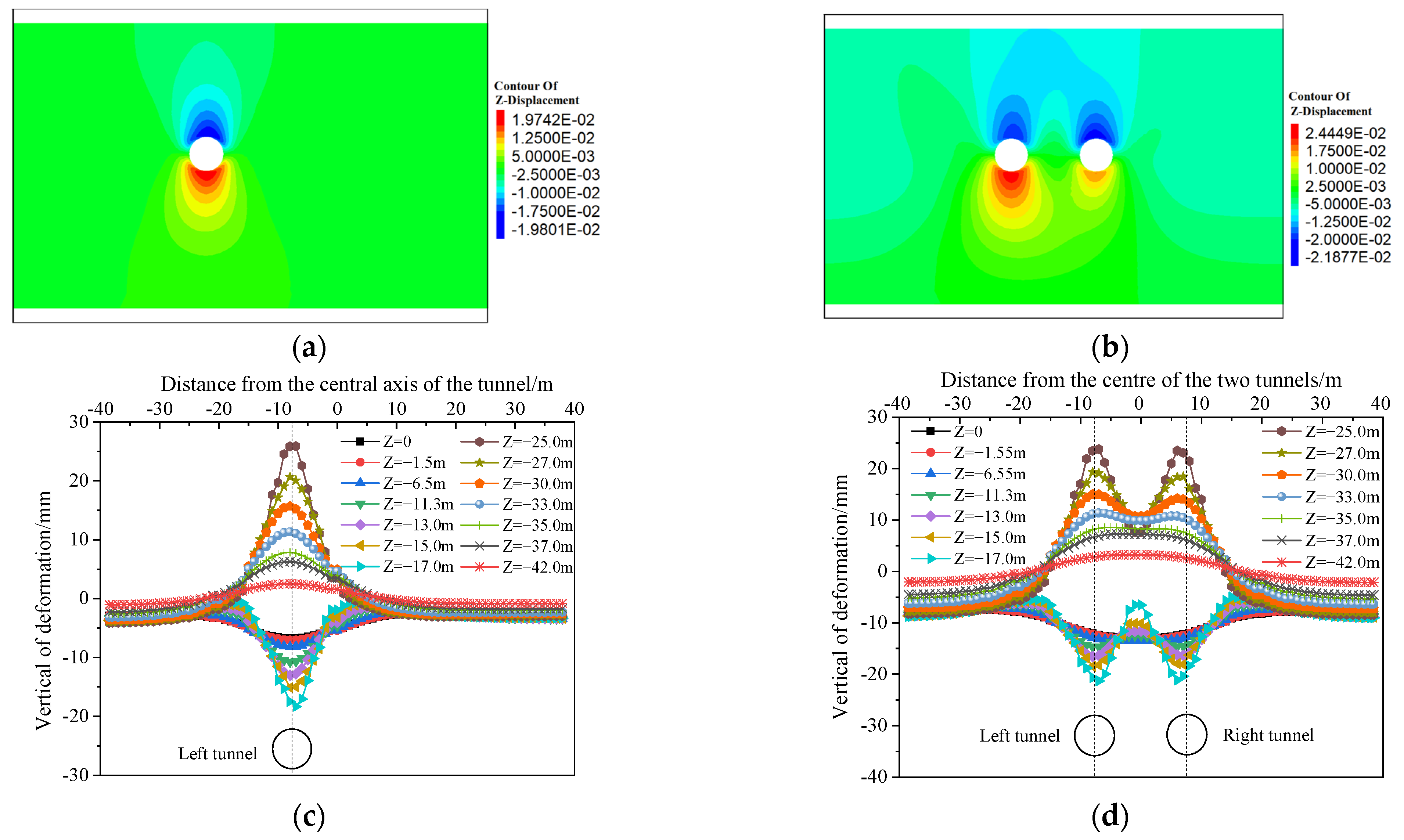
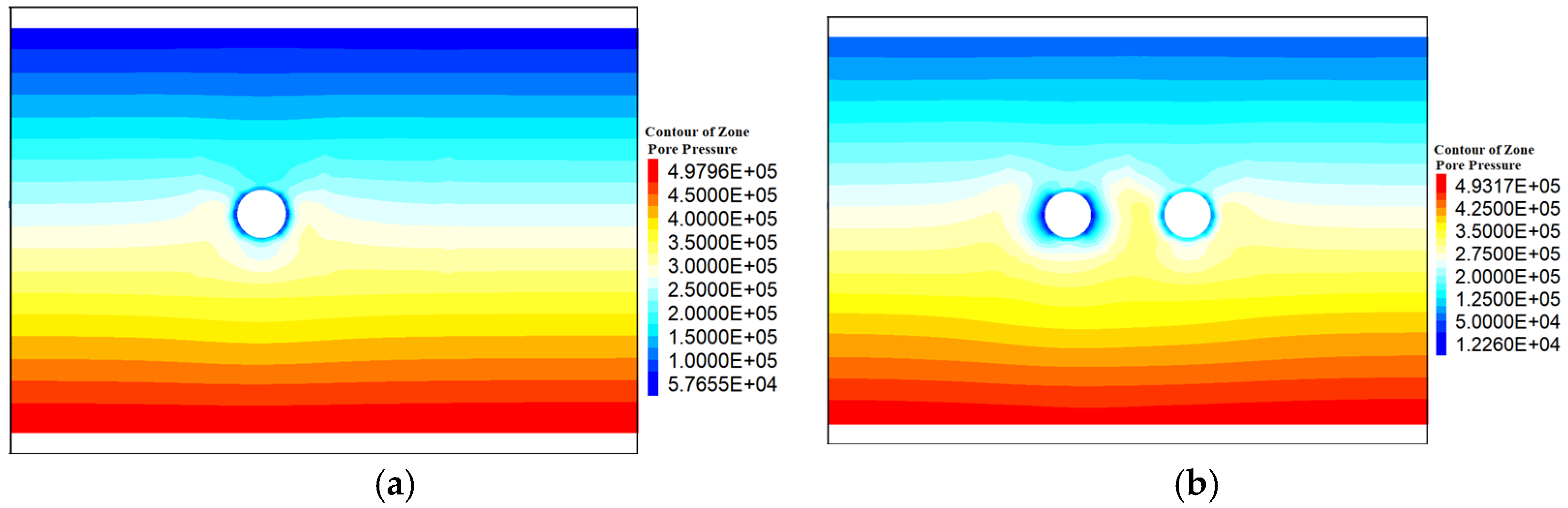
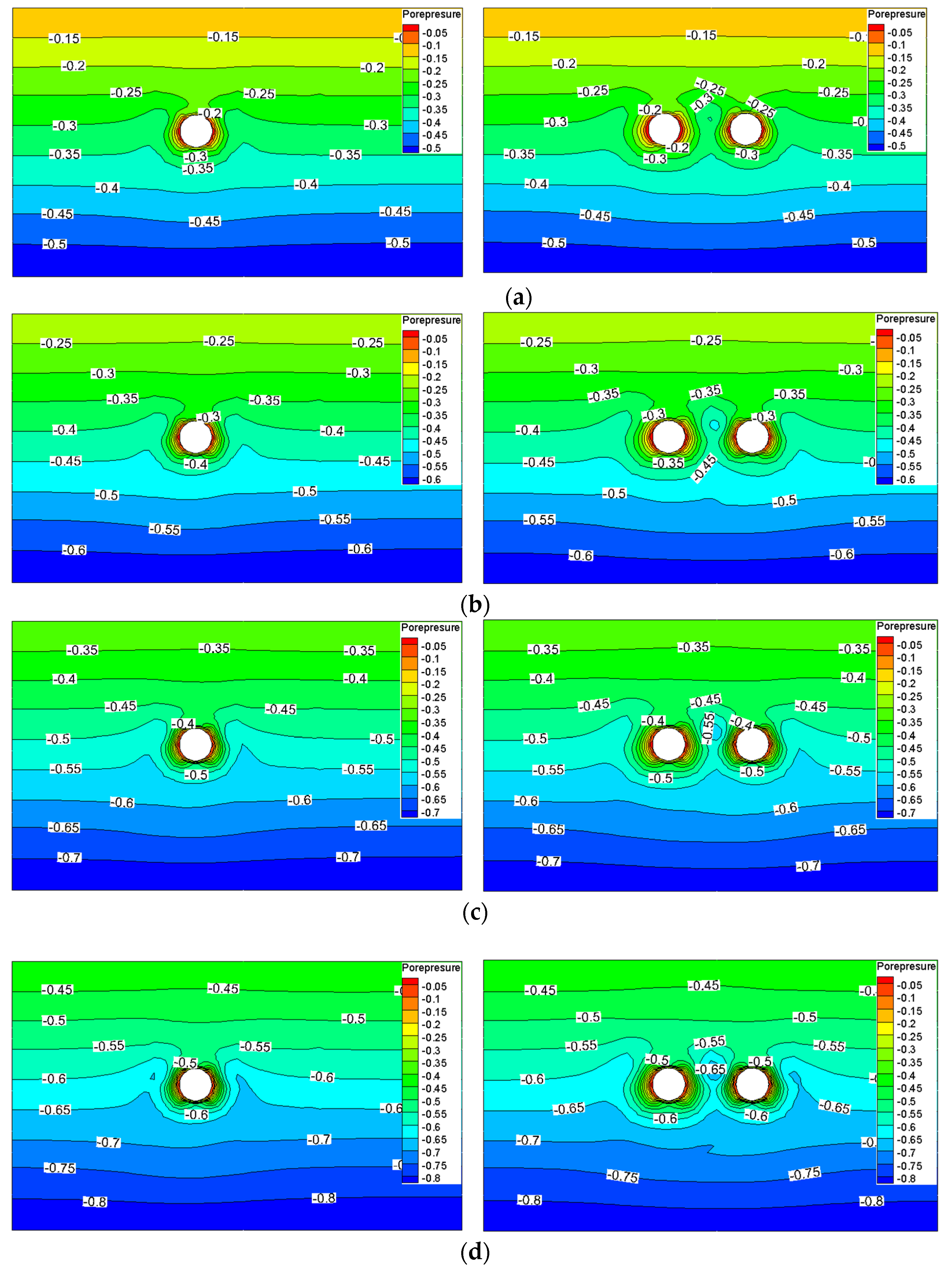
3.2. Analysis of Seepage Field
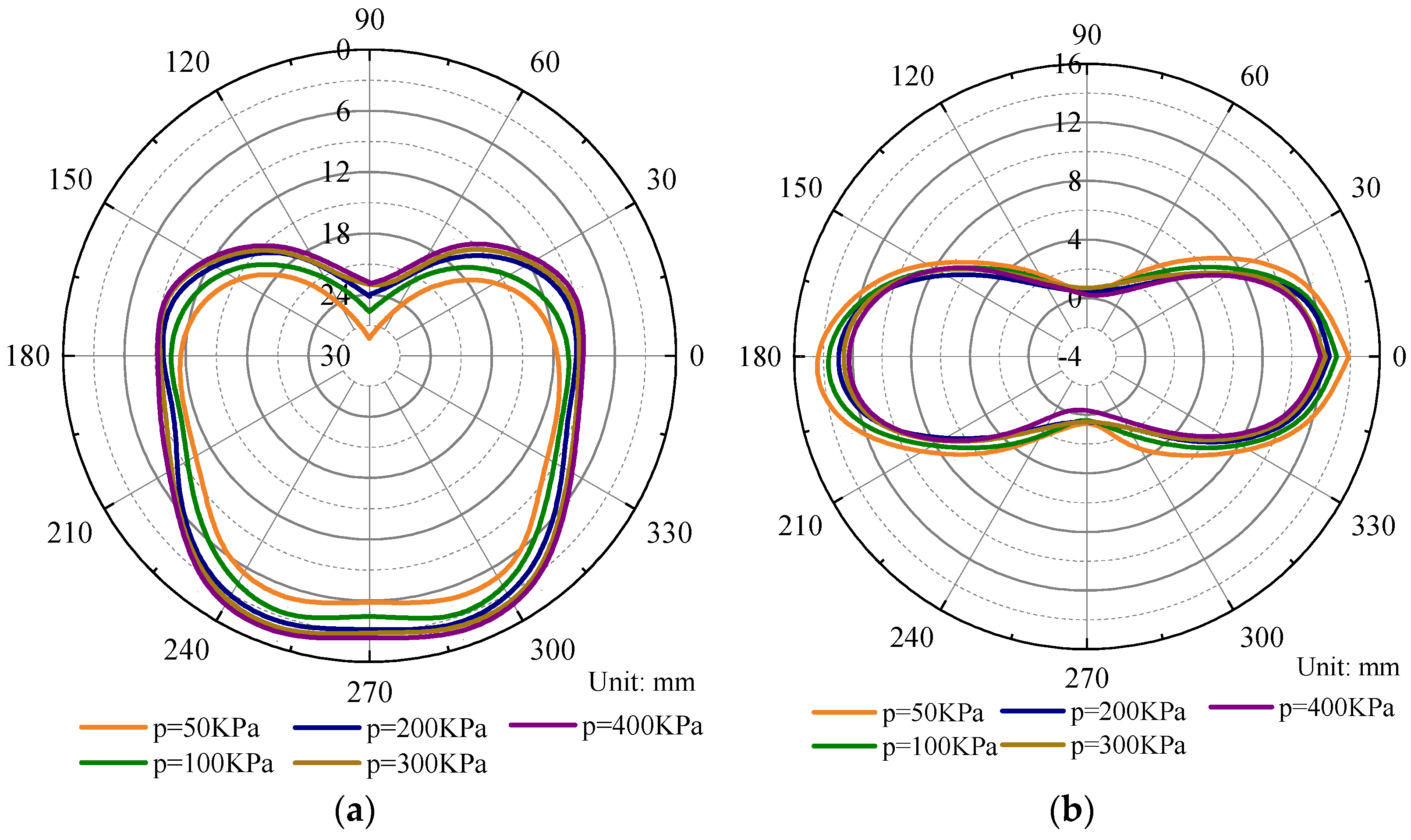
3.3. Analysis of Key Construction Parameters
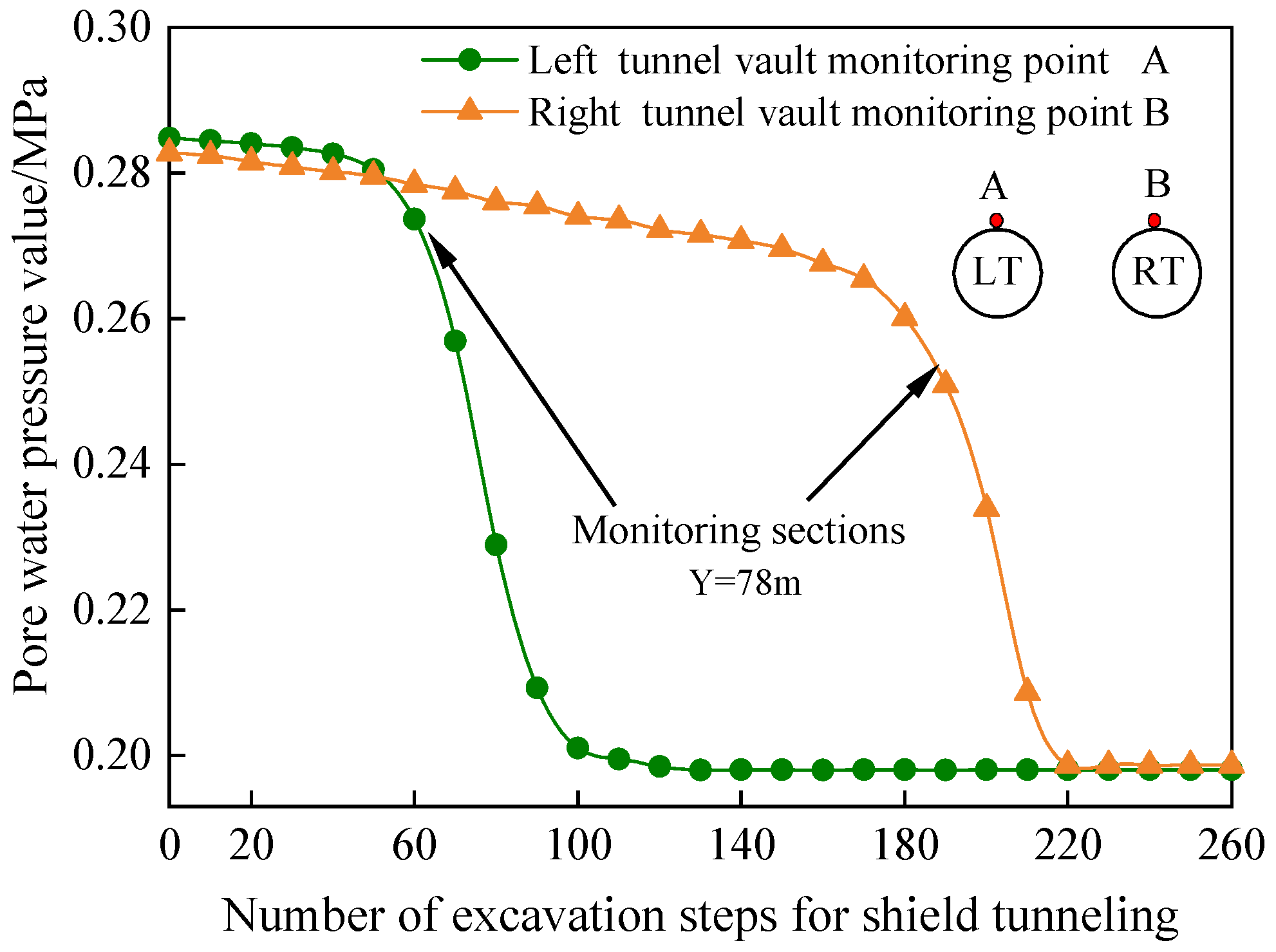
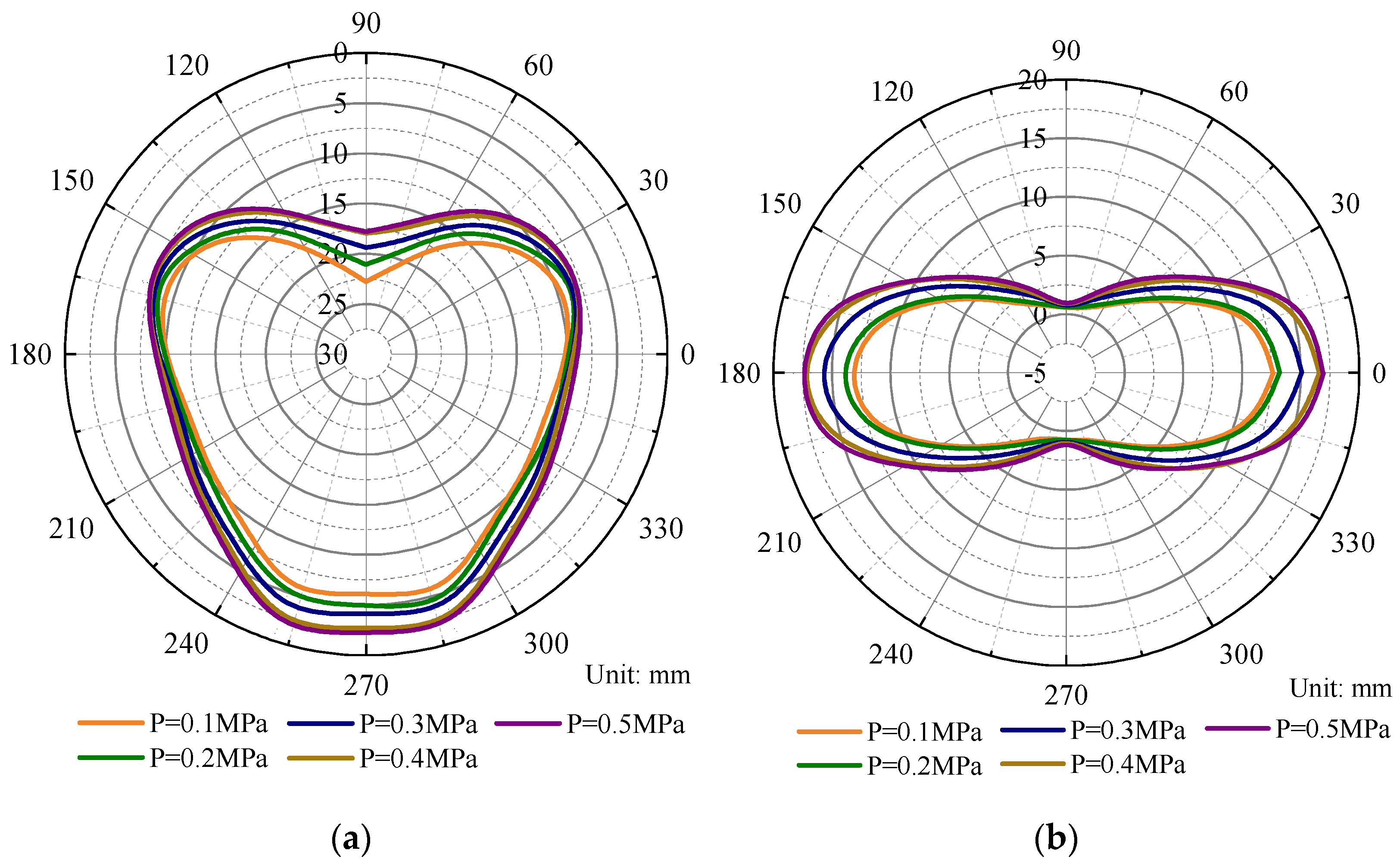
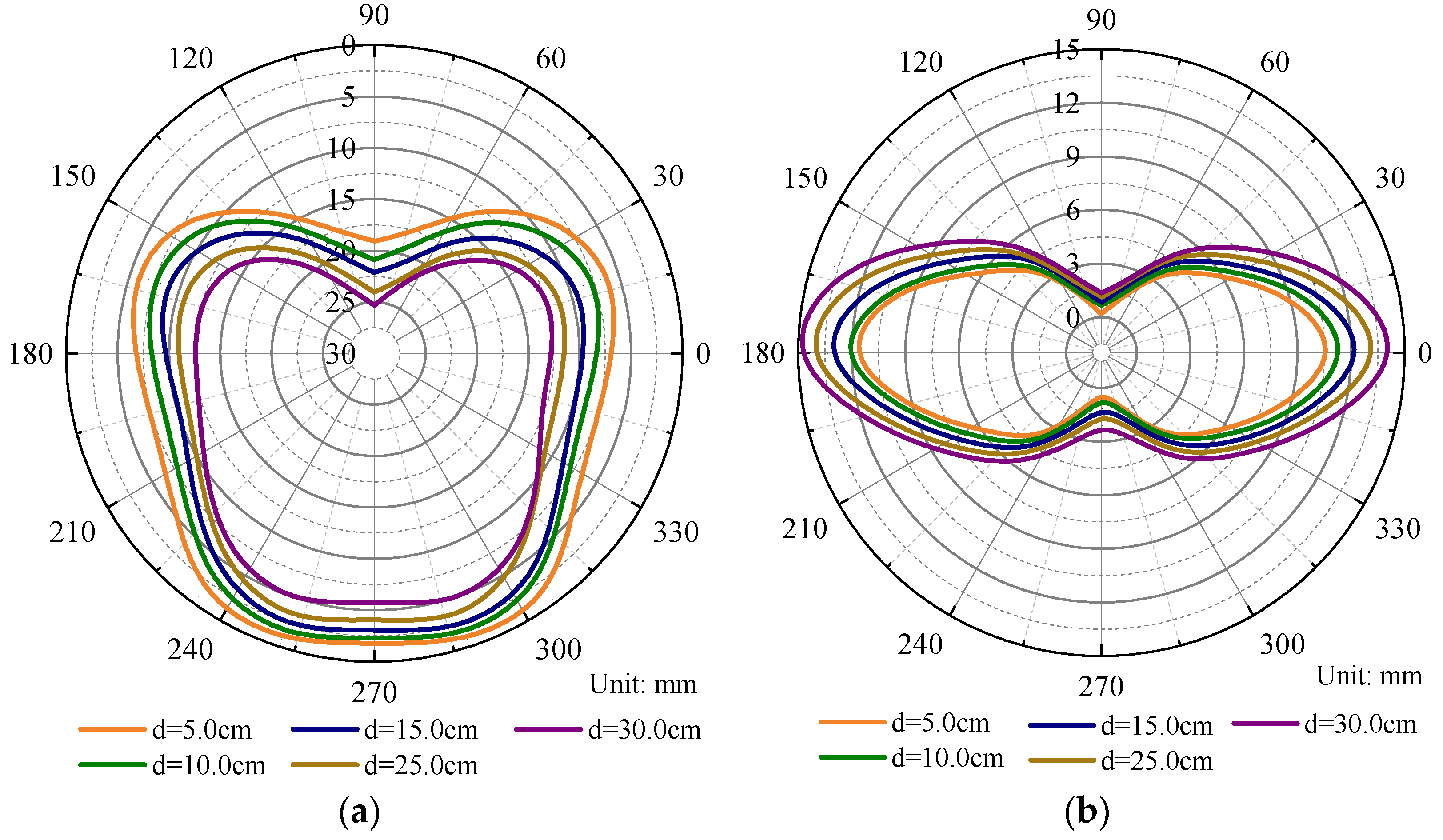
3.4. Seepage Characteristics of Shield Tunnel under High Water Pressure
3.4.1. Distribution Law of Seepage Field of Surrounding Rock
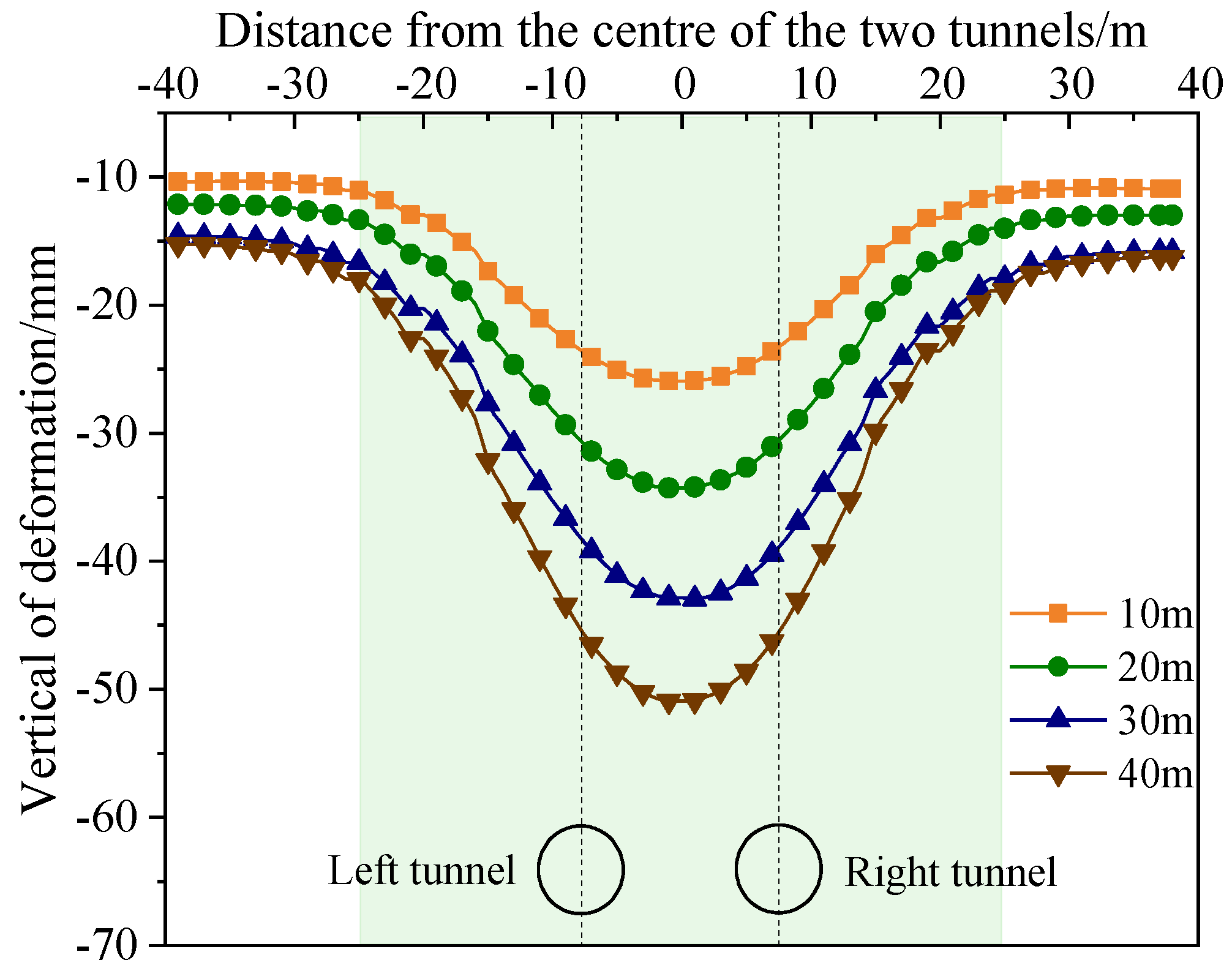
3.4.2. Surface Settlement
4. Conclusions
- (1)
- After shield excavation, the late consolidation settlement of the soil under seepage is enormous, accounting for about 25% of the total settlement, and the later tunnel will further enhance the seepage around the first tunnel.
- (2)
- During the construction of the underwater shield, the pore water pressure on both sides of the tunnel arch and arch waist is reduced by about 72% and 30%, respectively, compared with the initial value and requiring focused monitoring of the tunnel arch girdle area.
- (3)
- Within a specific range, increasing the digging pressure and grouting pressure and reducing the thickness of the grouting layer can effectively control the vertical deformation of the segment, and reducing the grouting stress and thickness of the grouting layer can effectively prevent the horizontal deformation of the segment.
- (4)
- The more prominent the overlying water level is, the more pronounced the seepage effect is, and the larger the maximum consolidation settlement and the influence range of the surface settlement. The influence of the water level on the force of the segment should be considered in the structural design of the segment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Li, S.C.; Li, L.P.; Zhang, Q.Q.; Xu, Z.H.; Wu, J.; He, P. Grouting effects evaluation of water-rich faults and its engineering application in Qingdao Jiaozhou Bay Subsea Tunnel China. Geomech. Eng. 2017, 12, 35–52. [Google Scholar] [CrossRef]
- Qiu, D.H.; Cui, J.H.; Xue, Y.G.; Liu, Y.; Fu, K. Dynamic risk assessment of the subsea tunnel construction process: Analytical model. J. Mar. Environ. Eng. 2019, 10, 195–210. [Google Scholar]
- Wu, Z.; Zou, S.L. A static risk assessment model for underwater shield tunnel construction. Sādhanā 2022, 45, 215. [Google Scholar] [CrossRef]
- Huang, M.; Zhan, J.W. Face stability assessment for underwater tunneling across a fault zone. J. Perform. Constr. Facil. 2019, 33, 04019034. [Google Scholar] [CrossRef]
- Shi, J.; Wang, F.; Zhang, D.; Huang, H. Refined 3D modelling of spatial-temporal distribution of excess pore water pressure induced by large diameter slurry shield tunneling. Comput. Geotech. 2021, 137, 104312. [Google Scholar] [CrossRef]
- Xu, J.H.; He, C.; Xia, W.Y. Research on coupling seepage field and stress field analyses of underwater shield tunnel. Rock Soil Mech. 2009, 30, 3519–3522. (In Chinese) [Google Scholar]
- Zhang, S.L.; Cheng, X.S.; Qi, L. Face stability analysis of large diameter shield tunnel in soft clay considering high water pressure seepage. Ocean Eng. 2022, 253, 111283. [Google Scholar] [CrossRef]
- Shin, Y.J.; Song, K.I.; Lee, I.M.; Cho, G.C. Interaction between tunnel supports and ground convergence—Consideration of seepage forces. Int. J. Rock Mech. Min. Sci. 2011, 48, 394–405. [Google Scholar] [CrossRef]
- Lu, X.L.; Li, F.D.; Huang, M.S. Numerical Simulation of the Face Stability of Shield Tunnel under Tidal Condition. Geo-Shanghai 2014, 742–750. [Google Scholar] [CrossRef]
- Broere, W. On the face support of microtunnelling tbms. Tunn. Undergr. Space Technol. 2015, 46, 12–17. [Google Scholar] [CrossRef]
- Wang, L.; Han, K.; Xie, T.; Luo, J. Calculation of limit support pressure for EPB shield tunnel face in water-rich sand. Symmetry 2019, 11, 1102. [Google Scholar] [CrossRef]
- Hu, Q.X.; Wang, S.Y.; Qu, T.M.; Xu, T.; Huang, S.; Wang, H. Effect of hydraulic gradient on the permeability characteristics of foam-conditioned sand for mechanized tunnelling. Tunn. Undergr. Space Technol. 2020, 99, 103377. [Google Scholar] [CrossRef]
- Wang, Y.C.; Li, Z.Y.; Jing, H.W.; Li, Y.B.; Wang, M.T. Study on the seepage characteristics of deep buried tunnels under variable high-pressure water heads. Bull. Eng. Geol. Environ. 2021, 80, 1477–1487. [Google Scholar] [CrossRef]
- Wei, Z.D.; Zhu, Y.P. A theoretical calculation method of ground settlement based on a groundwater seepage and drainage model in tunnel engineering. Sustainability 2021, 13, 2733. [Google Scholar] [CrossRef]
- Di, Q.G.; Li, P.F.; Zhang, M.J.; Zhang, W.J.; Wang, X.Y. Analysis of face stability for tunnels under seepage flow in the saturated ground. Ocean Eng. 2022, 266, 112674. [Google Scholar]
- Cheng, X.; Zhang, S.; Qi, L.; Zhou, X. Fluid-solid coupling response of shield tunnel lining structure under high water pressure. Mar. Georesources Geotechnol. 2022, 40, 1151–1161. [Google Scholar] [CrossRef]
- Anagnostou, G.; Kovari, K. Face stability condition with earth pressure balanced shields. Tunn. Undergr. Space Technol. 1996, 11, 165–173. [Google Scholar] [CrossRef]
- Zhang, D.M.; Liu, Y.; Huang, H.W. Leakage-induced Settlement of Ground and Shield Tunnel in Soft Clay. J. Tong Ji Univ. (Nat. Sci.) 2013, 41, 1185–1190+1212. (In Chinese) [Google Scholar]
- Tang, Y.; Chan, D.H.; Zhu, D.Z. Analytical solution for steady-state groundwater inflow into a circular tunnel in anisotropic soils. J. Eng. Mech. 2018, 144, 06018003. [Google Scholar] [CrossRef]
- Chen, R.P.; Yin, X.S.; Tang, L.J.; Chen, Y.M. Centrifugal model tests of tunneling face failure under seepage flow. Rock Soil Mech. 2015, 36, 225–229. (In Chinese) [Google Scholar]
- Feng, Y.; Chen, Y.M. Experimental study on water gushing-sand bursting in shield tunnels based on transparent soil. Tunn. Constr. 2023, 43, 75. (In Chinese) [Google Scholar]
- Zhang, Z.G.; Mao, M.D.; Pan, Y.T.; Zhang, M.X.; Ma, S.K.; Cheng, Z.; Wu, Z. Experimental study for joint leakage process of tunnel lining and particle flow numerical simulation. Eng. Fail. Anal. 2022, 138, 106348. [Google Scholar]
- Lu, X.L.; Wang, H.R.; Huang, M.S. Upper bound solution for the face stability of shield tunnel below the water table. Math. Probl. Eng. 2014, 2014, 727964. [Google Scholar]
- Lü, X.L.; Zhao, Y.C.; Cai, J.T. Numerical Simulation of Ground Subsidence Induced by Shield Tunnel Construction Disturbance in Water-rich Sandy Stratum. Mod. Tunneling Technol. 2020, 57, 104–109. (In Chinese) [Google Scholar]
- Li, K.; Guo, Z.; Wang, L.Z.; Jiang, H.Y. Effect of seepage flow on shields number around a fixed and sagging pipeline. Ocean Eng. 2019, 172, 487–500. [Google Scholar]
- Wongsaroj, J.; Soga, K.; Mair, R.J. Tunnelling-induced consolidation settlements in london clay. Geotechnique 2013, 63, 1103–1115. [Google Scholar]
- Avgerinos, V.; Potts, D.M.; Standing, J. The use of kinematic hardening models for predicting tunnelling-induced ground movements in London clay. Géotechnique 2016, 66, 106–120. [Google Scholar]
- Li, W.; Afshani, A.; Akagi, H.; Oka, S. Influence of lining permeability and temperature on long-term behavior of segmented tunnel. Soils Found. 2020, 60, 425–438. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Qiao, T.; Zhou, J.; Zhang, T.J.; Jiang, Y.C. Analytical Solution on Seepage Field of Underwater Non-circular Tunnel Considering Seepage Anisotropy. Adv. Eng. Sci. 2022, 26, 5328–5341. (In Chinese) [Google Scholar]
- Wu, Q.; Zhu, B.; Liu, S.Q. Flow-solid coupling simulation method analysis and time identification of lagging water-inrush near mine fault belt. Chin. J. Rock Mech. Eng. 2011, 30, 93–104. (In Chinese) [Google Scholar]
- Li, Z.; Luo, Z.J.; Xu, C.H.; Tan, J.Z. 3D fluid-solid full coupling numerical simulation of soil settlement induced by shield tunneling. Tunn. Undergr. Space Technol. 2019, 90, 174–182. [Google Scholar] [CrossRef]
- Wu, Z.S.; Liu, X.R.; Liang, B.; Zhong, Z.L. Study of seepage property and calculated watershed around underwater tunnels. Chin. J. Rock Mech. Eng. 2014, 33, 2402–2408. (In Chinese) [Google Scholar]
- Yang, F. Surface subsidence characteristic and control technology of subway tunnel construction in saturated loess. Master’s Thesis, Xi’an University of Science Technology, Xi’an, China, 2017. [Google Scholar]
- Zhu, C.H.; Li, N. Prediction and analysis of surface settlement due to shield tunneling for Xi’an Metro. Can. Geotech. J. 2017, 54, 529–546. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, S.; Peng, S.; Song, Y. Surface Settlement in Saturated Loess Stratum during Shield Construction: Numerical Modeling and Sensitivity Analysis. Tunn. Undergr. Space Technol. 2022, 119, 104205. [Google Scholar] [CrossRef]
- Li, J.B.; Chen, J.; Luo, H.X.; Cheng, H.Z.; Hu, Z.F.; Huang, J.H.; Zhang, S.K. Study on surrounding soil deformation induced by twin shield tunneling based on random field theory. Chin. J. Rock Mechan. Eng. 2018, 37, 1748–1765. [Google Scholar]
- Qiu, M.M.; Yang, G.L.; Duan, J.Y.; Zhang, P.R. Evolution rules and numerical simulation of stratum deformation induced by close-spaced twin tunnels shield construction. J. Nat. Disasters 2021, 30, 60–69. [Google Scholar]
- Niu, H.S.; Weng, X.L.; Yu, H.F.; Hu, J.B. Centrifugal test study on instability mode of shield tunnel excavation facein silty sand stratum under seepage. China Civ. Eng. J. 2020, 53, 99–104+118. (In Chinese) [Google Scholar]
- Wang, C.; Feng, K.; Dai, Z.C.; Wu, W.B.; Lin, H.; Chen, H.W. Study on the excavation face stability of small interval double-line earth pressure balance shield tunnel in water-rich stratum. Railw. Stand. Des. 2018, 62, 112–117+124. (In Chinese) [Google Scholar]
- Zhang, P.; Chen, R.; Wu, H.; Liu, Y. Ground settlement induced by tunneling crossing interface of water-bearing mixed ground: A lesson from Changsha, China. Tunn. Undergr. Space Technol. 2020, 96, 103224. [Google Scholar]
- Song, Z.; Ye, G.L.; Lei, H.; Wang, J.H. Key construction technologies for large river-crossing slurry shield tunnel: Case study. J. Aerosp. Eng. 2021, 34, 04020118. [Google Scholar]
- Liang, Y.; Jiang, K.; Gao, S.J.; Yin, Y.H. Prediction of Tunnelling Parameters for Underwater Shield Tunnels, Based on the GA-BPNN Method. Sustainability 2022, 14, 13420. [Google Scholar] [CrossRef]
- Fu, Y.; Zeng, D.; Xiong, H.; Li, X.; Chen, Y. Seepage effect on failure mechanisms of the underwater tunnel face via cfd–dem coupling. Comput. Geotech. 2022, 146, 104591. [Google Scholar] [CrossRef]
- Ying, H.; Zhu, C.; Gong, X. Tide-induced hydraulic response in a semi-infinite seabed with a subaqueous drained tunnel. Acta Geotech. 2018, 13, 149–157. [Google Scholar] [CrossRef]


| Floor Number | Thickness (m) | Porosity | Permeability Coefficient (cm·s−1) | Specific Weight (kN/m3) | Elastic Modules (MPa) | Cohesion (kPa) | Poisson’s Ratio | Friction Angle (°) | |
|---|---|---|---|---|---|---|---|---|---|
| Vertical | Level | ||||||||
| 2-4 | 3.1 | 0.386 | 2.69 × 10−4 | 6.37 × 10−4 | 20 | 12 | 6.78 | 0.25 | 35.8 |
| 2-3-1 | 7.1 | 0.418 | 1.72 × 10−6 | 2.91 × 10−6 | 19.7 | 9.3 | 10.9 | 0.31 | 17.9 |
| 2-2-1 | 2.2 | 0.456 | 1.65 × 10−7 | 2.72 × 10−7 | 19.3 | 11.5 | 22.2 | 0.34 | 10.7 |
| 2-4 | 8.7 | 0.386 | 2.69 × 10−4 | 6.37 × 10−4 | 20 | 12 | 6.78 | 0.25 | 35.8 |
| 2-5 | 10.5 | 0.363 | 8.01 × 10−4 | 1.89 × 10−3 | 20.4 | 10 | 8.53 | 0.29 | 35.9 |
| 2-3-3 | 6.7 | 0.418 | 1.55 × 10−6 | 2.34 × 10−6 | 19.8 | 7.6 | 11.6 | 0.3 | 14.7 |
| 3-6 | 7.7 | 0.319 | 9.61 × 10−4 | 2.26 × 10−3 | 20.4 | 10.03 | 13.6 | 0.28 | 32.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Xi, B.; Dong, Y.; He, S.; Shi, Y.; Gao, Q.; Liu, K.; Zhao, N. Study on the Stability and Seepage Characteristics of Underwater Shield Tunnels under High Water Pressure Seepage. Sustainability 2023, 15, 15581. https://doi.org/10.3390/su152115581
Chen L, Xi B, Dong Y, He S, Shi Y, Gao Q, Liu K, Zhao N. Study on the Stability and Seepage Characteristics of Underwater Shield Tunnels under High Water Pressure Seepage. Sustainability. 2023; 15(21):15581. https://doi.org/10.3390/su152115581
Chicago/Turabian StyleChen, Luhai, Baoping Xi, Yunsheng Dong, Shuixin He, Yongxiang Shi, Qibo Gao, Keliu Liu, and Na Zhao. 2023. "Study on the Stability and Seepage Characteristics of Underwater Shield Tunnels under High Water Pressure Seepage" Sustainability 15, no. 21: 15581. https://doi.org/10.3390/su152115581
APA StyleChen, L., Xi, B., Dong, Y., He, S., Shi, Y., Gao, Q., Liu, K., & Zhao, N. (2023). Study on the Stability and Seepage Characteristics of Underwater Shield Tunnels under High Water Pressure Seepage. Sustainability, 15(21), 15581. https://doi.org/10.3390/su152115581





