Distributed Control Scheme for Clusters of Power Quality Compensators in Grid-Tied AC Microgrids
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
- A distributed control protocol using the CPT for non-active power-sharing in a cluster of parallel PQCs connected to a grid-tied MG is proposed. This protocol allocates the contributions of the converters concerning the per-unit (p.u.) available power.
- A new observer-based control loop for controlling the sharing of compensations for non-active power in a PQC cluster is presented. Also, a stability analysis is included.
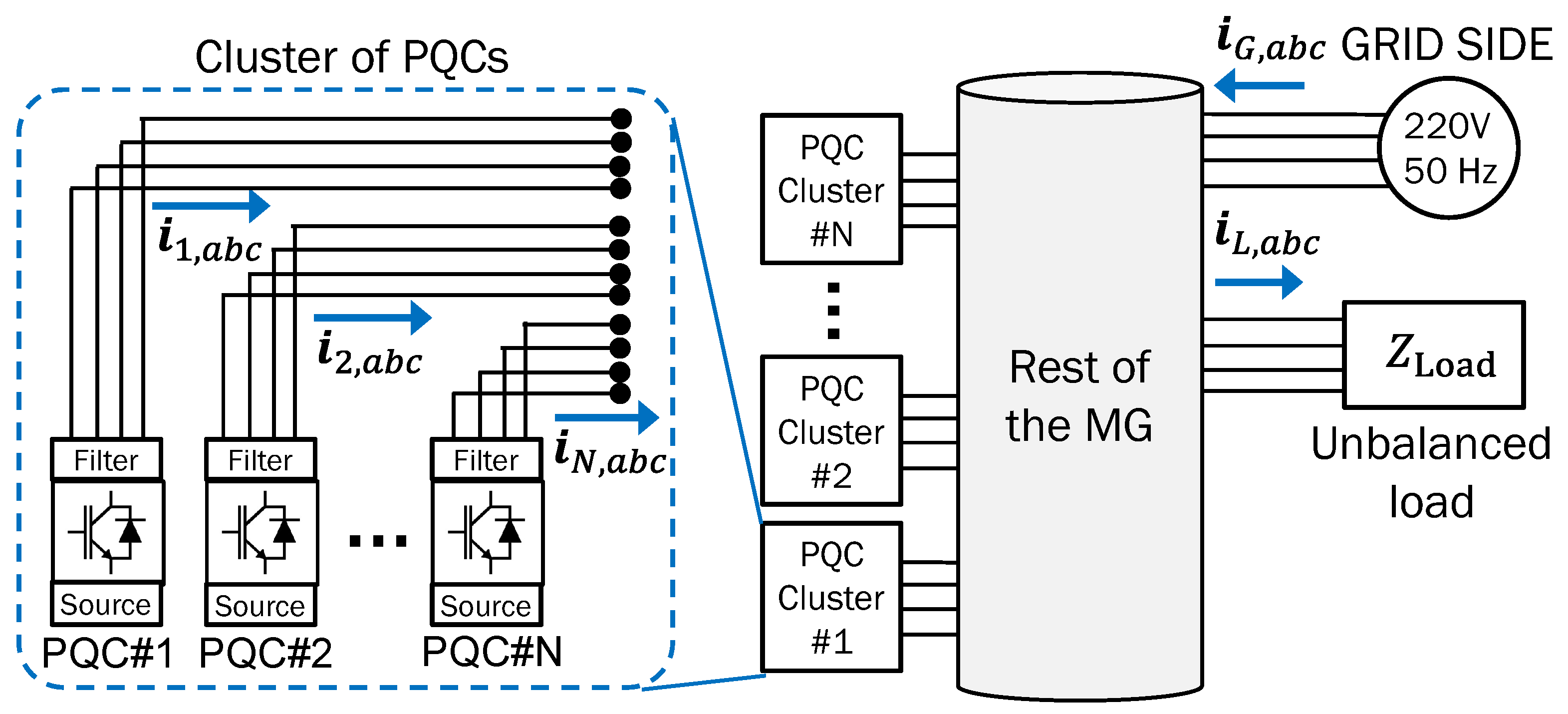
- A cooperative multi-purpose control scheme for current imbalance and harmonics in multiple buses is described. Each cluster of PQC performs a local and a grid-side compensation using the CPT framework.
- Online regulation via adjusted weights for the trade-off between grid-side and local CPT current components compensations is presented. The weights are adjusted according to deviations in defined power quality factors.
2. Preliminaries
2.1. Conservative Power Theory
2.2. Graph Theory
3. Design of Cooperative Control for Power Quality Compensators
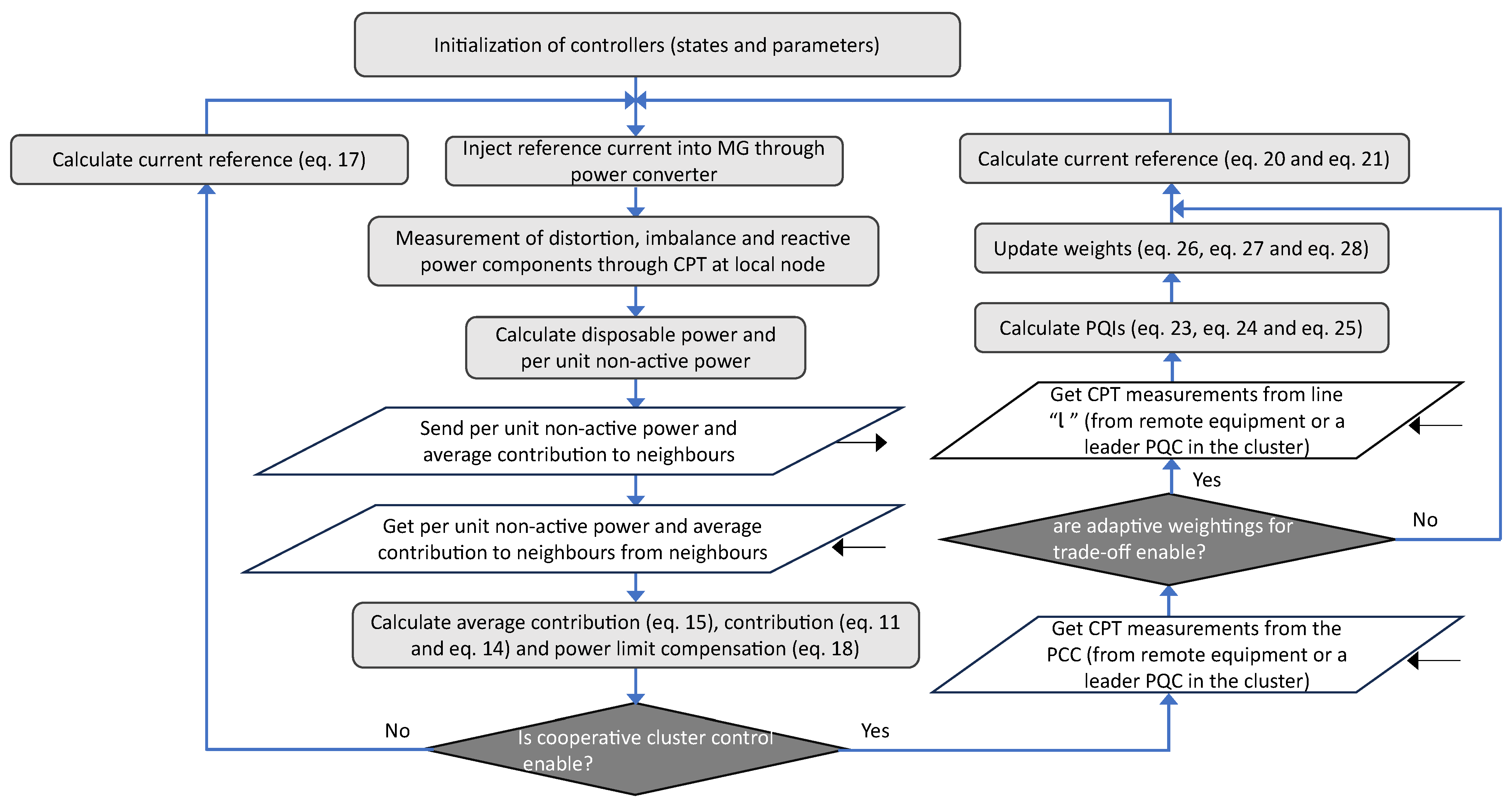
3.1. Consensus Algorithm for Non-Active Power-Sharing
3.2. Control Loop for Fulfilling the Required Compensation of Non-Active Power
3.3. Control Loop for Fulfilling Power Limit Constraints of PQCs
3.4. Stability Analysis
4. Design of Cooperative Control for Clusters of Power Quality Compensators
4.1. Multi-Purpose Compensation of PQCs for Power Quality Improvement in PCC and Local Node
4.2. Adaptive Weightings for Trade-Off between Grid and Local Power Quality Regulation
- General power factor
- Reactivity factor
- Unbalance factor
- Distortion factor
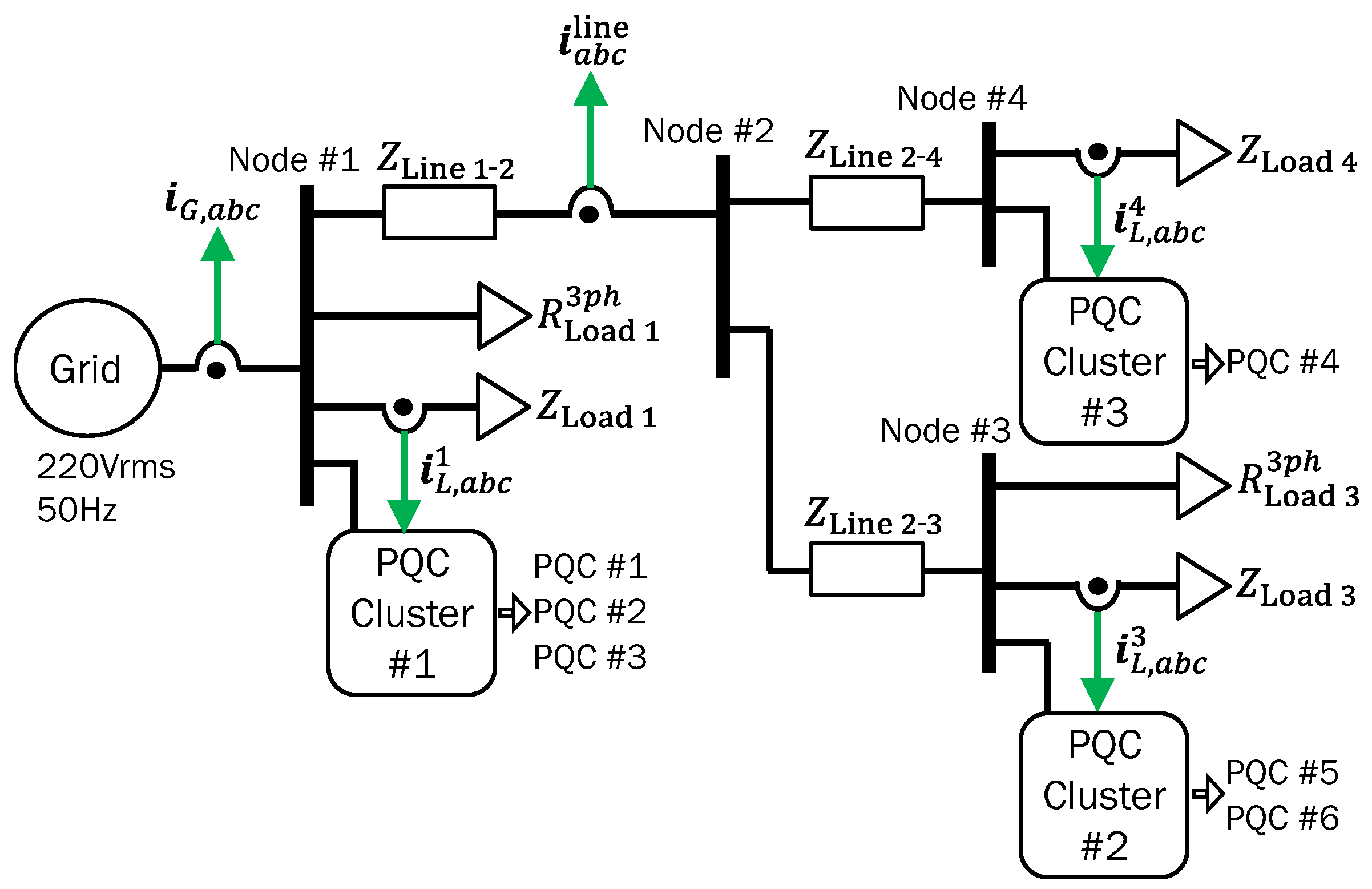
5. Case Study
5.1. Microgrid Model
5.2. Performance Tests
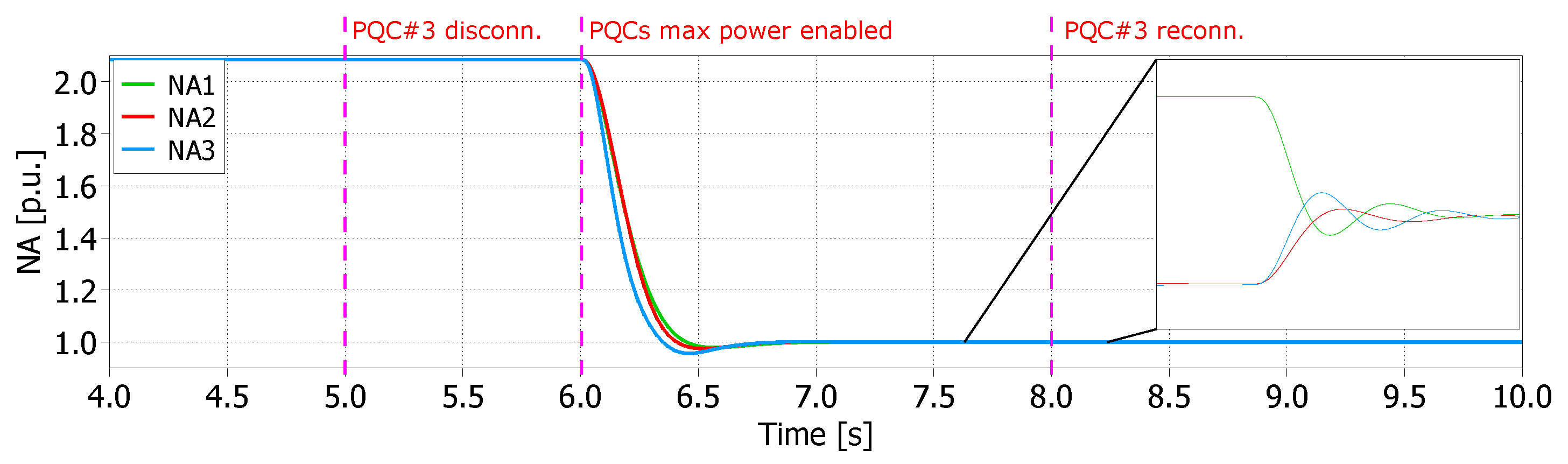
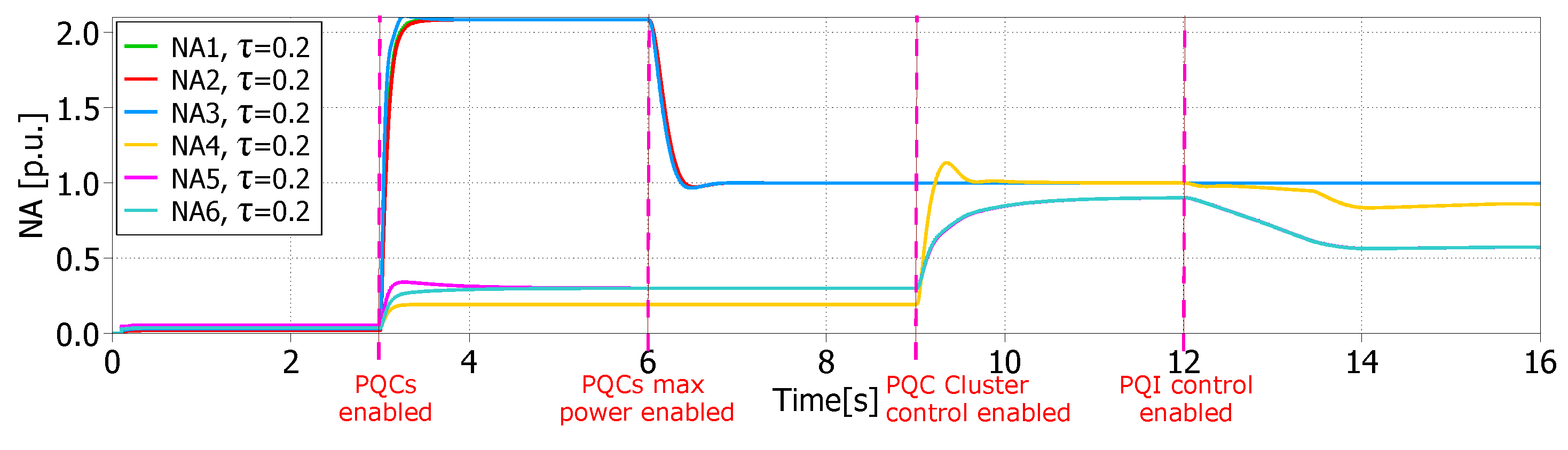
5.2.1. Case 1. Multi-Mode Operation
5.2.2. Case 2. Communication Issues within a Cluster of PQCs
5.2.3. Case 3. Communication Issues in PQI Compensation
6. Results and Discussions
6.1. Case 1
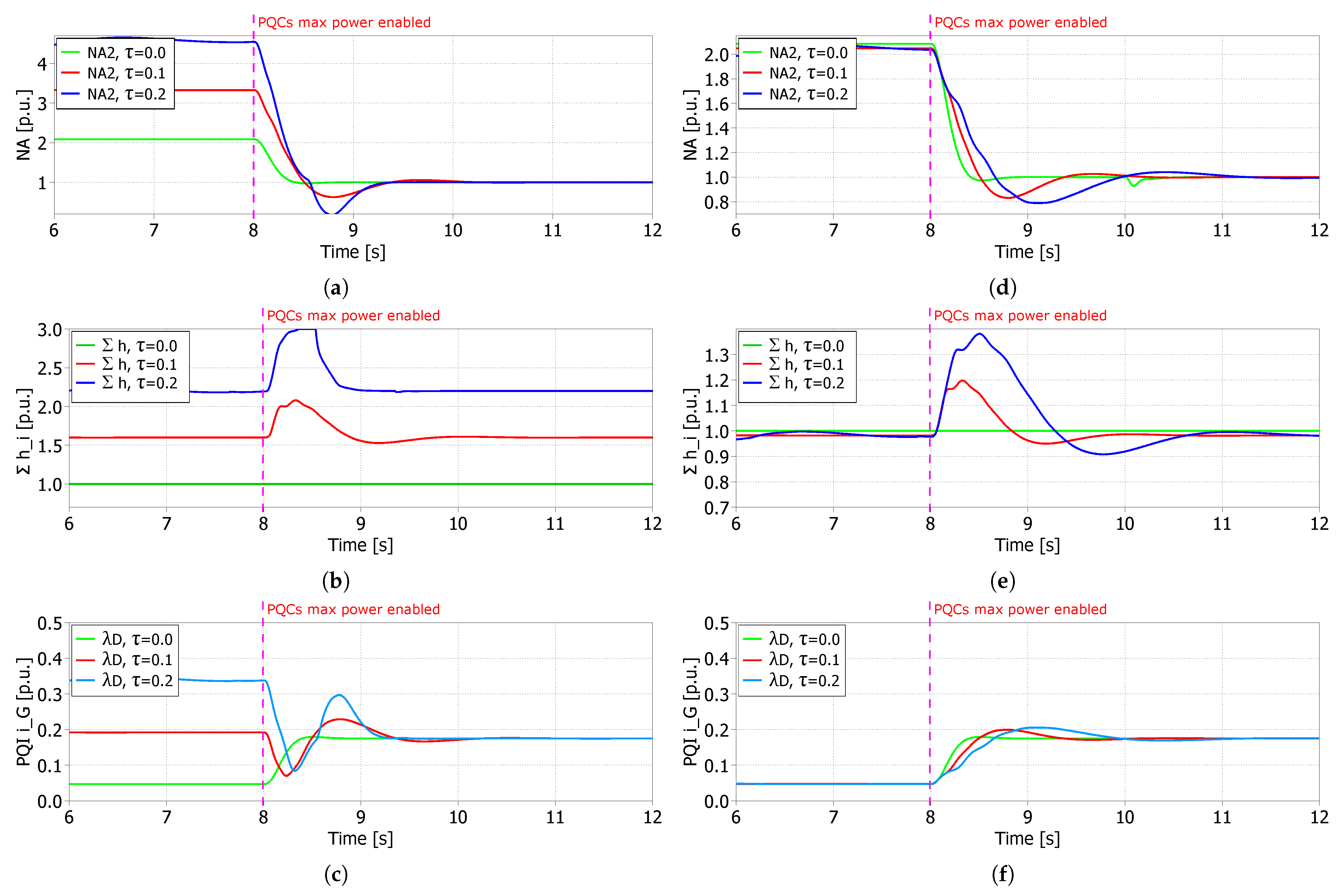
6.2. Case 2
6.2.1. Communication Link Failure inside PQC Cluster
6.2.2. Communication Delay inside PQC Cluster
6.3. Case 3
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MG | Microgrid |
| NCRE | Non-conventional renewable energy |
| LV | Low voltage |
| DFACTS | Distributed flexible AC transmission systems |
| SAPF | Shunt active power filter |
| STATCOM | Static synchronous compensator |
| PQC | Power quality compensator |
| PCC | Point of common coupling |
| CPT | Conservative power theory |
| VA | Volt-ampere |
| DSC | Delayed Signal Cancellation |
| MPPT | Maximum power point tracking |
| PQI | Power quality index |
References
- Schwaegerl, C.; Tao, L. The Microgrids Concept. In Microgrids; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 1; pp. 1–24. [Google Scholar] [CrossRef]
- Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cárdenas, R.; Martínez-Gómez, M.; Sáez, D. Distributed control strategies for microgrids: An overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Madrigal-Martínez, M.; Mina-Antonio, J.D.; Iracheta-Cortez, R.; Enríquez-Santiago, J.A.; Rodríguez-Rivera, O.; Martínez-Reyes, G.; Mendoza-Santos, E. A Comprehensive Review on Power-Quality Issues, Optimization Techniques, and Control Strategies of Microgrid Based on Renewable Energy Sources. Sustainability 2023, 15, 9847. [Google Scholar] [CrossRef]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.C.; Machado, L.; Sousa, T.J.C.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- Vineeth, G.; Aishwarya, J.; Sowmya, B.; Rani, B.; Narasimha, M. Power Quality Enhancement in Grid-Connected Renewable Energy Sources Using MC-UPQC. In Proceedings of the 2023 International Conference on Power, Instrumentation, Energy and Control (PIECON), Aligarh, India, 10–12 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, N.; Zheng, S.; Gao, W. Microgrid Harmonic Mitigation Strategy Based on the Optimal Allocation of Active Power and Harmonic Mitigation Capacities of Multi-Functional Grid-Connected Inverters. Energies 2022, 15, 6109. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Mahela, O.P.; Padmanaban, S.; Holm-Nielsen, J.B. Comprehensive Review of Distributed FACTS Control Algorithms for Power Quality Enhancement in Utility Grid With Renewable Energy Penetration. IEEE Access 2020, 8, 107614–107634. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Loh, P.C.; Lee, T.L.; Chandorkar, M. Advanced Control Architectures for Intelligent Microgrids—Part II: Power Quality, Energy Storage, and AC/DC Microgrids. IEEE Trans. Ind. Electron. 2013, 60, 1263–1270. [Google Scholar] [CrossRef]
- Pattery, J.M.; Jayaprakasan, S.; Cheriyan, E.P.; Ramchand, R. A Composite Strategy for Improved Power Quality Using Micro Compensators in Secondary Distribution Systems. IEEE Trans. Power Deliv. 2022, 37, 1027–1035. [Google Scholar] [CrossRef]
- Yang, J.; Qi, R.; Liu, Y.; Ding, Y. Coordinated Control Strategy for Harmonic Compensation of Multiple Active Power Filters. Energy Eng. 2022, 119, 609–620. [Google Scholar] [CrossRef]
- Soto, D.; Green, T. A comparison of high-power converter topologies for the implementation of FACTS controllers. IEEE Trans. Ind. Electron. 2002, 49, 1072–1080. [Google Scholar] [CrossRef]
- Perez, M.A.; Ceballos, S.; Konstantinou, G.; Pou, J.; Aguilera, R.P. Modular Multilevel Converters: Recent Achievements and Challenges. IEEE Open J. Ind. Electron. Soc. 2021, 2, 224–239. [Google Scholar] [CrossRef]
- Kontos, E.; Tsolaridis, G.; Teodorescu, R.; Bauer, P. High Order Voltage and Current Harmonic Mitigation Using the Modular Multilevel Converter STATCOM. IEEE Access 2017, 5, 16684–16692. [Google Scholar] [CrossRef]
- Morales Paredes, H.K.; Costabeber, A.; Tenti, P. Application of Conservative Power Theory to cooperative control of distributed compensators in smart grids. In Proceedings of the 2010 International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 15–18 June 2010; pp. 190–196. [Google Scholar] [CrossRef]
- Marini, A.; Ghazizadeh, M.S.; Mortazavi, S.S.; Piegari, L. A harmonic power market framework for compensation management of DER based active power filters in microgrids. Int. J. Electr. Power Energy Syst. 2019, 113, 916–931. [Google Scholar] [CrossRef]
- Mortezaei, A.; Simoes, M.G.; Savaghebi, M.; Guerrero, J.M.; Al-Durra, A. Cooperative Control of Multi-Master–Slave Islanded Microgrid With Power Quality Enhancement Based on Conservative Power Theory. IEEE Trans. Smart Grid 2018, 9, 2964–2975. [Google Scholar] [CrossRef]
- Munir, H.M.; Ghannam, R.; Li, H.; Younas, T.; Golilarz, N.A.; Hassan, M.; Siddique, A. Control of Distributed Generators and Direct Harmonic Voltage Controlled Active Power Filters for Accurate Current Sharing and Power Quality Improvement in Islanded Microgrids. Inventions 2019, 4, 27. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dorfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary Frequency and Voltage Control of Islanded Microgrids via Distributed Averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Ding, G.; Wei, R.; Zhou, K.; Gao, F. Communication-less harmonic compensation in a multi-bus microgrid through autonomous control of distributed generation grid-interfacing converters. J. Mod. Power Syst. Clean Energy 2015, 3, 597–609. [Google Scholar] [CrossRef]
- Skjong, E.; Suul, J.; Molinas, M.; Johansen, T. Optimal Compensation of Harmonic Propagation in a Multi-Bus Microgrid. Renew. Energy Power Qual. J. 2016, 236–241. [Google Scholar] [CrossRef]
- Gomez, J.S.; Llanos, J.; Espina, E.; Burgos-Mellado, C.; Rodriguez, J. Cooperative Power Conditioners for Microgrids in Mining. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Yang, Z.; Yi, H.; You, Y.; Zhuo, F.; Zhan, C.; Shi, S. Optimal Installation and System-level Control Strategy of SAPF Based on Extended-range Compensation of Multi-bus Harmonic Sources in Distribution Networks. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; pp. 1–9. [Google Scholar] [CrossRef]
- Wada, K.; Fujita, H.; Akagi, H. Considerations of a shunt active filter based on voltage detection for installation on a long distribution feeder. IEEE Trans. Ind. Appl. 2002, 38, 1123–1130. [Google Scholar] [CrossRef]
- Tenti, P.; Paredes, H.K.M.; Mattavelli, P. Conservative Power Theory, a Framework to Approach Control and Accountability Issues in Smart Microgrids. IEEE Trans. Power Electron. 2011, 26, 664–673. [Google Scholar] [CrossRef]
- Paredes, H.K.M.; Rodrigues, D.T.; Cebrian, J.C.; Bonaldo, J.P. CPT-Based Multi-Objective Strategy for Power Quality Enhancement in Three-Phase Three-Wire Systems Under Distorted and Unbalanced Voltage Conditions. IEEE Access 2021, 9, 53078–53095. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. Grid Synchronization PLL Based on Cascaded Delayed Signal Cancellation. IEEE Trans. Power Electron. 2011, 26, 1987–1997. [Google Scholar] [CrossRef]
- Svensson, J.; Bongiorno, M.; Sannino, A. Practical Implementation of Delayed Signal Cancellation Method for Phase-Sequence Separation. IEEE Trans. Power Deliv. 2007, 22, 18–26. [Google Scholar] [CrossRef]
- Neves, F.A.S.; Cavalcanti, M.C.; de Souza, H.E.P.; Bradaschia, F.; Bueno, E.J.; Rizo, M. A Generalized Delayed Signal Cancellation Method for Detecting Fundamental-Frequency Positive-Sequence Three-Phase Signals. IEEE Trans. Power Deliv. 2010, 25, 1816–1825. [Google Scholar] [CrossRef]
- Morales-Paredes, H.K.; Burgos-Mellado, C.; Bonaldo, J.P.; Rodrigues, D.T.; Quintero, J.S.G. Cooperative control of power quality compensators in microgrids. In Proceedings of the 2021 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 7–9 April 2021; pp. 380–386. [Google Scholar] [CrossRef]
- Stevanoni, C.; Deblecker, O.; Vallée, F. Cooperative Control Strategy of Multifunctional Inverters For Power Quality Enhancement in Smart Microgrids. Renew. Energy Power Qual. J. 2016, 73–78. [Google Scholar] [CrossRef]
- Spanos, D.; Olfati-Saber, R.; Murray, R. Dynamic consensus on mobile networks. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; pp. 1–6. [Google Scholar]
- Hedetniemi, S.M.; Hedetniemi, S.T.; Liestman, A.L. A survey of gossiping and broadcasting in communication networks. Networks 1988, 18, 319–349. [Google Scholar] [CrossRef]
- Llanos, J.; Olivares, D.; Simpson-Porco, J.; Mehrdad, K.; Sáez, D. A Novel Distributed Control Strategy for Optimal Dispatch of Isolated Microgrids Considering Congestion. IEEE Trans. Smart Grid 2019, 10, 6595–6606. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L.; Das, A. Optimal Design for Synchronization of Cooperative Systems: State Feedback, Observer and Output Feedback. IEEE Trans. Autom. Control. 2011, 56, 1948–1952. [Google Scholar] [CrossRef]
- Costabeber, A.; Tenti, P.; Caldognetto, T.; Liberado, E.V. Selective compensation of reactive, unbalance, and distortion power in smart grids by synergistic control of distributed switching power interfaces. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Moreira, A.C.; Paredes, H.K.M.; de Souza, W.A.; Marafão, F.P.; da Silva, L.C.P. Intelligent Expert System for Power Quality Improvement Under Distorted and Unbalanced Conditions in Three-Phase AC Microgrids. IEEE Trans. Smart Grid 2018, 9, 6951–6960. [Google Scholar] [CrossRef]
- Plexim. PLECS The Simulation Platform for Power Electronic Systems. Available online: https://www.plexim.com/products/plecs (accessed on 24 October 2023).
- Moradian, H.; Kia, S.S. On Robustness Analysis of a Dynamic Average Consensus Algorithm to Communication Delay. IEEE Trans. Control. Netw. Syst. 2019, 6, 633–641. [Google Scholar] [CrossRef]
- Martinez-Gomez, M.; Orchard, M.E.; Bozhko, S. Dynamic Average Consensus with Anti-windup applied to Interlinking Converters in AC/DC Microgrids under Economic Dispatch and Delays. IEEE Trans. Smart Grid 2023, 14, 4137–4140. [Google Scholar] [CrossRef]




| References | Additional Hardware | Communication (If Available) | Multi-Bus Compensation | Need Synchronizer or DSC | Implementation Costs |
|---|---|---|---|---|---|
| [6,14] | ✔ | centralized | × | ✔ | $ $ $ |
| [10,11,21,23,24] | ✔ | centralized | ✔ | ✔ | $ $ $ |
| [16,17,18] | × | centralized | × | ✔ | $ $ |
| [7] | × | centralized | ✔ | ✔ | $ $ |
| [15,26] | × | centralized | × | × | $ $ |
| [31] | × | centralized | ✔ | × | $ $ |
| [20,22] | × | distributed | ✔ | ✔ | $ |
| [30] | × | distributed | × | × | $ |
| Proposal | × | distributed | ✔ | × | $ |
| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| 0.3 () | 1.0 (mH) | 150 () | |||
| 0.1 () | 0.3 (mH) | 100 () | |||
| 0.3 () | 1.0 (mH) | ||||
| 10 () | 15 () | 7 () | |||
| 10 (mH) | 15 (mH) | 15 (mH) | |||
| 40 () | 56 () | 36 () | |||
| 15 (mH) | 15 (mH) | 15 (mH) | |||
| 100 () | 150 () | 100 () | |||
| 1 (mH) | 1 (mH) | 1 (mH) |
| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| 1.5 (kVA) | 1.5 (kVA) | 1.0 (kVA) | |||
| 1.7 (kVA) | 1.5 (kVA) | 2.0 (kVA) | |||
| 0.3 (kW) | 0.2 (kW) | 0.2 (kW) | |||
| 0.5 (kW) | 0.5 (kW) | 0.5 (kW) | |||
| 0.50 | 0.20 | 0.20 | |||
| 4.00 | 10.00 | 1.00 | |||
| 3.00 | 0.00 | 14.64 | |||
| 0.18 | 0.75 | 2.00 | |||
| 2.00 | 2.00 | 0.60 | |||
| 2.00 | 2.00 | 0.60 | |||
| 24.66 | 24.66 | 2.46 | |||
| 8.97 () | 0.20 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Gómez, M.; Burgos-Mellado, C.; Morales-Paredes, H.K.; Gómez, J.S.; Verma, A.K.; Bonaldo, J.P. Distributed Control Scheme for Clusters of Power Quality Compensators in Grid-Tied AC Microgrids. Sustainability 2023, 15, 15698. https://doi.org/10.3390/su152215698
Martínez-Gómez M, Burgos-Mellado C, Morales-Paredes HK, Gómez JS, Verma AK, Bonaldo JP. Distributed Control Scheme for Clusters of Power Quality Compensators in Grid-Tied AC Microgrids. Sustainability. 2023; 15(22):15698. https://doi.org/10.3390/su152215698
Chicago/Turabian StyleMartínez-Gómez, Manuel, Claudio Burgos-Mellado, Helmo Kelis Morales-Paredes, Juan Sebastián Gómez, Anant Kumar Verma, and Jakson Paulo Bonaldo. 2023. "Distributed Control Scheme for Clusters of Power Quality Compensators in Grid-Tied AC Microgrids" Sustainability 15, no. 22: 15698. https://doi.org/10.3390/su152215698
APA StyleMartínez-Gómez, M., Burgos-Mellado, C., Morales-Paredes, H. K., Gómez, J. S., Verma, A. K., & Bonaldo, J. P. (2023). Distributed Control Scheme for Clusters of Power Quality Compensators in Grid-Tied AC Microgrids. Sustainability, 15(22), 15698. https://doi.org/10.3390/su152215698










