A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm for PM2.5 Daily Concentration Prediction
Abstract
:1. Introduction
2. Materials
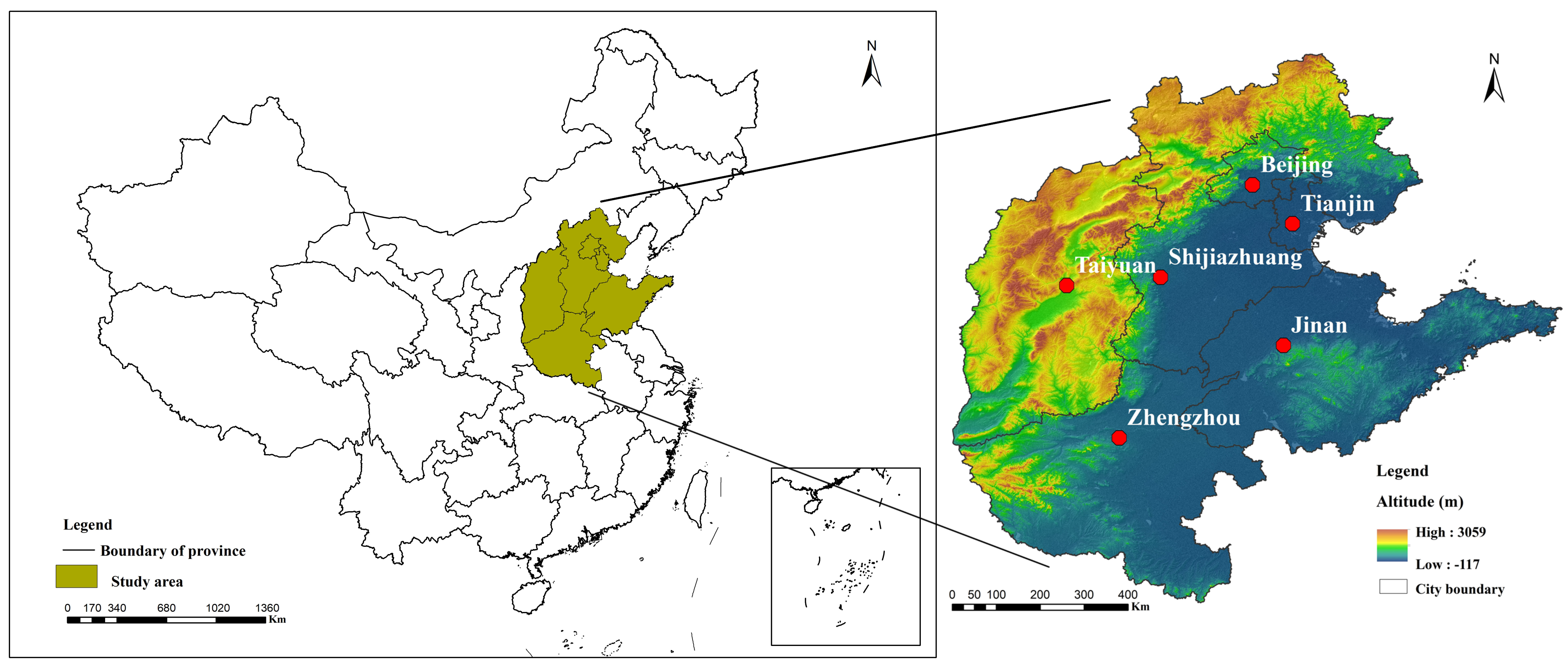
2.1. Study Area
2.2. Data Collection
3. Methods
3.1. Short-Term Trend Information-Based Time Series Forecasting Algorithm (STI-TSF)
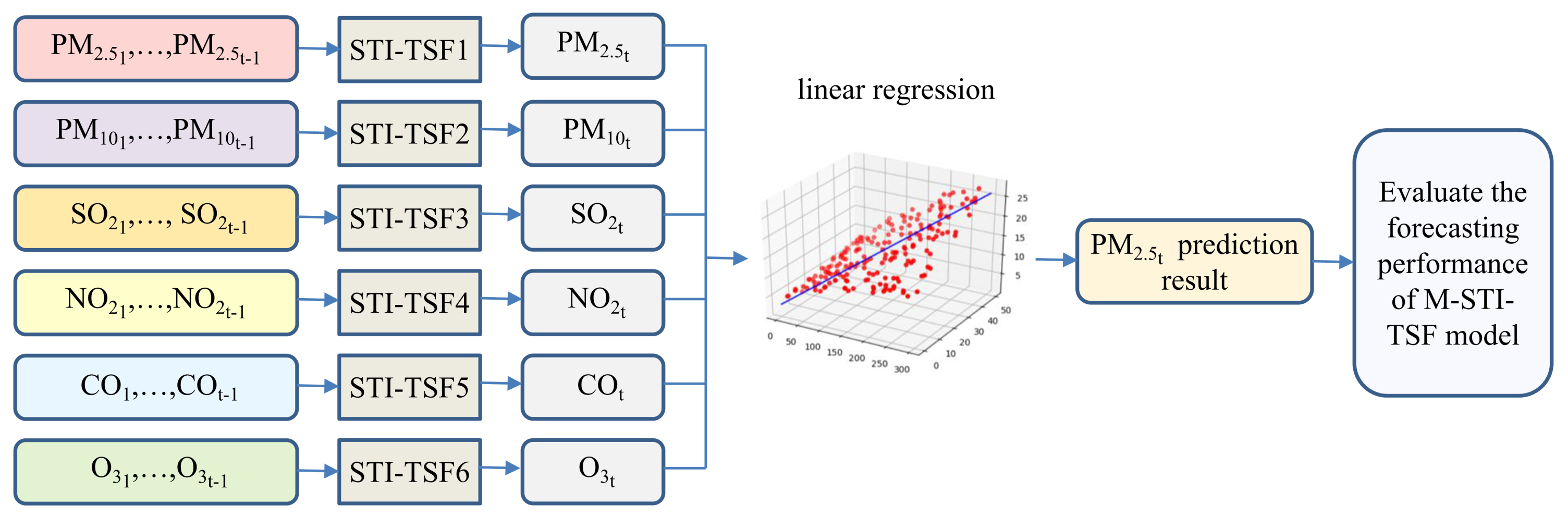
3.2. A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm (M-STI-TSF)
| Algorithm 1 A multivariate short-term trend information-based time series forecasting algorithm |
Require:the data set , where is the input vector of the prediction system composed of historical data of air pollutants, and is the PM concentration monitoring value at time t, which serves as the output of the prediction system. Ensure:the prediction results of PM concentration at time . 1: Each input feature forms a one-dimensional time series PM, PM, SO, NO,O and CO, which are respectively inputted into the STI-TSF model to obtain the prediction results , , , , and of each feature at time , where . 2: All nonzero feature prediction results and PM observations form a new training set , where , which contains short-term trend information for each feature time series and . 3: Construct the input vector at time considering the rule of the preceding step. 4: The linear regression model was trained and validated on training set to optimize its model parameters. 5: The final prediction result can be obtained by inputting into the trained linear regression model. Repeat step1 to step5 to get the prediction results at time . |
3.3. Evaluation of the Methods
4. Results and Discussion
4.1. Prediction Results of Input Features Combined with Short-Term Trend Information
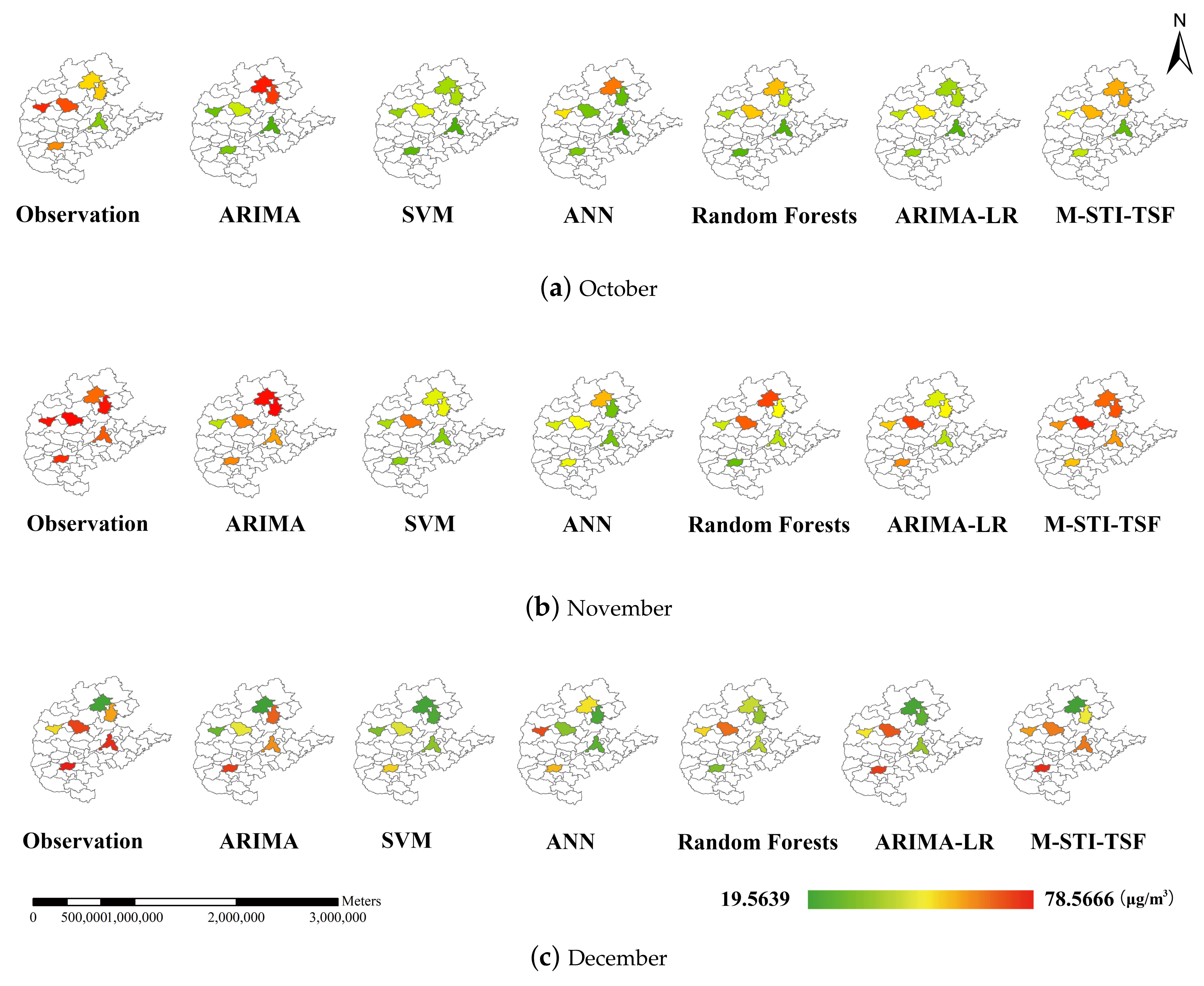
4.2. Comparison of Prediction Results between M-STI-TSF Model and Traditional Models
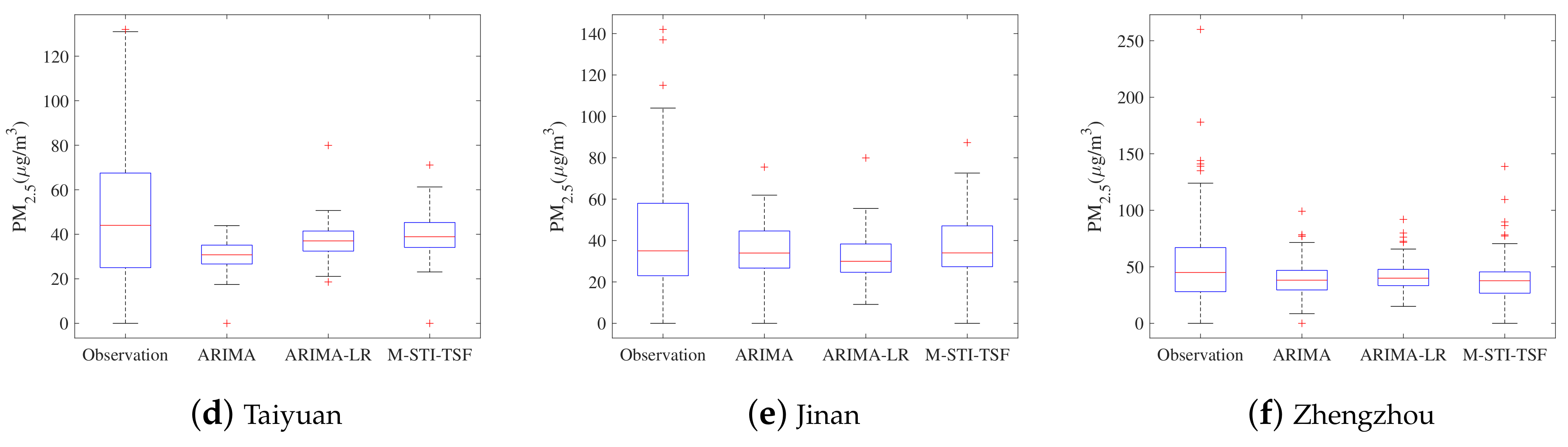
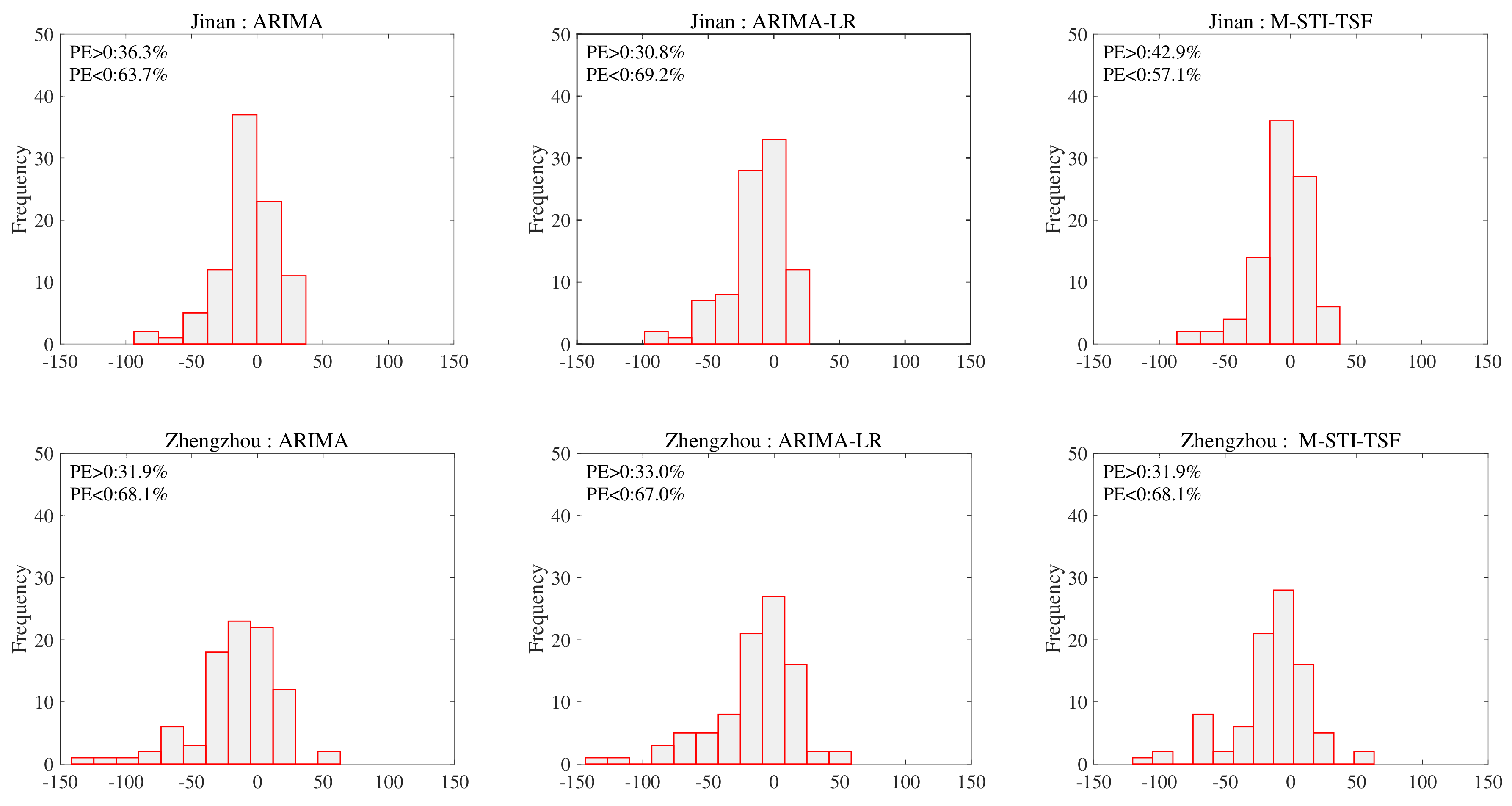
4.3. Comparison of Prediction Results between M-STI-TSF Model and Hybrid Model ARIMA-LR
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, F.Y.; Feng, C.Y.; Yang, Z.M.; Hsu, C.H.; Chan, K.W.; Lee, C.Y.; Chang, S.C. Evaluation of real-time PM2.5 forecasts with the WRF-CMAQ modeling system and weather-pattern-dependent bias-adjusted PM2.5 forecasts in Taiwan. Atmos. Environ. 2021, 244, 117909. [Google Scholar] [CrossRef]
- Jin, X.; Cai, X.; Yu, M.; Song, Y.; Wang, X.; Kang, L.; Zhang, H. Diagnostic analysis of wintertime PM2.5 pollution in the North China Plain: The impacts of regional transport and atmospheric boundary layer variation. Atmos. Environ. 2020, 224, 117346. [Google Scholar] [CrossRef]
- Yan, D.; Lei, Y.; Shi, Y.; Zhu, Q.; Li, L.; Zhang, Z. Evolution of the spatiotemporal pattern of PM2.5 concentrations in China—A case study from the Beijing-Tianjin-Hebei region. Atmos. Environ. 2018, 183, 225–233. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.J.; Chang, L.C.; Kao, I.F.; Wang, Y.S.; Kang, C.C. Multi-output support vector machine for regional multi-step-ahead PM2.5 forecasting. Sci. Total Environ. 2019, 651, 230–240. [Google Scholar] [CrossRef] [PubMed]
- Kow, P.Y.; Wang, Y.S.; Zhou, Y.; Kao, I.F.; Issermann, M.; Chang, L.C.; Chang, F.J. Seamless integration of convolutional and back-propagation neural networks for regional multi-step-ahead PM2.5 forecasting. J. Clean. Prod. 2020, 261, 121285. [Google Scholar] [CrossRef]
- Yeo, I.; Choi, Y.; Lops, Y.; Sayeed, A. Efficient PM2.5 forecasting using geographical correlation based on integrated deep learning algorithms. Neural Comput. Appl. 2021, 33, 15073–15089. [Google Scholar] [CrossRef]
- Samal, K.K.R.; Babu, K.S.; Das, S.K. Multi-directional temporal convolutional artificial neural network for PM2.5 forecasting with missing values: A deep learning approach. Urban Clim. 2021, 36, 100800. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, L.C.; Chang, F.J. Explore a Multivariate Bayesian Uncertainty Processor driven by artificial neural networks for probabilistic PM2.5 forecasting. Sci. Total Environ. 2020, 711, 134792. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Gao, S.; Jin, T.; Sato, S.; Zhang, X. A seasonal-trend decomposition-based dendritic neuron model for financial time series prediction. Appl. Soft Comput. 2021, 108, 107488. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, X. Predicting energy consumption: A multiple decomposition-ensemble approach. Energy 2019, 189, 116045. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, X. Predicting China’s energy consumption: Combining machine learning with three-layer decomposition approach. Energy Rep. 2021, 7, 5086–5099. [Google Scholar] [CrossRef]
- Bas, M.; Ortiz, J.; Ballesteros, L.; Martorell, S. Analysis of the influence of solar activity and atmospheric factors on 7Be air concentration by seasonal-trend decomposition. Atmos. Environ. 2016, 145, 147–157. [Google Scholar] [CrossRef]
- Song, Z.; Fu, D.; Zhang, X.; Han, X.; Song, J.; Zhang, J.; Wang, J.; Xia, X. MODIS AOD sampling rate and its effect on PM2.5 estimation in North China. Atmos. Environ. 2019, 209, 14–22. [Google Scholar] [CrossRef]
- Xu, W.; Wu, Q.; Liu, X.; Tang, A.; Dore, A.J.; Heal, M.R. Characteristics of ammonia, acid gases, and PM2.5 for three typical land-use types in the North China Plain. Environ. Sci. Pollut. Res. 2016, 23, 1158–1172. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Xiao, Q.; Meng, X.; Geng, G.; Wang, Y.; Lyapustin, A.; Gu, D.; Liu, Y. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain. Environ. Pollut. 2018, 242, 675–683. [Google Scholar] [CrossRef] [PubMed]
- China National Environmental Monitoring Center. Air Quality Status Report; China National Environmental Monitoring Center: Beijing, China, 2021. [Google Scholar]
- Feng, H.; Qian, Y. A Linear Differentiator Based on the Extended Dynamics Approach. IEEE Trans. Autom. Control 2022, 67, 6962–6967. [Google Scholar] [CrossRef]
- Feng, H.; Guo, B.Z. Extended dynamics observer for linear systems with disturbance. Eur. J. Control 2023, 71, 100806. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Liang, L. Spatio-temporal evolution of ozone pollution and its influencing factors in the Beijing-Tianjin-Hebei Urban Agglomeration. Environ. Pollut. 2020, 256, 113419. [Google Scholar] [CrossRef] [PubMed]
- Ordóñez, C.; Sánchez Lasheras, F.; Roca-Pardiñas, J.; de Cos Juez, F.J. A hybrid ARIMA–SVM model for the study of the remaining useful life of aircraft engines. J. Comput. Appl. Math. 2019, 346, 184–191. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]




| Monitoring Site | PM | PM | SO | NO | CO | O |
|---|---|---|---|---|---|---|
| Beijing | 3.4717 | 4.0569 | 0.4398 | 2.9285 | 0.1792 | 4.1748 |
| Tianjin | 3.7496 | 4.2947 | 1.4625 | 3.4132 | 0.2687 | 4.3273 |
| Shijiazhuang | 4.0727 | 4.6867 | 1.8496 | 3.5379 | 0.3877 | 4.5385 |
| Taiyuan | 4.0259 | 4.7017 | 2.2699 | 3.5498 | 0.4349 | 4.3875 |
| Jinan | 3.7403 | 4.3194 | 2.1140 | 3.3483 | 0.4116 | 4.4225 |
| Zhengzhou | 4.1133 | 4.6949 | 1.7382 | 3.2616 | 0.4111 | 4.5803 |
| Index | Model | Beijing | Tianjin | Shijiazhuang | Taiyuan | Jinan | Zhengzhou |
|---|---|---|---|---|---|---|---|
| MAE (g/m) | ARIMA | 22.9766 | 24.9719 | 22.9339 | 24.0437 | 16.9997 | 25.2036 |
| SVM | 20.1312 | 23.2731 | 21.5387 | 23.0336 | 18.5201 | 29.2287 | |
| ANN | 23.1709 | 25.0882 | 25.1652 | 23.5022 | 20.7495 | 27.3979 | |
| Random Forests | 22.3096 | 24.2858 | 21.2764 | 22.8206 | 19.5298 | 31.6621 | |
| ARIMA-LR | 20.6556 | 23.5358 | 20.9965 | 21.2971 | 18.2927 | 25.2138 | |
| M-STI-TSF | 18.9202 | 20.6108 | 19.1857 | 19.9263 | 15.5003 | 23.4288 | |
| RMSE (g/m) | ARIMA | 37.9598 | 35.2849 | 31.4454 | 32.5178 | 24.1315 | 37.4335 |
| SVM | 27.6051 | 31.4235 | 28.7260 | 31.6681 | 26.2627 | 42.1796 | |
| ANN | 31.1573 | 34.7872 | 33.7879 | 32.3894 | 27.9809 | 41.0037 | |
| Random Forests | 30.1424 | 33.9985 | 30.0709 | 31.5665 | 27.2551 | 48.1769 | |
| ARIMA-LR | 28.2249 | 32.0370 | 27.2791 | 29.4688 | 26.4061 | 37.9620 | |
| M-STI-TSF | 26.8017 | 27.5034 | 25.4315 | 26.7034 | 21.8855 | 34.6578 | |
| R | ARIMA | 0.7841 | 0.7971 | 0.7095 | 0.5672 | 0.6303 | 0.6668 |
| SVM | 0.5750 | 0.6592 | 0.7375 | 0.6027 | 0.6893 | 0.7183 | |
| ANN | 0.4493 | 0.6046 | 0.6866 | 0.1249 | 0.6568 | 0.7046 | |
| Random Forests | 0.4951 | 0.5029 | 0.6146 | 0.2843 | 0.5465 | 0.5484 | |
| ARIMA-LR | 0.5528 | 0.6440 | 0.6825 | 0.5525 | 0.6882 | 0.6834 | |
| M-STI-TSF | 0.5967 | 0.6924 | 0.7567 | 0.6119 | 0.7064 | 0.7224 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; He, X.; Feng, H.; Zhang, G. A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm for PM2.5 Daily Concentration Prediction. Sustainability 2023, 15, 16264. https://doi.org/10.3390/su152316264
Wang P, He X, Feng H, Zhang G. A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm for PM2.5 Daily Concentration Prediction. Sustainability. 2023; 15(23):16264. https://doi.org/10.3390/su152316264
Chicago/Turabian StyleWang, Ping, Xuran He, Hongyinping Feng, and Guisheng Zhang. 2023. "A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm for PM2.5 Daily Concentration Prediction" Sustainability 15, no. 23: 16264. https://doi.org/10.3390/su152316264
APA StyleWang, P., He, X., Feng, H., & Zhang, G. (2023). A Multivariate Short-Term Trend Information-Based Time Series Forecasting Algorithm for PM2.5 Daily Concentration Prediction. Sustainability, 15(23), 16264. https://doi.org/10.3390/su152316264





