Classification Study of New Power System Stability Considering Stochastic Disturbance Factors

Abstract

Power system instability causes many local or large-scale power outage accidents. To maintain sustainable development, a new power system construction aimed at maximizing new energy consumption is being put on the agenda. However, with a large increase in stochastic disturbance factors (SDFs), the system gradually shows strong stochasticity, and the stability presents greater complexity. It is necessary to analyze the impact on the system based on different processing methods of SDFs to maintain system stability. This paper delves into the impact of SDFs on system stability by analyzing and summarizing both stochastic variables and processes. Initially, the SDFs in the power system are meticulously analyzed and categorized. When the SDFs are treated as stochastic variables, the probabilistic stability is classified and evaluated based on a probability analysis method, which includes the probabilistic small-disturbance stability, the probabilistic transient stability, and the probabilistic voltage stability. When the SDFs are treated as stochastic processes, the stochastic stability is classified and evaluated by using a stochastic analysis method, including the stochastic small-disturbance stability, the stochastic transient stability, and the stochastic voltage stability. Finally, the research perspectives on SDFs and system stability are discussed and prospected.

1. Introduction

In December 2020, a white paper entitled “China’s Energy Development in the New Era” was issued by the Information Office of China’s State Council. In this white paper, the routes of “carbon peaking” and “carbon neutrality” are proposed, and the proportion of new energy in power systems will be further increased [1]. At the same time, the overall structure of the power grid has become more complex, and power outage accidents occur frequently around the world [2]. The blackout accidents caused by large-scale off-grid renewable energy also occurred [3,4,5], and the consequences are severe. While constructing a new power system, the influences of a large number of stochastic disturbance factors (SDFs), such as wind or photovoltaic (PV) power output with stochastic fluctuations on the power system’s stability, cannot be ignored [6,7,8].

The perceptions of “uncertainty” can be classified into three aspects: stochasticity, fuzziness, and ignorance, with stochasticity being the most widely discussed in power system analysis [9]. This review focuses on the “stochasticity” in power systems. The high penetration of renewable energy, such as wind/PV power, is greatly affected by the weather and environment, and their generation performance is characterized by intermittence and volatility. The large number of new energy electric vehicles (EVs) leads to system load display initiatives and complexity. The transmission grid is affected by stochastic load sources, and wide-ranging current fluctuations can also occur. At the same time, the increasingly complex overall grid structure and the mass access of power electronic equipment make the grid change from a deterministic system to a strong stochastic system. Whether the system can maintain stability is the prerequisite for safe and stable operations. The input of SDFs increases the overall or local instability and power outage risks, making the system more prone to extreme development. The traditional grid has a simple topology, low degree of regional interconnection, small unit capacity, and relatively simple equipment types, so the system stability analysis is mainly based on a deterministic method and has obtained quite rich research results [10,11]. However, the traditional deterministic analysis method ignores the SDFs’ influence on system stability, reducing the accuracy of the analysis results. It is necessary to adopt a stochastic analysis method to dissect the stability of a new power system with new energy as the main body.

Power system stability research under the consideration of SDFs has been carried out for nearly half a century, which can be mainly divided into two stages. In the first stage, R. C. Burchett first applied probability theory to describe the stochastic disturbance of power systems and solve the probability distribution of stochastic variables in the form of mathematical modeling [12]. Later, studies were continued based on the probabilistic analysis method. After 2000, the research hotspot of the probabilistic analysis method was shifted to new energy, and until now, there are still many scholars researching the relevant issues in this field [13,14]. In the second stage, scholars considered the SDFs as stochastic processes and integrated them into the stochastic modeling of power systems, using the stochastic differential equation (SDE) theory, crossing the probability theory and the differential equation to carry out the analysis. This approach has pioneered a new field of research in stochastic dynamics within power systems [15,16].

This paper synthesizes recent research on stochasticity, summarizing and analyzing the specific issue of how to approach SDFs and their impact on system stability. It categorizes SDFs into two types: stochastic variables and stochastic processes. Accordingly, system stability is classified into probabilistic stability and stochastic stability. Then, the analysis methods and the specific categories are dissected. Finally, some problems worth considering are discussed regarding the SDFs and system stability.

2. Stochastic Disturbance Factors

The specific meaning of the SDFs is the uncertainty with statistical law, which is a form of contingency. The SDFs in the power system exhibit a diverse range of attributes, varying from inconspicuous to prominent and from minor to substantial disturbances. The change rule in the SDFs cannot be accurately grasped, and it is generally portrayed by using statistical methods, such as providing the probability distribution function or fluctuation interval [17,18]. In traditional systems, SDFs also exist; however, due to their relatively insignificant stochastic nature, these SDFs are often overlooked in related studies. The impact of stochasticity becomes non-negligible in new power systems, and the SDFs are complex and diverse and can be classified in terms of the source, variable type, time scale, descriptive equation, and so on.

2.1. Sources of SDFs

The input of SDFs not only makes the power system surge in stochasticity but also greatly increases the complexity of the system, which is mainly reflected in the three links of “source–grid–load”.

In order to promote the overall green transformation and upgrading of energy, on the “source” side, a large amount of new energy power generation is being connected. Unlike traditional power generation, new energy power has a strong stochastic fluctuation, which is easy to impact the system’s stability [8].

Due to the demand for electricity, the power grid’s scale becomes larger. On the “grid” side, the emerging power electronics technology and control technology are commonly used in transmission and distribution links and bring more SDFs with greater intensity [19]. The heightened amplitude of system voltage and frequency fluctuations leads to a higher incidence of stochastic events such as network failure.

On the “load” side, EVs and electric trains increase uncertainty and flexibility. The load property shifts from “rigid” to “soft”; it is easy to increase the probability of the load loss time, which further increases the stochasticity [20].

2.2. Variable Types of SDFs

Statistically, the curves of load changes and new energy power changes are continuous and smooth, so they can be classified as continuous stochastic variables. Discrete events that occur by chance, such as stochastic charge and discharge behaviors of EVs, load shocks, power generation unit switching, system faults, and reclosing actions, can be classified as discrete stochastic variables [21].

2.3. Time Scales of SDFs

From a time-scale perspective, continuously varying stochastic variables caused by loads such as EVs are fast-varying SDFs. The variations in new energy sources, such as wind/PV, are generally between seconds and minutes and can be treated as slow-varying SDFs [22]. Stochastic system failures, as well as the actions of power electronic equipment, are usually performed in a very short period of time with a time scale of microseconds and thus can be considered as sudden-change SDFs [23].

2.4. Descriptive Equations for SDFs

The equations for describing the SDFs in the power system have three categories. The first one is the uncertainty of the initial value. The initial value is not the system equilibrium point before suffering a stochastic disturbance but rather the system value after the last operation. The initial value’s stochasticity is mainly caused by the uncertainty of the equilibrium point, and during the steady-state operation, the equilibrium point will fluctuate stochastically in a very small range. The main reason is that external environmental changes or internal structural changes lead to fluctuations in a small range of the equilibrium point. Such stochastic disturbances are generally analyzed using the probabilistic analysis method. Firstly, it is assumed that the initial value’s stochasticity obeys a certain probability distribution, and the probabilistic algebraic equation model is derived, and then the probability of the whole system stability is analyzed and calculated by using the probabilistic method. The system is judged whether it is stable or not according to the probabilistic results. With the depth of the study, for this type of stochastic disturbance, the contradiction between computation quantity and accuracy is gradually reduced.

The second category is the stochasticity of component parameters and coefficients, which is mainly caused by some internal or external factors that change the parameters or coefficients of lines and equipment. This type of stochastic disturbance is akin to the first type, which is used as a slow variable in dynamic analysis and is also assumed to obey a certain probability distribution, and then the system’s stability probability or the trajectory envelope is calculated [24,25].

The above two types of stochastic disturbances are based on the probability equation model, which is mainly analyzed by the probability theory method and is relatively mature.

The third category is the stochasticity of external excitation, which is different from the first two categories of stochastic disturbances. It is a fast variable in the dynamic process with time-variant properties, such as the intermittence of wind/PV power. When regional interconnected power grids are subject to external stochastic disturbances, probabilistic algebraic equations cannot satisfy the modeling and analysis of this type of stochastic disturbances. Therefore, the SDE and related theories should be introduced [26].

3. Research Framework of New Power System Stability

The research framework of new power system stability is shown in

Table 1. The research framework of new-type power system stability considering the stochastic disturbance factors (SDFs).

Processing Type of SDF	Stability Category	Research Content	Research Methodology	Theory
Stochastic variable	Probabilistic small- disturbance stability	Based on the deterministic small-disturbance stability analysis, considering the probability models of various stochastic uncertain sources, the small-disturbance stability is determined by the probability distributions of the key eigenvalues and other associated SDFs.	Simulation method, approximation method and analytical method based on probabilistic analysis methods	Probabilistic algebraic equation theory
	Probabilistic transient stability	Take the fault factors in the system as stochastic probabilistic events and consider the impact of a limited number of stochastic variables on the transient stability.
	Probabilistic voltage stability	Introduce the SDFs into the system and consider the possibility of the existence of a certain state together with the voltage stability in that state.
Stochastic process	Stochastic small- disturbance stability	Establish the model of stochastic small disturbance and introduce it into the system state equations, and study the impact of stochastic excitations on the system’s dynamic processes.	Mean value stability and mean square stability	Stochastic differential equation theory
	Stochastic transient stability	Study the system transient stability by considering stochastic disturbances with large intensity, such as stochastic faults superimposed on stochastic excitations.	Energy function method, extended equal-area method and analytical method considering stochastic excitations
	Stochastic voltage stability	Stochastic disturbances are modeled as stochastic excitations to study the system’s stochastic voltage dynamic response.	Voltage stability assessment method based on stochastic model

. System stability is classified into two major categories: probabilistic stability and stochastic stability, according to the processing type of SDFs. It can be sorted out as follows:

(1)

When the SDFs are treated as stochastic variables, the probabilistic stability is analyzed and evaluated based on probabilistic analysis method and probabilistic algebraic equation, including probabilistic small-disturbance stability, probabilistic transient stability, and probabilistic voltage stability.

(2)

If stochastic variables are replaced by stochastic processes considering the persistent disturbances by the SDFs, the stochastic stability is analyzed and evaluated based on the stochastic analysis method and SDE, including stochastic small-disturbance stability, probabilistic transient stability, and probabilistic voltage stability.

4. Probabilistic Stability Analysis

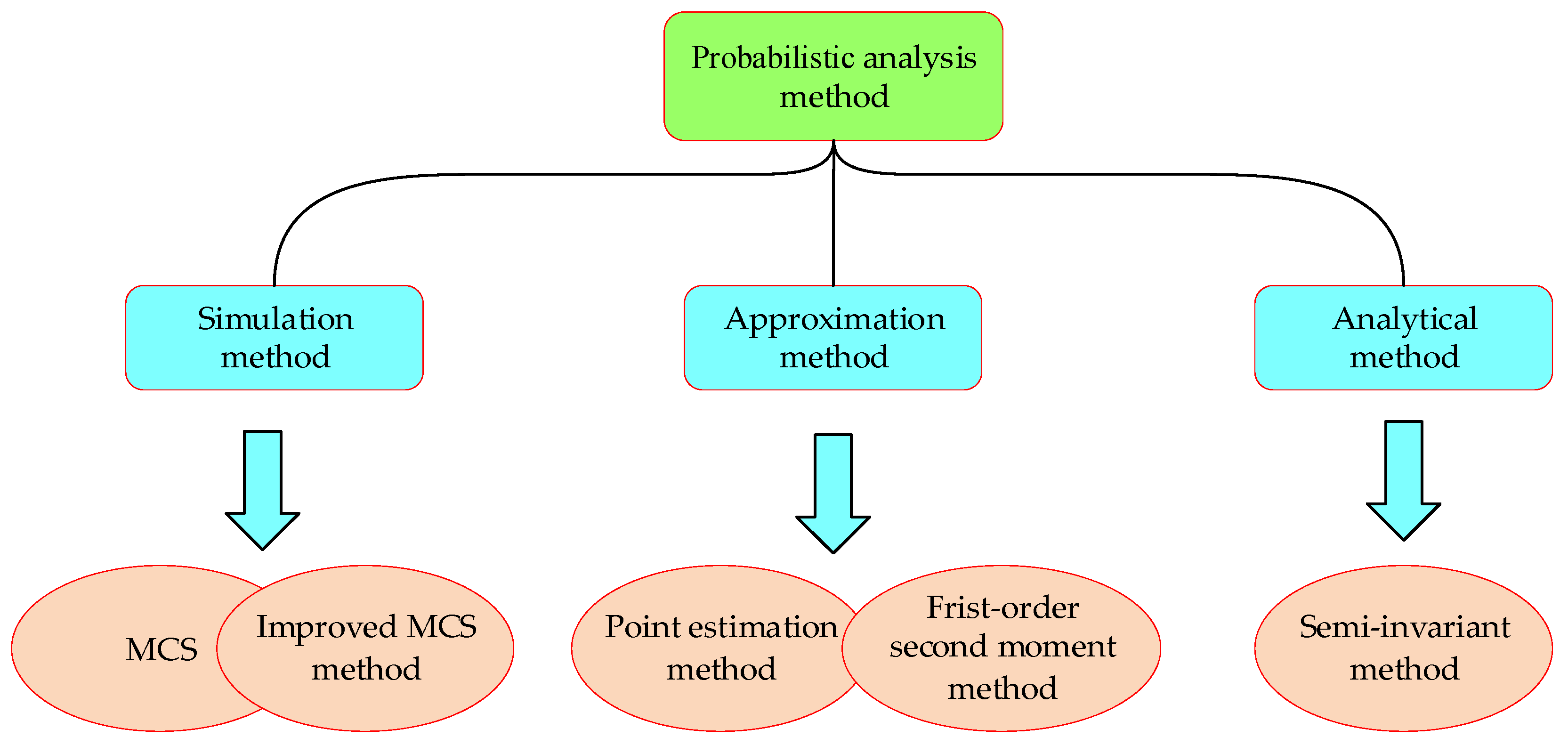
4.1. Probabilistic Analysis Method

Probabilistic analysis is the main method for studying probabilistic stability, and it is also used for stochastic analysis problems such as state estimation and probabilistic currents, etc. (The main goal is to obtain the probabilistic statistical characteristics of the system’s output variables, which can be used to quantify the impact of the system’s input stochastic variables [27,28,29]) By establishing the probability model of input stochastic variables, the probabilistic statistical characteristics of the system’s output variables can be obtained, which can be used to quantify the impact of the system’s input stochastic variables. The input random variables of the new power system mainly consist of renewable energy and uncertainty loads. The output power of the wind turbine changes with the fluctuation of the local wind speed. The probability model distribution of the wind speed can use the two-parameter Weibull distribution model [25]:

$$f(v)=\frac{k}{c}{(\frac{v}{c})}^{k-1}\exp (-{(\frac{v}{c})}^k)$$

(1)

where v is the wind speed; k and c are the shape and scale parameters of the Weibull distribution, respectively, and f(v) is the probability density function of the wind turbine.

The output power of the PV power supply is mainly affected by light intensity. The probability model of light intensity adopts the Beta distribution model [25]:

$$F(r)=\frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\cdot {(\frac{r}{r_{\max }})}^{a-1}\cdot {(1-\frac{r}{r_{\max }})}^{b-1}$$

(2)

where r is the light intensity, a and b are the shape parameters of the Beta distribution, r_max indicates the maximum light intensity of the place, and Γ is the Gamma function.

Loads adopt a normal distribution model [25]:

$$f(P_{\mathrm{L}})=\frac{1}{\sqrt{2\pi }{\sigma }_{\mathrm{L}}}\exp {\left[-\frac{(P_{\mathrm{L}}-P_{\mathrm{L}0})}{2{\sigma }_{\mathrm{L}}^2}\right]}^2$$

(3)

where P_L is the load power, P_L0 is the reference value of load power, σ_L is the standard deviation of load power.

As shown in Figure 1, common probabilistic analysis methods mainly include the simulation method, approximation method, and analytical method [30]. The simulation method mainly uses the Monte Carlo Simulation (MCS) [31], which obtains different sample scenarios by repeatedly sampling the stochastic input variables, and then analyses each specific scenario accordingly, and finally obtains the statistical characteristics of the stochastic output variables. MCS is computationally simple, can consider a variety of complex SDFs, and still has high computational accuracy as the number of sample scenarios is large. However, owing to its computational inefficiency, MCS is typically employed as a tool for verifying the accuracy of other simulation methods. Some effective sampling methods, such as Latin Hypercubic Sampling [32,33], Significant Sampling [34], and Low Bias Sequence [35], are currently proposed to accelerate the speed of convergence and reduce the number of required samples.

The approximation method employs a limited number of samples of stochastic variables to approximate the statistical characteristics of the object of study, e.g., the 1-order second-moment method [30] and the point estimation method [36,37]. Compared with MCS, the approximation method is computationally efficient, simple, and feasible, but it is difficult to obtain the higher-order moments of the output variables for complex stochastic variables, and there are errors between the statistical characteristics obtained from the moments of each order and the real situation.

The analytical method is mainly the semi-invariant method, which can represent the output stochastic variable as a linear superposition of the input stochastic variable by processing the system model, and the speed is better than MCS, but it requires complex mathematical processing of the original model of the system [38].

Considering the limitations of the above three probabilistic analysis methods, to obtain the statistical characteristics of the system’s stochastic output variables quickly and accurately, the surrogate model is widely used [39], whose essence is to carry out the computation by building a surrogate model that expresses the relationship between the input and output of the original system. It is used to reduce the computational complexity and ensure the calculation accuracy.

The more common methods used in building the surrogate models are the Polynomial Chaos Expression (PCE) method [40,41] and the polynomial approximation method based on the Galerkin method [42]. PCE is a method that uses the sum of orthogonal polynomials with stochastic variables to build a surrogate model of the system, and the polynomial coefficients are solved by the least-squares or collocation method to obtain the expression of the system’s input–output. The stochastic response surface method, in which the input variables are standard normally distributed stochastic variables and the Hermite orthogonal polynomials are the basis functions, is a special form of PCE [43]. The PCE model can be expressed as [40]

$$y=f(x)={\displaystyle \sum _{j=1}^m{\lambda }_j}{p}_j(x)$$

(4)

where j is the number of PCE items; λ_j is the j-th PCE coefficient to be solved; m is the total number of PCE items; p_j(x) is the product of the one-dimensional orthogonal polynomial basis function corresponding to the j-th dimensional standard stochastic variable, which can be characterized by Equation (5) [40]:

$$p_j(x)={\displaystyle \prod _{k=1}^d{\varphi }_k^j(x_k)}$$

(5)

where k represents the dimensionality of the stochastic variables; ϕ^j_k(x_k) is the one-dimensional orthogonal polynomial basis function corresponding to the kth dimension stochastic variable x_k; d is the dimensionality of the stochastic variables. The total number of terms m of PCE is determined jointly by the highest order p of the PCE and the dimensionality d of the stochastic variables. The specific functional relationship can be expressed as [40]

$$m=\frac{(d+p)!}{d!p!}$$

(6)

Galerkin method expands the state variable and algebraic variable polynomial of the original system model to obtain the corresponding surrogate model; its basic idea is to construct an equation that approximates the coefficients through projection calculation, thereby converting the stochastic equation into a deterministic equation, generalized polynomial chaos is one of its forms.

Table 2. Characteristics of MCS and surrogate models.

Method	Advantage	Disadvantage
MCS	Simple approach and strong achievability	Low computational efficiency
PCE	High computational efficiency	Curse of Dimensionality
Galerkin	High computational accuracy	Curse of Dimensionality

compares the characteristics of the PCE method, Galerkin method, and MCS.

The above two types of methods for building the surrogate models can improve computational efficiency and accuracy; in the uncertainty stability analysis, there may be a “Curse of Dimensionality” problem; that is, as the dimension of variables increases, the difficulty of analysis also increases, which seriously affects the application of the surrogate model method. Therefore, some scholars proposed the Sparse Polynomial Chaos Expansion (SPCE) method [44], Low-Rank Approximation (LRA) method [45], and Gaussian Process Regression (GPR) method [46], which can effectively solve the “Curse of Dimensionality” problem encountered by the traditional surrogate models, and at the same time, the optimal surrogate model construction method can be selected according to the nonlinear degree of the model. Among them, the SPCE method can be selected when the nonlinear degree is low, and the LRA method and GPR method can be selected when the nonlinear degree is high. A comparison of the three improved methods is listed in

Table 3. Characteristics of improved surrogate models.

Surrogate Model	Advantage	Disadvantage	Applicable Scene	Reference
SPCE	➢ Only the key polynomial basis function is retained. ➢ Strong generalization ability, can overcome the problem of “Curse of dimensionality” encountered by traditional polynomial chaos expansion method.	➢ Complex selection process of basis function. ➢ The construction of high order model requires a large amount of computing memory. ➢ Input stochastic variable independent.	High dimension and low order	[44]
LRA	➢ Reducing the number of basis function. ➢ Overcoming the problem of “Curse of dimensionality” encountered by traditional polynomial chaos expansion method.	➢ The solving process of complex coefficients to be solved. ➢ A lot of optimization problems need to be solved. ➢ Input stochastic variable independent.	High dimension and high order	[45]
GPR	➢ Obtain the output response’s confidence interval. ➢ By establishing a trend function, we can overcome the problem of “Curse of dimensionality” encountered by traditional polynomial chaos expansion method.	➢ Improper selection of trend function and correlation matrix will affect the fitting accuracy of the surrogate model.	High dimension and high order	[46]

.

4.2. Probabilistic Small-Disturbance Stability

Small-disturbance stability is the ability to maintain synchronous operation after the power system suffers small disturbances. Small-disturbance stability primarily relies on the eigenvalue analysis method, which linearizes the deterministic power system model. The study of probabilistic small-disturbance stability of power systems is based on the deterministic small-disturbance stability analysis, and the main task is to determine the probability distribution of the system’s key eigenvalues by the probability distribution of stochastic uncertainty sources so as to conclude the probabilistic small-disturbance stability [47].

The field of probabilistic small-disturbance stability analysis was first addressed by R.C. Burchett in his PhD thesis, which analyzed the impact of uncertain parameters on the small-disturbance stability by linearizing the system model for some of the uncertain parameters that conformed to a normal distribution. Since then, many scholars invested in the research on probabilistic small-disturbance stability, and the SDFs taken into account have been expanded from load fluctuations and generator damping coefficients at the beginning to probabilistic models of node injected power levels and component parameters (e.g., line impedance, controller parameters, etc.) [48].

Meanwhile, the analysis methods have also gradually formed three categories: the simulation method, analytical method, and approximation method, which are mainly based on probabilistic analysis. When adopting the probabilistic analysis method to analyze the probabilistic small-disturbance stability, it is mainly to study the system’s eigenvalues. The simulation method generates substantial scenarios by using MCS and other methods and calculates the probability distribution of the key eigenvalues for each scenario. The analytical method calculates the probability statistical information of the system’s eigenvalues after mathematically processing the system model. The approximation method approximates the system eigenvalues’ probability distribution using the probability statistical characteristics of stochastic input variables. In Literature [49], the operating state of transmission elements, load level, and generating unit output were described as discrete and normally distributed stochastic variables, and MCS was used to analyze the probabilistic features of the eigenvalues, eigenvectors and eigenparameters, and the probabilistic small-disturbance stability. A two-region 13-node system was used for simulation analysis, and it was verified that the uncertainty of the network topology has a significant impact on the small-disturbance stability.

Currently, the impact of the new energy output’s stochasticity on the small-disturbance stability cannot be ignored [50], and at the same time, the long simulation time and low computational efficiency problems of MCS also emerge. Aiming at the wind power’s stochastic fluctuations, Literature [51] calculated the probability distribution function of key eigenvalue’s real part stochastic variations, according to the Weibull function and the Gram–Charlier series expansion. MCS and the New England 39-node system were used to investigate the validity of this method. It is confirmed that the system’s probabilistic small-disturbance stability decreases rapidly when the grid-connected wind power increases.

Literature [52] analyzed the impact of stochastic fluctuations of PV output on the probabilistic small-disturbance stability by combining the stochastic response surface method and the Nataf method. The results show that this method has the advantages of fast computation and a high accuracy rate. Literature [53] studied the spatial distribution of wind farms and the stochastic characteristics of the wind speed on the probabilistic small-disturbance stability based on the Gram–Charlier series expansion. A 16-machine 3-wind farm system was used for analysis. It was also confirmed that the increase in the penetration rate of wind power will greatly reduce the probabilistic small-disturbance stability. Literature [54] constructed a detailed “2 m + 1” point estimation method by considering a variety of SDFs in wind farms to determine the probabilistic small-disturbance stability.

4.3. Probabilistic Transient Stability

At the beginning stage of the probabilistic transient stability research, the scholars mainly focused on the short-circuit, broken line, and other faults and their type, location, removal time, etc. The impact of lesser SDFs on the transient stability was considered. R. Billinton et al., for the first time, extended the transient stability problem from deterministic analysis to probabilistic analysis, and the direct method (DM) was used to solve the probabilistic transient stability for a multi-machine power system [55]. P. M. Anderson et al. analyzed the difference between the transient and probabilistic transient stability and introduced DM’s transient energy function into probabilistic transient stability, and MCS was used to calculate the probabilistic transient stability [56].

Literature [57] summarized the research conducted by previous scholars, providing a rigorous mathematical theory for the probabilistic stability calculation. It revealed the basic relationship between the probabilistic stability index and the main SDFs and later gave two methods for the calculation of transient probability. Literature [58] proposed a new computational method, the probabilistic collocation method, which performs a fast solution by establishing a polynomial model between the stochastic variable and the quantity to be solved.

After entering the 21st century, the research hotspot has been extended from the system fault to various SDFs (e.g., wind speed, light intensity, system load, etc.) in the power system. Literature [59,60,61] used the probabilistic analysis method to study the wind system’s transient stability and calculate the stability probability for wind power uncertainty using MCS, and the effects of wind turbine type and penetration on probabilistic transient stability were investigated, respectively. Literature [62] considered the wind farm’s uncertainty and correlation and solved the transient stability probability using the multipoint estimation method based on the Nataf transform and the transient stability probability indicator for the practical dynamic safety domain. Literature [63] used the extended equal area criterion (EEAC) as the basis, separated the multi-machine system into two groups according to the instability mode, and adopted the semi-invariant method combined with Gram–Charlier series approximation expansion to solve the analytical expression for the transient stability margin taking the two groups’ driving power and stability margin sensitivity as the coefficients, and obtained the probability distribution of transient stability margin, whose probability greater than 0 is the transient stability probability.

The probabilistic transient stability analysis methods are mainly classified into simulation and analytical methods. The simulation method, i.e., using MCS to sample the stochastic variables, performs time domain simulation for each sample to determine its transient stability and derive the corresponding statistical characteristics. The analytical method establishes the analytical expressions for probabilistic transient indicators based on different transient stability indicators and solves them analytically. One of the most important aspects of the analytical method is the calculation of the transient instability probability after the occurrence of a certain expected fault. With the progress of the research, faults include, but are not limited to, the type, component, location, time, and protection action time (or fault removal time) [64]. In general, the study of probability transient stability has attracted some attention, but with the increase in system structure complexity and the number of components, there is still much room for rise.

4.4. Probabilistic Voltage Stability

Voltage stability is the ability to maintain the bus voltage within an appropriate range after the power system suffers a disturbance. Voltage stability analysis is generally used to find the voltage collapse critical point in order to calculate the current voltage stability margin. The commonly used analysis methods are continuation power flow (CPF), DM, and the optimization method [65]. Conventional voltage stability study is based on the deterministic system, and when the SDFs such as load fluctuations, generator failures, and new energy power fluctuations are introduced into the system, the probabilistic voltage stability should be investigated, considering both a certain state’s possibility and the voltage stability in that state.

The load margin and the critical voltage are signal indicators for measuring voltage stability. Considering the influence of SDFs, these two types of indicators cease to be fixed values and instead adhere to a specific probability distribution. Probabilistic power flow (PPF) can better deal with the SDFs in the system and profoundly and comprehensively reflect the impact of SDFs on the state variables. However, PPF only yields the probability distribution parameters of bus voltage and branch power, which makes it difficult to comprehensively reflect the voltage stability problem.

CPF is a powerful tool to analyze voltage stability, which plays a key role in the calculation of the P–V curve and voltage collapse critical point. PPF is introduced into the CPF’s prediction, and the correction links can improve the applicability of CPF to the SDFs and obtain a more comprehensive system voltage stability condition [66]. Meanwhile, the analytical methods represented by semi-invariant and the approximation methods represented by point estimation are widely used in voltage stability analysis, which can effectively reduce the computation amount and improve computational efficiency. However, in the linearization processing of the semi-invariant method, when the stochastic disturbance is large, the linear relationship between the variables becomes worse, resulting in the calculation error becoming larger, and the semi-invariant method will no longer be applicable in the probabilistic voltage stability analysis. For this problem, there are two main solutions in the current research [67]. First, the probability density function of the stochastic variable is piecewise linearized. However, it brings in a larger computational amount, although the error is reduced. Second, the idea of scene partition is used to limit the stochastic fluctuations, and the computational accuracy is improved.

5. Stochastic Stability Analysis

Probability stability analysis employs statistical concepts, where statistical characteristics of stable indicators are obtained through repeated experiments. However, its limitation is that it only accounts for the effects of stochastic perturbations at a single point in time on system stability. The dynamic analysis of the system is different from the steady-state analysis. It needs to consider the changes in the system over time. Stochastic perturbations are unlikely to impact the system only at a singular moment, particularly for disturbances that continuously change, such as system load and wind turbine speed. Therefore, focusing solely on the influence of random variables on the system proves to be insufficient for a thorough analysis of dynamic characteristics. With the increase in SDFs in power systems, some scholars considered the continuous disturbances by the SDFs and replaced the stochastic variables with stochastic processes. Therefore, the research direction of power system stability has expanded from probabilistic stability to the field of stochastic stability research, and the theoretical research needs to draw on relevant knowledge of stochastic dynamics.

The deterministic function cannot define a stochastic process. It is only used as a stochastic path sample to analyze and observe the results. The implementation methods of stochastic processes can be classified into frequency domain and time domain methods.

The frequency domain method mainly describes the features of different stochasticity frequency components. The specific application is shown in Figure 2. Based on a series of methods, such as the power spectrum method and time–frequency transformation, the stochasticity in the power system is transformed to the frequency domain level, and the frequency domain characteristics are used to calculate the relevant indicators for the time domain. This method has a strong physical meaning and can also efficiently evaluate the operation state of power systems.

The time domain method is to model the system’s stochasticity and dynamics using SDEs and conduct a unified analysis with the help of relevant tools, which can better consider the system’s constraints and the stochastic states’ impacts. This section mainly reviews the research progress of time domain methods in stochastic processes. The system oscillation problem considering stochastic disturbances has not been elaborated on much.

Most of the stochasticity of stochastic excitations in power systems comes from the stochastic characteristics of new energy and load changes. Changes in stochastic excitation lead to stochastic fluctuations in the system state variables. For a more accurate description of the dynamic response under stochastic excitations, see Equation (7) [68]. The stochastic terms can be introduced into the system’s DE model, and then SDE is applied to this field. When analyzing the system stability based on the SDE theory, the establishment and solution of the dynamic model under stochastic excitations is the premise of obtaining the conclusion of the system stability analysis.

$$\left\{\begin{array}{l}\frac{dX(t)}{dt}=F_x\left[X(t),U(t),\theta ,t\right]+G_x\left[X(t),\theta ,t\right]\epsilon (t)\\ Y(t)=F_y\left[X(t),\theta ,t\right]+G_y\left[X(t),\theta ,t\right]\epsilon (t)\\ X(0)=X_0\end{array}\right.$$

(7)

where X(t) is the state vector; U(t) is the input vector; Y(t) is the output vector; θ is the parameter vector; F_x, F_y and G_x, G_y are nonlinear function vectors; X₀ is the initial value vector; ε(t) is the external stochastic excitation vector; t is the time.

5.1. Power System Stochastic Source Modeling

As the main component that converts other forms of energy into electrical energy, the generator is an indispensable key component in the energy conversion process. Therefore, the stochastic modeling for the generator plays a key role. There are three main sources of external stochastic excitations on the generator side: stochastic fluctuations in generator mechanical power; stochastic changes in the “source” side caused by stochastic changes in the “load” side; stochastic changes in generator output caused by stochastic fluctuations in the transmission of generation control signals.

The first kind of stochastic fluctuations are caused by the prime motor’s stochastic changes, such as the stochastic changes in the wind speed in wind farms, the changes in water level information in the water turbine, etc. The stochastic changes in the “load” side refer to the stochastic changes caused by the power consumer side fault, resulting in stochastic changes in the power generation side. The stochastic changes in generator control signal transmission are mainly due to the regional interconnection of the power grid, which leads to a substantial increase in transmission distance and transmission capacity. Digital controllers usually have stochastic disturbances in the control signal transmission process, leading to deviations in the signal, thereby causing stochastic changes in the generator output. Among the above three sources, the stochastic fluctuations of generator mechanical power account for the largest proportion, which is usually expressed as an additive noise [68], as shown in Equations (8) and (9).

$$P_{\mathrm{m}}=P_{\mathrm{m},0}+\Delta P_{\mathrm{W}}$$

(8)

$$d\Delta P_{\mathrm{W}}(t)=\eta dB(t)$$

(9)

In Equation (8), P_m = 0 is the determined part of the generator’s mechanical power, and ΔP_W is the stochastic part caused by external stochastic excitations, such as wind speed, light intensity, stochastic changes in water level pressure, etc. In Equation (9), B(t) represents the Winner process, and η represents the diffusion coefficient. When noise excitation is independent of the presence of stochastic variables, noise always causes interference in the power system through a superposition effect, and this type of noise is referred to as additive noise. On the other hand, when noise excitation is related to the presence of stochastic variables, the noise is termed multiplicative noise, and it is represented as having a multiplicative relationship with the stochastic variables. However, multiplicative noise is rarely used in power systems, and additive noise is primarily employed to describe stochastic perturbations.

When studying the impacts of stochastic excitations on the dynamic response of the “source” side, the generator model can be divided into 2-order, 3-order, and 5-order models according to accuracy requirements [69]. If the accuracy is required to be lower, a 2-order model can be used. If the excitation system needs to be considered when modeling, a 3-order or 5-order model needs to be used. Among them, the simplest 2-order model is as follows [70]:

$$\left\{\begin{array}{l}\frac{d{\delta }_i}{dt}={\omega }_i-{\omega }_0\\ \frac{d{\omega }_i}{dt}=\frac{1}{M}[P_{mi}-P_{ei}-D_i({\omega }_i-{\omega }_0)+{\sigma }_i{W}_i]\end{array}\right.$$

(10)

where, M_i is the inertia of the i-th generator, D_i is the damping coefficient; ω_i is the generator speed, and ω₀ is the initial angular velocity; P_mi is the mechanical power, and P_ei is the electromagnetic power; new energy output fluctuations, stochastic load changes and stochastic vibrations of generators are collectively referred to as the stochastic disturbance term W_i, and σ_i is the i-th generator’s stochastic disturbance intensity. When the generator is modeled using a classical second-order model and the load is represented by a constant impedance model, the rotor motion equation of the i-th generator can be expressed as follows:

$$\frac{d{\delta }_i}{dt}={\omega }_i-{\omega }_0$$

(11)

$$\frac{d{\omega }_i}{dt}=\frac{1}{M_i}\left[P_{mi}-P_{ei}-D_i({\omega }_i-{\omega }_0)\right]$$

(12)

In Equation (12),

$$P_{ei}=G_{ii}{E}_i^{\prime 2}+E_i^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{Y}_{ij}}{E}_j^{\prime }\sin ({\delta }_{ij}-{\alpha }_{ij})$$

(13)

$$P_{\mathrm{m}i}=G_{ii}{E}_i^{\prime 2}+E_i^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{Y}_{ij}}{E}_j^{\prime }\sin ({\delta }_{ij0}-{\alpha }_{ij})$$

(14)

$${\delta }_{ij}={\delta }_i-{\delta }_j$$

(15)

In the above equations, α_ij is the supplementary angle of the impedance angle between the i-th and j-th generators. Since generally the resistance is much smaller than the reactance, for simplification, it is sometimes approximated that α_ij ≈ 0. When the stochastic excitation is equivalent to a Gaussian process, the stochastic model is shown in the following equation [68]:

$$W_i(t)=\frac{dB(t)}{dt}$$

(16)

The standard Brown motion defined on [0,T] satisfies the following conditions:$B\left(0\right)=E\left[B\left(0\right)\right]=0$; Any $0\le s<x<y\le T$, increments $B\left(y\right)-B\left(x\right)$ and $B\left(t\right)-B\left(s\right)$ are independent of each other; Any $0\le s\le t\le T$, $B\left(t\right)-B\left(s\right)~\left[\sqrt{(t-s)}\right]N(0,1)$. When the stochastic excitation is equivalent to a Poisson process. The stochastic model is shown in the following equation [68]:

$$W_i(t)=\left\{\begin{array}{cc}0& N(t)=0\\ {\displaystyle \sum _{j=1}^{N(t)}{Y}_j}{\delta }_0(t-t_j)& N(t)>0\end{array}\right.$$

(17)

where N(t) is the Poisson counting process with the intensity λ, which represents the number of stochastic pulses in [0,t], Y_j and t_j are the intensity and time of occurrence of the jth stochastic pulse, respectively, Y_j and t_j are independent of each other, δ_D(·) is a Dirac function, ε(·) is the unit step function. When considering both continuous and discrete stochastic excitations, the stochastic dynamic differential equations with jumps can be used for modeling.

Regarding the uncertain factor analysis in transmission lines, although the intensity of stochastic disturbances is small, due to the wide coverage and large transmission capacity, their parameters and losses change all the time. Literature [71] started from the internal and external aspects that affect the operation state of transmission lines and proposed an evaluation method for the operation state and its risks based on the Markov chain model, which effectively overcomes the impact of certain information lack on the operation of transmission lines. Literature [72] summarized the research of visual detection for transmission lines based on deep learning in the past ten years, pointed out existing problems, and looked forward to future work. Research on the operation state and risk assessment of transmission lines under uncertain external factors have been abundant and mature, but there are few studies on using SDE to model the SDFs of transmission lines. Literature [73,74] applied the stochastic partial differential equation to transmission lines and analyzed the impact of noise on transmission lines. Literature [75] considered the stochastic changes in transmission line excitation sources and parameters, used the state variable method to establish the corresponding SDE model, and adopted the stochastic implicit Euler method to solve the mode and obtain the stochastic response of voltage and current.

Although there have been a lot of studies on stochastic excitation modeling, most stochastic excitations are simulated using Gaussian processes, and white noise or colored noise is used to simulate power fluctuations caused by stochastic changes in load noise. However, there is no practical basis for this assumption, and it only continues the premise of simulating the stochastic source when considering the probabilistic stability of power systems. Literature [76] studied the applicability of the Ornstein–Uhlenbeck process driven by various Levy processes in load modeling in power systems. The Wiener process was used to drive the stochastic fluctuations of small load sets, the Poisson process was used to drive discrete switching of high-power loads, and the statistical characteristics during the simulation process were compared with the actual data to verify the proposed method. Literature [77] applied the Poisson process to the stochastic modeling of fault occurrence, removal time, and reclosing process for the first time. Before and after the fault occurs, different SDEs were used for modeling according to the removal time and reclosing state, and the transient stability was simulated by the stochastic Euler method. Based on measured data, the literature [78] shows the characteristics of random disturbances in wind power plants using the Ornstein–Uhlenbeck process, using the Lyapunov exponent to determine the impact of fluctuating active power generated by stochastic energy sources in large interconnected power systems. In order to establish a more realistic trajectory of the wind speed, Literature [79] used the Ornstein–Uhlenbeck process to simulate wind turbine power and defined two autocorrelated Weibull distribution models by using SDE and the memoryless transformation method.

5.2. Solving SDE under Stochastic Excitations

Solving the SDE model is the key to analyzing the system state variables and exploring the impact of different stochastic excitations. The solutions to the SDE model can be divided into analytical solutions and numerical solutions. Some nonlinear models can generally be solved using the analytical solution formula of linear SDE after linearization. However, in most cases, the analytical solution method is not suitable for the SDE model, so the numerical solution method is usually used for solving [80]. The deterministic system model is a group of nonlinear stiff DEs. As shown in

Table 4. Comparison of methods for solving system dynamic models.

Power System Dynamic Simulation Model	No Stochastic Excitations	with Stochastic Excitations
Equation	Differential-algebraic equation	Stochastic differential-algebraic equation
Numerical solution method	Euler method, trapezoidal method, linear multi-step method, Runge–Kutta method, Matrix exponential method, distribution method and Taylor series method	Euler–Maruyan method, Milstein method, Random Runge–Kutta method, and Heun method

, the numerical solution methods include classic integration algorithms (Euler method and its deformations, trapezoidal integration method and its deformations, linear multi-step method, and Runge–Kutta method) and new-type integration algorithms [81] (Matrix exponential method, distribution method, and Taylor series method). When numerically solving the SDE model, the Euler method corresponds to the Euler–Maruyan method and its variant Milstein method. Mcshane proposed the Heun numerical method [82], which is similar to the prediction correction idea of the improved Euler method and transforms the Euler–Maruyan method based on the trapezoidal formula. The stochastic Runge–Kutta method is obtained by translating the Runge–Kutta method from the differential equation to the SDE [83]. Although it has high accuracy, it is rarely used in research due to the large amount of calculation.

The performance indicators to evaluate the quality of a numerical algorithm mainly include numerical stability, calculation accuracy, and calculation efficiency. Numerical stability affects calculation efficiency. Explicit integration does not require iteration, so it has a higher calculation efficiency, while implicit integration has a lower calculation efficiency, such as the forward Euler method and the backward Euler method. The calculation accuracy is determined by the local truncation error. The Euler–Maruyan method and Milstein method are obtained by truncating the random Taylor expansion in different places, and the Euler–Maruyan method has 1-order accuracy, and Milstein has 2-order accuracy. In addition, when solving the SDE numerically, there are two important indicators: the strong convergence and the weak convergence. The strong convergence indicates the degree to which the numerical simulation solution trajectory matches the real trajectory, while the weak convergence is related to the properties of each moment of the numerical solution [84].

5.3. Stability Analysis under Stochastic Excitations

In the early stage of stochastic stability research, the probabilistic stability analysis method only focused on the stochasticity of initial values, parameters, and disturbance modes, and it is an extension of the traditional stability analysis method. The probabilistic stability analysis cannot solve the behavior characteristics generated by the stochastic excitations in the dynamic process.

The power system model considering stochastic excitations is the SDE dynamic model, therefore, the stability analysis must also be expressed in the form of probabilistic statistics, such as Lyapunov stability with a probability of one, probabilistic asymptotic stability, and p-order average stability [85]. Stability analysis under stochastic excitations generally requires a quantitative and qualitative analysis. Quantitative analysis can determine the stability based on the curve fluctuation range by solving the change curve of state variables. Qualitative analysis uses relevant criteria to determine the system’s stability. If the stochastic excitation intensity (SEI) value is small, the model is generally linearized at the system’s equilibrium point to analyze the system’s stability. If SEI is large, the nonlinear model is more consistent with the actual situation. However, with the increase in new energy penetration rate, SEI also gradually increases, and the boundaries between small and large stochastic excitations gradually blur, which causes difficulties in selecting linear models and nonlinear models. Therefore, some scholars proposed the SEI threshold that the nonlinear model can be linearized. For example, Reference [86] established the linear and nonlinear models for the single-machine infinite system, used the Milstein-Euler algorithm to solve the two models, and quantitatively analyzed the impacts of different SEIs on the system stability; and a SEI threshold was proposed for the linearizable form of the nonlinear stochastic dynamic model.

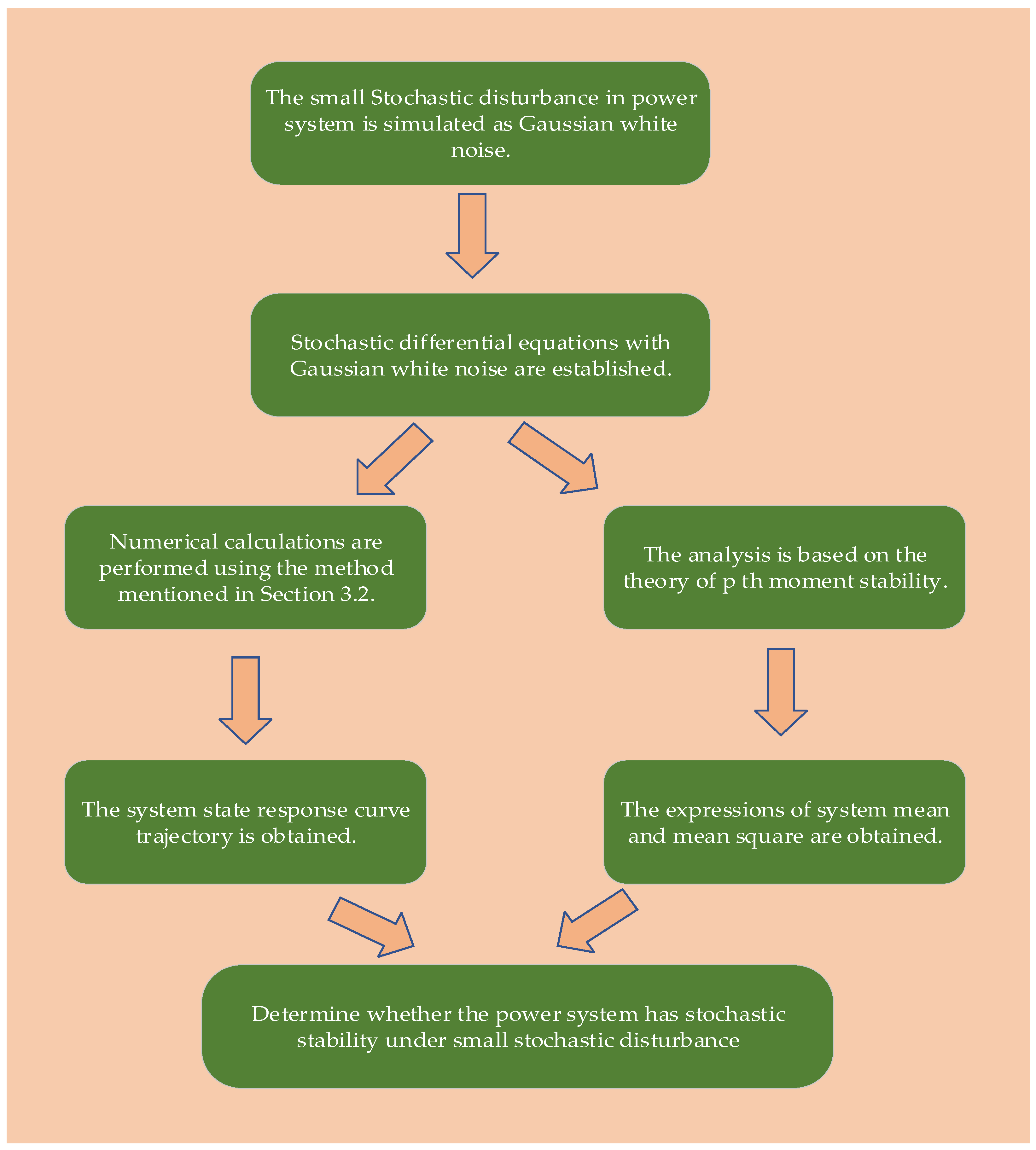
5.3.1. Stochastic Small-Disturbance Stability

Under the deterministic model, small-disturbance stability is usually described by static stability. The commonly used analysis method is eigenvalue analysis; that is, after establishing the system’s nonlinear DE, it is linearized at a specific operating point. In the form of the backstroke state space, eigenvalue analysis is conducted on the DE’s state matrix. The stochastic small-disturbance stability draws on the eigenvalue analysis and uses the SDE theory to judge the mean stability, mean square stability, and other order moment stability [87]. Mean stability and mean square stability are first-order and second-order moment stability, respectively. The former represents the average value of the system’s dynamic response, and the latter represents the degree to which the dynamic response deviates from the mean. The former is the premise of the latter. In addition, there are the Lyapunov method and the energy function method. The Lyapunov method is divided into the first method and the second method. The most used method is the Lyapunov second method, which is to directly judge the system stability by building the Lyapunov function. However, due to the uncertainty of stochastic excitations and complexity, it is impossible to quantitatively analyze the impact of stochastic excitation, so the energy function method is usually constructed based on the Lyapunov second method for analysis. The small stochastic disturbance stability analysis process is shown in Figure 3.

Literature [88] constructed a stochastic model of wind power systems under the condition of stochastic disturbances and parameter uncertainty and obtained the constraints between stochastic excitations, system parameters, and uncertain parameters when the system probability is stable by using the Lyapunov second method. The literature [89] represents the power system as a stochastic linear system and uses the calculation of moments associated with Lyapunov exponents to determine the optimal adjustment of the controller based on linear analysis. Literature [90] took the wind turbine mechanical power as a stochastic input to establish a small-disturbance stability analysis model. Taking a two-machine infinite system containing asynchronous wind turbines and synchronous generators as an example, an analytical solution to the stochastic state equation is obtained using a 1-order, 2-order moment stability to describe the small-disturbance steady-state characteristics. Literature [91] established a reduced-order SDE model of the DC distribution system, derived the analytical solution of SDE, gave the mean and mean square stability criteria, and comprehensively characterized the relationship between stochastic excitation and system mean stability and mean square stability. Literature [92] conducted a stochastic small-disturbance stability analysis based on a nonlinear SDE model that is closer to the actual system, proved the mean stability and mean square stability under stochastic small disturbances, and derived the stability criteria of SEI.

Stability criteria are conducive to further analyzing the impact of SEI on stability. In the literature mentioned in this section, linear and nonlinear stochastic dynamic models are used respectively in the analysis of stochastic small-disturbance stability. Among them, the linear model can reduce the calculation process and facilitate analysis, but it has larger errors than the real scene. The nonlinear model can improve the accuracy, which is close to the real scene, but its calculation process is more complex, which greatly increases the calculation time. Therefore, the stochastic dynamic model can be selected according to the following steps to better study the stochastic small-disturbance stability.

• The linear and nonlinear stochastic dynamic models of power systems are established, respectively;
• The same method is used to analyze and calculate the two models;
• According to the different research purposes, the corresponding indicator threshold is selected;
• When the indicator exceeds the threshold, the nonlinear model is selected; when the indicator is lower than the threshold, the linear model is selected;
• Carry out the stochastic stability analysis of power systems.

5.3.2. Stochastic Transient Stability

Transient stability analysis methods for deterministic systems can be divided into five categories: stepwise integration method, asymptotic expansion method, numerical approximation method, DM, and other methods [93]. Among them, the energy function and EEAC of DM can be extended to the study of stochastic transient stability. Stability analyses are performed by constructing an energy function containing stochastic disturbances and solving the fault removal time containing stochastic disturbances by improving the EEAC method. Literature [94] considered a variety of stochastic factors on a time scale, such as slow-changing factors of stochastic faults and fast-changing factors of load fluctuations, established the SDE model, and proposed a framework for evaluating stochastic transient stability. Literature [95,96] derived the quasi-Hamiltonian system equation based on the energy function using the stochastic averaging method and contrasting it with the MCS method. It was proved that the energy function weakly converges to a one-dimensional diffusion process, which has guiding significance for future stochastic transient stability research. Literature [97] proposed an improved EEAC method, which can convert the stochastic complex system into a stochastic simple system through coherence grouping and then construct an acceleration and deceleration area containing stochastic excitations and determine its transient stability by solving the limit removal time.

DM is extensively utilized in stochastic transient stability analysis, offering the benefits of rapid computation and the ability to determine stability. However, when compared to the time-domain simulation method, its model is simpler and less practical. At present, there are few pieces of literature on the stochastic transient analysis of power systems that can be retrieved, the advantages and disadvantages of time domain simulation and DM that take into account the stochastic process can be complemented, and the hybrid method that combines the two methods is a better choice, and it is also a direction of development for the stochastic transient stability analysis.

5.3.3. Stochastic Voltage Stability

Currently, there are few studies on stochastic voltage stability. In the past, when the influence of stochastic disturbances was not considered, the state matrix eigenvalues of ordinary differential equations were usually solved to analyze an operating point’s stability. If the eigenvalues all lie in the left half-complex plane, the operating point is stable. After considering the stochastic disturbance term, the voltage stability theory in deterministic analysis is no longer applicable. Literature [98] concluded that stochastic disturbances may destroy voltage stability. Stochastic disturbances in load will cause stochastic small-amplitude positive or negative accumulation of the load, causing the system to sudden voltage instability.

Deterministic bifurcation theory in nonlinear dynamics is also used in the mechanism analysis of voltage instability. As the bifurcation parameters gradually change, the shape of the nonlinear dynamic system will change, and bifurcation will occur. Common bifurcations in power systems are saddle-node and Hopf bifurcations. In wind/PV grid-connected systems, these two bifurcations are still the main types causing voltage instability or collapse [99]. However, when the interference of internal and external stochastic factors is considered at the same time, the deterministic bifurcation theory shows limitations. Therefore, the bifurcation theory is extended to stochastic systems, expanding a new research field, namely stochastic bifurcation. The concept of stochastic bifurcation is close to that of deterministic bifurcation. It refers to the phenomenon that in a stochastic excitation system when the system parameters change slightly and smoothly, its shape suddenly changes qualitatively. At present, stochastic bifurcation is mainly divided into dynamic bifurcation (D-bifurcation) and phenomenological bifurcation (P-bifurcation). D-bifurcation mainly studies the bifurcation of new invariant measures from a set of reference measures, which can be obtained by determining the sign of the maximum Lyapunov exponent. P-bifurcation is related to the qualitative change in the stationary probability density of the system response and is generally studied by finding the extreme value of the stationary probability density [100]. Research on nonlinear stochastic dynamics of Hamiltonian systems [85,101] provided a theoretical basis for the study of stochastic bifurcation. Although the research on stochastic bifurcation in power systems has attracted more attention, the research theory on stochastic bifurcation is not yet mature, which has brought many difficulties to related research.

6. Conclusions and Outlook

At present, there have been certain achievements in the research on power system stability considering the SDFs. Among them, probabilistic stability usually uses probability theory and statistics as mathematical tools to construct probabilistic stability indicators based on the static or dynamic model. By analyzing the probability distribution characteristics of variable parameters in the system and the probability distribution of model equation eigenvalues, the probabilistic stability can be evaluated. The related research results are more numerous and relatively mature.

The theory of SDE serves as a mathematical tool for analyzing stochastic nonlinear dynamic models, which include stochastic disturbances in power systems, and is employed to determine their stochastic stability. This research field started late, has relatively few results, and lacks corresponding research methods. Relevant research needs to be strengthened urgently.

This review describes and categorizes the probabilistic stability problems and stochastic stability problems of new power systems under construction and summarizes various analysis methods. The integration of diverse SDFs into power systems has significantly affected their stable operation. As the quantity of SDFs rapidly grows and their characteristics continually evolve, a multitude of theoretical and practical issues concerning stochasticity emerge, meriting deeper contemplation and exploration.

(1)

The existing research basically discusses and studies a certain type of specific stochasticity issues in power systems, which are only limited to a local scope. Even with the help of probability theory and statistical knowledge, the systematic theoretical research and processing method has not been formed, and it is difficult to reflect the stochasticity’s impact on the system stability.

(2)

With the increase in the new energy penetration rate and the number of SDFs, the boundary between large stochastic disturbances and small stochastic disturbances is no longer clear. The small stochastic disturbances will also be transformed into the large stochastic disturbances as the stochasticity of the system increases. The next research should focus on a more systematic and accurate characterization of SEI and its impact on system stability.

(3)

When studying the system’s stochastic stability, stochastic disturbances are usually treated as white noise that satisfies Gaussian distribution. This treatment is highly hypothetical and has poor applicability, and the real stochastic process is not white noise and may be colored noise. How to specifically and accurately characterize various stochastic disturbances is of great significance to future theoretical research and engineering applications.