Simulation and Experiment of the Smoothness Performance of an Electric Four-Wheeled Chassis in Hilly and Mountainous Areas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Structure and Working Principle of the Four-Wheel Robot
2.2. Establishing a Simulation Model
2.2.1. Creating Model Constraints
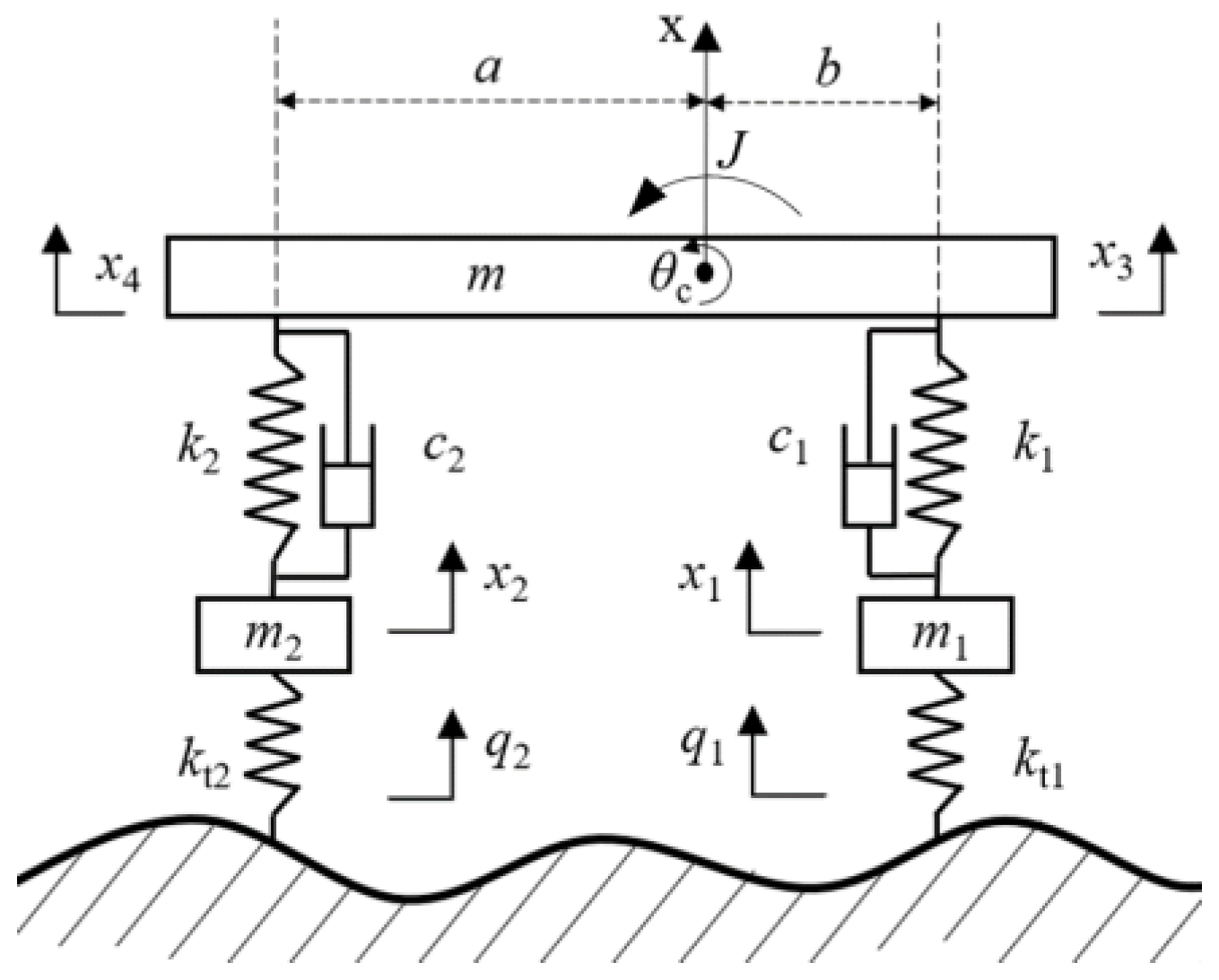
2.2.2. Establishing a Four-Degrees-of-Freedom Half-Car Vibration Model
- The chassis is symmetrical with respect to the longitudinal vertical plane passing through its center of mass, and only vertical direction vibration and longitudinal angular vibration are considered.
- The tire damping is small enough to be neglected.
- The forces exerted by each elastic element are linearly related to relative displacement, and the forces of each damper are linearly related to relative velocity.
- The excitation position of the road surface on the tires of the seeding robot chassis always remains at the contact point between the wheel center and the road surface.
- The seeding robot chassis is moving at a constant velocity in a straight line.
- The effect of air resistance on the seeding robot chassis can be ignored.
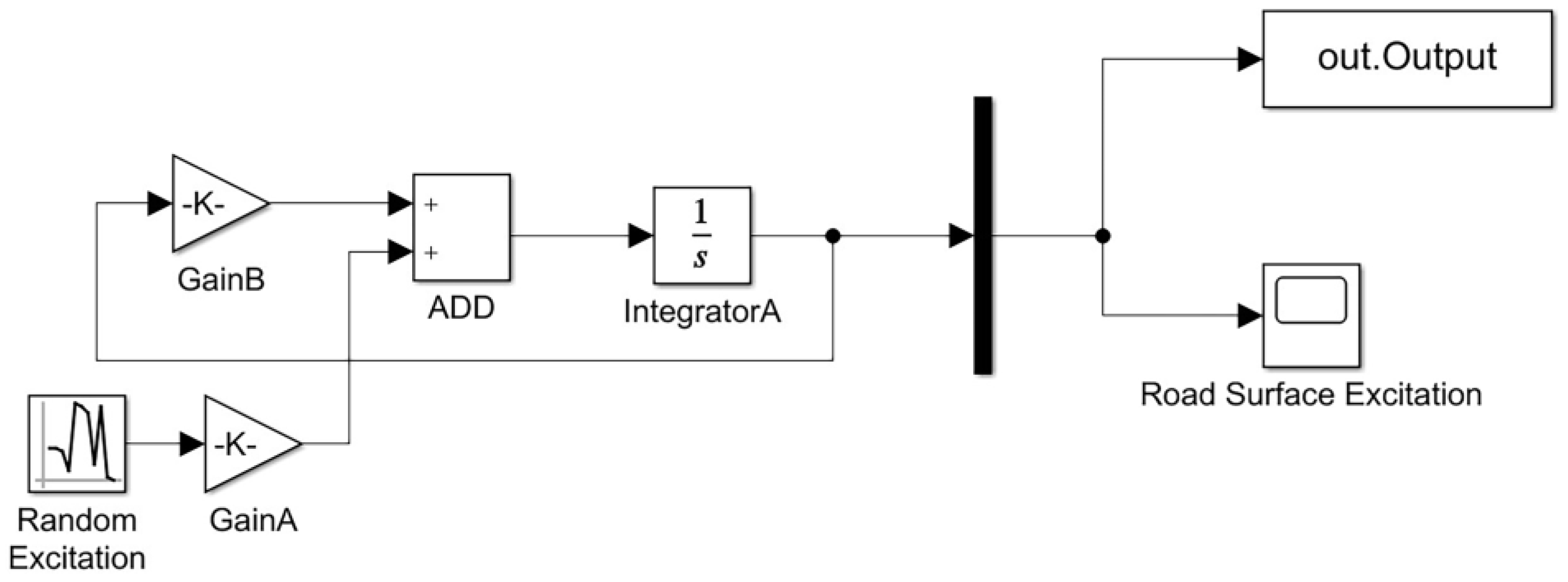
2.2.3. Establishing the Road Surface Model
3. Results
3.1. Straight-Line Travel Simulation
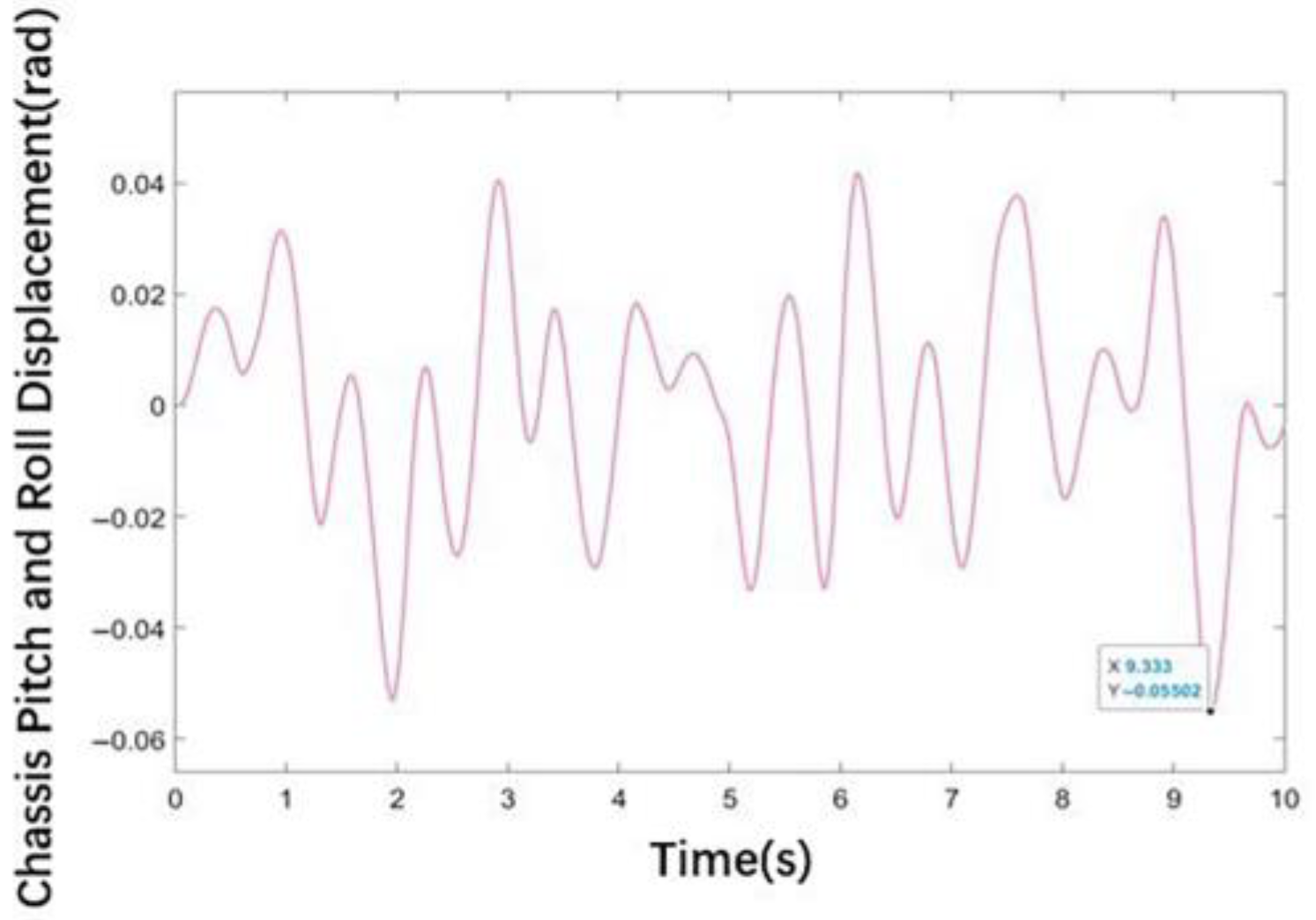
3.2. Vibration Simulation
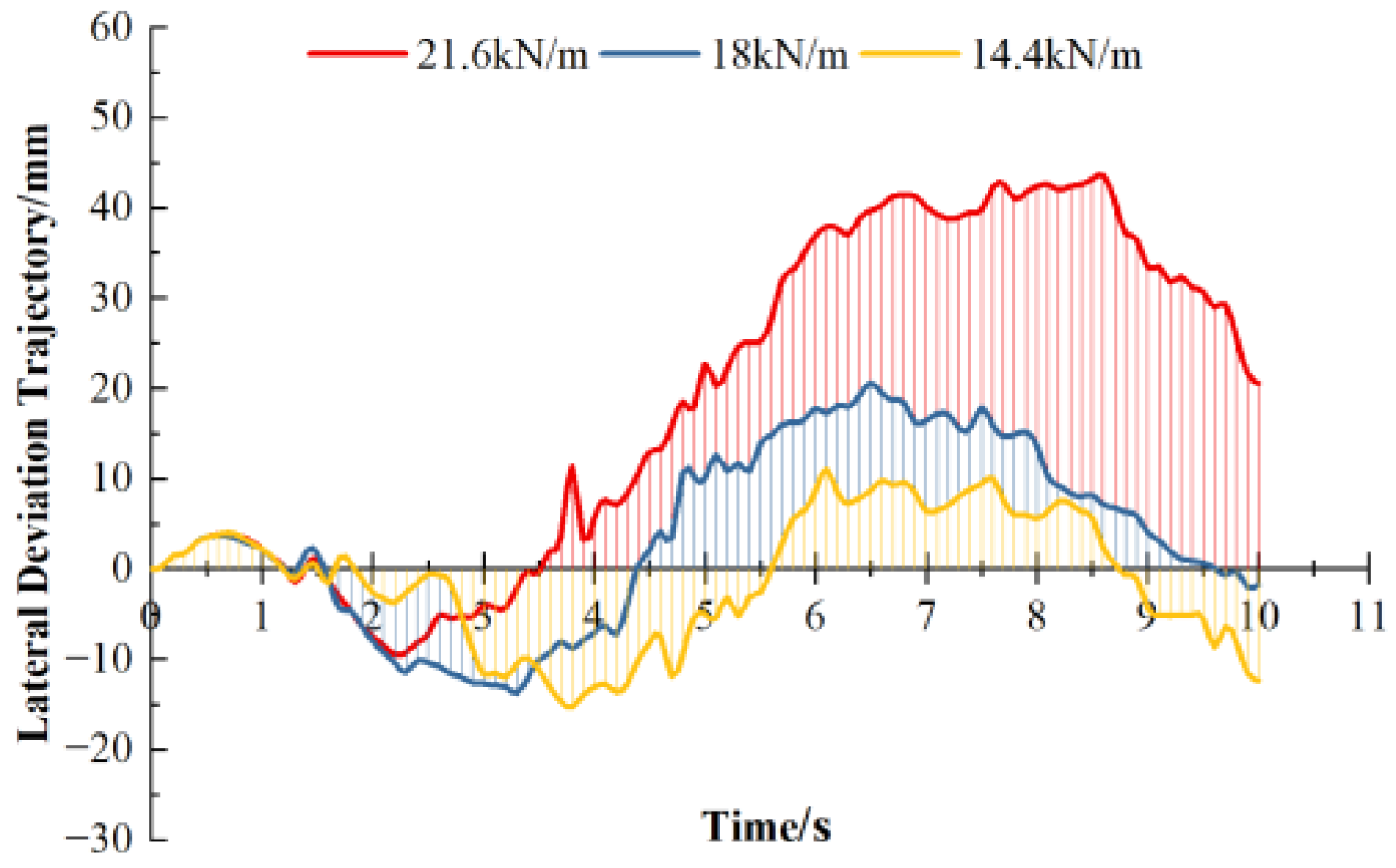
3.3. Simulation Results for Different Suspension Stiffness
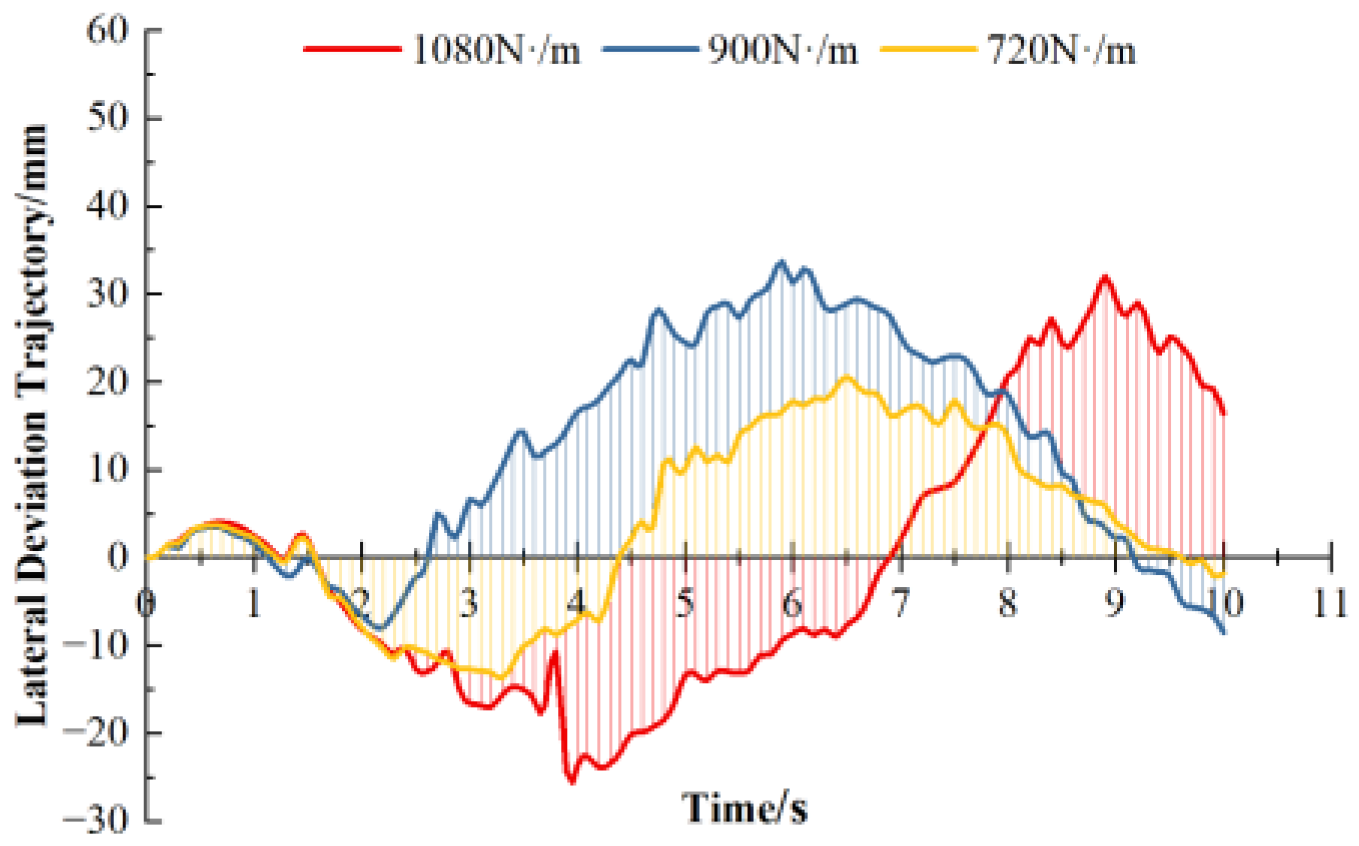
3.4. Simulation Results for Different Suspension Damping
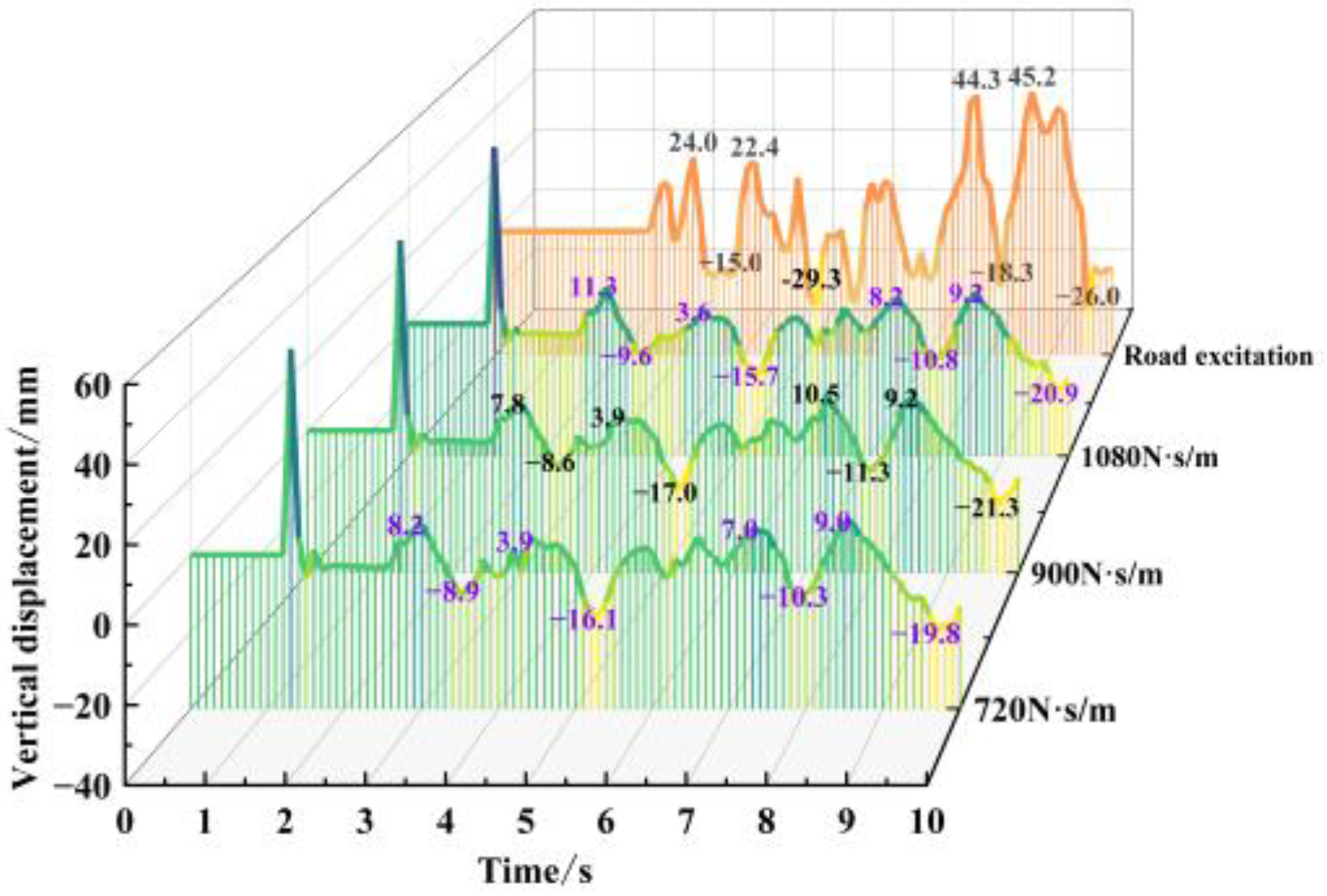
3.5. Simulation Analysis of Optimal Stiffness and Damping Combination
4. Experimental Validation
4.1. Test Equipment
4.2. Vibration Signal Acquisition
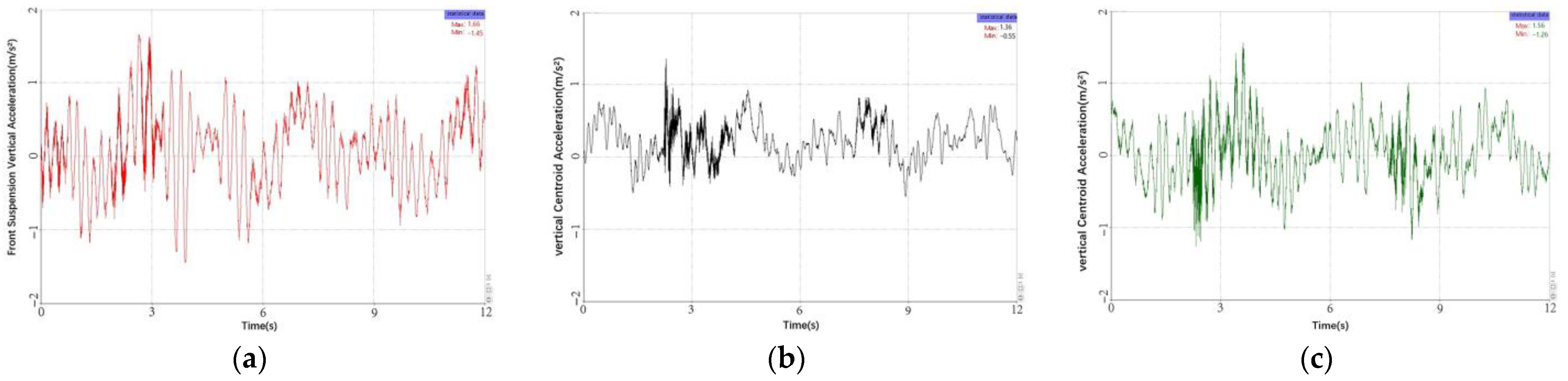
4.3. Experimental Results and Analysis
5. Discussion and Conclusions
- On the basis of the initial stiffness values, reducing the spring stiffness appropriately will improve the damping effect of the chassis. Specifically, when the stiffness is set to 14.4 kN/m, the vertical displacement of the chassis center of gravity is minimized, and the straight-line performance is optimized. This is because increasing stiffness leads to reduced spring deformation, weakening the damping effect, and causing vertical bouncing of the chassis due to reduced ground adhesion of the wheels, resulting in instability during travel.
- Comparing the simulation results under different damping settings, it can be concluded that the chassis exhibits the smallest vertical displacement of the center of gravity and the best straight-line performance when the damping coefficient is set to 900 N·s/m. This is because reducing damping increases the sensitivity of the shock absorbers to rebound while also increasing the extension displacement. Conversely, increasing damping, although reducing extension displacement, slows down the rebound speed of the shock absorbers, preventing them from quickly returning to their equilibrium position. This leads to a reduction in damping effectiveness when encountering continuous bumps in the road.
- The simulation results and experiments demonstrate that the four-wheel robot chassis exhibits good ride comfort and reliable operation. Future research will focus on field trials of the prototype under various road conditions and further in-depth parameter optimization. The road excitation generation method and dynamic simulation approach used in this paper are considered to be realistic and reliable, providing a method for optimizing suspension parameters for similar wheeled chassis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, J.; Ma, R. Research progress in the effects of mechanical compaction on soil properties and soil erosion in farmland. Trans. Chin. Soc. Agric. Eng. 2022, 38 (Suppl. S1), 27–36. [Google Scholar]
- Tang, Y.; Lu, X.; Yi, J. Evaluating the Spatial Spillover Effect of Farmland use Transition on Grain Production—An Empirical Study in Hubei Province. Ecol. Indic. 2021, 125, 107478. [Google Scholar] [CrossRef]
- Sun, W.; Li, C.; Wang, J. Research on Ride Comfort of an Off-road Vehicle with Compound Suspension. Chin. J. Autom. Eng. 2022, 44, 105–114+122. [Google Scholar]
- Zhang, J.; Chen, S.; Zhao, Y. Design and Testing of a Hydropneumatic Suspension with Continuously Adjustable Damping. Chin. J. Autom. Eng. 2015, 5, 282–289. [Google Scholar]
- Qiu, C.; Shen, Y.; Shi, D. Positive Real Optimization and Performance Analysis of New Type Vehicle Electromechanical Suspension. J. Vib. Shock 2021, 40, 76–81. [Google Scholar]
- Tian, R. Integrated Optimization Control and Software Architecture Design of Multi-dimensional Dynamics in Automotive Chassis Domain. Ph.D. Thesis, Jilin University, Changchun, China, 2023. [Google Scholar]
- Xie, J.; Zhang, Q. Simulation Analysis of Vehicle Ride Comfort Based on Simulink. Mech. Electr. Technol. 2013, 36, 14–18. [Google Scholar]
- Yu, X.; Liu, S. Simulation and Analysis of the Dissipative Control System of an Active Suspension. J. Beijing Univ. Technol. 2012, 38, 39–44. [Google Scholar]
- Tan, G.; Lu, Z. Steering Analysis of Tracked Wheeled Mobile Platform Based on RecurDyn. J. Agric. Mech. Res. 2023, 45, 238–243. [Google Scholar]
- Lv, X.; Meng, X. Design and Simulation of Small Tracked Vehicle Based on RecurDyn. Equip. Manuf. Technol. 2023, 02, 152–155. [Google Scholar]
- Zhang, Q.; Li, N. Joint Simulation of Small Wheeled Platform Based on RecurDyn and Matlab/Simulink. Comput. Meas. Control 2018, 26, 112–115. [Google Scholar]
- Ruchelshausen, A.; Biber, P.; Dorna, M. BoniRob: An Autonomous Field Robot Platform for Individual Plant Phenotyping. Precis. Agric. 2009, 9, 841–847. [Google Scholar]
- Analog Dialogue. Available online: https://www.analog.com/en/analog-dialogue/articles/inertial-sensors-and-autonomous-operation-in-robots.html (accessed on 18 October 2022).
- Zhang, J.; Chen, D. Design and Experiment of Four-wheel Independent Steering Driving and Control System for Agricultural Wheeled Robot. Trans. Chin. Soc. Agric. Eng. 2015, 31, 63–70. [Google Scholar]
- Sun, X.; Chu, Y.; Fan, J. Research of Simulation on the Effect of Suspension Damping on Vehicle Ride. Energy Procedia 2012, 17, 145–151. [Google Scholar] [CrossRef]
- Zhang, B.; Tan, C.; Dai, T. Ride Comfort and Energy Dissipation of Vehicle Suspension System under Non-stationary Random Road Excitation. J. Sound Vib. 2021, 511, 116347. [Google Scholar] [CrossRef]
- Rafael, T.; Joan, V.; Monzer, A. Modeling of an Active Torsion Bar Automotive Suspension for Ride Smoothness and Energy Analysis in Standard Road Profiles. IFAC PapersOnLine 2019, 52, 181–186. [Google Scholar]
- Huang, A. Yaw Stability of Four-wheel Independently Steering Unmanned Truck Control Research. Master’s Thesis, Hebei University of Technology, Tianjing, China, 2021. [Google Scholar]
- Li, M.; Li, L. Simulation of Vibration Characteristics of Lumped and Multibody Coupled Human-vehicle Model. J. Shandong Univ. Technol. 2024, 38, 61–67. [Google Scholar] [CrossRef]
- Gandhi, P.; Adarsh, S. Performance Analysis of Half Car Suspension Model with 4 DOF using PID, LQR, FUZZY and ANFIS Controllers. Proc. Comput. Sci. 2017, 115, 2–13. [Google Scholar] [CrossRef]
- Huang, D.; Wang, B. Research on Assessment Method of Vibration Control Feature of Suspension System of Vehicle. J. Ordnance Equip. Eng. 2021, 42, 142–146. [Google Scholar]
- ISO 8608:2016; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. International Organization for Standardization: Geneva, Switzerland, 2016.
- GB/T 7031-2005; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. Standards Press of China: Beijing, China, 2005.
- Yu, Z. Automotive Theory; Machinery Industry Press: Beijing, China, 2007; pp. 86–88. [Google Scholar]
- Zhao, B.; Dong, J. Establishment and simulation of time domain model for Band-Limited White Noise pavement roughness. Auto Appl. Technol. 2019, 3, 89–90+115. [Google Scholar]
- Pang, G.; Chen, L. Fundamentals of Automotive System Dynamics and Control Technology; Tsinghua University Press: Beijing, China, 2017; pp. 185–188. [Google Scholar]
- Liang, X. Research on Ride Comfort Analysis and Control Strategy Ofautomobile Air Suspension System. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2022. [Google Scholar]
- Gao, J. The Vehicle Ride Comfort Analysis and Research by Nonlinear Simulation Model and Test. Master’s Thesis, Dalian Jiaotong University, Dalian, China, 2021. [Google Scholar]
- Zhang, X.; Li, H. Analysis on Accelerations of Vehicle Body during Vertical Vibration. Railw. Stand. Des. 2011, 10, 8–11. [Google Scholar]

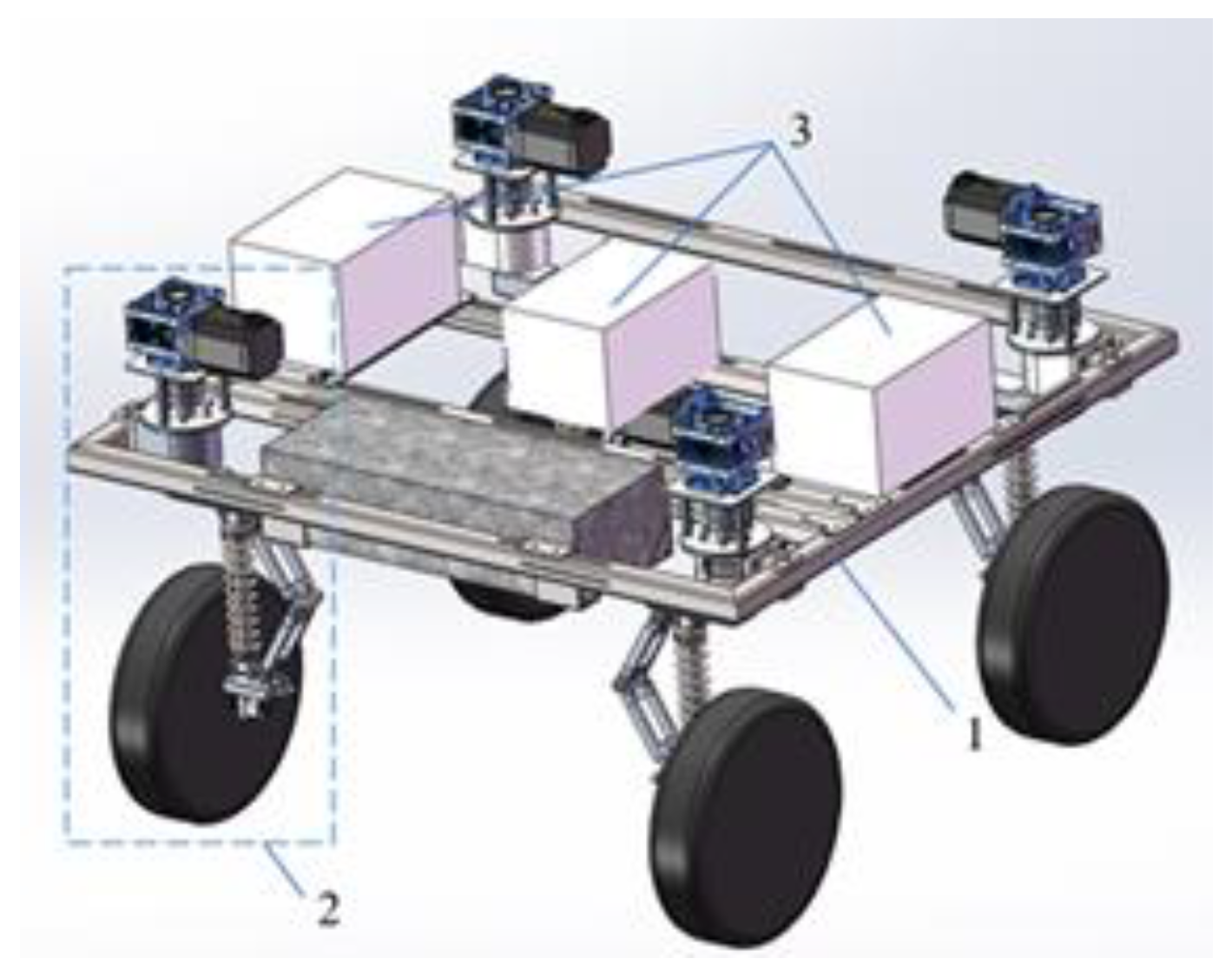
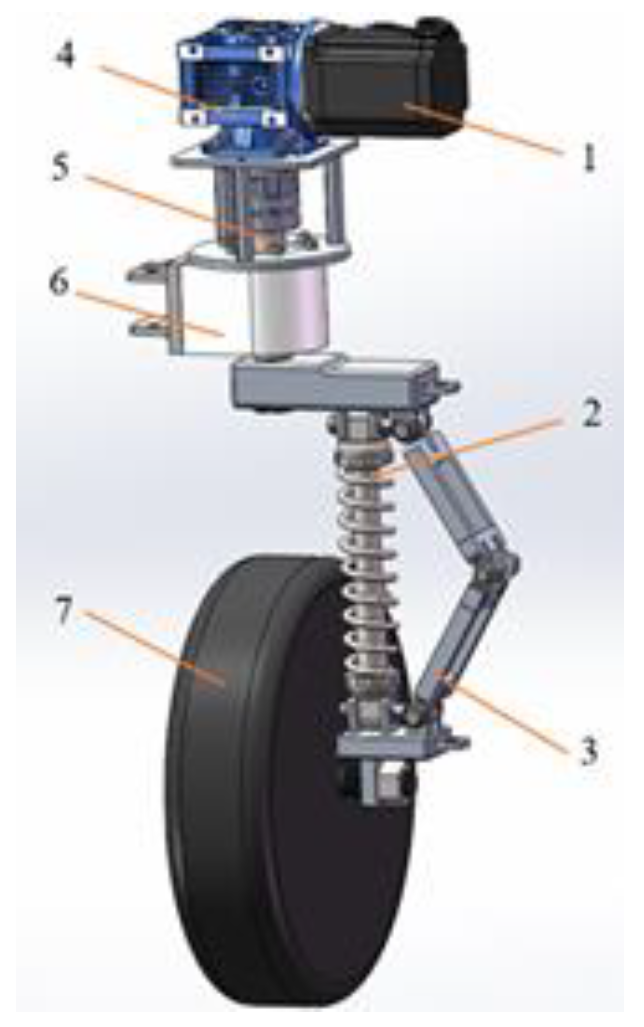











| Key Parameters | Units | Data |
|---|---|---|
| Machine size | mm | 1140 (Length) × 1200 (Width) × 870 (Height) |
| Travel Speed | m/s | 1 |
| Chassis total mass | kg | 200 |
| Damping type | Spring-damping damper | |
| Wheel diameter | mm | 388 |
| Name | Definition | Data | Name | Definition | Data |
|---|---|---|---|---|---|
| m | Chassis structure total ass | 200 kg | θc | Chassis angular displacement about center of mass | rad |
| J | Chassis pitch moment of inertia | 57.9 kg·m2 | x | Chassis vertical displacement of center of mass | m |
| a | Distance from chassis center of mass to rear axle | 0.475 m | b | Distance from center of mass to front axle | 0.375 m |
| q1 | Excitation on the front axle wheels due to road surface | m | q2 | Rear axle wheel excitation | m |
| kt1 | Vertical stiffness of the front axle tires | 25 kN/m | kt2 | Vertical stiffness of rear axle tire | 25 kN/m |
| m1 | Front axle unsprung mass | 10 kg | m2 | Rear axle unsprung mass | 10 kg |
| x1 | Front axle unsprung mass displacement | m | x2 | Displacement of rear axle unsprung mass | m |
| c1 | Front axle suspension vertical damping | 900 N·s/m | c2 | Vertical damping of rear axle suspension | 900 N·s/m |
| k1 | Front axle suspension vertical stiffness | 18 kN/m | k2 | Vertical stiffness of rear axle suspension | 18 kN/m |
| x3 | Front suspension vertical displacement | m | x4 | Vertical displacement of rear suspension | m |
| Test Number | Stiffness (kN/m) | Damping (N·s/m) | Standard Deviation (mm2) |
|---|---|---|---|
| 1 | 14.4 | 720 | 6.803 |
| 2 | 14.4 | 900 | 6.643 |
| 3 | 14.4 | 1080 | 6.966 |
| 4 | 18 | 720 | 6.980 |
| 5 | 18 | 900 | 6.789 |
| 6 | 18 | 1080 | 6.988 |
| 7 | 21.6 | 720 | 7.156 |
| 8 | 21.6 | 900 | 7.033 |
| 9 | 21.6 | 1080 | 7.282 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Liu, Z.; Jiang, Y.; Leng, Y.; Tang, J.; Wang, R.; Lv, X. Simulation and Experiment of the Smoothness Performance of an Electric Four-Wheeled Chassis in Hilly and Mountainous Areas. Sustainability 2023, 15, 16868. https://doi.org/10.3390/su152416868
Fu Y, Liu Z, Jiang Y, Leng Y, Tang J, Wang R, Lv X. Simulation and Experiment of the Smoothness Performance of an Electric Four-Wheeled Chassis in Hilly and Mountainous Areas. Sustainability. 2023; 15(24):16868. https://doi.org/10.3390/su152416868
Chicago/Turabian StyleFu, Yuan, Zheng Liu, Yuxiao Jiang, Yuancai Leng, Jialong Tang, Renqi Wang, and Xiaorong Lv. 2023. "Simulation and Experiment of the Smoothness Performance of an Electric Four-Wheeled Chassis in Hilly and Mountainous Areas" Sustainability 15, no. 24: 16868. https://doi.org/10.3390/su152416868
APA StyleFu, Y., Liu, Z., Jiang, Y., Leng, Y., Tang, J., Wang, R., & Lv, X. (2023). Simulation and Experiment of the Smoothness Performance of an Electric Four-Wheeled Chassis in Hilly and Mountainous Areas. Sustainability, 15(24), 16868. https://doi.org/10.3390/su152416868





