A Short Review on the Time-Domain Numerical Simulations for Structural Responses in Horizontal-Axis Offshore Wind Turbines
Abstract
:1. Introduction
2. Wind Field Modelling
3. Aerodynamic Modelling for Fluid–Structure Interaction (FSI)
4. Hydrodynamic Modelling for Offshore Wind Turbines
5. The Reduced Order Model
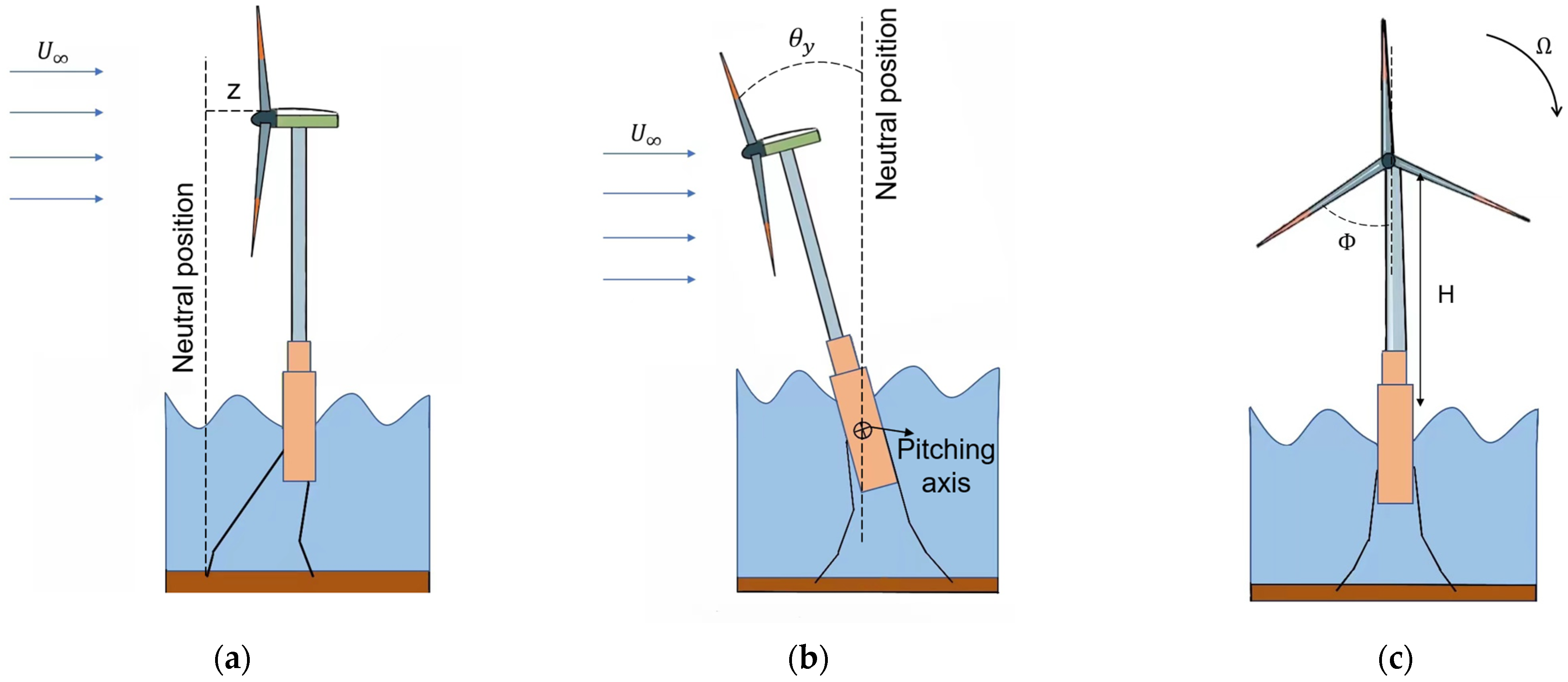
5.1. The Euler–Lagrange Approach
5.2. The Kane Approach
| Ref | Method | Turbine | DOFs | Description |
|---|---|---|---|---|
| [86,87,88,89,90] | Euler–Lagrange | NREL 5 MW/Offshore monopole | 14 | six DOFs for the blades, six DOFs for the tower, and two DOFs for the drivetrain. |
| [74,91] | Euler–Lagrange | NREL 5 MW/floating | 17 | six DOFs for the blade, three DOFs for the tower, two DOFs for the drivetrain, and six DOFs for the spar type platform. |
| [77,78] | Kane | NREL 5 MW/Floating | 22 | nine DOFs for the blades (six for flapwise and three for edgewise), six DOFs for the platform, four DOFs for the tower (two for fore–aft and two for side–side), two DOFs for the drivetrain, one DOF for the nacelle yaw |
| [79,80,81] | Euler–Lagrange | NREL 5 MW/offshore monopile | 12 | six DOFs for the blades, two DOFs for the tower, and four DOFs for the monopile (translation and rotation) |
| [92] | Euler–Lagrange | NREL 5 MW/onshore | 8 | six DOFs for the blade (three for the edgewise and three for the flapwise) and two DOFs for the tower. |
| [93] | Euler–Lagrange | NREL 5 MW/onshore | 3 | three DOFs for the modelling of edgewise vibration of the blade. |

6. Conclusions
- The wind profile model serves as the fundamental basis for accurately simulating the dynamics of HAWTs. Empirical wind profile models, such as the ones employed in the widely acknowledged code of TurbSim, show that the vertical variations in wind speeds could be described using the logarithm law or the power law.
- The estimates of aerodynamic loads acting on HAWTs concern the interactions between turbulent winds and the blades and the tower. The blade element momentum theory and its corrections are primarily used with consideration of floating platform motion on induced velocity and inflow angle.
- The classic wave models and hydrodynamic load calculations are necessary for the numerical simulation of floating HAWTs. Specifically, the wave kinematics shown from the potential flow theory and the empirical stochastic models are key for determining the hydrodynamic loads.
- Reduced-order models are applied to discern the structural responses of HAWTs. Specifically, the Euler–Lagrange approach and the Kane approach exhibit different computational efficiencies and result reliability, and hence should be employed under different situations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Renewables 2022. Available online: https://www.iea.org/reports/renewables-2022 (accessed on 10 August 2023).
- Summerfield-Ryan, O.; Park, S. The Power of Wind: The Global Wind Energy Industry’s Successes and Failures. Ecol. Econ. 2023, 210, 107841. [Google Scholar] [CrossRef]
- Government Energy Spending Tracker. Available online: https://www.iea.org/reports/government-energy-spending-tracker-2 (accessed on 15 August 2023).
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A Review of Recent Advancements in Offshore Wind Turbine Technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Y.; Liu, H.; Zhou, S.; Ni, Y.; Cai, C.; Zhou, T.; Li, Q. Review of Study on the Coupled Dynamic Performance of Floating Offshore Wind Turbines. Energies 2022, 15, 3970. [Google Scholar] [CrossRef]
- Subbulakshmi, A.; Verma, M.; Keerthana, M.; Sasmal, S.; Harikrishna, P.; Kapuria, S. Recent Advances in Experimental and Numerical Methods for Dynamic Analysis of Floating Offshore Wind Turbines—An Integrated Review. Renew. Sustain. Energy Rev. 2022, 164, 112525. [Google Scholar] [CrossRef]
- Otter, A.; Murphy, J.; Pakrashi, V.; Robertson, A.; Desmond, C. A Review of Modelling Techniques for Floating Offshore Wind Turbines. Wind Energy 2022, 25, 831–857. [Google Scholar] [CrossRef]
- Rezaei, M.; Behzad, M.; Haddadpour, H.; Moradi, H. Aeroelastic Analysis of a Rotating Wind Turbine Blade Using a Geometrically Exact Formulation. Nonlinear Dyn. 2017, 89, 2367–2392. [Google Scholar] [CrossRef]
- Peeters, M.; Santo, G.; Degroote, J.; Van Paepegem, W. High-Fidelity Finite Element Models of Composite Wind Turbine Blades with Shell and Solid Elements. Compos. Struct. 2018, 200, 521–531. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Yan, J.; Deng, X.; Korobenko, A. Computer Modeling of Wind Turbines: 2. Free-Surface FSI and Fatigue-Damage. Arch. Comput. Methods Eng. 2019, 26, 1101–1115. [Google Scholar] [CrossRef]
- Berg, J.C.; Resor, B.R. Numerical Manufacturing and Design Tool (Numad V2.0) for Wind Turbine Blades: User’s Guide. Available online: https://www.osti.gov/servlets/purl/1051715 (accessed on 21 August 2023).
- Yang, J.; Peng, C.; Xiao, J.; Zeng, J.; Xing, S.; Jin, J.; Deng, H. Structural Investigation of Composite Wind Turbine Blade Considering Structural Collapse in Full-Scale Static Tests. Compos. Struct. 2013, 97, 15–29. [Google Scholar] [CrossRef]
- Herbert, G.J.; Iniyan, S.; Sreevalsan, E.; Rajapandian, S. A Review of Wind Energy Technologies. Renew. Sustain. Energy Rev. 2007, 11, 1117–1145. [Google Scholar] [CrossRef]
- Tavares, R.P.; Bouwman, V.; Van Paepegem, W. Finite Element Analysis of Wind Turbine Blades Subjected to Torsional Loads: Shell Vs Solid Elements. Compos. Struct. 2022, 280, 114905. [Google Scholar] [CrossRef]
- Kim, S.-H.; Bang, H.-J.; Shin, H.-K.; Jang, M.-S. Composite Structural Analysis of Flat-Back Shaped Blade for Multi-Mw Class Wind Turbine. Appl. Compos. Mater. 2014, 21, 525–539. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Basu, B.; Nielsen, S.R. Active Tuned Mass Dampers for Control of in-Plane Vibrations of Wind Turbine Blades. Struct. Control Health Monit. 2013, 20, 1377–1396. [Google Scholar] [CrossRef]
- Vorpahl, F.; Schwarze, H.; Fischer, T.; Seidel, M.; Jonkman, J. Offshore Wind Turbine Environment, Loads, Simulation, and Design. WIREs Energy Environ. 2013, 2, 548–570. [Google Scholar] [CrossRef]
- Lu, H.; Porté-Agel, F. Large-Eddy Simulation of a Very Large Wind Farm in a Stable Atmospheric Boundary Layer. Phys. Fluids 2011, 23, 065101. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A Numerical Study of the Effects of Atmospheric and Wake Turbulence on Wind Turbine Dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows. Meas. Sci. Technol. 2001, 12, 2020–2021. [Google Scholar] [CrossRef]
- Thordal, M.S.; Bennetsen, J.C.; Koss, H.H.H. Review for Practical Application of CFD for the Determination of Wind Load on High-Rise Buildings. J. Wind. Eng. Ind. Aerodyn. 2019, 186, 155–168. [Google Scholar] [CrossRef]
- Mann, J. Wind Field Simulation. Probab. Eng. Mech. 1998, 13, 269–282. [Google Scholar] [CrossRef]
- Mann, J. The Spatial Structure of Neutral Atmospheric Surface-Layer Turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Hsieh, A.; Maniaci, D.C.; Herges, T.G.; Geraci, G.; Seidl, D.T.; Eldred, M.S.; Blaylock, M.L.; Houchens, B.C. Multilevel Uncertainty Quantification Using CFD and Openfast Simulations of the Swift Facility. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1949. [Google Scholar]
- Hübner, G.; Pinheiro, H.; de Souza, C.; Franchi, C.; Da Rosa, L.; Dias, J. Detection of Mass Imbalance in the Rotor of Wind Turbines Using Support Vector Machine. Renew. Energy 2021, 170, 49–59. [Google Scholar] [CrossRef]
- Somoano, M.; Battistella, T.; Rodríguez-Luis, A.; Fernández-Ruano, S.; Guanche, R. Influence of Turbulence Models on the Dynamic Response of a Semi-Submersible Floating Offshore Wind Platform. Ocean Eng. 2021, 237, 109629. [Google Scholar] [CrossRef]
- Malik, H.; Almutairi, A. Modified Fuzzy-Q-Learning (MFQL)-Based Mechanical Fault Diagnosis for Direct-Drive Wind Turbines Using Electrical Signals. IEEE Access 2021, 9, 52569–52579. [Google Scholar] [CrossRef]
- Pettas, V.; Costa García, F.; Kretschmer, M.; Rinker, J.M.; Clifton, A.; Cheng, P.W. A Numerical Framework for Constraining Synthetic Wind Fields with Lidar Measurements for Improved Load Simulations. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0993. [Google Scholar]
- Pokhrel, J.; Seo, J. Statistical Model for Fragility Estimates of Offshore Wind Turbines Subjected to Aero-Hydro Dynamic Loads. Renew. Energy 2021, 163, 1495–1507. [Google Scholar] [CrossRef]
- Jonkman, B.J. TurbSim User’s Guide: Version 1.50. Available online: https://www.osti.gov/biblio/965520 (accessed on 3 September 2023).
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Wan, D.; Pan, G.; Li, S. Exploring Inflow Wind Condition on Floating Offshore Wind Turbine Aerodynamic Characterisation and Platform Motion Prediction Using Blade Resolved CFD Simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Salzmann, D.C.; Van der Tempel, J. Aerodynamic Damping in the Design of Support Structures for Offshore Wind Turbines. In Proceedings of the Paper of the Copenhagen Offshore Conference, Copenhagen, Denmark, 23–25 November 2021. [Google Scholar]
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual. Available online: https://www.osti.gov/biblio/15014831 (accessed on 9 September 2023).
- Bai, C.J.; Wang, W.C. Review of Computational and Experimental Approaches to Analysis of Aerodynamic Performance in Horizontal-Axis Wind Turbines (HAWTs). Renew. Sustain. Energy Rev. 2016, 63, 506–519. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, D. Review of Numerical and Experimental Studies on Flow Characteristics around a Straight-Bladed Vertical Axis Wind Turbine and Its Performance Enhancement Strategies. Arch. Comput. Methods Eng. 2022, 29, 1839–1874. [Google Scholar] [CrossRef]
- Sant, T.; Cuschieri, K. Comparing Three Aerodynamic Models for Predicting the Thrust and Power Characteristics of a Yawed Floating Wind Turbine Rotor. J. Sol. Energy Eng. 2016, 138, 031004. [Google Scholar] [CrossRef]
- Wu, C.H.K.; Nguyen, V.T. Aerodynamic Simulations of Offshore Floating Wind Turbine in Platform-Induced Pitching Motion. Wind Energy 2017, 20, 835–858. [Google Scholar] [CrossRef]
- Micallef, D.; Rezaeiha, A. Floating Offshore Wind Turbine Aerodynamics: Trends and Future Challenges. Renew. Sustain. Energy Rev. 2021, 152, 111696. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.-J. Effects of Platform Motions on Aerodynamic Performance and Unsteady Wake Evolution of a Floating Offshore Wind Turbine. Renew. Energy 2019, 143, 9–23. [Google Scholar] [CrossRef]
- Wen, B.; Tian, X.; Dong, X.; Peng, Z.; Zhang, W. Influences of Surge Motion on the Power and Thrust Characteristics of an Offshore Floating Wind Turbine. Energy 2017, 141, 2054–2068. [Google Scholar] [CrossRef]
- Oukassou, K.; El Mouhsine, S.; El Hajjaji, A.; Kharbouch, B. Comparison of the Power, Lift and Drag Coefficients of Wind Turbine Blade from Aerodynamics Characteristics of Naca0012 and Naca2412. Procedia Manuf. 2019, 32, 983–990. [Google Scholar] [CrossRef]
- Almukhtar, A.H. Effect of drag on the Performance for an Efficient Wind Turbine Blade Design. Energy Procedia 2012, 18, 404–415. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Hsiao, F.-B. Aerodynamic Investigations of Low-Aspect-Ratio Thin Plate Wings at Low Reynolds Numbers. J. Mech. 2012, 28, 77–89. [Google Scholar] [CrossRef]
- Villeneuve, T.; Boudreau, M.; Dumas, G. Lift Enhancement and Drag Reduction of Lifting Blades through the Use of End-Plates and Detached End-Plates. J. Wind Eng. Ind. Aerodyn. 2019, 184, 391–404. [Google Scholar] [CrossRef]
- Jeon, M.; Lee, S.; Lee, S. Unsteady Aerodynamics of Offshore Floating Wind Turbines in Platform Pitching Motion Using Vortex Lattice Method. Renew. Energy 2014, 65, 207–212. [Google Scholar] [CrossRef]
- Hansen, M.O. Aerodynamics of Wind Turbines: Rotors, Loads and Structure; Earthscan: Oxford, UK, 2000; Volume 17. [Google Scholar]
- Shen, W.Z.; Mikkelsen, R.; Sørensen, J.N.; Bak, C. Tip Loss Corrections for Wind Turbine Computations. Wind Energy 2005, 8, 457–475. [Google Scholar] [CrossRef]
- Hansen, M. Aerodynamics of Wind Turbines; Routledge: Oxford, UK, 2015. [Google Scholar]
- Ning, S.A. A Simple Solution Method for the Blade Element Momentum Equations with Guaranteed Convergence. Wind Energy 2014, 17, 1327–1345. [Google Scholar] [CrossRef]
- Kim, M.-S.; Lee, K.-S. Hydrodynamic Force Calculation and Motion Analysis of OC3 Hywind Floating Offshore Wind Turbine Platform. J. Adv. Mar. Eng. Technol. 2013, 37, 953–961. [Google Scholar] [CrossRef]
- Bashetty, S.; Ozcelik, S. Review on Dynamics of Offshore Floating Wind Turbine Platforms. Energies 2021, 14, 6026. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Fundamental of Fluid Mechanics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Ishihara, T.; Zhang, S. Prediction of Dynamic Response of Semi-Submersible Floating Offshore Wind Turbine Using Augmented Morison’s Equation with Frequency Dependent Hydrodynamic Coefficients. Renew. Energy 2019, 131, 1186–1207. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; University of Colorado at Boulder: Boulder, CO, USA, 2007. [Google Scholar]
- Kvittem, M.I.; Bachynski, E.E.; Moan, T. Effects of Hydrodynamic Modelling in Fully Coupled Simulations of a Semi-Submersible Wind Turbine. Energy Procedia 2012, 24, 351–362. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.-H. The Coupled Dynamic Response Computation for a Semi-Submersible Platform of Floating Offshore Wind Turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Roald, L.; Jonkman, J.; Robertson, A.; Chokani, N. The Effect of Second-Order Hydrodynamics on Floating Offshore Wind Turbines. Energy Procedia 2013, 35, 253–264. [Google Scholar] [CrossRef]
- Hall, M.; Buckham, B.; Crawford, C. Evaluating the Importance of Mooring Line Model Fidelity in Floating Offshore Wind Turbine Simulations. Wind Energy 2014, 17, 1835–1853. [Google Scholar] [CrossRef]
- Masciola, M.; Robertson, A.; Jonkman, J.; Coulling, A.; Goupee, A. Assessment of the Importance of Mooring Dynamics on the Global Response of the Deepcwind Floating Semisubmersible Offshore Wind Turbine. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; p. ISOPE–I–13-129. [Google Scholar]
- Azcona, J.; Palacio, D.; Munduate, X.; Gonzalez, L.; Nygaard, T.A. Impact of Mooring Lines Dynamics on the Fatigue and Ultimate Loads of Three Offshore Floating Wind Turbines Computed with IEC 61400-3 Guideline. Wind Energy 2017, 20, 797–813. [Google Scholar] [CrossRef]
- Chen, L.; Basu, B.; Nielsen, S.R. A Coupled Finite Difference Mooring Dynamics Model for Floating Offshore Wind Turbine Analysis. Ocean Eng. 2018, 162, 304–315. [Google Scholar] [CrossRef]
- Li, Y.; Castro, A.; Sinokrot, T.; Prescott, W.; Carrica, P. Coupled Multi-Body Dynamics and CFD for Wind Turbine Simulation Including Explicit Wind Turbulence. Renew. Energy 2015, 76, 338–361. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Yuan, Z.; Gao, Y. Dynamic and Structural Performances of Offshore Floating Wind Turbines in Turbulent Wind Flow. Ocean Eng. 2019, 179, 92–103. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Fitzgerald, B.; Basu, B. Cable Connected Active Tuned Mass Dampers for Control of in-Plane Vibrations of Wind Turbine Blades. J. Sound Vib. 2014, 333, 5980–6004. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Basu, B. Structural Control of Wind Turbines with Soil Structure Interaction Included. Eng. Struct. 2016, 111, 131–151. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Zhang, J.; Gong, Z.; Guo, L.; Wu, H. Analysis of Mode and Dynamic Stability for Wind Turbine Rotating Blades. J. Offshore Mech. Arct. Eng. 2018, 140, 051902. [Google Scholar] [CrossRef]
- Fitzgerald, B.; Sarkar, S.; Staino, A. Improved Reliability of Wind Turbine Towers with Active Tuned Mass Dampers (ATMDs). J. Sound Vib. 2018, 419, 103–122. [Google Scholar] [CrossRef]
- Tong, W. Wind Power Generation and Wind Turbine Design; WIT Press: Billerica, MA, USA, 2010. [Google Scholar]
- Fitzgerald, B.; Basu, B. Vibration Control of Wind Turbines: Recent Advances and Emerging Trends. Int. J. Sustain. Mater. Struct. Syst. 2020, 4, 347–372. [Google Scholar] [CrossRef]
- Golnary, F.; Moradi, H.; Tse, K.T. Nonlinear Pitch Angle Control of an Onshore Wind Turbine by Considering the Aerodynamic Nonlinearities and Deriving an Aeroelastic Model. Energy Syst. 2021, 14, 197–227. [Google Scholar] [CrossRef]
- Høeg, C.E.; Zhang, Z. The Influence of Gyroscopic Effects on Dynamic Responses of Floating Offshore Wind Turbines in Idling and Operational Conditions. Ocean Eng. 2021, 227, 108712. [Google Scholar] [CrossRef]
- Jonkman, J.; Buhl, M. FAST User’s Guide. Golden, Co: National Renewable Energy Laboratory. 2005. Available online: https://www.nrel.gov/docs/fy06osti/38230.pdf (accessed on 19 September 2023).
- Sarkar, S.; Chen, L.; Fitzgerald, B.; Basu, B. Multi-Resolution Wavelet Pitch Controller for Spar-Type Floating Offshore Wind Turbines Including Wave-Current Interactions. J. Sound Vib. 2020, 470, 115170. [Google Scholar] [CrossRef]
- Mitra, A.; Sarkar, S.; Chakraborty, A.; Das, S. Sway Vibration Control of Floating Horizontal Axis Wind Turbine by Modified Spar-Torus Combination. Ocean Eng. 2021, 219, 108232. [Google Scholar] [CrossRef]
- Sarkar, S.; Fitzgerald, B. Use of Kane’s Method for MULTI-body Dynamic Modelling and Control of Spar-Type Floating Offshore Wind Turbines. Energies 2021, 14, 6635. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V. Bi-Directional Vibration Control of Offshore Wind Turbines Using a 3D Pendulum Tuned Mass Damper. Mech. Syst. Signal Process. 2018, 105, 338–360. [Google Scholar] [CrossRef]
- Sun, C. Semi-Active Control of Monopile Offshore Wind Turbines Under Multi-Hazards. Mech. Syst. Signal Process. 2018, 99, 285–305. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V.; Sun, H. Performance of a 3D Pendulum Tuned Mass Damper in Offshore Wind Turbines Under Multiple Hazards And System Variations. Smart Struct. Syst. 2019, 24, 53–65. [Google Scholar]
- Kane, T.R.; Levinson, D.A. Dynamics, Theory and Applications; McGraw Hill: New York, NY, USA, 1985. [Google Scholar]
- Ginsberg, J. Engineering Dynamics; Cambridge University Press: Cambridge, UK, 2008; Volume 10. [Google Scholar]
- Baruh, H. Applied Dynamics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ginsberg, J.H. Advanced Engineering Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Larsen, T.G.; Zhang, Z.; Høgsberg, J. Vibration Damping of an Offshore Wind Turbine by Optimally Calibrated Pendulum Absorber with Shunted Electromagnetic Transducer. J. Sound Vib. 2021, 505, 116144. [Google Scholar] [CrossRef]
- Zhang, Z. Passive and Active Vibration Control of Renewable Energy Structures. Ph.D. Thesis, Aalborg Universitetsforlag, Aalborg, Danmark, 2015. [Google Scholar]
- Chen, B.; Basu, B.; Hua, X.; Feng, Z.; Zhang, Z.; Chen, Z.; Nielsen, S.R. Online DWT Algorithm for Identification of Aerodynamic Damping in Wind Turbines. Mech. Syst. Signal Process. 2021, 152, 107437. [Google Scholar] [CrossRef]
- Chen, B.; Hua, X.; Zhang, Z.; Nielsen, S.R.; Chen, Z. Active Flutter Control of the Wind Turbines Using Double-Pitched Blades. Renew. Energy 2021, 163, 2081–2097. [Google Scholar] [CrossRef]
- Zhang, Z.; Basu, B.; Nielsen, S.R. Real-Time Hybrid Aeroelastic Simulation of Wind Turbines with Various Types of Full-Scale Tuned Liquid Dampers. Wind Energy 2019, 22, 239–256. [Google Scholar] [CrossRef]
- Zhang, Z.; Høeg, C. Inerter-Enhanced Tuned Mass Damper for Vibration Damping of Floating Offshore Wind Turbines. Ocean Eng. 2021, 223, 108663. [Google Scholar] [CrossRef]
- Sarkar, S.; Chakraborty, A. Development of Semi-Active Vibration Control Strategy for Horizontal Axis Wind Turbine Tower Using Multiple Magneto-Rheological Tuned Liquid Column Dampers. J. Sound Vib. 2019, 457, 15–36. [Google Scholar] [CrossRef]
- Zhang, Z.; Larsen, T.G. Optimal Calibration of the Rotational Inertia Double Tuned Mass Damper (Ridtmd) for Rotating Wind Turbine Blades. J. Sound Vib. 2021, 493, 115827. [Google Scholar] [CrossRef]
- Sarkar, S.; Fitzgerald, B. Vibration Control of Spar-Type Floating Offshore Wind Turbine Towers Using a Tuned Mass-Damper-Inerter. Struct. Control Health Monit. 2020, 27, e2471. [Google Scholar] [CrossRef]
- Kabeyi, M.J.B.; Olanrewaju, O.A. Sustainable Energy Transition for Renewable and Low Carbon Grid Electricity Generation and Supply. Front. Energy Res. 2022, 9, 1032. [Google Scholar] [CrossRef]
- Holechek, J.L.; Geli, H.M.; Sawalhah, M.N.; Valdez, R. A Global Assessment: Can Renewable Energy Replace Fossil Fuels by 2050? Sustainability 2022, 14, 4792. [Google Scholar] [CrossRef]
- Azémar, C.; Giroud, A. World Investment Report 2022: International Tax Reforms and Sustainable Investment: United Nations Conference on Trade and Development, Geneva and New York, 2022; Springer: Berlin/Heidelberg, Germany, 2023; p. 219. ISBN 978-9211130492. [Google Scholar]
- Newell, R.; Raimi, D.; Villanueva, S.; Prest, B. Global Energy Outlook 2020: Energy Transition or Energy Addition. Resour. Future 2020. Available online: https://media.rff.org/documents/GEO_2020_Report.pdf (accessed on 24 September 2023).
- Li, Y.; Yang, S.; Feng, F.; Tagawa, K. A Review on Numerical Simulation Based on CFD Technology of Aerodynamic Characteristics of Straight-Bladed vertical Axis Wind Turbines. Energy Rep. 2023, 9, 4360–4379. [Google Scholar] [CrossRef]
- Miller, A.; Chang, B.; Issa, R.; Chen, G. Review of Computer-Aided Numerical Simulation in Wind Energy. Renew. Sustain. Energy Rev. 2013, 25, 122–134. [Google Scholar] [CrossRef]



| Rating | 5 MW |
|---|---|
| Rotor orientation, Configuration | Upwind, 3 blades |
| Control | Variable speed, Collective pitch |
| Drivetrain | High speed, Multiple-stage gearbox |
| Rotor, Hub diameter | 126 m, 3 m |
| Hub height | 90 m |
| Cut-In, Rated, Cut-out wind speed | 3 m, 11.4 m, 25 m |
| Rated tip speed | 80 m/s |
| Overhang, Shaft tilt, Precone | |
| Rotor Mass | 110,000 Kg |
| Nacelle Mass | 240,000 Kg |
| Tower Mass | 347,460 Kg |
| Coordinate location of overall CM | (−0.2 m, 0.0 m, 64.0 m) |
| Node | Rnode | Aero-Twist | Chord | Airfoil Type |
|---|---|---|---|---|
| 1 | 2.8667 | 13.308 | 3.542 | Cylinder 1 |
| 2 | 5.6000 | 13.308 | 3.854 | Cylinder 2 |
| 3 | 8.3333 | 13.308 | 4.167 | Cylinder 2 |
| 4 | 11.7500 | 13.308 | 4.557 | DU40_A17 |
| 5 | 15.8500 | 11.480 | 4.652 | DU35_A17 |
| 6 | 19.9500 | 10.162 | 4.458 | DU35_A17 |
| 7 | 24.0500 | 9.011 | 4.249 | DU30_A17 |
| 8 | 28.1500 | 7.795 | 4.007 | DU25_A17 |
| 9 | 32.2500 | 6.544 | 3.748 | DU25_A17 |
| 10 | 36.3500 | 5.361 | 3.502 | DU21_A17 |
| 11 | 40.4500 | 4.188 | 3.256 | DU21_A17 |
| 12 | 44.5500 | 3.125 | 3.010 | NACA64_A17 |
| 13 | 48.650 | 2.319 | 2.764 | NACA64_A17 |
| 14 | 52.7500 | 1.526 | 2.518 | NACA64_A17 |
| 15 | 56.1667 | 0.863 | 2.313 | NACA64_A17 |
| 16 | 58.9000 | 0.370 | 2.086 | NACA64_A17 |
| 17 | 61.6333 | 0.106 | 1.419 | NACA64_A17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Y.; Peng, B.; Wang, J.; Golnary, F.; Li, W. A Short Review on the Time-Domain Numerical Simulations for Structural Responses in Horizontal-Axis Offshore Wind Turbines. Sustainability 2023, 15, 16878. https://doi.org/10.3390/su152416878
Ni Y, Peng B, Wang J, Golnary F, Li W. A Short Review on the Time-Domain Numerical Simulations for Structural Responses in Horizontal-Axis Offshore Wind Turbines. Sustainability. 2023; 15(24):16878. https://doi.org/10.3390/su152416878
Chicago/Turabian StyleNi, Yang, Bin Peng, Jiayao Wang, Farshad Golnary, and Wei Li. 2023. "A Short Review on the Time-Domain Numerical Simulations for Structural Responses in Horizontal-Axis Offshore Wind Turbines" Sustainability 15, no. 24: 16878. https://doi.org/10.3390/su152416878
APA StyleNi, Y., Peng, B., Wang, J., Golnary, F., & Li, W. (2023). A Short Review on the Time-Domain Numerical Simulations for Structural Responses in Horizontal-Axis Offshore Wind Turbines. Sustainability, 15(24), 16878. https://doi.org/10.3390/su152416878







