Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of the Nitrogen Dioxide Distribution in the Atmospheric Surface Layer
2.2. Characteristics of Parametric Identification IDM Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, F.; Rüdiger, C.; Redouté, J.; Yuce, M.R. Live Demonstration: An IoT Platform for Environmental Monitoring Using Self-Powered Sensors. In Proceedings of the IEEE Sensors, New Delhi, India, 28–31 October 2018. [Google Scholar] [CrossRef]
- Ferro, M.; Paciello, V.; Pietrosanto, A.; Sommella, P. A distributed measurement system for the estimation of air quality. IEEE Instrum. Meas. Mag. 2020, 23, 51–56. [Google Scholar] [CrossRef]
- Wu, F.; Rudiger, C.; Yuce, M.R. Design and field test of an autonomous iot wsn platform for environmental monitoring. In Proceedings of the 27th International Telecommunication Networks and Applications Conference (ITNAC), Melbourne, VIC, Australia, 22–24 November 2017; pp. 1–6. [Google Scholar]
- Oyjinda, P.; Pochai, N. Numerical simulation of air pollution emission control near an industrial zone. Adv. Math. Phys. 2017, 2017, 7. [Google Scholar] [CrossRef]
- Oyjinda, P.; Pochai, N. Numerical Simulation of an Air Pollution Model on Industrial Areas by Considering the Influence of Multiple Point Sources. Int. J. Differ. Equ. 2019, 2019, 2319831. [Google Scholar] [CrossRef]
- Velasco, A.; Ferrero, R.; Gandino, F.; Montrucchio, B.; Rebaudengo, M. On the design of distributed air quality monitoring systems. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2015; Volume 1702, p. 180014. [Google Scholar]
- Miskell, G.; Salmond, J.A.; Williams, D.E. Use of a handheld low-cost sensor to explore the effect of urban design features on local-scale spatial and temporal air quality variability. Sci. Total Environ. 2018, 619, 480–490. [Google Scholar] [CrossRef] [PubMed]
- Shiang, Y.-L.; Wang, J.-C.; Sun, C.-H.; Wen, T.-H.; Juang, J.-Y.; Jiang, J.-A. Mobile Measurement of Particulate Matter Concentrations on Urban Streets: System Development and Field Verification. In IEEE Access; IEEE: New York, NY, USA, 2020; pp. 197617–197629. [Google Scholar]
- Korunoski, M.; Stojkoska, B.R.; Trivodaliev, K. Internet of Things Solution for Intelligent Air Pollution Prediction and Visualization. In Proceedings of the IEEE EUROCON 2019—18th International Conference on Smart Technologies, Novi Sad, Serbia, 1–4 July 2019; pp. 1–6. [Google Scholar]
- Kalajdjieski, J.; Korunoski, M.; Stojkoska, B.R.; Trivodaliev, K. Smart City Air Pollution Monitoring and Prediction: A Case Study of Skopje. In Proceedings of the International Conference on ICT Innovations, Skopje, North Macedonia, 24–26 September 2020; pp. 15–27. [Google Scholar]
- Savinykh, V.; Maiorov, A.; Materukhin, A. Spatial modeling of air pollution based on data streams from geosensor networks. Geod. Cartogr. 2017, 78, 39–43. [Google Scholar] [CrossRef]
- Kaivonen, S.; Ngai, E. Real-time air pollution monitoring with sensors on city buses. Digit. Commun. Netw. 2019, 6, 23–30. [Google Scholar] [CrossRef]
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; Di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 607, 691–705. [Google Scholar] [CrossRef] [PubMed]
- Boubrima, A.; Bechkit, W.; Rivano, H. Optimal WSN deployment models for air pollution monitoring. IEEE Trans. Wireless Commun. 2017, 16, 2723–2735. [Google Scholar] [CrossRef]
- Boubrima, A.; Bechkit, W.; Rivano, H. On the Deployment of Wireless Sensor Networks for Air Quality Mapping: Optimization Models and Algorithms. IEEE/ACM Trans. Netw. 2019, 27, 1629–1642. [Google Scholar] [CrossRef]
- Kalajdjieski, J.; Stojkoska, B.R.; Trivodaliev, K. IoT Based Framework for Air Pollution Monitoring in Smart Cities. In Proceedings of the 2020 28th Telecommunications Forum (TELFOR), Belgrade, Serbia, 24–25 November 2020; pp. 1–4. [Google Scholar]
- Atmosphere Monitiring Service. Available online: https://atmosphere.copernicus.eu (accessed on 20 July 2022).
- Ministry of Environmental Protection and Natural Resources of Ukraine. Available online: https://mepr.gov.ua// (accessed on 20 July 2022).
- Korolev, A.V. Differential and Difference Equations: A Textbook and Workshop for Academic Bachelor’s Degrees; M: Urayt Publishing House: Moscow, Russia, 2017; p. 281. [Google Scholar]
- Glyzin, S.D.; Marushkina, E.A. Differential and Difference Equations and Systems in Examples and Problems; Tutorial; YarSU: Yaroslavl, Russia, 2017; p. 80. [Google Scholar]
- Urmanchev, V.I. Difference Equations; The National Academy of Statistics, Accounting and Auditing: Kyiv, Ukraine, 2018; p. 44c. [Google Scholar]
- Polyanin, A.; Zaitsev, V. Handbook of Ordinary Differential Equations: Exact Solutions, Methods, and Problems; CRC Press: Boca Raton, FL, USA, 2017; 1496. [Google Scholar]
- Dyvak, M.; Rot, A.; Pasichnyk, R.; Tymchyshyn, V.; Huliyev, N.; Maslyiak, Y. Monitoring and Mathematical Modeling of Soil and Groundwater Contamination by Harmful Emissions of Nitrogen Dioxide from Motor Vehicles. Sustainability 2021, 13, 2768. [Google Scholar] [CrossRef]
- Dyvak, M. Parameters Identification Method of Interval Discrete Dynamic Models of Air Pollution Based on Artificial Bee Colony Algorithm. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 13–15 May 2020; pp. 130–135. [Google Scholar]
- Porplytsya, N.; Dyvak, M.; Spivak, I.; Voytyuk, I. Mathematical and algorithmic foundations for implementation of the method for structure identification of interval difference operator based on functioning of bee colony. In Proceedings of the 13th International Conference on the Experience of Designing and Application of CAD Systems in Microelectronics (CADSM), Lviv, Ukraine, 24–27 February 2015; pp. 196–199. [Google Scholar]
- Dyvak, M.; Porplytsya, N.; Borivets, I.; Shynkaryk, M. Improving the computational implementation of the parametric identification method for interval discrete dynamic models. In Proceedings of the 12th International Conference on International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 5–8 September 2017; pp. 533–536. [Google Scholar]
- Dyvak, M.; Pukas, A.; Oliynyk, I.; Melnyk, A. Selection the “Saturated” Block from Interval System of Linear Algebraic Equations for Recurrent Laryngeal Nerve Identification. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 444–448. [Google Scholar] [CrossRef]
- Krepych, S.; Spivak, I. Model of human weight correction based on interval data analysis. Int. J. Comput. 2020, 19, 128–136. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithms: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Christou, I.T.; Darrell, W.L.; De Long, K.; Martin, W. Evolutionary Algorithms; Springer-Verlag: New York, NY, USA, 2021; 602p. [Google Scholar]
- Petrowski, A.; Ben-Hamida, S. Evolutionary Algorithms (Computer Engineering: Metaheuristics Book 9), 1st ed.; Wiley-ISTE: Hoboken, NJ, USA, 2017; p. 305. [Google Scholar]
- Abraham, A.; Jatoth, R.K.; Rajasekhar, A. Hybrid differential artificial bee colony algorithm. J. Comput. Theor. Nanosci. 2012, 9, 249–257. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Alshattnawi, S.; Afifi, L.; Shatnawi, A.M.; Barhoush, M.M. Utilizing Genetic Algorithm and Artificial Bee Colony Algorithm to Extend the WSN Lifetime. Int. J. Comput. 2022, 21, 25–31. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D.; Gorkemli, B.; Kaya, E. A survey on the artificial bee colony algorithm variants for binary, integer and mixed integer programming problems. Appl. Soft Comput. 2021, 106, 107351. [Google Scholar] [CrossRef]
- Slowik, A. Swarm Intelligence Algorithms: Modification and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020; 378p. [Google Scholar]
- Kumar, A.; Negi, G.; Pant, S.; Ram, M.; Dimri, S.C. Availability-Cost Optimization of Butter Oil Processing System by Using Nature Inspired Optimization Algorithms. Reliab. Theory Appl. 2021, SI 2, 188–200. [Google Scholar]
- Akay, B.; Karaboga, D. A survey on the applications of artificial bee colony in signal, image, and video processing. Signal Image Video Process 2015, 9, 967–990. [Google Scholar] [CrossRef]
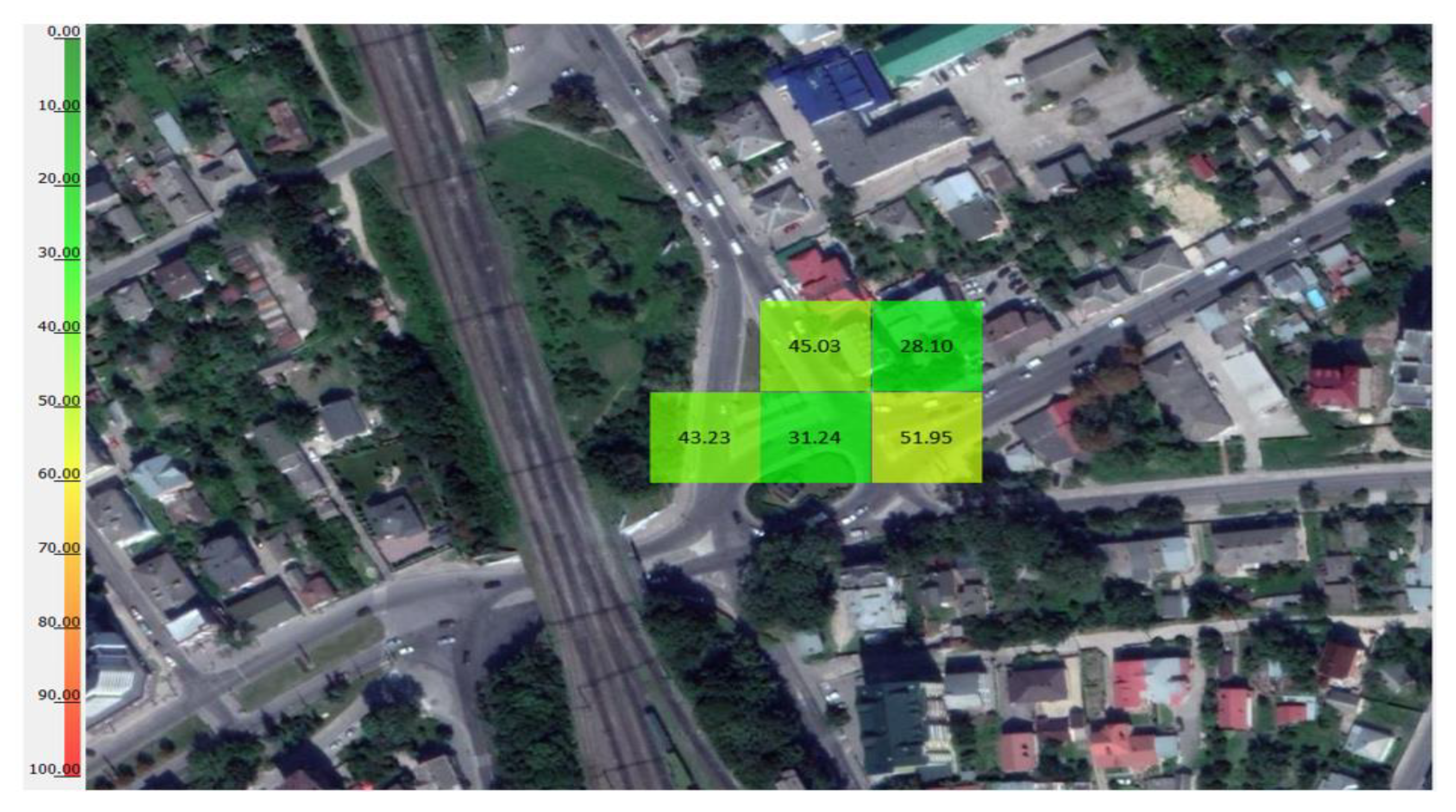
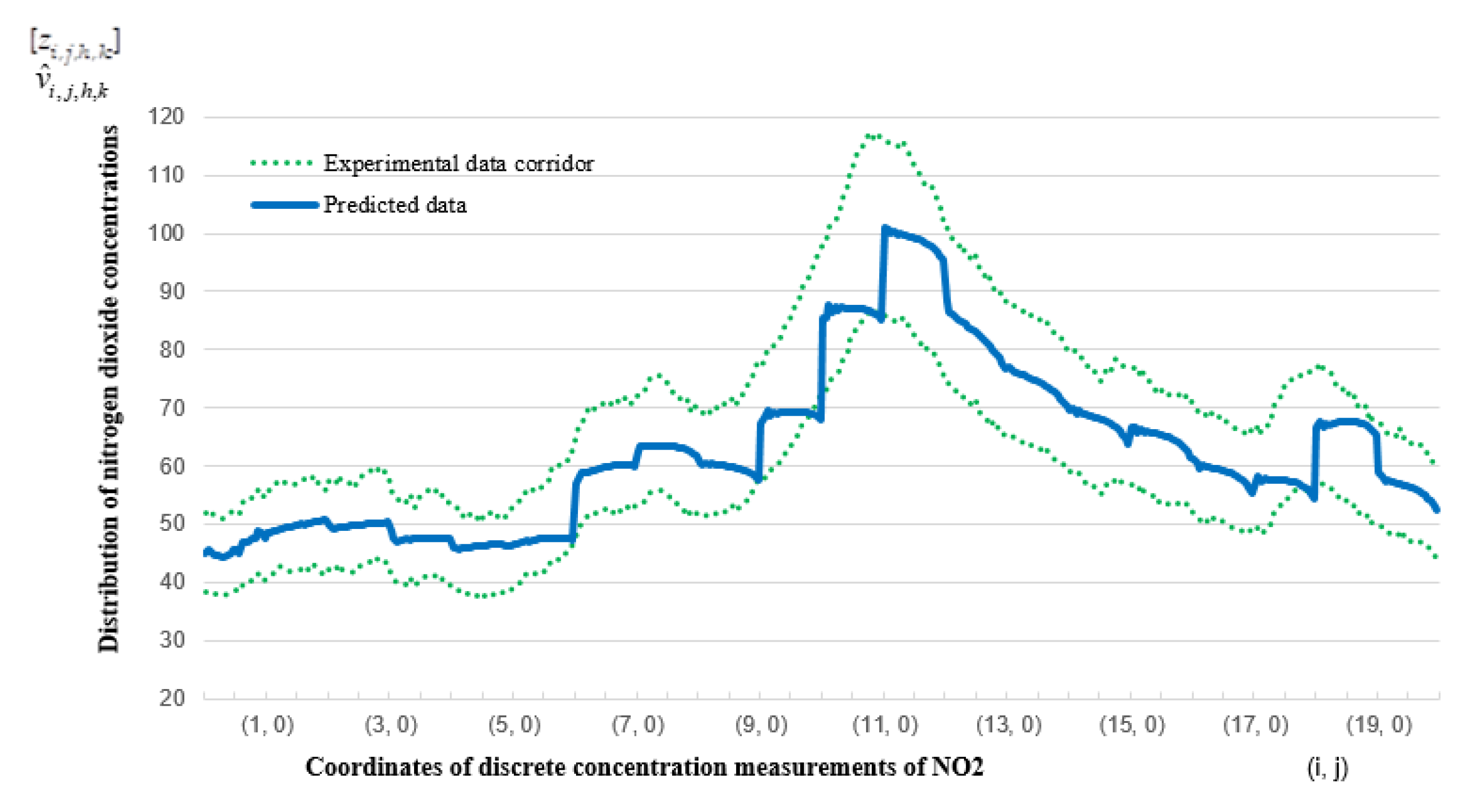
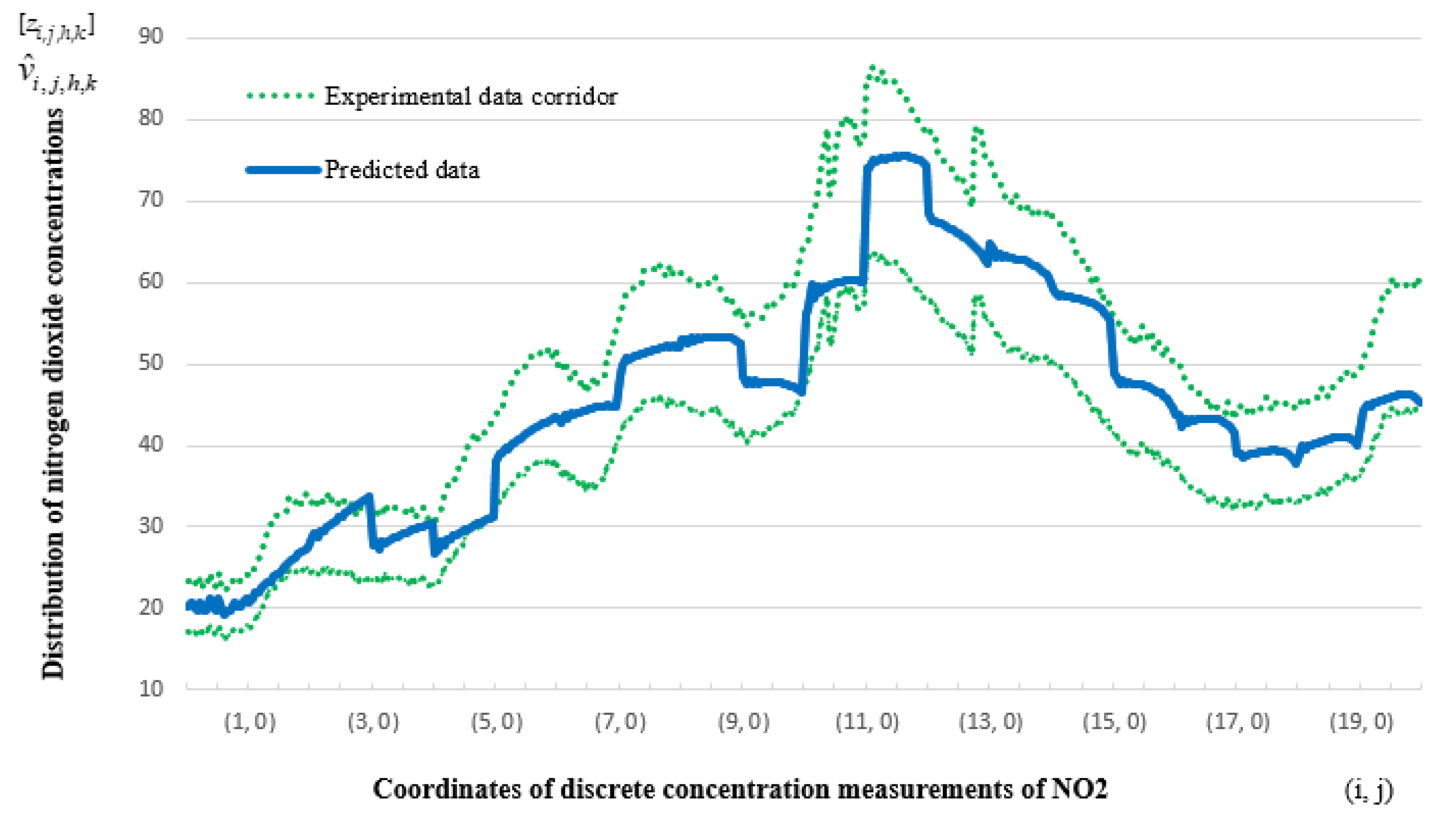
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 0 | 45.13 | 45.6 | 45.13 | 44.66 | 44.66 | 44.19 | 44.19 | 44.66 | 45.13 | 45.6 | 45.6 | 45.13 | 47.01 | 47.01 | 47.01 | 47.48 | 47.48 | 48.89 | 48.42 | 47.48 |
| 1 | 48.42 | 48.42 | 48.89 | 49.84 | 50.31 | 49.84 | 49.36 | 49.36 | 49.36 | 49.36 | 49.84 | 49.84 | 50.31 | 49.84 | 49.84 | 50.78 | 49.84 | 48.89 | 48.89 | 48.42 |
| 2 | 49.84 | 49.36 | 49.36 | 50.78 | 49.84 | 49.84 | 49.84 | 49.36 | 48.89 | 49.84 | 50.31 | 50.78 | 51.25 | 51.25 | 51.72 | 52.19 | 51.25 | 50.78 | 51.25 | 50.78 |
| 3 | 48.89 | 47.48 | 47.01 | 47.01 | 47.01 | 46.54 | 47.95 | 47.01 | 46.07 | 47.48 | 47.95 | 47.95 | 48.42 | 47.95 | 47.95 | 48.89 | 48.42 | 47.48 | 47.48 | 46.54 |
| 4 | 46.07 | 46.07 | 45.6 | 44.66 | 45.13 | 44.66 | 45.13 | 44.66 | 44.19 | 45.13 | 44.19 | 44.19 | 45.13 | 44.66 | 44.19 | 45.13 | 45.13 | 44.66 | 45.6 | 45.6 |
| 5 | 46.54 | 46.54 | 47.01 | 47.48 | 48.89 | 48.89 | 48.42 | 48.89 | 48.42 | 49.36 | 49.36 | 49.84 | 51.72 | 51.72 | 51.72 | 52.66 | 52.66 | 53.13 | 53.13 | 55.01 |
| 6 | 56.89 | 58.3 | 58.77 | 59.71 | 60.65 | 61.12 | 60.65 | 61.59 | 61.59 | 61.59 | 62.06 | 61.59 | 61.12 | 62.06 | 61.59 | 61.59 | 62.53 | 62.06 | 61.59 | 62.53 |
| 7 | 62.53 | 63.47 | 63.47 | 63.94 | 65.35 | 65.35 | 65.35 | 65.82 | 65.82 | 64.88 | 64.41 | 63.47 | 63 | 63 | 62.06 | 61.59 | 62.06 | 60.65 | 60.18 | 61.12 |
| 8 | 60.65 | 60.18 | 60.65 | 60.18 | 60.65 | 61.12 | 60.65 | 61.59 | 61.59 | 61.12 | 62.06 | 62.53 | 61.59 | 62.06 | 63 | 63.47 | 64.88 | 65.35 | 67.23 | 67.7 |
| 9 | 67.23 | 68.17 | 69.58 | 70.05 | 70.05 | 70.99 | 71.46 | 72.4 | 73.34 | 73.81 | 75.22 | 76.16 | 77.1 | 78.51 | 79.92 | 80.39 | 81.33 | 82.27 | 83.22 | 84.63 |
| 10 | 85.57 | 85.57 | 87.92 | 88.39 | 88.86 | 89.8 | 92.15 | 93.09 | 94.03 | 96.38 | 97.32 | 99.2 | 99.67 | 100.14 | 101.08 | 102.02 | 101.08 | 102.02 | 101.55 | 101.55 |
| 11 | 101.08 | 100.61 | 100.14 | 100.14 | 100.14 | 99.67 | 100.61 | 99.67 | 98.26 | 97.79 | 96.38 | 95.91 | 94.97 | 94.03 | 94.5 | 94.03 | 93.09 | 92.15 | 90.74 | 88.39 |
| 12 | 88.39 | 86.51 | 86.04 | 86.04 | 85.1 | 84.16 | 84.63 | 83.69 | 83.22 | 84.16 | 82.74 | 81.33 | 80.86 | 79.92 | 80.39 | 78.98 | 78.04 | 78.51 | 77.57 | 76.63 |
| 13 | 77.1 | 76.63 | 76.16 | 76.16 | 75.69 | 75.22 | 75.69 | 74.75 | 74.75 | 74.75 | 74.28 | 73.81 | 74.28 | 73.34 | 72.4 | 71.93 | 71.46 | 71.46 | 70.52 | 69.58 |
| 14 | 69.58 | 70.05 | 69.11 | 69.11 | 68.17 | 67.23 | 67.23 | 66.29 | 66.29 | 65.35 | 64.88 | 65.35 | 66.76 | 66.29 | 67.23 | 68.17 | 67.7 | 67.23 | 67.23 | 66.76 |
| 15 | 66.76 | 66.76 | 65.82 | 66.76 | 65.35 | 64.88 | 64.88 | 64.41 | 63 | 63.47 | 63.47 | 62.53 | 63 | 62.53 | 62.53 | 63 | 62.53 | 62.06 | 63 | 62.06 |
| 16 | 61.12 | 60.65 | 59.71 | 60.18 | 59.71 | 59.24 | 60.18 | 59.71 | 59.24 | 59.71 | 59.24 | 58.77 | 58.3 | 57.83 | 57.83 | 57.83 | 57.36 | 56.89 | 57.83 | 56.89 |
| 17 | 57.36 | 58.3 | 57.36 | 57.36 | 58.3 | 58.3 | 61.12 | 61.59 | 62.06 | 63.94 | 63.94 | 64.41 | 65.35 | 65.82 | 65.82 | 65.82 | 65.82 | 65.82 | 66.76 | 66.76 |
| 18 | 66.76 | 67.7 | 66.76 | 66.76 | 66.29 | 65.82 | 64.41 | 64.41 | 63.47 | 63.94 | 63.47 | 62.06 | 62.53 | 61.12 | 61.12 | 60.65 | 61.12 | 58.77 | 59.24 | 58.77 |
| 19 | 58.77 | 58.3 | 57.36 | 56.89 | 57.36 | 56.89 | 56.42 | 57.83 | 56.42 | 55.48 | 55.48 | 55.48 | 55.95 | 55.48 | 55.01 | 54.07 | 54.07 | 53.13 | 52.19 | 52.19 |
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 0 | 20.22 | 20.69 | 20.22 | 19.75 | 20.69 | 19.75 | 19.75 | 21.16 | 20.22 | 19.75 | 21.16 | 19.75 | 19.28 | 19.75 | 19.75 | 20.69 | 20.22 | 20.22 | 20.69 | 21.16 |
| 1 | 20.69 | 21.16 | 22.10 | 22.57 | 23.51 | 24.45 | 25.86 | 26.33 | 26.33 | 27.27 | 27.74 | 27.74 | 27.74 | 29.15 | 28.68 | 28.68 | 29.15 | 28.68 | 29.62 | 29.15 |
| 2 | 28.68 | 29.15 | 28.68 | 28.21 | 29.15 | 29.62 | 28.68 | 29.15 | 28.68 | 28.68 | 29.15 | 28.68 | 28.21 | 28.68 | 27.74 | 27.27 | 28.21 | 27.74 | 27.74 | 27.74 |
| 3 | 27.74 | 28.21 | 27.27 | 27.27 | 28.68 | 27.74 | 27.74 | 28.21 | 28.21 | 27.74 | 27.74 | 27.74 | 27.27 | 28.21 | 27.27 | 27.27 | 28.21 | 27.27 | 26.80 | 27.27 |
| 4 | 26.80 | 27.27 | 28.21 | 29.15 | 30.56 | 30.56 | 30.56 | 31.97 | 32.44 | 32.44 | 34.32 | 34.79 | 35.26 | 36.2 | 35.26 | 35.26 | 36.2 | 36.2 | 37.14 | 37.61 |
| 5 | 38.08 | 39.02 | 39.02 | 40.43 | 40.9 | 41.37 | 41.84 | 42.78 | 42.78 | 42.78 | 43.72 | 44.19 | 44.19 | 44.66 | 44.66 | 44.19 | 44.66 | 45.13 | 44.19 | 45.13 |
| 6 | 43.25 | 42.78 | 43.72 | 42.78 | 41.84 | 42.78 | 41.84 | 41.37 | 41.84 | 40.43 | 41.37 | 41.84 | 40.9 | 41.84 | 42.31 | 42.31 | 44.66 | 44.66 | 46.07 | 47.48 |
| 7 | 48.42 | 49.84 | 50.78 | 50.78 | 51.25 | 52.19 | 52.19 | 52.19 | 53.6 | 53.6 | 53.6 | 53.6 | 53.13 | 54.07 | 53.13 | 52.66 | 54.07 | 53.13 | 52.66 | 53.13 |
| 8 | 53.13 | 53.13 | 52.66 | 52.19 | 52.19 | 52.19 | 51.72 | 51.72 | 52.19 | 52.19 | 52.19 | 52.66 | 51.72 | 51.25 | 50.78 | 49.84 | 50.31 | 49.36 | 48.42 | 49.36 |
| 9 | 48.42 | 47.48 | 47.95 | 48.89 | 48.89 | 48.89 | 48.42 | 48.89 | 49.84 | 49.36 | 49.84 | 50.31 | 50.31 | 51.25 | 52.19 | 51.72 | 51.72 | 52.66 | 54.07 | 55.95 |
| 10 | 55.95 | 56.89 | 59.71 | 60.18 | 61.12 | 64.88 | 66.29 | 68.64 | 71.46 | 72.87 | 76.16 | 78.98 | 78.98 | 79.92 | 82.74 | 82.74 | 83.22 | 84.63 | 84.16 | 84.16 |
| 11 | 84.16 | 84.16 | 85.1 | 84.16 | 83.69 | 84.63 | 83.69 | 83.22 | 83.22 | 83.69 | 82.74 | 82.27 | 82.27 | 81.33 | 80.86 | 79.92 | 79.45 | 79.45 | 78.51 | 78.04 |
| 12 | 78.51 | 77.57 | 77.57 | 75.69 | 75.22 | 75.22 | 74.75 | 74.28 | 74.28 | 73.34 | 72.87 | 73.34 | 71.93 | 71.46 | 70.05 | 68.64 | 68.17 | 68.64 | 65.82 | 64.88 |
| 13 | 64.88 | 63.94 | 63 | 63 | 62.06 | 61.12 | 60.65 | 60.65 | 61.59 | 60.65 | 59.71 | 60.18 | 60.18 | 59.24 | 60.18 | 59.71 | 59.24 | 59.24 | 58.77 | 58.77 |
| 14 | 59.24 | 58.77 | 58.3 | 58.3 | 57.36 | 57.36 | 56.89 | 56.42 | 55.01 | 54.54 | 54.54 | 54.54 | 53.13 | 52.19 | 52.66 | 52.19 | 50.31 | 50.78 | 50.78 | 48.89 |
| 15 | 48.89 | 48.42 | 47.48 | 47.48 | 46.54 | 46.07 | 46.54 | 45.6 | 46.07 | 47.48 | 47.01 | 46.07 | 46.54 | 45.13 | 46.07 | 45.13 | 44.19 | 45.13 | 44.19 | 43.72 |
| 16 | 43.72 | 43.72 | 42.31 | 41.84 | 41.37 | 40.9 | 40.9 | 40.43 | 40.43 | 39.96 | 39.49 | 38.55 | 39.49 | 39.02 | 38.55 | 38.55 | 38.08 | 39.49 | 38.55 | 37.61 |
| 17 | 39.02 | 39.02 | 38.55 | 38.08 | 39.02 | 38.08 | 38.08 | 38.55 | 39.02 | 39.96 | 39.02 | 38.55 | 39.49 | 39.02 | 39.02 | 39.02 | 39.49 | 39.02 | 39.02 | 38.55 |
| 18 | 39.02 | 39.96 | 39.49 | 39.49 | 39.96 | 39.96 | 39.96 | 40.9 | 40.43 | 39.96 | 40.9 | 40.9 | 41.37 | 41.84 | 41.84 | 42.78 | 42.31 | 41.84 | 42.31 | 42.78 |
| 19 | 42.78 | 44.19 | 45.13 | 45.6 | 47.95 | 48.42 | 48.89 | 51.25 | 51.25 | 51.25 | 52.66 | 52.19 | 51.72 | 51.72 | 51.72 | 52.19 | 51.72 | 51.72 | 52.66 | 52.19 |
| Finding Solutions of the Optimization Problem (24) | Finding Solutions of the Optimization Problem (12) | |||
|---|---|---|---|---|
| Number of Search Iterations | Total Search Time in Seconds | Number of Search Iterations | Total Search Time in Seconds | |
| Try 1 | 500 | 560 | 706 | 732 |
| Try 2 | 604 | 627 | 1590 | 1563 |
| Try 3 | 1208 | 1239 | 5468 | 4973 |
| Try 4 | 1745 | 1758 | 2072 | 1886 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyvak, M.; Spivak, I.; Melnyk, A.; Manzhula, V.; Dyvak, T.; Rot, A.; Hernes, M. Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases. Sustainability 2023, 15, 2163. https://doi.org/10.3390/su15032163
Dyvak M, Spivak I, Melnyk A, Manzhula V, Dyvak T, Rot A, Hernes M. Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases. Sustainability. 2023; 15(3):2163. https://doi.org/10.3390/su15032163
Chicago/Turabian StyleDyvak, Mykola, Iryna Spivak, Andriy Melnyk, Volodymyr Manzhula, Taras Dyvak, Artur Rot, and Marcin Hernes. 2023. "Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases" Sustainability 15, no. 3: 2163. https://doi.org/10.3390/su15032163
APA StyleDyvak, M., Spivak, I., Melnyk, A., Manzhula, V., Dyvak, T., Rot, A., & Hernes, M. (2023). Modeling Based on the Analysis of Interval Data of Atmospheric Air Pollution Processes with Nitrogen Dioxide due to the Spread of Vehicle Exhaust Gases. Sustainability, 15(3), 2163. https://doi.org/10.3390/su15032163











