Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Analysis of Posture and Endpoint Trajectory for Planter
3.2. Working Principle and Model Establishment
3.2.1. Working Principle
3.2.2. Model Establishment
3.2.3. Displacement Equation
3.2.4. Velocity Equation
3.2.5. Acceleration Equation
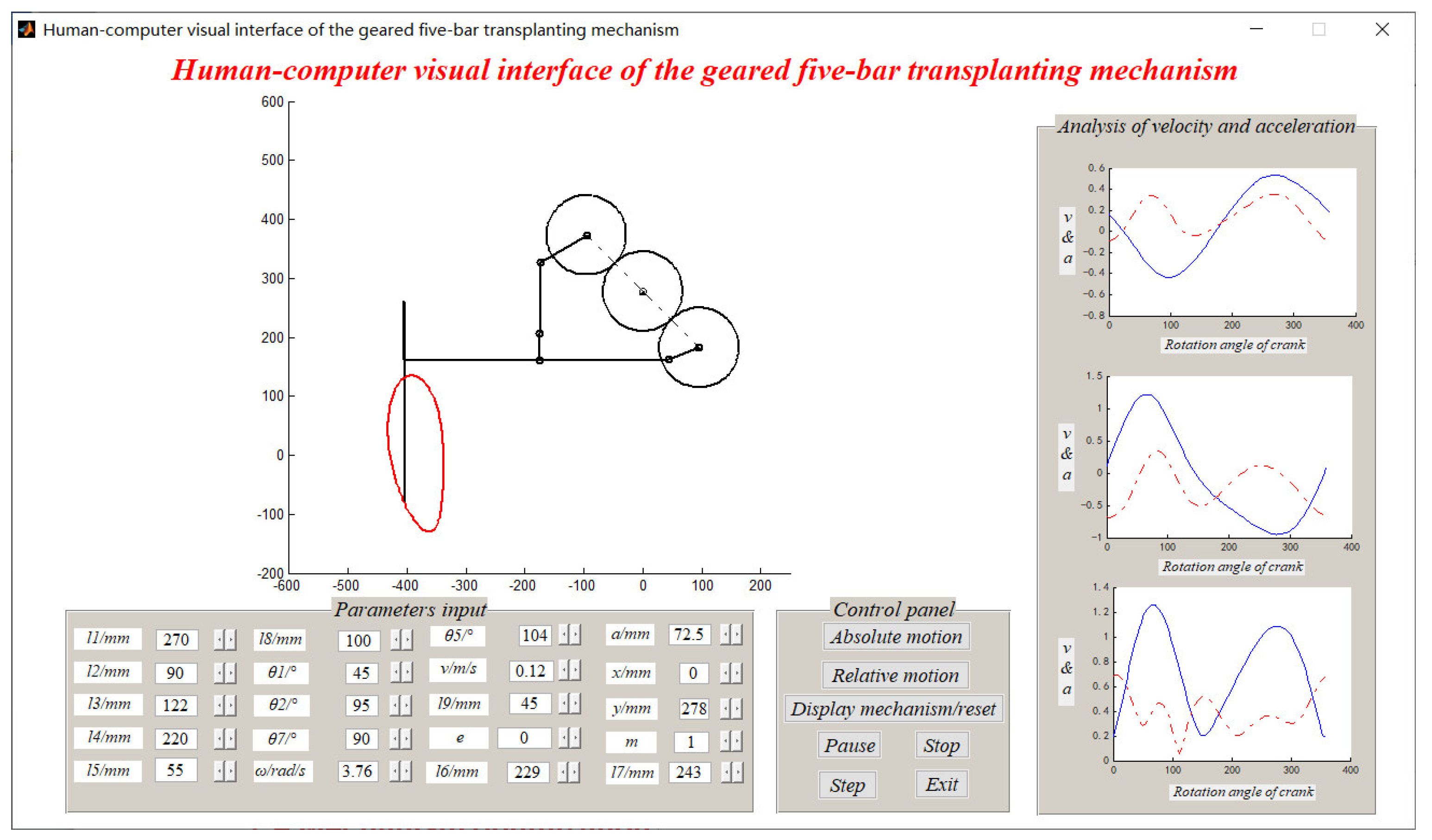
3.3. Human–Computer Interaction Visual Auxiliary Interface
3.4. Mechanism Optimization
3.4.1. Determination of Factor Level
3.4.2. Determination of Response Indicators
3.4.3. Method and Result Analysis
4. Results and Discussion
4.1. Results Analysis
4.1.1. Determination of Optimal Result
4.1.2. Comparing Results before and after Optimization
4.2. Mechanism Development
4.3. Bench Test
5. Conclusions
- (1)
- On the basis of analyzing the structural composition and working principle for the transplanting mechanism, the human–computer interactive auxiliary interface was established through the kinematics model.
- (2)
- With the aid of the auxiliary interface and orthogonal design, the combination of parameters that improve the operation performance and quality of the geared five-bar transplanting mechanism for Salvia miltiorrhiza were obtained (l1 = 290 mm, l2 = 100 mm, l3 = 124 mm, l4 = 231 mm, l5 = 64 mm, l6 = 229 mm, l7 = 243 mm, l8 = 100 mm, l9 = 45 mm, θ1 = 45°, θ5–θ2 = 19°, θ7 = 90°, and θ8 = 90°). Compared to before optimization, the optimized h1, β1, and α2 were basically unchanged. The optimized α1 increased approximately 1.9°, while the optimized l reduced by approximately 13.6 mm, which means that the length of the hole formed by the transplanting mechanism was reduced by 13.6 mm.
- (3)
- According to the optimal combination of parameters, a test bench system of the transplanting mechanism was built. The actual trajectory of the transplanting mechanism prototype was obtained by using high-speed photography technology. The bench test results showed that the comparison between the actual measurements and the theoretical analysis results was basically consistent, thus verifying the accuracy of the mechanism optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.; Song, J.; Lai, M.; Song, Z. Influence of fertigation integrated cultivation of Salvia miltiorrhiza on weed biomass. Shandong Agric. Sci. 2020, 52, 96–99. [Google Scholar]
- Lei, L.; Guo, Q.; Wang, C.; Ma, Z.; Cao, Y.; An, J. Effects of compound planting on growth and quality of Salvia miltiorrhiza. China J. Chin. Mater. Med. 2018, 43, 1818–1824. [Google Scholar]
- Chen, X.; He, C.; Yan, B.; Li, W.; Geng, Y.; Hou, J.; Wang, W. Investigation and analysis on difference of cultivation technique situation of Salvia miltiorrhiza. China J. Chin. Mater. Med. 2019, 44, 1314–1320. [Google Scholar]
- Wang, K.; Chao, J.; Gu, W.; Sheng, Y.; Su, S.; Xia, Y.; Wang, Y.; Hui, X.; Wang, Y. Effects of different seedling raising methods on the morphology, agronomic characters and physiological and biochemical indexes of Salvia miltiorrhiza Bunge seedlings. J. South. Agric. 2020, 51, 162–168. [Google Scholar]
- Jiang, L.; Tian, C.; Li, J.; Sun, J. Standardized and industrialized planting technology of Salvia miltiorrhiza. J. Zhejiang Agric. Sci. 2019, 60, 1842–1845+1849. [Google Scholar]
- Zhao, Y.; Fan, F.; Song, Z.; Na, M.; Zuo, Y.; Feng, Y.; Ji, H. Design and simulation of inverted vegetable pot seedling transplanting mechanism with conjugate cam. Trans. Chin. Soc. Agric. Eng. 2014, 30, 8–16. [Google Scholar]
- Hwang, S.; Park, J.; Lee, J.; Shim, S.; Nam, J. Optimization of Main Link Lengths of Transplanting Device of Semi-Automatic Vegetable Transplanter. Agronomy 2020, 10, 1938. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, C.; Xu, T.; Fu, J.; Chen, Y.; Yang, Y.; Gao, Q. Design and experiment of transplanting machine for cabbage substrate block seedlings. INMATEH Agric. Eng. 2021, 64, 375–384. [Google Scholar] [CrossRef]
- Xu, G.; Jian, S.; Song, Y.; Fang, H.; Qiu, X.; Ming, X. Design and Experiment of Cellar Cavitation Mechanism for Crops of Hilly Mountains Transplanter. Trans. Chin. Soc. Agric. Mach. 2022, 53, 105–113+125. [Google Scholar]
- Cui, W.; Liu, S.; Gao, L.; Wang, R.; Wang, J. Development of 2ZFS-1A multifunctional tobacco transplanting machine. Trans. Chin. Soc. Agric. Eng. 2012, 28, 36–41. [Google Scholar]
- Xie, Q.; Liu, F.; Yang, M.; Liu, J.; Yang, S.; Xie, S. DEM simulation and evaluation of well cellar making performance. INMATEH Agric. Eng. 2021, 63, 41–50. [Google Scholar] [CrossRef]
- Wu, J.; Yu, W.; Zhang, M.; Wu, C.; Jiang, L.; Tang, Q. Design and experiment of 2ZY-6 rapeseed blanket seedling transplanting machine. Trans. Chin. Soc. Agric. Mach. 2020, 51, 95–102+275. [Google Scholar]
- Sri, M.; Hwang, S.; Nam, J. Experimental safety analysis of transplanting device of the cam-type semi-automatic vegetable transplanter. J. Terramechanics 2022, 103, 19–32. [Google Scholar] [CrossRef]
- Iqbal, M.; Islam, M.; Ali, M.; Kiraga, S.; Kim, Y.; Chung, S. Theoretical overturning analysis of a 2.6-kW two-Row walking-type automatic pepper transplanter. J. Biosyst. Eng. 2022, 47, 79–91. [Google Scholar] [CrossRef]
- Reza, M.; Islam, M.; Chowdhury, M.; Ali, M.; Islam, S.; Kiraga, S.; Lim, S.; Choi, L.; Chung, S. Kinematic analysis of a gear-Driven rotary planting mechanism for a six-row self-propelled onion transplanter. Machines 2021, 9, 183. [Google Scholar] [CrossRef]
- Wang, K.; Gu, Y.; Sheng, Y.; Shen, X.; Han, Y.; Su, S.; Wang, Y.; Hui, X.; Gu, W.; Chao, J. Screening and optimization of nutrient solution for soilless seedling raising of Salvia miltiorrhiza. Soil Fertil. Sci. China 2020, 5, 243–249. [Google Scholar]
- Stubbs, S.; Colton, J. The Design of a Mechanized Onion Transplanter for Bangladesh with Functional Testing. Agriculture 2022, 12, 1790. [Google Scholar] [CrossRef]
- Liu, M.; Hu, X.; Liao, Y.; Liao, Y.; Wan, X.; Yi, M. Morphological parameters characteristics of mechanically transplanted plant in suitable transplanting period for different rape varieties. Trans. Chin. Soc. Agric. Eng. 2015, 31, 243–249. [Google Scholar]
- Xu, G.; Liu, H.; Jian, S.; Shi, S.; He, T. Design and Test of Transplanting Mechanism on Mulch-film of Salvia miltiorrhiza Based on Five-bar Mechanism. Trans. Chin. Soc. Agric. Mach. 2018, 49, 55–65. [Google Scholar]
- Yu, G.; Tong, Z.; Sun, L.; Tong, J.; Zhao, X. Novel gear transmission mechanism with twice unequal amplitude transmission Ratio. J. Mech. Des. 2019, 141, 092304. [Google Scholar] [CrossRef]
- Hu, J.; Pan, J.; Zhang, C.; Zhang, S.; Fei, W.; Pan, H. Optimization design and experiment on planetary gears planting mechanism of self-propelled transplanting machine. Trans. Chin. Soc. Agric. Mach. 2018, 49, 78–86. [Google Scholar]
- Wang, Y.; Chen, J.; Zhao, X.; Sun, X. Parameter optimization and experiment of planting mechanism driven by plantary non-circular gears. Trans. Chin. Soc. Agric. Mach. 2015, 46, 85–93. [Google Scholar]
- Zhou, H.; Yang, W.; Yu, G.; Wang, B.; Ye, B. Optimization design and experiments of ditching multi-bar seedling planting mechanism. Trans. Chin. Soc. Agric. Mach. 2023, 1–10. Available online: http://kns.cnki.net/kcms/detail/11.1964.S.20230112.0909.003.html (accessed on 16 January 2023).
- Wu, G.; Yu, G.; Ye, B.; Yu, Y. Forward-reverse design method for rice potted-seedling transplanting mechanism with compound planetary gear train. Trans. Chin. Soc. Agric. Mach. 2020, 51, 85–93+102. [Google Scholar]
- Sun, L.; Shen, J.; Zhou, Y.; Ye, Z.; Yu, G.; Wu, C. Design of non-circular gear linkage combination driving type vegetable pot seedling transplanting mechanism. Trans. Trans. Chin. Soc. Agric. Mach. 2019, 35, 26–33. [Google Scholar]
- Chen, J.; Huang, Q.; Wang, Y.; Sun, L.; Zhao, X.; Wu, C. Parametric analysis and inversion of transplanting mechanism with planetary non-circular gears for potted-seedling transplanter. Trans. Chin. Soc. Agric. Eng. 2013, 29, 18–26. [Google Scholar]
- Liao, Q.; Liu, M.; Zhang, Z.; Hu, X. Multi-objective optimization design of double five-bar transplanting mechanism for rape pot seedling. Trans. Chin. Soc. Agric. Mach. 2015, 46, 49–56. [Google Scholar]
- Zhu, W.; Zhang, C.; Pang, Q. Design and Optimization of the Crawling Mechanism of Rotary Sidewall Coring Device in Shale Gas Wells. Pet. Drill. Tech. 2021, 49, 100–104. [Google Scholar]
- Zhao, X.; Guo, J.; Li, K.; Dai, L.; Chen, J. Optimal design and experiment of 2-DoF five-bar mechanism for flower seedling transplanting. Comput. Electron. Agric. 2020, 178, 105746. [Google Scholar] [CrossRef]
- Chen, J.; Huang, Q.; Wang, Y.; Zhang, G. Kinematics modeling and analysis of transplanting mechanism with planetary elliptic gears for pot seedling transplanter. Trans. Chin. Soc. Agric. Eng. 2012, 28, 6–12. [Google Scholar]
- Ye, B.; Zeng, G.; Deng, B.; Yang, Q.; Liu, J.; Yu, G. Design and tests of a rotary plug seedling pick-up mechanism for vegetable automatic transplanter. Int. J. Agric. Biol. Eng. 2020, 13, 70–78. [Google Scholar] [CrossRef]
- Hu, S.; Hu, M.; Yan, W.; Zhang, W. Design and experiment of an integrated automatic transplanting mechanism for picking and planting pepper hole tray seedlings. Agriculture 2022, 12, 557. [Google Scholar] [CrossRef]


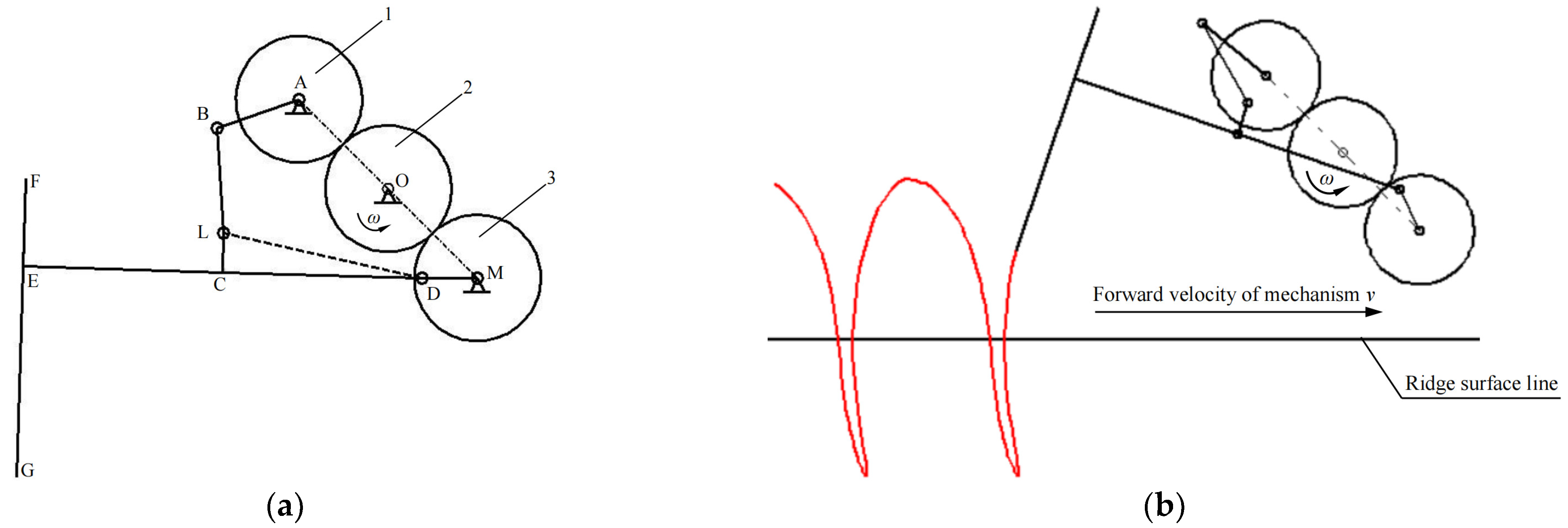







| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| l1/(mm) | The length of frame AM | θ/(°) | The angular displacement of crank AB and MD |
| l2/(mm) | The length of crank AB | θ1/(°) | The initial installation angle of rack AM |
| l3/(mm) | The length of connecting rod BC | θ3/(°) | The angular displacement of connecting rod BC |
| l4/(mm) | The length of connecting rod DC | θ2/(°) | The initial installation angle of crank AB |
| l5/(mm) | The length of crank MD | θ4/(°) | The angular displacement of connecting rod DC |
| l6/(mm) | The length of the connecting rod CE for planter | θ5/(°) | The initial installation angle of crank MD |
| l7/(mm) | The length of the bottom for the planter EG | θ6/(°) | The angular displacement of connecting rod CE |
| l8/(mm) | The length of the upper for the planter FE | θ7/(°) | The angle of between planter FG and the rod CE |
| l9/(mm) | The length of lower link articulated connecting rod CL | θ8/(°) | The initial installation angle of articulated connecting rod CL and lower connecting rod DE |
| l10/(mm) | The distance between hinge point D and L | ω/(rad/s) | The angular velocity of crank |
| Level | Factors | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| The Length l2 of Crank AB/mm | The Length l5 of Crank MD/mm | The Difference between Installation Angles θ5–θ2 of Double Cranks/° | The Length l3 of Connecting Rod BC/mm | The Distance l10 between Hinge Point D and L/mm | |
| 1 | 94 | 58 | 18 | 116 | 231 |
| 2 | 96 | 60 | 19 | 118 | 233 |
| 3 | 98 | 62 | 20 | 120 | 235 |
| 4 | 100 | 64 | 21 | 122 | 237 |
| 5 | 102 | 66 | 22 | 124 | 239 |
| Serial Number | Factors | Response Index | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | h1/mm | β1/° | l/mm | α1/° | α2/° | |
| 1 | 1 | 1 | 1 | 1 | 1 | 129.5 | 87.2 | 4.7 | 88.1 | 81.0 |
| 2 | 1 | 2 | 2 | 2 | 2 | 130.9 | 89.7 | 7.8 | 88.2 | 81.6 |
| 3 | 1 | 3 | 3 | 3 | 3 | 132.3 | 92.4 | 11.5 | 88.3 | 82.1 |
| 4 | 1 | 4 | 4 | 4 | 4 | 133.5 | 95.3 | 15.6 | 88.3 | 82.9 |
| 5 | 1 | 5 | 5 | 5 | 5 | 134.6 | 98.2 | 20.2 | 88.4 | 83.6 |
| 6 | 2 | 1 | 2 | 3 | 4 | 139.4 | 88.6 | 12.3 | 89.6 | 81.8 |
| 7 | 2 | 2 | 3 | 4 | 5 | 140.5 | 91.1 | 15.7 | 89.4 | 82.2 |
| 8 | 2 | 3 | 4 | 5 | 1 | 146.4 | 90.8 | 15.1 | 90.3 | 82.4 |
| 9 | 2 | 4 | 5 | 1 | 2 | 127.5 | 92.9 | 9.6 | 87.6 | 82.1 |
| 10 | 2 | 5 | 1 | 2 | 3 | 127.5 | 91.9 | 0.3 | 87.0 | 81.9 |
| 11 | 3 | 1 | 3 | 5 | 2 | 153.3 | 87.2 | 15.7 | 91.2 | 81.3 |
| 12 | 3 | 2 | 4 | 1 | 3 | 134.6 | 89.0 | 9.9 | 89.8 | 82.4 |
| 13 | 3 | 3 | 5 | 2 | 4 | 135.8 | 91.5 | 13.6 | 92.9 | 82.5 |
| 14 | 3 | 4 | 1 | 3 | 5 | 135.9 | 90.8 | 4.8 | 88.5 | 81.6 |
| 15 | 3 | 5 | 2 | 4 | 1 | 141.8 | 90.6 | 4.3 | 89.1 | 82.4 |
| 16 | 4 | 1 | 4 | 2 | 5 | 142.7 | 88.0 | 14.3 | 90.0 | 80.9 |
| 17 | 4 | 2 | 5 | 3 | 1 | 148.7 | 87.5 | 12.9 | 90.4 | 81.9 |
| 18 | 4 | 3 | 1 | 4 | 2 | 148.8 | 86.9 | 5.0 | 89.9 | 81.7 |
| 19 | 4 | 4 | 2 | 5 | 3 | 150.1 | 89.5 | 8.7 | 90.5 | 82.5 |
| 20 | 4 | 5 | 3 | 1 | 4 | 131.1 | 91.3 | 2.9 | 87.7 | 82.2 |
| 21 | 5 | 1 | 5 | 4 | 3 | 156.8 | 86.5 | 17.2 | 91.7 | 82.2 |
| 22 | 5 | 2 | 1 | 5 | 4 | 157.0 | 86.0 | 9.7 | 91.4 | 85.5 |
| 23 | 5 | 3 | 2 | 1 | 5 | 138.2 | 87.6 | 4.1 | 89.1 | 81.6 |
| 24 | 5 | 4 | 3 | 2 | 1 | 144.0 | 87.4 | 2.6 | 93.5 | 85.4 |
| 25 | 5 | 5 | 4 | 3 | 2 | 145.3 | 89.9 | 6.5 | 93.6 | 82.5 |
| K1 | 660.8 | 721.7 | 698.7 | 660.9 | 710.4 | h1 | ||||
| K2 | 681.3 | 711.7 | 700.4 | 677.9 | 705.8 | |||||
| K3 | 701.4 | 701.5 | 701.2 | 701.6 | 701.3 | |||||
| K4 | 721.4 | 691.0 | 702.5 | 721.4 | 696.8 | |||||
| K5 | 741.2 | 680.3 | 703.4 | 741.4 | 691.9 | |||||
| R | 80.6 | 41.4 | 4.7 | 80.5 | 18.5 | |||||
| Factor order | A > D > B > E > C | |||||||||
| K1 | 462.8 | 437.5 | 442.8 | 448.0 | 443.5 | β1 | ||||
| K2 | 455.3 | 443.3 | 446.0 | 448.5 | 446.6 | |||||
| K3 | 449.1 | 449.2 | 449.4 | 449.2 | 449.3 | |||||
| K4 | 443.2 | 455.9 | 453.0 | 450.4 | 452.7 | |||||
| K5 | 437.4 | 461.9 | 456.6 | 451.7 | 455.7 | |||||
| R | 25.4 | 24.4 | 13.8 | 3.7 | 12.2 | |||||
| Factor order | A > B > C > E > D | |||||||||
| K1 | 59.8 | 64.2 | 24.5 | 31.2 | 39.6 | l | ||||
| K2 | 53.0 | 56.0 | 37.2 | 38.6 | 44.6 | |||||
| K3 | 48.3 | 49.3 | 48.4 | 48.0 | 47.6 | |||||
| K4 | 43.8 | 41.3 | 61.4 | 57.8 | 44.4 | |||||
| K5 | 40.1 | 34.2 | 73.5 | 69.4 | 59.1 | |||||
| R | 19.7 | 30 | 49 | 38.2 | 19.5 | |||||
| Factor order | C > D > B > A > E | |||||||||
| K1 | 441.3 | 450.6 | 444.9 | 442.3 | 451.4 | α1 | ||||
| K2 | 443.9 | 449.2 | 446.5 | 451.6 | 450.5 | |||||
| K3 | 451.5 | 450.5 | 450.1 | 450.4 | 447.3 | |||||
| K4 | 448.5 | 448.4 | 452.0 | 448.4 | 449.9 | |||||
| K5 | 459.3 | 445.8 | 451.0 | 451.8 | 445.4 | |||||
| R | 18.0 | 4.8 | 6.1 | 9.5 | 5.1 | |||||
| Factor order | A > D > C > E > B | |||||||||
| K1 | 411.2 | 407.2 | 411.7 | 409.3 | 413.1 | α2 | ||||
| K2 | 410.4 | 413.6 | 409.9 | 412.3 | 409.2 | |||||
| K3 | 410.2 | 410.3 | 413.2 | 409.9 | 411.1 | |||||
| K4 | 409.2 | 414.5 | 411.1 | 411.4 | 414.9 | |||||
| K5 | 417.2 | 412.6 | 412.3 | 415.3 | 409.9 | |||||
| R | 7.0 | 6.4 | 3.3 | 6.0 | 5.7 | |||||
| Factor order | A > B > D > E > C | |||||||||
| l2/mm | l5/mm | θ5–θ2/° | l3/mm | l10/mm | h1/mm | β1/° | l/mm | α1/° | α2/° | |
|---|---|---|---|---|---|---|---|---|---|---|
| Before optimization | 100 | 60 | 24 | 120 | 235 | 150.3 | 90.3 | 22.3 | 88.7 | 82.6 |
| After optimization | 100 | 64 | 19 | 122 | 233 | 150.1 | 89.5 | 8.7 | 90.5 | 82.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Fang, H.; Song, Y.; Du, W.; Wang, N. Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface. Sustainability 2023, 15, 2219. https://doi.org/10.3390/su15032219
Xu G, Fang H, Song Y, Du W, Wang N. Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface. Sustainability. 2023; 15(3):2219. https://doi.org/10.3390/su15032219
Chicago/Turabian StyleXu, Gaowei, Huimin Fang, Yumin Song, Wensheng Du, and Ning Wang. 2023. "Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface" Sustainability 15, no. 3: 2219. https://doi.org/10.3390/su15032219
APA StyleXu, G., Fang, H., Song, Y., Du, W., & Wang, N. (2023). Performance Improvement of a Geared Five-Bar Transplanting Mechanism for Salvia miltiorrhiza by Orthogonal Design Based on an Interactive Human–Computer Auxiliary Interface. Sustainability, 15(3), 2219. https://doi.org/10.3390/su15032219






