Multi-Objective Intercity Carpooling Route Optimization Considering Carbon Emission
Abstract
:1. Introduction
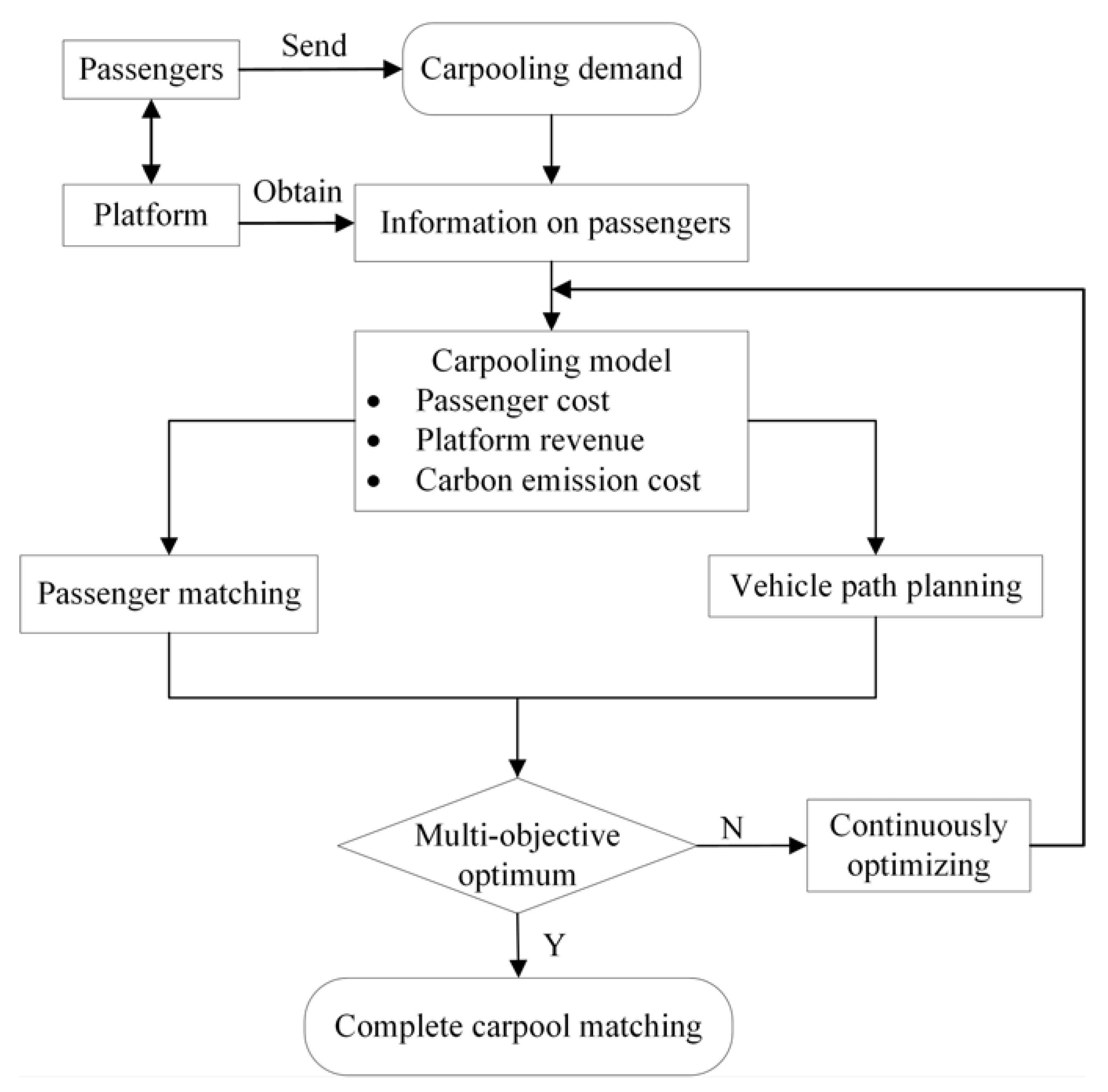
2. Problem Description
2.1. Intercity Carpooling
2.2. Assumptions
3. Model Construction
3.1. Multi-Objective Function Determination
3.1.1. Passenger Perspective: Cost Minimization
3.1.2. Platform Perspective: Revenue Maximization
3.1.3. Government Perspective: Carbon Emission Minimization
3.2. Multi-Objective Model Construction
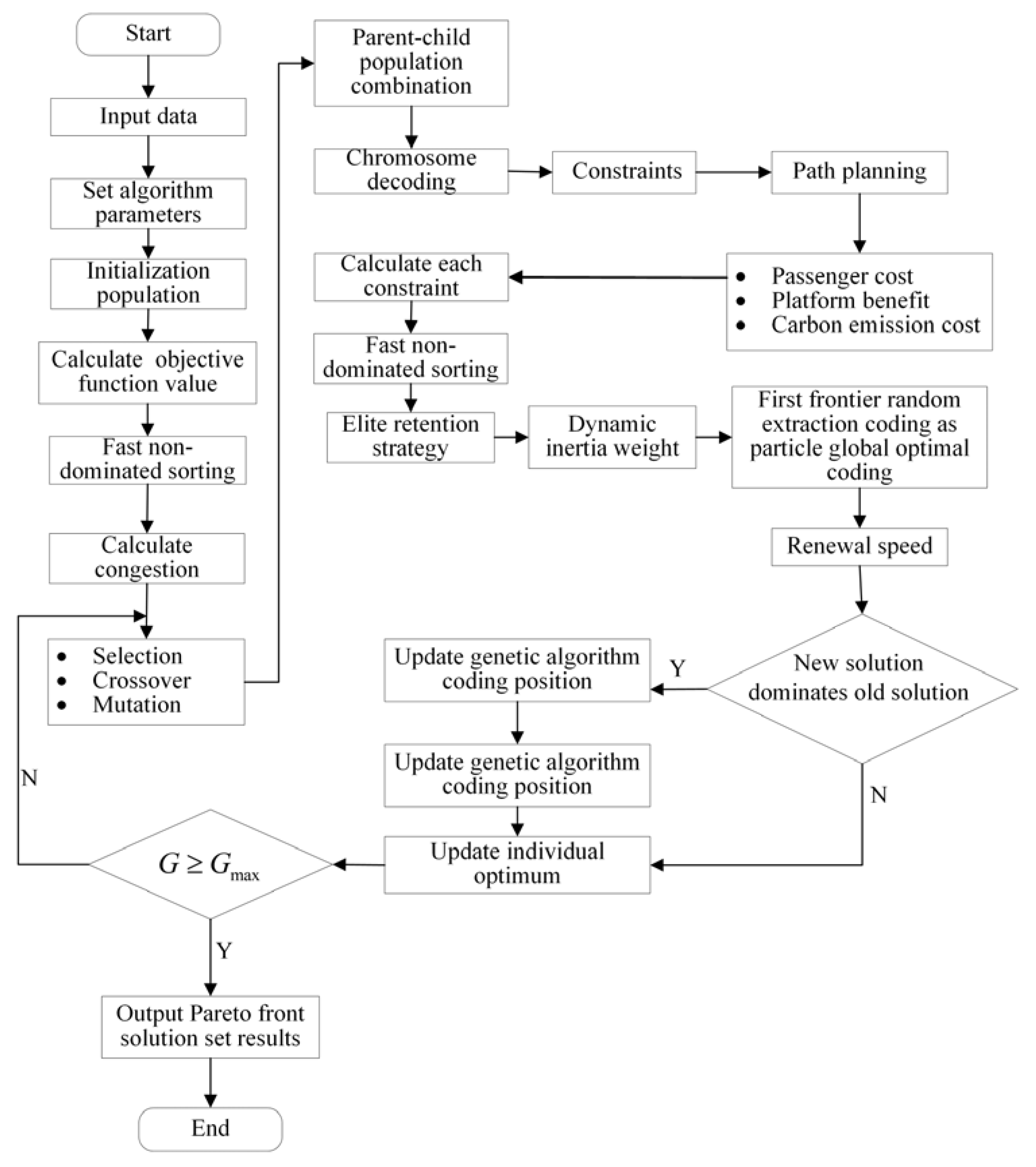
4. Algorithm Design
- (1)
- Initialize population
- (2)
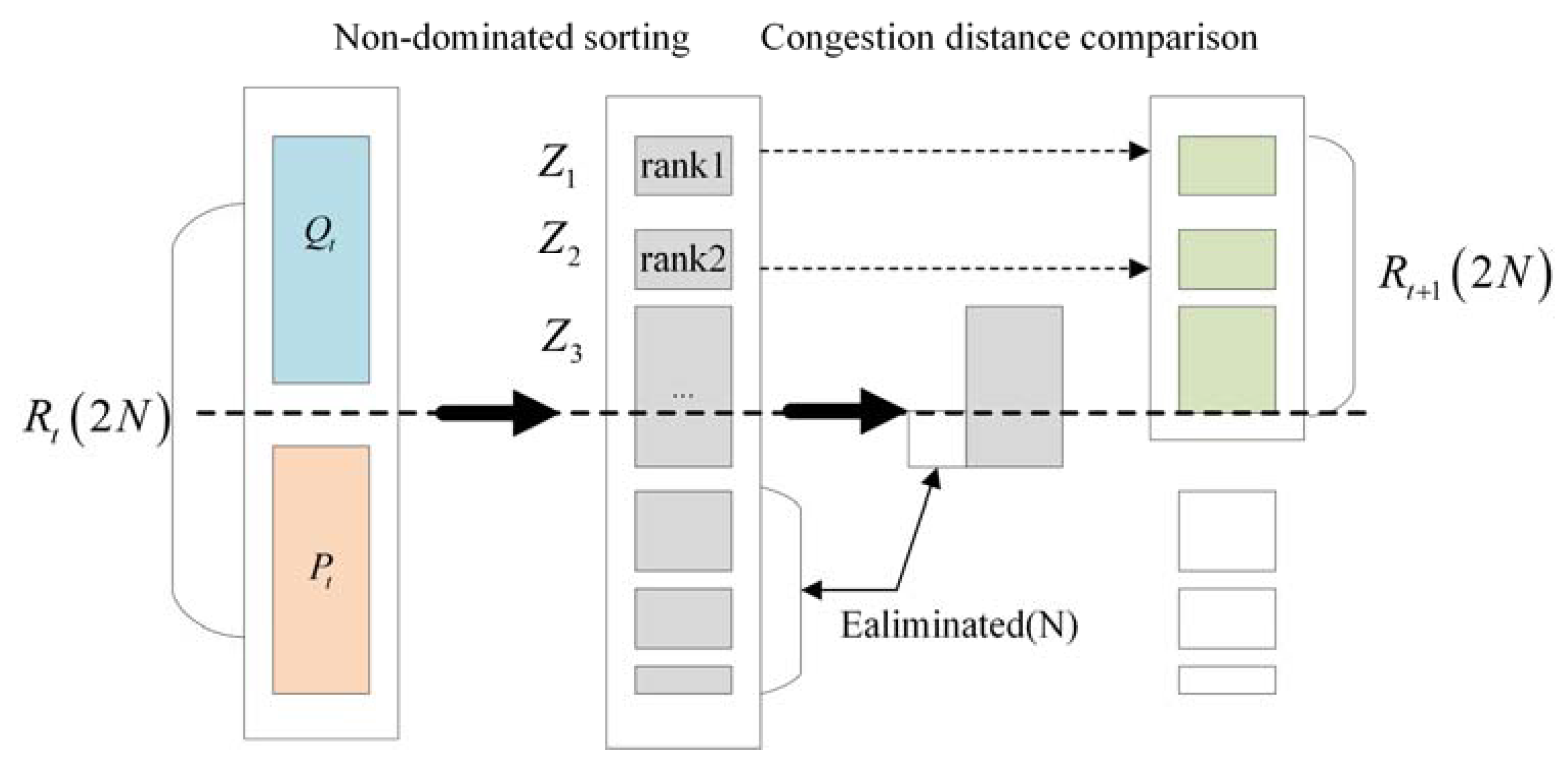
- Fast non-dominated sorting
- (3)
- Crowded degree sorting
- (4)
- Elite retention strategy
- (5)
- Improved particle swarm optimization operator
5. Example Analysis
5.1. Data Source
- (1)
- Passenger information
- (2)
- Node distance
- (3)
- Parameters value
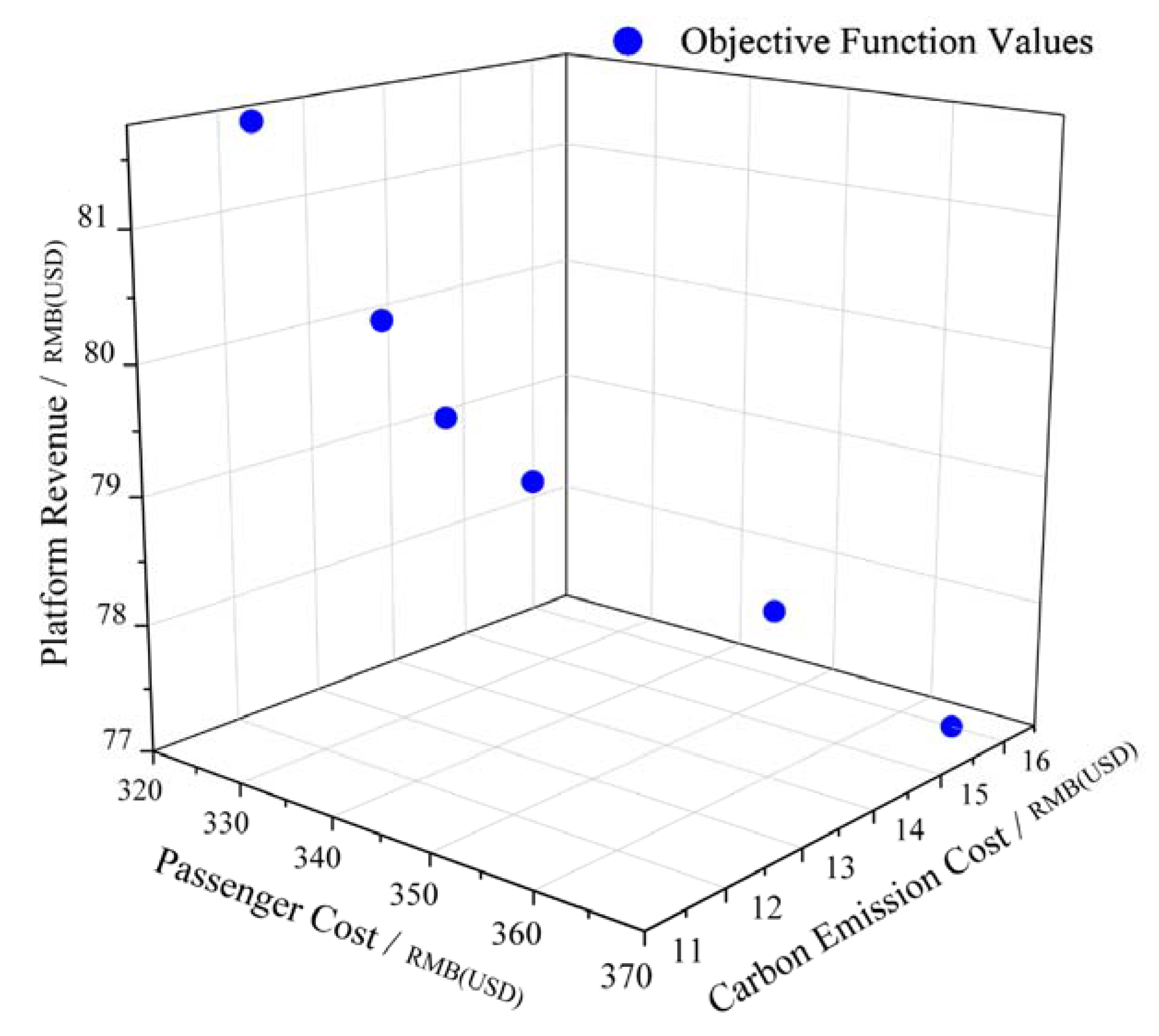
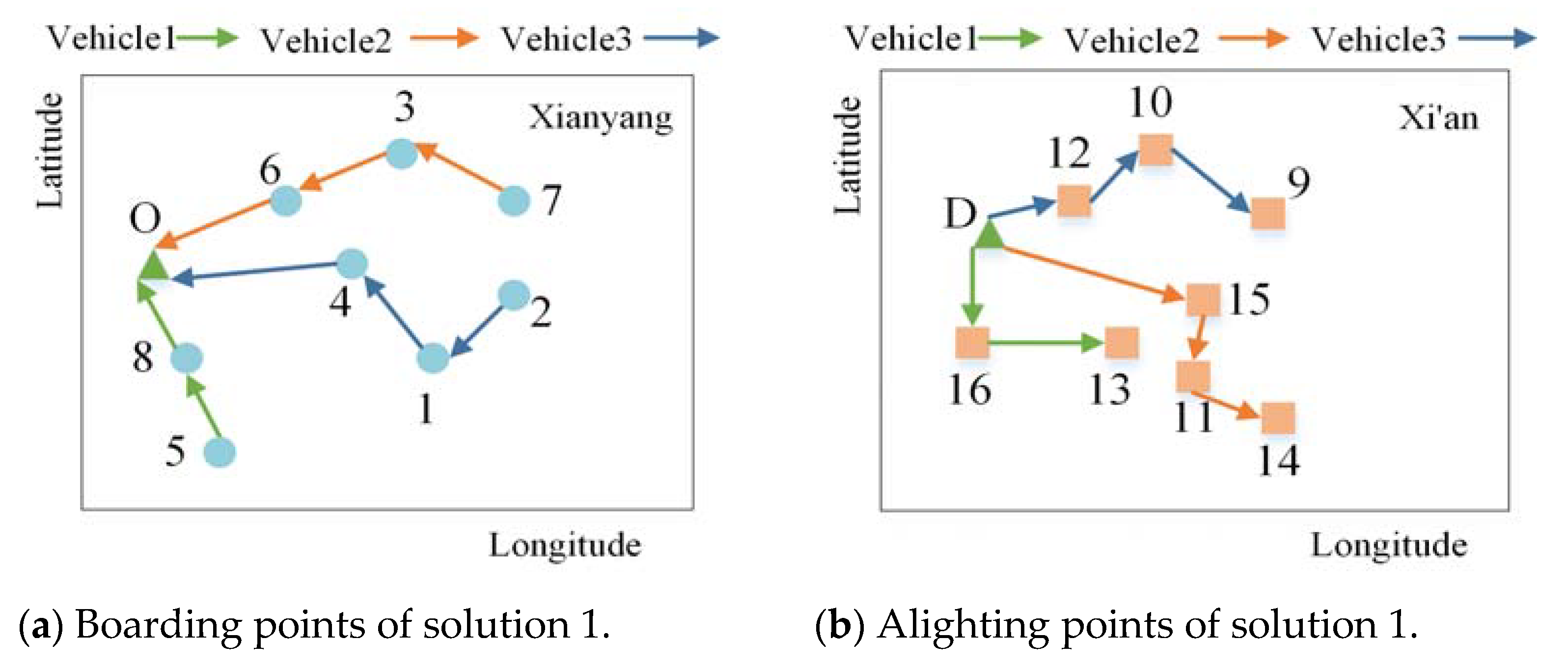
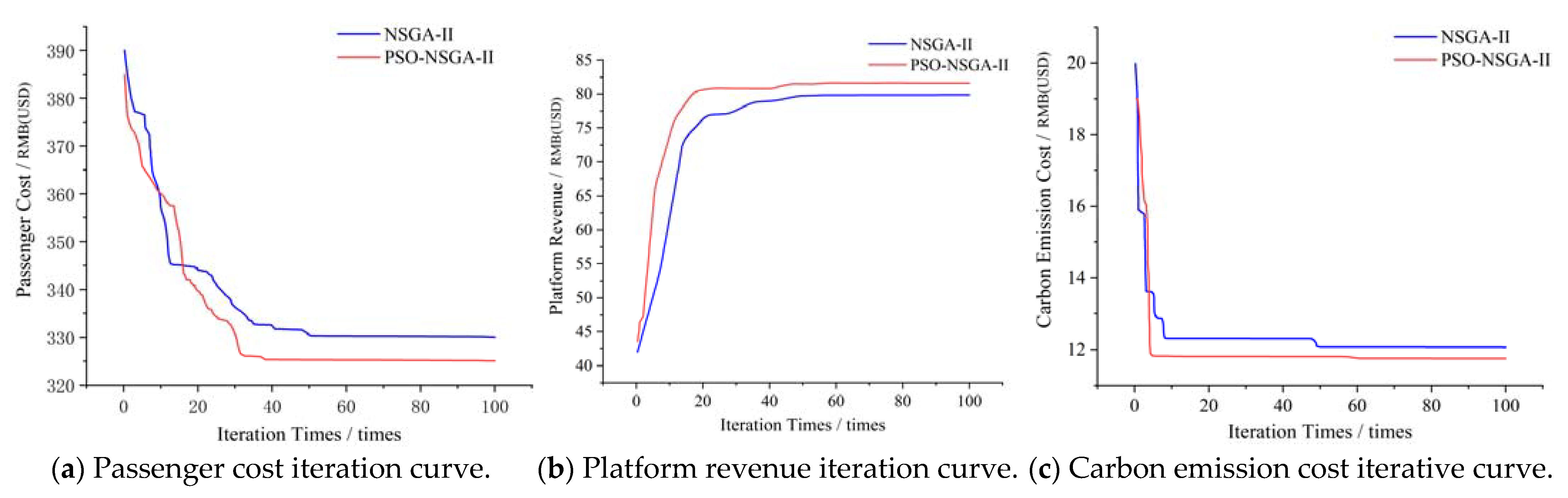
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Sets | Definitions |
|---|---|
| V | Node set |
| A | Link set |
| P | Passenger demand point set |
| P+ | Passenger boarding point number set |
| P− | Passenger alighting point number set |
| K | Vehicle set |
| Parameters | Descriptions |
| Z1 | Passenger cost |
| Z2 | Platform revenue |
| Z3 | Carbon emission cost |
| C11 | Passenger time cost in vehicle |
| C12 | Passenger time cost outside vehicle |
| W1 | Passenger waiting cost per unit time in vehicle |
| Tijk | Travelling time between point i and point j of vehicle k |
| WTik | Waiting time at point i of vehicle k |
| Ts | Average service time per passenger |
| Qi | Number of passengers in vehicle before arriving at point i |
| Tik | Arrival time at point i of vehicle k |
| FT0k | Vehicle departure time from the parking lot |
| W2 | Passenger waiting cost per unit time outside vehicle |
| I | Platform income |
| C21 | Fixed and variable costs of the platform |
| C22 | Penalty cost of vehicle arriving later than time window |
| F | Fare for a single trip |
| W3 | The fixed cost of a single trip |
| W4 | Freeway toll per unit mileage |
| W5 | Fuel consumption cost per unit mileage |
| dij | Distance between point i and point j |
| Average speed between point i and point j | |
| [ETi, LTi] | Time window at point i, ETi is the earliest arrival time and LTi is the latest arrival time |
| θ1 | Penalty coefficient arriving later than time window |
| tik | Departure time of vehicle k from point i |
| f | Load limit of vehicle |
| w | Vehicle weight |
| fij | Real-time load |
| Pij | Fuel consumption between point i and point j |
| aij | Parameters related to links |
| β1 | Parameters related to vehicle |
| ε | Carbon tax rate |
| δ | Fuel consumption factor |
| ε0 | Fuel consumption rate at no-load |
| ε* | Fuel consumption rate at full load |
| Maximum travelling time for passenger at point i | |
| Decision Variables | Definitions |
| Xijk | 0–1 variable, Xijk = 1 if vehicle k travels from point i to point j; otherwise, Xijk = 0. |
| Xik | 0–1 variable, Xik = 1 if the passenger at point i is transported by vehicle k; otherwise, Xik = 0. |
References
- CIR. China Intercity Travel Industry Present Situation Investigation and Future Development Trend Analysis Report. 2022. Available online: https://www.cir.cn/7/33/ChengJiChuXingHangYeXianZhuangYu.html (accessed on 10 January 2023).
- Rey-Merchán, M.D.C.; López-Arquillos, A.; Pires Rosa, M.; Gómez-de-Gabriel, J.M. Proposal for an institutional carpooling system among workers from the public-education sector. Sustainability 2022, 14, 14601. [Google Scholar] [CrossRef]
- Liu, X.; Yan, X.; Liu, F.; Wang, R.; Leng, Y. A trip-specific model for fuel saving estimation and subsidy policy making of carpooling based on empirical data. Appl. Energy 2019, 240, 295–311. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Sabar, N.R.; Bhaskar, A.; Chung, E.; Turky, A.; Song, A. A self-adaptive evolutionary algorithm for dynamic vehicle routing problems with traffic congestion. Swarm Evol. Comput. 2019, 44, 1018–1027. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Zhou, F.; Lin, Y. Dynamic vehicle routing problem considering simultaneous dual services in the last mile delivery. Kybernetes 2020, 49, 1267–1284. [Google Scholar] [CrossRef]
- Bruglieri, M.; Mancini, S.; Pezzella, F.; Pisacane, O. A new mathematical programming model for the green vehicle routing problem. Electron. Notes Discret. Math. 2016, 55, 89–92. [Google Scholar] [CrossRef] [Green Version]
- Solomon, M.M.; Desrosiers, J. Time window constrained routing and scheduling problems. Transp. Sci. 1988, 22, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Truden, C.; Maier, K.; Armbrust, P. Decomposition of the vehicle routing problem with time windows on the time dimension. Transp. Res. Procedia. 2022, 62, 131–138. [Google Scholar] [CrossRef]
- Wang, Y.; Zhe, J.; Wang, X.; Sun, Y.; Wang, H. Collaborative multidepot vehicle routing problem with dynamic customer demands and time windows. Sustainability 2022, 14, 6709. [Google Scholar] [CrossRef]
- Schaap, H.; Walther, G.; Schiffer, M.; Schneider, M. A large neighborhood search for the vehicle routing problem with multiple time windows. Transp. Sci. 2022, 56, 1369–1392. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; He, Z.; Yang, Z.; Guan, Y. Bi-Objective vehicle routing for hazardous materials transportation with actual load dependent risks and considering the risk of each vehicle. IEEE Trans. Eng. Manag. 2019, 66, 429–442. [Google Scholar] [CrossRef]
- Liu, X.; Titheridge, H.; Yan, X.; Wang, R.; Tan, W.; Chen, D.; Zhang, J. A passenger-to-driver matching model for commuter carpooling: Case study and sensitivity analysis. Transp. Res. Part C Emerg. Technol. 2020, 117, 102702. [Google Scholar] [CrossRef]
- De Carvalho, V.R.; Golpayegani, F. Satisfying user preferences in optimised ridesharing services: A multi-agent multi-objective optimisation approach. Appl. Intell. 2022, 52, 11257–11272. [Google Scholar] [CrossRef]
- Ma, N.; Zeng, Z.; Wang, Y.; Xu, J. Balanced strategy based on environment and user benefit-oriented carpooling service mode for commuting trips. Transportation 2021, 48, 1241–1266. [Google Scholar] [CrossRef]
- Asghari, M.; Al-e-hashem, S.M.J.M.; Rekik, Y. Environmental and social implications of incorporating carpooling service on a customized bus system. Comput. Oper. Res. 2022, 142, 105724. [Google Scholar] [CrossRef]
- Shen, J.; Liu, K.; Ma, C.; Zhao, Y.; Shi, C. Bibliometric analysis and system review of vehicle routing optimization for emergency material distribution. J. Traffic Transp. Eng. 2022, 9, 893–911. [Google Scholar] [CrossRef]
- Beed, R.S.; Biswas, S.D.; Biswas, S.; Sarkar, S.; Roy, A. A hybrid multi-objective carpool route optimization technique using genetic algorithm and A* algorithm. Comput. Res. Model. 2021, 13, 67–85. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Zhan, F.M.; Guo, Y.H. A solution methodology for carpooling systems based on double auctions and cooperative coevolutionary particle swarms. Appl. Intell. 2019, 49, 741–763. [Google Scholar] [CrossRef]
- Huang, S.C.; Lin, J.J.; Jiau, M.K. Global and local pareto optimality in coevolution for solving carpool service problem with time windows. IEEE Trans. Intell. Transp. Syst. 2020, 21, 934–946. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, S.; Wang, J.; Huang, M. A branch-and-price algorithm for the heterogeneous fleet green vehicle routing problem with time windows. Transp. Res. Part B Methodol. 2019, 122, 511–527. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Chen, B.; Feng, Z.; Qin, Y.; Liu, Q.; Liu, Y. Multi-objective optimization of shield construction parameters based on random forests and NSGA-II. Adv. Eng. Inform. 2022, 54, 101751. [Google Scholar] [CrossRef]
- Brahami, M.A.; Dahane, M.; Souier, M.; Sahnoun, M. Sustainable capacitated facility location/network design problem: A Non-dominated Sorting Genetic Algorithm based multiobjective approach. Ann. Oper. Res. 2022, 311, 821–852. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Zhe, J.; Sun, Y.; Wang, X.; Wang, H. Electric vehicle charging Station location-routing problem with time windows and resource sharing. Sustainability 2022, 14, 11681. [Google Scholar] [CrossRef]
- Xu, A.; Chen, J.; Liu, Z. Exploring the effects of carpooling on travelers’ behavior during the COVID-19 pandemic: A case study of metropolitan city. Sustainability 2021, 13, 11136. [Google Scholar] [CrossRef]
- Guan, D.; Cong, X.; Li, J.; Wang, P.; Yang, Z.; Jing, X. Theoretical modeling and optimal matching on the damping property of mechatronic shock absorber with low speed and heavy load capacity. J. Sound Vibr. 2022, 535, 117113. [Google Scholar] [CrossRef]
- Guan, D.; Pan, B.; Chen, Z.; Li, J.; Shen, H.; Pang, H. Quantitative modeling and bio-inspired optimization the clamping load on the bipolar plate in PEMFC. Energy 2023, 263, 125951. [Google Scholar] [CrossRef]
- Bektaş, T.; Lapote, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]

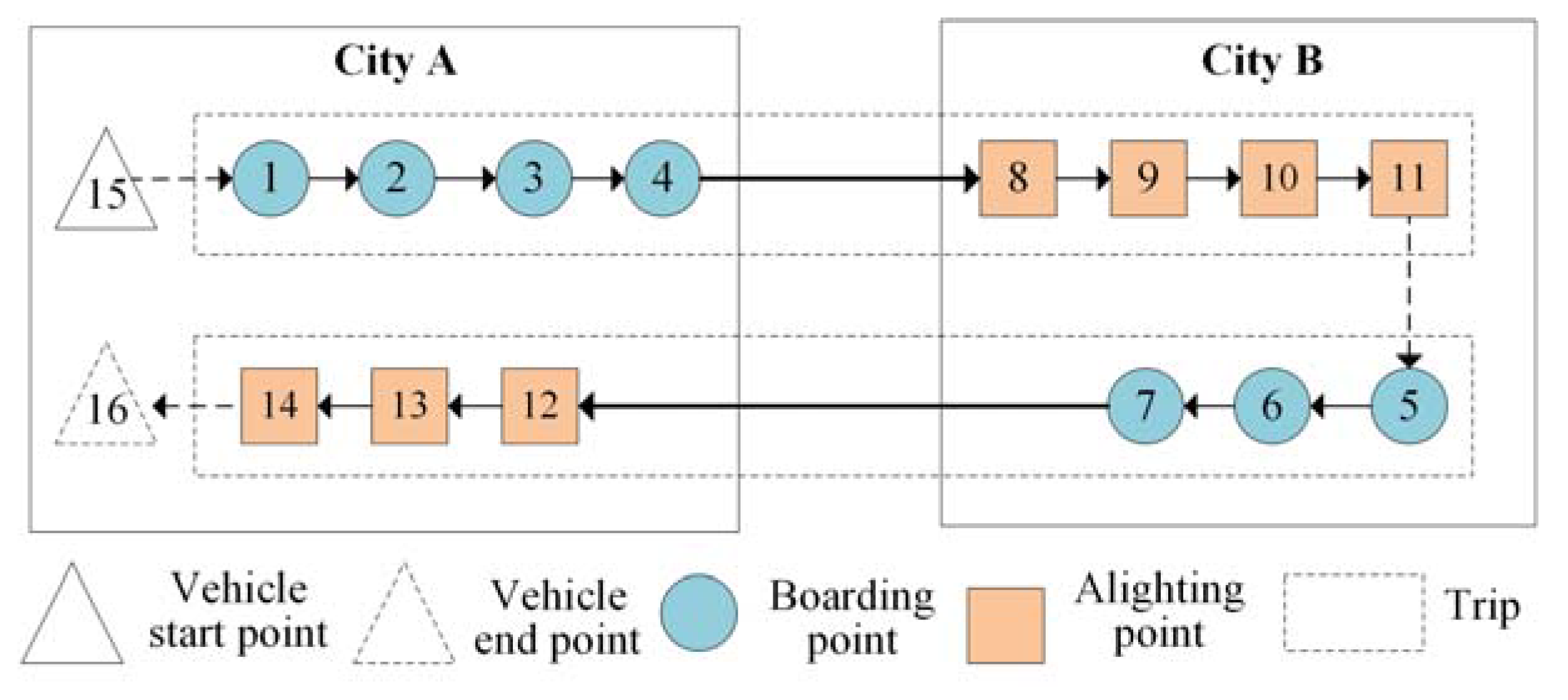

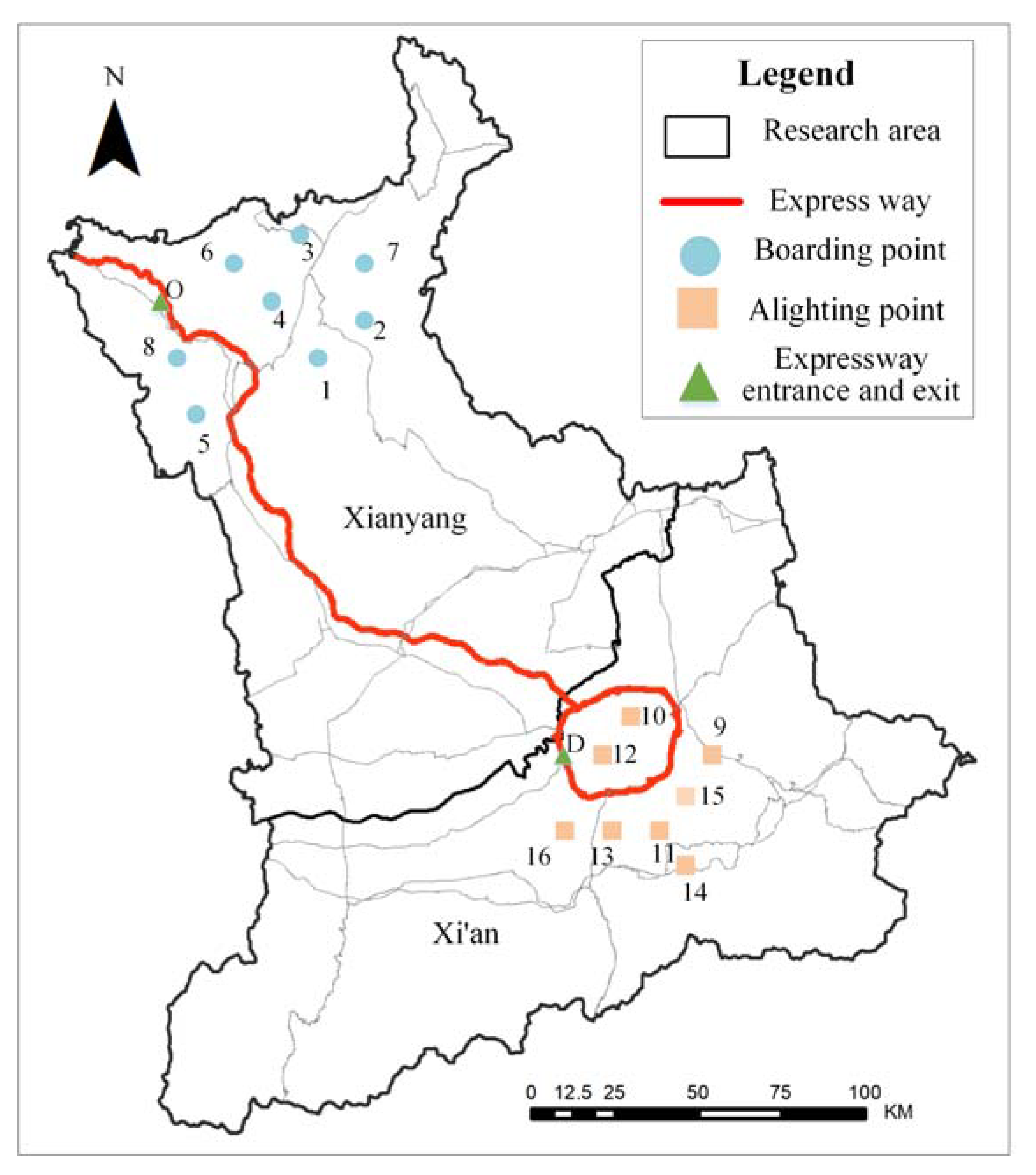
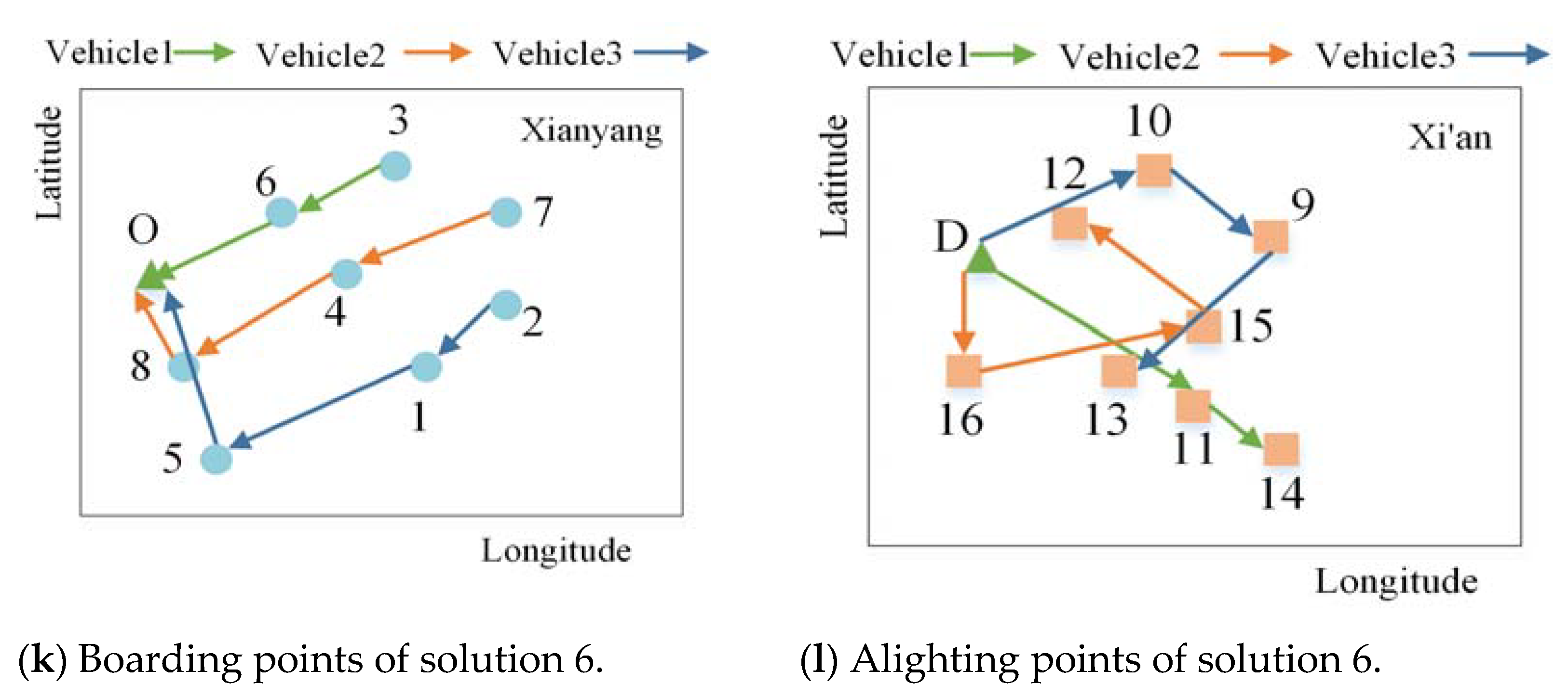

| Boarding Point | Longitude and Latitude | Alighting Point | Longitude and Latitude | Time Window [ETi, LTi]/min | Maximum Travelling Time /min |
|---|---|---|---|---|---|
| 1 | (108.24, 35.05) | 9 | (109.12, 34.21) | [15, 20] | 50 |
| 2 | (108.36, 35.06) | 10 | (108.94, 34.32) | [15, 20] | 55 |
| 3 | (108.26, 35.22) | 11 | (108.88, 34.10) | [10, 15] | 55 |
| 4 | (108.15, 35.12) | 12 | (108.89, 34.26) | [20, 25] | 60 |
| 5 | (108.01, 34.93) | 13 | (108.78, 34.11) | [20, 25] | 55 |
| 6 | (108.08, 35.19) | 14 | (109.01, 34.06) | [10, 15] | 60 |
| 7 | (108.36, 35.13) | 15 | (109.04, 34.15) | [5, 10] | 45 |
| 8 | (107.94, 35.03) | 16 | (108.71, 34.14) | [25, 30] | 65 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3.45 | 6.39 | 4.12 | 8.23 | 7.21 | 4.72 | 9.32 | … |
| 2 | 3.45 | 0 | 6.53 | 6.80 | 11.49 | 9.67 | 2.68 | 12.77 | … |
| 3 | 6.39 | 6.53 | 0 | 4.96 | 13.07 | 5.78 | 4.35 | 12.22 | … |
| 4 | 4.12 | 6.80 | 4.96 | 0 | 8.21 | 3.09 | 6.47 | 7.35 | … |
| 5 | 8.23 | 11.49 | 13.07 | 8.21 | 0 | 9.57 | 12.90 | 4.06 | … |
| 6 | 7.21 | 9.67 | 5.78 | 3.09 | 9.57 | 0 | 8.81 | 7.31 | … |
| 7 | 4.72 | 2.68 | 4.35 | 6.47 | 12.90 | 8.81 | 0 | 13.41 | … |
| 8 | 9.32 | 12.77 | 12.22 | 7.35 | 4.06 | 7.31 | 13.41 | 0 | … |
| … | … | … | … | … | … | … | … | … | … |
| Parameter | Description | Value |
|---|---|---|
| W1 | Passenger waiting cost per unit time in vehicle (RMB(USD)/min) | 0.2 |
| W2 | Passenger waiting cost per unit time outside vehicle (RMB(USD)/min) | 0.4 |
| W3 | The fixed cost of a single trip (RMB(USD)) | 10 |
| W4 | Freeway toll per unit mileage (RMB(USD)/km) | 0.3 |
| W5 | Fuel consumption cost per unit mileage (RMB(USD)/km) | 0.5 |
| F | Fare for a single trip (RMB(USD)) | 30 |
| Ts | Average service time per passenger (min) | 1 |
| θ1 | Penalty coefficient arriving later than the time window | 0.2 |
| The average speed between point i and point j (km/h) | 50 | |
| w | Vehicle weight (kg) | 1500 |
| fij | Real-time load (kg) | 100 |
| ε | Carbon tax rate (RMB(USD)/t) | 5 |
| δ | Fuel consumption factor | 2.544 |
| ε0 | Fuel consumption rate at no-load | 0.254 |
| ε* | Fuel consumption rate at full load | 0.276 |
| Number of Non-Dominated Solutions | Passenger Cost /RMB (USD) | Platform Revenue /RMB (USD) | Carbon Emission Cost/RMB (USD) |
|---|---|---|---|
| 1 | 325.68 | 81.75 | 11.8 |
| 2 | 328.25 | 80.26 | 12.8 |
| 3 | 334.75 | 79.52 | 13.5 |
| 4 | 342.13 | 79.81 | 13.2 |
| 5 | 355.64 | 78.64 | 14.8 |
| 6 | 365.58 | 77.52 | 15.7 |
| Vehicle Number | Path | Travel Time (min) | Passenger Cost/RMB (USD) | Platform Revenue/RMB (USD) | Carbon Emission Cost/RMB (USD) |
|---|---|---|---|---|---|
| Vehicle 1 | 5-8-O-D-16-13 | 59.08 | 75.26 | 14.58 | 3.39 |
| Vehicle 2 | 7-3-6-O-D-15-11-14 | 81.60 | 126.15 | 28.32 | 4.36 |
| Vehicle 3 | 2-1-4-O-D-12-10-9 | 72.35 | 124.27 | 38.85 | 4.05 |
| Total | 213.03 | 325.68 | 81.75 | 11.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Wang, J.; Yuen, C.W.; Liu, Q. Multi-Objective Intercity Carpooling Route Optimization Considering Carbon Emission. Sustainability 2023, 15, 2261. https://doi.org/10.3390/su15032261
Lu X, Wang J, Yuen CW, Liu Q. Multi-Objective Intercity Carpooling Route Optimization Considering Carbon Emission. Sustainability. 2023; 15(3):2261. https://doi.org/10.3390/su15032261
Chicago/Turabian StyleLu, Xiaojuan, Jianjun Wang, Choon Wah Yuen, and Qian Liu. 2023. "Multi-Objective Intercity Carpooling Route Optimization Considering Carbon Emission" Sustainability 15, no. 3: 2261. https://doi.org/10.3390/su15032261
APA StyleLu, X., Wang, J., Yuen, C. W., & Liu, Q. (2023). Multi-Objective Intercity Carpooling Route Optimization Considering Carbon Emission. Sustainability, 15(3), 2261. https://doi.org/10.3390/su15032261






