Research on the Damage Diagnosis Model Algorithm of Cable-Stayed Bridges Based on Data Mining
Abstract
:1. Introduction
2. Data Mining Algorithm for Damage Diagnosis of Cable-Stayed Bridges
2.1. Damage Location Using the SVM Algorithm
2.2. Damage Quantification Using the XGBoost Algorithm
3. Performance Optimization of Data Mining Algorithms
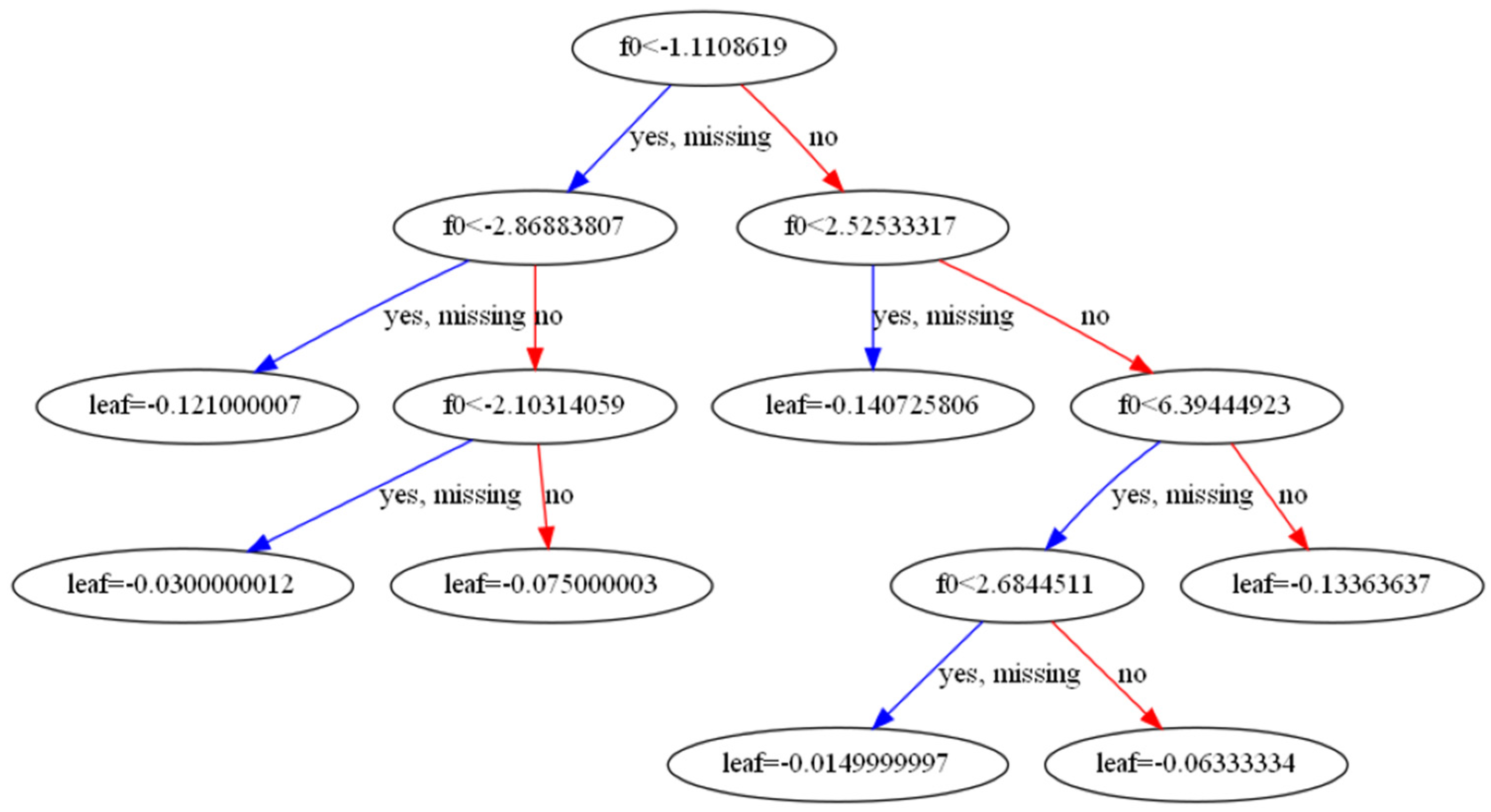
3.1. The Optimization Method
3.2. The Optimization Implementation
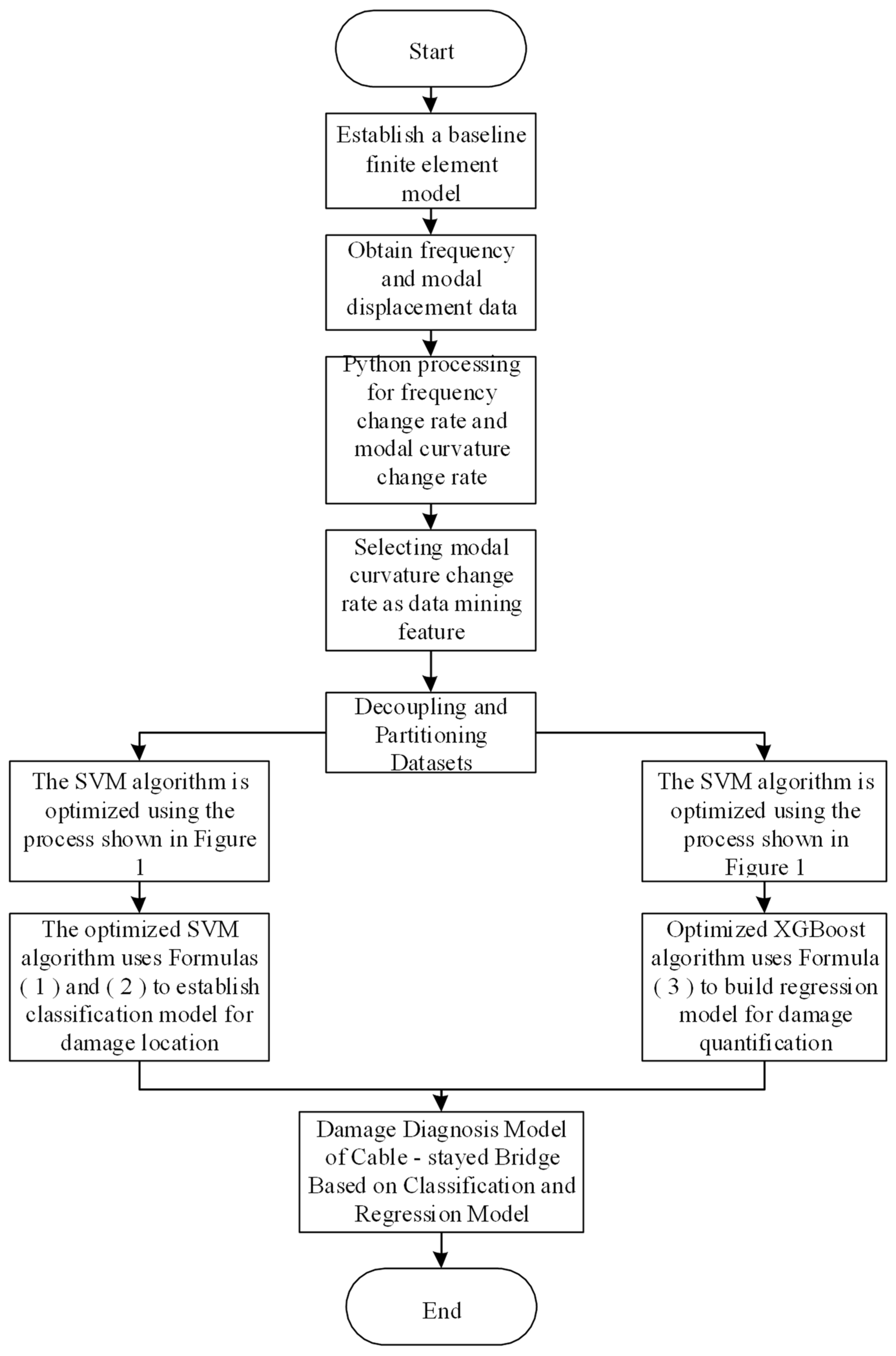
4. Attainment and Application of the Damage Diagnosis Model
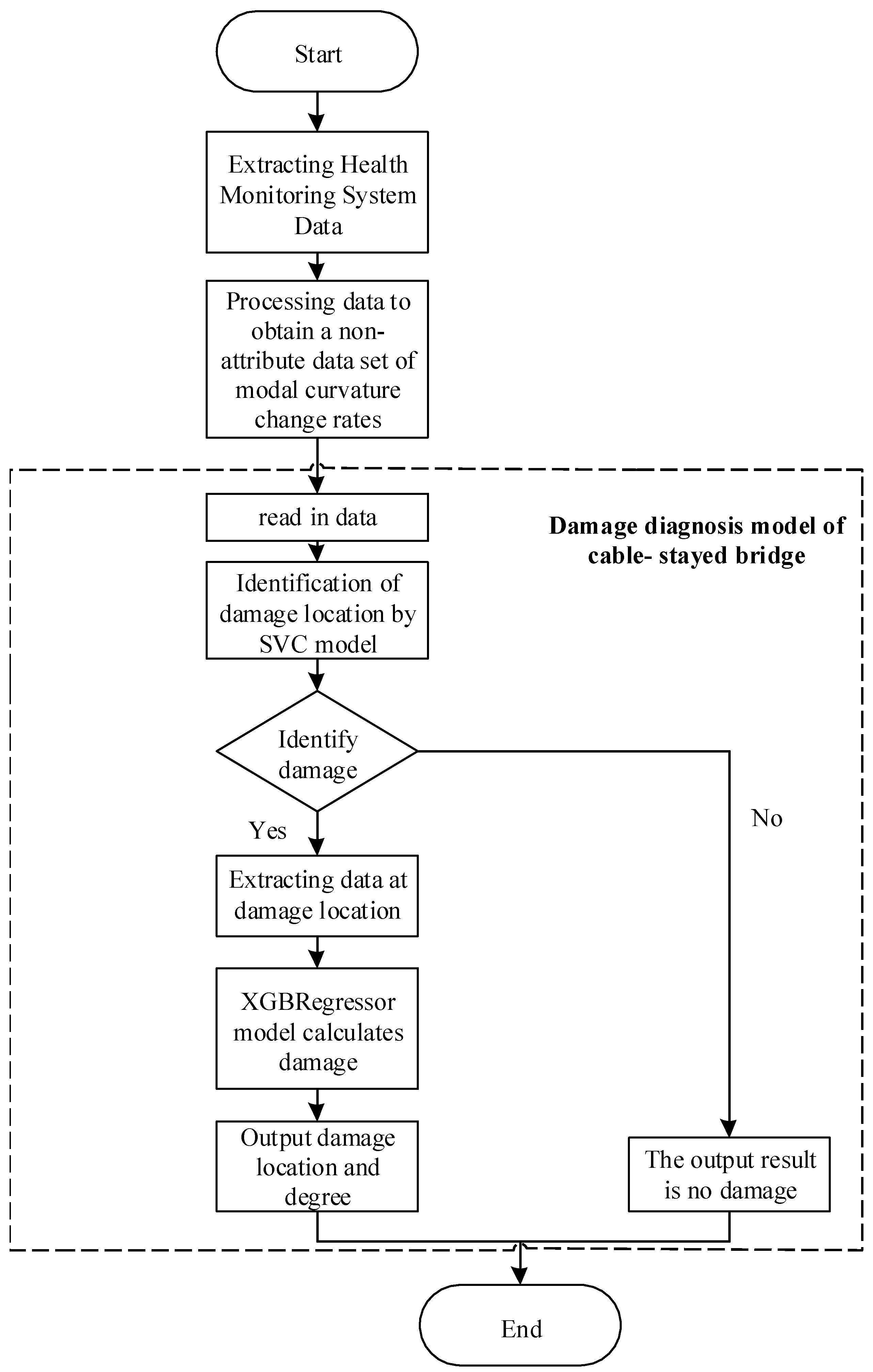
4.1. Implementation Process for the Damage Diagnosis Model
4.2. Use of Damage Diagnosis Models
5. Example and Analysis of a Cable-Stayed Bridge
5.1. Overview of the Cable-Stayed Bridge Project
5.2. Datum Finite Element Model of a Cable-Stayed Bridge
5.3. Damage Condition Setting of Cable-Stayed Bridge
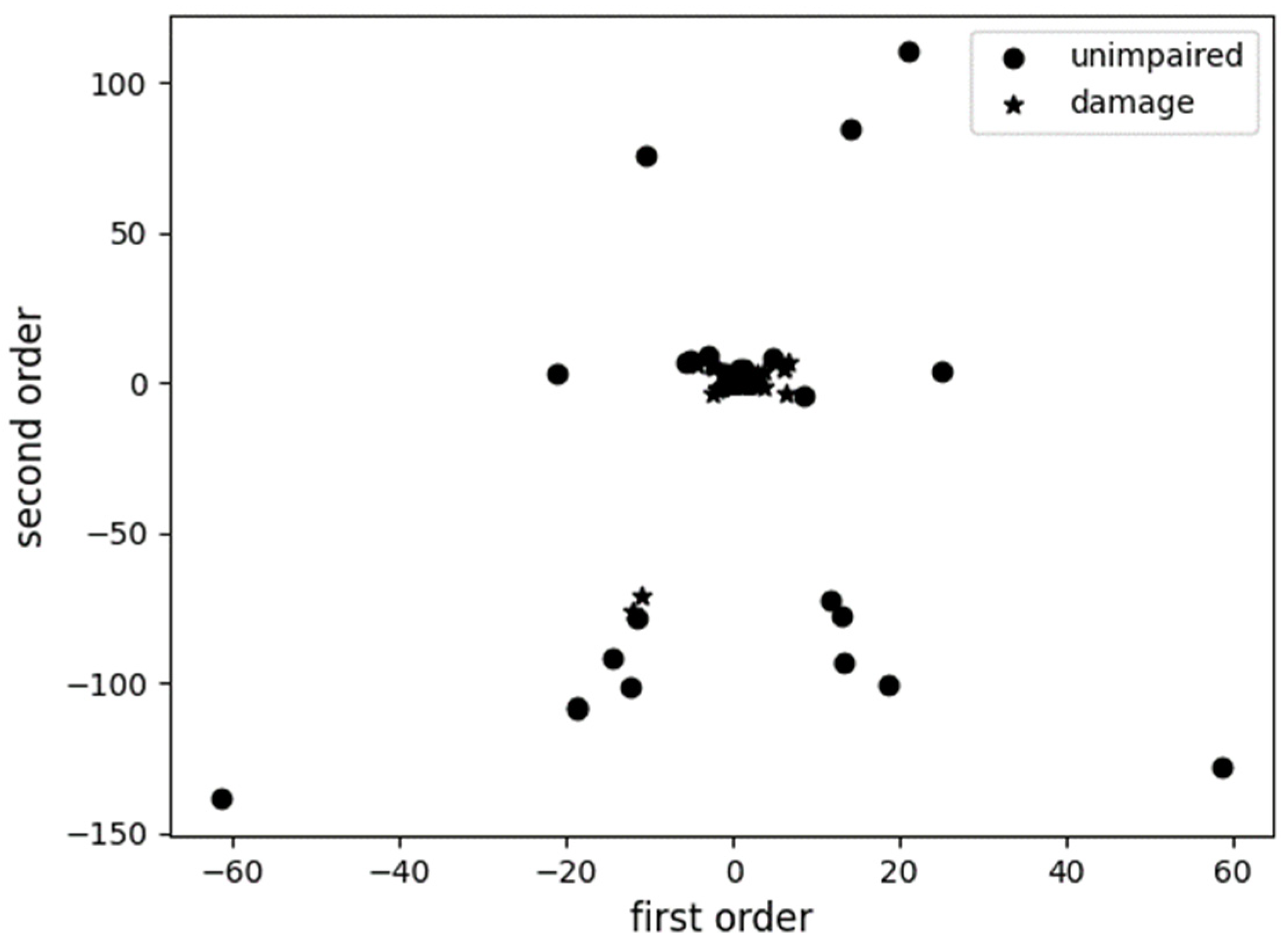
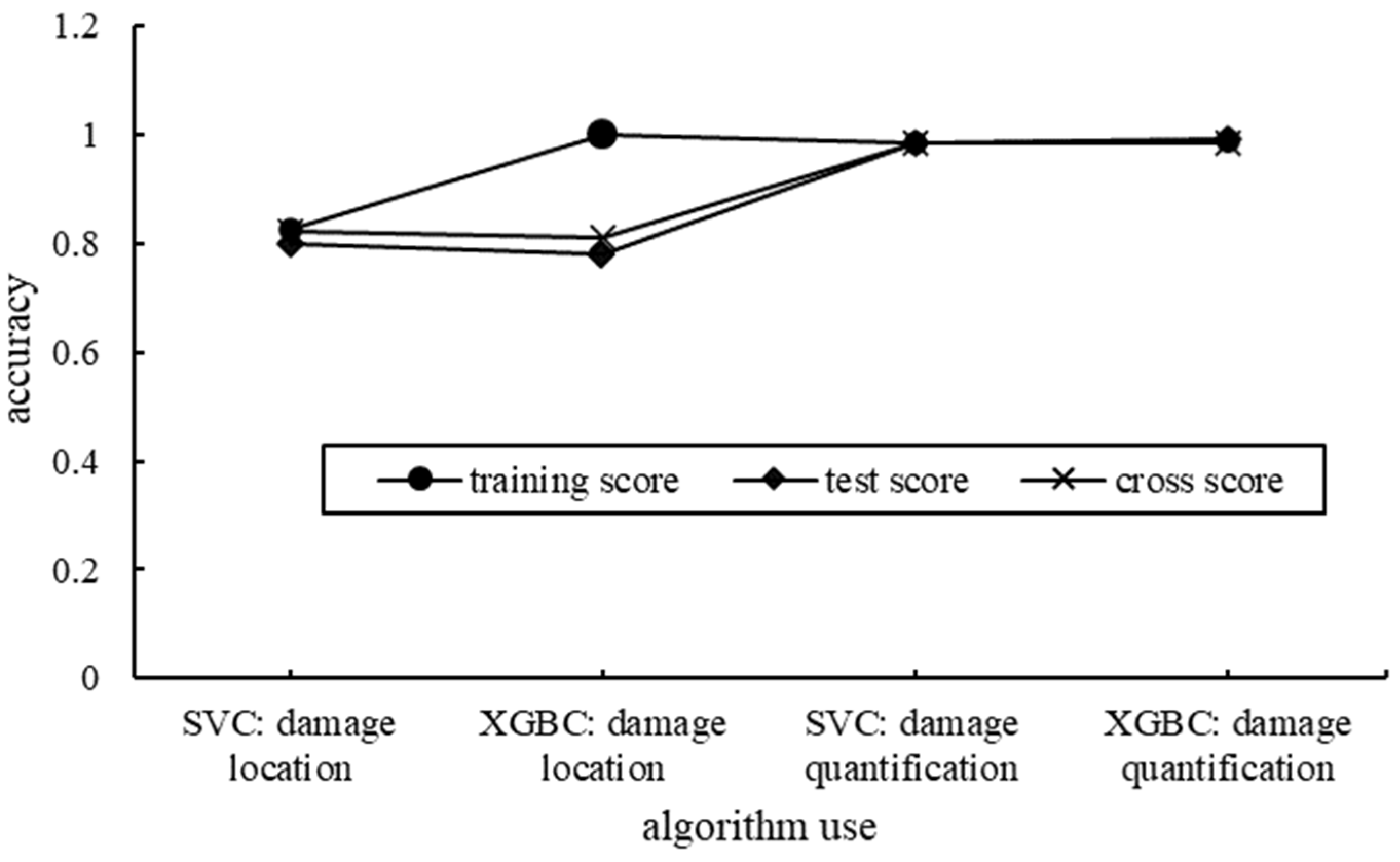
5.4. Damage Diagnosis of Cable-Stayed Bridges Based on Data Mining
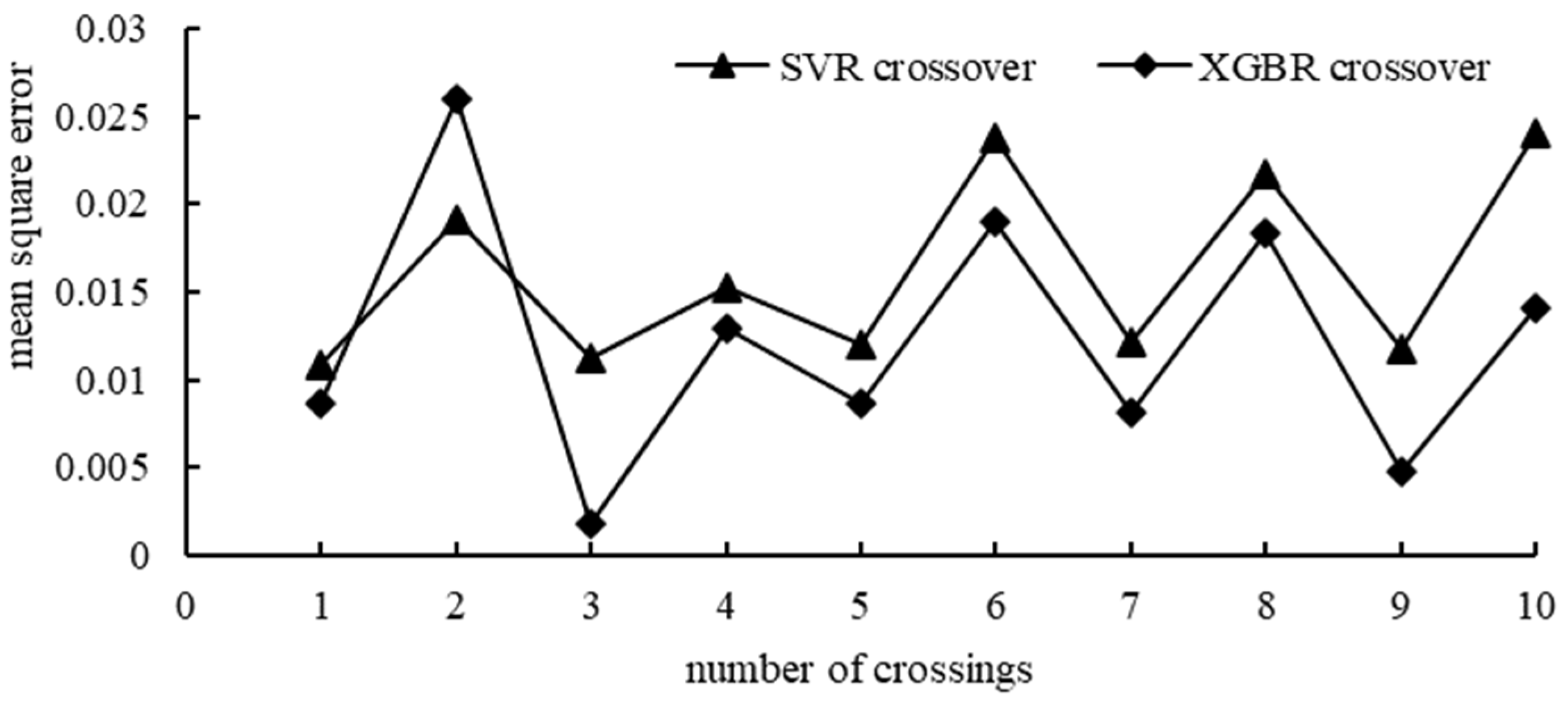
5.5. Performance Optimization of the Damage Diagnosis Model for Cable-Stayed Bridges
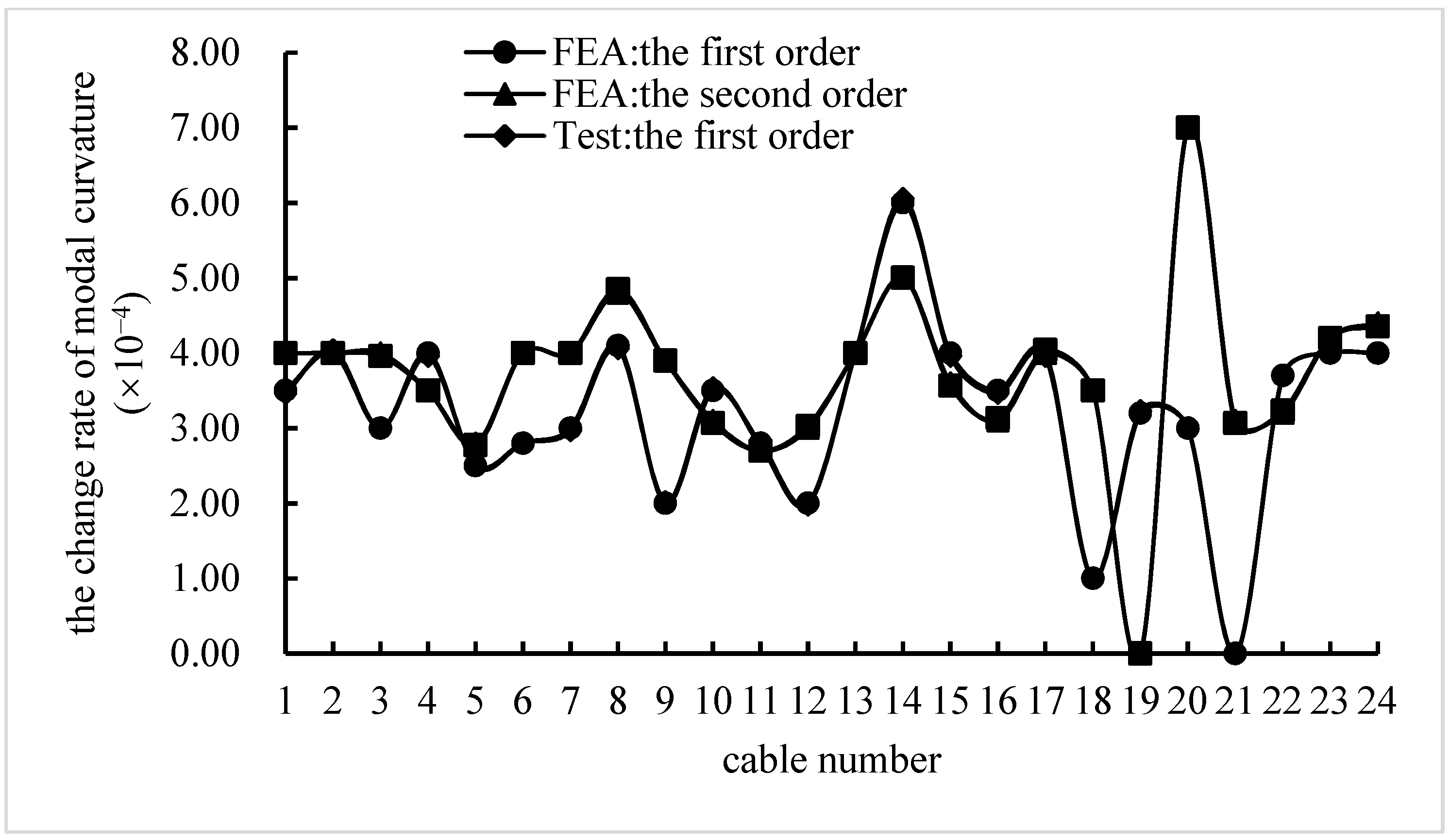
5.6. Application of the Model in a Practical Cable-Stayed Bridge
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, Z.-G.; Yue, Q.; Shi, Z. Design of Structural Health Monitoring System for Hutong Changjiang River Bridge. Bridge Constr. 2017, 47, 7–12. [Google Scholar]
- Editorial Department of China Journal of Highway and Transport. Review on China’s Bridge Engineering Research: 2021. China J. Highw. Transp. 2021, 34, 1–97. [Google Scholar]
- Ke, J.; Dong, H.; Tan, C.; Liang, Y. PBWA: A Provenance-Based What-If Analysis Approach for Data Mining Processes. Chin. J. Electron. 2017, 26, 986–992. [Google Scholar] [CrossRef]
- Guo, Q.; Nan, P.; Wan, J. Signal classification method based on data mining for multi-mode radar. J. Syst. Eng. Electron. 2016, 27, 1010–1017. [Google Scholar] [CrossRef]
- Gordan, M.; Razak, H.A.; Ismail, Z.; Ghaedi, K. Recent Developments in Damage Identification of Structures Using Data Mining. Lat. Am. J. Solids Struct. 2017, 14, 2373–2401. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, N.; Zhang, Z. Structural Damage Identification Study Based on Kernel Component Analysis and Support Vector Machine. J. Basic Sci. Eng. 2018, 26, 888–900. [Google Scholar]
- Sun, C.; Lü, Q.; Zhu, S.; Zheng, W.; Cao, Y.; Wang, J. Ultra-short-term Power Load Forecasting Based on Two-layer XGBoost Algorithm Considering the Influence of Multiple Features. High Volt. Eng. 2021, 47, 2885–2898. [Google Scholar]
- Zhao, Y.-P.; Yu, T.-L.; Jiao, Y.-B.; Gong, Y.-F.; Song, G. Damage identification method and factor evaluation for irregular-shaped bridge. J. Jilin Univ. (Eng. Technol. Ed.) 2016, 46, 1858–1866. [Google Scholar]
- Zhang, J.; Zhang, Q.; Qin, X.; Sun, Y. A two-stage fault diagnosis methodology for rotating machinery combining optimized support vector data description and optimized support vector machine. Measurement 2022, 200, 111651. [Google Scholar] [CrossRef]
- An, P.; Wu, X. Multi position damage identification of beam-bridges based on support vector machine. J. Railw. Sci. Eng. 2019, 16, 1231–1236. [Google Scholar]
- Liu, Z.; Jin, M.; Zhou, L.; Tu, C.; Tang, L.; Jiang, Z.; Liu, Y. Bridge Damage Identification Method Based on Structural Response Vectors and Support Vector Machine Algorithms. J. Univ. Jinan (Sci. Technol.) 2020, 34, 106–112. [Google Scholar]
- Guo, X.; Gong, R.; Bao, H. Modeling of wind speed uncertainty based on evidence theory. Electr. Power Autom. Equip. 2019, 39, 73–77. [Google Scholar]
- Li, Y.; Huang, Y.X.; Zhao, L.J.; Liu, C.L. Multi-condition Wear Evaluation of Tool Based on T-SNE and XGBoost. J. Mech. Eng. 2020, 56, 132–140. [Google Scholar]
- Huang, X. Research on Damage Identification of Long-Span Bridges Based on Optimal Sensor Placement and Integrated Learning. Doctoral Thesis, Wuhan University of Technology, Wuhan, China, 2020. [Google Scholar]
- Ling, D.; Li, C.; Wang, Y.; Zhang, P. Fault Detection and Identification of Furnace Negative Pressure System with CVA and GA-XGBoost. Energies 2022, 15, 6355. [Google Scholar] [CrossRef]
- Fu, C.; Shan, D.; Li, Q. The Static Damage Identification Method Based on the Support Vector Machine. China Railw. Sci. 2010, 31, 47–53. [Google Scholar]
- Wan, H.-P.; Ren, W.-X.; Yan, W.-J. Analytical global sensitivity analysis for uncertainty in structural dynamic properties of bridges. J. Vib. Eng. 2016, 29, 429–435. [Google Scholar]
- Xiao, R.; Wei, Z.; Zhai, X. Hourly Energy Consumption Forecasting for Office Buildings Based on Support Vector Machine. J. Shanghai Jiao Tong Univ. 2021, 55, 331–336. [Google Scholar]
- Ma, L.; Yu, S.; Zhao, S. Superheated Steam Temperature Prediction Models Based on XGBoost Optimized with Random Search Algorithm. J. North China Electr. Power Univ. 2021, 48, 99–105. [Google Scholar]
- Zhang, H.-S.; Wang, Y.-Y. Cooling Method Numerical Analysis of Suspender Cable Tension and Cable Saddle Pushing. J. Railw. Eng. Soc. 2017, 34, 39–44. [Google Scholar]
- Wang, H.; Liu, J.; Wang, X.; Zhang, Z. A New Method and Implementation of Building Baseline FE Model of Cable-Stayed Bridge. J. Vib. Meas. Diagn. 2014, 34, 458–462. [Google Scholar]



| Damage no | Damage Location | Degree of Damage |
|---|---|---|
| 1 | A9 | 10%, 20%, 30%, 35%, 40% |
| 2 | A8 | 10%, 20%, 30%, 35%, 40% |
| 3 | A9, A8 | 10%, 20%, 30%, 35%, 40% |
| 4 | A9, A3 | 10%, 20%, 30%, 35%, 40% |
| 5 | A9, A7 | 10%, 20%, 30%, 35%, 40% |
| Test Set No | Expected Output | Actual Output |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 1 | 1 |
| Algorithm Combination | Parameter Combination |
|---|---|
| SVR-RSM | C=2.07, epsilon=0.034, gamma=0.22 |
| SVR-GSM | C=1.03, epsilon=0.034, gamma=0.083 |
| SVC-GSM | C=7.241455172413793, gamma=0.07242137931034483 |
| SVC-RSM | C=6.2069758620689655, gamma=0.08276586206896551 |
| XGBR-RSM | n_estimators=100, max_depth=3, min_child_weight=4, learning_rate=0.07 |
| XGBC-RSM | n_estimators=50, max_depth=3, min_child_weight=8.72, learning_rate=0.22 |
| Algorithm | svc | svr | ||||
|---|---|---|---|---|---|---|
| optimization method | gsm | rsm | gsm | rsm | ||
| optimization time | 21.43 | 0.36 | 265 | 0.13 | ||
| performance not optimized | 0.822 | 0.822 | 0.015 | 0.015 | ||
| performance after optimization | 0.860 | 0.858 | 0.008 | 0.011 |
| Algorithm | XGBClassifier | XGBRegressor |
|---|---|---|
| optimization time | 9.14 | 8.70 |
| performance not optimized | 0.809 | 0.01 |
| performance after optimization | 0.822 | 0.006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Cheng, H.; Liu, Q.; Wang, H.; Bu, J. Research on the Damage Diagnosis Model Algorithm of Cable-Stayed Bridges Based on Data Mining. Sustainability 2023, 15, 2347. https://doi.org/10.3390/su15032347
Liu J, Cheng H, Liu Q, Wang H, Bu J. Research on the Damage Diagnosis Model Algorithm of Cable-Stayed Bridges Based on Data Mining. Sustainability. 2023; 15(3):2347. https://doi.org/10.3390/su15032347
Chicago/Turabian StyleLiu, Jie, Han Cheng, Qingkuan Liu, Hailong Wang, and Jianqing Bu. 2023. "Research on the Damage Diagnosis Model Algorithm of Cable-Stayed Bridges Based on Data Mining" Sustainability 15, no. 3: 2347. https://doi.org/10.3390/su15032347
APA StyleLiu, J., Cheng, H., Liu, Q., Wang, H., & Bu, J. (2023). Research on the Damage Diagnosis Model Algorithm of Cable-Stayed Bridges Based on Data Mining. Sustainability, 15(3), 2347. https://doi.org/10.3390/su15032347








