Cooperative Efficiency Evaluation System for Intelligent Transportation Facilities Based on the Variable Weight Matter Element Extension
Abstract
:1. Introduction
2. Materials and Methods
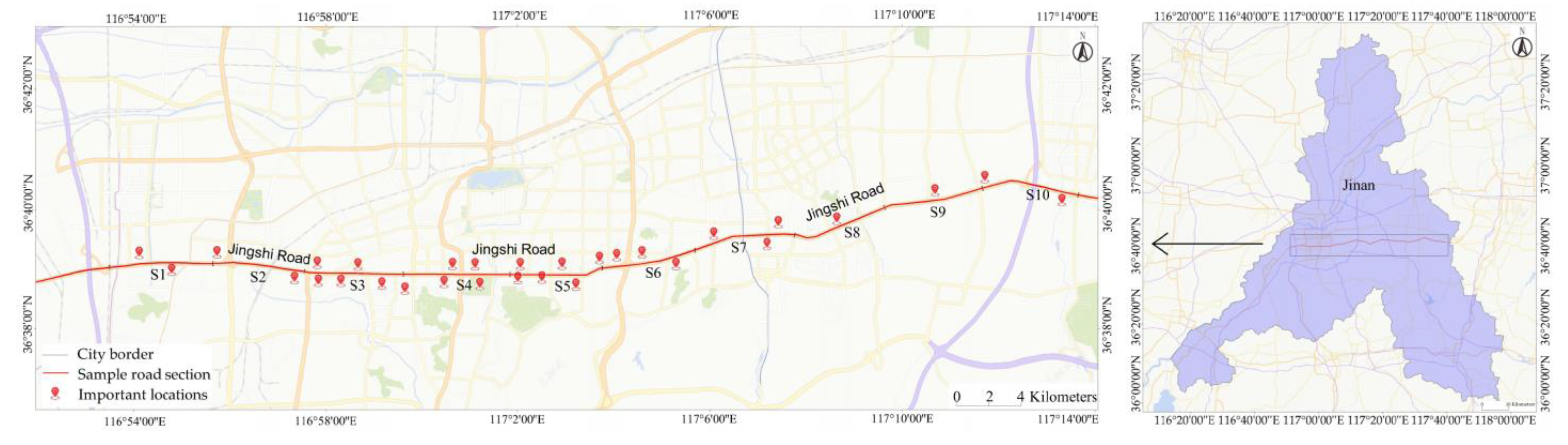
2.1. Study Area
2.2. Collection and Preparation of Data
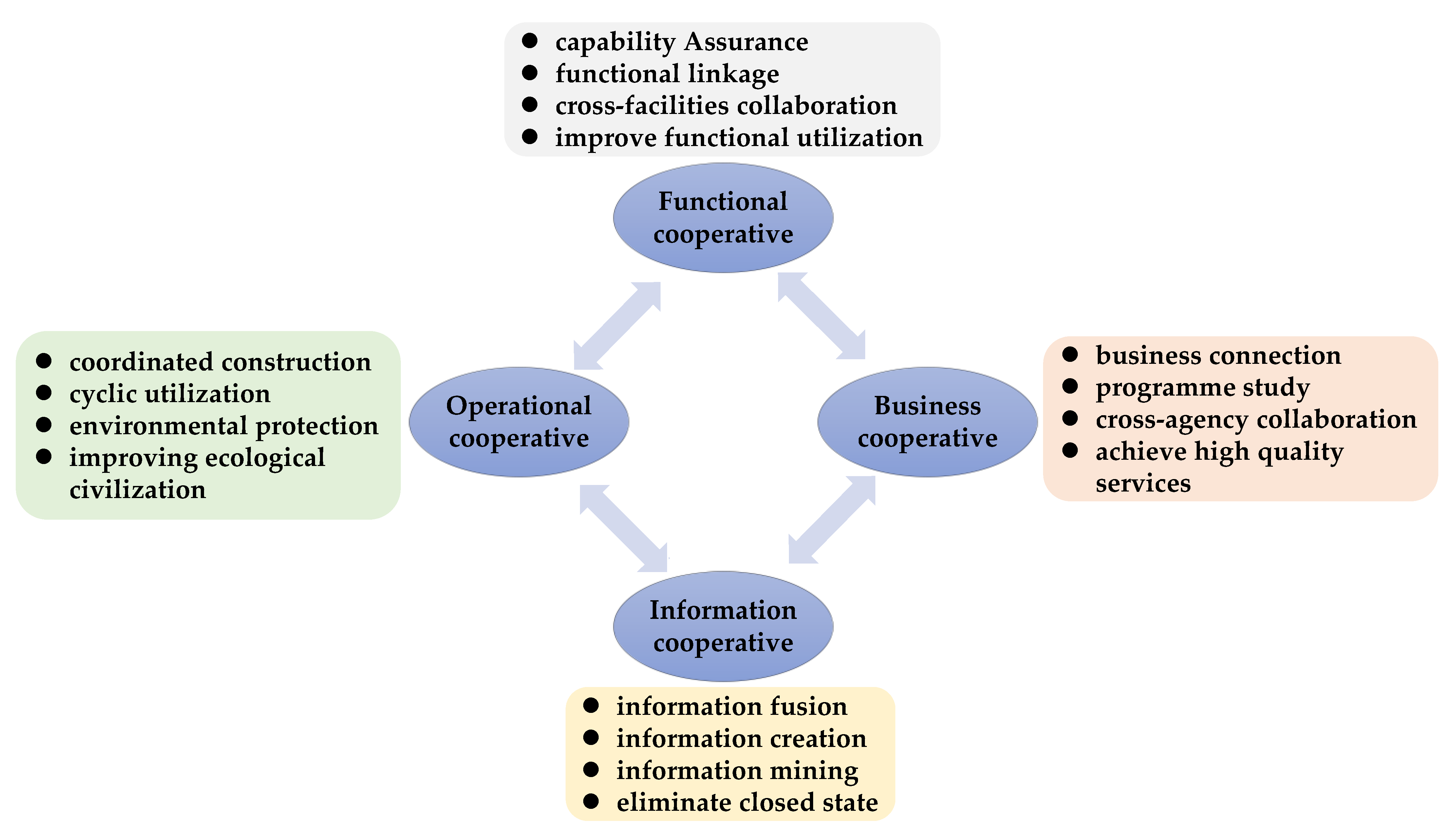
2.3. Establishment of a Cooperative Evaluation System for the Effectiveness of Intelligent Transportation Facilities
2.4. Determination of Index Weights
2.4.1. Index Normalization
2.4.2. Determine the Constant Weight
2.4.3. Determination of Variable Weight
2.5. Matter-Element Extension Evaluation Model
2.5.1. Determine the Evaluation Matter-Element
2.5.2. Determining Classical Domains, Node Domains, and Evaluation Objects
2.5.3. Determine the Close Degree
2.5.4. Rating
3. Results
3.1. Weights of Assessment Index
3.2. Evaluation Results
4. Discussion
4.1. Sensitivity Analysis
4.2. Reliability Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.M.; Chen, X.J. Design of digital control system for traffic facilities based on K-means clustering algorithm. J. Xiangtan Univ. 2022, 44, 101–108. [Google Scholar]
- Ivanitskaya, N.V.; Baybulov, A.K.; Safronchuk, M.V. Modelling of the stress-strain state of a transport tunnel under load as a measure to reduce operational risks to transportation facilities. J. Phys. 2020, 1703, 012024. [Google Scholar]
- Stivin, A.N.; Mussa, A.D.; Gerrit, K.J.; Janeth, M.; Michael, K. MAGITS: A Mobile-based Information Sharing Framework for Integrating Intelligent Transport System in Agro-Goods e-Commerce in Developing Countries. IJACSA. 2021, 12, 714–725. [Google Scholar]
- Yu, H.; Dai, H.; Tian, G.; Xie, Y.; Wu, B.; Zhu, Y.; Li, H.; Wu, H. Big-Data-Based Power Battery Recycling for New Energy Vehicles: Information Sharing Platform and Intelligent Transportation Optimization. IEEE Access. 2020, 8, 99605–99623. [Google Scholar] [CrossRef]
- Feng, W.; Shi, Q.D. On Problems, Causes and Governance Approaches of Repetitive Construction of Characteristic Databases in Provincial Public Libraries. Res. Libr. Sci. 2021, 08, 50–56. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Long, L.H.; Basenda, T.P.; Tran, D.H. Tradeoff time cost quality in repetitive construction project using fuzzy logic approach and symbiotic organism search algorithm. Alex. Eng. J. 2022, 61, 1499–1518. [Google Scholar] [CrossRef]
- Li, P.; Jiang, F.T.; Cao, J.H. Industrial Overcapacity and Duplicate Construction in China: Reasons and Solutions; World Scientific Publishing Company: Singapore, 2019. [Google Scholar]
- David, B. Redefining Digital Library Boundaries: Being More than an Information Silo. SRELS J. Inf. Manag. 2019, 56, 274–287. [Google Scholar]
- Li, G.L.; Wang, L.; Yang, X.Y.; Li, Y.L.; Liu, Y. Comparative Study on Development Level of Transport Infrastructure in China. J. Highw. Transp. Res. Dev. 2021, 38, 97–105. [Google Scholar]
- Felbermayr, G.J.; Tarasov, A. Trade and The Spatial Distribution of Transport Infrastructure. J. Urban Econ. 2022, 130, 103473. [Google Scholar] [CrossRef]
- Sun, C.; Chen, X.; Zhang, H.M.; Huang, Z. An Evaluation Method of Urban Public Transport Facilities Resource Supply Based on Accessibility. J. Adv. Transp. 2018, 2018, 3754205. [Google Scholar] [CrossRef]
- Qi, Z.; Zheng, T.; Liu, N.; Zhong, H. Study on energy consumption index system and calculation method of highway transportation infrastructure in Qinghai Province. IOP Conf. Ser. Earth Environ. Sci. IOP Publ. 2020, 440, 032003. [Google Scholar] [CrossRef]
- Verweij, S.; Loomans, O.; Leendertse, W. The Role of the Public Partner in Innovation in Transport Infrastructure PPPs: A Qualitative Comparative Analysis of Nine Dutch DBFM Projects. Public Work. Manag. Policy. 2020, 25, 5–32. [Google Scholar] [CrossRef]
- Hu, J.; Ning, C. Research on Partner Selection of Transportation Infrastructure Projects under PPP Mode. Sci. J. Econ. Manag. Res. 2022, 4, 43–47. [Google Scholar]
- Chen, Z.Y. Research on Comprehensive Evaluation Index System of Traffic Infrastructure Construction. IOP Conf. Ser. Mater. Sci. Eng. 2019, 688, 022021. [Google Scholar] [CrossRef]
- Shen, J.; He, X.Y.; Hou, B.R.; Xia, H.J.; Fang, Z.X. Current situation of corrosion of transportation infrastructure. Port Waterw. Eng. 2022, 9, 15–21+79. Available online: https://www.sygc.com.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20220903&journal_id=sygc (accessed on 19 December 2022).
- Pang, R.; Yuan, Y.; Guo, X.L.; Zhou, L.J.; Su, Y.F.; Jiang, M.X.; Li, X. Discussion on operation safety and countermeasures of Highway tunnel Traffic Engineering Facilities. IOP Conf. Ser. Earth Environ. Sci. 2021, 638, 012115. [Google Scholar] [CrossRef]
- Shteyn, A.; Zaytsev, A.; Cherkasov, A.; Cherbakov, A.; Philipov, S. Evaluation of options for strengthening weak bases of embankments of transport infrastructure facilities. MATEC Web Conf. 2019, 265, 02013. [Google Scholar] [CrossRef]
- Alexey, V.S.; Maxim, A.S. A Fast-Track Method for Assessing the Risk of a Terrorist Attack on Transportation Facilities. Eur. J. Secur. Res. 2019, 4, 265–271. [Google Scholar]
- Zhang, Y.L.; Li, W.X.; Deng, H.P.; Li, Y. Evaluation of public transport-based accessibility to health facilities considering spatial heterogeneity. J. Adv. Transp. 2020, 2020, 7645153. [Google Scholar] [CrossRef]
- Ren, Y.; Zhao, C.R.; Fu, J.L. The Effect of Traffic Facilities Accessibility on Residents’ Travel under Block Scale. Open J. Soc. Sci. 2020, 8, 98–110. [Google Scholar] [CrossRef]
- Bayrakci, B.M.; Donaldson, B.; Diefenderfer, B. Use of Solar Photovoltaic Energy Systems in Department of Transportation Facilities: A Review of Practice and Preliminary Assessment for Virginia Department of Transportation. SAE Int. J. Sustain. Transp. Energy Environ. Policy. 2022, 3, 101–114. [Google Scholar] [CrossRef]
- Wang, B.; Teng, Q.; Bao, F.; Song, X.M. Designs of Intelligent Safety Monitoring and Early Warning Systems for Urban Rail Transit Facilities. Urban Rapid Rail Transit. 2021, 34, 58–64. [Google Scholar]
- Kerimov, M.; Safiullin, R.; Marusin, A.; Marusin, A. Evaluation of functional efficiency of automated traffic enforcement sys-tems. Transp. Res. Procedia. 2017, 20, 288–294. [Google Scholar] [CrossRef]
- Liu, S.T.; Sun, Y. Research on the Intelligent Level of Public Transport Infrastructure in Tianjin. City 2020, 4, 56–63. Available online: https://mall.cnki.net/magazine/article/CSHI202004008.htm (accessed on 19 December 2022).
- Kutela, B.; Combs, T.; Mwekh’iga, R.J.; Langa, N. Insights into the long-term effects of COVID-19 responses on transportation facilities. Transp. Res. Part D Transp. Environ. 2022, 111, 103463. [Google Scholar] [CrossRef] [PubMed]
- Kossov, E.E.; Muginshtein, L.A.; Kuchumov, V.A.; Ermolenko, D.V.; Kossova, L.E. Comparative Assessment of Effectiveness of Transport Facilities. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 2680–2684. [Google Scholar]
- Sun, D.L.; Wu, J.P.; Zhang, F.T.; Su, W.C.; Hui, H. Evaluating Water Resource Security in Karst Areas Using DPSIRM Modeling, Gray Correlation, and Matter–Element Analysis. Sustainability 2018, 10, 3934. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, F.S.; Gao, M.; Liu, L.; Wang, X.P. Impact of the Stress Status of Employees on the Enterprise Technology Management Cost Through Matter-Element Analysis Under Psychological Health Education. Front. Psychol. 2021, 12, 593813. [Google Scholar] [CrossRef]
- Sun, C.; Quan, W. Multiple Classifier of Traffic Accident Based on Matter-Element Analysis. IOP Conf. Ser. Earth Environ. Sci. 2020, 587, 012038. [Google Scholar] [CrossRef]
- Liu, B.; Li, X.L.; Zhang, P.; Zhu, G.Y. Evaluationon operational risk of urban rail transit line based on entropy weight extension matter-element model. J. Saf. Sci. Technol. 2019, 15, 175–181. [Google Scholar]
- Zhao, Y.N.; Xue, X.Z.; Huang, Y.; Kong, H. Evaluating comprehensive carrying capacity of coastal area using the matter-element extension method: A case study in Fujian Province of China. Ocean Coast. Manag. 2021, 214, 105902. [Google Scholar] [CrossRef]
- Chen, J.H.; Chen, Y.; Yang, S.; Zhong, X.D.; Han, X. A prediction model on rockburst intensity grade based on variable weight and matter-element extension. PLoS ONE 2019, 14, e0218525. [Google Scholar] [CrossRef]
- Pan, Y.; Mao, T.F. Toll road PPP project risk early warning based on variable weight extension matter-element model. Transp. Syst. Eng. Inf. 2018, 18, 5–11. [Google Scholar]
- Huang, J.; Shuai, Y.H.; Liu, Q.; Zhou, H.; He, Z.G. Synergy Degree Evaluation Based on Synergetics for Sustainable Logistics Enterprises. Sustainability 2018, 10, 2187. [Google Scholar] [CrossRef]
- Han, X.; Wang, D. Research on the Application of System Theory in Traffic Engineering. J. Phys. Conf. Ser. 2021, 1972, 012112. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Ahmad, A.D.; Abubaker, A.M.; Mohamed, M.A.; Hassan, M.A.; Akafuah, N.K. Optimal sizing of country-scale renewable energy systems towards green transportation sector in developing countries. Case Stud. Therm. Eng. 2022, 39, 102442. [Google Scholar] [CrossRef]
- Zhang, T. Interpretation of “Action Plan for Carbon Peak Before 2030”. Ecol. Econ. 2022, 38, 9–12. [Google Scholar]
- Heilongjiang Provinces carbon peak implementation plan introduced “ten actions” to ensure “the provinces carbon peak by 2030” goal. Environ. Sci. Manag. 2022, 47, 1.
- Wang, P.B.; Wang, W.; Meng, N.N.; Xu, D.G. Multi-objective energy management system for DC microgrids based on the maximum membership degree principle. J. Mod. Power Syst. Clean Energy. 2018, 6, 668–678. [Google Scholar] [CrossRef]
- Zhao, H.B.; Ma, Y.J. Study on early-warning model based on variable weight-matter element analysis for ecological security in old industrial bases: A case study of Jilin Province. Acta Ecol. Sin. 2014, 34, 4720–4733. [Google Scholar]
- Li, D.Q.; Hao, F.L. Weights Transferring Effect of State Variable Weight Vector. Syst. Eng.-Theory Pract. 2009, 29, 127–131. [Google Scholar] [CrossRef]
- Gao, Z.W.; Ma, D.H.; Wang, W.; Guo, X.D.; Ge, Q.Z. Development and Application of Ancient Timber Buildings Structural Condition Assessment Model Based on a Fuzzy Matter-Element Model that Includes Asymmetric Proximity. Math. Probl. Eng. 2018, 2018, 7426915. [Google Scholar] [CrossRef]
- Wen, Y.Y.; You, T.G.; Xu, Y.H.; Lin, S.H.; Ning, J.; You, X.M.; Xiao, Y.L. Comprehensive Evaluation of the Level of Water Ecological Civilization Construction in the Min River Basin, China. Sustainability 2022, 14, 15753. [Google Scholar] [CrossRef]

| Target Layer | Criterion Layer | Index Layer | |
|---|---|---|---|
| Index | Type | ||
| Functional cooperative, | Functional integrity, | Functional coverage, | + |
| Functional peak level, | + | ||
| Functional reproducibility, | - | ||
| Function guarantee level, | + | ||
| Function expansion, | Functional upgrading level, | + | |
| Interface reservation level, | + | ||
| Functional variability, | + | ||
| Functional sharing breadth, | Function scheduling level, | + | |
| Functional combination effect, | + | ||
| Business cooperative, | Project level, | Plan autonomy, | + |
| Plan executability, | + | ||
| Option evaluation level, | Program plan efficiency, | + | |
| Option evaluation accuracy, | + | ||
| Option evaluation efficiency, | + | ||
| Information cooperative, | Information fusion level, | Space-time registration rate, | + |
| Information interactivity, | + | ||
| Multi-sectoral information fusion level, | + | ||
| Information evaluation level, | Traffic environment evaluation, | + | |
| multi-department mobility evaluation, | + | ||
| Control ability evaluation, | + | ||
| Information evaluation efficiency, | + | ||
| Information expression level, | Information updating rate, | + | |
| Completeness of information elements, | + | ||
| Information display accuracy, | + | ||
| Information forecast level, | Facilities status, | + | |
| Road condition alarm, | + | ||
| situation prediction efficiency, | + | ||
| Operational cooperative, | Repeated construction level, | Vertical cooperative construction, | - |
| Facility consolidation level, | + | ||
| Reliability level, | Annual failure rate, | - | |
| Mean time between failure, | - | ||
| Recoverable level, | + | ||
| Facilities replacement cycle, | + | ||
| Resources utilization level, | Cycle level of facilities, | + | |
| Spatial intensification level, | + | ||
| Renewable resources utilization level, | + | ||
| Index | Constant Weight | Dynamic Weight | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | ||
| 0.0351 | 0.0324 | 0.0312 | 0.0341 | 0.0317 | 0.0325 | 0.0324 | 0.0330 | 0.0329 | 0.0317 | 0.0331 | |
| 0.0191 | 0.0177 | 0.0176 | 0.0187 | 0.0184 | 0.0194 | 0.0199 | 0.0198 | 0.0201 | 0.0203 | 0.0204 | |
| 0.0227 | 0.0245 | 0.0207 | 0.0234 | 0.0237 | 0.0234 | 0.0245 | 0.0269 | 0.0223 | 0.0235 | 0.0273 | |
| 0.0166 | 0.0162 | 0.0161 | 0.0178 | 0.0176 | 0.0176 | 0.0177 | 0.0164 | 0.0165 | 0.0161 | 0.0168 | |
| 0.0139 | 0.0138 | 0.0121 | 0.0120 | 0.0139 | 0.0139 | 0.0135 | 0.0135 | 0.0137 | 0.0135 | 0.0138 | |
| 0.0154 | 0.0124 | 0.0152 | 0.0152 | 0.0157 | 0.0162 | 0.0162 | 0.0151 | 0.0234 | 0.0151 | 0.0154 | |
| 0.0195 | 0.0232 | 0.0182 | 0.0191 | 0.0216 | 0.0221 | 0.0231 | 0.0197 | 0.0214 | 0.0203 | 0.0198 | |
| 0.0448 | 0.0433 | 0.0717 | 0.0432 | 0.0469 | 0.0467 | 0.0466 | 0.0472 | 0.0461 | 0.0857 | 0.0471 | |
| 0.0390 | 0.0393 | 0.0401 | 0.0403 | 0.0378 | 0.0399 | 0.0397 | 0.0397 | 0.0381 | 0.0378 | 0.0450 | |
| 0.0245 | 0.0326 | 0.0241 | 0.0257 | 0.0266 | 0.0234 | 0.0236 | 0.0261 | 0.0254 | 0.0214 | 0.0236 | |
| 0.0128 | 0.0148 | 0.0113 | 0.0134 | 0.0132 | 0.0128 | 0.0126 | 0.0135 | 0.0132 | 0.0132 | 0.0135 | |
| 0.0331 | 0.0318 | 0.0313 | 0.0389 | 0.0324 | 0.0342 | 0.0322 | 0.0297 | 0.0364 | 0.0281 | 0.0322 | |
| 0.0157 | 0.0178 | 0.0142 | 0.0142 | 0.0181 | 0.0163 | 0.0163 | 0.0178 | 0.0156 | 0.0123 | 0.0147 | |
| 0.0263 | 0.0224 | 0.0224 | 0.0254 | 0.0257 | 0.0261 | 0.0241 | 0.0223 | 0.0226 | 0.0180 | 0.0243 | |
| 0.0147 | 0.0144 | 0.0142 | 0.0135 | 0.0153 | 0.0138 | 0.0138 | 0.0176 | 0.0158 | 0.0131 | 0.0146 | |
| 0.0383 | 0.0348 | 0.0314 | 0.0362 | 0.0374 | 0.0375 | 0.0374 | 0.0413 | 0.0363 | 0.0314 | 0.0394 | |
| 0.0403 | 0.0411 | 0.0582 | 0.0397 | 0.0410 | 0.0425 | 0.0407 | 0.0438 | 0.0397 | 0.0476 | 0.0453 | |
| 0.0219 | 0.0215 | 0.0194 | 0.0217 | 0.0277 | 0.0219 | 0.0223 | 0.0186 | 0.0221 | 0.0153 | 0.0196 | |
| 0.0268 | 0.0325 | 0.0245 | 0.0241 | 0.0258 | 0.0226 | 0.0243 | 0.0241 | 0.0241 | 0.0220 | 0.0269 | |
| 0.0197 | 0.0208 | 0.0181 | 0.0184 | 0.0216 | 0.0201 | 0.0207 | 0.0192 | 0.0211 | 0.0171 | 0.0204 | |
| 0.0261 | 0.0243 | 0.0243 | 0.0263 | 0.0263 | 0.0252 | 0.0249 | 0.0243 | 0.0257 | 0.0226 | 0.0185 | |
| 0.0163 | 0.0181 | 0.0152 | 0.0171 | 0.0168 | 0.0169 | 0.0157 | 0.0157 | 0.0167 | 0.0141 | 0.0157 | |
| 0.0411 | 0.0417 | 0.0422 | 0.0437 | 0.0427 | 0.0387 | 0.0387 | 0.0425 | 0.0431 | 0.0617 | 0.0442 | |
| 0.0259 | 0.0224 | 0.0212 | 0.0283 | 0.0249 | 0.0263 | 0.0261 | 0.0214 | 0.0219 | 0.0212 | 0.0219 | |
| 0.0207 | 0.0275 | 0.0153 | 0.0204 | 0.0217 | 0.0180 | 0.0206 | 0.0231 | 0.0217 | 0.0176 | 0.0194 | |
| 0.0266 | 0.0251 | 0.0226 | 0.0258 | 0.0271 | 0.0270 | 0.0241 | 0.0264 | 0.0239 | 0.0194 | 0.0268 | |
| 0.0337 | 0.0327 | 0.0287 | 0.0324 | 0.0335 | 0.0357 | 0.0334 | 0.0319 | 0.0376 | 0.0283 | 0.0285 | |
| 0.0576 | 0.0582 | 0.0971 | 0.0580 | 0.0551 | 0.0582 | 0.0547 | 0.0553 | 0.0542 | 0.0802 | 0.0601 | |
| 0.0289 | 0.0297 | 0.0294 | 0.0293 | 0.0264 | 0.0274 | 0.0293 | 0.0297 | 0.0286 | 0.0279 | 0.0357 | |
| 0.0403 | 0.0421 | 0.0413 | 0.0406 | 0.0387 | 0.0421 | 0.0411 | 0.0421 | 0.0422 | 0.0386 | 0.0412 | |
| 0.0284 | 0.0277 | 0.0223 | 0.0282 | 0.0263 | 0.0278 | 0.0305 | 0.0298 | 0.0282 | 0.0256 | 0.0303 | |
| 0.0322 | 0.0310 | 0.0287 | 0.0367 | 0.0334 | 0.0334 | 0.0347 | 0.0318 | 0.0320 | 0.0278 | 0.0293 | |
| 0.0278 | 0.0242 | 0.0203 | 0.0268 | 0.0264 | 0.0238 | 0.0278 | 0.0261 | 0.0264 | 0.0243 | 0.0243 | |
| 0.0276 | 0.0216 | 0.0242 | 0.0262 | 0.0253 | 0.0281 | 0.0295 | 0.0274 | 0.0258 | 0.0244 | 0.0268 | |
| 0.0357 | 0.0337 | 0.0341 | 0.0336 | 0.0336 | 0.0368 | 0.0361 | 0.0360 | 0.0336 | 0.0347 | 0.0335 | |
| 0.0309 | 0.0327 | 0.0211 | 0.0316 | 0.0297 | 0.0317 | 0.0312 | 0.0312 | 0.0316 | 0.0281 | 0.0306 | |
| Sections | Evaluation of the Accessible Degree of the Grade | Maximum Proximity | Character Value | Grades | |||
|---|---|---|---|---|---|---|---|
| S1 | 0.1052 | 0.0473 | 0.0231 | 0.0193 | 0.1052 | 1.3025 | Excellent |
| S2 | 0.0763 | 0.0975 | 0.0165 | 0.1049 | 0.1049 | 2.5105 | Poor |
| S3 | 0.0861 | 0.0824 | 0.0237 | 0.0493 | 0.0861 | 1.9237 | Excellent |
| S4 | 0.1331 | 0.0756 | 0.0193 | 0.0128 | 0.1331 | 1.3998 | Excellent |
| S5 | 0.0877 | 0.1862 | 0.0760 | 0.0262 | 0.1862 | 1.9569 | Good |
| S6 | 0.1606 | 0.0741 | 0.0193 | 0.0127 | 0.1606 | 1.3455 | Excellent |
| S7 | 0.0873 | 0.1651 | 0.0346 | 0.0358 | 0.1651 | 1.7272 | Good |
| S8 | 0.1925 | 0.0729 | 0.0564 | 0.0639 | 0.1925 | 1.2436 | Excellent |
| S9 | 0.1085 | 0.0305 | 0.0425 | 0.1837 | 0.1837 | 2.9885 | Poor |
| S10 | 0.0387 | 0.1699 | 0.0275 | 0.0397 | 0.1699 | 2.0796 | Good |
| Section | Constant Weight | Variable Weight | ||
|---|---|---|---|---|
| Grades | Results | Grades | Results | |
| S1 | I | Excellent | I | Excellent |
| S2 | II | Good | IV | Poor |
| S3 | I | Excellent | I | Excellent |
| S4 | I | Excellent | I | Excellent |
| S5 | I | Good | II | Good |
| S6 | I | Excellent | I | Excellent |
| S7 | II | Good | II | Good |
| S8 | I | Excellent | I | Excellent |
| S9 | III | Medium | IV | Poor |
| S10 | II | Good | II | Good |
| Single regression: , | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Bai, H.; Yan, X.; Zhao, L.; Wang, X. Cooperative Efficiency Evaluation System for Intelligent Transportation Facilities Based on the Variable Weight Matter Element Extension. Sustainability 2023, 15, 2411. https://doi.org/10.3390/su15032411
Li K, Bai H, Yan X, Zhao L, Wang X. Cooperative Efficiency Evaluation System for Intelligent Transportation Facilities Based on the Variable Weight Matter Element Extension. Sustainability. 2023; 15(3):2411. https://doi.org/10.3390/su15032411
Chicago/Turabian StyleLi, Kailei, Han Bai, Xiang Yan, Liang Zhao, and Xiuguang Wang. 2023. "Cooperative Efficiency Evaluation System for Intelligent Transportation Facilities Based on the Variable Weight Matter Element Extension" Sustainability 15, no. 3: 2411. https://doi.org/10.3390/su15032411
APA StyleLi, K., Bai, H., Yan, X., Zhao, L., & Wang, X. (2023). Cooperative Efficiency Evaluation System for Intelligent Transportation Facilities Based on the Variable Weight Matter Element Extension. Sustainability, 15(3), 2411. https://doi.org/10.3390/su15032411







