Analysis of Sub-Optimization Impact on Partner Selection in VMI
Abstract
:1. Introduction
2. Literature Review
3. Preparation Work
3.1. Model Assumptions
3.2. Parameter Settings
4. Benefits Analysis in VMI
4.1. Modeling
4.2. Revenue Fluctuation Analysis
5. Numerical Experiment
5.1. Simulation Parameter Settings
5.2. Parameter Scope Determination
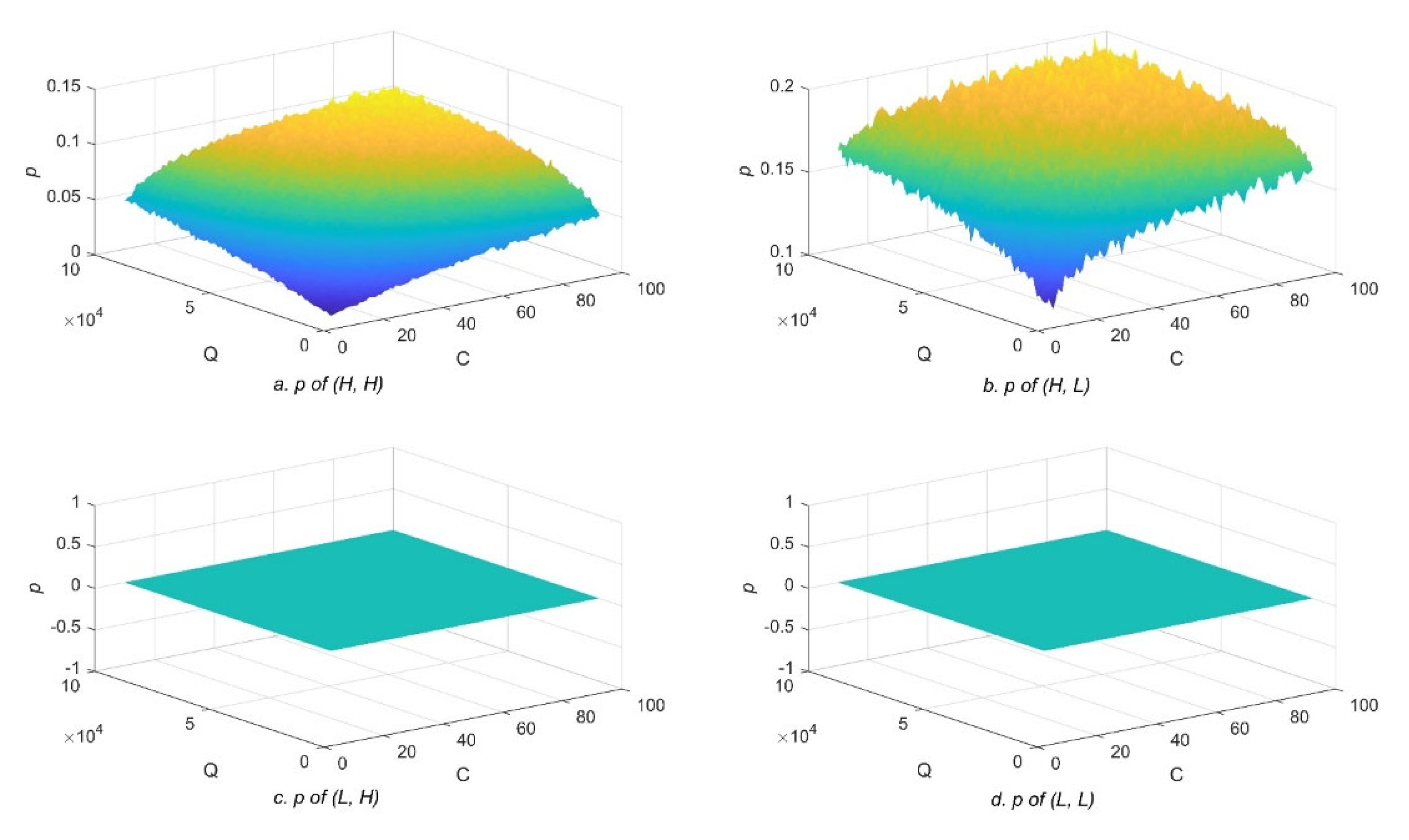
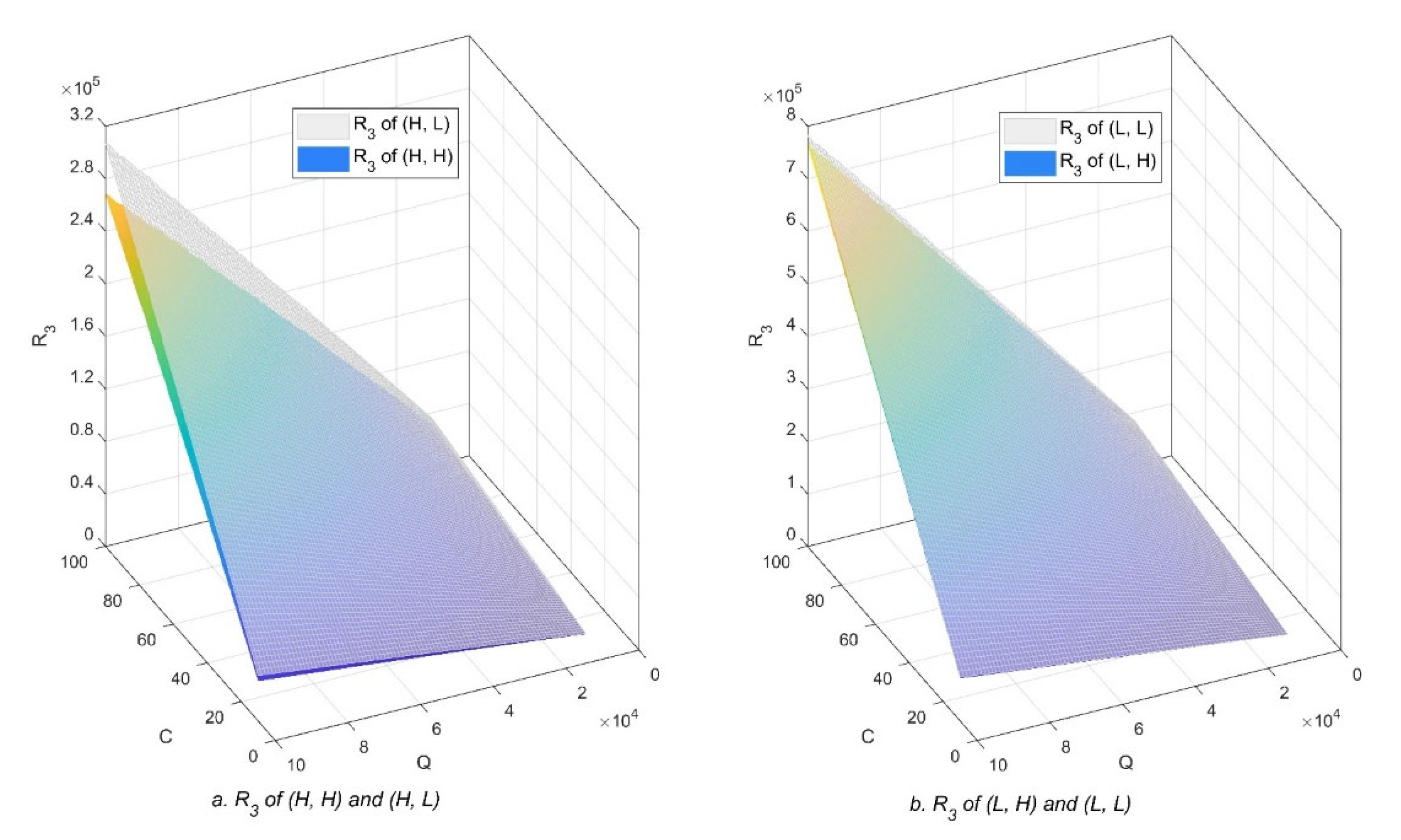
5.3. Analysis Object Selection
5.4. Experiment and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Disney, S.M.; Towill, D.R. The effect of vendor managed inventory (VMI) dynamics on the Bullwhip Effect in supply chains. Int. J. Prod. Econ. 2003, 85, 199–215. [Google Scholar] [CrossRef]
- Ma, J.; Lou, W.; Tian, Y. Bullwhip effect and complexity analysis in a multi-channel supply chain considering price game with discount sensitivity. Int. J. Prod. Res. 2019, 57, 5432–5452. [Google Scholar] [CrossRef]
- Yao, Y.; Dresner, M. The inventory value of information sharing, continuous replenishment, and vendor-managed inventory. Transp. Res. Part E: Logist. Transp. Rev. 2008, 44, 361–378. [Google Scholar] [CrossRef]
- Graham, T.S.; Daugherty, P.J.; Dudley, W.N. The long-term strategic impact of purchasing partnerships. J. Supply Chain. Manag. 1994, 30, 13. [Google Scholar] [CrossRef]
- Sha, J.; Wang, A.; Lv, T.; Wu, W. Coordination of advertising free riding in hybrid channel supply chain. Discret. Dyn. Nat. Soc. 2016, 2016, 7423043. [Google Scholar] [CrossRef]
- Ryu, C. Investigation on How VMI affects Ongoing Performance of Supply Chain System. J. Distrib. Sci. 2020, 18, 85–94. [Google Scholar]
- Kim, S.C.; Shin, K.S. Negotiation Model for Optimal Replenishment Planning Considering Defects under the VMI and JIT Environment. Asian J. Shipp. Logist. 2019, 35, 147–153. [Google Scholar] [CrossRef]
- Beklari, A.; Nikabadi, M.S.; Farsijani, H.; Mohtashami, A. A Hybrid Algorithm for Solving Vendors Managed Inventory (VMI) Model with the Goal of Maximizing Inventory Turnover in Producer Warehouse. Ind. Eng. Manag. Syst. 2018, 17, 570–587. [Google Scholar] [CrossRef]
- Torres, F.; García-Díaz, C. Evolutionary dynamics of two-actor VMI-driven supply chains. Comput. Math. Organ. Theory 2018, 24, 351–377. [Google Scholar] [CrossRef]
- Chen, M.C.; Hsiao, Y.H.; Huang, H.Y. Semiconductor supply chain planning with decisions of decoupling point and VMI scenario. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 856–868. [Google Scholar] [CrossRef]
- Cai, J.; Zhong, M.; Shang, J.; Huang, W. Coordinating VMI supply chain under yield uncertainty: Option contract, subsidy contract, and replenishment tactic. Int. J. Prod. Econ. 2017, 185, 196–210. [Google Scholar] [CrossRef]
- Verma, N.K.; Chatterjee, A.K. A multiple-retailer replenishment model under VMI: Accounting for the retailer heterogeneity. Comput. Ind. Eng. 2017, 104, 175–187. [Google Scholar] [CrossRef]
- Lee, D. VMI with Upper Limit of Inventory for Vendor and Retailer. J. Soc. Korea Ind. Syst. Eng. 2017, 40, 105–111. [Google Scholar] [CrossRef]
- Golmohammadi, A.M.; Javid, N.J.; Poursoltan, L.; Esmaeeli, H. Modeling and analyzing one vendor-multiple retailers VMI SC using Stackelberg game theory. Ind. Eng. Manag. Syst. 2016, 15, 385–395. [Google Scholar] [CrossRef]
- Choudhary, D.; Shankar, R. The value of VMI beyond information sharing under time-varying stochastic demand. Int. J. Prod. Res. 2015, 53, 1472–1486. [Google Scholar] [CrossRef]
- Laganà, D.; Longo, F.; Vocaturo, F. Vendor-managed inventory practice in the supermarket supply chain. Int. J. Food Eng. 2016, 12, 827–834. [Google Scholar] [CrossRef]
- De Maio, A.; Laganà, D. The effectiveness of vendor managed inventory in the last-mile delivery: An industrial application. Procedia Manuf. 2020, 42, 462–466. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Tadikamalla, P.R.; Shang, J. Flexible contract design for VMI supply chain with service-sensitive demand: Revenue-sharing and supplier subsidy. Eur. J. Oper. Res. 2017, 261, 143–153. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Wang, Z.; Jiang, H. Multi-Period Coordination Mechanism Based on Revenue Sharing Contract in VMI Model. Adv. Appl. Math. Mech. 2019, 11, 980–1004. [Google Scholar]
- Phan, D.A.; Vo, T.L.H.; Lai, A.N.; Nguyen, T.L.A. Coordinating contracts for VMI systems under manufacturer-CSR and retailer-marketing efforts. Int. J. Prod. Econ. 2019, 211, 98–118. [Google Scholar] [CrossRef]
- Choudhary, D.; Shankar, R.; Tiwari, M.K.; Purohit, A.K. VMI versus information sharing: An analysis under static uncertainty strategy with fill rate constraints. Int. J. Prod. Res. 2016, 54, 3978–3993. [Google Scholar] [CrossRef]
- Huynh, C.H.; Pan, W. Operational strategies for supplier and retailer with risk preference under VMI contract. Int. J. Prod. Econ. 2015, 169, 413–421. [Google Scholar] [CrossRef]
- Jiang, N.; Zhang, L.L.; Yu, Y. Optimizing cooperative advertizing, profit sharing, and inventory policies in a VMI supply chain: A Nash bargaining model and hybrid algorithm. IEEE Trans. Eng. Manag. 2015, 62, 449–461. [Google Scholar] [CrossRef]
- Mateen, A.; Chatterjee, A.K.; Mitra, S. VMI for single-vendor multi-retailer supply chains under stochastic demand. Comput. Ind. Eng. 2015, 79, 95–102. [Google Scholar] [CrossRef]
- Jing, X.; Liu, Z. Formulation on VMI System Integration and Income Sharing Contract. In Proceedings of the 2011 International Conference on Information Management, Innovation Management and Industrial Engineering, Shenzhen, China, 26–27 November 2011; Volume 2, pp. 33–37. [Google Scholar]

| Symbol | Description | Additional Information |
|---|---|---|
| Q | Market demand faced by retailer | Q ≥ 0 |
| C | Purchase price of wholesaler | C ≥ 0 |
| C0 | Wholesaler’s sale price at the end of the selling period | C0 ≥ 0 and C0 < C |
| P1, P2 | Product price of upstream wholesaler and downstream retailer | Pi ≥ 0 |
| V1A, V1B | Profits of wholesaler before and after the implementing of VMI | - |
| V2A, V2B | Profits of retailer before and after the implementing of VMI | - |
| S1, S2, S3 | Inventory cost per unit of upstream wholesaler, downstream retailer and VMI | Si ≥ 0 |
| D1, D2, D3 | Ordering cost of upstream wholesaler, downstream retailer and VMI | Di ≥ 0 |
| Q1*, Q2*, Q3* | Economic order quantity (EOQ) of upstream wholesaler, downstream retailer and VMI | Qi* ≥ 0 |
| R1, R2, R3 | Revenue change of wholesaler, retailer and overall supply chain | - |
| λ | Demand amplification factor | λ > 1 |
| α | Reduction coefficient of inventory cost | 0≤α≤1 |
| Inventory Management Level | High | Low | |
|---|---|---|---|
| Supply Chain Location | |||
| Upstream | λ∼U (1, 1.05) C0∼U (0.4C, 0.8C) S1∼U (0.01C, 0.02C) α∼U (0.5, 1) D1∼U (500, 750) | λ∼U (1.05, 1.1) C0∼U (0, 0.4C) S1∼U (0.02C, 0.03C) α∼U (0, 0.5) D1∼U (750, 1000) | |
| Downstream | S2∼U (0.03C, 0.04C) D2∼U (500, 750) | S2∼U (0.04C, 0.05C) D2∼U (750, 1000) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, J.; Zheng, S. Analysis of Sub-Optimization Impact on Partner Selection in VMI. Sustainability 2023, 15, 2742. https://doi.org/10.3390/su15032742
Sha J, Zheng S. Analysis of Sub-Optimization Impact on Partner Selection in VMI. Sustainability. 2023; 15(3):2742. https://doi.org/10.3390/su15032742
Chicago/Turabian StyleSha, Jin, and Sisi Zheng. 2023. "Analysis of Sub-Optimization Impact on Partner Selection in VMI" Sustainability 15, no. 3: 2742. https://doi.org/10.3390/su15032742
APA StyleSha, J., & Zheng, S. (2023). Analysis of Sub-Optimization Impact on Partner Selection in VMI. Sustainability, 15(3), 2742. https://doi.org/10.3390/su15032742







