Development and Implementation of Photovoltaic Integrated Multi-Skin Façade (PV-MSF) Design Based on Geometrical Concepts to Improve Building Energy Efficiency Performance

Abstract

This study presents the influence of multi-skin façade (MSF) design with photovoltaic (PV) systems on the thermal behaviors and power generation potential when installed on the entire southern façade of an office building model. This study considers various flexible changes in MSF system design based on geometrical concepts. For the simulation model development, this study uses the medium-sized prototype office building model, developed based on the ASHRAE 90.1-2019. A total of 24 different patterns are created based on a pyramid configuration: triangular pyramid (TP) and rectangular pyramid (RP). Changing the tilt angle for PV integrated surfaces is the main method used to compare the power generation efficiency of different MSF configurations. Results from this analysis indicate that the proposed PV-integrated MSF system with generated patterns tends to reduce cooling and heating demands. The system also presents increased PV power generation performance compared to vertically installed PV systems (i.e., the base case). The designed pattern has the highest performance in the RP configuration, 49.4% and 46.6% higher than the base case when compared based on energy yield and energy yield per unit area parameter, respectively. Increasing the cavity depth and installing the PV-integrated roof surface angle to coincide with the local latitude can achieve efficient power generation for the TP configuration, provided that only one unit is required for a pattern. As for the RP configuration, reducing the cavity depth and combining the number of units (up to nine units) on the pattern surface can achieve the best-performing power generation, while the heating and cooling demands of the perimeter zone are not significantly impacted. The results show the influence of geometrical design aspects of MSF systems on energy efficiency and the potential to generate energy from PV systems. This study is a part of developing an energy-efficient design method for multi-skin façade systems for commercial buildings.

1. Introduction

Sustainable building envelopes have recently received increasing attention due to their benefits in reducing the environmental impact of building development [1]. The building sector contributes over a third of the world’s total energy consumption and greenhouse gas emissions impact [2,3]. Today, many countries worldwide have enacted energy policies to meet Net-Zero Energy Buildings (NZEBs) criteria, responding to such global energy and environmental issues [1]. The design and development of NZEBs with a sustainable envelope has become a challenge for building architects and designers [4]. For example, the European Union initiated the Energy Performance of Buildings Directive (EPBD), according to which entire newly developed buildings will be ‘’nearly zero-energy buildings’’ from 2021 [5]. The US Army issued a policy in January 2014 directing all facilities to adopt net-zero energy policies by reducing energy use and increasing renewable energy production. Gibson [6] compared and concluded with persistent and successful anchoring of a change in Army culture towards net-zero energy strategies. Sustainable construction is recognized as the best solution for the construction industry to minimize the negative impact of work to achieve the goal of sustainable development and balance environmental, social, and economic factors [7,8].

For many years, solar PV systems have been one of the most prominent renewable technologies for building applications [9]. The advantages of PV systems include green technologies with no noise or pollution and adaptability to various applications. Such benefits make PV systems durable and dependable, with greatly reduced maintenance requirements. On the other hand, PV systems also have some disadvantages, such as high initial costs compared to competing power generation technologies, requiring a relatively large array area to generate a significant amount of power, and the availability of solar radiation resources at a given location [10]. PV integration into a building is imperative through building-integrated PV (BIPV) or building-attached/applied PV (BAPV) techniques to achieve high-energy-efficient building performance [11]. BIPV replaces the building envelope with components such as PV modules and directly absorbs solar radiation to generate electrical energy on-site [12], which is suitable for new construction. BAPV does not replace the structural component, but can be installed directly on the shell or be rooftop mounted. It has a shielding effect in summer and contributes to some impacts such as lowering indoor temperature [11], which is suitable for the energetic optimization of existing buildings [13]. Moschetti et al. [14] studied a Norwegian NZEB with PV modules and low-carbon insulation materials. The results showed that using PV modules was the most effective in reducing operational energy, and the embodied energy and emissions from the materials for NZEBs were significant.

There is already a significant amount of research on the potential of applying PV to rooftop areas [15,16,17,18]. However, research on the application of PV to building façades only started a few years ago [19,20,21,22,23]. The façade, as one of the most important and largest components of a building, could have a significant impact on the sustainability performance of the entire building [24]. According to the previous literature, façades can help minimize buildings’ harmful environmental effects [25]. In other studies, façades, floors, and roofs bring large heat losses to the building. The façade causes 60% of the heat losses, while the floor and roof only account for 15% and 25% [26]. Adding and integrating passive strategies into building envelopes is a step towards achieving NZEBs [27]. Changying et al. [28] researched and developed an overall architectural approach to support the design of typical residential high-rise buildings with façade-integrated photovoltaics (FIPV) in Trondheim, Norway. The results showed that roof and façade areas integrated with PV could cover up to 60% of the household energy consumption of an 11-story high-rise building. Adi et al. [29] explored the power generation potential of building-integrated PV in typical residential building types in Rishon Lezion, Israel, by evaluating the shadows cast on façades and roofs. The results showed that some façades (mainly south- and east-facing) could still significantly contribute to the total solar potential of urban buildings. It is predicted that by 2050 more than half of the world’s PV capacity will be installed on building envelopes [30].

Multi-skin façade (MSF) technologies with PV systems integrated into building façades have also been considered to improve the indoor thermal environment and reduce cooling and heating demands because they have a high energy-saving potential for building applications. Engineers and architects have introduced the air layer as an internal structure in façade construction in the last decade to create energy-efficient façades. This strategy is widely used in buildings with glass façades to reduce energy consumption [31]. Several options for incorporating air layers in building envelopes include Trombe walls, solar chimneys, unglazed transpired collectors, double-skin façades (DSFs), three-skin façades, and quadruple-skin façades [32]. Among them, DSFs have been considered one of the most promising responsive building elements as one of the building retrofitting options [33,34,35]. However, the MSF concept is used in this study to evaluate their performance when applied to commercial office building façades. In principle, the structure and operating mechanism of DSF and MSF are closely similar. The MSF model in this study adds a layer of foam insulation in the system’s innermost layer.

In the literature, although many studies have been published on the thermal and electrical performance of DSF systems [36,37,38,39], the evaluation of the MSF with renewable systems is still insufficient. The review of existing studies shows that the DSF and MSF systems in this study are similar, so the previous studies on DSF technologies can also be used for the literature review. A DSF consists of two or more layered structures with outer and inner spaces separated by the air cavity thickness [40]. Moreover, the DSF system also brings aesthetic appearance benefits and sound insulation to the building envelope [41]. In the case of the south-facing façade, the solar-heated air is used for heating purposes in winter but must be removed in summer to prevent the building from overheating [42]. As confirmed by several studies, Pomponi et al. [43] investigated many DSF systems in temperate climates. The cavity size can vary between 0.20 m and 2 m according to building features and circumstances. Such systems can reduce energy consumption by 90% and 30% for heating and cooling, respectively, in buildings. Gratia and De Herde [44] extensively studied the effects of natural ventilation on DSFs. In another study [45], the performance of a DSF south façade was optimized by considering multiple configurations and factors. An open configuration has solved the overheating effect in the air cavity to allow air to escape from the cavity [46]. DSF systems have been studied and adopted as promising passive building technology with renewables. For example, the systems can also be integrated into building-integrated photovoltaic (BIPV) windows, called PV-DSF [47]. These PV windows can replace the outer layer windows, generating renewable energy. Peng et al. [48] developed a type of ventilated façade (BIPV) with a DSF. This PV-DSF model can generate electricity on-site and reduce heat gains and heat losses through the building façades. Kim et al. [49] compared the thermal and daylighting effects of a DSF system with interior and exterior blinds and an office space where no passive technologies were applied. Results showed that the simulated DSF model could save up to 40% on heating, 2% on cooling, and 5% on total consumption, compared to the base case with no blinds or controls. Zomorodian and Tahsildoost [50] applied the optimal DSF system to reduce the building’s energy consumption. According to the results, DSF configurations reduce 14.8% of the energy consumption of the building.

Commercial buildings typically have a large façade-to-roof area ratio in the buildings category, with façades considered, relatively, more attractive than the roof as possible surfaces for energy production [51]. Office buildings have one of the highest energy consumption values compared to other building areas [52]. This study was conducted to evaluate the performance of PV multi-skin façade (PV-MSF) systems integrated into the façade of a medium-sized office building prototype model [53].

Several factors that affect the performance of the PV system include the solar radiation incident on solar panels, ambient temperature, cell temperature, shading effect, tilt angle, direction, etc. [10]. Factors that cannot be controlled include solar radiation, ambient temperature, dirt, etc. Factors that can be controlled include tilt angle and direction, installation techniques, etc. For medium/large PV systems, the tilt angle and orientation angle significantly impact the energy and the specific yield [54]. Some studies on tropical countries have shown that PV arrays facing east receive higher irradiance than those facing the equator [55], and the orientation influence at a low tilt angle is assumed to be negligible [56]. Jafarkazemi and Saadabadi [57] used a simulation method to assess the effect of orientation on the optimal tilt angle of solar panels on power generation. The results showed that the optimal orientation angle is to the south.

Although many studies on PV-DSF or PV-MSF technology have been reported, there are very few studies on changing the tilt angle of PV modules integrated into the skin layer. The differences between the geometric configurations of the system also affect the efficiency and potential of power generation. Hachem et al. [58] studied the impact of the geometric design of equatorially oriented DSF on energy efficiency. A base case was an office model with a modular area of 3 × 3 m², with a south orientation, in the middle of a twelve-story office building. Results showed that the fold position and the cavity depth significantly impact thermal load and power generation potential, with the total annual power generation potential from the multifold configurations exceeding that of the flat façade by up to 80%. Another study [59] examined the impact of equatorially oriented façade design on energy efficiency. The author has studied the geometric configuration equivalent to two units (upper plates and lower plates) of the module system by changing the tilt angle and the orientation angle (70°/15° and 60°/20°) of the surface-integrated PV. The results show that the electricity generated by the PV system is integrated into 50% of the façade surface in the form of folded plates, increasing by up to 56% compared to a south-facing flat.

Existing studies have mainly examined the creation of geometric configurations with PV integrated and applied to a space of a given size (module), enclosed and surrounded by adjacent rooms. There are also studies using such modules for attachment to building façades, but the variety of geometries and differences in angular variation of PV panels are still limited. The simulation of certain size modules in a certain space has the advantage that the output data are extracted accurately and intensively, because the installation data are not large. However, the limitation is that if these modules are attached to a building with a large façade area, the output will be inaccurate compared to the module size because the sample installation data are large. In this case, the strong shading effect when many similar modules are installed on building façades leads to strongly deviating result data compared to a module with a specific sample size.

This study proposes various geometric configurations of the PV-MSF system and arranges them uniformly over the south façade of a medium-sized model office building [53]; the building’s orientation angle is set to south. Changing the tilt angle for PV arrays is the main objective to compare the power generation efficiency of different MSF configurations. The MSF system model of the test facility is used for validation purposes, with the simulation environment set up so that the output parameters match the actual measurement parameters. The validated MSF model is used to assemble the entire south façade of the office building. An additional result is a shading effect on the building energy performance when a row of identical modules is arranged on the building façade. Based on the results, the options between the geometric configurations are compared to find the optimal solution for the power generation potential.

2. The Development of a Simulation Model

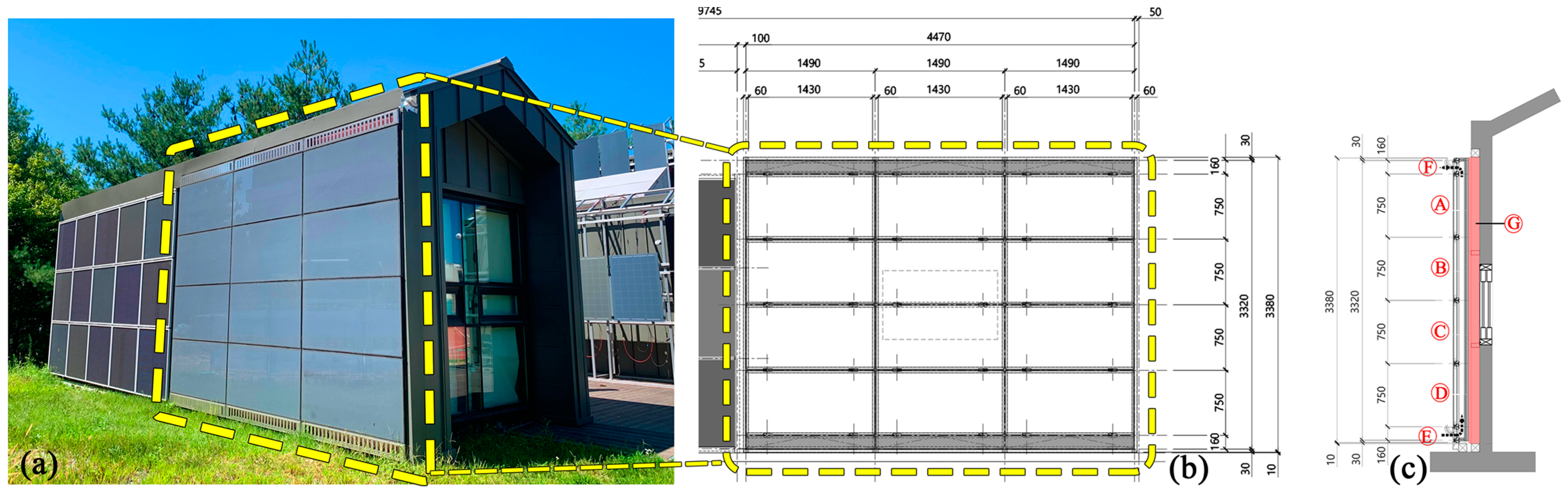
2.1. The Overview of the Full-Scale BIPV Mock-Up

The PV-MSF system used for this study is integrated into an experimental facility shown in Figure 1 at Hanbat National University in Daejeon, South Korea (Latitude: 36.35 °N, Longitude: 127.38 °E). This facility was intentionally constructed to study the thermal behavior of the multi-skin system and to analyze the power generation potential of PV panels integrated on the external surface of the system. The test facility is a lightweight prefabricated construction with a total area of 21 m², a width of 3 m, a depth of 7 m, and a height of 4.47 m. The east side is equipped with glazing over a total area of 7 m². The glazing configuration is shown in

Table 1. Construction and window details of optical thermal values of the experimental facility and the MSF system.

	U-Value (W/m²K)	Visible Transmittance	Solar Heat Gain Coefficient (SHGC)
External wall	0.219	N/A	N/A
Floor	0.227	N/A	N/A
Roof	0.334	N/A	N/A
Double clear window	2.665	0.781	0.703
Insulation (G, Figure 1c)	0.217	N/A	N/A
Aluminum frame	5.881	N/A	N/A
PV module (A, B, C, D, Figure 1c)	2.690	0.260	0.590

. The MSF system is integrated into the south side of the experimental facility. The system consists of prefabricated lightweight constructions with a width of 0.31 m and a height of 3.3 m. Figure 2 shows the longitudinal and cross-sectional drawings of the test facility with the MSF system.

The PV modules are used for positions A, B, C, and D of this experimental MSF system, as shown in Figure 1c. Optical and thermal properties (i.e., U-value, solar heat gain coefficient (SHGC), and visible transmittance) are considered to validate the simulated MSF model. Top and bottom ventilation dampers (positions F and E of Figure 1c) are manually controlled to bring outdoor air through the cavity of the MSF. Table 1 summarizes the main input parameters of the components that construct the test facility and the MSF system. These parameters are used directly in the modeling process described in the following section.

2.2. Field Measurement for Model Validation

The experimental PV-MSF system has a total of 12 PV integration areas, as shown in Figure 2. However, in this study, to simplify the simulation of the MSF computational domain, these 12 spaces are converted into 09 spaces to allow the temperature data collection process to extract data with a high degree of accuracy. Since spaces from the medium-top and medium-bottom are merged into medium spaces, data of nine zones are converted from Z1 to Z9 (Figure 2). Therefore, for the PV back surface temperature measurement, data from the medium-top and medium-bottom surfaces are added to the average value of the two adjacent top and bottom panels, corresponding to Z2, Z8, and Z5.

The temperature data that need to be collected for the validation process are the inside air cavity temperature and PV back surface temperature. The inside air cavity temperature data are measured at 9 nodes with the positions depicted in Figure 3a,b. A thermocouple-with-stone technique keeps these positions at the central position of each zone. Each measuring point is connected to a data logger with the thermocouple. Data are collected every minute and transferred to the GL820 data logger (GRAPHTECCORP Inc.). T-type thermocouples with a measuring range of −100 to 400 °C and an accuracy of 0.1% of the reading +0.5 °C are used [49].

A similar measurement method is used to collect PV backsides temperature data for all PV configurations (Figure 3c), using foil tape to attach thermocouples to the PV back surfaces, as aluminum foil tape has high reflectivity and low emissivity, thereby minimizing excessive exposure to solar radiation.

The monitoring system is installed concurrently with the construction of the MSF system to analyze the integrated PV panels’ performance and power generation potential. Power and voltage are monitored.

Table 2. The PV modules’ specifications and power supply inputs.

Dimensions [mm]	1.07 m² (730 × 470 × 11)
Cells on module	32 (4 × 8)
Maximum Power (Pmax)	177.9 W
Surface	Glass
Module efficiency	16.60%
Module voltage at max power (Vmp)	19.8 V
Open circuit voltage (Voc)	23.2 V
Module current at max power (Imp)	9 A
Short circuit current (Isc)	9.4 A

summarizes the PV modules’ specifications and the input power supply parameters.

The measured parameters and the input data from the test facility are used for further analysis and validation. It is significantly important to measure the data carefully. They are the fundamental basis for the correct development of the simulation model.

2.3. Description of the Simulation Model Development

2.3.1. Airflow Network Algorithm Model

To model the experimental facility with the MSF system, EnergyPlus is used for thermal analysis and empirical validation. EnergyPlus is recommended software for modeling advanced passive systems [60,61]. The airflow network (AFN) model provided by EnergyPlus allows the calculation of air flows between thermal air nodes from outside the system, such as ventilation and infiltration of a building. The building is a network consisting of a collection of nodes representing zones and environments.

Figure 4 describes in detail and visualizes how the nodes used in EnergyPlus are linked to calculate actual air flows in the test facility. The alignment between nodes means there are airflow paths between openings such as vents, windows, doors, and cracks.

The vertical and horizontal airflow rates are also detailed in Figure 4 to easily visualize how the external airflows penetrate further into the inner spaces of the MSF system and the test facility. The ventilation dampers on the top and bottom of the MSF system (vertical openings) are manually closed/opened at specified intervals for data measurement. The horizontal openings are set to be always open to show that the airflows are always moving back and forth inside the MSF system. The input data for vertical and horizontal openings are detailed in

Table 3. List of input values used for the AFN model calculation in EnergyPlus obtained directly from Refs. [61,65].

Parameter		Value
Building Type		Low-Rise Building
Vertical Opening	Air Mass Flow Coefficient When Opening is Closed	0.00006 (kg/s-m)
	Air Mass Flow Exponent When Opening is Closed	0.7 (Dimensionless)
	Discharge Coefficient	0.65 (Dimensionless)
Horizontal Opening	Air Mass Flow Coefficient When Opening is Closed	0.001 (kg/s-m)
	Air Mass Flow Exponent When Opening is Closed	0.5 (Dimensionless)
	Discharge Coefficient	0.65 (Dimensionless)
Effective Leakage Area (ELA)	Air Mass Flow Exponent	0.667 (Dimensionless)
	Discharge Coefficient	1 (Dimensionless)
	Reference Pressure Difference	4 (Pa)
Opening/Crack Factor		0.5 (Dimensionless)
Minimum Venting Open Factor		0.3 (Dimensionless)

.

The procedure for the AFN model in EnergyPlus is described as follows in this part. The AFN model consists of three sequential steps [60,62], including (1) pressure and airflow calculations, (2) node temperature and humidity calculations, and (3) sensible and latent load calculations. A connection used in the AirflowNetwork model has two nodes, inlet and outlet nodes, and is linked by a component that has a relationship between the airflow and pressure. The Bernoulli equation is used to predict the pressure difference, as presented in the equation (Equation (1)) in the AFN model:

$$\Delta P=\left(P_n+\frac{\rho V_n^2}{2}\right)-\left(P_m+\frac{\rho V_m^2}{2}\right)+\rho ɡ\left(z_n-z_m\right)+P_w$$

(1)

where $\rho$(kg/m³) and ɡ (9.81 m/s²) are air density and acceleration due to gravity. $P_n$ and $P_m$ (Pa) are entry and exit static pressure. $z_n$ and $z_m$ (m) are entry and exit elevations. $P_w$ is the wind pressure through outside air.

Bernoulli’s equation also determines wind pressure, assuming no change in altitude or pressure losses [60]. The wind pressure through the outside air can be expressed as

$$P_w=C_p\rho \frac{V_{ref}^2}{2}$$

(2)

where $C_p$ is the wind surface pressure coefficient (dimensionless) and V_ref is the reference wind speed at local height (kg/m³). In this study, the wind pressure coefficient input values were obtained directly from published values used for the geometry of office buildings in EnergyPlus [61]. The wind speed of the reference building is adjusted from the measured meteorological wind speed. The estimation of the reference wind speed and the velocity of the airflow can be determined by Ref. [63].

The Effective Leakage Area (ELA) object is used in the AFN model to estimate and calculate the air mass flow rate due to infiltration through building surfaces. The relationship between pressure and airflow can be defined as [60]:

$${\dot{m}}_{Leak}=ELA\times C_d\sqrt{2\rho }\times {\left(\Delta P_r\right)}^{0.5-n}{\left(\Delta P\right)}^n$$

(3)

where ELA is an effective leakage area (m²), $C_d$ is the discharge coefficient (dimensionless), $\Delta P_r$ is a reference pressure difference, and $\Delta P$ is the pressure difference across each component. Since ELA values are generally applied in the case of geometric buildings and structures, the infiltration calculation is derived from the ASHRAE Handbooks of Fundamentals [64]. Finally, the sums of mass flow rate and latent loads are used in the zone heat balance equation to calculate the heating and cooling loads [60,62].

2.3.2. Simulation Model Setups

After converting all data from DesignBuilder to EnergyPlus, the MSF system is modeled into seventeen different zones. Fifteen zones are stacked vertically and two zones are insulating material (width 0.1 m) (as shown in Figure 5). Vertical and horizontal openings are also described and illustrated in Figure 2 and Figure 3. The experimental MSF system described is a closed system with a single thermal zone. Fifteen stacked zones are considered for MSF modeling and airflow path generation. The airflow network model in EnergyPlus makes it possible to calculate the air pressure and temperature differences between the connection zones.

Three vertical openings at the top and three at the bottom are used as ventilation dampers (positions F and G in Figure 2b) to bring fresh outside air through the inner spaces. The opening/closing plan is carried out and checked manually. There is a window on the exterior wall of the facility (behind zone Z8, Figure 2), but the insulating foam layer has covered it (as mentioned in Figure 2b). Therefore, the MSF system model is considered a closed model to only focus on monitoring data such as PV generation power, PV back surfaces temperature, and inside air cavity temperature.

2.3.3. Weather Data Modification

Daejeon, South Korea’s weather is characterized by four distinct seasons (i.e., hot and humid summer, cold winter, and two transitional periods). Outdoor variables monitored for the validation period were dry-bulb temperature and solar radiation (global horizontal, diffuse horizontal, and direct normal irradiance). These variables are carefully measured at Hanbat National University, South Korea’s testing facility then merged into a single file and packaged into Elements software for use with the EnergyPlus simulation program. According to [66], the Elements software is an open-source, cross-platform software tool used to create and edit custom weather files for building energy modeling. The variables used for the validation process will be adjusted in Elements software using an EPW weather data file, which the National Weather Station collected in Daejeon, South Korea [67].

2.4. Validation Process of the PV-MSF Model

2.4.1. Validation Flowchart

An overall summary of the validation process is illustrated in Figure 6. The software Design Builder version 6.0 [68] is used to develop the initial geometry and inputs of the test facility with the MSF system, while the program engine is EnergyPlus version 8.9. The developed model is translated into surface coordinates in EnergyPlus as an IDF file to deal with the detailed analysis, with more inputs and output available. Therefore, the creation of a model with complete parameters of the structural dimensions, materials used, or thermophysical properties of the base case model is completed.

2.4.2. Model Validation for Thermal Behaviors

Data from the MSF model after simulation are compared with measured data. For the highest level of reliability, the validation process must be performed continuously. This research will provide a validation process with two time periods corresponding to two different MSF conditions. Accordingly, the tests must be set with the specific conditions of the MSF system established for all the ventilation dampers to be always opened (from 5 December to 11 December 2021), and the second condition is set for all the ventilation dampers always closed (from 6 April to 12 April 2022). Figure 7 illustrates two different MSF conditions used for the thermal behavior validation.

The parameters that compare simulated data with measured data include inside air cavity temperature, PV back surfaces temperature and power generation. Each parameter is applied in the two different conditions of the MSF mentioned above. The validation process must quantify the accuracy of the results and compare them to measured data. The MSF system simulation results are manually updated by adding the same values using the same materials, environment, weather, etc., until the simulated data and measured data values meet the level of accuracy that conforms to the criteria defined in ASHRAE Guideline 14 [69]. The recommended statistical indicators to evaluate the simulation model’s accuracy are normalized mean bias error (NMBE) and root means square error (CV-RMSE). According to the ASHRAE guideline 14 and the FEMP Criteria [70], a simulation model with hourly measured data is considered correct if the NMBE is within ±10% and the coefficient of variation of the CV-RMSE is within ±30% between the measured data and the simulated data.

To easily visualize the difference in parameters between zones, the position of the graphs is arranged based on the actual parts of the zones, from zone 1 to zone 9, according to Figure 3a and Figure 7.

2.5. Validated Results

2.5.1. Validated Results under Condition 1

Figure 8, Figure 9 and Figure 10 compare inside air cavity temperatures, PV surface temperatures, and PV power generation, respectively, for measured versus simulated data under Condition 1. Condition 1 indicates that all the ventilation dampers are set to be always opened from 5 December to 11 December 2021. The simulated data of each property represent good agreement against measured data for each position with a higher than 0.9 coefficient of determination values.

Table 4. Statistical indicators use to evaluate the accuracy of the simulated data and measured data of condition 1.

Inside Air Cavity Temperature	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	24	14.2	15.1	20.5	14.4	13.2	16.8	13.6	15
NMBE (%)	−1.4	−4.2	−0.5	7.5	−9.6	1.8	−6.58	2.5	1.6
PV surface temperature	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	16.4	15.1	16	15.2	16.2	17.1	14.8	16.7	16.6
NMBE (%)	−3.5	4.7	5.2	−0.8	9	7.9	9.1	9.9	6.7
PV power generation	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	27.7	26.9	28.2	21.8	26.8	29.3	29.5	27.1	29.3
NMBE (%)	−3.3	−7.8	−7.6	−5.1	−7.6	−7.6	−6.8	−8.9	−8.7

presents that the simulated and measured data values meet the accuracy following the criteria outlined in the ASHRAE Guidelines 14. The NMBE indices are within ±10%, and the CV-RMSE indices are within ±30%. The calculated NMBE and CV-RMSE of condition 1 are within tolerance. Based on such statistical indicators, this study validated the simulation analysis model and used this simulation for further façade design analysis.

2.5.2. Validated Results under Condition 2

Figure 11, Figure 12 and Figure 13 compare inside air cavity temperatures, PV surface temperatures, and PV power generation, respectively, for measured versus simulated data under Condition 2. Condition 2 indicates that all the ventilation dampers are set to be always closed from 6 April to 12 April 2022. The simulated data of each property represent good agreement against measured data for each position with a higher than 0.9 coefficient of determination values.

Table 5. Statistical indicators use to evaluate the accuracy of the simulated data and measured data of condition 2.

Inside Air Cavity Temperature	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	10.1	10.1	8.2	9.9	9.9	8.6	11.4	9.7	8.2
NMBE (%)	2	1.6	1.6	2.4	1.7	2.4	4.5	2.8	2.2
PV surface temperature	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	15.5	14.3	11.2	16.4	14.5	12.6	15.9	14.3	12.3
NMBE (%)	−2.1	−2	1.4	−2.5	−1.3	0.3	−0.5	−0.5	1.6
PV power generation	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	Z9
CV-RMSE (%)	19.2	12.4	19.4	19	17.7	20.7	19	12.9	19.9
NMBE (%)	4.2	6.3	6.1	4.4	6.9	8.3	3.4	5.4	7.1

presents that the simulated and measured data values meet the accuracy following the criteria outlined in the ASHRAE Guidelines 14. The NMBE indices are within ±10% and the CV-RMSE indices are within ±30%. The calculated NMBE and CV-RMSE of condition 1 are within tolerance as well.

3. The Proposal for Geometrical Designs

3.1. Design Concepts

Since this study focuses on changing the tilt angles of the PV-integrated surfaces to estimate the PV power generation potential, and the building’s orientation angle is set to the south, the design is based on the idea that solar panels are more efficient when angled to a vertical plane (compared to a flat façade) [58]. This principle leads to a multi-faceted design strategy, which is achieved by creating many surfaces. This study selected two folding plate geometries that are based on a pyramid, one of the developed geometrical configurations. The first configuration is the triangular pyramid unit (TP) configuration, and the second configuration is the rectangular pyramid unit (RP). The TP and RP configurations’ sizes are taken from the experimental MSF system’s dimensions (as shown in Figure 1). The apex of the TP is defined as the intersection of the two diagonals of the 3 m × 4 m rectangle, dividing the surface into four triangles, with the roof surface and two side surfaces PV integrated, and the bottom surface glass emerges. Similar to the RP configuration but for a different concept, the midpoints of the diagonals are joined to form a rectangle in the center measuring 1.5 m × 2.2 m. The RP configuration has five surfaces: the top surface (roof surface) and two sides surface integrated with PV, the rectangular surface in the middle position, the bottom surface, and the glass surface. Figure 14a describes the dimensions, configuration, and surfaces on which PV and glazing are to be installed.

Solar radiation is a major contributor to the performance of PV systems. In general, high solar irradiance means better PV performance. The optimal performance of a PV module depends on the amount of incoming solar radiation. To obtain the maximum solar radiation, the PV panel must be tilted in a direction perpendicular to the sun’s rays hitting the module. The tilt angle of PV is the angle of the PV panel inclination with its horizontal [10]. The tilt angle of an array can be changed in summer or winter to be optimized, depending on energy demand.

For a region in the northern hemisphere, the annual maximum solar energy from arrays on a fixed surface is obtained by adjusting the surface at a tilt angle value roughly equal to the local latitude value (latitude −15° for summer, and latitude +15° for winter) [58,71]. Variations of the above two configurations are formed based on a change in the angle of the roof surfaces. As mentioned earlier, the experimental MSF system is in Hanbat National University in Daejeon, South Korea (Latitude: 36.35°N), so the tilt angle change is based on the latitude of Daejeon city plus or minus 15° for each case which, in turn, applies to two configurations, TP and RP. Figure 14a,b shows that three different tilt angle options are created: Daejeon latitude (36.35°), Daejeon latitude + 15° (51.35°), and Daejeon latitude −15° (21.35°).

There are three patterns based on three different tilt angles for each configuration. From there, more diverse variations are created by dividing the surface area of the MSF system into equal parts corresponding to one unit, four units, nine units and sixteen units. Therefore, there is one flat pattern, and 24 patterns are based on the two main configurations, TP and RP (Figure 15). All patterns are based on the size of the experimental MSF system (as shown in Figure 1).

Dividing into variations can result in different cavity depths, PV mounting areas, and shadow effects. Through simulation, the most optimal configuration for the power generation potential can be found. In addition, the objective is to diversify the arrangements integrated into the façade of the office building to provide more options and comparisons.

The two main façade parameters that affect energy efficiency are the fold’s position and the cavity’s maximum depth [58]. The position of the fold determines the side’s glazing size, and the maximum cavity depth is measured from the inner insulating surface to the top of the corrugation. A single clear glass surface (3 mm), with a transmittance rate of about 89%, an SHGC value of 0.86, and a U-value of 5.89 (W/m²-K), is applied to take into account the cooling and heating energy needs. Three vertical openings at the top and three at the bottom are used as ventilation dampers (positions F and E in Figure 1c), with the condition that all ventilation dampers are opened. There is also an insulation layer on the back of the configurations, with the input parameters described in Table 1.

3.2. The Selection of Base Case Building

Prototype building energy models are of great importance as they are a starting point for analyzing numerous applications; for example, building energy saving potential investigation, building design, building energy market evaluation, and building energy strategy [72]. Prototype building models are intended to depict the building stock, so the simulation results represent the actual energy consumption [53,73]. These models have been widely adopted to facilitate the simulation and validation of measurements for development, and compliance calculations of building energy performance codes and standards such as ASHRAE Standard 90.1 [53]. Figure 16 depicts the main spaces and dimensions of the medium-size office building model from a 3D perspective combined with a floor plan drawing.

This study uses prototype building energy models to model a base case medium office building serving the integration of the MSF system on the southern façade. It then uses the EnergyPlus tool to conduct simulations and extract data on PV panels’ energy efficiency and performance. To accommodate MSF systems mounted south of the building, the three-floor window-to-wall ratio (WWR) will be modified from the original prototype building energy model. The remaining input parameters of the office (internal heat gain, HVAC system, material properties, etc.) remain the same and are presented in

Table 6. Representative input parameter of the medium-sized office model base case [74,75].

Parameter		Characteristic
Weather/Location		Daejeon, South Korea
Total conditioned floor area		4982 m²
Floor-to-ceiling height		2.74 m (1.22 m above-ceiling plenum)
Window-to-wall ratio (South façade)		27% (1st floor), 32% (2nd and 3rd floor)
Window-to-wall ratio (North, East, and West façade)		33%
PV area (MSF)		67.5 m² (1st floor), 82.5 m² (2nd floor), 82.5 m² (3rd floor)
Glazing area (MSF)		52.3 m² (1st floor), 64 m² (2nd floor), 64 m² (3rd floor)
Glazing (MSF)	U-factor	5.89 W/m²-K
	SHGC	0.86
Window	U-factor	0.36 W/m²-K
	SHGC	0.36
Exterior wall construction	Type	Steel-frame walls
	U-factor	0.36 W/m²-K
Roof construction	Type	Built-up roof: roof membrane, insulation, and metal decking
	U-factor	0.18 W/m²-K
Floor construction	Type	Slab-on-grade floors
	U-factor	0.23 W/m²-K
Occupancy density		18.57 m²/person
HVAC type		Rooftop unit (RTU) with variable air volume (VAV) fan and reheat box
Lighting power density (LPD)		6.89 W/m²
Equipment power density (EPD)		8.1 W/m²
Zone thermostat set-point		Cooling: 24 °C/Heating: 21 °C
Zone thermostat set-back		Cooling: 26.7 °C/Heating:15.6 °C

.

The MSF system (flat pattern) is integrated into the façade with a configuration created based on the dimensions of the facility MSF system (Figure 1). However, to match the existing model of the medium-sized office building, the flat pattern is divided into five stacked zones, as shown in Figure 17a, to avoid obstructing the view from the interior spaces. Accordingly, Zone 1 and Zone 2 are ventilation dampers, Zone 3 has single glazing on the outer skin, and Zone 4 and Zone 5 have PV-integrated external surfaces. The insulation layer on the back of all the MSF configurations is installed over the entire surface, except for the building window area.

Figure 17b illustrates the base case modeling and converting model data process from DesignBuilder to EnergyPlus, by modifying the WWR and window size on each floor, combined with the integration of flat pattern systems into the south façade. There is a total of 31 identical modules installed horizontally. Table 6 details the input parameters of the medium-sized office building and the integrated MSF system on the south façade of the building.

Using 24 patterns (as shown in Figure 15) to install on the south façade of the prototype medium office building energy models, Figure 18 shows images of 24 completed patterns, using DesignBuilder software for the modeling process. After the model development with DesignBuilder, all patterns are converted to EnergyPlus as an IDF file, fully adding input and output data and performing simulations.

All options have a total of 31 identical modules installed horizontally on the three-story south-facing surface of the office building. Figure 19a shows that the cavity depth parameter and the PV and glazing area are calculated based on 31 installed modules.

The PV installation area on the roof surface of the TP and RP patterns is the same in each configuration. However, the difference is displayed in the glazing area on each unit pattern (one-, four-, nine- and sixteen-unit patterns), resulting in the two PV integrated side areas of each pattern being different, and this parameter also affects the power generation potential difference between configurations. Patterns of TP configuration have a larger PV installation area on the roof surface compared to RP configuration because the folds of the TP configuration are higher and farther away, resulting in greater cavity depth. Additionally, it can also be seen that the glazing area of the RP configuration is larger due to its original structure, as can be seen in Figure 14c.

The cavity depth tends to decrease steadily in each pattern as the number of units increases and decreases steadily in each unit as the tilt angle on the PV-installed roof surface increases. The pattern with the largest cavity depth is 1TP_21.35, with 1.6 m, much larger than pattern 16RP_51.35, with 0.11 m. Creating different cavity depths results in shadow effects from the top rows above or a non-optimal tilt angle, resulting in differences in the annual power generation.

3.3. Comparative Analysis of Proposed Design Conditions

Comparative studies with different cases are carried out to investigate the energy-saving potential of the MSF system. Comparative studies include the following cases:

Case 1: Base case versus triangular pyramid patterns

Case 2: Base case versus rectangular pyramid patterns

Case 3: Triangular pyramid with rectangular pyramid patterns

Comparison of the base case versus one-unit patterns, four-unit patterns, nine-unit patterns, and sixteen-unit patterns.

This study examines the influence of the façade’s geometric design on the energy efficiency of a medium-sized office building, to identify which geometries can increase the façade’s power generation potential without significantly affecting heating and cooling loads. The reference office is assumed to be located in the northern perimeter area, combined with the optimal façade orientation for the location (in the northern hemisphere). The MSF patterns’ size and material input parameters are constant in all iterations. The model takes into account the mutual shading effect of adjacent modules.

4. Results and Discussion

This section contains an analysis of the simulation results of all the patterns within the base case. Results include the impact of the designs on the annual PV power generated across the modules and the PV generation potential per unit area of each configuration. In addition, the parameters of the annual cooling and heating energy are also analyzed. Heating energy output includes the sum of electricity and natural gas, while cooling energy output contains only the electricity value. With all the MSF cases described above, the top and bottom ventilation dampers are set up with the function of always opening for ventilation, helping to reduce the heating and cooling load of the perimeter zones. The results first discuss the parameters’ impact and then highlight the overall energy performance across all cases. The following are the main results.

4.1. Base Case Versus Triangular Pyramid Patterns

With the triangular pyramid patterns, the area of the PV modules is gradually reduced according to the configuration, with roof surface inclination angles of 21.35°, 36.35°, and 51.35°. The larger the tilt angle, the smaller the glazing area (Figure 19b).

The results show that the heating and cooling energy are significantly reduced in all TP configurations compared to the base case. The top and bottom ventilation dampers of all patterns are set up with the function of always opening for ventilation, and then the heating and cooling demands are almost the same value as the TP configurations. The remaining façades are not in direct contact with adjacent structures, so then the end use efficiency in the office buildings is not optimally achieved when installed with MSF patterns.

In terms of annual power generation output, when the area is divided into multiple units the power production is based on the number of units in a pattern, and all three tilt angle options show a slight downtrend. The pattern with the highest generation value is the 1TP pattern (one unit), decreasing from 4TP, 9TP, and 16TP, respectively. This is explained by the fact that although all TP configurations have the same roof slope when split into multiple units in a pattern, the cavity depth is significantly reduced, creating many small areas for PV integration, increasing the potential for a shading effect from the rows above. Since there is the same PV installation area in all patterns (Figure 20b), the result of the energy yield rate per unit area is similar to the total annual electricity production.

Figure 20a shows the base case option’s lowest PV power generation potential. Since the PV installation is 90° vertical (flat façade) when the PV slope of the roof surface is changed, the 1TP pattern gives a relative efficiency of power production of 18%, 20% and 17% for the patterns 1TP_21.35, 1TP_36.35 and 1TP_51.35 compared to the base case. The lowest power generation efficiency pattern is the sixteen-unit pattern, but compared to the base case it is still 13%, 16% and 15% higher for 16TP_21.35, 16TP_36.35 and 16TP_51.35, respectively. Of all the patterns in the TP configuration, the design with the roof slope angle of 36.35 dominates the rest, and the pattern 1TP_36.35 has the highest performance. This demonstrates the effectiveness of installing PV module tilt angles according to local latitudes (for the Northern Hemisphere), as described earlier.

Figure 20b shows that when comparing TP configurations to the base case, the base case has a much higher power generation rate per unit area, even though the base case has the smallest PV installation area. It explains that, although the base case is installed at 90° (flat pattern), the row spacing of the PV modules in the base case is widely spaced (Figure 17b) and the cavity depth is minimal. This tendency should not be adversely affected by the shadow of the upper rows. Therefore, the base case’s power production per unit area has the largest output compared to the TP patterns, larger than the 1TP_51.35, 1TP_36.35, and 1TP_21.35 patterns with 16.5%, 17.5%, and 20.6%, respectively.

4.2. Base Case Versus Rectangular Pyramid Patterns

Similar to the TP configuration, the RP configuration creates multiple folding surfaces and increases the shading effect of adjacent units and rows above, performing the same function as a window awning, creating a positive shading effect when installing MSF systems. In this case, the base case configuration has a PV module area close to that of the RP configurations, but the PV power generation potential and the energy yield rate per unit area are the lowest. The power generation potential tends to increase with the PV-integrated roof slopes of 21.35°, 36.35° and 51.35°.

Slightly different from TP patterns, the RP patterns themselves do not have a peak point (Figure 14a), so the patterns with the PV roof surface angle according to the local latitude do not have much influence on the electrical power production potential. Two factors that directly affect the power generation potential, in this case, are an increase in the slope of the roof surface angle and a decrease in the cavity depth. According to Figure 19a, the patterns of the RP_51.35 configuration have the smallest cavity depth and the largest roof slope. The units (divided on the surface of the designs) are not greatly affected by the effect of shadows from adjacent units. As shown in Figure 21, the nine-unit patterns lead in power generation potential and energy yield rate per unit area in each design with the identical tilt angle. The highest-ranked design is 9RP_51.35, which follows the second 9RP_36.35 and 9RP_21.35 with less than 2.2% and 6.1%, respectively. The difference is not significant, but the nine-unit patterns show that this is the optimal solution for the MSF installation since it has a PV area that is neither too small nor too large, so it can collect energy from the absorbing sun potential, and the ability to remain unaffected by shade is most valued. Moreover, compared to other patterns with energy yield parameters, pattern 9RP_51.35 is almost 20% higher than pattern 16RP_21.35 and almost double (49.4%) compared to the base case.

Regarding the power generation potential per unit area on the patterns of the RP configuration compared to the base case, as a result, all the designs have a higher potential than the base case. In particular, the pattern 9RP_51.35 has the highest value, 15% higher than the pattern with the lowest value 16RP_21.35 and 46.6% higher than the base case.

4.3. Detailed Comparison of Base Case Versus Triangular Pyramid and Rectangular Pyramid Patterns

Considering the PV power generation potential of the patterns of the two configurations with the base case shown in Figure 22a, the RP patterns dominate in terms of the total annual revenue ratio, indicating that the RP configuration has a major advantage in installing MSF systems in office buildings. In addition, as shown in Figure 22b, it can again be seen that, despite the smaller PV installation area, the power generation efficiency per unit area of the RP patterns is significantly higher than that of the TP patterns. They also turn out great economic benefits, and the capability to maintain and troubleshoot the power generation of the RP patterns is more appreciated.

Comparing the highest PV power generation pattern of the TP configuration (1TP_36.35) and the lowest generation capacity of the RP configuration (16RP_21.35), the design of the RP configuration is still 18.1% higher. Additionally, when compared with the most increased PV generation of the RP configuration (9RP_51.35), the difference is up to 38.1%. This is an extremely large number and worth considering as designers and investors considering installing MSF systems in office building façades.

In terms of impact on heating and cooling loads, as seen in Figure 22a, the difference between end uses of the TP and RP patterns is not significant, which was shown above for the reason that the installation of MSF systems is only on the building’s south-facing surface; MSF systems or adjacent buildings do not dominate the remaining directions, so the difference between heating and cooling energy is not large and almost the equivalent. The second reason is that all ventilation dampers are opened, resulting in stable air circulation, so heating and cooling demands are always balanced and the same across all TP and RP patterns. Additionally, when compared to the base case, the integration of the MSF patterns TP and RP on the south façade brings a desirable effect when it comes to reducing the heating and cooling demands.

Regarding the power production per unit area, as shown in Figure 22b, the base case ratio is higher than all TP patterns and lower than all RP patterns. This has been illustrated in Section 4.1 and Section 4.2 and helps demonstrate the outstanding power generation efficiency of the RP configuration. By combining Figure 19 and Figure 22, creating only one unit in one pattern for the TP configuration is most appropriate. The power generation efficiency is 1TP_36.35, 1TP_51.35, and 1TP_21.35, respectively, for a cavity depth of 1.41 m, 1.14 m, and 1.6 m. For the RP configuration, generating nine units in one pattern is the most favorable power generation potential. The efficiency of 9RP_51.35, 9RP_36.35 and 9RP_21.35 correspond to the cavity depths of 0.15 m, 0.2 m and 0.23 m, respectively.

Figure 22c depicts the percentage of electricity, an important parameter in determining the high or low power generation efficiency of solar panels integrated into the façade of a building. The base case parameter is the lowest, with 0.27%, and the patterns of both TP and RP configurations are higher than that of the base case. The output shows an increase in the number of units in each pattern. Sixteen-unit patterns account for the highest percentage of all patterns. Therein, the 9TP_36.35 pattern leads in the TP configuration, with a current percentage share of 9.91%, showing the importance of placing roof-PV panels tilted according to local latitude, but the difference with the other two tilt angles is not too high. In the RP configuration, 16RP_51.35 leads with 18.94% and the difference between the other two tilt angles is also relatively small. It can be seen that the percent electricity of the patterns of the RP profile is overwhelming compared to that of the TP profile. Parameters appear to be approximately twice as high when compared with each corresponding pattern of each configuration, which again confirms the great power generation potential of the RP configuration. However, the difference between the base case and the one-unit patterns of both structures is not too large.

4.3.1. Base Case Versus One-Unit Patterns and Four-Unit Patterns

Increasing the roof slope inclination for one-unit patterns reduces the PV installation area but increases annual power generation efficiency. In terms of annual power generation efficiency, the most efficient pattern is the one with a roof angle that equals local latitude, in both TP and RP configurations (pattern 1TP_36.35 and pattern 1RP_36.35). It offers high sunlight absorption capacity efficiency and generates electricity since the reach of the peak fold is wide enough (with cavity depths of 1.41 m and 0.6 m for pattern 1TP_36.35 and pattern 1RP_36.35, respectively) when the roof angle corresponds with the local latitude.

The difference in annual power generation efficiency and energy yield rate per unit area of the patterns in the design is relatively low. According to Figure 23, the RP configuration dominates the TP configuration and also the base case. Although the TP configuration has a larger PV installation area and a higher annual power generation efficiency than the base case, the energy yield rate per unit area efficiency is lower (the base case is 10% larger than the pattern with the highest output of TP configuration, which is 1TP_51.35).

For the four-unit designs, the results tend to be similar to the one-unit designs (Figure 23). The only difference is that installing patterns of the RP configuration with roof pitches that coincide with the local latitude no longer carries the efficiency of a one-unit design. With a cavity depth of pattern 4RP_51.35 of 0.23m, this pattern has an annual power generation efficiency 1.6% higher than the 4RP_36.35 pattern and a 4.1% higher energy yield per unit area. As in Figure 24a,b, the performance of pattern 4RP_51.35 is the highest of any pattern in either configuration.

4.3.2. Base Case Versus Nine-Unit Patterns and Sixteen-Unit Patterns

In both nine-unit patterns (Figure 25) and sixteen-unit patterns (Figure 26), the results show an upward trend similar to the four-unit patterns in both TP and RP configurations. In the TP configuration, the pattern with the highest annual power generation efficiency is still the pattern where the roof pitch coincides with the local latitude of 36.35°, and the patterns in the TP configuration have an incredibly small difference in energy yield rate. The pattern with the highest percentage is the pattern with the highest number of units (nine units and sixteen units). In the RP configuration, there is always an increase in both energy yield and energy yield rate per unit area as the roof slope tilt angle increases and the cavity depth decreases. It is expected that, in the RP configuration, although the area of the PV modules can be reduced, the annual power generation efficiency can be increased, and the energy savings from the annual heating and cooling energy can be maintained.

For sixteen-unit patterns in the TP configuration, the results have been analyzed in the content above. Although the RP configuration has the largest number of units on the configuration surface, the generation potential is lower than that of the nine-unit patterns. It can be seen that the power generation potential tends to increase as the number of units on the surface increases. Splitting many units leads to the risk of shadowing each unit’s surface. Therefore, by analyzing the simulation results according to each type of unit pattern of the RP configuration, a maximum of nine units is considered the most optimal option to achieve power generation benefits.

5. Conclusions

A comparative study of heating and cooling energy consumption, power generation potential, and energy yield rate per unit area were quantitatively conducted to examine the impact of different multi-skin façade design integrated photovoltaic (PV-MSF) surfaces installed on the south face of a medium-sized office building, based on the ASHRAE Standard 90.1-2019. The PV-MSF system model was based on the basic geometric configurations developed as pyramids: triangular pyramid (TP) and rectangular pyramid (RP). Twenty-four different patterns were created based on these two configurations, dividing the surfaces into equal units with numbers ranging from one, four, nine and sixteen units. Combined with changing the inclination angle of the PV integrated roof surface based on the local latitude of 36.35 (Daejeon City, South Korea), the remaining two tilt angles were 51.35° and 21.35° (corresponding to the local latitude degrees ±15°).

All the above 24 patterns were compared with the base case, where the PV external surface was installed at an angle of 90° which resulted in the optimal PV installation angle plan for the roof surface of the configurations. Cavity depth had also been studied and compared, and the option had optimal power generation efficiency which could save on heating and cooling demands. Before performing simulations for the analytical investigation, the MSF system was validated with measurement data from an experimental facility. Additionally, the airflow network (AFN) model in EnergyPlus was used to study thermal analysis and power generation performance. The key findings of this study are as follows:

• The heating and cooling energy were significantly reduced in all TP and RP configurations compared to the base case. The heating and cooling demands difference between the TP and RP patterns was insignificant. The designs of the above two arrangements acted as window awnings, providing positive effects in the form of effective shading and reducing the building’s energy end uses.
• Creating only one unit in one pattern for the TP configuration was most efficient. The highest electricity generation potential pattern was the 1TP_36.35 pattern, with the inclination of the roof-integrated PV corresponding with the local latitude (the local degree 36.35°) since the reach of the peak point was wide enough with the cavity depth of 1.41 m.
• For the RP configuration, the roof PV-integrated surface angle according to the local latitude did not significantly impact the power generation potential. The power generation potential of RP patterns tended to increase with a roof slope of 21.35°, 36.35° and 51.35°. Generating nine units in one design was the most efficient power generation potential.
• The base case had a much smaller PV module area than the TP patterns, so the energy yield was also lower. However, in terms of energy yield rate per unit area, the base case was slightly more dominant, 17.5% higher than the 1TP_36.35 pattern—which was the highest performance pattern in the TP patterns. The base case had a PV module area close to that of the RP patterns, but the PV power generation potential and energy yield per unit area were the lowest. Specifically, the plan with the highest energy yield value of RP patterns was 9RP_51.35, which was 49.4% higher than the base case and 46.6% higher in comparison based on the energy yield rate per unit area.
• Considering the power generation potential and energy yield rate per unit area of the entire patterns of the two TP and RP configurations with the base case, the RP patterns accounted for the highest and most optimal proportion, with the conclusion that RP patterns had a great potential to achieve high efficiency in the design and installation of the MSF systems. RP patterns also improved practical efficiency for smaller PV installation areas, and maintainability was highly appreciated in the event of power generation problems.
• This result could help to find specific solutions to increase the number of units (up to nine units) on a surface of a pattern (RP configuration) to decrease the cavity depth and maintain the best-performing PV installation area while keeping the heating and cooling loads of the perimeter zone not significantly affected. As for the TP configuration, it was necessary to increase the cavity depth and install the PV with a roof slope according to the local latitude for power generation efficiency and overall energy efficiency.

The research presented in this study fills the gap in the existing studies regarding applying the PV-MSF system to a large area of a medium-sized office building. We provide an objective assessment result with a large sample file that can be applied to solve energy-saving problems and highlight the role of geometric patterns designed with different built-in complexities used on the building façade, compared to the conventional flat façade module.

The workflow used in this study helps architects, engineers, and investors build and package options earlier to create an energy-saving office building model. In the future, the results can also guide the design of various geometric configurations to further develop kinetic façade systems with renewables.