Influence of a Soft Story on the Seismic Response of Non-Structural Components
Abstract
1. Introduction
2. Modelling and Analysis of Buildings
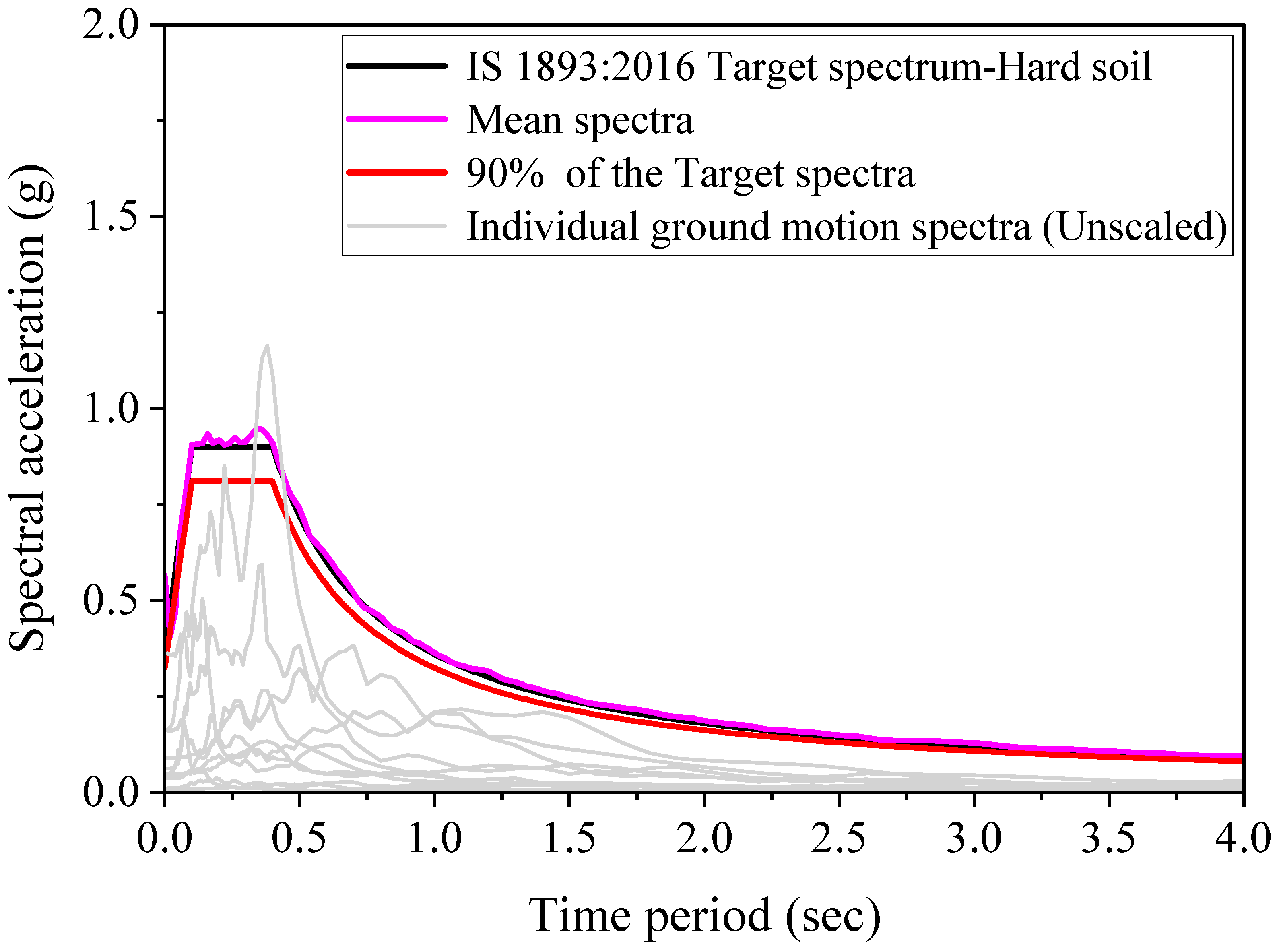
3. Selection and Scaling of Ground Motions
4. Results and Discussion
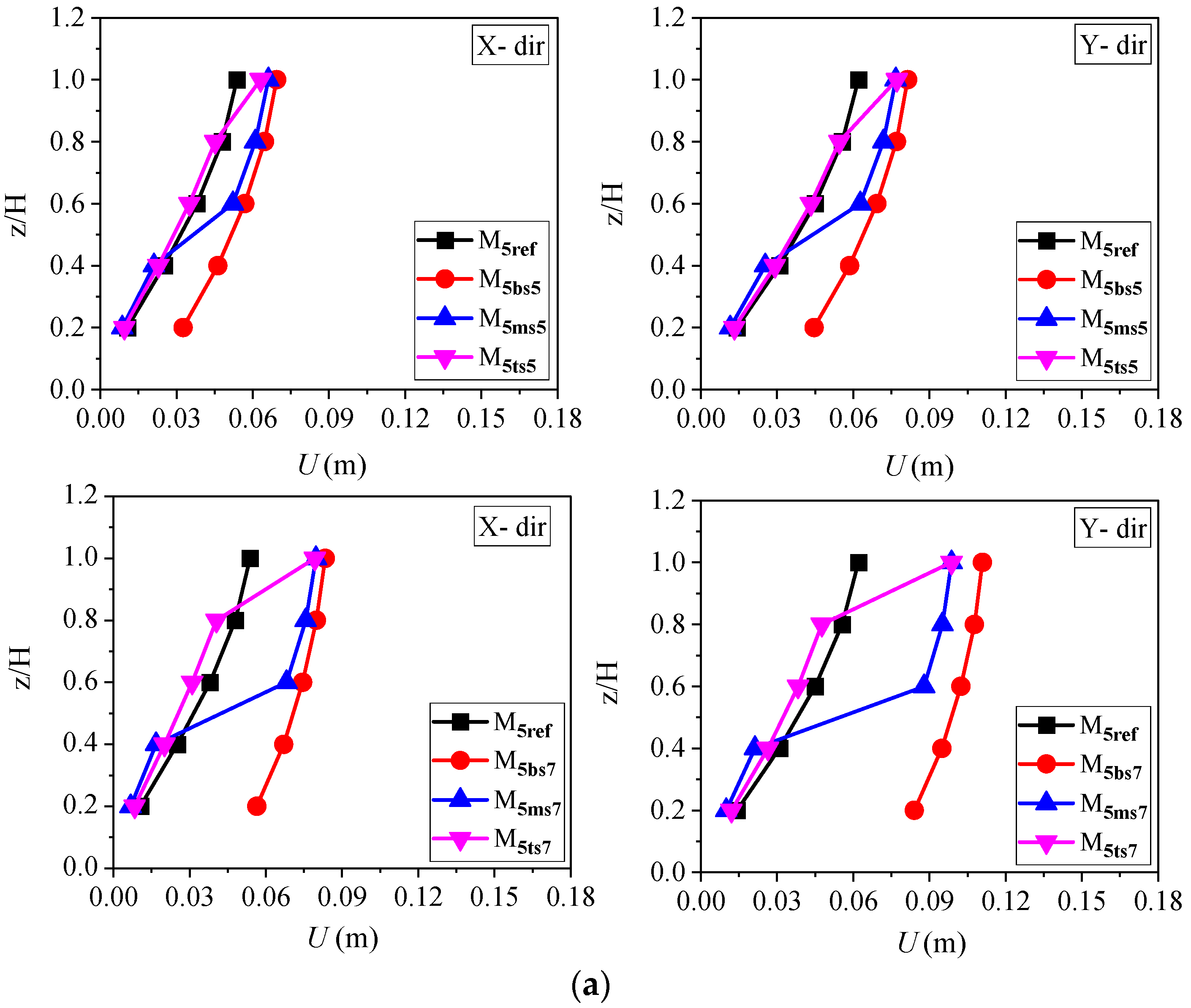
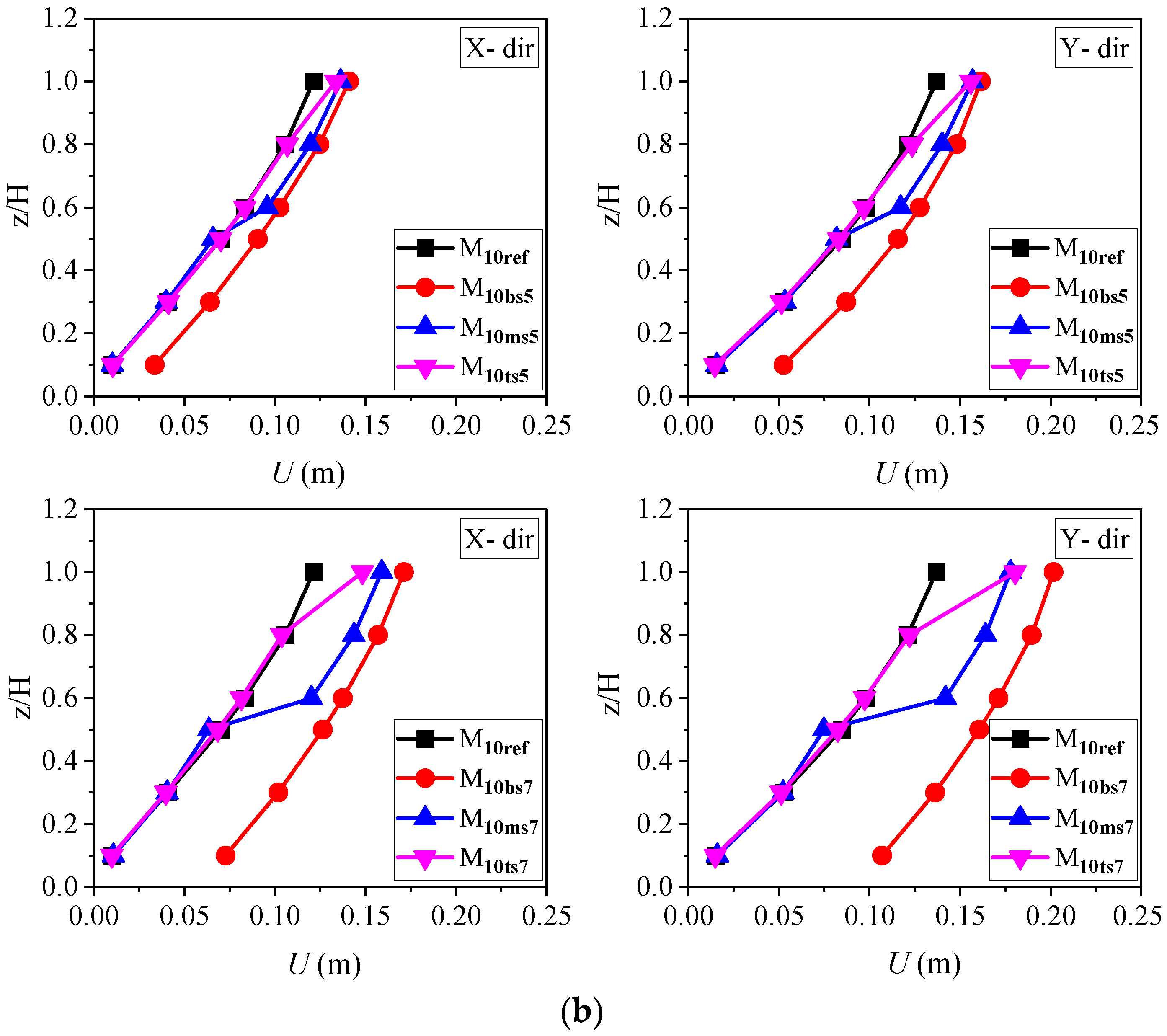
4.1. Peak Story Displacement
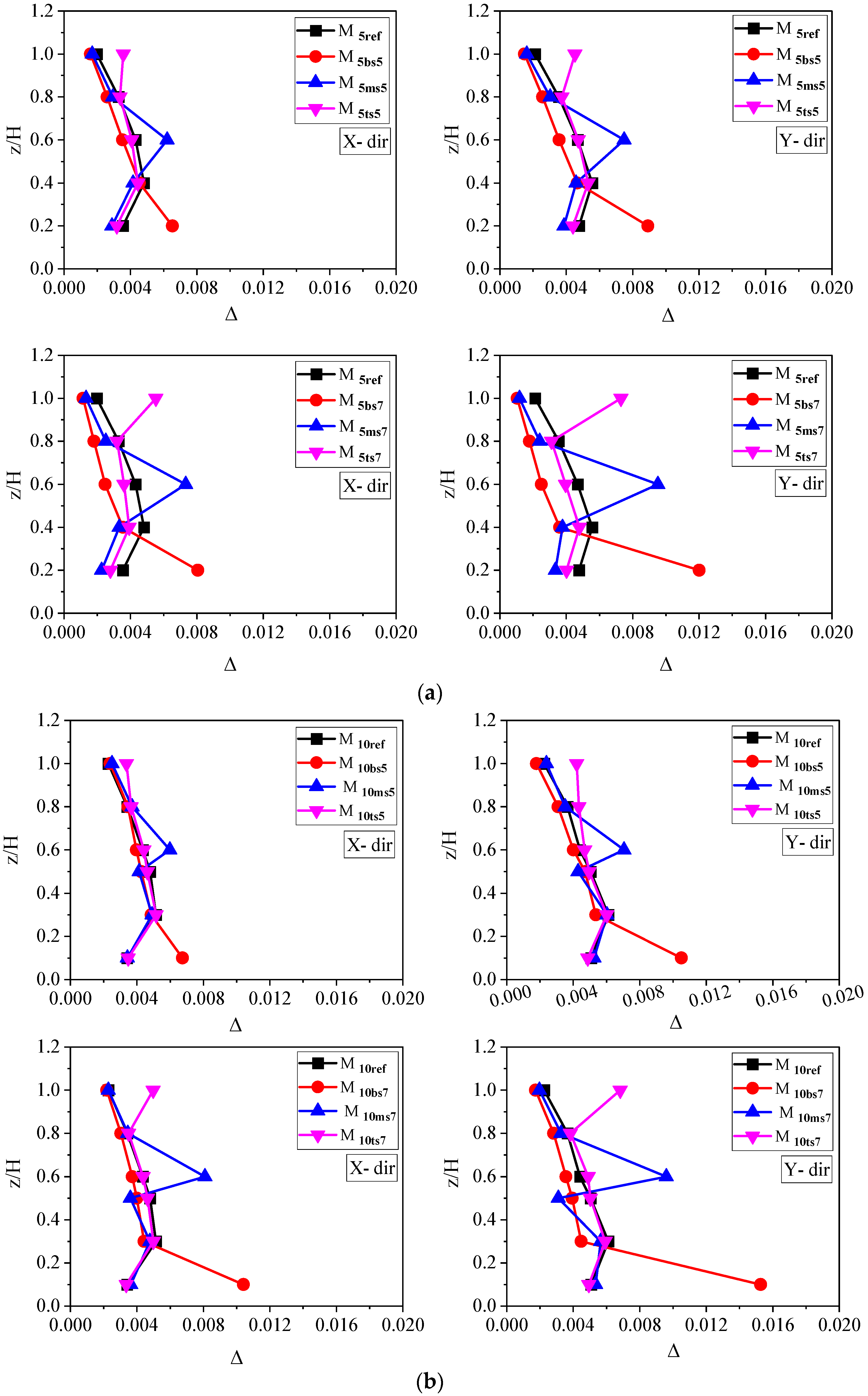
4.2. Inter-Story Drift Ratio (IDR)
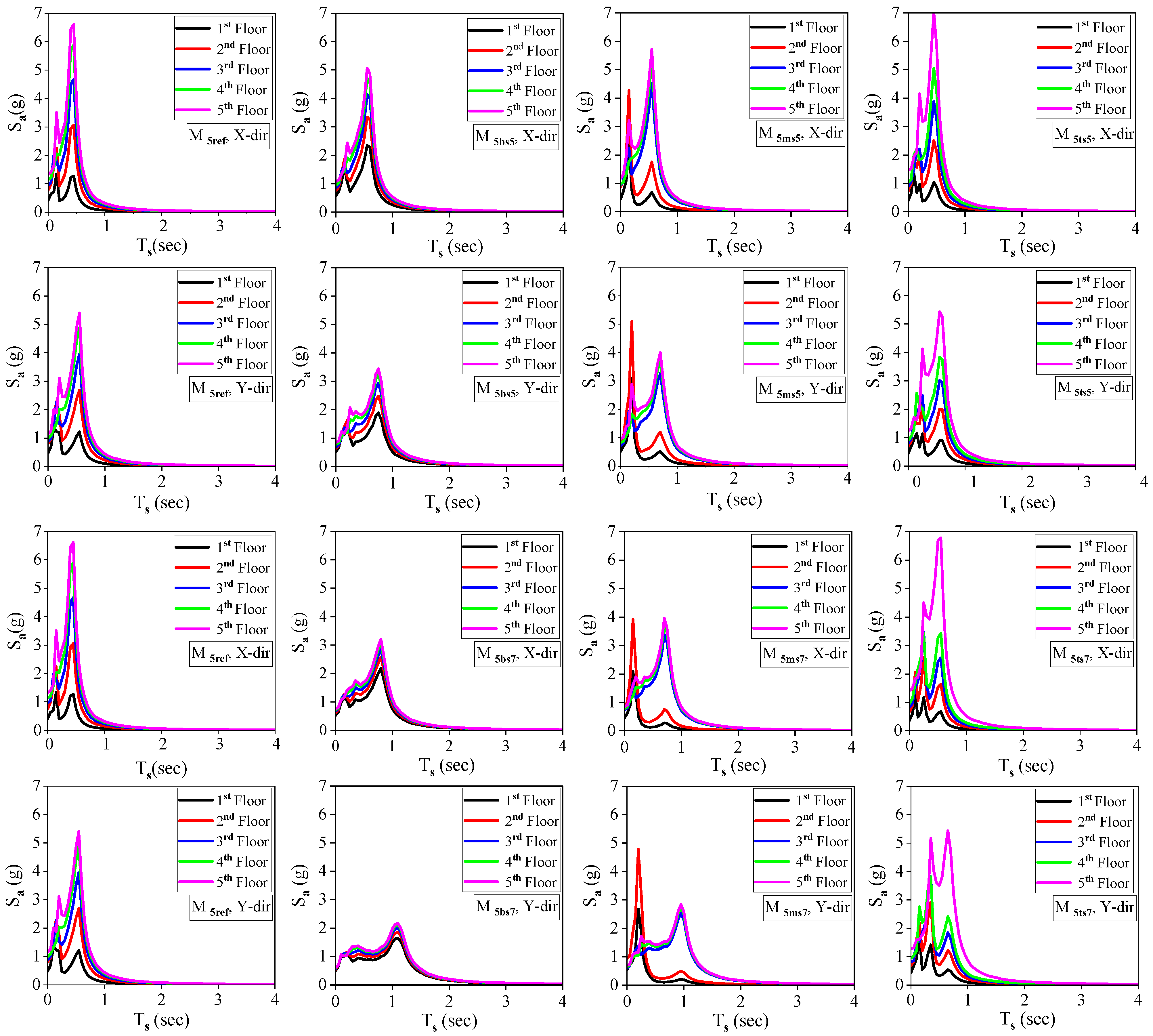
4.3. Floor Response Spectra (FRS)
4.4. Evaluation of Floor Amplification
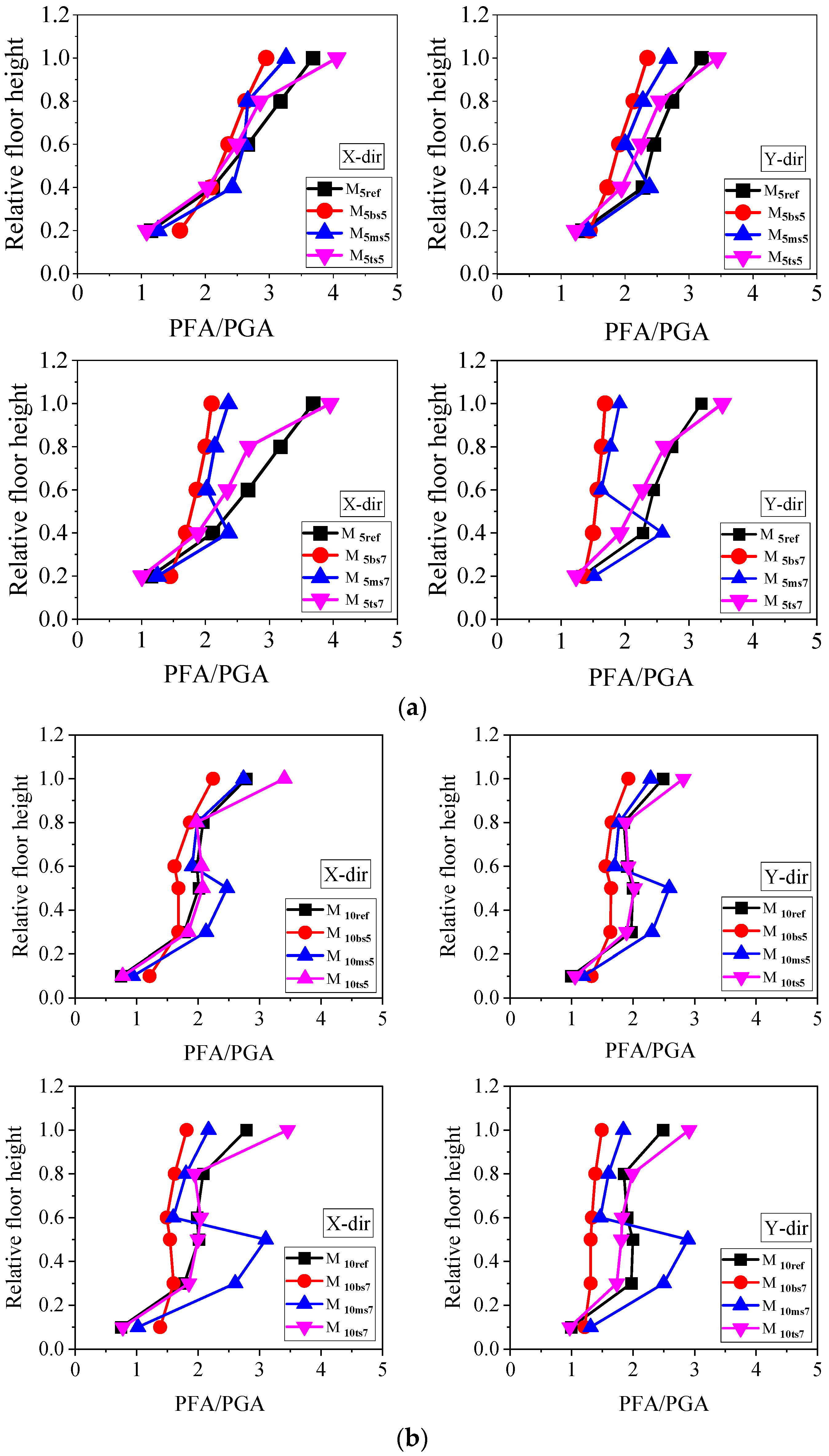
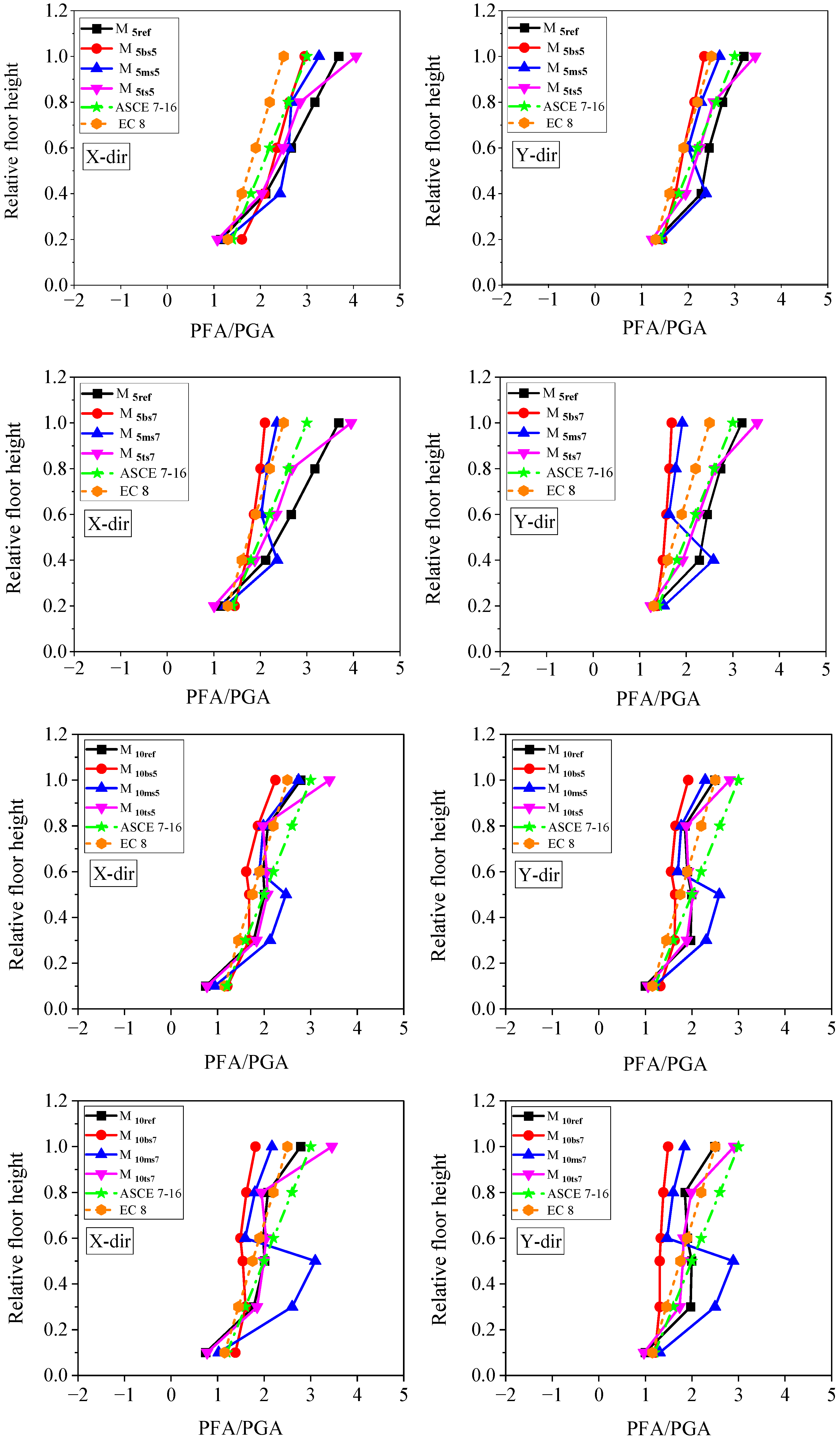
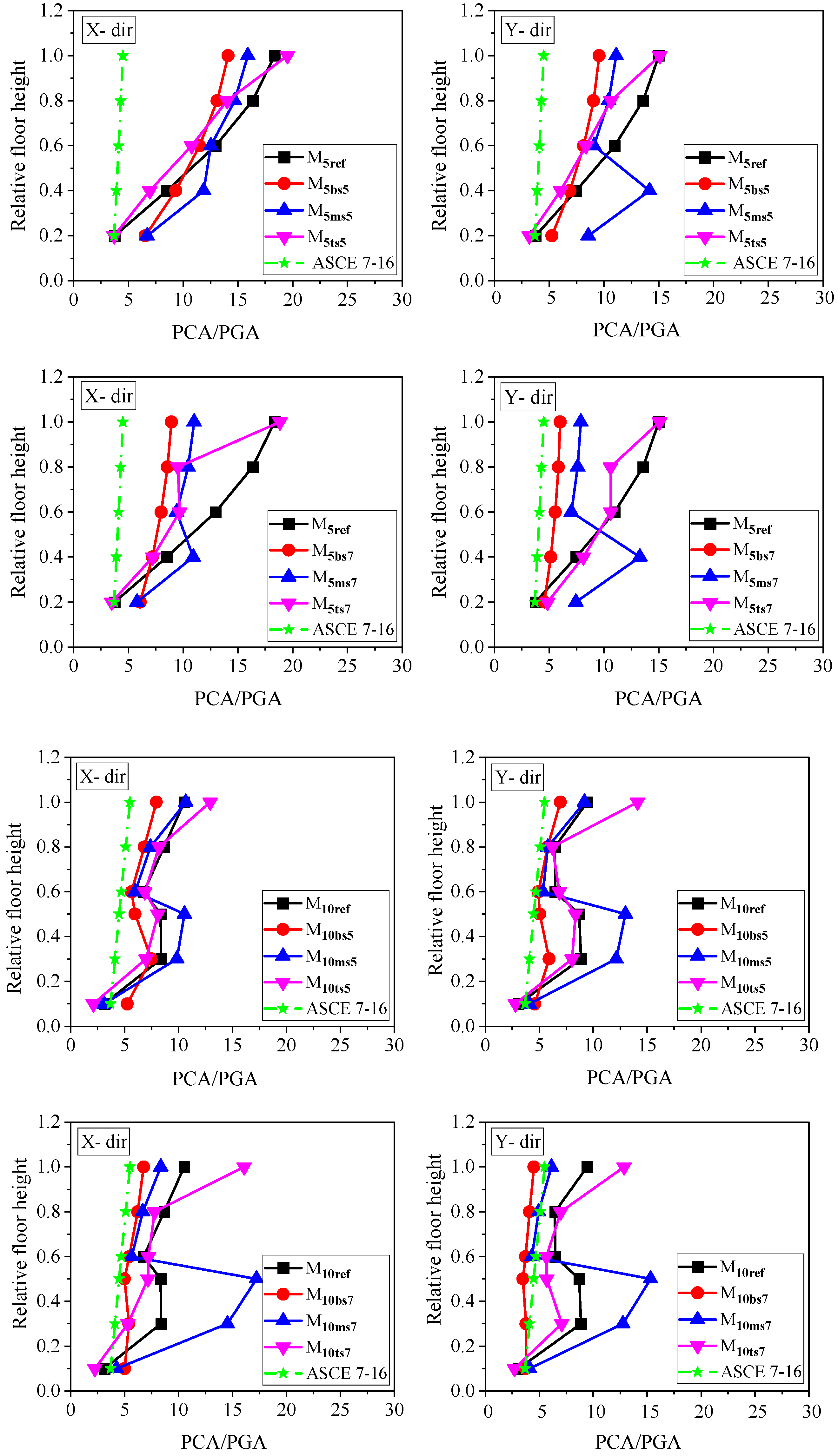
4.5. Peak Component Acceleration
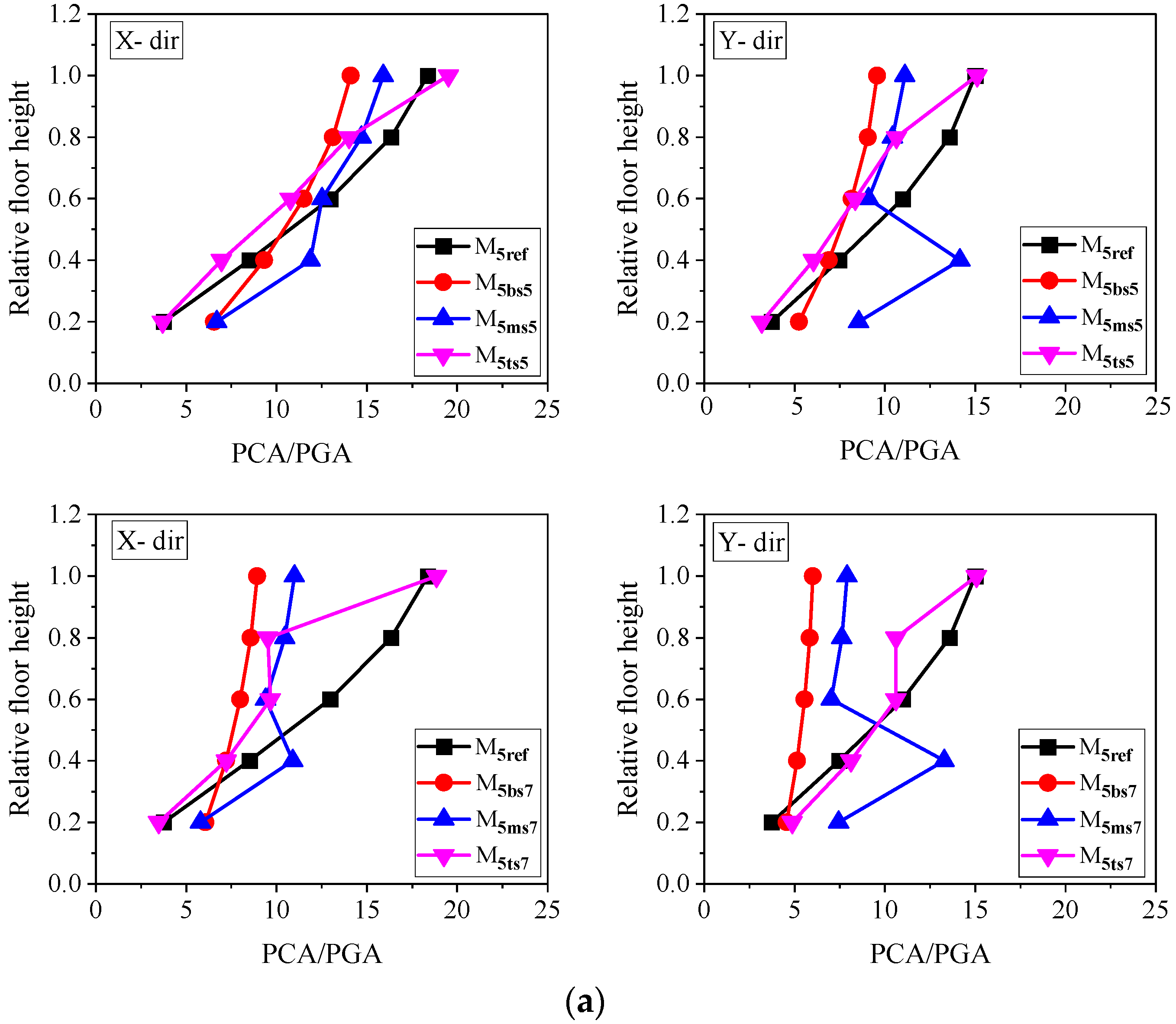
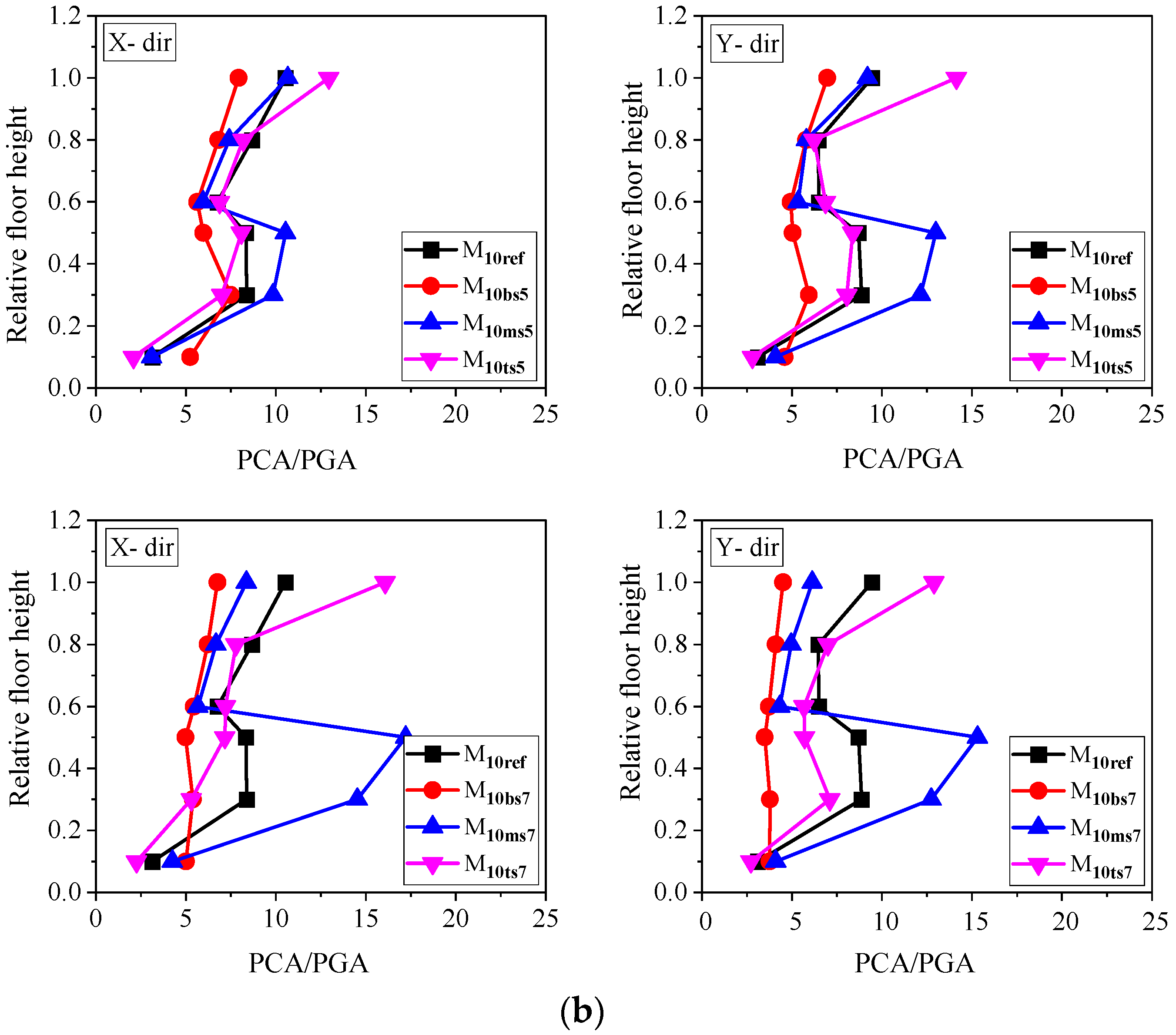
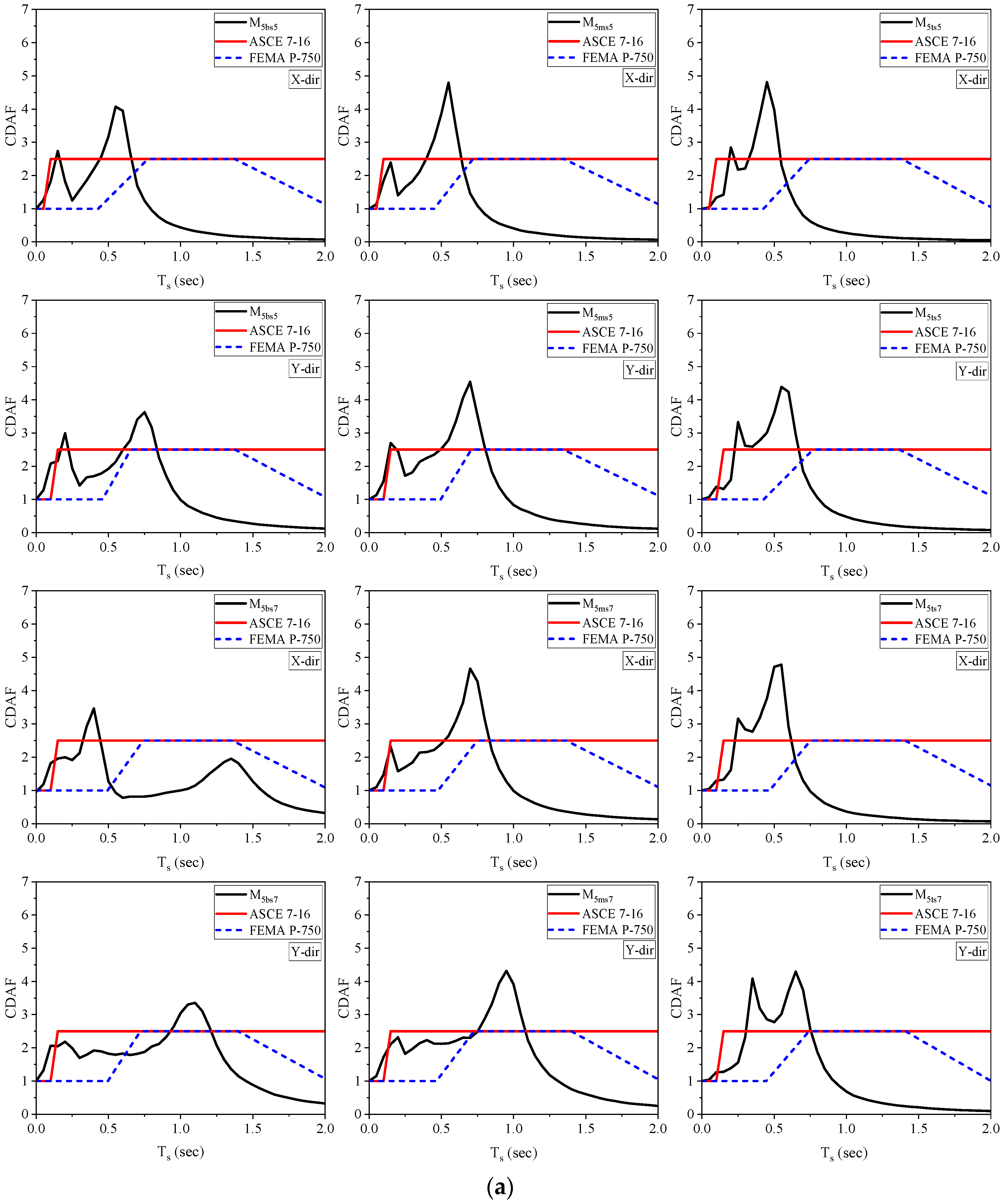
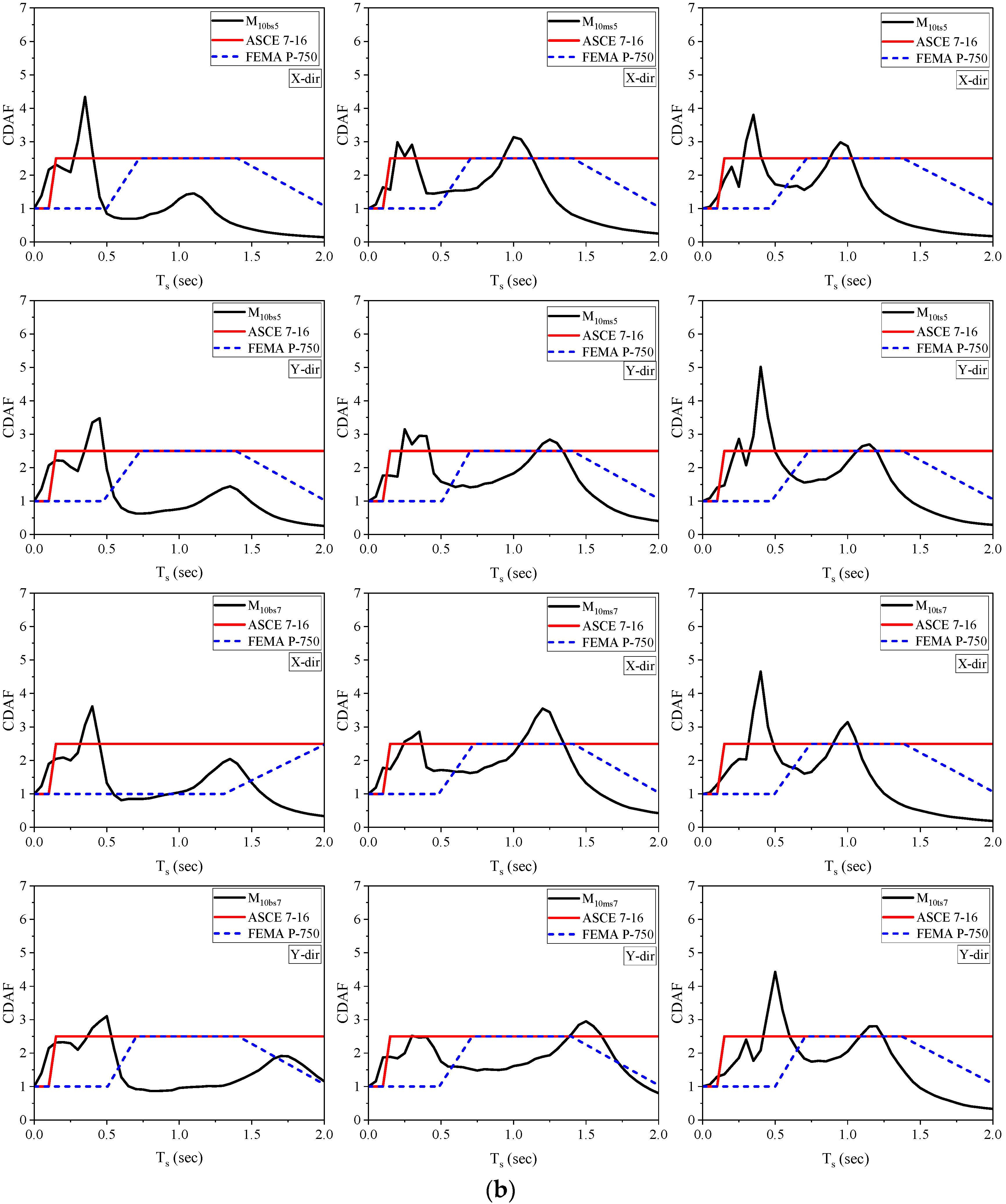
4.6. Component Dynamic Amplification Factor
5. Summary and Conclusions
- The existence of a soft story at different levels has an insignificant effect on the top-story displacement of the building models. The amplification in the peak story displacements of a building with a middle and top soft story was smaller than that of the building with a bottom soft story at the respective floor level. As the soft-story height increases, the peak story displacements increase for all the building models.
- The magnitude of the peak inter-story drift ratio is more significant in the soft-story building models at the soft-story level than that of the reference building models. The building models with a soft story have a sudden increase in the drift ratio at the specified story level in the two orthogonal directions. The maximum rapid change in drift values was observed in a building with a bottom soft story compared to the other models.
- The short-period NSCs will experience a high seismic demand when attached to the lower floor levels in a building without any vertical stiffness irregularity. Building models exhibit more substantial floor-to-floor amplification of spectral accelerations when the soft-story height is 5 m. As the soft-story height increases to 7 m, the spectra on various levels merge.
- The floor amplification factors and normalized peak component accelerations were amplified at the soft-story level in the bottom and top soft-story models. In the case of middle soft-story buildings, such amplification was observed in the immediate floors below the soft-story level.
- The middle soft-story buildings exhibit the greatest amplification in the component’s acceleration (CDAF). The average amplification factor values at the soft-story level are 2.72, 3.74, and 4.24 for the bottom, top, and middle soft-story building models correspond to the fundamental vibration period of the NSC when considering all the building models and soft-story heights.
- Code formulations underestimate the PFA demands at a soft-story level in all the considered building models. Therefore, it can be inferred that the linear hypothesis in the code-based formulae may result in an under- or overestimation of PFA demands together with building height.
- The code definitions underestimate the peak component acceleration and dynamic amplification factors at the soft-story level. Hence, the current code-based formulation should be modified by incorporating the effects of vertical stiffness irregularity into the analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Filiatrault, A.; Sullivan, T. Performance-Based Seismic Design of Nonstructural Building Components: The Next Frontier of Earthquake Engineering. Earthq. Eng. Eng. Vib. 2014, 13, 17–46. [Google Scholar] [CrossRef]
- Pardalopoulos, S.I.; Pantazopoulou, S.J. Seismic Response of Nonstructural Components Attached on Multistorey Buildings. Earthq. Eng. Struct. Dyn. 2015, 44, 139–158. [Google Scholar] [CrossRef]
- Perrone, D.; Filiatrault, A. Seismic Demand on Non-Structural Elements: Influence of Masonry Infills on Floor Response Spectra. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Shang, Q.; Wang, T.; Li, J. Seismic Fragility of Flexible Pipeline Connections in a Base Isolated Medical Building. Earthq. Eng. Eng. Vib. 2019, 18, 903–916. [Google Scholar] [CrossRef]
- Di Sarno, L.; Magliulo, G.; D’Angela, D.; Cosenza, E. Experimental Assessment of the Seismic Performance of Hospital Cabinets Using Shake Table Testing. Earthq. Eng. Struct. Dyn. 2019, 48, 103–123. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A. Evaluation of ASCE 7 Equations for Designing Acceleration-sensitive Nonstructural Components Using Data from Instrumented Buildings. Earthq. Eng. Struct. Dyn. 2018, 47, 1075–1094. [Google Scholar] [CrossRef]
- Suarez, L.E.; Singh, M.P. Floor Response Spectra with Structure–Equipment Interaction Effects by a Mode Synthesis Approach. Earthq. Eng. Struct. Dyn. 1987, 15, 141–158. [Google Scholar] [CrossRef]
- Adam, C. Dynamics of Elastic–Plastic Shear Frames with Secondary Structures: Shake Table and Numerical Studies. Earthq. Eng. Struct. Dyn. 2001, 30, 257–277. [Google Scholar] [CrossRef]
- Menon, A.; Magenes, G. Definition of Seismic Input for Out-of-Plane Response of Masonry Walls: II. Formulation. J. Earthq. Eng. 2011, 15, 195–213. [Google Scholar] [CrossRef]
- Challagulla, S.P.; Bhargav, N.C.; Parimi, C. Evaluation of Damping Modification Factors for Floor Response Spectra via Machine Learning Model. Structures 2022, 39, 679–690. [Google Scholar] [CrossRef]
- D’Angela, D.; Magliulo, G.; Cosenza, E. Seismic Damage Assessment of Unanchored Nonstructural Components Taking into Account the Building Response. Struct. Saf. 2021, 93, 102126. [Google Scholar] [CrossRef]
- Yasui, Y.; Yoshihara, J.; Takeda, T.; Miyamoto, A. Direct Generation Method for Floor Response Spectra; IASMiRT: Raleigh, NC, USA, 1993. [Google Scholar]
- Vukobratović, V.; Fajfar, P. A Method for the Direct Determination of Approximate Floor Response Spectra for SDOF Inelastic Structures. Bull. Earthq. Eng. 2015, 13, 1405–1424. [Google Scholar] [CrossRef]
- Jiang, W.; Li, B.; Xie, W.C.; Pandey, M.D. Generate Floor Response Spectra: Part 1. Direct Spectra-to-Spectra Method. Nucl. Eng. Des. 2015, 293, 525–546. [Google Scholar] [CrossRef]
- Ruggieri, S.; Vukobratović, V. Acceleration Demands in Single-Storey RC Buildings with Flexible Diaphragms. Eng. Struct. 2023, 275, 115276. [Google Scholar] [CrossRef]
- Calvi, P.M.; Sullivan, T.J. Estimating Floor Spectra in Multiple Degree of Freedom Systems. Earthquakes Struct. 2014, 7, 17–38. [Google Scholar] [CrossRef]
- Zhai, C.H.; Zheng, Z.; Li, S.; Pan, X.; Xie, L.L. Seismic Response of Nonstructural Components Considering the Near-Fault Pulse-like Ground Motions. Earthq. Struct. 2016, 10, 1213–1232. [Google Scholar] [CrossRef]
- Petrone, C.; Magliulo, G.; Manfredi, G. Floor Response Spectra in RC Frame Structures Designed According to Eurocode 8. Bull. Earthq. Eng. 2016, 14, 747–767. [Google Scholar] [CrossRef]
- Berto, L.; Bovo, M.; Rocca, I.; Saetta, A.; Savoia, M. Seismic Safety of Valuable Non-Structural Elements in RC Buildings: Floor Response Spectrum Approaches. Eng. Struct. 2020, 205, 110081. [Google Scholar] [CrossRef]
- Shang, Q.; Li, J.; Wang, T. Floor Acceleration Response Spectra of Elastic Reinforced Concrete Frames. J. Build. Eng. 2022, 45, 103558. [Google Scholar] [CrossRef]
- Vukobratović, V.; Fajfar, P. Code-Oriented Floor Acceleration Spectra for Building Structures. Bull. Earthq. Eng. 2017, 15, 3013–3026. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Inelastic Floor Spectra for Designing Anchored Acceleration-Sensitive Nonstructural Components. Bull. Earthq. Eng. 2020, 18, 2115–2147. [Google Scholar] [CrossRef]
- Vukobratović, V.; Ruggieri, S. Floor Acceleration Demands in a Twelve-Storey RC Shear Wall Building. Buildings 2021, 11, 38. [Google Scholar] [CrossRef]
- Landge, M.V.; Ingle, R.K. Comparative Study of Floor Response Spectra for Regular and Irregular Buildings Subjected to Earthquake. Asian J. Civ. Eng. 2021, 22, 49–58. [Google Scholar] [CrossRef]
- Landge, M.V.; Ingle, R.K. Influence of Torsional Irregularity on Tri-Directional Floor Response Spectra Used in Industrial Buildings. Innov. Infrastruct. Solut. 2022, 7, 34. [Google Scholar] [CrossRef]
- Singh, M.P.; Suarez, L.E. Seismic Response Analysis of Structure–Equipment Systems with Non-classical Damping Effects. Earthq. Eng. Struct. Dyn. 1987, 15, 871–888. [Google Scholar] [CrossRef]
- Perez, Y.M.; Guerra, E.M.; Bazan-zurita, E.; Engineer, P.; Associates, R.; Engineer, S.P.; Associates, R.; Associates, R. Seismic Response of Equipment Supported on Structures. In Proceedings of the 23rd Conference on Structural Mechanics in Reactor Technology, Manchester, UK, 10–14 August 2015. [Google Scholar]
- IS 1893; Criteria for Earthquake Resistant Design of Structures. Bureau of Indian Standards: New Delhi, India, 2016.
- ASCE. Minimum Design Loads and Associated Criteria for Buildings and Other Structures (ASCE/SEI 7–16); American Society of Civil Engineers: Reston, VA, USA, 2016. [Google Scholar]
- Setia, S.; Sharma, V. Seismic Response of RCC Building with Soft Storey. Int. J. Appl. Eng. Res. 2012, 7, 180–186. [Google Scholar]
- Mahmoud, S.; Genidy, M.; Tahoon, H. Time-History Analysis of Reinforced Concrete Frame Buildings with Soft Storeys. Arab. J. Sci. Eng. 2017, 42, 1201–1217. [Google Scholar] [CrossRef]
- Alam, T.; Amanat, K.M. Seismic Response of Randomly Infilled Reinforced Concrete Frames with Soft Ground Storey. Aust. J. Civ. Eng. 2020, 18, 153–163. [Google Scholar] [CrossRef]
- Das, S.; Nau, J.M. Seismic Design Aspects of Vertically Irregular Reinforced Concrete Buildings. Earthq. Spectra 2003, 19, 455–477. [Google Scholar] [CrossRef]
- Chintanapakdee, C.; Chopra, A.K. Seismic Response of Vertically Irregular Frames: Response History and Modal Pushover Analyses. J. Struct. Eng. 2004, 130, 1177–1185. [Google Scholar] [CrossRef]
- Choi, B.J. Hysteretic Energy Response of Steel Moment-resisting Frames with Vertical Mass Irregularities. Struct. Des. Tall Spec. Build. 2004, 13, 123–144. [Google Scholar] [CrossRef]
- Fragiadakis, M.; Vamvatsikos, D.; Papadrakakis, M. Evaluation of the Influence of Vertical Stiffness Irregularities on the Seismic Response of a 9-Story Steel Frame. In Proceedings of the 4th European Workshop on the Seismic Behavior of Irregular and Complex Structures, Thessaloniki, Greece, 26–27 August 2005. [Google Scholar]
- Satheesh, A.J.; Jayalekshmi, B.R.; Venkataramana, K. Effect of In-Plan Eccentricity on Vertically Stiffness Irregular Buildings under Earthquake Loading. Soil Dyn. Earthq. Eng. 2020, 137, 106251. [Google Scholar] [CrossRef]
- Parekar, S.D.; Datta, D. Seismic Behaviour of Stiffness Irregular Steel Frames under Mainshock–Aftershock. Asian J. Civ. Eng. 2020, 21, 857–870. [Google Scholar] [CrossRef]
- Abd-Alghany, M.M.; El-Kashif, K.F.; Abdalla, H.A. Seismic Response of Multi-Storey Reinforced Concrete Buildings with Soft Floor. HBRC J. 2021, 17, 407–428. [Google Scholar] [CrossRef]
- Filiatrault, A.; Perrone, D.; Merino, R.J.; Calvi, G.M. Performance-Based Seismic Design of Nonstructural Building Elements. J. Earthq. Eng. 2018, 25, 237–269. [Google Scholar] [CrossRef]
- Gabbianelli, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Seismic Acceleration and Displacement Demand Profiles of Non-Structural Elements in Hospital Buildings. Buildings 2020, 10, 243. [Google Scholar] [CrossRef]
- FEMA. Seismic Performance Assessment of Buildings Volume 1-Methodology; FEMA: Washington, DC, USA, 2012.
- Sani, H.P.; Gholhaki, M.; Banazadeh, M. Simplified Direct Loss Measure for Seismic Isolated Steel Moment-Resisting Structures. J. Constr. Steel Res. 2018, 147, 313–323. [Google Scholar] [CrossRef]
- FEMA. Multi-Hazard Loss Estimation Methodology, Earthquake Model, Hazus-MH 2.1, Technical Manual; FEMA: Washington, DC, USA, 2013.
- Hejazi, F.; Jilani, S.; Noorzaei, J.; Chieng, C.Y.; Jaafar, M.S.; Ali, A.A.A. Effect of Soft Story on Structural Response of High Rise Buildings. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2011; Volume 17, p. 12034. [Google Scholar]
- IS 875; Part Code of Practice for Design Loads (Other than Earthquake) for Buildings and Structures: Part 2—Imposed Loads (Second Revision). Bureau of Indian Standards: New Delhi, India, 1987.
- IS 13920; Ductile Design and Detailing of Reinforced Concrete Structures Subjected to Seismic Forces—Code of Practice. Bureau of Indian Standards: New Delhi, India, 2016.
- SeismoStruct. Release-1—A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures 2016. Available online: https://seismosoft.com/product/seismostruct/ (accessed on 1 October 2022).
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Menegotto, M. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Pinho, R.; Bhatt, C.; Antoniou, S.; Bento, R. Modelling of the Horizontal Slab of a 3D Irregular Building for Nonlinear Static Assessment. In the Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008; pp. 15–17. [Google Scholar]
- Bagheri, B.; Nivedita, K.A.; Firoozabad, E.S. Comparative Damage Assessment of Irregular Building Based on Static and Dynamic Analysis. Int. J. Civ. Struct. Eng. 2013, 3, 505. [Google Scholar]
- Senaldi, I.; Magenes, G.; Penna, A.; Galasco, A.; Rota, M. The Effect of Stiffened Floor and Roof Diaphragms on the Experimental Seismic Response of a Full-Scale Unreinforced Stone Masonry Building. J. Earthq. Eng. 2014, 18, 407–443. [Google Scholar] [CrossRef]
- Pacific Earthquake Engineering Research Center. PEER Ground Motion Database; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2013; Available online: https://ngawest2.berkeley.edu (accessed on 1 October 2022).
- FEMA P-2082-1; NEHRP Recommended Seismic Provisions for New Buildings and Other Structures. Part 1, Provisions. FEMA: Washington, DC, USA, 2009.
- Khy, K.; Chintanapakdee, C.; Wijeyewickrema, A.C. Application of Conditional Mean Spectrum in Nonlinear Response History Analysis of Tall Buildings on Soft Soil. Eng. J. 2019, 23, 135–150. [Google Scholar] [CrossRef]
- Alatik, L.; Abrahamson, N. An Improved Method for Nonstationary Spectral Matching. Earthq. Spectra 2010, 26, 601–617. [Google Scholar] [CrossRef]
- Shooshtari, M.; Saatcioglu, M.; Naumoski, N.; Foo, S. Floor Response Spectra for Seismic Design of Operational and Functional Components of Concrete Buildings in Canada. Can. J. Civ. Eng. 2010, 37, 1590–1599. [Google Scholar] [CrossRef]
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2005.
- FEMA P-750; Nehrp Recommended Seismic Provisions for New Buildings and Other Structures. FEMA: Washington, DC, USA, 2009.
- Surana, M.; Singh, Y.; Lang, D.H. Effect of Irregular Structural Configuration on Floor Acceleration Demand in Hill-Side Buildings. Earthq. Eng. Struct. Dyn. 2018, 47, 2032–2054. [Google Scholar] [CrossRef]
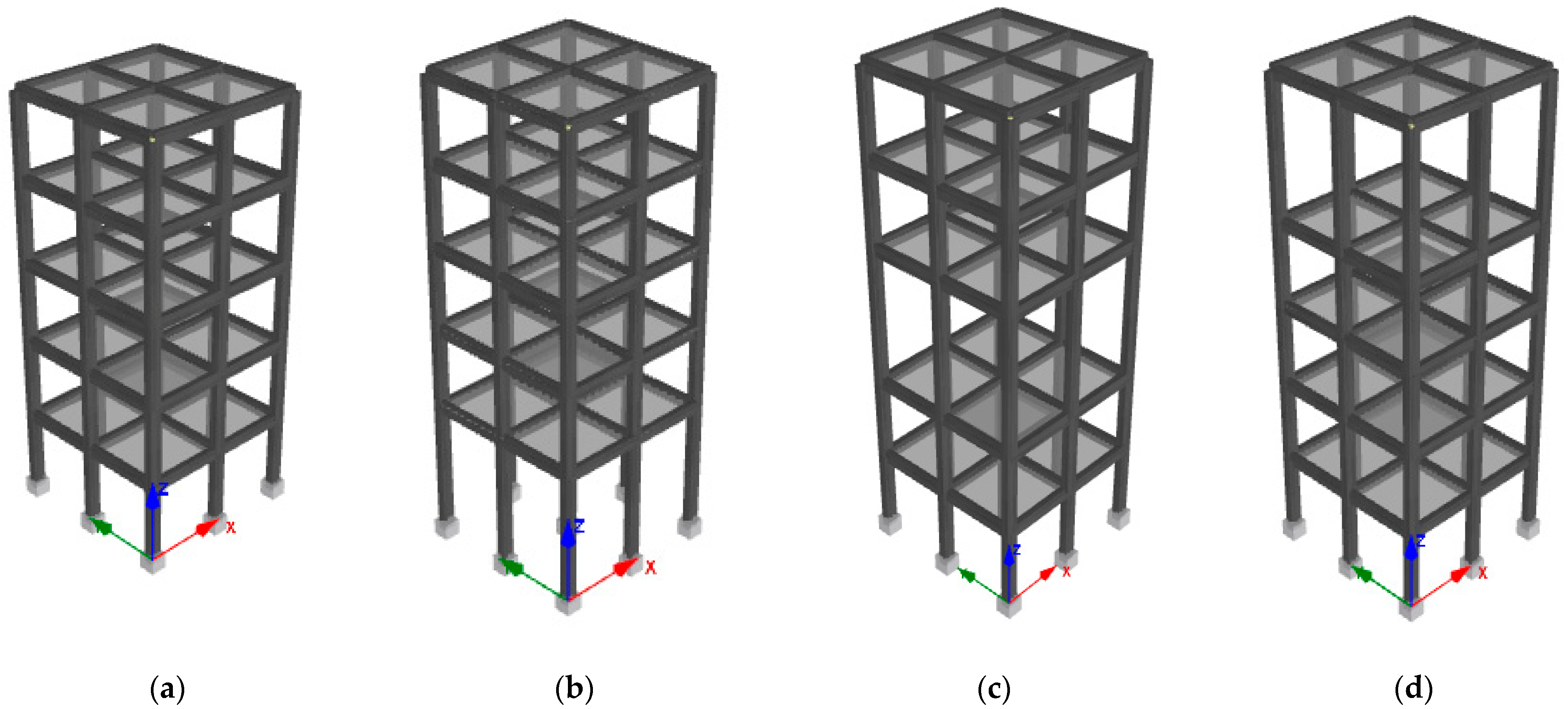


| Building Model | Heigh of a Soft Story (m) | Soft Story Location (Floor Level) | ||
|---|---|---|---|---|
| X-Dir | Y-Dir | |||
| M5bs5 | 5 | 1 | 0.495 | 0.373 |
| M5ms5 | 5 | 3 | 0.407 | 0.334 |
| M5ts5 | 5 | 5 | 0.348 | 0.302 |
| M10bs5 | 5 | 1 | 0.522 | 0.389 |
| M10ms5 | 5 | 6 | 0.449 | 0.365 |
| M10ts5 | 5 | 10 | 0.330 | 0.305 |
| M5bs7 | 7 | 1 | 0.231 | 0.159 |
| M5ms7 | 7 | 3 | 0.211 | 0.154 |
| M5ts7 | 7 | 5 | 0.173 | 0.134 |
| M10bs7 | 7 | 1 | 0.245 | 0.168 |
| M10ms7 | 7 | 6 | 0.235 | 0.172 |
| M10ts7 | 7 | 10 | 0.188 | 0.151 |
| Earthquake | Year | Station | Mw | Rjb (km) | Vs30 (m/s) |
|---|---|---|---|---|---|
| Helena_Montana-01 | 1935 | Carroll College | 6 | 2.07 | 593.35 |
| Helena_Montana-02 | 1935 | Helena Fed Bldg. | 6 | 2.09 | 551.82 |
| Kern County | 1952 | Pasadena—CIT Athenaeum | 7.36 | 122.65 | 415.13 |
| Kern County | 1952 | Santa Barbara Courthouse | 7.36 | 81.3 | 514.99 |
| Kern County | 1952 | Taft Lincoln School | 7.36 | 38.42 | 385.43 |
| Southern Calif | 1952 | San Luis Obispo | 6 | 73.35 | 493.5 |
| Parkfield | 1966 | Cholame—Shandon Array #12 | 6.19 | 17.64 | 408.93 |
| Parkfield | 1966 | San Luis Obispo | 6.19 | 63.34 | 493.5 |
| Parkfield | 1966 | Temblor pre-1969 | 6.19 | 15.96 | 527.92 |
| Borrego Mtn | 1968 | Pasadena—CIT Athenaeum | 6.63 | 207.14 | 415.13 |
| Borrego Mtn | 1968 | San Onofre—So Cal Edison | 6.63 | 129.11 | 442.88 |
| 1(Y) | 2(X) | 3(R) | 4(Y) | 5(X) | 6(R) | 7(Y) | 8(X) | 9(R) | 10(Y) | 11(X) | 12(R) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M5ref | 0.54 | 0.44 | 0.42 | 0.18 | 0.14 | 0.13 | 0.1 | 0.08 | 0.07 | 0.06 | 0.05 | 0.11 |
| M5bs5 | 0.76 | 0.58 | 0.56 | 0.23 | 0.18 | 0.17 | 0.12 | 0.1 | 0.09 | 0.08 | 0.06 | 0.05 |
| M5ms5 | 0.71 | 0.56 | 0.53 | 0.2 | 0.16 | 0.15 | 0.14 | 0.1 | 0.09 | 0.08 | 0.07 | 0.06 |
| M5ts5 | 0.59 | 0.47 | 0.45 | 0.25 | 0.19 | 0.18 | 0.14 | 0.11 | 0.1 | 0.09 | 0.07 | 0.06 |
| M5bs7 | 1.11 | 0.81 | 0.76 | 0.25 | 0.2 | 0.19 | 0.13 | 0.1 | 0.09 | 0.08 | 0.07 | 0.06 |
| M5ms7 | 0.96 | 0.73 | 0.68 | 0.22 | 0.17 | 0.16 | 0.15 | 0.12 | 0.11 | 0.08 | 0.07 | 0.06 |
| M5ts7 | 0.67 | 0.53 | 0.5 | 0.34 | 0.25 | 0.24 | 0.14 | 0.11 | 0.1 | 0.08 | 0.06 | 0.05 |
| M10ref | 1.13 | 0.94 | 0.83 | 0.37 | 0.3 | 0.27 | 0.21 | 0.17 | 0.16 | 0.15 | 0.12 | 0.11 |
| M10bs5 | 1.37 | 1.11 | 0.98 | 0.45 | 0.36 | 0.32 | 0.24 | 0.19 | 0.18 | 0.16 | 0.13 | 0.12 |
| M10ms5 | 1.28 | 1.06 | 0.93 | 0.41 | 0.33 | 0.31 | 0.24 | 0.19 | 0.18 | 0.17 | 0.13 | 0.12 |
| M10ts5 | 1.16 | 0.98 | 0.85 | 0.4 | 0.33 | 0.29 | 0.25 | 0.19 | 0.18 | 0.17 | 0.14 | 0.13 |
| M10bs7 | 1.77 | 1.37 | 1.21 | 0.52 | 0.42 | 0.36 | 0.25 | 0.2 | 0.19 | 0.17 | 0.14 | 0.13 |
| M10ms7 | 1.54 | 1.24 | 1.07 | 0.46 | 0.36 | 0.35 | 0.26 | 0.21 | 0.19 | 0.18 | 0.14 | 0.13 |
| M10ts7 | 1.2 | 1.01 | 0.87 | 0.49 | 0.38 | 0.35 | 0.3 | 0.23 | 0.23 | 0.18 | 0.15 | 0.14 |
| 1(Y) | 2(X) | 3(R) | 4(Y) | 5(X) | 6(R) | 7(Y) | 8(X) | 9(R) | 10(Y) | 11(X) | 12(R) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M5ref | UX | 0 | 83 | 83 | 83 | 94 | 94 | 94 | 94 | 97.8 | 97.8 | 97.8 | 97.8 |
| UY | 84.9 | 84.9 | 84.9 | 95.1 | 95.1 | 95.1 | 98.3 | 98.3 | 98.3 | 99.6 | 100 | 100 | |
| M5bs5 | UX | 0 | 94 | 94 | 94 | 99.2 | 99.2 | 99.2 | 99.2 | 99.8 | 99.8 | 99.8 | 99.8 |
| UY | 96 | 96 | 96 | 99.5 | 99.5 | 99.5 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | |
| M5ms5 | UX | 0 | 76.3 | 76.3 | 76.3 | 94.7 | 94.7 | 94.7 | 97 | 97 | 97 | 97 | 97 |
| UY | 76 | 76 | 76 | 95.6 | 95.6 | 95.6 | 96.9 | 96.9 | 96.9 | 99.6 | 99.6 | 99.6 | |
| M5ts5 | UX | 0 | 78.7 | 78.7 | 78.7 | 90.4 | 90.4 | 90.4 | 90.4 | 96.6 | 96.6 | 96.6 | 96.6 |
| UY | 80.1 | 80.1 | 80.1 | 91.2 | 91.2 | 91.2 | 97.2 | 97.2 | 97.2 | 99.9 | 99.9 | 99.9 | |
| M5bs7 | UX | 0 | 98.1 | 98.1 | 98.1 | 99.8 | 99.8 | 99.8 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 |
| UY | 99 | 99 | 99 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | 100 | 100 | 100 | |
| M5ms7 | UX | 0 | 69.7 | 69.7 | 69.7 | 69.7 | 95.5 | 95.5 | 96.4 | 96.4 | 96.4 | 96.4 | 96.4 |
| UY | 68.8 | 68.8 | 68.8 | 96.6 | 96.6 | 96.6 | 96.9 | 96.9 | 96.9 | 99.9 | 100 | 100 | |
| M5ts7 | UX | 0 | 78.7 | 78.7 | 78.7 | 90.4 | 90.4 | 90.4 | 90.4 | 96.6 | 96.6 | 96.6 | 96.6 |
| UY | 80.1 | 80.1 | 80.1 | 91.2 | 91.2 | 91.2 | 97.2 | 97.2 | 97.2 | 99.4 | 99.9 | 99.9 | |
| M10ref | UX | 0 | 78.6 | 78.6 | 78.6 | 91.3 | 91.3 | 91.3 | 95 | 95 | 95 | 95 | 97 |
| UY | 80.7 | 80.7 | 80.7 | 92.3 | 92.3 | 92.3 | 95.8 | 95.8 | 95.8 | 97.5 | 98.6 | 98.6 | |
| M10bs5 | UX | 0 | 87 | 87 | 87 | 97.5 | 97.5 | 97.5 | 99.1 | 99.1 | 99.1 | 99.6 | 99.6 |
| UY | 90.3 | 90.3 | 90.3 | 98.9 | 98.9 | 98.9 | 100 | 100 | 100 | 100 | 100 | 100 | |
| M10ms5 | UX | 0 | 74.5 | 74.5 | 74.5 | 91.6 | 91.6 | 91.6 | 93.4 | 93.4 | 93.4 | 97.1 | 97.1 |
| UY | 75.5 | 75.5 | 75.5 | 92.6 | 92.6 | 92.6 | 93.9 | 93.9 | 93.9 | 97.6 | 97.6 | 97.6 | |
| M10ts5 | UX | 0 | 77.8 | 77.8 | 77.8 | 90.1 | 90.1 | 90.1 | 93.9 | 93.9 | 93.9 | 96.3 | 96.3 |
| UY | 79.8 | 79.8 | 79.8 | 90.9 | 90.9 | 90.9 | 94.4 | 94.4 | 94.4 | 96.8 | 96.8 | 96.8 | |
| M10bs7 | UX | 0 | 93.8 | 93.8 | 93.8 | 99.4 | 99.4 | 99.4 | 99.8 | 99.8 | 99.8 | 99.9 | 99.9 |
| UY | 96.4 | 96.4 | 96.4 | 99.6 | 99.6 | 99.6 | 99.8 | 99.8 | 99.8 | 99.9 | 99.9 | 99.9 | |
| M10ms7 | UX | 0 | 69.1 | 69.1 | 69.1 | 91.9 | 91.9 | 91.9 | 92.3 | 92.3 | 92.3 | 97.1 | 97.1 |
| UY | 68.5 | 68.5 | 68.5 | 92.7 | 92.7 | 92.7 | 92.9 | 92.9 | 92.9 | 97.5 | 97.5 | 97.5 | |
| M10ts7 | UX | 0 | 76.1 | 76.1 | 76.1 | 87.1 | 87.1 | 87.1 | 93 | 93 | 93 | 96 | 96 |
| UY | 77.7 | 77.7 | 77.7 | 87.2 | 87.2 | 87.2 | 93.7 | 93.7 | 93.7 | 96.6 | 96.6 | 96.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesaralanka, V.; Challagulla, S.P.; Vicencio, F.; Chandra Babu, P.S.; Hossain, I.; Jameel, M.; Ramakrishna, U. Influence of a Soft Story on the Seismic Response of Non-Structural Components. Sustainability 2023, 15, 2860. https://doi.org/10.3390/su15042860
Pesaralanka V, Challagulla SP, Vicencio F, Chandra Babu PS, Hossain I, Jameel M, Ramakrishna U. Influence of a Soft Story on the Seismic Response of Non-Structural Components. Sustainability. 2023; 15(4):2860. https://doi.org/10.3390/su15042860
Chicago/Turabian StylePesaralanka, Vyshnavi, S. P. Challagulla, Felipe Vicencio, P. Suresh Chandra Babu, Ismail Hossain, Mohammed Jameel, and Uppari Ramakrishna. 2023. "Influence of a Soft Story on the Seismic Response of Non-Structural Components" Sustainability 15, no. 4: 2860. https://doi.org/10.3390/su15042860
APA StylePesaralanka, V., Challagulla, S. P., Vicencio, F., Chandra Babu, P. S., Hossain, I., Jameel, M., & Ramakrishna, U. (2023). Influence of a Soft Story on the Seismic Response of Non-Structural Components. Sustainability, 15(4), 2860. https://doi.org/10.3390/su15042860







