Energy Consumption, Carbon Emission and Economic Growth at Aggregate and Disaggregate Level: A Panel Analysis of the Top Polluted Countries

Abstract

Economic expansion leads to higher CODe₂ emissions, which puts pressure on environmental degradation. More than 30% of carbon emissions are contributed by the top0polluting countries in the world through their energy consumption. Therefore, the current study examines the association between CO₂ emissions, energy consumption, GDP and industrial production, along with other control variables at the aggregated and disaggregated levels for the top emitter countries for the 1990–2019 period. The short- and long-term results indicate that CO₂ emissions are positively and significantly linked with energy consumption, except carbon emissions from the gas model, by employing the PARDL model using pooled mean group (PMG) analysis. Thus, gas consumption is less polluting to the environment than other sources of energy; therefore, countries need to reduce the consumption of coal and oil, which will lead to a decrease in CO₂ emissions. This refers to the composition effect, which focuses on the use of clean energy instead of dirty energy in the production and consumption processes. The shift from oil or coal to gas in the production process will help to reduce the oil demand, which ultimately controls its consumption and prices, which may help to control the prices of various other goods and services.

1. Introduction

Environmental degradation, greenhouse gases and the changing climate have become the most debated issues for several years around the world [1,2]. This environmental degradation puts billions of precious lives at risk, so this area has received huge focus from researchers and academia [3]. It has been revealed that about 75% of greenhouse gas emissions are comprised of CO₂ emissions, which are the main contributor to global warming [3,4,5].

The UNFCC (United Nations Framework on Climate Change) treaty is considered the most important environmental agreement. It was approved in 1992 and opened for signatures at the UNFCCC on climate and development in Rio de Janeiro. The main theme of the UNFCCC was to decrease CO₂ emissions across countries and to tackle the related climate issues and greenhouse gas (GHG) effects [6]. To control the global challenge of environmental degradation, many other steps were taken to resolve this serious issue, such as the KP (Kyoto Protocol) in 1997 and the PCA (Paris Climate Agreement) in 2015. The major goal of the Kyoto Protocol was to operationalize the UNFCCC into action by requiring industrialized countries and economies in transition to set individual objectives that restrict and reduce greenhouse gas emissions [7].

The European Union’s (EU) goal for sustainable development is part of the Europe (2020–2030) strategy for sustainable growth that also sets a goal for the reduction in CO₂ emissions. Furthermore, climate actions will attempt to decrease GHG emissions from 20% and 40% by 2020 and 2030, respectively. Moreover, these objectives are also involved in the framework of the EU-2050 to lower CO₂ emissions by emphasizing that all segments of the economy ought to contribute to the lessening of GHG (where GHG represents greenhouse gas emissions) release, which might attain the objective of an 80% reduction in GHG emissions compared to their levels in 1990 [7].

Energy is one of the major components in the manufacturing process and is as important as labor and capital in the production process [8]. Energy plays a key role in diverse segments of the economy such as “agriculture, transportation, trade, and economic development”. Moreover, it is considered a major compliment for poverty reduction, sustaining human development, and enhancing economic prosperity through the consumption of several types of energy [9]. On the other hand, these consumption patterns may increase CO₂ emissions, which are the most important components of GHG emissions [10]. The energy sector, especially fossil fuel consumption, contributes a massive amount of CO₂ emissions. According to the report from the IEA (2019), carbon dioxide emissions grew by 1.7% in 2018, which approached 33.1%, owing to increasing energy consumption demand [11].

Even though the consumption of energy is rising continuously, with a growth rate of 10.9% from 2003–2007, the total amount of energy consumed by coal, crude oil and natural gas increased by 3.5 times from 7.67 million tons in 1992 to 26.56 million tons in 2007. Hence, individuals, corporate sectors and government sectors are taking an interest in tackling these environmental concerns with the awareness of emissions and climate issues [12].

The recent report issued by the IEA (International Energy Agency) revealed that the use of fossil fuels contributes to a higher level of CO₂ emissions, which affects the climate negatively. The report further elaborated that worldwide energy consumption will increase up to 7.6% in 2040 as compared to 2012, i.e., 32.3% billion metric tons. Moreover, the report further argued that growth in emissions is extremely sensitive in industrialized countries that are heavily reliant on the usage of fossil fuels for accelerating their GDP and meeting their demand for energy [13]. A varied range of literature sources is available on the association between CO₂ emissions and economic growth [14,15]. This relationship has been studied by researchers through the environmental Kuznets curve hypothesis: the curve identifies the association between income inequality and economic growth and proposes that when income reaches a particular level, economic development will contribute to income disparity. However, as income rises above a certain level, this income distribution will be non-discriminatory. The EKC curve features an upward portion that worsens the environment in the first half then turns in a descending direction after reaching its highest point, indicating that the environment improves with the incline in economic growth. The environmental Kuznets curve hypothesis shows that as PCI (per capita income) improves in a country, it will cause environmental degradation up to a specified level, and beyond that certain level, the upward shift in per-capita income will lead to improving the environment [16].

1.1. Rationale of Study

The association between CO₂ emissions, energy consumption and economic growth has been studied in many ways with different methodologies [3,4,12,15,17]. Increasing economic expansion is resulting in higher CO₂ emissions from economic activities which pose great threats to environmental degradation. When a country expands its production of various commodities, it emits more carbon dioxide into the environment, which has a detrimental effect on economic development [18]. Researchers are more concerned about those policies which are implemented for the reduction in CO₂ emissions that might slow down economic growth. There is a need to consider effective and implementable policies to arrive at the optimal strategy based on analysis that determines the affiliation between GDP and CO₂ emissions in-depth [19].

Policymakers first check for the existence of a normal environmental Kuznets curve and, in case one exists, whether the turning point has been achieved or not while identifying the relationship between GDP and CO₂ outflows. If the turning point has been achieved, then higher economic growth will not affect an increasing level of CO₂ emissions [20]. After a while, industrialized countries began to organize substantial environmental agreements and agendas to reduce and manage GHG emissions and their concentrations in the atmosphere [21]. The estimated entire cost of the changing climate due to CO₂ emissions is proportional to around 5% of economic growth every year and is projected to reach 20% by the end of the year if rigorous actions are not be adopted [22]. Recent statistics on CO₂ emissions with respect to the share of the top-emitting countries are depicted in the following graph (Reported by IEA in August 2020).

Figure 1 explains that China is the highest contributor to carbon emissions and is responsible for the emission of 10.06 (Metric Gigatons) of carbon into the environment. The United States holds the second position and emits 5.41 (Metric Gigatons) of carbon into the atmosphere, followed by India, contributing 2.65 (Metric Gigatons) of carbon emissions; Russia, contributing 1.71 (Metric Gigatons) of CO₂ emissions; Japan, contributing 1.16 (Metric Gigatons) of CO₂ emissions; and so on. Germany contributes 0.75 (Metric Gigatons), South Korea 0.65 (Metric Gigatons), Indonesia 0.61 (Metric Gigatons), Canada 0.56 (Metric Gigatons), Brazil 0.45 (Metric Gigatons), and France is contributing 0.33 (Metric Gigatons) of CO₂ emissions.

A wide range of literature is available on CO₂ emissions, consumption of energy, and economic growth on the aggregated level, but there are very few studies [23,24] available on the disaggregated level. The literature provides varying results on the possible relationship between energy consumption, carbon emission, and economic growth on the aggregated level. Researchers [12,19,21,25] have found that there is a one-way causation moving from GDP to energy consumption in the short run, whereas unidirectional causation is moving from GDP and consumption of energy to CO₂ emissions in the long run. In contrast, several other findings [5,25,26,27] have investigated a positive two-way causality between energy consumption, CO₂ emissions, and GDP growth in the long run. Recently, other studies [24,28] have found that consumption of energy negatively impacts CO₂ emissions, moreover the renewable energy production reduces carbon emissions in African countries. Additionally, energy generated through oil, natural gas, and coal has an adverse effect on carbon releases, while energy generated from hydropower eases carbon emissions.

On the contrary, the consumption of petrol and GHG emissions have asymmetric impacts on economic growth and carbon emission, while the non-renewable use of energy has a positive outcome on GDP and reduces CO₂ emissions [29]. However, it is found that an upward shift in the percapita income increase CO₂ emissions, which indicates a monotonic relationship between per capita income and carbon emissions at the aggregated level both for electricity and oil consumption models [19,30]. On contrary, there appears to be no causal relation between CO₂ emissions and income [21]. Furthermore, the disaggregated analysis shows that the rise in the consumption of biomass energy was effective at reducing CO₂ emissions in Germany, Japan, France and the United States, while the use of hydroelectricity helped to decrease carbon emissions in the United Kingdom and Italy [3,31].

1.2. Gap

The reason for choosing the top emitting countries for this study (Canada, Brazil, China, Indonesia, India, France, Japan, Germany, Russia, South Korea and the United States) is because these countries produce 36.6% of global energy production and emit 33.7% of the world’s carbon emissions (WDI). More precisely, we may conclude from the above discussion that there are contradictory findings regarding the relationship between CO₂ emissions, energy consumption and economic growth. The current study contributes to the existing body of literature in many ways. First, this study examines the association between CO₂ emissions, energy consumption and GDP at both the aggregated and disaggregated levels of high-consumption economies that were not examined in the earlier studies. Secondly, to obtain deeper insight, the current study investigates the impact of carbon emissions from coal, oil and gas at the disaggregate level for the top emitting countries specifically. Third, to the best of our knowledge, this is the first study that inspects this association among the top-emitting countries especially, so the sample selection is also a contribution of this study.

To fulfill this research gap, the current study not only highlights the role of CO₂ emissions from coal, oil and gas at the disaggregated level for the top-emitting countries, but also employs the panel autoregressive distributive lag (PARDL) model. Previous studies have employed (ARDL), (DOLS), and (FMOLS) models to identify the association between “carbon emissions, energy consumption & GDP” at the aggregated level; hence, this study will be a new contribution to the existing body of literature.

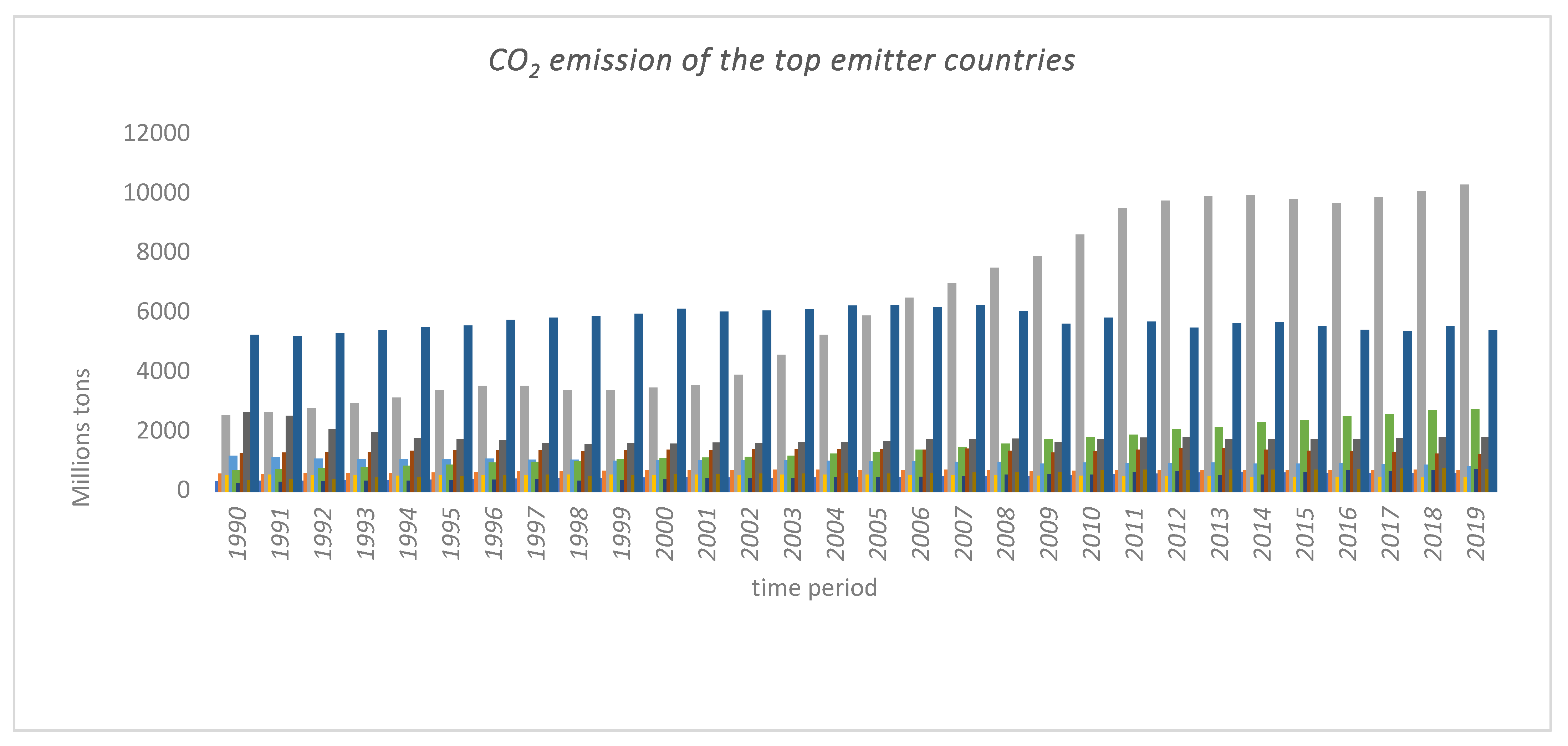
2. Data and Methodology

The study analyzes the determinants of CO₂ emissions from energy consumption, economic growth, industrial production and a set of other control variables such as population density and international trade for the top emitting countries for the period from 1990 to 2019. In this study, the top emitting countries are selected for analysis because they contributed more to CO₂ emissions, accounting for about 33.7% of the total CO₂ emissions of the entire world (WDI). Developed countries are still heavily dependent on the use of fossil fuels, and that is why these countries are facing a serious threat of environmental pollution (31). The data for CO₂ emissions (million tons), CO₂ emissions from coal (million tons), CO₂ emissions from gas (million tons) and CO₂ emissions from oil (million tons) have been extracted from “British Petroleum (BP)statistics”. The data for industrial production (IP, at constant 2010 USD) were obtained from World Bank global economic monitoring. The data for energy consumption (kg of oil equivalent per capita), GDP (constant 2010 USD) and X, which is a set of control variables that involve population density (people per sq. km of land area) and international trade as a % of GDP, were obtained from the world development indicator (WDI). (All variables are expressed in the Log form except population density and international trade. The complete data sources are given in Appendix A). The current study examines two models for deeper insight regarding their objectives and aggregated analysis and disaggregated analysis of CO₂ emissions for the top emitter countries (Canada, Brazil, France, Germany, China, Indonesia, India, Russia, Japan, South Korea and the United States.) The basic functional form of the aggregated model of CO₂ emissions is as follows [30,32]:

$${ \mathrm{CO}}_{2\mathrm{i},\mathrm{t} = \mathrm{f} \left({\mathrm{EC}}_{\mathrm{i},\mathrm{t}},{ \mathrm{GDP}}_{\mathrm{i},\mathrm{t}},{\mathrm{IP}}_{\mathrm{i},\mathrm{t},}{ \mathrm{X}}_{\mathrm{i},\mathrm{t}}\right) }$$

(1)

where CO₂ represents carbon emissions, energy consumption is represented by EC, GDP represents economic growth, IP represents industrial production and X represents a set of control variables that involve population density and international trade. “t” denotes the number of time periods, and “i” denotes the number of cross-sections in all equations.

The disaggregated level of CO₂ emissions from coal, oil and gas for the top emitting countries is as follows.

The model used for CO₂ emissions from coal is as follows:

$${ \mathrm{CCO}}_{2\mathrm{i},\mathrm{t}}={\mathsf{\beta }}_0+{\mathsf{\beta }}_1{\mathrm{EC}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\beta }}_2{\mathrm{GDP}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\beta }}_3{\mathrm{IP}}_{\mathrm{i},\mathrm{t},}+{\mathsf{\beta }}_4{\mathrm{X}}_{\mathrm{i},\mathrm{t}}+\mathsf{\epsilon }$$

(2)

where CCO₂ is the CO₂ emissions from coal, EC represents energy consumption, GDP represents economic growth, IP represents industrial production and X is a set of control variables. β₀ represents the intercept of the model and β₁, β₂, β₃ and β₄ are the coefficients of energy consumption, economic growth and industrial production, respectively, and ε is the random term [33].

The model used for CO₂ emissions from gas is as follows:

$${\mathrm{GCO}}_{2\mathrm{i},\mathrm{t}}={\mathsf{\gamma }}_0+{\mathsf{\gamma }}_1{\mathrm{EC}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\gamma }}_2{\mathrm{GDP}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\gamma }}_3{\mathrm{IP}}_{\mathrm{i},\mathrm{t},}+{ \mathsf{\gamma }}_4{\mathrm{X}}_{\mathrm{i},\mathrm{t}}+\mathsf{\mu }$$

(3)

where GCO₂ is the CO₂ emissions from gas, “EC indicates energy consumption, GDP represents economic growth”, IP represents industrial production and X is a set of control variables that involve population density and international trade [34]. ${\mathsf{\gamma }}_0$ shows the intercept of the model, whereas ${\mathsf{\gamma }}_1,{ \mathsf{\gamma }}_2, { \mathsf{\gamma }}_3 {\mathrm{and} \mathsf{\gamma }}_4$ are the coefficients of energy consumption, economic growth and industrial production, respectively, and μ is the random term.

The model used for CO₂ emissions from oil is as follows:

$${\mathrm{OCO}}_{2\mathrm{i},\mathrm{t}}={\mathsf{\delta }}_0+{\mathsf{\delta }}_1{\mathrm{EC}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\delta }}_2{\mathrm{GDP}}_{\mathrm{i},\mathrm{t}}+{\mathsf{\delta }}_3{\mathrm{IP}}_{\mathrm{i},\mathrm{t},}+{\mathsf{\delta }}_4{\mathrm{X}}_{\mathrm{i},\mathrm{t}}+\mathsf{\omega }$$

(4)

where OCO₂ is the CO₂ emissions from oil, EC represents energy consumption, GDP represents economic growth, IP represents industrial production and X is a set of control variables that involve population density and international trade [30]. ${\mathsf{\delta }}_0$represents the intercept of the model, while ${\mathsf{\delta }}_1,{ \mathsf{\delta }}_2,{ \mathsf{\delta }}_3{ \mathrm{and} \mathsf{\delta }}_{4 }$ are the coefficients of energy consumption, economic growth and industrial production, respectively, and $\mathsf{\omega }$ is the error term.

2.1. Tests of Cross-Sectional Dependence

Consider the standard panel data model:

$${\mathrm{y}}_{\mathrm{it}}= \mathsf{\alpha }\mathrm{i}+{\mathsf{\beta }}^{\prime }{\mathrm{X}}_{\mathrm{it}}+{ \mathsf{\mu }}_{\mathrm{it}}, \mathrm{i}=1,\dots ,\mathrm{N} \mathrm{and} \mathrm{t}=1,\dots ,\mathrm{T}$$

(5)

where β is a K × 1 vector of parameters to be estimated and β denotes individual time-invariant disturbance parameters, whereas the K × 1 vector of repressor is represented by X_it. ${\mathsf{\mu }}_{\mathrm{it}}$ is presumed to be “independent and identically distributed” across time and composed of cross-sectional units under the null hypothesis [3]. ${\mathsf{\mu }}_{\mathrm{it}}$may be associated across cross-sections under the ${\mathrm{H}}_0$hypothesis, whereas the assumption of no serial correlation remains constant. Hence, the hypothesis of interest is:

$${\mathrm{H}}_0: {\mathrm{p}}_{\mathrm{ij}}={\mathrm{p}}_{\mathrm{ji}}=\mathrm{cor} ({\mathrm{U}}_{\mathrm{it}}, {\mathrm{U}}_{\mathrm{jt}}) \_0 \mathrm{for} \mathrm{i} \ne \mathrm{j}$$

(6)

against

$${\mathrm{H}}_1: {\mathrm{p}}_{\mathrm{ij}}={\mathrm{p}}_{\mathrm{ji}} \ne 0 \mathrm{for} \mathrm{some} \mathrm{i} \ne \mathrm{j}$$

where ${\mathrm{p}}_{\mathrm{ji}}$ is the disturbance of the product–moment correlation constant and assumed to be

$${\mathrm{p}}_{\mathrm{ij}}={\mathrm{p}}_{\mathrm{ji}}=\frac{{{\displaystyle \sum }}_{\mathrm{t} =\mathrm{i}}^{\mathrm{T}}{ \mathrm{U}}_{\mathrm{it}}{\mathrm{U}}_{\mathrm{jt}}}{({{\displaystyle \sum }}_{\mathrm{t}=\mathrm{i}}^{\mathrm{T}}{\mathrm{u}}_{\mathrm{it}}^2)\frac{1}{2}({{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{u}}_{\mathrm{jt}}^2)\frac{1}{2}}$$

The number of possible pairings (${\mathrm{u}}_{\mathrm{it}}$, ${\mathrm{u}}_{\mathrm{jt}}$) increases with N.

Pesaran’s CD Test

Breusch and Pagan [35] introduced an LM statistic in the context of seemingly unrelated regression estimates, which is valid for fixed N as $\mathrm{T} \to \infty$and denoted by

$$\mathrm{LM}=\mathrm{T} {{\displaystyle \sum }}_{\mathrm{i} 1}^{\mathrm{N}-1}{{\displaystyle \sum }}_{\mathrm{j} \frac{\mathrm{i}}{1}}^{\mathrm{N}}\mathfrak{J}\mathrm{ij}$$

The residuals pairwise correlation for sample estimation is denoted by $(\Im$ij)

$${\Im }_{\mathrm{ij}}={\Im }_{\mathrm{ji}}=\frac{{{\displaystyle \sum }}_{\mathrm{t} =1}^{\mathrm{T}}\Im \mathrm{it} \Im \mathrm{jt}}{\left( {{\displaystyle \sum }}_{\mathrm{t} =1}^{\mathrm{T}}{\mathsf{Û}}_{\mathrm{it}}^2\right)\frac{1}{2 }({{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}{\mathsf{Û}}_{\mathrm{jt}}^2)\frac{1}{2}}$$

where ${\mathsf{Û}}_{\mathrm{it}}^2$is the estimate of ${\mathrm{U}}_{\mathrm{it}}$ in Equation (6). Under the null hypothesis of interest, LM is asymptotically distributed as χ² with N (N − 1)/2 degrees of freedom.

The following alternative test proposed by Pesaran [36]

$$\mathrm{CD}=\frac{\sqrt{2\mathrm{T}}}{\mathrm{N} \left( \mathrm{N}-1\right)}({{\displaystyle \sum }}_{\mathrm{i} =1}^{\mathrm{N} -1}{{\displaystyle \sum }}_{\mathrm{j} = \mathrm{i}+1}^{\mathrm{N}}{\Im }_{\mathrm{ij}})$$

(7)

shows no cross-sectional dependence when CD $\begin{array}{c}d\\ \to \end{array}$ (0,1) for N →$\infty ,$and T is sufficiently large under the null hypothesis.

In a variety of panel-data models, including homogeneous/heterogeneous dynamic models and nonstationary models, the CD statistic has a mean of exactly zero for given values of T and N, in contrast to the LM statistic. For both homogeneous and heterogeneous dynamic models, classic fixed effect and random effect estimators are biased [37,38] The cross-sectional dependence test, on the other hand, is still valid because, even if the parameter estimations have a small sample bias, the fixed effect/random effect residuals will have a mean of exactly zero for fixed (T) if the disturbances are symmetrically distributed.

For imbalanced panels, Pesaran [36] suggests a slightly modified version of Equation (7), which is represented by:

$$\mathrm{CD}=\frac{\sqrt{2}}{\mathrm{N} \left( \mathrm{N} -1\right)}( {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N} -1}{{\displaystyle \sum }}_{\mathrm{j}=\mathrm{i}+1}^{\mathrm{N}}\sqrt{\mathrm{Tij}\Im \mathrm{ij}})$$

(8)

where Tij = # (Ti ∩ Tj) (i.e., the number of time-series observations that are similar across units i and j)

$$\Im \mathrm{ij}=\Im \mathrm{ji}=\frac{\sum \mathrm{t}ϵ\mathrm{Ti}\cap \mathrm{Tj}\left({\mathsf{Û}}_{\mathrm{it} }-{\overline{\mathsf{Ü}}}_{\mathrm{i}}\right)\left({\mathsf{Û}}_{\mathrm{jt} }-{\overline{\mathsf{Ü}}}_{\mathrm{j}}\right)}{\sum \mathrm{t}ϵ\mathrm{Ti}\cap \mathrm{Tj}{\left({\mathsf{Û}}_{\mathrm{it} }-{\overline{\mathsf{Ü}}}_{\mathrm{i}}\right)}^2\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\sum \mathrm{t}ϵ\mathrm{Ti}\cap \mathrm{Tj}{\left({\mathsf{Û}}_{\mathrm{jt} }-{\overline{\mathsf{Ü}}}_{\mathrm{j}}\right)}^2\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

and

$${\overline{\mathsf{Ü}}}_{\mathrm{i}}=\frac{\sum \mathrm{t}ϵ\mathrm{Ti}\cap {\mathrm{Tj} \mathsf{Û}}_{\mathrm{it} }}{\#\left({ \mathrm{T}}_{\mathrm{i}}\cap {\mathrm{T}}_{\mathrm{j}}\right)}$$

the revised statistic adjusts for the fact that subsets of (t) errors do not always have a mean zero.

The findings of CSD are presented in

Table 1. CD Test.

Variables	Breusch–Pagan LM	Pesaran-Scaled LM	Bias-Corrected Scaled LM	Pesaran CD
LCO2	730.84 ***	64.44 ***	64.25 ***	3.560 *
LCCO2	995.45 ***	85.85 ***	85.66 ***	0.150 ***
LGCO2	861.84 ***	76.93 ***	76.74 ***	27.60 ***
LOCO2	753.17 ***	66.57 ***	66.38 ***	0.750 ***
LEC	758.14 ***	67.04 ***	66.85 ***	1.070 ***
LGDP	1458.02 ***	133.77 ***	133.58 ***	38.02 ***
LIP	623.75 ***	54.23 ***	54.04 ***	9.120 ***
PD	1204.56 ***	109.61 ***	109.42 ***	21.930 ***
TR	557.38 ***	47.90 ***	47.71 ***	15.600 ***

Note: The level of significance is determined by 1% indicated through ***.

, as introduced earlier [36]. In panel data econometrics, cross-sectional dependency is a central issue that poses serious problems, including dimensional disorders and unit root errors [39,40]. Therefore, the scaled LM test proposed and interpreted [35] and the CD test [36] are used in the study. Before estimating the model, it is necessary to find out the CSD among the considered variables. The outcomes of the CSD test indicate that all variables appear to be cross-sectionally dependent.

The third part of

Table 2. Test for slope heterogeneity [41].

Models	Delta	Adjusted Delta Tilde
Model-1 LCO2 = f (LEC, LGDP, LIP, PD, TR)	−6.30 ***	−10.45 ***
Model-2 LCCO2 = f (LEC, LGDP, LIP, PD, TR)	−5.28 ***	−8.75 ***
Model-3 LGCO2 = f (LEC, LGDP, LIP, PD, TR)	−6.81 ***	−11.23 ***
Model-4 LOCO2 = f (LEC, LGDP, LIP, PD, TR)	−6.76 ***	−11.20 ***

Note: The level of significance is determined by 1% indicated through ***.

employs the homogeneity test, which was introduced by Pesaran and Yamagata [41], to determine whether the slope is homogeneous or not. The reason for employing [41] is that previous heterogeneity tests fail to report the problem of cross-sectional dependency; therefore, it is superior to earlier heterogeneity tests [39]. The slope heterogeneity results demonstrate that all models have an issue of heterogeneity, implying that unit root tests and cointegration techniques will yield biased results [40]. The significant values of the delta tilde ($\tilde{\Delta }$) and the adjusted delta tilde ($\tilde{\Delta }$ Adjusted) are presented in Table 2. This shows that there is a problem of slope heterogeneity and that the test statistics are statistically significant for all models.

2.2. Panel Unit Root Test

The study uses the panel unit root test because of the higher chances of CSD (cross-sectional dependency) in the data. Baltagi [42] separates panel unit root tests into two categories, that is, the unit root tests of the first and second generations, which increases the strength of the unit root tests [43]. The assumption of cross-sectional dependence is the primary dissimilarity between the two generations of unit root tests. All cross-sections are assumed to be independent in first-generation tests; however, this assumption is relaxed for the second-generation unit root tests. To resolve the issue of CSD, the study employs the second-generation CIPS unit root test introduced by Pesaran (2007).

The equation of CIPS is presented as:

$$\Delta {\mathrm{y}}_{\mathrm{it}}={\mathsf{\alpha }}_{\mathrm{i}}+{\mathsf{\rho }}_{\mathrm{i}}{\mathrm{y}}_{\mathrm{it}-1}+{\mathsf{\beta }}_{\mathrm{i}}{\overline{\mathrm{y}}}_{\mathrm{t}-1}+{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{k}}{\mathsf{\Upsilon }}_{\mathrm{ij}}\Delta {\overline{\mathrm{y}}}_{\mathrm{it}-1}+{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{k}}{\mathsf{\delta }}_{\mathrm{ij}}{\mathrm{y}}_{\mathrm{it}-1}+{\mathsf{\epsilon }}_{\mathrm{it}}$$

(9)

where the deterministic term is represented by ${\mathsf{\alpha }}_{\mathrm{i}}$, the lag of order is indicated by k and t is the cross-sectional average. According to Pesaran [44] this approach allows for CSD across the observed countries, as well as consistent conclusions, even when the sample size is small. The test statistics of CIPS are determined as follows when compared to the CIPS statistics calculated by using cross-sectional Augmented Dickey–Fuller (CADF) statistics:

$$\widehat{\mathrm{CIPS}}={\mathrm{N}}^{-1}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{CDF}}_{\mathrm{i}}$$

(10)

where (CADF) is denoted by CDF.

The study uses the Cross-Sectionally Augmented IPS 2007 [44] test to check the order of integration of different variables presented in the fourth step of

Table 3. Stationarity and Order of Integration.

Cross-Sectionally Augmented IPS (CIPS, 2007)
Variables	Level	Order of Integration
LCO2	−3.48 ***	I (0)
LCCO2	−3.14 ***	I (0)
LGCO2	−1.94	I (1)
LOCO2	−2.49 ***	I (0)
LEC	−1.61	I (1)
LGDP	−3.06 ***	I (0)
LIP	−3.59 ***	I (0)
PD	−1.43	I (1)
TR	−1.91	I (1)

Note: Critical values at 1%, 5% and 10%, respectively, are −2.340, −2.170 and −2.070 with (N, T = 30, 11). The level of significance is determined at 1 % indicated through ***.

. This is a unit root test of the second generation. For heterogeneous panels, this test is more essential since it implies the cross-sectional dependency caused by a single common component. This study employed the lag of the variables to adjust serial correlations [39]. The findings of the IPS (CIPS, 2007) show that carbon emissions, CCO₂, OCO₂, GDP and industrial production are integrated into the order I (0), whereas GCO₂, energy consumption, population density and international trade are integrated order I (1).

Hence, for this study panel, the autoregressive distributive lag (PARDL) technique is appropriate. Moreover, the results of the test confirm that none of the variables are integrated of order I (2), so the Pooled Mean Group (PMG) technique is applied for the estimation of PARDL, which is reported in table [45]. Furthermore, the outcomes of the CIPS unit root test are shown in

Table 4. Second-Generation Panel Co-integration Test [46].

Models	Variance Ratio (Statistic)	p-Value	Co-Integration Exists
Model-1 LCO2 = f (LEC, LGDP, LIP, PD, TR)	4.8812	0.0000	Yes
Model-2 LCCO2 = f (LEC, LGDP, LIP, PD, TR)	2.404	0.0081	Yes
Model-3 LGCO2 = f (LEC, LGDP, LIP, PD, TR)	22.874	0.0000	Yes
Model-4 LOCO2 = f (LEC, LGDP, LIP, PD, TR)	14.567	0.0000	Yes

, which proves the existence of unit root for entire variables. Then the panel cointegration test is employed to deal with the issue of a unit root [46].

2.3. Panel Co-Integration Test

The two nonparametric tests proposed [46] that was the extension of earlier test [47] on time series methodology to address the panel issues. WP is a pooled test that is therefore defined against the homogeneous alternative, whereas WG is a group-mean test that is specified against the heterogeneous alternative [40]. The OLS residuals ${\overline{\mathsf{Ü}}}_{\mathrm{i},\mathrm{t}}$ from Equation (1) is the starting point for Pedroni tests. Define ${\overline{\mathsf{Ü}}}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{t}=1}^{\mathrm{T}}{û}_{\mathrm{it}}^2$, $û={\mathrm{N}}^{-1}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\overline{\mathsf{Ü}}}_{\mathrm{i}}$ and ${\mathsf{ȇ}}_{\mathrm{it}}={{\displaystyle \sum }}_{\mathrm{j}=\mathrm{i}}^{\mathrm{t}}{û}_{\mathrm{ij}}$. The essential parts of the test statistics are then supplied by using these quantities:

$${\mathrm{WP}}^0={ \mathrm{N}}^{-1/2}\left({{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}^2/û\left({\mathrm{T}}^{-4}{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}{\mathsf{ȇ}}_{\mathrm{it}}^2\right)\right)$$

(11)

$${\mathrm{WG}}^0={ \mathrm{N}}^{-1/2} {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{T}}^2/\overline{\mathsf{Ü}} \left({\mathrm{T}}^{-4}{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}{\mathsf{ȇ}}_{\mathrm{it}}^2\right)$$

(12)

When the Delta technique is used for WP⁰ and a central limit theorem is applied to WG⁰ (easily shown again by writing ${\mathrm{WG}}^0={ \mathrm{N}}^{-1/2}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{WG}}_{\mathrm{i}}^0$), asymptotic standard normality is obtained in the sequential limit under the null hypothesis when suitable mean and variance correction factors are used, i.e.,

$$\mathrm{WP}=\frac{{\mathrm{WP}}^0-{ \mathrm{N}}^{1/2}{ \mathrm{M}}_{\mathrm{WP}}\left(\mathrm{s}, \mathrm{l}\right)}{\left({\mathrm{V}}_{\mathrm{WP}}\left(\mathrm{s}, \mathrm{l}\right) \right)1/2}\to \mathrm{N}\left(0, 1\right)$$

$$\mathrm{WG}=\frac{{\mathrm{WG}}^0-{ \mathrm{N}}^{\frac{1}{2}}{ \mathrm{M}}_{\mathrm{WG}}\left(\mathrm{s}, \mathrm{l}\right) }{\frac{\left({\mathrm{V}}_{\mathrm{WG}}\left(\mathrm{s}, \mathrm{l}\right)\right)1}{2}}\to \mathrm{N}\left(0, 1\right)$$

Table 4 presents the outcomes of the Panel Co-integration test. After the confirmation of the CIPS test for stationarity, the study employs the Wester Lund [46] test for co-integration [40]. The ${\mathrm{H}}_0$ of the test shows no co-integration, while the ${\mathrm{H}}_1$ shows the existence of co-integration. The outcomes of the test reject the null hypothesis of no co-integration and accept the alternative hypothesis of co-integration for both the aggregated and disaggregated models, as stated by the outcomes of the study (H₀ and H₁ are the null and alternative hypotheses).

2.4. Panel Autoregressive Distributed Lag (PARDL) Model

The PARDL model is used for econometric analysis [34]. The application of this method is appropriate in this case for the following reasons. First, it is appropriate for large time periods and small cross-sectional panels. The second and most significant motive is that it aids in the detection of linear inconsistencies, which is the key objective of this study. Finally, it is more appropriate when the integration order is less than I (1).

The two most common approaches for estimating dynamic heterogeneous panel data models are the PMG (Pooled Mean Group) and MG (Mean Group) estimators. The current study used the PMG method because it provides homogeneous coefficients in the long run as well as heterogeneous coefficients of all countries for the panel in the short run, too [30]. The PMG method is used because the association between CO₂ emissions, GDP, energy consumption, industrial production, international trade and population density may change in the short term for each cross-section. However, the same pattern can also be observed between these variables in the long term. It is also worth mentioning that alternative methods, such as FMOLS and DOLS, can also be applied, but they simply consider the long-run relationship between the series but ignore the short-run dynamics [30]. This argument further emphasizes the fact that PMG is most relevant for the current study.

$$\begin{gathered} {\mathrm{CO}}_{2\mathrm{it}}={\mathsf{\beta }}_{0\mathrm{i}}+{\mathsf{\beta }}_{1\mathrm{i}}{\mathrm{EC}}_{\mathrm{i},\mathrm{t}-1}+{\mathsf{\beta }}_{2\mathrm{i}}{\mathrm{GDP}}_{,\mathrm{t}-1}+{\mathsf{\beta }}_{3\mathrm{i}}{\mathrm{IP}}_{\mathrm{t}-1}+{\mathsf{\beta }}_{4\mathrm{i}}{\mathrm{PD}}_{\mathrm{t}-1}+{\mathsf{\beta }}_{5\mathrm{i}}{\mathrm{IT}}_{\mathrm{t}-1} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{N}1}{\mathsf{\lambda }}_{\mathrm{ij}}\Delta {\mathrm{EC}}_{\mathrm{i},\mathrm{t}-\mathrm{j}}+{\displaystyle \sum }_{\mathrm{j}=0}^{\mathrm{N}2}{\mathsf{\gamma }}_{\mathrm{ij}}\Delta {\mathrm{GDP}}_{\mathrm{t}-\mathrm{j}}+{\displaystyle \sum }_{\mathrm{j}=0}^{\mathrm{N}3}{\mathsf{\eta }}_{\mathrm{ij}}\Delta {\mathrm{IP}}_{\mathrm{t}-\mathrm{j}}+{\displaystyle \sum }_{\mathrm{j}=0}^{\mathrm{N}4}{\mathsf{\alpha }}_{\mathrm{ij}}\Delta {\mathrm{PD}}_{\mathrm{t}-\mathrm{j}} \\ +{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{N}5}{\mathsf{\phi }}_{\mathrm{ij}}\Delta {\mathrm{IT}}_{\mathrm{t}-\mathrm{j}}+{\mathsf{\epsilon }}_{\mathrm{it}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ \mathrm{i}=1, 2, 3,\dots \mathrm{N};\mathrm{t}=1, 2, 3,\dots \mathrm{T}. \end{gathered}$$

(13)

The panel ARDL is defined as: where ${\mathrm{CO}}_{2\mathrm{it}}$ is the log of CO₂ emissions over a period of time t for each cross-sectional unit i, ${\mathrm{Ec}}_{\mathrm{t}}$ represents energy consumption, ${\mathrm{GDP}}_{\mathrm{t}}$ denotes economic growth,${ \mathrm{IP}}_{\mathrm{t}}$ represents industrial production, ${\mathrm{PD}}_{\mathrm{t}}$ represents population density, ${\mathrm{IT}}_{\mathrm{t}}$ represents international trade and sample units are indicated by “i”, whereas the number of time periods is represented by “t”. It is probable to re-specify Equation (13) to include the ECM (error correction term) as follows:

$$\begin{gathered} \Delta {\mathrm{CO}}_{2\mathrm{it}}={\mathsf{\delta }}_{\mathrm{i}}{ \mathrm{v}}_{\mathrm{i},\mathrm{t}-1}+{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{N}1}{\mathsf{\lambda }}_{\mathrm{ij}}\Delta \mathrm{EC}+{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{N}2}{\mathsf{\gamma }}_{\mathrm{ij}}\Delta {\mathrm{GDP}}_{\mathrm{t}-\mathrm{j}}+{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{N}3}{\mathsf{\eta }}_{\mathrm{ij}}\Delta {\mathrm{IP}}_{\mathrm{t}-\mathrm{j}} \\ +{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{N}4}{\mathsf{\alpha }}_{\mathrm{ij}}\Delta {\mathrm{PD}}_{\mathrm{t}-\mathrm{j}}+{{\displaystyle \sum }}_{\mathrm{j}=0}^{\mathrm{N}5}{\mathsf{\phi }}_{\mathrm{ij}}\Delta {\mathrm{IT}}_{\mathrm{t}-\mathrm{j}}+{\mathsf{\epsilon }}_{\mathrm{it}} \end{gathered}$$

(14)

where ${\mathrm{v}}_{\mathrm{i},\mathrm{t}-1}={ \mathrm{EC}}_{\mathrm{i},\mathrm{t}-1}-{\mathsf{\varphi }}_{0\mathrm{i}}-{\mathsf{\varphi }}_{1\mathrm{i}}{\mathrm{GDP}}_{\mathrm{t}-1}-{\mathsf{\varphi }}_{2\mathrm{i}}{\mathrm{IP}}_{\mathrm{t}-1}-{\mathsf{\varphi }}_{3\mathrm{i}}{\mathrm{PD}}_{\mathrm{t}-1}-{\mathsf{\varphi }}_{4\mathrm{i}}{\mathrm{IT}}_{\mathrm{t}-1}$ shows the linear error correction term for each unit and the parameter $\mathsf{\delta }\mathrm{i}$ is the error-correcting speed of adjustment term for each unit, which is also equivalent to${ \mathsf{\beta }}_{1\mathrm{i}}$. The parameters${\mathsf{\varphi }}_{0\mathrm{i}}$, ${\mathsf{\varphi }}_{1\mathrm{i}}$, ${\mathsf{\varphi }}_{2\mathrm{i}}$, ${\mathsf{\varphi }}_{3\mathrm{i}}$ and ${\mathsf{\varphi }}_{4\mathrm{i}}$ are computed as $-\frac{{\mathsf{\beta }}_{0\mathrm{i}}}{{\mathsf{\beta }}_{1\mathrm{i}}}$, $-\frac{{\mathsf{\beta }}_{2\mathrm{i}}}{{\mathsf{\beta }}_{1\mathrm{i}}}$, $-\frac{{\mathsf{\beta }}_{3\mathrm{i}}}{{\mathsf{\beta }}_{2\mathrm{i}}}$,$-\frac{{\mathsf{\beta }}_{4\mathrm{i}}}{{\mathsf{\beta }}_{3\mathrm{i}}}$ and $-\frac{{\mathsf{\beta }}_{5\mathrm{i}}}{{\mathsf{\beta }}_{4\mathrm{i}}}$, respectively.

The study uses the same methodology to estimate the disaggregate analysis by applying the panel ARDL technique.

3. Results

3.1. Aggregate Model Results of (PARDL)

Table 5. The short- and long-run results of the aggregate model of Equation (1) are estimated by PARDL.

Variable	Coefficient	Std. Error	t-Statistic	Prob. *
Dependent variable; CO2	Long-Run Equation
LEC	0.949593	0.079269	11.97942	0.0000
LGDP	0.123012	0.051654	2.381476	0.0182
LIP	0.012787	0.055625	0.229878	0.8184
PD	0.004258	0.000412	10.33698	0.0000
TR	−0.002628	0.000558	−4.707642	0.0000
Dependent variable; CO2	Short-Run Equation
COINTEQ01	−0.177040	0.082753	−2.139374	0.0337
D(LEC)	0.446371	0.222972	2.001913	0.0467
D(LGDP)	0.453656	0.156210	2.904138	0.0041
D(LIP)	−0.057310	0.045241	−1.266792	0.2068
D(PD)	−0.044685	0.060031	−0.744370	0.4576
D(TR)	0.000416	0.000475	0.874857	0.3827
C	1.645752	0.717668	2.293195	0.0229
Mean dependent var	0.016463	S.D. dependent var		0.053726
S.E. of regression	0.042846	Akaike info criterion		−4.717007
Sum squared resid	0.354311	Schwarz criterion		−3.638552
Log-likelihood	730.5885	Hannan–Quinn criteria.		−4.284192

* Note: p-values and any subsequent tests do not account for model selection. The model is estimated by PMG.

indicates the short- and long-term estimates for the association between CO₂ emission and the given explanatory variables, namely, energy consumption, GDP, industrial production, international trade and population density. Table 5 also illustrates the outcomes of the error-correction term, which has a significant negative effect, implying that the system converts to long-run equilibrium after a shock.

The short- and long-term results indicate that CO₂ emissions are positively associated with energy consumption and are statistically significant. More specifically, a one percent intensification in the consumption of energy will tend to increase CO₂ emissions by 0.446 million tons each year in the short run, while a 1% growth in the use of energy leads to a rise in carbon emissions by 0.949 million tons in the long run. The outcomes of the study are consistent and supported by different studies [15,45].

The rationale for this relationship is based on the scale effect, which argues that an increase in the scale of the economy increases the demand for energy, which causes CO₂ emissions at early stages of development; in the long run, as countries become more developed, energy consumption will further increase, which leads to increased CO₂ emissions [45]. Both the short- and long-run CO₂ emissions are positively related to GDP and statistically significant. Specifically, in the short run, an increase of 1% in economic growth will lead to a rise in carbon emissions by 0.453 million tons per year, whereas, in the long run, a one percent incline in GDP tends to an upsurge in CO₂ emissions by 0.123 million tones. The results of this study are consistent with the findings of a few studies [48] but also contradict the findings of some other studies [3]. This might be explained by the N-shaped EKC, which illustrates that the incline in income may once again lead to a positive association between GDP and environmental distortions [14]. The results also indicate that CO₂ emissions are negatively associated with industrial production in the short term and positively associated in the long term but are statistically insignificant. The CO₂ emissions are inversely but insignificant associated with population density in the short run and positively and significantly related to CO₂ emissions in the long run. More specifically, a one percent increase in population density leads to an increase in carbon emission by 0.004 million tons in the long run [49,50]. The rationale of this study is based on the higher economic activities of the studied countries, which indicates that as the population increases, the demand for goods and services increases, causing economic activity shifts and leading to higher CO₂ emissions [49]. It is also found that CO₂ emissions are positively associated and statistically insignificant with international trade in the short run while being negatively and significantly associated with CO₂ emissions in the long run. Specifically, a 1% incline in international trade tends to a decline in carbon emissions by 0.002 million tons in the long run. These conclusions are consistent with a reported study [51] and inconsistent with the findings of some other studies [25]. The reason for this might be traded gains/surpluses from international trade, which may lead to a decline in CO₂ emissions in the long term [51].

3.2. Panel ARDL Results of Disaggregate CO₂ Emissions from Coal Model

Table 6. Disaggregate the Coal Consumption Model of (PARDL) from Equation (2).

Variable	Coefficient	Std. Error	t-Statistic	Prob. *
Dependent variable; CCO2	Long-Run Equation
LEC	2.349141	0.227240	10.33773	0.0000
LGDP	−0.915808	0.134216	−6.823393	0.0000
LIP	−0.020424	0.066491	−0.307166	0.7590
PD	0.011191	0.002904	3.854142	0.0001
TR	0.006239	0.002172	2.872824	0.0044
Dependent variable; CCO2	Short-Run Equation
COINTEQ01	−0.206805	0.054009	−3.829110	0.0002
D(LEC)	0.166457	0.385363	0.431948	0.6662
D(LGDP)	0.427531	0.209855	2.037270	0.0427
D(LIP)	0.067281	0.063426	1.060782	0.2898
D(PD)	0.198828	0.111873	1.777273	0.0767
D(TR)	0.002819	0.001434	1.965354	0.0505
C	5.253246	1.467027	3.580878	0.0004
Mean dependent var	0.014665	S.D. dependent var		0.114659
S.E. of regression	0.087832	Akaike info criterion		−2.868478
Sum squared resid	1.913201	Schwarz criterion		−1.924461
Log-likelihood	555.2988	Hannan–Quinn criteria		−2.491923

* Note: p-values and any subsequent tests do not account for model selection. The model is estimated by PMG.

indicates the short- and long-run estimates for the association between CO₂ emission from coal and the given explanatory variables (explanatory variables are GDP, energy consumption, industrial production, international trade and population density). The outcomes of the error-correction term indicate significant and negative effects, which shows that the system converts to long-run equilibrium after a shock. It is evident from the results of this study that a short-term positive and insignificant association between CCO₂ and energy consumption exists while, in the long run, the relationship is positive and significance is found. This means that a 1% growth in energy consumption tends to decrease CCO₂ emissions by 2.349 million tons in the long run, and the results of this study are supported by the findings of some other studies [31,48] but contrary to the findings of [52]. The economic perspective behind this result signifies that coal is the main source of energy combustion which contributes significantly to CO₂ emissions and affects the environment in long run [31,48].

The bond between CCO₂ and economic growth is positively and statistically significantly related in the short run, while an inverse and significant association is observed in the long run. Precisely, an increase of 1% in economic growth will tend to grow CCO₂ emissions by 0.427 million tons each year in the short run while a 1% incline in GDP tends to decline carbon emissions by 0.915 million tons in the long run. These findings, which are based on coal emissions, are supported by [53] and inconsistent with the findings of [8]. This result may confirm the Environmental Kuznets Curve, which indicates that in the first half, degrading the environment can help in achieving economic growth while achieving the threshold level of increasing economic growth will not increase CO₂ emissions [20]. The association between CCO₂ emissions and industrial production is positively but insignificantly connected in the short run, while a negative and insignificant relationship is found in the long run. The relationship between CCO₂ emissions and population density is positive in both the short and long run and is statistically significant. More precisely, an increase of 1% in population density will lead to an increase in CO₂ emissions by 0.198 million tons each year in the short run while a 1% incline in population density adds to CO₂ emissions by 0.011 million tons in the long run, which supports the findings of [49]. The acceleration in economic activities indicates that when the population increases, the demand increases, and this production increase contributes to CO₂ emissions [49]. Furthermore, in the short and long run, the association between CCO₂ and international trade is positive and significant. More, specifically a one percent increase in international trade will tend to grow CCO₂ emissions by 0.002 million tons each year in the short run while a 1% incline in international trade rises carbon emissions from coal by 0.006 million tons in the long term, but these results are inconsistent with a previous study [14].

3.3. Panel ARDL Results of Disaggregate CCO₂ Emissions from Gas Model

Table 7. Disaggregate Gas Consumption Model (PARDL) from Equation (3).

Variable	Coefficient	Std. Error	t-Statistic	Prob. *
Dependent variable; GCO2	Long Run Equation
LEC	−1.789820	0.436701	−4.098500	0.0001
LGDP	−0.733948	0.325836	−2.252506	0.0254
LIP	1.277670	0.387333	3.298635	0.0012
PD	0.013408	0.003536	3.791650	0.0002
TR	−0.010776	0.002707	−3.980935	0.0001
Dependent variable; GCO2	Short Run Equation
COINTEQ01	−0.187061	0.070491	−2.653703	0.0086
D(LEC)	0.896923	0.366204	2.449241	0.0152
D(LGDP)	0.218600	0.276265	0.791271	0.4298
D(LIP)	−0.402277	0.141615	−2.840650	0.0050
D(PD)	0.031365	0.034774	0.901971	0.3682
D(TR)	0.000799	0.002418	0.330425	0.7414
C	3.119797	1.125986	2.770723	0.0061
Mean dependent var	0.040745	S.D. dependent var		0.104016
S.E. of regression	0.205264	Akaike info criterion		−2.823305
Sum squared resid	8.131719	Schwarz criterion		−1.744850
Log-likelihood	470.2045	Hannan–Quinn criteria		−2.390490

* Note: p-values and any subsequent tests do not account for model selection. The model is estimated by PMG.

presents the estimates for the association between CCO₂ emission from gas and the given variables for the short and long term. The results of the error-correction term indicate that the system transforms to a long-run equilibrium after a shock. The outcomes of the study specify a positive relation between GCO₂ and consumption of energy in the short run but are inversely and significantly associated in the long run. That is, a onepercent increase in the use of energy will tend to increase CO₂ emissions from gas by 0.896 million tons each year in the short run while a rise of 1% in the consumption of energy will lead to reduction in GCO₂ by 1.789 million tons in the long run, which is supported by the findings of the cited study [29] and contrary to the findings of the reported study [32].

The rationale behind this result may be that natural gas is often defined as clean energy, and compared to the combustion of other sources of energy such as coal and oil, it emits less CO₂ emissions; it is also considered more energy efficient [29]. The affiliation between GCO₂ and GDP is positive but insignificant in the short term while inversely and significantly connected in the long term. This means that an increase of 1% in economic growth decreases carbon emissions from gas by 0.733 million tons in the long term [26]. In the short run, the relationship between GCO2 and industrial production is negative but significant, whereas it is positive and significant in the long term. More precisely, a one percent increase in industrial production will tend to a decline in GCO₂ by 0.402 million tons each year in the short run, while a 1% growth in industrial production leads to an incline in carbon emission by 1.277 million tons in the long run, which is contrary to the findings of [9]. The affiliation between GCO₂ emissions and population density is positive and associated in the short run and the long run but insignificant and significant, respectively. This means that an increase of 1% in population density would result in contributing 0.013 million tons of GCO₂ per year [49]. The association between CO₂ emissions from gas and international trade is positively and insignificantly associated in the short run, while it is inversely and significantly connected in the long run. More specifically, an incline of 1% in international trade reduces GCO₂ by 0.010 million tons in the long run, and these results are supported by the cited literature [14].

3.4. Panel ARDL Results of Disaggregate CO₂ Emissions from Oil Model

Table 8. Disaggregate Oil Consumption Model (PARDL) Equation (4).

Variable	Coefficient	Std. Error	t-Statistic	Prob. *
Dependent variable; OCO2	Long-Run Equation
LEC	0.717997	0.109664	6.547216	0.0000
LGDP	0.369502	0.077766	4.751479	0.0000
LIP	−0.116989	0.067136	−1.742563	0.0826
PD	−0.000982	0.001875	−0.523936	0.6008
TR	−0.006615	0.000643	−10.28572	0.0000
Dependent variable; OCO2	Short-Run Equation
COINTEQ01	−0.195378	0.085964	−2.272778	0.0239
D(LEC)	0.485550	0.125315	3.874649	0.0001
D(LGDP)	0.427650	0.162573	2.630516	0.0091
D(LIP)	−0.027958	0.048725	−0.573781	0.5666
D(PD)	0.073759	0.051448	1.433652	0.1529
D(TR)	−0.000374	0.000840	−0.444896	0.6568
C	1.427686	0.604875	2.360298	0.0190
Mean dependent var	0.011617	S.D. dependent var		0.062187
S.E. of regression	0.036311	Akaike info criterion		−3.930103
Sum squared resid	0.326993	Schwarz criterion		−2.986086
Log-likelihood	730.4671	Hannan–Quinn criteria.		−3.553549

* Note: p-values and any subsequent tests do not account for model selection. The model is estimated by PMG.

express the short- and long-term estimates for the association between CO₂ emissions from oil and the given independent variables. The results of the error-correction term in Table 8 shows a significant negative effect, indicating that the system transforms to a long-run equilibrium after a shock. The results of the test indicate that a positive association exists between OCO₂ (OCO₂ is CO₂ emissions from oil) and consumption of energy in the short and long run that is statistically significant. Specifically, an incline of 1% in energy consumption will lead to a rise in OCO₂ emissions by 0.485 million tons each year in the short run, while a 1% increase in consumption of energy tends to a shift in CO₂ emissions from oil by 0.717 million tons in the long run [13,54,55]. As oil is also the main source of fossil fuel combustion, it leads to a higher contribution in CO₂ emissions [54]. The bond between OCO₂ and GDP is positively and statistically significant in both the short and the long run. A 1% rise in GDP will lead to an increase in CO₂ emissions from oil by 0.427 million tons each year in the short run, while a rise of 1% in GDP leads to an increase in OCO₂ by 0.369 million tons in the long run, and these results are both supported by the literature [34] and are contrary to a previously cited study [4].

The relation between OCO₂ and industrial production is negative in both the short run and long run but insignificant and significant, respectively. A 1% growth in industrial production leads to a decline in OCO₂ emissions by 0.116 million tons in the long term, and these outcomes are contrary to a few studies [9,55]. Our results can be supported by some economic reasoning that technological innovation and transformation help to decline carbon emissions in the long run [55]. The connection between OCO₂ and population density is positive in the short run and inversely related in the long run, but statistically insignificant for both periods. The association between OCO₂ and international trade is inverse and insignificant in the short run but positively and significantly related in the long term. From the table, an incline of 1% in international trade tends to increase CO₂ emissions by 0.006 million tons in the long run [56] and is inconsistent with the results of another reported study [50].

4. Conclusions

The above discussion regarding the findings of this study indicates a strong association between carbon emissions and energy consumption from both aggregated and disaggregated models. It is revealed that an increase of 1% in energy consumption tends to increase the carbon emissions of the top carbon-emitting countries by 0.94% in the long run (Table 6), while an increase of 1% in energy consumption tends to grow carbon emissions from coal by 2.34% in the long run (Table 7). However, Table 8 reveals that a rise of 1% in energy consumption tends to decline carbon emissions from gas by 1.78%, whereas Table 8 shows that a rise of 1% in energy consumption positively shifts carbon emissions from oil by 0.71% in the long run. Moreover, the results of error correction models for all models reveal that after a shock, the system converges to the equilibrium in the long run. Additionally, the results of this study also verify the findings of WDI that the top emitting countries produce 36.6% of all energy and emit 33.7% of the world’s carbon emissions. The results of economic growth and emissions of CO₂, CCO₂, GCO₂ and OCO₂ indicate that an increase of 1% in EC (EC is energy consumption) shifts economic growth in the long term for all models, which further presents that emissions are positive for CO₂ and OCO₂ while being inversely related with emission from coal and gas models. There are mixed results of industrial production between energy consumption and CO₂ emissions from gas, coal and oil in the long run. Population density data show that an incline of 1% in EC shifts carbon emissions by 0.004, 0.0111 and 0.013% in the long run for the CO₂, CCO₂, and GCO₂ models. The findings of international trade indicate that an upsurge of 1% in EC contributes to carbon emissions by −0.002, 0.006, −0.010 and −0.006% for all models in the long run. This means that countries need to reduce their consumption of coal and oil, which may help to decrease carbon emissions and help control the environmental degradation, specifically for the top carbon-emitting countries, but and for other countries as well. This refers to the composition effect, which focuses on the use of clean energy instead of dirty energy in the production and consumption process. This is supported by our findings in Table 6 and Table 8, where we have found a positive association between carbon emissions from coal and oil and energy consumption in the long run for the top carbon-emitting countries.

So, it is the need of the hour that the top emitting countries and other nations shift their consumption patterns to reduce carbon emissions by focusing on gas consumption. The shift from oil or coal to gas in the production process will also help to reduce the pressure on oil consumption and its prices, which will ultimately control the prices of various economic goods and services. This shift also helps to solve geopolitical issues by reducing the demand for oil from the international market by switching the consumption of oil and coal to gas. There is a need to increase clean energy use that requires optimal pricing of alternative energy products to smoothly run the markets. Column four of Table 7 specifies a negative relationship between carbon emissions from gas and energy consumption in the long run, elaborating that increasing gas consumption will aid in a decline in carbon emissions in the top carbon-emitting countries.

The industrial sector is emitting a significant amount of carbon emissions to meet higher market demand; therefore, developed nations and other nations need to use environmentally friendly technologies which may mitigate carbon emissions. The governments of developed nations and other countries need to implement policies for regulating population density, which may help to decline the carbon emissions from the household level by providing clean energy because the provision of any public good or service such as gas and water sanitation is comparatively easy in high-density areas. The provision of a gas facility will reduce the demand for fossil fuels and forest products for cooking purposes. These findings are supported by our findings in column eight of Table 5, Table 6 and Table 7 that carbon emissions and population density are positively related in the long run for the top carbon-emitting countries. Moreover, the developed countries need to reduce trade barriers, which will promote international trade and will create opportunities for adopting new environmentally friendly technologies to other nations that will bring a negative change in emission levels across the world.

We can formulate the following policy based on our findings to control further environmental degradation. These suggestions may not only help the top emitting countries but also the rest of the world in achieving a better and sustained environment;

➢

Optimal pricing of alternative energy is required for the adoption of clean energy;

➢

There is a need to shift the consumption pattern from oil and coal to gas;

➢

The geopolitical crisis can also be resolved by lowering the demand for oil from the international market;

➢

There is a need to adopt environmentally friendly and advanced technology by lowering trade barriers.