Creep Characteristic Test and Creep Model of Frozen Soil

Abstract

In order to research the creep deformation characteristics of frozen soil and the effect of various influencing factors on creep, indoor uniaxial creep tests were carried out on frozen soil specimens at temperatures of −5, −4, −3 and −2 °C under loads of 0.25, 0.5, and 0.75 σ_t, respectively. The creep deformation characteristics of frozen soil under different temperatures and load conditions are analyzed under unconfined conditions. The results show that under the uniaxial creep test conditions, when the load is low, there is no accelerated creep stage in the creep curve, which belongs to the decaying type creep; when the load is 0.75 σ_t, the creep curve enters the stage of accelerated creep, and the creep turns non-attenuated; temperature is the most important external factor affecting permafrost soil creep, and the proportion of ice is the key internal factor for affecting permafrost soil creep, the temperature is negatively correlated with the proportion of ice and the sensitivity of creep rate to temperature and load increases with the decrease of the proportion of ice; the damage variable D is introduced to modify the creep constitutive equation of the frozen soil, the creep process of frozen soil is well described by the modified creep constitutive equation for frozen soil.

1. Introduction

The Qinghai-Tibet Plateau is the largest high-altitude permafrost region on earth [1]. In the negative temperature environment, the water in the soil pores condenses and freezes into ice, resulting in frost heave deformation of the soil. When it comes to engineering construction in permafrost regions, changes in the mechanical properties of frozen soil and their consequences must be considered [2,3]. The most essential difference between frozen soil and conventional thawed or unfrozen soil is the rheological properties of ice and unfrozen water [4,5]. The existence of ice makes the soil change from a three-phase system to that of four phases consisting of solid mineral particles, poly crystalline ice, unfrozen water and gas. Creep is one of the most important mechanical behaviors of frozen soil and is defined as the change in deformation with time when the stress is constant.

Research on the creep of frozen soil has always been a frontier topic in the mechanics of frozen soil mechanics. Many scholars have observed microstructure changes during uniaxial creep of frozen soil. The results show that the creep process is the result of the combined action of the development of micro-cracks in the frozen soil, the destruction of the skeleton particle structure and the evolution of other defects under the action of external loads [6,7,8]. Through systematic experimental research, Zhu [9,10] found that when the temperature of frozen soil is higher than −1 °C, the axial strain lowers sharply with rising soil temperature, and a small temperature change can also cause a large change in strain, and the time for deformation stabilization of frozen soil is usually long, if ever, such as tens of days or even months. Possibly this is due to a large amount of unfrozen water in the frozen soil, and the unfrozen water under pressure in the soil undergoes slow phase changes, migration, infiltration and recrystallization. Mcrobert et al. [11] analyzed the stable creep rate of frozen soil with high ice content in the range of −0.8~−4.0 °C through experiments, and found that under the same conditions, the higher the ice content, the greater the creep rate of frozen soil. Ma et al. [12] studied the creep characteristics of frozen soil with high ice content. The test results show that no matter how much stress and how long the action time is, the creep process of uniaxial compression of frozen clay with high ice content has attenuation characteristics. In order to make the test conditions more in line with the deformation conditions of permafrost soil under climate warming, Zheng et al. [13] carried out a constant load heating test of permafrost soil indoors. It is found that the compressibility of frozen soil at higher temperature is much larger than that at lower temperature, and temperature is the main factor for affecting the compressibility of frozen soil. Eckardt et al. [14] carried out uniaxial creep test research by means of hierarchical loading and obtained the functional relationship between the mechanical parameters of the frozen specimen and soil temperature. Yao et al. [15] carried out uniaxial compression and graded loading creep tests on clay in deep mines under negative temperature conditions. Liu et al. [16] conducted in-depth research on the permafrost layer of Niangmute coal mine and pointed out that the permafrost layer has special creep characteristics. Shang et al. [17] revealed the law of structural deformation and fracture of the overlying permafrost through the stope “thin plate” theory. The above studies have well revealed the creep properties of frozen soil but the research on the creep properties of frozen soil under various influencing factors is far from adequate.

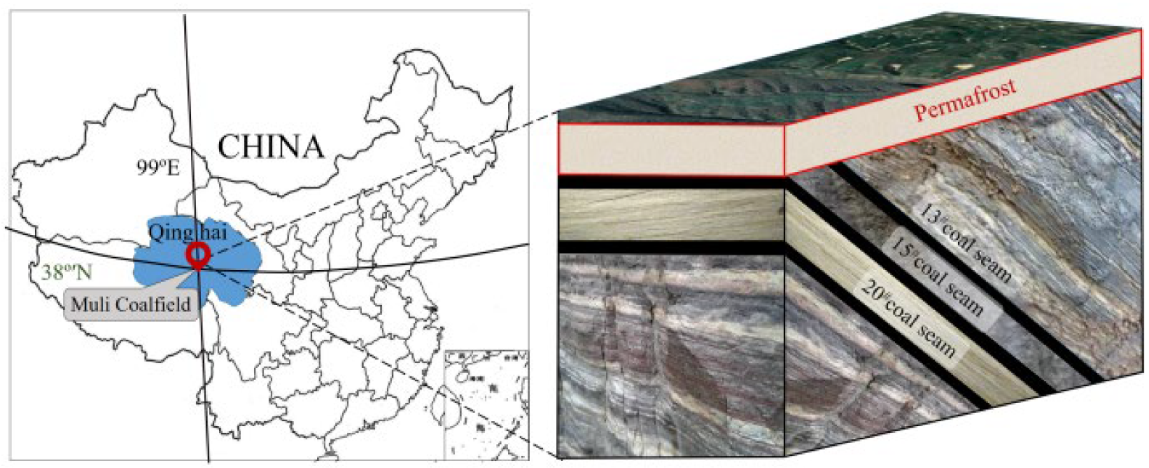
In this study, the overburden frozen soil of Jiangcang coal mine in the permafrost region on the Qinghai-Tibet Plateau was taken as the specimen, and the creep deformation characteristics of frozen soil in the high temperature range and their relationships with various influencing factors were investigated by conducting indoor uniaxial creep tests. A new permafrost creep model was established based on the revised Nishihara model. The distribution characteristics of frozen soil and underlying coal seams in Jiangcang Coal Mine are shown in Figure 1. The research results can provide a theoretical basis for the mining of underlying coal in the Jiangcang coal mine and green mining and reclamation in Muli coalfield mining area.

2. Experimental Design

2.1. Sample Preparation

The experimental frozen soil was collected from the overlying permafrost layer of Jiangcang Mine in the Muli Coalfield in the headwater area of the Daton River on the east Qinghai-Tibet Plateau. The main components are gravels, loamy sands and ice crystals. The retrieved soil samples were air-dried, rolled, and passed through the 2.0 mm sieve. A cylindrical standard specimen of Φ50 × 100 mm was prepared, with the moisture content at 23%, and dry density at 2.1 g/cm³. The production process of frozen soil specimens strictly follows the frozen soil uniaxial compression test method standard for frozen soils. A total of four groups of cylindrical frozen soil specimens were processed in this experiment, and the experimental temperatures were −5, −4, −3 and −2 °C, respectively, to ensure that there are not less than three frozen soil samples under the same conditions. The frozen soil sample used for creep test is named FSC_i-j, where i and j are the absolute value of test temperature and specimen number respectively (For example, the number of the second test piece at −3 °C is FSC₃-b).

2.2. Experimental System

We used the TAW-1000 microcomputer-controlled single-triaxial creep testing machine (Zhongqiao Bolian Instrument Equipment Co., Ltd., Beijing, China). As shown in Figure 2, for the low temperature control, we adopted (Zhejiang Danfu Environmental Technology Co., Ltd. Hangzhou, China) TMS8019-E5000-R40 low temperature circulation device, with the temperature range at −60 to −40 °C, the accuracy of temperature fluctuation is ±0.1 °C. The maximum axial load of the loading system is 1000 kN, and the accuracy is ±1% [18]. The suitable sample size is Φ50 × 100 mm, and the accuracy of deformation measurement is ±0.005 mm.

2.3. Experimental Program

First, a conventional uniaxial compression test was carried out on the frozen soil specimens at −5~−2 °C, and the mechanical parameters of the frozen soil specimens were obtained to provide a basis for determining the creep loading level. The average uniaxial compressive strengths of the four frozen soil specimens at different temperatures are 4.58, 5.18, 5.47 and 6.53 MPa, respectively (

Table 1. Results of permafrost uniaxial compression test.

Sample No.	Soil Temperature (°C)	Average Compressive Strength (MPa)
FS1-1,2,3	−2	4.58
FS2-1,2,3	−3	5.18
FS3-1,2,3	−4	5.47
FS4-1,2,3	−5	6.53

).

The creep test was carried out on the frozen soil under four different temperature conditions by the method of graded loading. The test load was divided into three grades. The creep loading grades were 0.25, 0.5 and 0.75 σ_t and keep it at 0.75 σ_t until the frozen soil sample is destroyed. The graded loading stress values under different stress states are shown in

Table 2. Frozen soil creep test design.

Sample No.	Sample Temperature (°C)	Axial Loading Stress (MPa)
		0.25 σt	0.5 σt	0.75 σt
FSC2-a,b,c	−2	1.15	2.29	3.43
FSC3-a,b,c	−3	1.30	2.59	3.89
FSC4-a,b,c	−4	1.37	2.74	4.10
FSC5-a,b,c	−5	1.63	3.27	4.90

.

3. Creep Test Results and Analysis

Due to the limited space,

Table 3. Creep deformation characteristics under different conditions.

Sample Number	Destruction Form	Binarization	Creep Curve	Brief Description
FSC2-b				(1) The number of tensile failures increases; (2) The shear failure of the main oblique fissure dominates the failure of the specimen, and a few small fissures appear around it; (3) The maximum axial deformation is 0.54.
FSC3-c				(1) Increased number of tensile and shear failures; (2) The mixed failure of tension and shear leads to the failure of the specimen, and the distribution of cracks is complex; (3) The maximum axial deformation is 0.63.
FSC4-a				(1) The distribution area of cracks increased, concentrated in the middle of the specimen, and the number of shear failures increased significantly; (2) The mixed failure of tension and shear leads to the failure of the specimen; (3) The maximum axial deformation is 0.78.
FSC5-b				(1) The average track length of cracks increased, concentrated in the middle and upper part of the specimen, and the number of shear failures increased significantly; (2) The mixed failure of tension and shear leads to the failure of the specimen, and the failure form of the specimen is complex; (3) The maximum axial deformation is 0.86.

only lists a set of typical creep curves under each test condition for description. The creep behavior of frozen soil can be regarded as the external macroscopic manifestation of the microscopic damage evolution of the internal structure of the sample. In general, the crack development of frozen soil is relatively slow when it is in the initial creep and stable creep stages, and the increase rate of cracks in frozen soil is very rapid when it is in the accelerated creep stage. The soil temperature has a great influence on the failure mode of the frozen soil sample. When the soil temperature is −2 °C, a main oblique crack appears in the frozen soil sample, and some small cracks, around it. At −5 °C~−3 °C, the damage cracks of the frozen soil samples also gradually increased, and tiny cracks appeared. The crack spacing of the samples gradually formed, and the tensile characteristics appeared [19].

In the case of the same soil moisture content and axial stress, the soil temperature of the frozen soil specimens at −5, −4, −3 and −2 °C, respectively, the creep deformation increases with the decrease of soil temperature and the lowest, the creep strain (0.54) at −5 °C increased by 59.26% compared to the highest soil temperature −2 °C (0.86). The higher the temperature, the shorter the specimen in the stable creep stage during the creep process, and the larger the slope of the soil curve in the accelerated creep stage.

As shown in Table 3, when the axial stress is 0.25 σ_t, the axial stress at this stage is mainly borne by the pore pressure of the specimen, and the pores and cracks in the frozen soil are compacted and closed. The lower the temperature, the larger the proportion of ice and the smaller the unfilled porosity. The smaller the compressible space of the sample, the smaller the deformation. When the axial stress is 0.5 σ_t, the initial cracks of the specimen expand and new cracks sprout, and the external load is transferred from the pore pressure to the soil particle skeleton. As soil temperature decreases, the effective stress of the specimen increases. The coupling effect of effective stress is complex, resulting in an insignificant regularity of creep deformation. When the axial stress is 0.75 σ_t, the crack breaks rapidly at this stage, and the axial stress is mainly borne by the soil particle skeleton. When entering the accelerated creep stage, the creep rate of the specimen increases; the lower the temperature is, the later it enters the accelerated creep stage, and the greater the deformation after entering the accelerated creep stage.

4. Creep Constitutive Equation of Frozen Soil

The classic Nishihara model is mainly composed of two parts in series: the generalized Kelvin body and the viscoplastic body (Figure 3). This model can describe the visco-elastic-plastic change characteristics during the creep process of frozen soil and can be used for featuring the creep characteristics of geotechnical materials.

The following Formula (1) is the creep equation of this model.

$$\epsilon =\left\{\begin{array}{ll}\frac{\sigma }{E_0}+\frac{\sigma }{E_1}(1-e^{-\frac{E_1}{{\eta }_1}t})\hfill & \sigma <{\sigma }_s\\ \frac{\sigma }{E_0}+\frac{\sigma }{E_1}(1-e^{-\frac{E_1}{{\eta }_1}t})+\frac{\sigma -{\sigma }_s}{{\eta }_2}t\hfill & \sigma \ge {\sigma }_s\end{array}\right.$$

(1)

In the formula: E₀ represents the elastic modulus of the Hooke elastomer; η₁ and E₁ represent the viscous coefficient and elastic modulus in the Kelvin model; η₂ represents the viscous coefficient in the viscoplastic body; σ represents the Creep stress; σ_s represents the yield stress.

4.1. Modification of Frozen Soil Creep Constitutive Model

The creep of frozen soil is nonlinear, and the current classical creep models are basically composed of linear elements. The obvious disadvantage is that it can only describe the primary and stable stages of the frozen soil creep process; the accelerated creep phase is not well described. Therefore, some scholars suggest introducing nonlinear elements or damage variables into the creep model for model improvement. By borrowing this method, as shown in Figure 4, this is corrected based on the classical Nishihara model, and the viscous coefficient in the viscoelastic element in the model is corrected as a function of creep time and stress level. The damage variable is considered in the plastic element, and a modified frozen soil creep model is thereupon established [20].

(1)

Viscoelastic part

The viscoelastic part of the frozen soil model is mainly composed of nonlinear viscous elements and a spring in parallel. In the creep process of frozen soil, its nonlinear characteristics are significant, and the nonlinear characteristics are affected by the magnitude of the load and its duration at the same time. In this paper, by referring to the relevant literature on the frozen soil creep model [21], the viscosity coefficient is modified as a function of creep time and stress level, which can be expressed as the following expression:

$${\eta }_1\left(t,\sigma \right)={\eta }_{10}\left(\frac{2{\sigma }_0-\sigma }{\sigma }\right)\frac{{\left(t/t_0\right)}^{1/3}}{\left[{\left(t/t_0\right)}^{1/3}+1\right]}$$

(2)

In the formula: σ₀ represents the compressive strength of the frozen soil at the same temperature; σ represents the creep stress; η₁₀ represents the initial viscosity coefficient of the viscoelastic body; t₀ represents the frozen soil creep time reference value, the unit is h, and t₀ = 1 for this frozen soil test.

Derivative of the time in Equation (3), we can get:

$${\dot{\eta }}_1(\mathit{t},\sigma )={\eta }_{10}(\frac{2{\sigma }_0-\sigma }{\sigma })\frac{\frac{1}{3}{(t/t_0)}^{-2/3}}{{\left[{\left(t/t_0\right)}^{1/3}+1\right]}^2}\ge 0$$

(3)

Thus, the constitutive equation of the modified Kelvin style can be obtained as:

$$\sigma =E_1\epsilon \left(t\right)+{\eta }_1\left(t,\sigma \right)\frac{d\epsilon \left(t\right)}{dt}$$

(4)

The above Formula (4) can be obtained by definite integration of the separated variables under the condition of constant stress (t = 0, ε(t) = 0), and finally the creep equation of the unsteady Kelvin body can be obtained as:

$$\epsilon \left(t\right)=\frac{{\sigma }_0}{E_1}\left[1-e^{\left(-\alpha t-\frac{3}{2}\alpha {\left(t/t_0\right)}^{2/3}\right)}\right]$$

(5)

In the above expression:

$$\alpha =\frac{E_1}{{\eta }_{10}}\left(\frac{\sigma }{2{\sigma }_0-\sigma }\right)$$

(6)

Therefore, the Kelvin style after the above correction can be well-used to describe the decay creep process of frozen soil.

(2)

Viscoplastic part

The relevant permafrost creep test research [22] shows that there is a damage effect in the frozen soil. When the stress is greater than a certain critical value, the damage effect of the frozen soil will occur. When it is dominant, the frozen soil will be damaged. Non-attenuated creep occurs. Introducing the damage variable D into the frozen soil creep model can better describe the stable and accelerated creep stages in the permafrost creep process. On the basis of the damage mechanisms, the damage variable D in the frozen soil is defined [23]:

$$E\left(\sigma ,t\right)=\left\{\begin{array}{l}{E}_0,\sigma -{\sigma }_{\infty }<0\hfill \\ E_0{e}^{-c{t}^R},\sigma -{\sigma }_{\infty }\ge 0\hfill \end{array}\right.$$

(7)

$$D\left(\sigma ,t\right)=1-\frac{E\left(\sigma ,t\right)}{E_0}$$

(8)

$$D\left(\sigma ,t\right)=\left\{\begin{array}{l}0,\sigma -{\sigma }_{\infty }<0\hfill \\ 1-e^{-c{t}^R},\sigma -{\sigma }_{\infty }\ge 0\hfill \end{array}\right.$$

(9)

where D(σ,t) is the damage variable of the frozen soil; E(σ,t) is the function of the elastic modulus changing with time; E₀ is the initial elastic modulus; c, R are the material parameters related to the damage degree of the frozen soil; σ_∞ is the long-term strength of the frozen soil.

According to the definition of effective stress [24]:

$${\sigma }^{\prime }=\frac{\sigma }{1-D}$$

(10)

$${\sigma }^{\prime }=\left\{\begin{array}{l}\sigma ,\sigma -{\sigma }_{\infty }<0\hfill \\ \sigma e^{c{t}^R},\sigma -{\sigma }_{\infty }\ge 0\hfill \end{array}\right.$$

(11)

where σ′ is the effective stress and σ_∞ is the creep stress.

The accelerated creep stage of frozen soil is described by adopting a viscoplastic element in which the unsteady cohesive body and the plastic body are connected in parallel. When σ < σ_∞, the plastic body will not deform; when σ ≥ σ_∞, the plastic body will yield. Therefore, the viscosity coefficient of an unsteady viscous body is expressed as:

$${\eta }_2\left(t,\sigma \right)={\eta }_{20}\left[1+\frac{2{\sigma }_{\infty }}{\sigma }\left(1-e^{-t/t_0}\right)\right]$$

(12)

where η₂₀ represents the initial viscosity coefficient of the viscoplastic element.

According to the establishment method of the creep model method, the modified frozen soil creep constitutive equation is obtained as follows:

$$\epsilon =\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-e^{\left(-\alpha t-\frac{3}{2}\alpha \left(t/t_0\right)2/3\right)}\right]\sigma <{\sigma }_{\infty }$$

(13)

$$\epsilon =\frac{\sigma }{E_0}+\frac{\sigma }{E_1}\left[1-e^{\left(-\alpha t-\frac{3}{2}\alpha \left(t/t_0\right)2/3\right)}\right]+\frac{\sigma \prime -{\sigma }_{\infty }}{{\eta }_2\left(t,\sigma \right)}\sigma <{\sigma }_{\infty }$$

(14)

4.2. Creep Model Parameters

According to the uniaxial creep test results, the modified frozen soil creep model is used for fitting analysis, as shown in Figure 5. The correlation coefficient R² ≥ 0.89 obtained from the fitting is 0.94 on average. The fitted curve is in good agreement with the measured curve as a whole. The initial creep stage is in good agreement with the stable creep stage, and in poor agreement with the accelerated creep stage. At the beginning of the 0.75 σ_t loading stage, with the increase of time, the coefficient of fitting was significantly improved. It shows that the modified creep constitutive model can better describe the decaying and non-attenuating creep processes of frozen soil well.

The initial elastic modulus E₀ represents the deformation resistance at the moment of loading.

Table 4. Frozen soil creep model parameters.

Sample Number	Temperature/°C	Stress/MPa	c	R	E0	E1	η10	η20	R2
FSC2-b	−2	1.15	1.7658	0.3496	2.2188	1.3763	2.0852	8.6866	0.8945
		2.29			2.6575	1.9158	1.8960		0.9909
		3.43			2.4864	1.5326	1.5266		0.9950
FSC3-c	−3	1.30	1.4622	0.1039	3.0760	1.1810	3.9870	14.7524	0.9482
		2.59			3.5324	1.3213	3.5333		0.9971
		3.89			3.1660	1.4639	3.2542		0.9845
FSC4-a	−4	1.37	1.3493	0.0808	3.3755	2.2417	6.2449	20.5709	0.9846
		2.74			3.8462	2.7647	5.9199		0.9594
		4.10			3.6132	2.4076	5.6791		0.9941
FSC5-b	−5	1.63	0.7620	0.0571	4.2981	2.8563	8.7446	26.4141	0.9805
		3.27			5.3059	3.1279	7.4421		0.9964
		4.90			5.1398	3.0202	6.2154		0.9948

shows that E₀ increases with the decrease of rising temperature but increases with the elevating of the loading level. The progressive elastic modulus E₁ represents the deformation resistance of the soil in the initial creep stage, which is very close to the change trend of E₀. The values of η₁₀ and η₂₀ represent the initial viscosity coefficient of viscoelastic bodies and viscoplastic body, respectively, which can reflect the deformation rates of soil.

5. Discussion

In the early stage of this study, many frozen soil basic tests were done to determine the physical and mechanical parameters of the frozen soil specimens. After they were consistent with the frozen soil field specimens of Jiangcang Coal Mine, the permafrost creep test was carried out. Aiming at the deformation and failure characteristics of the overlying frozen soil in the coal mine, the failure characteristics of frozen soil specimens with different stress states, different creep types and different creep stages are mainly studied.

The deformation properties of frozen soil are comprehensively affected by factors such as soil temperature, proportion of soil ice content and load. No matter what the conditions are, the creep type of the final creep curve can be divided into attenuated creep and non-attenuated creep. Attenuated creep only goes through the initial stage and the stable stage, and there is no acceleration stage. The creep rate of the initial stage gradually decreases with elapsing time, and the stable creep curve gradually develops into an approximately straight line, showing a slowly decaying state; the non-attenuated creep can be divided into three stages: initial, stable and accelerating creep stages [25]. In the initial stage, the creep rate gradually decreases with elapsing time until its nadir. In the stable stage, the creep rate remains unchanged at this minimum value. At the accelerating creep stage, the creep rate increases until the frozen soil column fails. When the axial stress is 0.25 σ_t and 0.5 σ_t, the creep curve shows obvious initial and stable creep stages, respectively. The creep deformation rate decreases with passing time, and the creep curve smooths out. The creep type is decaying when the axial stress is 0.75 σ_t, the creep curve goes through the initial creep stage, the stable and the accelerating creep stage, and the creep deformation rate shows a trend of first decreasing and then increasing, showing a curve of a typical non-attenuated creeping.

Temperature, soil ice content and graded load have great influences on the creep properties and failure modes of frozen soil. The higher the soil temperature, the smaller the proportion of soil ice content, the greater the load, the more unstable the mechanical properties of the frozen soil, the greater the creep deformation, the greater the stable creep rate, and the smaller the peak stress of the frozen soil. The lower the soil temperature, the greater the proportion of soil ice content and the smaller the load. As the soil temperature decreases, the proportion of soil ice content and the load increase, the time in the stable creep stage becomes longer, and the specimen enters the longer accelerated creep stage, and the accelerated creep stage is longer. The greater the slope of the curve, the greater the peak value of the frozen soil stress. The above basic research is consistent with the results of most permafrost studies.

However, most scholars believe that the non-attenuating creep of frozen soil has an important influence on the settlement of the foundation and the attenuating creep is ignored. However, both attenuated creep and non-attenuated creeps have a significant impact on the safe production of coal mines. Therefore, this paper analyzes the movement of the coal mine overlying rock and the occurrence of rock pressure according to the mechanical behavior and fracture law of the overlying frozen soil in the coal mine. It goes as follows: The lower the soil temperature, the greater the proportion of soil ice content, the greater the peak stress, the more complex the failure patterns of frozen soil and the more complex the crack evolution path.

With the increase of stress peak value, the failure mode of frozen soil changed from simple shear failure to complex mixed failure, the larger the expansion capacity. At the same time, it shows that temperature is an important factor affecting the mechanical properties and failure form of frozen soil.

6. Conclusions

In order to study the creep deformation characteristics of high-temperature frozen soil and the influence of factors such as temperature and load, this study carried out indoor uniaxial creep tests and the main conclusions are as follows:

(1) Soil temperature is the most important external factor for affecting frozen soil creep, and the proportion of soil ice content is the key internal factor affecting permafrost to the creep. The lower the soil temperature, the higher the proportion of soil ice content in the specimen, the lower the creep rate of frozen soil and the smoother the curve. The greater the number of cracks and the trace length of the specimen, the more complex the failure type. The sensitivity of creep rate to soil temperature and load increases as the proportion of soil ice content decreases.

(2) For the frozen soil specimen under load, the external load in the early stage is mainly borne by the pore pressure and the pores and cracks of the specimen are compacted. With the increase of external load, cracks expand and germinate and the structure bearing external load transfers from pore pressure to soil particle skeleton. The coupling effect of pore pressure and effective stress is complex, leading to the non-obvious regularity of creep deformation. At 0.75σt, the structure bearing the external load transforms into the soil particle skeleton, enters the accelerated creep stage and the failure speed of the specimen increases.

(3) Based on the classical Nishiplasma model, the modified permafrost creep model is obtained, which can better describe the decaying creep and non-attenuating creep processes of frozen soil. The model is relatively simple and has relatively fewer parameters. It can provide a theoretical basis for the mitigation and control of surface subsidence in the mining of underlying coal seams in Jiangcang Coal Mine.