Reliability and Criticality Analysis of a Large-Scale Solar Photovoltaic System Using Fault Tree Analysis Approach
Abstract
1. Introduction
2. Literature Survey
- Different methodologies used for data collection (Section 2.1);
- Methods/techniques used for system reliability modeling and analysis (Section 2.2); and
- Approaches used for estimating best-fit (most suitable) probability distributions for the given data set (time to failure data). The given data set is the failure rate of basic events or failure modes (Section 2.3).
2.1. Methodologies Used for Data Collection
| Sr. No. | Author(s) and Reference(s) | Data Collection Methodologies | |||
|---|---|---|---|---|---|
| Field Data | Test Data | Literature | Expert Judgments | ||
| 1 | Stember et al. [46] | √ | |||
| 2 | Mishra and Joshi [20] | √ | |||
| 3 | Maish et al. [39] | √ | |||
| 4 | Jahn and Nasse [40] | √ | |||
| 5 | Oozeki et al. [41] | √ | |||
| 6 | Huffman et al. [47] | √ | |||
| 7 | Collins et al. [42] | √ | √ | ||
| 8 | Zini et al. [35] | √ | |||
| 9 | Golnas [43] | √ | |||
| 10 | Theristies and Papazoglou [21] | √ | |||
| 11 | Hu et al. [22] | √ | |||
| 12 | Charki et al. [36] | √ | |||
| 13 | Ghaedi et al. [24] | √ | |||
| 14 | Ahadi et al. [25] | √ | |||
| 15 | Ahadi et al. [27] | √ | √ | ||
| 16 | Colli [26] | √ | |||
| 17 | Sulaeman et al. [28] | √ | |||
| 18 | Cai et al. [48] | √ | |||
| 19 | Sulaeman et al. [31] | √ | √ | ||
| 20 | Nemes et al. [36] | √ | |||
| 21 | El- Metwally et al. [37] | √ | |||
| 22 | Gupta et al. [17] | √ | |||
| 23 | Perveen et al. [34] | √ | √ | ||
| 24 | Baschel et al. [32] | √ | √ | ||
| 25 | Chiacchio et al. [18] | √ | |||
| 26 | Sayed et al. [19] | √ | |||
| 27 | Rajput et al. [15] | √ | |||
| 28 | Sayed et al. [29] | √ | |||
| 29 | Aguisti et al. [44] | √ | |||
| 30 | Rajput et al. [38] | √ | √ | ||
| 31 | Fara and Craciunescu [33] | √ | |||
| 32 | Qadeer and Ikram [16] | √ | |||
| 33 | Yian Liu [45] | √ | |||
| 34 | Ong et al. [30] | √ | |||
| 35 | Simon et al. [49] | √ | |||
| 36 | Spertino et al. [50] | √ | |||
| 37 | Li et al. [51] | √ | |||
| 38 | Luo et al. [52] | √ | |||
| 39 | Yinan Liu [45] | √ | |||
| 40 | Ostovar et al. [53] | √ | |||
| 15 | 5 | 24 | 2 | ||
2.2. Methods/Techniques Used for System Reliability Modeling and Analysis
2.3. Methodologies Used for Data Collection, Sorting, and Estimating Best-Fit Probability Distributions
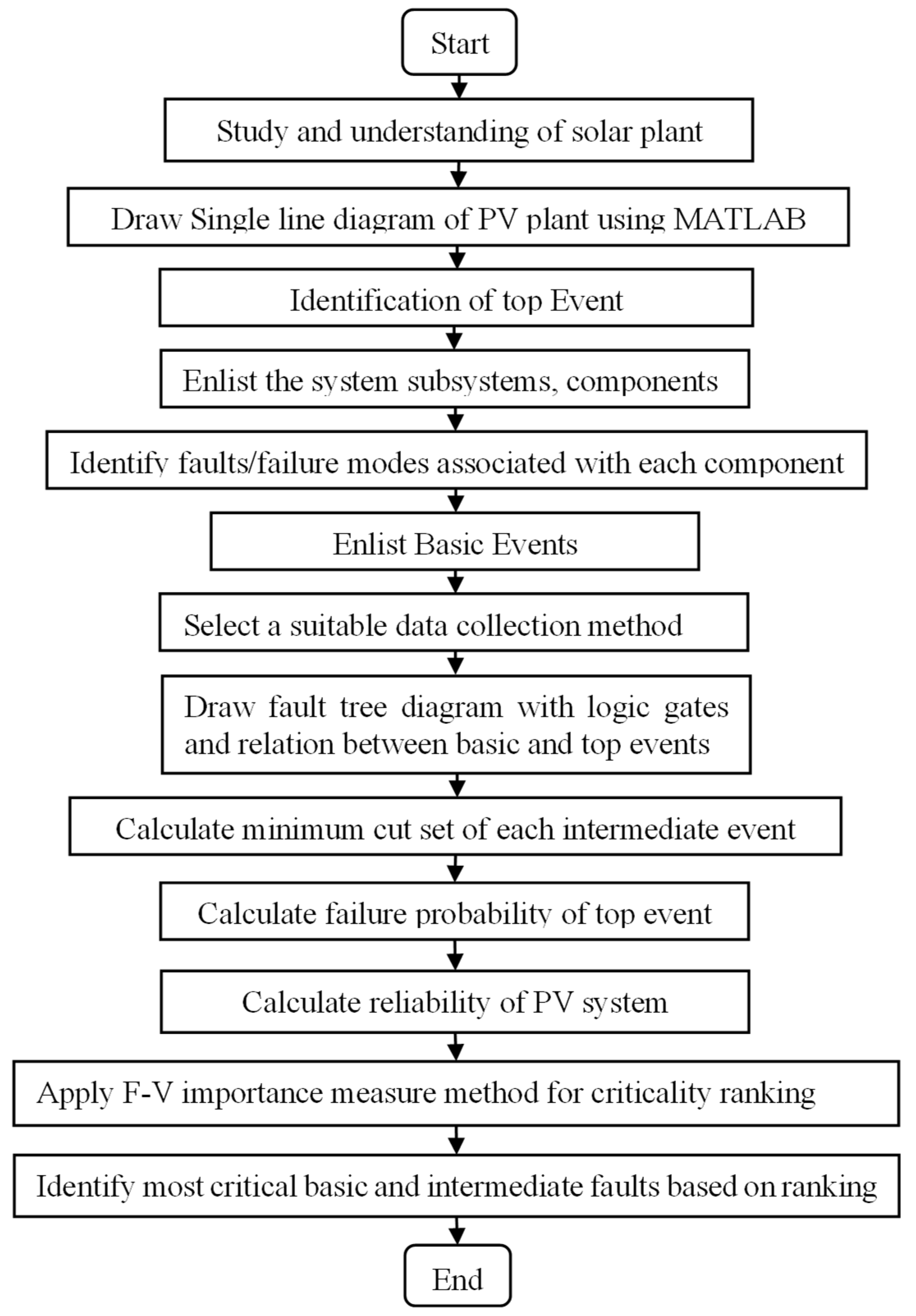
3. Methodology
- A process to identify various subsystems, components, and failure modes of a solar PV system (Section 3.1);
- How to construct a fault tree diagram for a given system (Section 3.2);
- Data collection strategy (Section 3.3);
- Steps to calculate the minimum cut set of each basic and intermediate events (Section 3.4), and finally;
- Criticality ranking of intermittent and basic events (Section 3.5).
3.1. Identification of Subsystems, Components, and Faults Related to Components
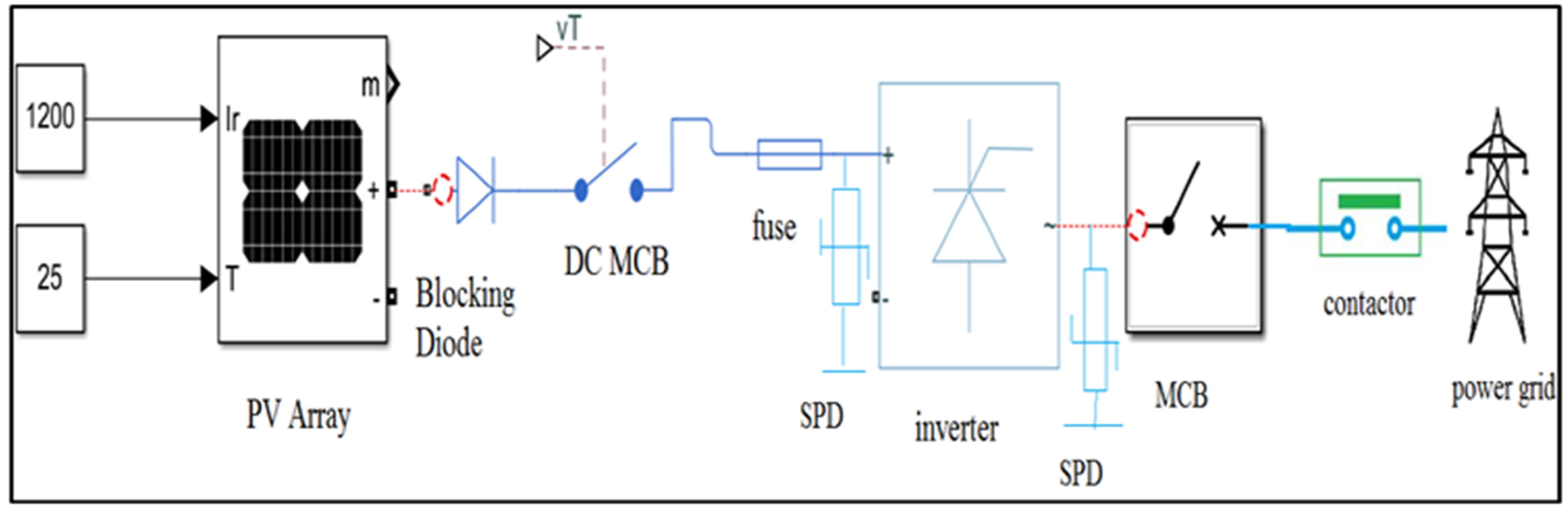
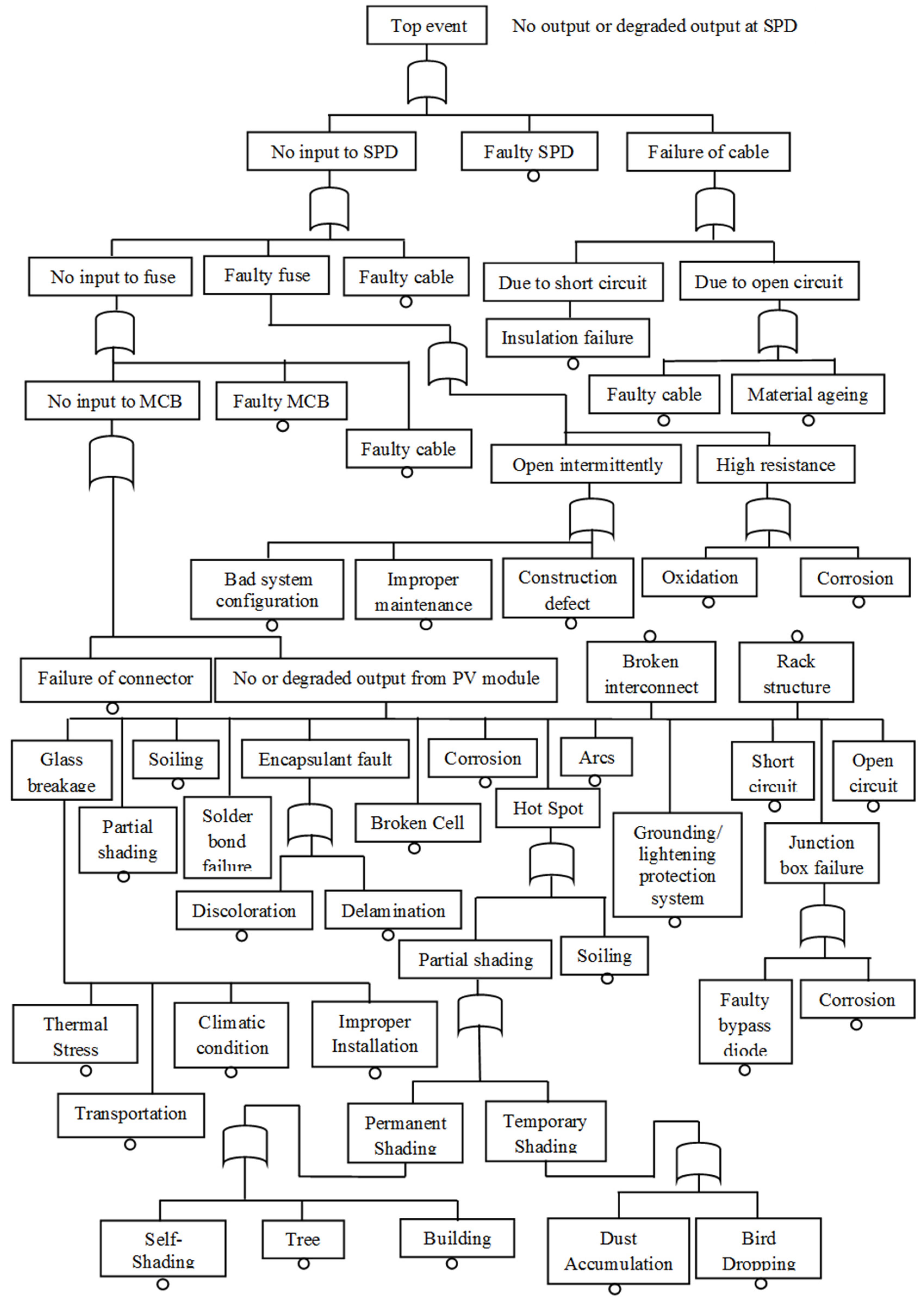
3.2. Construction of Fault Tree Diagram of Solar PV System
- Identification of top event. The top occurrence/event in this study is “No output or reduced power output”.
- Using a top-down approach, it is necessary to determine the basic events and intermediate ones that led to the top event. The dominating external events, such as weather conditions and radiation levels, are considered while constructing the FT diagram.
- Create a FT diagram with logic gates and symbols (as depicted in Table 5) that can be represented by a Boolean equation. The OR gate connects all basic and intermediate events. A rectangle represents the top event.
3.3. Data Collection
3.4. Calculate the Minimum Cut Set of Each Basic Event
Calculation of Reliability of a Solar PV System
3.5. Criticality Ranking of MCSs of Basic Events
4. Reliability Analysis of Solar PV System
4.1. FT Diagram of Solar PV System under Study
4.2. Qualitative FTA of a Solar PV System
4.3. Quantitative Reliability Analysis of Solar PV System
4.4. Comparison of the Results Obtained by the Proposed Methodology with the Published Results
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature & Abbreviations
| Failure probability | |
| Failure rate | |
| Mission time | |
| Importance measure of ith minimum cut set | |
| Probability of a top event | |
| Reliability of solar PV | |
| AC | Alternating Current |
| BDD | Binary Decision Diagram |
| BOS | Balance Of System |
| DBN | Dynamic Bayesian Network |
| DC | Direct Current |
| EVA | Ethylene Vinyl Acetate |
| FFTA | Fuzzy Fault Tree Analysis |
| FMEA | Failure Mode and Effect Analysis |
| FMECA | Failure Mode, Effects, and Criticality Analysis |
| FTA | Fault Tree Analysis |
| FT | Fault Tree |
| F-V | Fussel Vesely |
| GW | Gigawatt |
| HASS | Highly Accelerated Stress Screening |
| IEA | International Energy Agency |
| IM | Importance Measure |
| MCB | Miniature Circuit Breaker |
| MCS | Minimum Cut Set |
| MPPT | Maximum Power Point Tracking |
| MTTF | Mean Time To Failure |
| PV | Photovoltaic |
| PR | Performance Ratio |
| RAM | Reliability, Availability, Maintainability |
| RBD | Reliability Block Diagram |
| SHyFTA | Stochastic hybrid FTA |
| SMUD | Municipal Utility District |
| SPD | Surge Protection Device |
| TE | Top Event |
References
- IEA-Photovoltaic Power Systems Programme. Snapshot of Global PV Markets 2022; IEA: Paris, France, 2022. [Google Scholar]
- Wolfe, P. pv Magazine Group GmbH & Co. KG. 2021. Available online: https://www.pv-magazine.com/2021/09/23/the-worlds-largest-solar-parks/ (accessed on 1 January 2023).
- GlobalData. Global Solar Photovoltaic Capacity Expected to Exceed 1500GW by 2030, Says GlobalData. Available online: https://pes.eu.com/wind/global-solar-photovoltaic-capacity-expected-to-exceed-1500gw-by-2030-says-globaldata/ (accessed on 1 January 2023).
- Dhimish, M.; Ahmad, A.; Tyrrell, A.M. Inequalities in Photovoltaics Modules Reliability: From Packaging to PV Installation Site. Renew. Energy 2022, 192, 805–814. [Google Scholar] [CrossRef]
- Cristaldi, L.; Faifer, M.; Lazzaroni, M.; Khalil, M.M.A.F.; Catelani, M.; Ciani, L. Failure Modes Analysis and Diagnostic Architecture for Photovoltaic Plants. In Proceedings of the 13 th IMEKO TC10 Workshop on Technical Diagnostics Advanced Measurement Tools in Technical Diagnostics for Systems’ Reliability and Safety, Warsaw, Poland, 26–27 June 2014; pp. 186–191. [Google Scholar]
- Atsu, D.; Seres, I.; Aghaei, M.; Farkas, I. Analysis of Long-Term Performance and Reliability of PV Modules under Tropical Climatic Conditions in Sub-Saharan. Renew. Energy 2020, 162, 285–295. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, M.; Yadav, K. Degradation and Reliability Analysis of Photovoltaic Modules after Operating for 12 Years: A Case Study with Comparisons. Renew. Energy 2022, 196, 1170–1186. [Google Scholar] [CrossRef]
- Aboagye, B.; Gyamfi, S.; Ofosu, E.A.; Djordjevic, S. Degradation Analysis of Installed Solar Photovoltaic (PV) Modules under Outdoor Conditions in Ghana. Energy Rep. 2021, 7, 6921–6931. [Google Scholar] [CrossRef]
- Quansah, D.A.; Adaramola, M.S. Comparative Study of Performance Degradation in Poly- and Mono-Crystalline-Si Solar PV Modules Deployed in Different Applications. Int. J. Hydrogen Energy 2018, 43, 3092–3109. [Google Scholar] [CrossRef]
- Cui, C.; Li, Z.; Zhang, J. Building a Prediction Model of Solar Power Generation Based on Improved Grey Markov Chain. Int. J. Glob. Energy Issues 2022, 44, 139–149. [Google Scholar] [CrossRef]
- Manohar, P.; Atla, C.R. Development of Predictive Reliability Model of Solar Photovoltaic System Using Stochastic Diffusion Process for Distribution System. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 279–289. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K.; Tian, G.; Xu, G.; Zhao, H. Reliability Assessment of Power Generation System Using an Optimized State Enumeration Method. Recent Patents Eng. 2021, 16, 89–96. [Google Scholar] [CrossRef]
- Stember, L.H. Reliability Considerations in the Design of Solar Photovoltaic Power Systems. Sol. Cells 1981, 3, 269–285. [Google Scholar] [CrossRef]
- Nageh, M.; Abdullah, M.P.; Yousef, B. Reliability Evaluation and Cost Analysis for Optimized Large Scale Solar PV System. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 22–23 November 2021; pp. 195–200. [Google Scholar]
- Rajput, P.; Malvoni, M.; Kumar, N.M.; Sastry, O.S.; Tiwari, G.N. Risk Priority Number for Understanding the Severity of Photovoltaic Failure Modes and Their Impacts on Performance Degradation. Case Stud. Therm. Eng. 2019, 16, 100563. [Google Scholar] [CrossRef]
- Qadeer, A.; Huawei, L.; Ikram, M.T. Research on Reliability of Grid Connected Photovoltaic Renewable Generation System. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 032058. [Google Scholar] [CrossRef]
- Gupta, N.; Garg, R.; Kumar, P. Sensitivity and Reliability Models of a PV System Connected to Grid. Renew. Sustain. Energy Rev. 2017, 69, 188–196. [Google Scholar] [CrossRef]
- Chiacchio, F.; Famoso, F.; D’Urso, D.; Brusca, S.; Aizpurua, J.I.; Cedola, L. Dynamic Performance Evaluation of Photovoltaic Power Plant by Stochastic Hybrid Fault Tree Automaton Model. Energies 2018, 11, 306. [Google Scholar] [CrossRef]
- Sayed, A.; El-Shimy, M.; El-Metwally, M.; Elshahed, M. Reliability, Availability and Maintainability Analysis for Grid-Connected Solar Photovoltaic Systems. Energies 2019, 12, 1213. [Google Scholar] [CrossRef]
- Mishra, P.; Joshi, J. Reliability Estimation for Components of Photovoltaic Sysyems. Energy Stud. 1995, 37, 1371–1382. [Google Scholar]
- Theristis, M.; Papazoglou, I.A. Markovian Reliability Analysis of Standalone Photovoltaic Systems Incorporating Repairs. IEEE J. Photovolt. 2014, 4, 414–422. [Google Scholar] [CrossRef]
- Hu, R.; Mi, J.; Hu, T.; Fu, M.; Yang, P. Reliability Research for PV System Using BDD-Based Fault Tree Analysis. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 359–363. [Google Scholar] [CrossRef]
- Charki, A.; Bigaud, D. Availability Estimation of a Photovoltaic System. In Proceedings of the 2013 Proceedings Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2013; pp. 4–8. [Google Scholar] [CrossRef]
- Ghaedi, A.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M.; Othman, M. Reliability Evaluation of a Composite Power System Containing Wind and Solar Generation. In Proceedings of the 2013 IEEE 7th International Power Engineering and Optimization Conference (PEOCO), Langkawi, Malaysia, 3–4 June 2013; pp. 483–488. [Google Scholar] [CrossRef]
- Ahadi, A.; Ghadimi, N.; Mirabbasi, D. Reliability Assessment for Components of Large Scale Photovoltaic Systems. J. Power Sources 2014, 264, 211–219. [Google Scholar] [CrossRef]
- Colli, A. Failure Mode and Effect Analysis for Photovoltaic Systems. Renew. Sustain. Energy Rev. 2015, 50, 804–809. [Google Scholar] [CrossRef]
- Ahadi, A.; Hayati, H.; Miryousefi Aval, S.M. Reliability Evaluation of Future Photovoltaic Systems with Smart Operation Strategy. Front. Energy 2016, 10, 125–135. [Google Scholar] [CrossRef]
- Sulaeman, S.; Member, S.; Benidris, M. Modeling the Output Power of PV Farms for Power. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Sayed, A.; EL-Shimy, M.; El-Metwally, M.; Elshahed, M. Impact of Subsystems on the Overall System Availability for the Large Scale Grid-Connected Photovoltaic Systems. Reliab. Eng. Syst. Saf. 2020, 196, 106742. [Google Scholar] [CrossRef]
- Mohd Nizam Ong, N.A.F.; Sadiq, M.A.; Md Said, M.S.; Jomaas, G.; Mohd Tohir, M.Z.; Kristensen, J.S. Fault Tree Analysis of Fires on Rooftops with Photovoltaic Systems. J. Build. Eng. 2022, 46, 103752. [Google Scholar] [CrossRef]
- Sulaeman, S.; Benidris, M.; Mitra, J. Modeling and Assessment of PV Solar Plants for Composite System Reliability Considering Radiation Variability and Component Availability. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016. [Google Scholar] [CrossRef]
- Baschel, S.; Koubli, E.; Roy, J.; Gottschalg, R. Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance. Energies 2018, 11, 1579. [Google Scholar] [CrossRef]
- Fara, L.; Craciunescu, D. Reliability Analysis of Photovoltaic Systems for Specific Applications. Reliab. Ecol. Asp. Photovolt. Modul. 2020, 1–14. [Google Scholar] [CrossRef]
- Perveen, S.; Ashfaq, H.; Asjad, M. Reliability Assessment of Solar Photovoltaic Systems Based on Fuzzy Fault Tree Analysis. Life Cycle Reliab. Saf. Eng. 2019, 8, 129–139. [Google Scholar] [CrossRef]
- Zini, G.; Mangeant, C.; Merten, J. Reliability of Large-Scale Grid-Connected Photovoltaic Systems. Renew. Energy 2011, 36, 2334–2340. [Google Scholar] [CrossRef]
- Nemes, C.; Munteanu, F.; Rotariu, M.; Astanei, D. Availability Assessment for Grid-Connected Photovoltaic Systems with Energy Storage. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 908–911. [Google Scholar] [CrossRef]
- El-Metwally, M.; Elshahed, M.; El-Shimy, M.; Sayad, A. Detailed Analyses of the Failure and Repair Rates of Wind and Solar-PV Systems for RAM Assessment Military Technical College Kobry El-Kobbah, Cairo, Egypt 11 Th International Conference on Electrical Engineering ICEENG 2018 Detailed Analyses of the Fail. In Proceedings of the International Conference on Electrical Engineering ICEENG 2018, Cairo, Egypt, 3–5 April 2018; pp. 3–5. [Google Scholar]
- Rajput, P.; Malvoni, M.; Sastry, O.S.; Tiwari, G.N. Failure Mode and Effect Analysis of Monocrystalline Silicon Photovoltaic Modules after 24 Years Outdoor Exposure in Semi-Arid Climate. AIP Conf. Proc. 2020, 2276, 020004. [Google Scholar] [CrossRef]
- Maish, A.B.; Atcitty, C.; Hester, S.; Greenberg, D.; Osborn, D.; Collier, D.; Brine, M. Photovoltaic System Reliability. Conf. Rec. IEEE Photovolt. Spec. Conf. 1997, 3, 1049–1054. [Google Scholar] [CrossRef]
- Jahn, U.; Nasse, W. Operational Performance of Grid-Connected PV Systems on Buildings in Germany. Prog. Photovoltaics Res. Appl. 2004, 12, 441–448. [Google Scholar] [CrossRef]
- Oozeki, T.; Yamada, T.; Kato, K.; Yamamoto, T. An Analysis of Reliability for Photovoltaic Systems on the Field Test Project for Photovoltaic in Japan. In Proceedings of ISES World Congress 2007 (Vol. I–Vol. V) Solar Energy and Human Settlement; Springer: Berlin/Heidelberg, Germany, 2007; Volume 3, pp. 1628–1632. [Google Scholar] [CrossRef]
- Collins, E.; Miller, S.; Stein, J.; Sorensen, R.; Granata, J.; Auintana, M. A Reliability and Availability Sensitivity Study of a Large Photovoltaic System. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 4463–4469. [Google Scholar]
- Golnas, A. PV System Reliability: An Operator’s Perspective. IEEE J. Photovoltaics 2013, 3, 416–421. [Google Scholar] [CrossRef]
- Causia Aguisti, F.; Musyafa’, A.; Khamim Asy’ari, M. Analysis of RAM (Reliability, Availability, Maintainability) Production of Electric Voltage from 48 v PV (Photovoltaic) at Pantai Baru Pandansimo, Indonesia. E3S Web Conf. 2020, 190, 00010. [Google Scholar] [CrossRef]
- Liu, Y. Reliability Analysis of Photovoltaic Module Based on Measured Data. IOP Conf. Ser.: Earth Environ. Sci. 2021, 793, 012019. [Google Scholar] [CrossRef]
- Stember, L.H.; Huss, W.R.; Bridgman, M.S. A Methodology for Photovoltaic System Reliability & Economic Analysis. IEEE Trans. Reliab. 1982, R-31, 296–303. [Google Scholar] [CrossRef]
- Huffman, D.L.; Antelme, F. Availability Analysis of a Solar Power System with Graceful Degradation. Proc. Annu. Reliab. Maintainab. Symp. 2009, 348–352. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Ma, Y.; Huang, L.; Liu, Z. A Framework for the Reliability Evaluation of Grid-Connected Photovoltaic Systems in the Presence of Intermittent Faults. Energy 2015, 93, 1308–1320. [Google Scholar] [CrossRef]
- Simon, D.F.; Teixeira, M.; da Costa, J.P. Availability Estimation in Photovoltaic Generation Systems Using Timed Petri Net Simulation Models. Int. J. Electr. Power Energy Syst. 2022, 137, 106897. [Google Scholar] [CrossRef]
- Spertino, F.; Amato, A.; Casali, G.; Ciocia, A.; Malgaroli, G. Reliability Analysis and Repair Activity for the Components of 350 Kw Inverters in a Large Scale Grid-Connected Photovoltaic System. Electronics 2021, 10, 564. [Google Scholar] [CrossRef]
- Li, T.; Tao, S.; Zhang, R.; Liu, Z.; Ma, L.; Sun, J.; Sun, Y. Reliability Evaluation of Photovoltaic System Considering Inverter Thermal Characteristics. Electronics 2021, 10, 1763. [Google Scholar] [CrossRef]
- Luo, W.; Khoo, Y.S.; Hacke, P.; Jordan, D.; Zhao, L.; Ramakrishna, S.; Aberle, A.G.; Reindl, T. Analysis of the Long-Term Performance Degradation of Crystalline Silicon Photovoltaic Modules in Tropical Climates. IEEE J. Photovolt. 2019, 9, 266–271. [Google Scholar] [CrossRef]
- Ostovar, S.; Esmaeili-Nezhad, A.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Reliability Assessment of Distribution System with the Integration of Photovoltaic and Energy Storage Systems. Sustain. Energy Grids Netw. 2021, 28, 100554. [Google Scholar] [CrossRef]
- Hamdy, M.A.; Beshir, M.E.; Elmasry, S.E. Reliability Analysis of Photovoltaic Systems. Appl. Energy 1989, 33, 253–263. [Google Scholar] [CrossRef]
- Cristaldi, L.; Khalil, M.; Soulatiantork, P. A Root Cause Analysis and a Risk Evaluation of PV Balance of Systems Failures. Acta IMEKO 2017, 6, 113–120. [Google Scholar] [CrossRef]
- Yan, W.; Liu, W.; Kong, W. Reliability Evaluation of PV Modules Based on Exponential Dispersion Process. Energy Rep. 2021, 7, 3023–3032. [Google Scholar] [CrossRef]
- Xiao, H.; Lin, C.; Kou, G.; Peng, R. Reliability Modeling and Configuration Optimization of a Photovoltaic Based Electric Power Generation System. Reliab. Eng. Syst. Saf. 2022, 220, 108285. [Google Scholar] [CrossRef]
- Hefaidh, H.; Mébarek, D.; Belkhir, N.; Driss, Z. Reliability Degradation Prediction of Photovoltaic Modules Based on Dependability Methods. Int. J. Qual. Reliab. Manag. 2021, 40, 478–495. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault Tree Analysis: A Survey of the State-of-the-Art in Modeling, Analysis and Tools. Comput. Sci. Rev. 2015, 15, 29–62. [Google Scholar] [CrossRef]
- Gupta, S.; Bhattacharya, J. Reliability Analysis of a Conveyor System Using Hybrid Data. Qual. Reliab. Eng. Int. 2007, 23, 867–882. [Google Scholar] [CrossRef]
- Cristaldi, L.; Khalil, M.; Faifer, M.; Soulatiantork, P. Markov Process Reliability Model for Photovoltaic Module Encapsulation Failures. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; 5, pp. 203–208. [Google Scholar] [CrossRef]
- Ferdous, R.; Khan, F.I.; Veitch, B.; Amyotte, P.R. Methodology for Computer-Aided Fault Tree Analysis. Process Saf. Environ. Prot. 2007, 85, 70–80. [Google Scholar] [CrossRef]
- Lavasani, S.M.; Zendegani, A.; Celik, M. An Extension to Fuzzy Fault Tree Analysis (FFTA) Application in Petrochemical Process Industry. Process Saf. Environ. Prot. 2015, 93, 75–88. [Google Scholar] [CrossRef]
- Prasanna, R.; Karthik, C.; Chowdhury, S.; Khan, B. Comprehensive Review on Modelling, Estimation, and Types of Faults in Solar Photovoltaic System. Int. J. Photoenergy 2022, 2022, 3053317. [Google Scholar] [CrossRef]
| Sr. No. | Author(s) and Reference(s) | Methods Used for System Reliability Evaluation | |||||
|---|---|---|---|---|---|---|---|
| FTA | FMEA | RBD | Hybrid FTA | Markov Chain | Any Other Method | ||
| 1 | Stember et al. [46] | √ | √ | ||||
| 2 | Hamdy et al. [54] | √ | |||||
| 3 | Mishra and Joshi [20] | √ (Failure data) | |||||
| 4 | Maish et al. [39] | √ (Monte Carlo) | |||||
| 5 | Jahn and Nasse [40] | √ (Performance Ratios) | |||||
| 6 | Oozeki et al. [41] | √ (Failure data) | |||||
| 7 | Huffman et al. [47] | √ | |||||
| 8 | Collins et al. [42] | √ | |||||
| 9 | Zini et al. [35] | √ | |||||
| 10 | Golnas [43] | √ (Failure data) | |||||
| 11 | Theristies and Papazoglou [21] | √ | |||||
| 12 | Hu et al. [22] | √ (BDD FTA) | |||||
| 13 | Charki et al. [23] | √ (Petri Networks) | |||||
| 14 | Ghaedi et al. [24] | √ (State Enumeration Method) | |||||
| 15 | Ahadi et al. [25] | √ | |||||
| 16 | Ahadi et al. [27] | √ | √ | ||||
| 17 | Colli [26] | √ | |||||
| 18 | Sulaeman et al. [28] | √ (Discrete convolution) | |||||
| 19 | Cai et al. [48] | √ | √ (Dynamic Bayesian Networks) | ||||
| 20 | Sulaeman et al. [31] | √ (Monte Carlo simulation) | |||||
| 21 | Nemes et al. [36] | √ (Monte Carlo simulation) | |||||
| 22 | El- Metwally et al. [37] | √ (Failure data) | |||||
| 23 | Gupta et al. [17] | √ (Logic gate) | |||||
| 24 | Perveen et al. [34] | √ (Fuzzy FTA) | |||||
| 25 | Baschel et al. [32] | √ | √ | ||||
| 26 | Chiacchio et al. [18] | √ (SHyFTA) | |||||
| 27 | Sayed et al. [19] | √ | |||||
| 28 | Rajput et al. [15] | √ | |||||
| 29 | Sayed et al. [29] | √ | |||||
| 30 | Aguisti et al. [44] | √ (Control Chart) | |||||
| 31 | Rajput et al. [38] | √ | |||||
| 32 | Fara and Craciunescu [33] | √ | |||||
| 33 | Qadeer and Ikram [16] | √ | |||||
| 34 | Liu [45] | √ | |||||
| 35 | Ong et al. [30] | √ | |||||
| 36 | Cristaldi et al. [55] | √ (FMECA) and Markov Process | |||||
| 37 | Simon et al. [49] | √ (Petri Networks) | |||||
| 38 | Spertino et al. [50] | √ (Failure data) | |||||
| 39 | Li et al. [51] | √ | |||||
| 40 | Yan et al. [56] | √ (Exponential Dispersion) | |||||
| 41 | Xiao et al. [57] | √ (Optimization model) | |||||
| 42 | Hefaidh et al. [58] | √ | √ (FMECA) | ||||
| 43 | Ostovar et al. [53] | √ | √ (Multi-state model) | ||||
| Sr. No. | Author(s) and Reference(s) | Methods Used for System Reliability Evaluation | ||||
|---|---|---|---|---|---|---|
| Weibull | Exponential | Lognormal | Arithmetic | β | ||
| 1 | Mishra and Joshi [20] | √ | ||||
| 2 | Collins et al. [42] | √ | √ | |||
| 3 | Zini et al. [35] | √ | ||||
| 4 | Charki et al. [23] | √ | √ | |||
| 5 | Ahadi et al. [25] | √ | ||||
| 6 | Ahadi et al. [27] | √ | ||||
| 7 | Sulaeman et al. [28] | √ | ||||
| 8 | Sulaeman et al. [31] | √ | ||||
| 9 | Nemes et al. [36] | √ | ||||
| 10 | Gupta et al. [17] | √ | ||||
| 11 | Perveen et al. [34] | √ | ||||
| 12 | Baschel et al. [32] | √ | ||||
| 13 | Chiacchio et al. [18] | √ | ||||
| 14 | Sayed et al. [19] | √ | √ | √ | √ | |
| 15 | Sayed et al. [29] | √ | ||||
| 16 | Aguisti et al. [44] | √ | ||||
| 17 | Fara and Craciunescu [33] | √ | ||||
| 18 | Liu [45] | √ | ||||
| 19 | Simon et al. [49] | √ | ||||
| 20 | Li et al. [51] | √ | ||||
| 21 | Yinan Liu [45] | √ | ||||
| Sr. No. | Subsystems | Components | Faults Related to Components |
|---|---|---|---|
| 1 | PV module | Solar cells, solar glass, EVA sheet, back sheet, aluminum frame, junction box, interconnector | Module failure, glass breakage, encapsulation fault, hot spot, junction box failure, broken cell, solder bond failure, discoloration, delamination, etc. |
| 2 | Balance of system components | DC MCB, fuse, DC switches, AC switches, DC SPD, DC to DC converter, etc. | Faulty MCB, faulty cable, insulation failure, faulty SPD, failure of connector, fuse failure, switch failure, converter fault, open circuit fault, short circuit fault, etc. |
| Sr. No. | Name of Event/Gate | Symbol | Description |
|---|---|---|---|
| 1 | Basic Events |  | These events occurred spontaneously |
| 2 | Intermediate event | 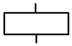 | These events are caused by one or more other events |
| 3 | Transfer in |  | These symbols are employed to combine the occurrences of numerous FTs into one FT when fault three is too vast to fit on a single page (act as an output) |
| 4 | Transfer out |  | These symbols are employed to combine the occurrences of numerous FTs into one FT when fault three is too vast to fit on a single page (acts as an input) |
| 5 | Underdeveloped event |  | If subsystems are not Bes, there is insufficient information, or events are not significant enough to develop a subsystem into a subtree. |
| 6 | External Event |  | An occurrence that is typically anticipated |
| 7 | Conditioning event |  | A precise prerequisite or constraint that could be imposed on any gate |
| 8 | AND gate |  | When the output event will occur if all input events occur, this gate is employed. |
| 9 | OR gate |  | When any one of the input events occurs, this gate is utilized to control an output event. |
| 10 | k/N gate |  | If any k of the N numbers of input events happen, an output event will also happen. |
| 11 | INHIBIT gate | 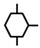 | If the input events happen and the conditioning event specified to the right of them too, then there is an output event. |
| Sr. No. | Basic Events | Failure Rate | Failure Probability | Reference(s) |
|---|---|---|---|---|
| 1 | Failure of SPD | NA | 5.515×10−3 | [34] |
| 0.313 | NA | [18] | ||
| 2 | Discoloration | 8.48 | NA | [61] |
| 3 | Delamination | 5.44 | NA | [23] |
| 15.4 | NA | [61] |
| Sr. No. | F-V Measure Ranking | Severity Level |
|---|---|---|
| 1 | 1–8 | Highly critical |
| 2 | 9–18 | Medium |
| 3 | 19 onwards | Low |
| Sr. No. | Notation | Meaning |
|---|---|---|
| 1 | Reliability of Glass Breakage | |
| 2 | Reliability of Encapsulation Fault | |
| 3 | Reliability of Hot Spot | |
| 4 | Reliability of Junction Box Failure | |
| 5 | Reliability of PV Module | |
| 6 | Reliability of Miniature Circuit Breaker | |
| 7 | Reliability of Open Intermittently | |
| 8 | Reliability of High Resistance | |
| 9 | Reliability of Faulty Fuse | |
| 10 | Reliability of No Input to Fuse | |
| 11 | Reliability of Open Circuit | |
| 12 | Reliability of Short Circuit | |
| 13 | Reliability of Failure of Cable | |
| 14 | Reliability of No Input to SPD |
| Sr. No. | Component | Failure Rate 10−6 Failures/hour | ||||
|---|---|---|---|---|---|---|
| Mean | Median | Mode | Lowest | Highest | ||
| 1 | Failure of SPD (E1) | 1.048 | 1.048 | NA | 0.313 | 1.783 |
| 2 | Faulty cable (E2) | 0.099 | 0.099 | NA | 0.099 | 0.099 |
| 3 | Failure of cable due to insulation failure (E3) | 0.018 | 0.018 | NA | 0.018 | 0.018 |
| 4 | DC Circuit Breaker (E4) | 0.25 | 0.25 | NA | 0.1 | 0.4 |
| 5 | Failure of cable due to material ageing (E5) | 0.054 | 0.054 | NA | 0.054 | 0.054 |
| 6 | Failure of fuse-bad system configuration (E6) | 0.015 | 0.015 | NA | 0.015 | 0.015 |
| 7 | Failure of fuse -improper maintenance (E7) | 0.049 | 0.049 | NA | 0.049 | 0.049 |
| 8 | Failure of fuse-construction defect (E8) | 0.0001 | 0.0001 | NA | 0.0001 | 0.0001 |
| 9 | Failure of fuse–oxidation (E9) | 0.001 | 0.001 | NA | 0.001 | 0.001 |
| 10 | Failure of fuse–corrosion (E10) | 0.048 | 0.048 | NA | 0.048 | 0.048 |
| 11 | Broken interconnect (E11) | 28.5 | 28.5 | NA | 28.5 | 28.5 |
| 12 | Rack structure (E12) | 24.40 | 24.40 | NA | 24.40 | 24.40 |
| 13 | Failure of connector (E13) | 0.00268 | 0.00024 | 0.00024 | 0.00024 | 0.01 |
| 14 | Soiling (E14) | 0.433 | 0.433 | NA | 0.433 | 0.433 |
| 15 | Arcs (E15) | 0.493 | 0.493 | NA | 0.493 | 0.493 |
| 16 | Short contacts (E16) | 1.041 | 1.041 | NA | 1.041 | 1.041 |
| 17 | Open contacts (E17) | 1.677 | 1.677 | NA | 1.677 | 1.677 |
| 18 | Broken Cell (E18) | 38.1 | 38.1 | NA | 38.1 | 38.1 |
| 19 | Shading (E19) | 2.840 | 2.840 | NA | 2.840 | 2.840 |
| 20 | Solder bond failure (E20) | 51.9 | 51.9 | NA | 51.9 | 51.9 |
| 21 | Discoloration (E21) | 8.48 | 8.48 | NA | 8.48 | 8.48 |
| 22 | Delamination (E22) | 10.42 | 10.42 | NA | 5.44 | 15.4 |
| 23 | Grounding/Lightening protection system (E23) | 16.2 | 16.2 | NA | 16.2 | 16.2 |
| 24 | Thermal stress (E24) | 0.020 | 0.020 | NA | 0.020 | 0.020 |
| 25 | Cable failure due to extreme weather conditions (E25) | 0.020 | 0.020 | NA | 0.020 | 0.020 |
| 26 | Improper installation (E26) | 0.049 | 0.049 | NA | 0.049 | 0.049 |
| 27 | Bypass diode (E27) | 1.529 | 0.677 | NA | 0.45 | 3.46 |
| Event | Basic Event | Event | Basic Event | ||||
|---|---|---|---|---|---|---|---|
| E1 | Faulty SPD | 0.0032 | 0.9968 | E18 | Broken Cell | 0.1115 | 0.8885 |
| E2 | Faulty cable | 0.0003 | 0.9997 | E19 | Partial shading | 0.0088 | 0.9912 |
| E3 | Insulation failure | 0.0001 | 0.9999 | E20 | Solder bond failure | 0.1487 | 0.8513 |
| E4 | Faulty MCB | 0.0008 | 0.9992 | E21 | Discoloration | 0.0260 | 0.9740 |
| E5 | Material aging | 0.0002 | 0.9998 | E22 | Delamination | 0.0318 | 0.9682 |
| E6 | Bad system configuration | 0.0000 | 1.0000 | E23 | Grounding/lightning protection system | 0.0490 | 0.9510 |
| E7 | Improper maintenance | 0.0002 | 0.9998 | E24 | Thermal Stress | 0.0001 | 0.9999 |
| E8 | Construction defect | 0.0000 | 1.0000 | E25 | Climatic condition | 0.0001 | 0.9999 |
| E9 | Oxidation | 0.0000 | 1.0000 | E26 | Improper Installation | 0.0002 | 0.9998 |
| E10 | Corrosion | 0.0001 | 0.9999 | E27 | Faulty bypass diode | 0.0021 | 0.9979 |
| E11 | Broken interconnect | 0.0846 | 0.9154 | E28 | Transportation | NA | 1 |
| E12 | Rack structure | 0.0729 | 0.9271 | E29 | Self-Shading | NA | 1 |
| E13 | Failure of connector | 0.0001 | 1.0000 | E30 | Tree | NA | 1 |
| E14 | Soiling | 0.0013 | 0.9987 | E31 | Building | NA | 1 |
| E15 | Arcs | 0.0015 | 0.9985 | E32 | Dust Accumulation | NA | 1 |
| E16 | Short circuit | 0.0032 | 0.9968 | E33 | Bird Dropping | NA | 1 |
| E17 | Open circuit | 0.0052 | 0.9948 |
| Basic Event No. | Basic Event | Failure Probability | F-V Importance Measure | Critical Ranking |
|---|---|---|---|---|
| E1 | Faulty SPD | 0.0032 | 5.7971 × 10−3 | 10 |
| E2 | Faulty cable | 0.0003 | 5.4348 × 10−4 | 16 |
| E3 | Insulation failure | 0.0001 | 1.8116 × 10−4 | 20 |
| E4 | Faulty MCB | 0.0008 | 1.4493 × 10−3 | 15 |
| E5 | Material ageing | 0.0002 | 3.6232 × 10−4 | 17 |
| E6 | Bad system configuration | 0.0000 | 0.0000 | 25 |
| E7 | Improper maintenance | 0.0002 | 3.6232 × 10−4 | 18 |
| E8 | Construction defect | 0.0000 | 0.0000 | 26 |
| E9 | Oxidation | 0.0000 | 0.0000 | 27 |
| E10 | Corrosion | 0.0001 | 1.8116 × 10−4 | 21 |
| E11 | Broken interconnect | 0.0846 | 1.5326 × 10−1 | 3 |
| E12 | Rack structure | 0.0729 | 1.3207 × 10−1 | 4 |
| E13 | Failure of connector | 0.0001 | 1.8116 × 10−4 | 22 |
| E14 | Soiling | 0.0013 | 2.3551 × 10−3 | 14 |
| E15 | Arcs | 0.0015 | 2.7174 × 10−3 | 13 |
| E16 | Short circuit | 0.0032 | 5.7971 × 10−3 | 11 |
| E17 | Open circuit | 0.0052 | 9.4203 × 10−3 | 9 |
| E18 | Broken cell | 0.1115 | 2.0199 × 10−1 | 2 |
| E19 | Partial shading | 0.0088 | 1.5942 × 10−2 | 8 |
| E20 | Solder bond failure | 0.1487 | 2.6938 × 10−1 | 1 |
| E21 | Discoloration | 0.0260 | 4.7101 × 10−2 | 7 |
| E22 | Delamination | 0.0318 | 5.7609 × 10−2 | 6 |
| E23 | Grounding/ lightning protection system | 0.0490 | 8.8768 × 10−2 | 5 |
| E24 | Thermal stress | 0.0001 | 1.8116 × 10−4 | 23 |
| E25 | Climatic condition | 0.0001 | 1.8116 × 10−4 | 24 |
| E26 | Improper installation | 0.0002 | 3.6232 × 10−4 | 19 |
| E27 | Faulty bypass diode | 0.0021 | 3.8043 × 10−3 | 12 |
| Event No. | Sub-System/Intermediate Event | Abbreviation | ||
|---|---|---|---|---|
| F1 | Glass Breakage | GB | 0.0003 | 0.9997 |
| F2 | Encapsulation fault | EF | 0.0570 | 0.9430 |
| F3 | Hot Spot | HS | 0.0101 | 0.9899 |
| F4 | Junction Box Failure | JBF | 0.0022 | 0.9978 |
| F5 | Photovoltaic Module | PVM | 0.4372 | 0.5628 |
| F6 | Miniature Circuit Breaker | MCB | 0.4372 | 0.5628 |
| F7 | Open Intermittently | OIMT | 0.0002 | 0.9998 |
| F8 | High Resistance | HRS | 0.0002 | 0.9998 |
| F9 | Faulty Fuse | FFUSE | 0.0004 | 0.9996 |
| F10 | No input to Fuse | NIF | 0.4378 | 0.5622 |
| F11 | Open Circuit | OC | 0.0005 | 0.9995 |
| F12 | Short Circuit | SC | 0.0001 | 0.9999 |
| F13 | Failure of Cable | FOC | 0.0005 | 0.9995 |
| F14 | No Input to SPD | NISPD | 0.4380 | 0.5620 |
| Sr. No. | Intermediate Event | Failure Probability | F-V Importance Measure | Critical Ranking |
|---|---|---|---|---|
| 1 | Glass Breakage | 0.000276 | 0.0005 | 11 |
| 2 | Encapsulation fault | 0.056951 | 0.1032 | 5 |
| 3 | Hot Spot | 0.010103 | 0.0041 | 6 |
| 4 | Junction Box Failure | 0.002247 | 0.0041 | 7 |
| 5 | PV Module | 0.437232 | 0.7921 | 4 |
| 6 | Miniature Circuit Breaker | 0.437232 | 0.7921 | 3 |
| 7 | Open Intermittently | 0.000199 | 0.0004 | 12 |
| 8 | High Resistance | 0.000152 | 0.0003 | 13 |
| 9 | Faulty Fuse | 0.000351 | 0.0006 | 10 |
| 10 | No input to Fuse | 0.437841 | 0.7932 | 2 |
| 11 | Open Circuit | 0.000475 | 0.0009 | 9 |
| 12 | Short Circuit | 5.58 × 10−5 | 0.0001 | 14 |
| 13 | Failure of Cable | 0.00053 | 0.0010 | 8 |
| 14 | No Input to SPD | 0.437955 | 0.7934 | 1 |
| Sr. No. | Intermediate Events | Proposed Methodology Criticality Ranking | [34] | [29] | [35] | [25] | [48] | [37] | [55] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | No Input to SPD | 1 | |||||||
| 2 | No input to Fuse | 2 | |||||||
| 3 | Miniature Circuit Breaker | 3 | 6 | 8 | 7 | ||||
| 4 | PV Module | 4 | 2 | 3 | 3 | 2 | 4 | ||
| 5 | Encapsulation fault | 5 | |||||||
| 6 | Hot Spot | 6 | |||||||
| 7 | Junction Box Failure | 7 | |||||||
| 8 | Failure of Cable | 8 | 11 | 5 | |||||
| 9 | Open Circuit | 9 | 5 | ||||||
| 10 | Faulty Fuse | 10 | |||||||
| 11 | Glass Breakage | 11 | |||||||
| 12 | Open Intermittently | 12 | 11 | ||||||
| 13 | High Resistance | 13 | |||||||
| 14 | Short Circuit | 14 | 6 |
| Sr. No. | Basic event | Proposed Methodology Criticality Ranking | [34] | [29] | [37] | [55] |
|---|---|---|---|---|---|---|
| 1 | Solder bond failure | 1 | - | |||
| 2 | Broken Cell | 2 | - | |||
| 3 | Broken interconnect | 3 | - | |||
| 4 | Rack structure | 4 | - | |||
| 5 | Grounding/ lightning protection system | 5 | - | |||
| 6 | Delamination | 6 | - | |||
| 7 | Discoloration | 7 | - | |||
| 8 | Partial shading | 8 | 3 | |||
| 9 | Open circuit | 9 | 5 | |||
| 10 | Faulty SPD | 10 | 4 | 7 | ||
| 11 | Short circuit | 11 | 6 | |||
| 12 | Faulty bypass diode | 12 | 9 | 2 | 2 | |
| 13 | Arcs | 13 | 7 | |||
| 14 | Soiling | 14 | 2 | |||
| 15 | Faulty MCB | 15 | ||||
| 16 | Faulty cable | 16 | 11 | 5 | ||
| 17 | Material ageing | 17 | 12 | |||
| 18 | Improper maintenance | 18 | 13 | |||
| 19 | Improper Installation | 19 | - | |||
| 20 | Insulation failure | 20 | 17 | |||
| 21 | Corrosion | 21 | 14 | |||
| 22 | Failure of connector | 22 | 8 | 10 | ||
| 23 | Thermal Stress | 23 | 16 | |||
| 24 | Climatic condition | 24 | 16 | |||
| 25 | Bad system configuration | 25 | 18 | |||
| 26 | Construction defect | 26 | 22 | |||
| 27 | Oxidation | 27 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sonawane, P.R.; Bhandari, S.; Patil, R.B.; Al-Dahidi, S. Reliability and Criticality Analysis of a Large-Scale Solar Photovoltaic System Using Fault Tree Analysis Approach. Sustainability 2023, 15, 4609. https://doi.org/10.3390/su15054609
Sonawane PR, Bhandari S, Patil RB, Al-Dahidi S. Reliability and Criticality Analysis of a Large-Scale Solar Photovoltaic System Using Fault Tree Analysis Approach. Sustainability. 2023; 15(5):4609. https://doi.org/10.3390/su15054609
Chicago/Turabian StyleSonawane, Pramod R., Sheetal Bhandari, Rajkumar Bhimgonda Patil, and Sameer Al-Dahidi. 2023. "Reliability and Criticality Analysis of a Large-Scale Solar Photovoltaic System Using Fault Tree Analysis Approach" Sustainability 15, no. 5: 4609. https://doi.org/10.3390/su15054609
APA StyleSonawane, P. R., Bhandari, S., Patil, R. B., & Al-Dahidi, S. (2023). Reliability and Criticality Analysis of a Large-Scale Solar Photovoltaic System Using Fault Tree Analysis Approach. Sustainability, 15(5), 4609. https://doi.org/10.3390/su15054609








