Energy Measurement in Standard Penetration Tests

Abstract

The standard penetration test (SPT) is a widely used in situ test method worldwide that can evaluate soil properties based on the blow counts (N-value). The N-value depends on soil properties, and the energy transferred to the drill pipe during hammering. Currently, European and American scholars generally believe that variation in the amount of hammer energy transmitted to the drill pipe due to different types of drop hammer systems is the primary factor that leads to variations in N-value. In China, there is a lack of research on the quantitative energy transfer efficiency of the drop hammer system based on test data from a penetration test instrument. In this study, an in-situ test in Jiangsu Province was performed at a test site using standard penetration test instruments that are commonly used in China. Corresponding time history curves and strain, acceleration, force, velocity, energy and penetration degree data were obtained through the stress wave test. The propagation law of the stress wave and energy in a drill pipe was analyzed, and the energy transfer efficiency of the domestic SPT system was measured. In the stress wave test, most of the measured hammer energy efficiency was between 74.5 and 84.5%, and the measured average energy was 0.3723 kJ; the average energy efficiency was 78.7%; the standard deviation (SD) of the energy efficiency was 3.82, and the coefficient of variation (CV) of energy transfer efficiency(E_R) was 4.9%. The average energy efficiency of 78.7% can be considered to be the energy efficiency of the domestic SPT system. The calculated results reported in this article can be used to improve the quantitative level of domestic investigation. Based on the calculated E_r, the results obtained from different SPT systems at home and abroad can be corrected.

1. Introduction

A standard penetration test (SPT) consists of a heavy hammer with a mass of 63.5 kg falling freely from a specified drop distance (76 cm) and a standard specification penetration device being driven into a given formation. The nature of the soil layer is then determined based on the hammering number of the penetration device and the depth reached by the device during the test [1]. The SPT is a widely used in-situ test method worldwide and the required test equipment is simple, easy to operate, low-cost, widely applicable to soil layers, can take soil samples, and produces rich engineering data in different regions. With the advancement of the national belt and road strategy in recent years, more Chinese enterprises are moving abroad. In these international projects, Chinese enterprises must often perform surveys, develop designs and construct projects in accordance with the regulations of Europe and the United States [2]. Therefore, it is necessary to bring domestic survey methods into line with international standards and further promote domestic standard quantitative studies of penetration tests.

The quantitative research on the hammering energy of SPT systems began in the 1970s. Schmertmann and Palacios tested different standard penetration test systems through experiments in 1979 and put forward the concept of the energy efficiency ratio of the drop hammer; it was concluded that the energy efficiency ratio E_R is inversely proportional to the value of the standard penetration test hammering number N. The study showed that the safety hammer’s energy efficiency than E_R was close to 60%; therefore, Seed [3] and Skempton [4] suggested that 60% could be used as the benchmark to compare the energy efficiency ratio of various standard penetration test drop hammer systems, and the benchmark energy efficiency ratio of 60% was also widely used in the world [5]. Therefore, we now have the currently more commonly used hammering energy-corrected standard penetration number:

$$N_{60}=\frac{E_R}{60}\times N$$

(1)

where, N₆₀ is the hammer number after the hammer energy correction, and N is the hammer number of the measured standard penetration test.

Currently, European and American scholars generally believe that the variability in hammer energy that is transmitted to drill pipes due to different types of drop hammer systems is the most important factor that leads to variations in N [6,7,8,9,10]. These drop hammer systems vary markedly between countries. A numerical comparative study of hammer energies measured in the field showed that different drop hammer release modes would also lead to a difference in N [11,12]. In China and the United States, the main difference between the drop hammer system is the type of heavy hammer. Different types of heavy hammers have different degrees of influence on force wave propagation and energy transfer [13]. The primary difference between Chinese and U.S. drop hammer systems is the difference in hammer mass, which also affects the stress wave propagation and energy transfer [14]. In recent years, scholars have performed field measurements and analyses on the transmission efficiency in the hammer energy of standard penetration tests [15,16,17,18], but there is little research on this topic in China.

Both the SPT and cone penetration test (CPT) are commonly used for the evaluation of the mechanical properties of soil. Compared with the CPT, the SPT is cheaper, but its accuracy is highly dependent on the operator experience and the system used in the test. There are limited reports on the energy transfer efficiency of drop hammer systems in the SPT in China. In this study, the energy transfer efficiency (E_R) of the Chinese drop hammer system is calculated. Based on the calculated E_R, the results obtained from different SPT systems at local and international projects can be corrected.

2. Materials and Methods

2.1. Quantitative Research Method of Standard Penetration Test

The primary factors that affect the standard penetration test hammer for N are that the real hammer system is passed to the drill pipe and penetration of energy, due to the difficulty of the injection device in the test. For energy measurement, strain sensors and acceleration sensors are installed in the drill pipe to perform fluctuation tests, and the real transmitted energy is then determined by calculation. According to the measured energy, the hammer number N obtained by different standard penetration test equipment is energy-corrected. The determination of the hammer energy is based on one-dimensional fluctuation theory and can be divided into two primary methods such as the force square method and the force velocity method.

2.1.1. Force-Leveling Method to Determine the Hammer Strike Energy

The force-leveling method is a standard penetration test energy measurement method proposed by Schmertmann and Palacios [3] in 1977. The idea is to install a strain sensor (force gauge) somewhere in the drill rod and calculate the hammer energy according to the measured stress time course curve. According to the functional principle, the hammer energy E is the total work W acting at the particle; that is:

$$E=W={{\displaystyle \int }}_0^{\Delta t}{F}_r\left(t\right)v\left(t\right)dt$$

(2)

The force-leveling method assumes the same cross-section of the drill; it is not a reflected wave interference:

$$F_r\left(t\right)=A_r\times \sigma \left(t\right)$$

(3)

where, A_r is the section area of the drill rod measurement, σ(t) is the stress of the drill rod measurement, and v(t) is the speed of the drill rod measurement.

The drill rod material is made of steel with line elastic properties, according to the line elasticity assumption:

$$\sigma \left(t\right)={\rho }_r\times c_r\times v\left(t\right)=\frac{E_{r}v\left(t\right)}{c}$$

(4)

where, ρ_r is the density of the drill pipe, C_r is the propagation speed of elastic waves in the drill pipe, and E_r is the elastic modulus of the drill pipe material.

Substituting Equation (4) with Equation (3) gives:

$$v\left(t\right)=\frac{F_r\left(t\right)\times c_r}{A_r}$$

(5)

Substituting Equation (5) with Equation (2), we see that the energy generated by hammering E_i is

$$E_i={{\displaystyle \int }}_0^{\Delta t}{F}_r\left(t\right)v\left(t\right)dt=\frac{c_r}{A_r{E}_r}{{\displaystyle \int }}_0^{\Delta t}{F}_r{(t)}^{2}dt$$

(6)

The standard penetration test drill rod is a finite long rod. When the stress wave from the hammer travels down to the tip of the penetration rod, the reflected wave travels up along the drill rod; when the reflected wave reaches the strain sensor position, it is offset with the compression wave of the continuous input. At this point, the force and speed will no longer be proportional, and the power level method chooses the energy at this time as the hammer energy. The time required for the first pressure wave generated for the hammer, starting from the measuring point position, and being transmitted to the bottom of the penetration device to again reflect back to the drill rod, is $\Delta t$:

$$\Delta t=2L^{\prime }/c_r$$

(7)

where, $L^{\prime }$ is the distance from the position of the measuring point to the tip of the penetrator.

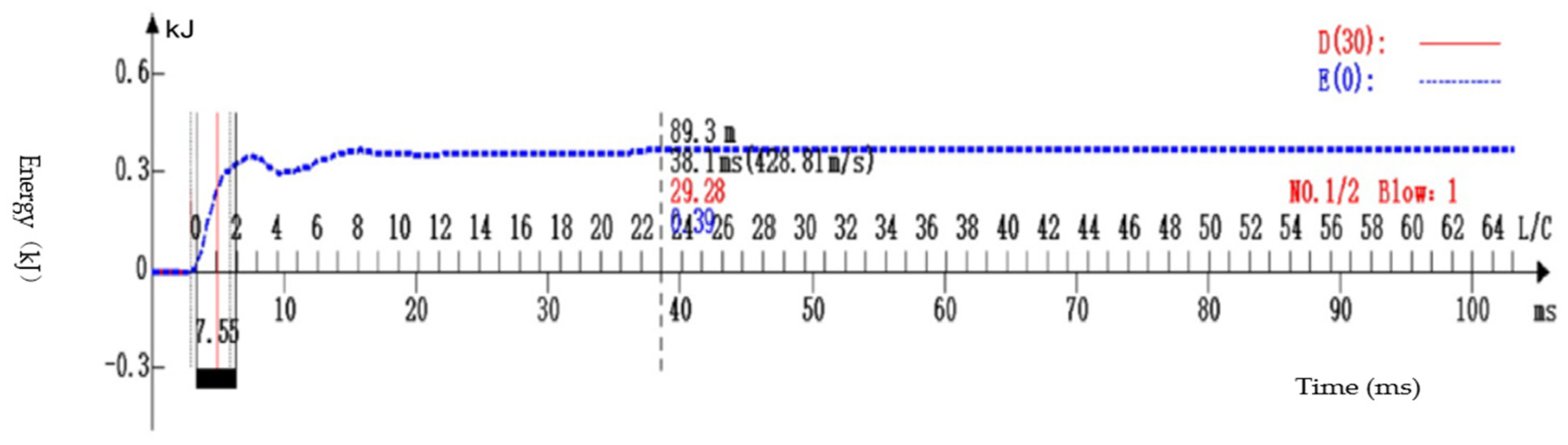
2.1.2. Force-Speed Method

The force-velocity method was developed by Abou-matar and Goble [19] in 1997; it was proposed that hammer energy is directly integrated from the time of the drill measurement of section area F_r(t) and speed v(t):

$$E={{\displaystyle \int }}_0^{max}{F}_r\left(t\right)v\left(t\right)dt$$

(8)

where max is the corresponding time when the energy accumulates to the maximum energy.

The force-velocity method differs from the force-leveling method in that the force-velocity method requires increasing the acceleration a(t) of the measuring position of the drill rod measured by the acceleration sensor, and the velocity v(t) is then integrated by Equation (9).

$$v\left(t\right)=\int a\left(t\right)dt$$

(9)

The force leveling method assumes that the drill rod is an equal cross-section, which requires that the force be proportional to the speed, while the force-velocity method does not require this assumption, and can track the energy transfer of the whole hammer process.

2.2. Fluctuation Test of the In Situ SPT

In this study, a test field in Jiangsu Province was selected for an in-situ test. Data were obtained from a fluctuation test; the propagation law of the stress wave and energy in the drill rod were analyzed; the two energy calculation methods of the comparative force-leveling method and force-velocity method were analyzed; in addition, the energy and energy efficiency actually transmitted by the heavy hammer to the drill rod were calculated.

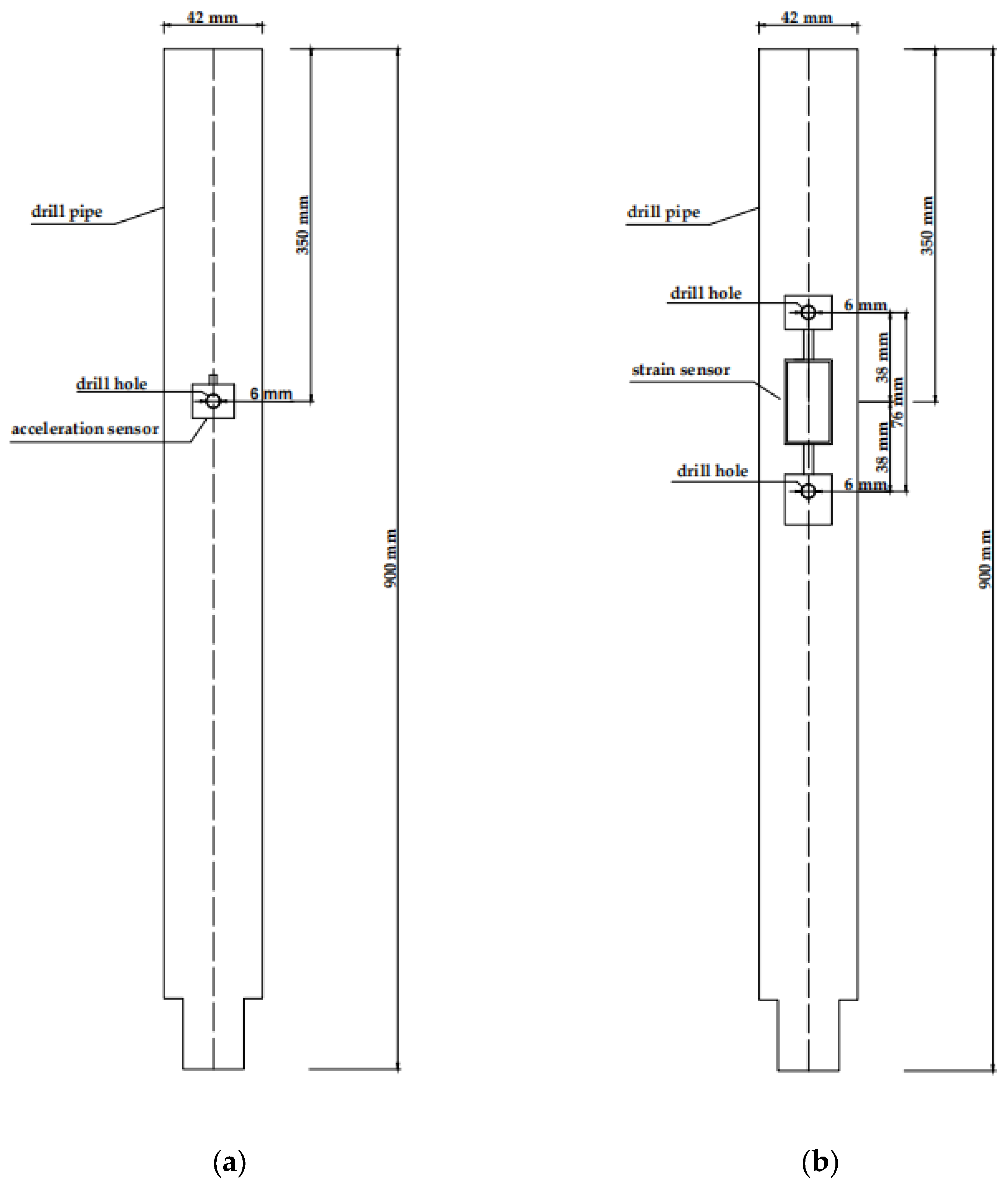
2.2.1. Volatility Test Instruments and Equipment

A high-strain base pile detector was used for the test. Pictures of the test instrument and supporting sensors are shown in Figure 1 and Figure 2.

The data acquisition module of the device adopts a high-precision AD resolution of 24 bit, and the sampling frequency is divided into 10 kHz, 20 kHz, 30 kHz and 40 kHz four stages adjustable, with the sampling length of 1024, 2048 and 4096 points optional. During the standard penetration fluctuation test, the sampling frequency was 40 kHz, the sampling length was 4096 points, and the sampling length was 100 ms.

Both sides of the strain sensor are protected, which makes the performance more stable and reliable. The acceleration sensor was originally imported from the United States, and the maximum acceleration range can reach 5000 g. The main parameters of the strain sensors and acceleration sensors are shown in

Table 1. Technical parameters table of strain sensor of pile driving analyzer selected in the experiment.

Measurement Range (με)	Sensitivity (mV/V)	Weight (g)	Temperature Range (°C)	Overall Dimensions (mm)
2000	3.37	90	−30~80	115 × 37 × 11

and

Table 2. Technical parameters of acceleration sensor of pile driving analyzer selected in the experiment.

Sensitivity (Pc/g)	Frequency Range (kHz)	Weight (g)	Temperature Range (°C)	Overall Dimensions (mm)
1.02	0.5~10	100	−54~+120	80 × 27 × 25

.

2.2.2. Geology of the Test Site

The foundation soil of the test site has four layers; the first layer is mixed fill, plain fill, pond filling or cultivated soil; the second largest layer is silty clay, commonly known as the hard shell layer; the third layer is soft soil layer, with certain deposition rules, mainly silty clay; the fourth layer is a hard clay layer, mainly plastic or hard clay, with a thin layer of silty clay.

According to the site survey report and drilling data, within the range of the survey depth (the maximum depth is 56 m) are the quaternary Late Pleistocene and Holocene deposits, and the overall soil is relatively uniform, which is suitable for the development of this paper.

2.2.3. Standard Test Fluctuation Test Process

For the fluctuation test in the SPT, a strain sensor was installed on the drill rod and an acceleration sensor was placed under the hammer pad; the strain duration curve and acceleration duration curve below the hammer pad were measured to obtain the corresponding force duration curve and speed duration curve; additionally, the real hammer energy transmitted by the drop hammer system to the drill rod was obtained through the force−velocity method.

To ensure a valid test, we prepared the required instruments in advance, including a standard penetration instrument, the high strain base pile detector that was equipped with a suitable strain sensor and acceleration sensor; a drilling rod; a steel support; and a hoist to lift the hammer as shown in Figure 3. The schematic diagram of the drilling hole and sensor installation position and sensor installation positions is shown in Figure 4, while Figure 5 shows the schematic of the field installation.

The steps and key points of the in situ test are as follows:

• We used the crane to lift the steel support to the test position to maintain stability. We used a winch that met the lifting requirements, fixed a pulley to guide the steel wire rope on the top of the support, and connected the power supply.
• We determined the appropriate drilling position to ensure that the drop hammer’s centerline and the desired hole’s centerline were located on the same vertical line. During hammering, we ensured the vertical alignment of the falling hammer and the drill rod to mitigate unnecessary friction between the falling hammer and the guide rod, and any eccentricity in the contact between the heavy hammer and the hammer pad, which would have affected the collected data.
• The drill rod of the installed sensor was connected between the hammer pad and the drill rod under the standard penetration instrument; the drilling hole was located 30 cm under the hammer pad, and the drilling position was kept approximately 0.6 m above the ground.
• We installed the strain and acceleration sensors on the drill rod securely, and connected the high strain collection instrument.
• We turned the high-strain acquisition instrument on; set the appropriate engineering parameters, pile parameters and sensor parameters, selected the appropriate trigger voltage; adjusted and confirmed that the sensor was ready, and waited for the hammer to impact the test sample.
• We commanded the operator to use the winch to lift the hammer until it automatically fell and impacted the hammer pad. We then ceased data acquisition and saved all data that were recorded 100 ms after the trigger.
• We commanded the drilling operator to lift the hammer in order to repeat the test. We then repeated step 6 until the end of the SPT. We then recorded the test depth, rod length, mark, stroke number and other relevant data.
• We removed the sensor and wire, arranged the relevant instruments, removed the standard penetration device and cleaned any debris from it. We then placed the device back into the borehole for the next depth of the SPT. Photographs of the in situ trials are shown in Figure 6.

3. Results

Data Wrangling

A total of two boreholes were tested, each with a test depth of 10 m, while the test soil layer was mainly conducted on layer 2 of silty clay. There were 21 standard penetration hits and 189 standard penetration hits, and 172 sets of hammer signals were collected by the strain and acceleration sensors mounted directly below the hammer pad.

Using the high-strain base pile detector analysis software to analyze the collected data, we could obtain the corresponding strain, acceleration, force, speed, energy, penetration time course curve and data.

Through a comparative analysis of the above data, the effectiveness of the acquisition instrument and data was first verified, and the effective hammer data were selected.

The verification steps performed in this study are as follows:

• Comparison of force time course curve calculated by force-velocity method and force-leveling method.

The force-time range curve can be integrated by the strain signal measured by the strain sensor, and similarly, the velocity time curve can be integrated by the acceleration signal measured by the acceleration sensor.

Force data can also be calculated by velocity data via Equation (10)

$$F\left(t\right)=\frac{A\times E}{c}\times v\left(t\right)=Z\times v\left(t\right)$$

(10)

where A is the area of the cross-section of the drill pipe (6.79 × 10⁻⁴ m²), E is the elastic modulus of the drill pipe (206,840 MPa), and c is the theoretical wave velocity ($c={\left(E/\rho \right)}^{0.5}=5120\mathrm{m}/\mathrm{s}$), $\rho$ is the density of the drill pipe (7850 kg/m³), v is the measured wave velocity and Z is the drill pipe wave impedance.

The F and ZV time course curves are at the initial time point (t_i) and the time when the tensile wave reaches the measuring point position (t_i + 2L’/c) is proportional, L’ is the length of the sensor measured point position to the tip of the penetrator.

• Comparison of the displacement and measured penetration

The calculated displacement can be obtained by the velocity curve $u={{\displaystyle \int }}_0^{\infty }vdt$ and judged by comparing the measured displacement with the standard penetration test.

Comparison of acceleration time curve on both sides of the drill rod; whether the hammer produces an eccentric effect is determined by comparing the acceleration time curves on both sides of the drill rod.

After the above three steps, the measured hammer data were filtered, and 44 effective hits were obtained.

4. Discussion

4.1. Stress Wave and Energy Transfer Law

Typical hammer data were selected to analyze the characteristics of hammer stress waves and the energy transfer. Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 illustrate the hammer data of 7.55 m of the rod length (sensor measuring point position to the penetration tip), including the time course curve of acceleration, speed, force, penetration and energy.

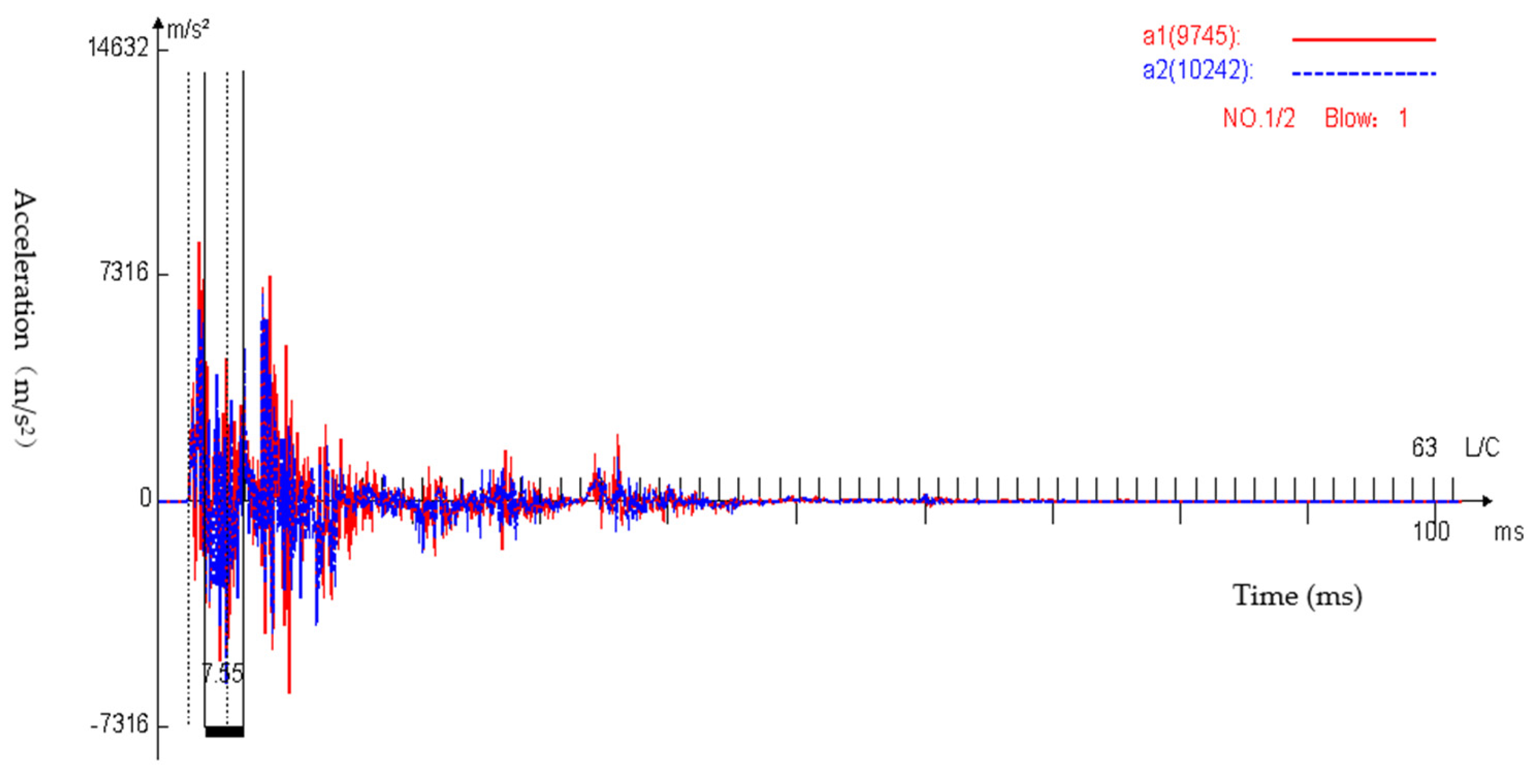
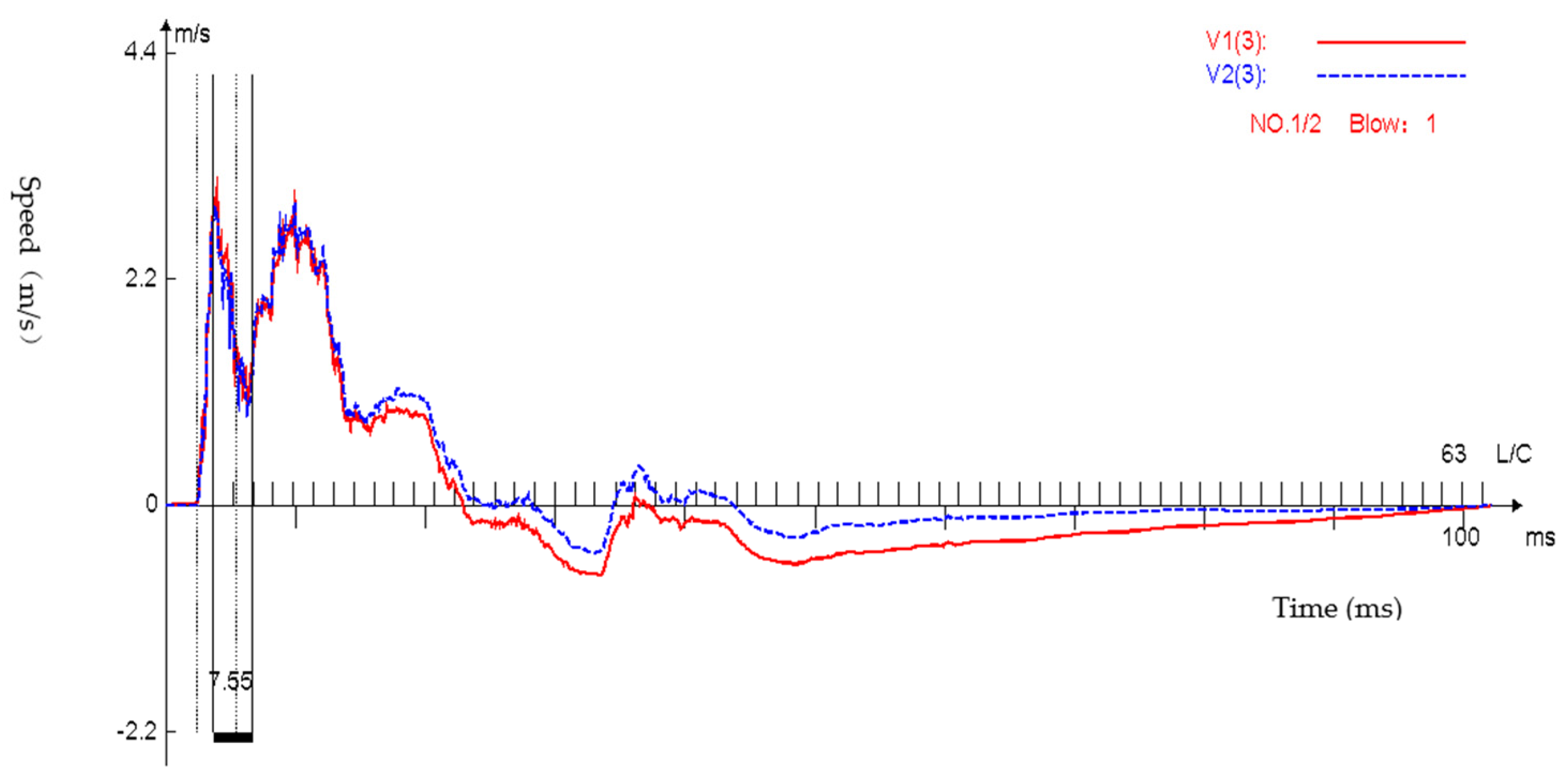
4.1.1. Acceleration and Speed

Figure 7 shows that when the heavy hammer falls freely and hits the hammer pad, the acceleration rises rapidly, reaches its maximum and then gradually returns to zero. The signals corresponding to the two acceleration sensors mounted on both sides of the drill pipe are nearly identical during the impact, which indicates no eccentric effect during the hammering.

Figure 8 shows that all the measured maximum accelerations of effective hammering are summarized. The maximum acceleration of some hammering can reach 25,000 m/s², and most of them are 8500~12,500 m/s². The range of the acceleration sensor meets the requirements. All acceleration time-history curves were analyzed, and the acceleration value −5000~5000 m/s² accounts for the main part. The velocity time-history curve can be obtained by integrating the acceleration time-history curve, while the maximum hammer speed can reach about 3.0 m/s.

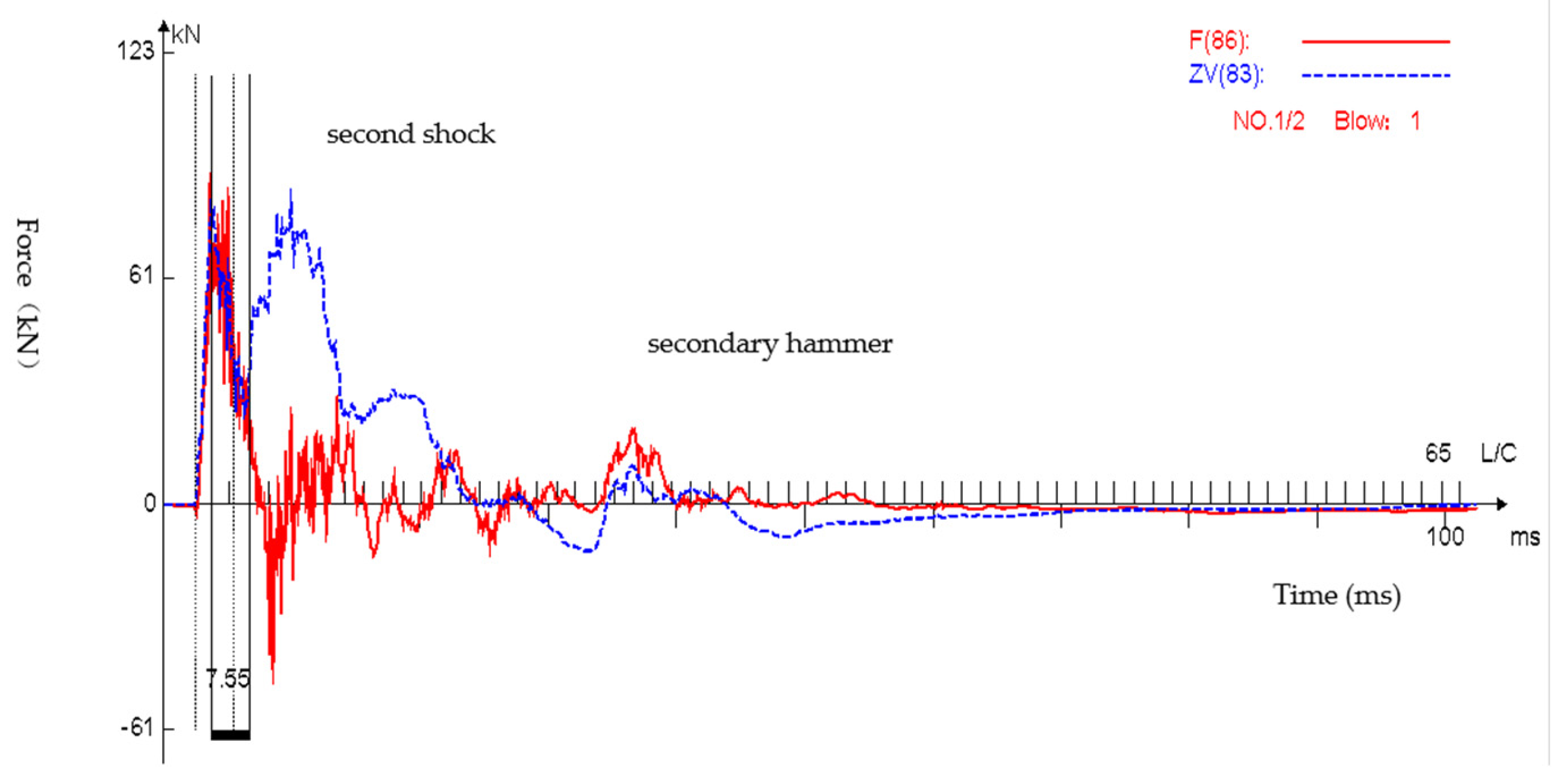
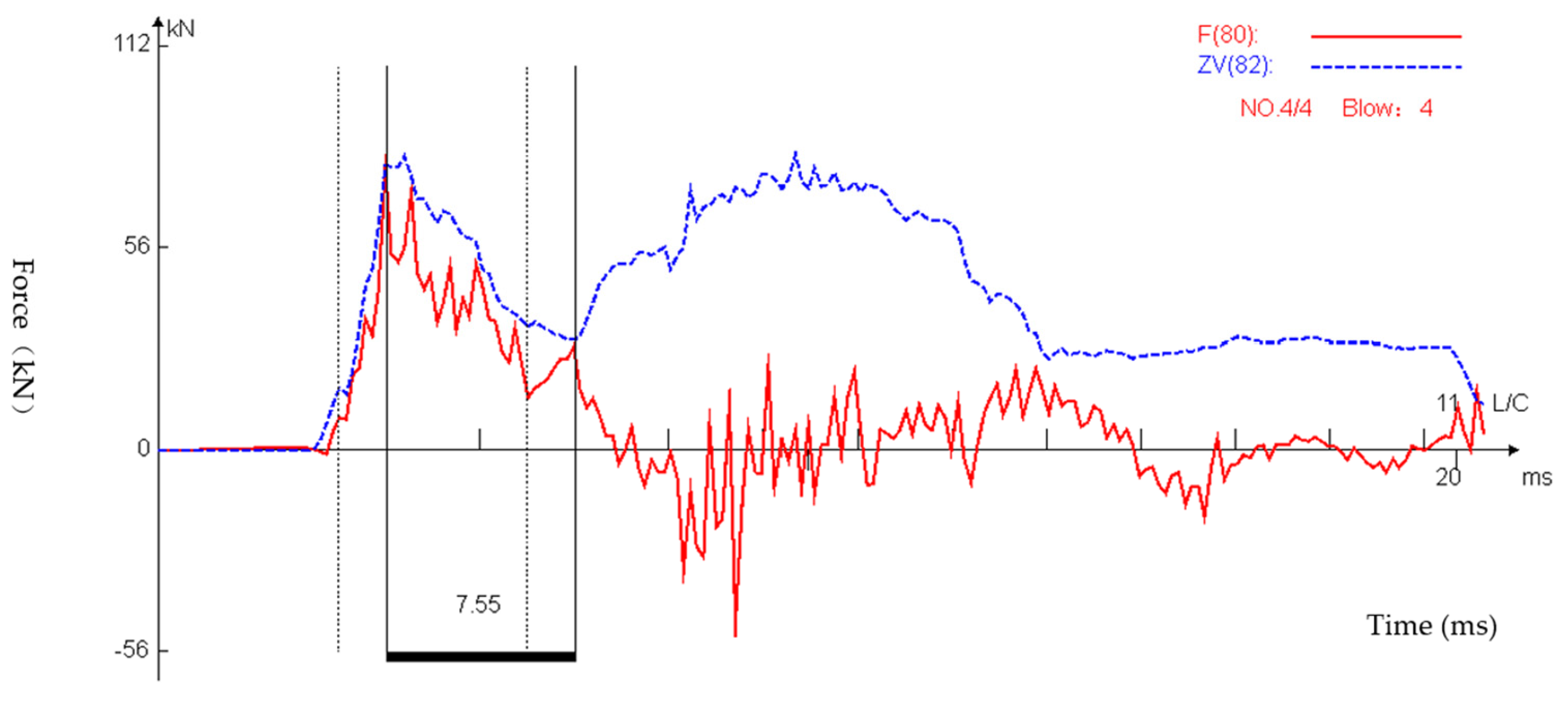
4.1.2. Force

All measured hammer force time-history curves were analyzed and the force-time history curve could be calculated by the strain-time history curve. The maximum force can reach 100 kN. The strain sensor range meets the requirements. The force value is −50~50 kN and accounts for the main part, as shown in Figure 9.

4.1.3. Stress Wave and Energy Propagation

The force-time history and ZV time-history curves show that the strain and acceleration signals are generated at the moment when the heavy hammer falls freely and hits the hammer pad. The force data and the ZV data are then obtained. The impact of the drop hammer produces the first compression wave, which propagates down the drill pipe to the tip of the penetrator, and the penetrator moves downward under the action of the compression wave. Reaching the tip of the penetrator part of the energy at the end is used to cause soil penetration, and a portion of the energy is dissipated into the soil as radiation damping. The downward movement of the tip of the penetrator is then reflected back to the rod in the form of a stretching wave (or a compression wave if the soil resistance is sufficient) due to the soil resistance. In the first strike of the standard penetration test, the tip of the penetrator should be free (i.e., the tip resistance is low), and this situation is clearly shown.

This downward movement of the tip of the penetrator produces a corresponding stretch wave, and the stretch wave reflects up along the drill pipe, returns to the measuring point position, and then continues up to the hammer pad. The time interval between the initial peak of the compression wave at the measuring point position and the reflected stretching wave is 2 L’/c, where L’ is the distance from the measuring point position to the tip of the penetrator, c is the propagation speed of the stress wave in the drill pipe, and the propagation speed of c in steel is 5120 m/s. In Figure 9, the rod length is 7.55 m, the time interval 2 L’/c is 3.04 ms, and the wave velocity is 4970 m/s. The propagation speed of the stress wave in the drill pipe is similar to the theoretical wave velocity, and the measured data are generally slightly smaller than the corresponding theoretical values, because in the prototype test, there are joints between the drill pipes, joint tightness, and silt between threads, etc. which will affect the wave velocity. Therefore, there will be a certain deviation between the wave velocity measured in the field and the theoretical wave velocity. Thus, the test results are consistent with the one-dimensional wave theory.

The force-time history and ZV time-history curve show that the time histories of the force and speed are similar. After the signal is triggered, the force and speed rapidly increase to the maximum value, and after the initial peak, the force and speed smoothly decrease to zero. The F and ZV time history curves nearly coincide before the reflected wave is reflected back to the measured point position. At 2 L’/c after the initial peak of the compression wave, the stretching wave reaches the measuring point position, and the F and ZV time history curves are separated. After the initial peak of the compression wave, the tensile wave reaches the measurement point position, and the F and ZV time-course curves separately. After separation, the ZV time curve is still positive because the inertial drill rod continues down, while the F time curve turns negative within the influence range of the tensile wave. When the length of the drill rod from the hammer to the point of the penetration tip is short, the initial tensile wave returning from the bottom of the drill rod reaches the top of the drill rod before the full compression force is successfully transmitted from the hammer to the drill rod, canceling out part of the compression wave, and resulting in a decrease in the transmitted energy, which is the rod length effect.

4.1.4. Comparison of the Force-Speed Method (FV) and Force-Flat Method (F²)

The stretching wave returning from the bottom of the bar when reaching the top of the bar typically results in a physical separation between the heavy hammer and the bar, and this stretching wave is then reflected back again along the bar as compression waves to produce a second shock. The heavy hammer falls due to gravity for a short distance after separation and recontacts the top of the drill at some point in time to provide a secondary hammer. Each impact increases the energy delivered to the drill system. The hammering energy time-history curve measured under the hammer pad in Figure 11 shows the energy transmission process throughout the hammering process, and the energy change caused by the first and second impact is clearly shown and is consistent with the theoretical analysis. In Figure 11, the total hammering energy measured is 0.39 kJ, and one impact contributes most of this energy. Secondary impact also contributes to approximately 6% of the total energy in this test. As shown in the penetration time-course curve in Figure 10, secondary impacts contribute to the total penetration degree and cannot be ignored; this has also been confirmed by Lee et al. [20]. Therefore, the real energy transferred to the rod should consider all impacts. Compared to the force-square (F²) method, the energy measured by the force-velocity (FV) method can more truly describe the energy transmitted by the drop hammer system to the drill rod.

4.1.5. Penetration

In Figure 10, the penetration time-course curve shows that the displacement obtained by the measured acceleration integration is consistent with the real penetration degree. As shown in the curve, the penetration degree first peaks and then partially decreases, indicating that the drill rod has moved up, which may be caused by the rebound of the mud in the borehole and the soil at the bottom of the penetration device.

4.1.6. Impact of Drill Joints

From the local force–time-course curve in Figure 12, the ratio between force and velocity is not completely consistent, even before the tensile wave reflects back to the test point position. This phenomenon may be due to variations in impedance (such as loose joints or a sudden variation in the cross-sectional area). These variations can lead to energy reflections, disrupting the transmission of the first shock, and further breaking the ratio assumption of F and ZV in the initial time period. For example, a loose joint in the rig disrupts the initial compression transfer and causes a tensile reflection, and in this particular case, the energy will be underestimated if the force-flat method is used. Similarly, if the cross-sectional area at the joint increases at the junction site, then this will produce a partial compressive reflection, which then decomposes the initial compression wave passing through the bar. In this case, the energy may be marginally overestimated if the force-flat method is used. The force-velocity method does not require this scaling relationship, which accurately yields exactly the true energy transfer in these cases if accurate acceleration data can be obtained. As accelerometers improve, it is now becoming possible to track these effects, including joint loosening and joint impedance changes, etc. and to analyze the effects of these factors on energy transmission.

4.2. Hammer Strike Energy

After screening, a total of 44 effective hammer data were obtained; according to the measured hammer energy E_mea, the corresponding energy transfer efficiency E_R is obtained by Equation (11):

$$E_R=\frac{E_{mea}}{E_{theo}}$$

(11)

where E_mea is the measured maximum energy and E_theo is the theory of hammer energy.

The theory of hammer energy E_theo is equal to the potential energy of the heavy hammer that can be obtained by Equation (12):

$$E_{theo}=mgh=0.473\mathrm{kJ}$$

(12)

where m is the weight of a heavy hammer of 3.5 kg and h is the falling distance of 76 cm.

Statistics were performed for the measured hammer hit energy E_mea and the energy transfer and the statistical results are shown in

Table 3. Measured hammering energy and energy efficiency.

Measured Hammer Energy E (kJ)	Energy Transfer Efficiency ER (%)	Measured Hammer Energy E (kJ)	Energy Transfer Efficiency ER (%)
0.3810	80.5	0.3749	79.3
0.3740	79.1	0.3807	80.5
0.3746	79.2	0.3887	82.2
0.4085	86.4	0.3678	77.8
0.3841	81.2	0.3705	78.3
0.3899	82.4	0.3913	82.7
0.3430	72.5	0.3860	81.6
0.3904	82.5	0.3685	77.9
0.3916	82.8	0.3787	80.1
0.3731	78.9	0.3603	76.2
0.3657	77.3	0.3687	77.9
0.3899	82.4	0.3541	74.9
0.3571	75.5	0.3555	75.2
0.3374	71.3	0.3599	76.1
0.3618	76.5	0.3235	68.4
0.3923	82.9	0.3982	84.2
0.3813	80.6	0.3792	80.2
0.3922	82.9	0.3608	76.3
0.3758	79.5	0.3970	83.9
0.3716	78.6	0.3445	72.8
0.3324	70.3	0.3719	78.6
0.3637	76.9	0.3696	78.1

Measured hammer stroke energy transfer efficiency E_R distribution diagram is shown in Figure 13.

.

Most of the measured hammer energy transfer efficiency is between 74.5% and 84.5%. The measured average energy is 0.3723 kJ; the average energy transfer efficiency is 78.7%; the standard deviation in energy transfer efficiency SD is 3.82%; and the coefficient of variation of the energy transfer efficiency CV is 4.9%. Considering the many influencing factors on the standard penetration test, the data errors obtained in this trial are in a reasonable range. Thus, we use 78.7% as the standard hammer system of the instrument in China.

5. Conclusions

In this study, a test site in Jiangsu province was used as a prototype test and fluctuation test in a region that consists primarily of uniform silty clay. The results of this study describe the reduction in drop hammer energy and the primary contribution of this study is the determination of energy transfer efficiency (E_R) of a drop hammer system in a SPT test in China. Based on the calculated E_R, the results obtained from different SPT systems at home and abroad can be corrected. Analysis of the collected fluctuation test data can determine the corresponding strain, acceleration, force, speed, energy, penetration time-course curve and data. The above hammer data collected in this study were then analyzed, and the following conclusions were obtained:

• As shown in the measured force (F) time curve and ZV time curve, the impact of the falling hammer produces a compression wave that propagates down along the drill rod to the tip of the inflow device. The inflow device moves down under the action of the compression wave and produces the corresponding stretching wave, and the stretching wave then reflects upward along the drill rod. When the length of the drill rod from the hammer to the penetration tip is short, the initial tensile wave returning from the bottom of the drill rod begins to reach the top of the drill rod before the full compression force is successfully transferred from the heavy hammer to the drill rod, counteracting the partial compression wave, and resulting in reduced energy transmission.
• The F and ZV time-course curves nearly coincide, before the reflection wave is reflected back to the measurement point position; however, after that time, these curves are no longer proportional to each other. The arrival of the reflected stretching wave typically results in a physical separation between the heavy hammer and the drill rod, and this stretching wave then reflects back again as the compression waves along the drill rod. The heavy hammer falls again due to gravity, and recontacts the top of the drill rod at some point in time, providing a secondary hammer. The secondary impact of the reflected wave and the secondary hammer of the heavy hammer will increase the energy transmitted to the drill rod. The real energy transmitted to the rod should thus include all subsequent impacts. Therefore, when compared to the force-square (F²) method, the force-speed (FV) method can more accurately obtain all the energy transmitted by the drop hammer system.
• The ratio between force and speed is not completely consistent until the tensile wave reflects back to the test point position. This phenomenon may be due to changes in the impedance (e.g., loose joints; sudden changes in the cross-sectional area).
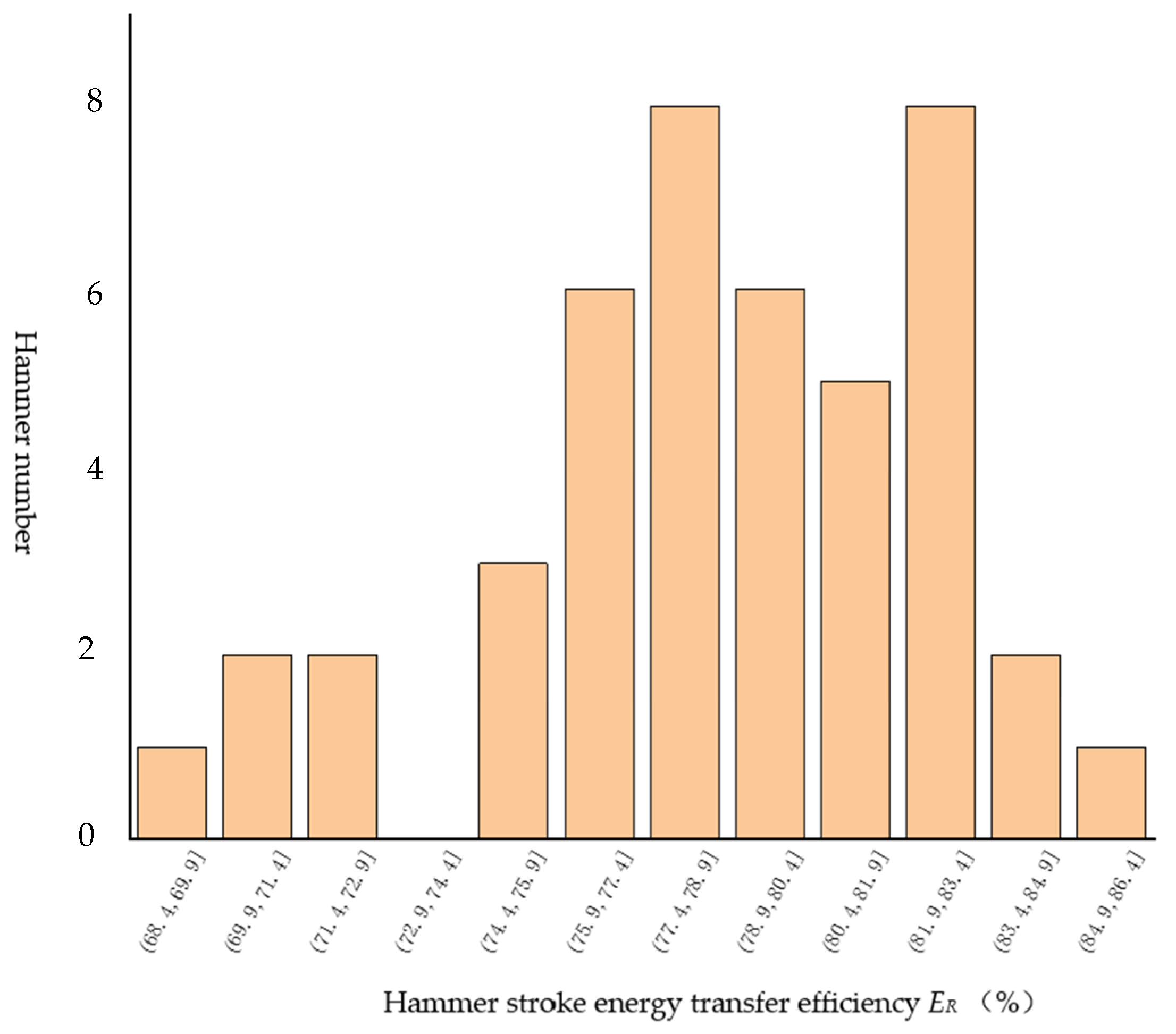
• Most of the measured hammer energy transfer efficiency of the site in situ tests is between 74.5% and 84.5%. The average measured energy is 0.37 kJ; the average energy transfer efficiency is 78.7%; the standard deviation in energy transfer efficiency SD is 3.82; and the variation coefficient of the energy transfer efficiency CV is 4.9%. The average energy transfer efficiency of 78.7% can be used as the standard energy transfer efficiency of a hammer system with a common penetration instrument in China.