Thermodynamic Analysis of the Solubility of Propylparaben in Acetonitrile–Water Cosolvent Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Solvent Mixtures
2.3. Solubility Determination
- Sample saturation: PP was added to each of the cosolvent mixtures {MeCN (1) + W (2)} until a saturated solution in equilibrium with the solid phase was obtained. The samples were subjected to ultrasound for 30 min and then placed in a recirculating water bath (thermostat) at each of the study temperatures (278.15, 283.15, 288.15, 293.15, 298.15, 303.15, 308.15, 313.15 and 318.15 K) for a period of 72 h (a constant concentration was verified).
- Phase separation: The filtration method was employed using membranes with a pore diameter of 0.45 m (Millipore Corp. Swinnex, Burlington, VT, USA). Using a syringe previously thermostatted to the study temperature, an aliquot of the supernatant was taken and then poured through the membrane. In order to reduce the possible effects of solute sorption on the filter membrane, the first drops of the filtrate were discarded.
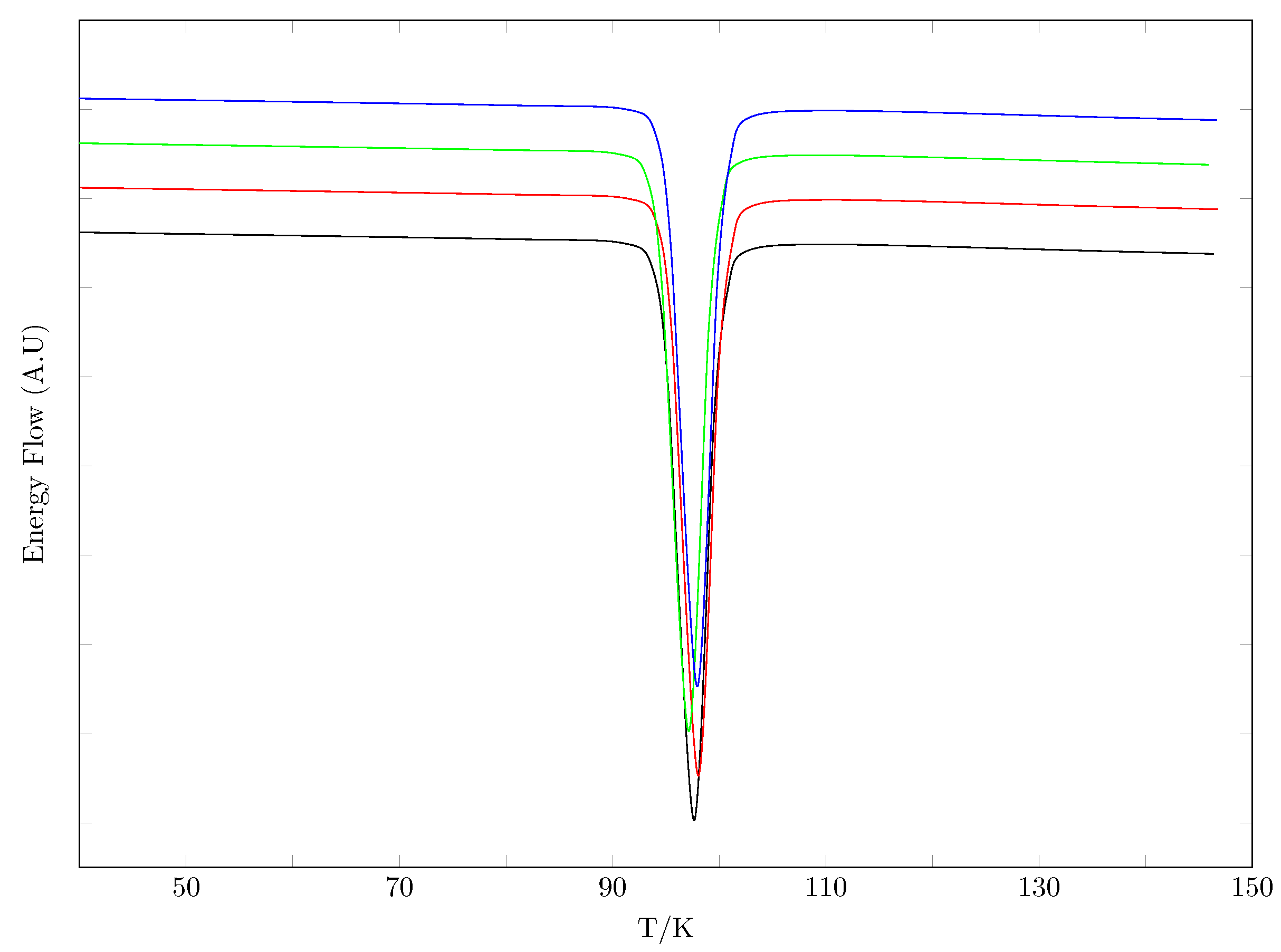
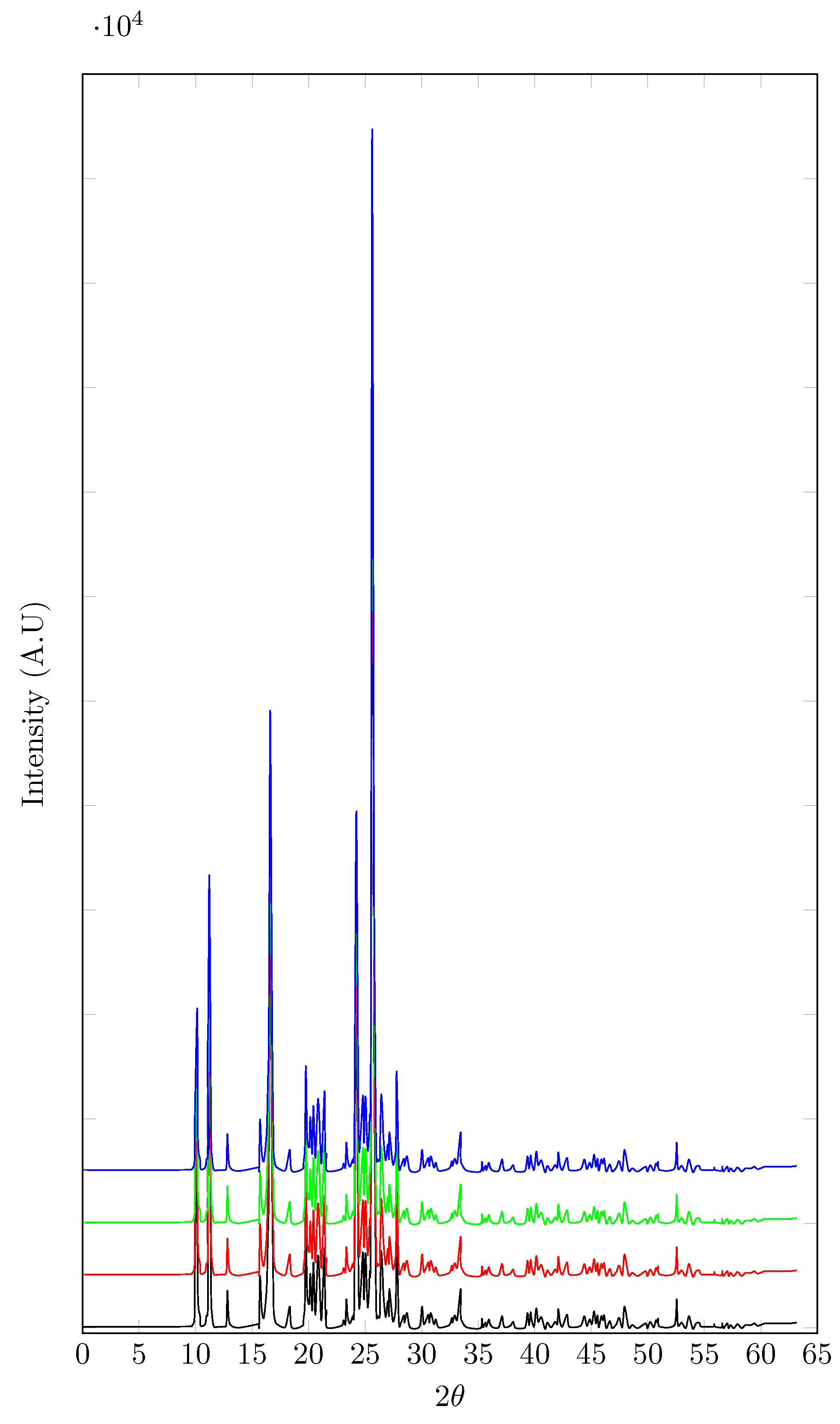
- Saturated solution and solid phase analysis: The concentration of PP in each of the samples was determined by UV/Vis spectrophotometry. From the filtered aliquot, gravimetric dilutions were performed with NaOH 0.1 N (NaOH 0.1 N was used since mixing the saturated solution with the NaOH solution forms the sodium salt of PP, and as the salt is very soluble in aqueous media, the probability of PP precipitation decreases). After dilution, the samples were analyzed in a UV/Vis spectrophotometer UV/Vis (UV/VIS EMC-11- UV spectrophotometer, Dresden, Germany) at 256 nm (the wavelength of maximum absorbance) for the prior construction of the calibration curve. In order to identify possible polymorphic changes, solid samples in equilibrium were analyzed using differential scanning calorimetry (DSC) and X-ray powder diffraction (XRPD).
3. Results and Discussion
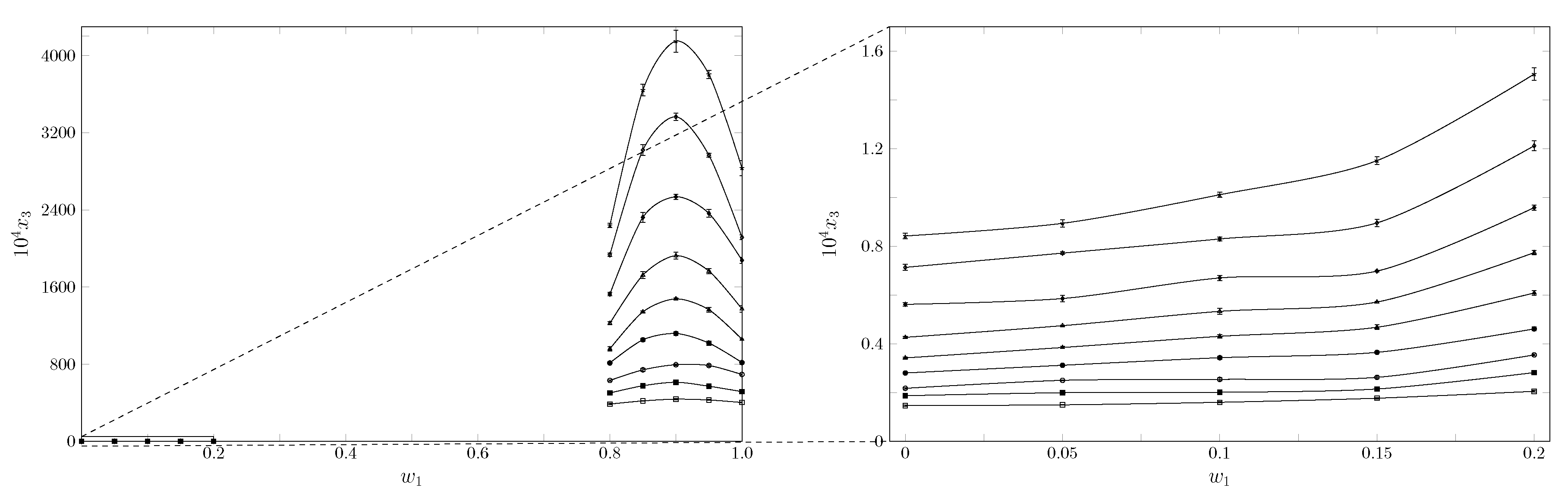
3.1. Solubility () of Propylparaben (3) in 10 Cosolvent Mixtures {Acetonitrile (1) + Water (2)}
| b | Temperatures | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 278.15 | 283.15 | 288.15 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | |
| 0.00 | 0.1468 | 0.1873 | 0.2176 | 0.2804 | 0.3422 | 0.4265 | 0.5617 | 0.7132 | 0.842 |
| 0.05 | 0.1498 | 0.1995 | 0.2502 | 0.3121 | 0.3849 | 0.4743 | 0.5856 | 0.7717 | 0.8939 |
| 0.10 | 0.1603 | 0.2013 | 0.2543 | 0.343 | 0.4307 | 0.533 | 0.6699 | 0.8298 | 1.0109 |
| 0.15 | 0.1771 | 0.2149 | 0.2625 | 0.365 | 0.4679 | 0.5712 | 0.698 | 0.8956 | 1.1508 |
| 0.20 | 0.2053 | 0.2819 | 0.3545 | 0.4612 | 0.6085 | 0.7737 | 0.9582 | 1.2116 | 1.5053 |
| 0.80 | 387.3 | 502.2 | 631.8 | 813.6 | 959.2 | 1224.4 | 1527.4 | 1934.9 | 2238.3 |
| 0.85 | 419.9 | 576.8 | 741.8 | 1053.1 | 1342.9 | 1723.9 | 2322.8 | 3019.9 | 3642.3 |
| 0.90 | 438.0 | 613.2 | 795.4 | 1118.4 | 1477.2 | 1925.1 | 2535.5 | 3365.1 | 4148.8 |
| 0.95 | 429.5 | 572.0 | 786.6 | 1019.1 | 1364.4 | 1765.4 | 2363.6 | 2966.9 | 3804.4 |
| 1.00 | 403.2 | 516.1 | 693.4 | 817.8 | 1058.8 | 1373.0 | 1877.7 | 2115.1 | 2834.2 |
| Sample | Enthalpy of Melting, /kJ·mol | Melting Point /K |
|---|---|---|
| Original sample | 27.0 ± 0.5 | 369.6 ± 0.5 |
| 26.150 a | 369.7 a | |
| 27.9 ± b | 369.5 ± 0.5 b | |
| 28.4 ± 0.6 c | 369.4 ± 0.5 c | |
| 27.2 ± 0.8 d | 369.4 ± 0.5 d | |
| 28.0 e | 369.65 e | |
| 26.51 f | 369.6 f | |
| 24.75 g | 370.92 g | |
| Water | 26.8 ± 0.5 | 369.4 ± 0.5 |
| 27.1 ± 0.5 | 369.9 ± 0.5 | |
| Acetonitrile | 26.9 ± 0.5 | 370.1 ± 0.5 |
3.2. Thermodynamic Functions of Solution
| b | / (kJ·mol) | (kJ·mol) | (J·mol·K | (kJ·mol) | c | c |
|---|---|---|---|---|---|---|
| 0.00 | 25.37 | 32.62 | 24.35 | 7.25 | 0.818 | 0.182 |
| 0.05 | 25.17 | 32.70 | 25.30 | 7.53 | 0.813 | 0.187 |
| 0.10 | 24.97 | 34.36 | 31.57 | 9.40 | 0.785 | 0.215 |
| 0.15 | 24.79 | 34.76 | 33.51 | 9.97 | 0.777 | 0.223 |
| 0.20 | 24.12 | 36.47 | 41.48 | 12.34 | 0.747 | 0.253 |
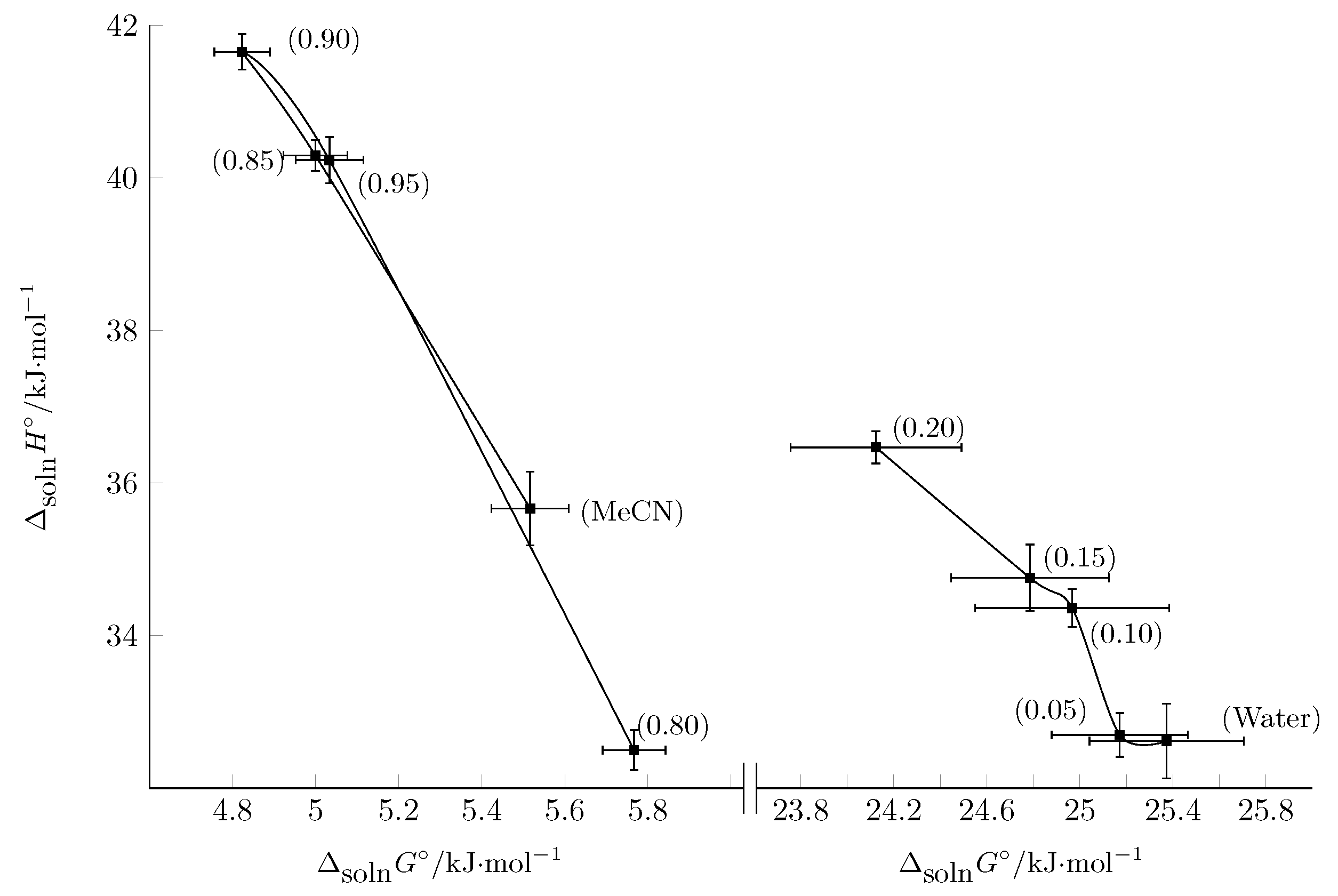
| 0.80 | 5.77 | 32.50 | 89.83 | 26.73 | 0.549 | 0.451 |
| 0.85 | 5.03 | 40.23 | 118.28 | 35.2 | 0.533 | 0.467 |
| 0.90 | 4.82 | 41.65 | 123.76 | 36.83 | 0.531 | 0.469 |
| 0.95 | 5.00 | 40.29 | 118.60 | 35.29 | 0.533 | 0.467 |
| 1.00 | 5.52 | 35.67 | 101.32 | 30.15 | 0.542 | 0.458 |
3.3. Thermodynamic Functions of Mixing
| Variable | Temperatures | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 278.15 | 283.15 | 288.15 | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | |
| IS a | 0.1468 | 0.1873 | 0.2176 | 0.2804 | 0.3422 | 0.4265 | 0.5617 | 0.7132 | 0.842 |
| 4.84 kJ·mol | |||||||||
| 22.45 kJ·mol | |||||||||
| 59.16 J·mol·K | |||||||||
| 17.60 kJ·mol | |||||||||
| b | ||||
|---|---|---|---|---|
| (kJ·mol) | (kJ·mol) | (J·mol) | (kJ·mol) | |
| 0.00 | 20.53 | 10.17 | −34.81 | −10.36 |
| 0.05 | 20.33 | 10.25 | −33.86 | −10.08 |
| 0.10 | 20.12 | 11.92 | −27.58 | −8.21 |
| 0.15 | 19.94 | 12.31 | −25.64 | −7.63 |
| 0.20 | 19.28 | 14.02 | −17.68 | −5.26 |
| 0.80 | 0.92 | 10.05 | 30.68 | 9.13 |
| 0.85 | 0.19 | 17.79 | 59.13 | 17.60 |
| 0.90 | −0.02 | 19.21 | 64.60 | 19.22 |
| 0.95 | 0.16 | 17.85 | 59.45 | 17.69 |
| 1.00 | 0.67 | 13.22 | 42.16 | 12.55 |
3.4. Enthalpy–Entropy Compensation Analysis
3.5. Mathematical Assessment of Solubility
| a | A | B | ARD b |
|---|---|---|---|
| 0.00 | 3.56 ± 0.36 | −4116.30 ± 111.63 | 3.79 |
| 0.05 | 3.22 ± 0.32 | −3987.13 ± 99.51 | 2.07 |
| 0.10 | 3.73 ± 0.11 | −4112.51 ± 33.57 | 1.30 |
| 0.15 | 4.52 ± 0.33 | −4330.91 ± 101.26 | 3.43 |
| 0.20 | 4.91 ± 0.10 | −4362.04 ± 30.01 | 1.21 |
| 0.80 | 10.82 ± 0.27 | −3913.52 ± 83.91 | 1.49 |
| 0.85 | 14.00 ± 0.33 | −4770.38 ± 101.79 | 2.30 |
| 0.90 | 14.72 ± 0.24 | −4958.96 ± 73.08 | 1.33 |
| 0.95 | 14.31 ± 0.13 | −4858.76 ± 40.13 | 0.99 |
| 1.00 | 12.63 ± 0.51 | −4424.53 ± 158.78 | 4.17 |
| Overall ARD | 2.08 |
| a | A | B | C | ARD b |
|---|---|---|---|---|
| 0.00 | −0.052 ± 0.004 | 2.174 ± 0.177 | 0.008 ± 0.001 | 3.70 |
| 0.05 | −0.049 ± 0.005 | 2.035 ± 0.232 | 0.007 ± 0.001 | 4.01 |
| 0.10 | −0.054 ± 0.003 | 2.255 ± 0.121 | 0.008 ± 0.0 | 1.85 |
| 0.15 | −0.07 ± 0.007 | 2.916 ± 0.329 | 0.01 ± 0.001 | 3.81 |
| 0.20 | −0.087 ± 0.006 | 3.608 ± 0.246 | 0.013 ± 0.001 | 3.18 |
| 0.80 | −116.6 ± 10.0 | 4835.8 ± 444.1 | 17.636 ± 1.494 | 3.21 |
| 0.85 | −235.6 ± 16.1 | 9871.4 ± 713.2 | 35.57 ± 2.399 | 4.14 |
| 0.90 | −280.3 ± 18.1 | 11771.6 ± 802.1 | 42.288 ± 2.698 | 4.73 |
| 0.95 | −251.8 ± 17.1 | 10576.2 ± 757.7 | 37.992 ± 2.548 | 4.41 |
| 1.00 | −174.6 ± 22.5 | 7322.6 ± 998.7 | 26.346 ± 3.359 | 5.01 |
| Overall ARD | 3.81 |
| a | h | ARD b | |
|---|---|---|---|
| 0.00 | 0.0003 ± 2 | 11,301,162 ± 525,076 | 2.97 |
| 0.05 | 0.0003 ± 2 | 10,420,554 ± 353,844 | 2.01 |
| 0.10 | 0.0004 ± 2 | 8,606,763 ± 278,840 | 1.88 |
| 0.15 | 0.0005 ± 3 | 7,765,353 ± 348,425 | 2.62 |
| 0.20 | 0.0008 ± 3 | 5,352,830 ± 161,122 | 1.72 |
| 0.80 | 1.42 ± 0.08 | 2846.3 ± 101.3 | 1.60 |
| 0.85 | 5.83 ± 0.46 | 954.6 ± 55.6 | 3.06 |
| 0.90 | 8.31 ± 0.76 | 714.0 ± 49.5 | 3.81 |
| 0.95 | 6.10 ± 0.51 | 919.4 ± 57.4 | 2.90 |
| 1.00 | 2.49 ± 0.27 | 1877.5 ± 150.7 | 4.55 |
| Overall ARD | 2.71 |
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Molar heat capacity | |
| CAS | Chemical Abstracts Service Registry Number |
| DSC | Differential scanning calorimetry |
| g | grams |
| G | Gibbs Energy |
| GC | Gas Chromatography |
| H | Enthalpy |
| hm | Harmonic mean |
| HPLC | High Performance Liquid Chromatography |
| id | Ideal |
| J | Joule |
| K | Kelvin |
| k | kilo |
| m | Melting |
| MeCN | Acetonitrile |
| mix | Mixing |
| PEG | Polyethylene glycol 200 |
| PP | Propylparaben |
| R | Gas constant |
| S | Entropy |
| sol | Solution |
| tr | Transfer |
| T | Temperature |
| Harmonic temperature | |
| UV | Ultraviolet |
| W | Water |
| w | Mass fraction |
| x | Mole fraction |
| Solubility parameter | |
| X-ray powder diffraction |
References
- Shahvar, A.; Soltani, R.; Saraji, M.; Dinari, M.; Alijani, S. Covalent triazine-based framework for micro solid-phase extraction of parabens. J. Chromatogr. A 2018, 1565, 48–56. [Google Scholar] [CrossRef]
- Han, J.H.; Cui, Y.Y.; Yang, C.X. Tailored amino/hydroxyl bifunctional microporous organic network for efficient stir bar sorptive extraction of parabens and flavors from cosmetic and food samples. J. Chromatogr. A 2021, 1655, 462521. [Google Scholar] [CrossRef]
- Yang, X.S.; Wang, L.L.; Liu, Y.S.; Yang, C.X.; Zhao, J.; Ji, S.L.; Liu, Q.W.; Hu, Z.H.; Liu, F.J.; Wang, P. Fabrication of magnetic covalent organic framework for effective and selective solid-phase extraction of propylparaben from food samples. Food Chem. 2022, 386, 132843. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas, Z.J.; Jiménez, D.M.; Delgado, D.R.; Almanza, O.A.; Jouyban, A.; Martínez, F.; Acree, W.E. Solubility and preferential solvation of some n-alkyl-parabens in methanol+water mixtures at 298.15 K. J. Chem. Thermodyn. 2017, 108, 26–37. [Google Scholar] [CrossRef]
- Rudyanto, M.; Ihara, M.; Takasu, K.; Yoshida, M.; Poerwono, H.; Sudiana, I.K.; Indrayanto, G.; Brittain, H.G. Propylparaben: Physical Characteristics. In Profiles of Drug Substances, Excipients and Related Methodology; Academic Press: Cambridge, MA, USA, 2003; Volume 30, pp. 235–269. [Google Scholar] [CrossRef]
- Jouyban, A. Handbook of Solubility Data for Pharmaceuticals; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Yalkowsky, S.H. Solubility and Solubilization in Aqueous Media; American Chemical Society: Washington, DC, USA, 1999. [Google Scholar]
- Sinko, P.; Martin, A. Martin’s Physical Pharmacy and Pharmaceutical Sciences: Physical Chemical and Biopharmaceutical Principles in the Pharmaceutical Sciences; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
- Trujillo-Trujillo, C.F.; Angarita-Reina, F.; Herrera, M.; Ortiz, C.P.; Cardenas-Torres, R.E.; Martinez, F.; Delgado, D.R. Thermodynamic Analysis of the Solubility of Sulfadiazine in (Acetonitrile 1-Propanol) Cosolvent Mixtures from 278.15 K to 318.15 K. Liquids 2023, 3, 7–18. [Google Scholar] [CrossRef]
- Torres-Cardozo, A.; Cerquera, N.E.; Ortiz, C.P.; Osorio-Gallego, J.; Cardenas-Torres, R.E.; Angarita-Reina, F.; Martinez, F.; Delgado, D.R. Thermodynamic analysis of the solubility of progesterone in 1-octanol + ethanol cosolvent mixtures at different temperatures. Alex. Eng. J. 2023, 64, 219–235. [Google Scholar] [CrossRef]
- Zhao, Y.; Zada, A.; Yang, Y.; Pan, J.; Wang, Y.; Yan, Z.; Xu, Z.; Qi, K. Photocatalytic Removal of Antibiotics on g-C3N4 Using Amorphous CuO as Cocatalysts. Front. Chem. 2021, 9, 797738. [Google Scholar] [CrossRef]
- Liu, S.; Zada, A.; Yu, X.; Liu, F.; Jin, G. NiFe2O4/g-C3N4 heterostructure with an enhanced ability for photocatalytic degradation of tetracycline hydrochloride and antibacterial performance. Chemosphere 2022, 307, 135717. [Google Scholar] [CrossRef]
- Yue, D.; William, E.A., Jr.; Abraham, M.H. Applications of Abraham solvation parameter model: Estimation of the lethal median molar concentration of the antiepileptic drug levetiracetam towards aquatic organisms from measured solubility data. Phys. Chem. Liq. 2020, 58, 302–308. [Google Scholar] [CrossRef]
- Liu, X.; Abraham, M.H.; William, E.A., Jr. Abraham Model Descriptors for Melatonin; Prediction of Solution, Biological and Thermodynamic Properties. J. Solut. Chem. 2022, 51, 992–999. [Google Scholar] [CrossRef]
- van Oss, C.J. Interfacial Forces in Aqueous Media, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Rubino, J.; Yalkowsky, S. Cosolvency and cosolvent polarity. Pharm. Res. 1987, 4, 220–230. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas, Z.J.; Jiménez, D.M.; Rodríguez, G.A.; Delgado, D.R.; Martínez, F.; Khoubnasabjafari, M.; Jouyban, A. Solubility of methocarbamol in some cosolvent+water mixtures at 298.15 K and correlation with the Jouyban–Acree model. J. Mol. Liq. 2013, 188, 162–166. [Google Scholar] [CrossRef]
- Rubino, J.T. Cosolvents and Cosolvency. In Encyclopedia of Pharmaceutical Science and Technology, 4th ed.; Swarbrick, J., Ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 61–73. [Google Scholar]
- Romero-Nieto, A.M.; Caviedes-Rubio, D.I.; Polania-Orozco, J.; Cerquera, N.E.; Delgado, D.R. Temperature and cosolvent composition effects in the solubility of methylparaben in acetonitrile + water mixtures. Phys. Chem. Liq. 2020, 58, 722–735. [Google Scholar] [CrossRef]
- Romero-Nieto, A.M.; Cerquera, N.E.; Martínez, F.; Delgado, D.R. Thermodynamic study of the solubility of ethylparaben in acetonitrile + water cosolvent mixtures at different temperatures. J. Mol. Liq. 2019, 287, 110894. [Google Scholar] [CrossRef]
- Dittert, L.W.; Higuchi, T.; Reese, D.R. Phase solubility technique in studying the formation of complex salts of triamterene. J. Pharm. Sci. 1964, 53, 1325–1328. [Google Scholar] [CrossRef]
- Mader, W.J.; Higuchi, T. Phase solubility analysis. C R C Crit. Rev. Anal. Chem. 1970, 1, 193–215. [Google Scholar] [CrossRef]
- Higuchi, T.; Connors, K. Advances in Analytical Chemistry and Instrumentation; Interscience Publishers, Inc.: New York, NY, USA, 1965. [Google Scholar]
- Koley, S.; Ghosh, S. Study of Microheterogeneity in Acetonitrile–Water Binary Mixtures by using Polarity-Resolved Solvation Dynamics. ChemPhysChem 2015, 16, 3518–3526. [Google Scholar] [CrossRef]
- Marcus, Y. The structure of and interactions in binary acetonitrile + water mixtures. J. Phys. Org. Chem. 2012, 25, 1072–1085. [Google Scholar] [CrossRef]
- Paruta, A.N. Solubility of the Parabens in Dioxane—Water Mixtures. J. Pharm. Sci. 1969, 58, 204–206. [Google Scholar] [CrossRef]
- Paruta, A.N.; Sciarrone, B.J.; Lordi, N.G. Solubility profiles for the xanthines in dioxane—water mixtures. J. Pharm. Sci. 1965, 54, 838–841. [Google Scholar] [CrossRef]
- Peña, M.A.; Bustamante, P.; Escalera, B.; Reíllo, A.; Bosque-Sendra, J.M. Solubility and phase separation of benzocaine and salicylic acid in 1,4-dioxane–water mixtures at several temperatures. J. Pharm. Biomed. Anal. 2004, 36, 571–578. [Google Scholar] [CrossRef]
- Hildebrand, J. Regular and Related Solutions: The Solubility of Gases, Liquids and Solids; Van Nostrand Reinhold: New York, NY, USA, 1970. [Google Scholar]
- Alexander, K.; Laprade, B.; Mauger, J.; Paruta, A.N. Thermodynamics of Aqueous Solutions of Parabens. J. Pharm. Sci. 1978, 67, 624–627. [Google Scholar] [CrossRef]
- Prankerd, R. Solid-state properties of drugs. I. Estimation of heat capacities for fusion and thermodynamic functions for solution from aqueous solubility-temperature dependence measurements. Int. J. Pharm. 1992, 84, 233–244. [Google Scholar] [CrossRef]
- Yang, H.; Rasmuson, A.C. Ternary phase diagrams of ethyl paraben and propyl paraben in ethanol aqueous solvents. Fluid Phase Equilibria 2014, 376, 69–75. [Google Scholar] [CrossRef]
- Ouyang, J.; Chen, J.; Zhou, L.; Liu, Z.; Zhang, C. Solubility Measurement, Modeling, and Dissolution Thermodynamics of Propylparaben in 12 Pure Solvents. J. Chem. Eng. Data 2020, 65, 4725–4734. [Google Scholar] [CrossRef]
- Yang, H.; Svärd, M.; Zeglinski, J.; Rasmuson, A.C. Influence of Solvent and Solid-State Structure on Nucleation of Parabens. Cryst. Growth Des. 2014, 14, 3890–3902. [Google Scholar] [CrossRef] [Green Version]
- Martin, A.; Carstensen, J. Extended Solubility Approach: Solubility Parameters for Crystalline Solid Compounds. J. Pharm. Sci. 1981, 70, 170–172. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Rodionov, S.V.; Bauer-Brandl, A. Thermodynamics of solubility, sublimation and solvation processes of parabens. Eur. J. Pharm. Sci. 2005, 24, 25–33. [Google Scholar] [CrossRef]
- Giordano, F.; Bettini, R.; Donini, C.; Gazzaniga, A.; Caira, M.R.; Zhang, G.G.; Grant, D.J. Physical properties of parabens and their mixtures: Solubility in water, thermal behavior, and crystal structures. J. Pharm. Sci. 1999, 88, 1210–1216. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of va not Hoff and Arrhenius data. J. Phys. Chem. 1976, 80, 2335–2341. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Aydi, A.; Dali, I.; Ghachem, K.; Al-Khazaal, A.Z.; Delgado, D.R.; Kolsi, L. Solubility of Hydroxytyrosol in binary mixture of ethanol + water from (293.15 to 318.15) K: Measurement, correlation, dissolution thermodynamics and preferential solvation. Alex. Eng. J. 2021, 60, 905–914. [Google Scholar] [CrossRef]
- Cárdenas-Torres, R.E.; Ortiz, C.P.; Acree, W.E.; Jouyban, A.; Martínez, F.; Delgado, D.R. Thermodynamic study and preferential solvation of sulfamerazine in acetonitrile + methanol cosolvent mixtures at different temperatures. J. Mol. Liq. 2022, 349, 118172. [Google Scholar] [CrossRef]
- Agredo-Collazos, J.J.; Ortiz, C.P.; Cerquera, N.E.; Cardenas-Torres, R.E.; Peña, M.A.; Martínez, F. Equilibrium Solubility of Triclocarban in (Cyclohexane + 1,4-Dioxane) Mixtures: Determination, Correlation, Thermodynamics and Preferential Solvation. J. Solut. Chem. 2022, 51, 1603–1625. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Wu, M. Estimation of the ideal solubility (crystal-liquid fugacity ratio) of organic compounds. J. Pharm. Sci. 2010, 99, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Neau, S.H.; Flynn, G.L. Solid and Liquid Heat Capacities of n-Alkyl Para-aminobenzoates Near the Melting Point. Pharm. Res. 1990, 7, 157–1162. [Google Scholar] [CrossRef]
- Neau, S.H.; Bhandarkar, S.V.; Hellmuth, E.W. Differential Molar Heat Capacities to Test Ideal Solubility Estimations. Pharm. Res. 1997, 14, 601–605. [Google Scholar] [CrossRef]
- Opperhuizen, A.; Gobas, F.A.P.C.; Van der Steen, J.M.D.; Hutzinger, O. Aqueous solubility of polychlorinated biphenyls related to molecular structure. Environ. Sci. Technol. 1988, 22, 638–646. [Google Scholar] [CrossRef]
- Delgado, D.R.; Mogollon-Waltero, E.M.; Ortiz, C.P.; Peña, M.A.; Almanza, O.A.; Martínez, F.; Jouyban, A. Enthalpy-entropy compensation analysis of the triclocarban dissolution process in some {1,4-dioxane (1) + water (2)} mixtures. J. Mol. Liq. 2018, 271, 522–529. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Tkachev, V.V.; Strakhova, N.N.; Kazachenko, V.P.; Volkova, T.V.; Surov, O.V.; Schaper, K.; Raevsky, O.A. Thermodynamic and structural aspects of sulfonamide crystals and solutions. J. Pharm. Sci. 2009, 98, 4738–4755. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Strakhova, N.N.; Kazachenko, V.P.; Volkova, T.V.; Tkachev, V.V.; Schaper, K.J.; Raevsky, O.A. Sulfonamides as a subject to study molecular interactions in crystals and solutions: Sublimation, solubility, solvation, distribution and crystal structure. Int. J. Pharm. 2008, 349, 300–313. [Google Scholar] [CrossRef]
- Ryde, U. A fundamental view of enthalpy–entropy compensation. RSC Med. Chem. 2014, 5, 1324–1336. [Google Scholar] [CrossRef] [Green Version]
- Sharp, K. Entropy—enthalpy compensation: Fact or artifact? Protein Sci. 2001, 10, 661–667. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L. Entropy-Enthalpy Compensation: Role and Ramifications in Biomolecular Ligand Recognition and Design. Annu. Rev. Biophys. 2013, 42, 121–142. [Google Scholar] [CrossRef] [Green Version]
- Delgado, D.R.; Peña, M.A.; Martínez, F. Extended Hildebrand solubility approach applied to sulphadiazine, sulphamerazine and sulphamethazine in some 1-propanol (1) + water (2) mixtures at 298.15 K. Phys. Chem. Liq. 2019, 57, 388–400. [Google Scholar] [CrossRef]
- Vargas-Santana, M.S.; Cruz-González, A.M.; Cerquera, N.E.; Escobar Rodriguez, A.S.; Cardenas, R.E.; Calderón-Losada, O.; Ortiz, C.P.; Delgado, D.R. Método extendido de Hildebrand y modelo de Yalkowsky- Roseman en la estimación de la solubilidad de sulfadiazina y sulfametazina en algunas mezclas etilenglicol (1) + agua (2) a varias temperaturas. Rev. Colomb. De Cienc. Químico-Farm. 2022, 50, 812–836. [Google Scholar] [CrossRef]
- Cárdenas, R.E.; Tinoco, L.E.; Galindres, D.M.; Beltrán, A.; Oviedo, C.D.; Osorio, J. Predicción de la solubilidad de la sulfadiazina en algunas mezclas cosolventes utilizando modelos de solución no ideales. Rev. Colomb. De Cienc. Químico-Farm. 2020, 49, 822–842. [Google Scholar] [CrossRef]
- Tinoco, L.E.; Galindres, D.M.; Osorio, J.; Cárdenas, R.E. Predicción de la solubilidad de sulfamerazina y sulfametazina en algunas mezclas cosolventes utilizando modelos de solución no ideales. Rev. Colomb. De Cienc. Químico-Farm. 2021, 50, 292–313. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Sotomayor, R.G.; Holguín, A.R.; Cristancho, D.M.; Delgado, D.R.; Martínez, F. Extended Hildebrand Solubility Approach applied to piroxicam in ethanol+water mixtures. J. Mol. Liq. 2013, 180, 34–38. [Google Scholar] [CrossRef]
- Blokhina, S.V.; Ol’khovich, M.V.; Sharapova, A.V.; Levshin, I.B.; Perlovich, G.L. Thermodynamic insights to solubility and lipophilicity of new bioactive hybrids triazole with thiazolopyrimidines. J. Mol. Liq. 2021, 324, 114662. [Google Scholar] [CrossRef]
- Ksiazczak, A.; Kosinski, J.J. Vapour pressure of binary, three-phase (S-L-V) systems and solubility. Fluid Phase Equilibria 1988, 44, 211–236. [Google Scholar] [CrossRef]
- Jouyban, A. Review of the cosolvency models for predicting solubility of drugs in water-cosolvent mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jouyban, A.; Acree, W.E. Mathematical derivation of the Jouyban-Acree model to represent solute solubility data in mixed solvents at various temperatures. J. Mol. Liq. 2018, 256, 541–547. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortiz, C.P.; Cardenas-Torres, R.E.; Herrera, M.; Delgado, D.R. Thermodynamic Analysis of the Solubility of Propylparaben in Acetonitrile–Water Cosolvent Mixtures. Sustainability 2023, 15, 4795. https://doi.org/10.3390/su15064795
Ortiz CP, Cardenas-Torres RE, Herrera M, Delgado DR. Thermodynamic Analysis of the Solubility of Propylparaben in Acetonitrile–Water Cosolvent Mixtures. Sustainability. 2023; 15(6):4795. https://doi.org/10.3390/su15064795
Chicago/Turabian StyleOrtiz, Claudia Patricia, Rossember Edén Cardenas-Torres, Mauricio Herrera, and Daniel Ricardo Delgado. 2023. "Thermodynamic Analysis of the Solubility of Propylparaben in Acetonitrile–Water Cosolvent Mixtures" Sustainability 15, no. 6: 4795. https://doi.org/10.3390/su15064795
APA StyleOrtiz, C. P., Cardenas-Torres, R. E., Herrera, M., & Delgado, D. R. (2023). Thermodynamic Analysis of the Solubility of Propylparaben in Acetonitrile–Water Cosolvent Mixtures. Sustainability, 15(6), 4795. https://doi.org/10.3390/su15064795









