Semi-Open Multi-Distribution Center Path Planning with Time Windows

Abstract

A well-planned robot dispatching platform reduces costs and increases efficiency for companies while also reducing carbon emissions and achieving sustainable development. At the moment, the solution to the difficulty of warehouse logistics is use of multiple distribution centers with autonomous mobile robots (AMR). To solve this problem, this paper establishes a semi-closed model of multiple distribution centers, considering the number of cycles and the number of vehicles. An improved ant colony algorithm is proposed to improve the heuristic function based on the node distance relationship to improve the quality of path search. Dynamic variable pheromone concentration and volatility factors are set to accelerate the convergence speed of the algorithm while effectively reducing the problem of the premature algorithm. The traditional ant colony algorithm and the improved ant colony algorithm are used to solve the established model. In addition, the results show that the traditional ant colony algorithm has a certain rate of dominance in the single-day cost of the closed distribution model, but the overall comprehensive cost is lower than that of the improved ant colony algorithm. The single-day cost of the semi-open multi-distribution center logistics and distribution model is lower than that of the closed multi-distribution center logistics and distribution model, and the 7 day average cost is reduced by 12%. The improved ant colony algorithm can save about 119 kWh of electricity under the same target volume requirement, which achieves the company’s goals of cost reduction and increased efficiency, as well as green and sustainable development.

1. Introduction

The autonomous mobile robot (AMR) is part of a new generation of robot technology with intelligent sensing and autonomous mobility developed after the traditional automated guided vehicle (AGV). Over the past two years, as industrial automation and intelligent manufacturing have become mainstream trends, the AMR industry has embraced important development opportunities [1]. At present, the technologies affecting the deep development of AMR technology mainly include navigation technology [2,3], wireless sensor networks [4], control technology [5], and the development of a scheduling system and path planning platform [6,7]. A good scheduling system and path planning platform can ensure that the AMR can still ensure the normal operation of the warehouse logistics system; on the other hand, enterprises can achieve cost reduction and increased efficiency and can reduce consumption while achieving sustainable development.

Dantzig G. B. and Ramser J. H. [8] proposed a linear programming solution procedure to solve the problem of transporting gasoline in refineries, and the vehicle routing problem was thus created. The path planning and scheduling system can be divided into single distribution centers and multiple distribution centers according to the number of distribution centers. The multiple depot vehicle routing problem (MDVRP) has gradually become the mainstream of logistics system research in large-scale warehouse logistics [9]. The difference is whether the AMR needs to return to the original starting point after completing the transportation task. If the AMR must return to the original distribution center, it is a closed vehicle path problem; and if the AMR still needs to return to the distribution center but does not specify a specific distribution center, it is a semi-open vehicle path problem. In the semi-open model, AMR can supplement goods in the midway.

At present, research on MDVRP is mainly focused on model building and model optimization [10]. Sartorl [11] proposed an improved hybrid algorithm for this problem and a new method for generating path problem instances based on open data. Naccache [12] presented the multiple pickup and delivery problem with time windows and developed a hybrid adaptive large neighborhood search algorithm with improved operations for solving this problem. Bae [13] developed a multi-site vehicle path model with time windows and solved the specific algorithm using a genetic algorithm. The optimization study of the model solution is crucial to improving the performance of the algorithm. Ray [14] studied a centralized model for solving the multi-warehouse logistics distribution problem and used a heuristic algorithm to solve it. Moshref-Javadi [15] represented the customer-centric multi-commodity distribution problem as two mixed integer linear programming models and combined two intelligent algorithms with complementary advantages to propose a heuristic method for solving the large-scale problem. Bullnheimer [16] proposed an improved ant colony algorithm to solve the vehicle path problem for a single distribution center and compared it with five other heuristic methods, proving that the improved ant colony algorithm is more effective in solving the single distribution center vehicle distribution problem.

The semi-open model is more in line with the actual warehouse logistics situation than the closed model [17] and, at the same time, can bring greater economic benefits. In terms of algorithms, most scholars have used heuristic algorithms to solve this type of problem, which improves the efficiency of the solution. The ant colony algorithm was first used to solve the traveler problem [18]. In addition, Pureza [19] used the ant colony algorithm in combination with the forbidden search algorithm in the exploration of the vehicle path problem to complement each other’s advantages and improve the computational efficiency. Liang [20] proposed a hybrid algorithm by combining the ant colony algorithm and the genetic algorithm to further improve the quality of marine survey path schemes. In addition, experiments showed that the hybrid algorithm is efficient and robust for obtaining ideal paths for single or multiple research vessels. Zhao [21] proposed an improved ant colony algorithm and applied it to crane path planning. Yang [22] proposed a two-layer ant colony algorithm for robot navigation, which consists of two independent ant colony algorithms for successive operations, and the simulation results showed that the method can generate collision-free paths more effectively. Song [23] developed a VRP model considering the delivery time window and variable service time and improved the computational efficiency by improving the ant colony algorithm.

In summary, current research on the theoretical stage is more developed, and no practical modeling frameworks and considerations of specific problems have been conducted for specific models. In addition, the research samples are generally based on single-cycle data, which is incidental, and the data samples with multiple cycles have not been studied by scholars. Therefore, the main contributions of this paper are as follows:

• A semi-open model of multiple distribution centers is established based on the actual problem in light of the number of vehicles, the number of operations, and other factors;
• An improved ant colony algorithm is proposed, and the improved ant colony algorithm is used to solve the semi-open model. In addition, the reliability of the improved ant colony algorithm is compared with the traditional ant colony algorithm to verify the reliability of the improved ant colony algorithm;
• The validity of the semi-open model considering the number of runs is verified against the closed model.

The paper is structured in the following layout. The problem description and mathematical modeling framework are outlined in Section 2. In Section 3, the algorithmic solving process is introduced. An example of the algorithm is provided in Section 3.3. Finally, some conclusions and future recommendations are provided in Section 4.

2. Problem Description and Mathematical Modeling

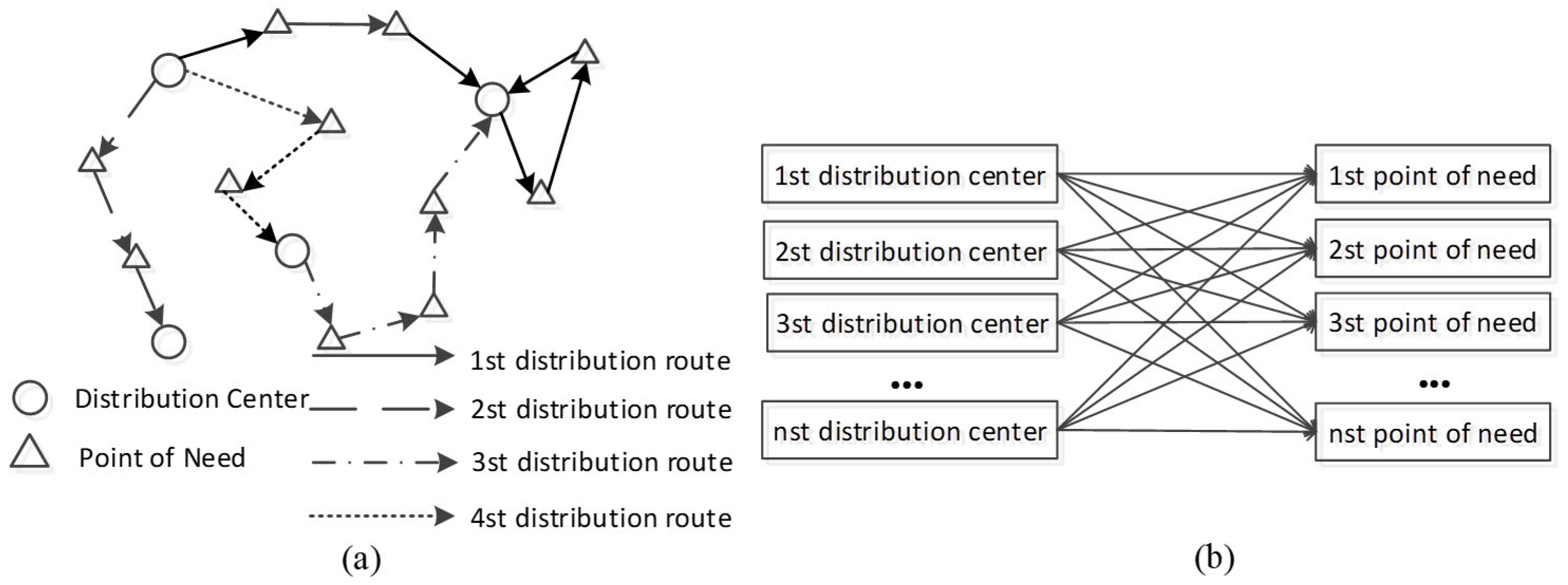
2.1. AMR Problem Description

The semi-open multi-distribution center AMR path problem can be described as follows: there are n warehouse distribution centers (hereafter referred to as distribution centers) with known location coordinates and m demand service points. The daily demand at the demand points is known before the AMR conducts distribution operations, and the number of AMRs is limited. After the AMR receives the distribution task, it starts from the distribution center and delivers to each demand point according to the AMR load quality and soft time window requirements and arrives early or beyond the time to bear the corresponding penalty cost. The AMR can choose any distribution center for replenishment or stopping when it does not meet the distribution requirements and is not forced to return to the original distribution center until all demand points are served, completing the single-cycle distribution task. A schematic diagram of the AMR path is shown in Figure 1.

The model aims to achieve the lowest integrated cost and considers the service time window and the limitation of the number of AMRs. It also saves the opening or idle cost of the distribution centers, the transportation cost, the time window penalty cost, and the cargo damage cost, and then finally integrates them. The distribution center will be open or idle according to the actual demand at the demand point, so it will incur the corresponding open or idle cost. The AMR transport costs include two aspects: the fixed cost of AMR use on the one hand and the cost proportional to the distance traveled by the AMR on the other. Each demand point has specific requirements for the delivery time of goods. In addition, in the actual operation process, there will be early or late arrivals, and the process generates the corresponding time window penalty cost. The quality of the goods may be affected during the transportation process, so we need to set up the cost of goods damage.

Based on the above analysis, the model makes the following assumptions: (1) the number of AMRs in the distribution center is constant, and each vehicle is of the same type and has a certain load capacity; (2) the distribution center has sufficient goods, and there is no shortage of goods; (3) each demand point will be served only once by one vehicle, and the service will meet the demand at one time; (4) once the AMR starts the distribution operation, it will not accept other assignments in the middle; and (5) the sum of the demand quantity demanded by each transport AMR on a single transport route cannot be greater than the maximum load capacity of that AMR for one delivery. In addition, if the AMR needs to continue its operation, the replenishment operation will be carried out.

2.2. Mathematical Modeling

2.2.1. Decision Variables

The distribution center and vehicle distribution mark are described by the following formula.

$${\omega }_i=\{\begin{array}{l}1,\mathrm{Distribution}\mathrm{center}\mathrm{open}\mathrm{for}\mathrm{operation}\\ 0,\mathrm{else}\end{array}$$

(1)

$$v_{ij}^k=\{\begin{array}{l}1,\mathrm{The}\mathrm{kth}\mathrm{AMR}\mathrm{serves}\mathrm{between}i\mathrm{and}j\\ 0,\mathrm{else}\end{array}$$

(2)

where i, j, and k denote the distribution center, demand point, and vehicle serial number, respectively.

2.2.2. Model Parameters

$\left\{i|i\in I,i=1,2,\dots ,n\right\}$, where i denotes a distribution center, I denotes a collection of distribution centers, and denotes the maximum number of distribution centers.

$\left\{j|j\in J,j=1,2,\dots ,m\right\}$, where $j$ denotes the demand point, $J$ denotes the demand point set, and $m$ denotes the maximum number of demand points.

$\left\{k|k\in K,k=1,2,\dots ,g\right\}$, where $k$ denotes the AMR, $K$ denotes the AMR set, and $g$ denotes the maximum number of AMRs.

$C_{i1}$ denotes the open-use cost of the distribution center $i$ and $C_{i2}$ denotes the idle cost.

$C_k$ denotes the single-use cost of the AMR and $C_{ij}$ denotes the transportation cost per unit distance of the AMR.

$Q_i$ denotes the capacity of the distribution center $i$ and $Q_j$ denotes the demand quantity at the demand point. $Q_{ij}$ denotes the volume of transportation from node $i$ to node $j$. $p$ denotes the unit cost of the goods and $\theta$ denotes the damage factor of the goods.

$d_{ij}$ indicates the distance between node $i$ and node $j$.

$Q$ indicates the maximum mass of the AMR in a single load.

$T_j$ indicates the actual time of delivery of the goods.

$E_j$, $L_j$ is the hard time window, while $e_j$, $l_j$ is the soft time window, indicating the earliest or latest time required or acceptable for delivery.

$\epsilon$, $\eta$ indicates the penalty factor for arriving earlier or later than the required time.

$F_j\left(T_j\right)$ denotes the penalty cost factor function resulting from arrivals outside the specified time frame, which can be expressed as:

$$F_j\left(T_j\right)=\{\begin{array}{ll}\infty & T_j<e_j\backslash T_j>l_j\\ \epsilon & e_j\le T_j<E_j\\ 0& E_j\le T_j\le L_j\\ \eta & L_j<T_j\le l_j\end{array}$$

(3)

2.2.3. Objective Function

The semi-open distribution target can be described as Equations (4)–(8).

$$\min C=C_1+C_2+C_3+C_4$$

(4)

$$C_1={\displaystyle \sum _{i\in I}{\omega }_i{C}_{i1}+(n-{\displaystyle \sum _{i\in I}{\omega }_i)C_{i2}}}$$

(5)

$$C_2={\displaystyle \sum _{k\in K}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{v}_{{}_{ij}}^k{C}_k+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{v}_{{}_{ij}}^k{d}_{ij}{C}_{ij}}}}}}$$

(6)

$$C_3={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{v}_{{}_{ij}}^k{Q}_{ij}p\theta }}$$

(7)

$$C_4={\displaystyle \sum _{j\in J}p{Q}_j{F}_j(T_j)\max \left\{(E_j-T_j),(T_j-L_j),0\right\}}$$

(8)

2.2.4. Binding Conditions

Related constraints of ant colony algorithm can be set as Equations (9)–(16).

$${\displaystyle \sum _{i\in I}{\omega }_i}\le n$$

(9)

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\nu }_{ij}^k\le g}}}$$

(10)

$${\displaystyle \sum _{j\in J}{Q}_{ij}\le Q_i}$$

(11)

$${\displaystyle \sum _{i\in I}{Q}_{ij}\ge Q_j}$$

(12)

$$Q_{ij}\le Q$$

(13)

$${\displaystyle \sum _{k\in K}{\displaystyle \sum _{j\in J}{\nu }_{ij}^k}=1}$$

(14)

$${\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\nu }_{ij}^k}}={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\nu }_{ji}^k}}$$

(15)

$${\displaystyle \sum _{j\in J}{\displaystyle \sum _{k\in K}{\nu }_{ij}^k}}={\displaystyle \sum _{j\in J}{\displaystyle \sum _{k\in K}{\nu }_{ji}^k}},i=1,2,3,4$$

(16)

Equations (3)–(15) establish the complete semi-open multi-distribution center AMR path problem model. Equation (4) is the objective function of minimizing the total cost of distribution, and Equations (5)–(8) are the equation interpretations, where C₁ denotes the open operation cost and idle cost of the distribution center, C₂ denotes the transportation cost of goods, C₃ denotes the damage cost during the transportation of goods, and C₄ denotes the time window penalty cost arising from the failure of goods to be delivered within the specified time due to various reasons. Equations (9)–(15) are the solution constraints; Equations (9) and (10) are the constraints on the number of distribution centers and the number of AMRs; Equations (11) and (12) are the constraints on the capacity of distribution centers and the demand quantity of demand points; Equation (13) indicates that the freight volume of the AMR cannot exceed its maximum transportation capacity; Equation (14) indicates that each demand point can and will be served by one vehicle only once; Equation (15) indicates that the AMR departs from a distribution center and needs to return to a distribution center after completing the distribution task; and Equation (16) indicates that the number of vehicles departing from the distribution center is equal to the number of vehicles returning to the distribution center and is a closed model constraint. When this constraint is not included, the model is a semi-open model.

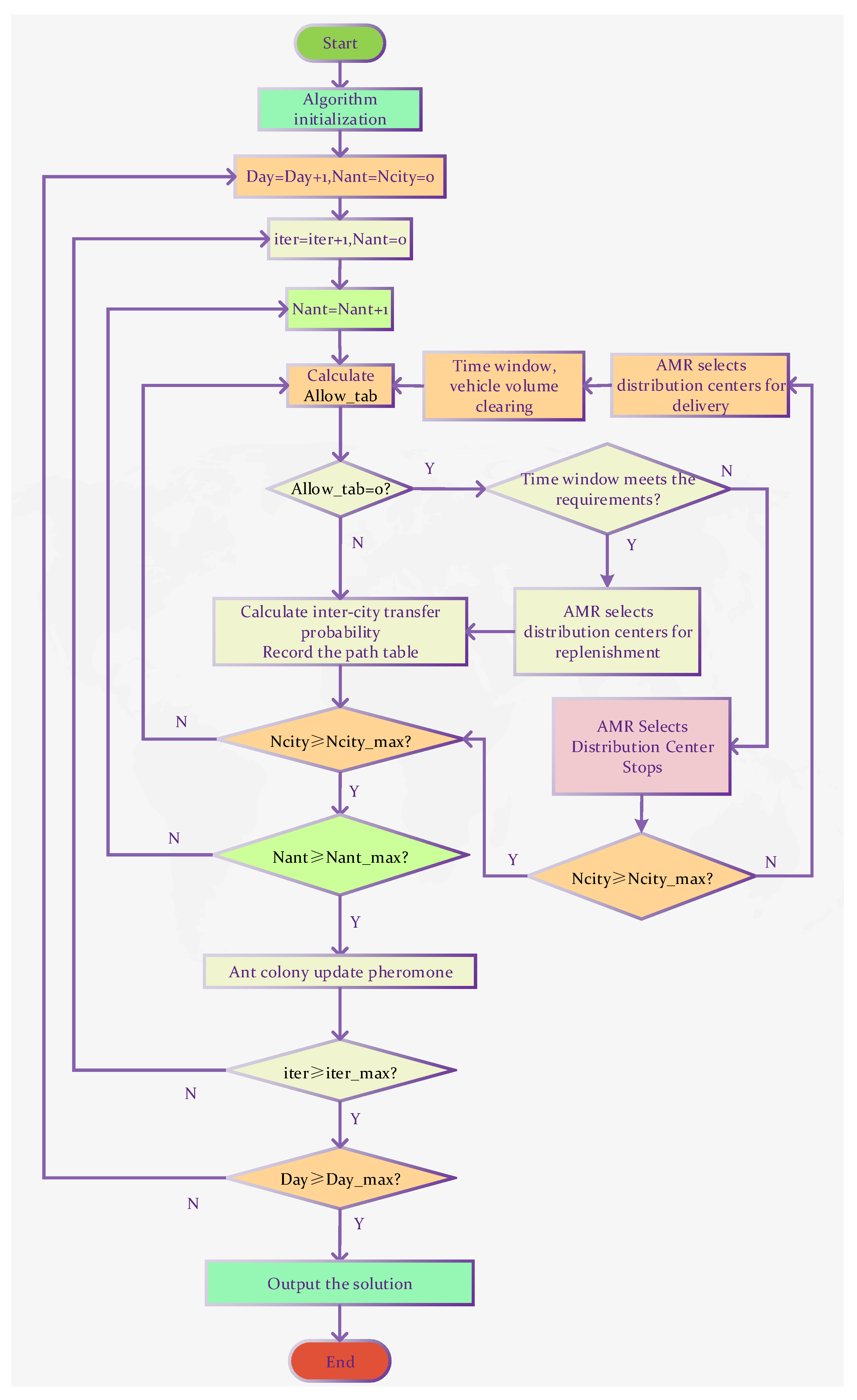
3. Algorithm Solving

3.1. Overview of the Traditional Ant Colony Algorithm

The ant colony algorithm abstracts the actual ant activity captured into a mathematical model, and the ants choose the next destination by transfer probability. In the iterative process, the pheromone update strategy will continuously guide the search direction of the ant colony.

The nodes $i$ and $j$ denote the start and end points, respectively. ${\tau }_{ij}\left(t\right)$ indicates the pheromone concentration between $i$ and $j$, at the time of $t$. ${\eta }_{ij}$ denotes the visibility in ${\eta }_{ij}=1/d_{ij}$. $A_{allow}$ is the set of nodes allowed to be visited by ants at a given time. $\alpha$ is the weighted value of the pheromone. $\beta$ is the weighted value of visibility. $p_{ij}^k\left(t\right)$ denotes the probability of ants moving from $i$ to $j$, and ants choose the next location to be visited according to the probability of moving.

$$p_{ij}^k\left(t\right)=\{\begin{array}{l}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }\cdot {\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}{{\displaystyle \sum _{k\in A_{allow}}{\left[{\tau }_{ik}\left(t\right)\right]}^{\alpha }\cdot {\left[{\eta }_{ik}\left(t\right)\right]}^{\beta }}}{,}_{}k\in A_{allow}\\ 0,k\notin A_{allow}\end{array}$$

(17)

The ants release and volatilize pheromones during pathfinding. $\rho (0<\rho <1)$ denotes the pheromone volatilization factor. $\Delta {\tau }_{ij}^k$ denotes the pheromone increment released by the $k_{th}$ ant between $i$ and $j$. $C_k$ denotes the total length of the first ant moving on a complete path. $Q$ denotes the total amount of pheromones left by an ant at the end of one traversal. The pheromone update expression is:

$${\tau }_{ij}\left(t\right)=\left(1-\rho \right){\tau }_{ij}+{\displaystyle \sum _{k=1}^m\Delta {\tau }_{ij}^k}$$

(18)

$$\Delta {\tau }_{ij}^k=\{\begin{array}{l}Q/C_k,\mathrm{The}\mathrm{kth}\mathrm{ant}\mathrm{passes}\mathrm{through}\mathrm{point}(\mathrm{i},\mathrm{j})\mathrm{in}\mathrm{this}\mathrm{cycle}\\ 0,\mathrm{else}\end{array}$$

(19)

3.2. Algorithm Improvement

3.2.1. Heuristic Factors

The heuristic factor $n_{ij}$ only considers the distance between the node $i$ and the node $j$, ignoring the distance relationship between the start point and the end point. To improve the ant colony search in the direction of the global optimum, the heuristic factor is also improved. In the following equation, $d_{oj}$ represents the distance relationship between the starting point and the target node, and $d_{js}$ represents the distance relationship between the target node and the termination point.

$${\eta }_{ij}=\frac{1}{d_{oj}\cdot d_{ij}\cdot d_{js}}$$

(20)

3.2.2. Pheromone Volatility Factor

The pheromone volatility factor $\rho$ reflects the persistence of the pheromone amount, and setting it to a certain value may cause the algorithm to fall into a local optimum, so the value of $\rho$ is improved. In the following equation, $iter$ denotes the number of iterations, and $ite{r}_{\max }$ denotes the maximum number of iterations.

$$\rho =\{\begin{array}{l}0.2,iter\in \left[0,0.25ite{r}_{max}\right]\\ 0.3,iter\in \left[0.25ite{r}_{max},0.75ite{r}_{max}\right]\\ 0.4,iter\in \left[0.75ite{r}_{max},1\right]\end{array}$$

(21)

3.2.3. Pheromone Concentration

The size of the pheromone concentration ${\tau }_{ij}$ greatly affects the optimization process of the ant colony algorithm. If ${\tau }_{ij}$ is set too high, it will reduce the randomness; if ${\tau }_{ij}$ is set too low, it will cause the algorithm to converge prematurely. Controlling ${\tau }_{ij}$ within a reasonable interval can avoid the suboptimal situation caused by a sharp increase or decrease in the pheromone concentration.

$${\tau }_{ij}=\{\begin{array}{l}{\tau }_{max},{\tau }_{ij}\ge {\tau }_{max}\\ {\tau }_{ij},{\tau }_{min}\le {\tau }_{ij}\le {\tau }_{max}\\ {\tau }_{min},{\tau }_{min}\ge {\tau }_{ij}\end{array}$$

(22)

3.3. Implementation Scheme of an Improved Ant Colony Algorithm

Step 1. Initialize. Initialize the parameters. The maximum number of iterations is $ite{r}_{max}$; the initial number of iterations is shown by $I_{iter}=0$ and $I_{ite}{}_r\le ite{r}_{max}$; the number of ants is represented by $m$, so that the initial value is $m=0$; and the initial number of cycles $day=0$;

Step 2. Start iteration. Count the number of AMRs in each distribution center and start the iteration;

Step 3. Derive the allowable table based on the remaining onboard volume and time window;

Step 4. Determine whether the permission table is empty. If the permission table is not empty, select the next point to be visited according to the transfer probability, record it in the path table, and perform step (5). If the permission table is empty, perform step (6);

Step 5. Determine whether all the demand points are visited. If yes, perform step (10). Otherwise, perform step (3);

Step 6. Judge whether the time window meets the distribution requirements. If it does not, perform step (7). Otherwise, perform step (8);

Step 7. Select the distribution center with the lowest total cost to make a stop. Determine whether the ant runs all the demand points. If yes, perform step (5). Otherwise, perform step (9);

Step 8. Select the distribution center with the lowest total cost for replenishment. Select the next point to be visited according to the transfer probability, record it in the route table, and perform step (5);

Step 9. Randomly select a distribution center that has an AMR at this time to perform the distribution service, assign initial values to the vehicle volume and time window, and perform step (3);

Step 10. Update information. Determine whether all ants complete the task. If they do, record the best path at this time and update the pheromone concentration. Otherwise, $m=m+1$ and perform step (3);

Step 11. Determine whether the iteration is finished or not. If not, add 1 to the number of iterations and perform step (3). Otherwise, perform step (12);

Step 12. Output results. Determine whether the distribution cycle is complete. If it is, finish the task and display the result. Otherwise, the number of cycles is increased by 1 and the number of iterations is initialized to return to the execution of step (2).

In order to describe the algorithm steps more conveniently, the steps are sorted and drawn. The algorithm flowchart is shown in Figure 2.

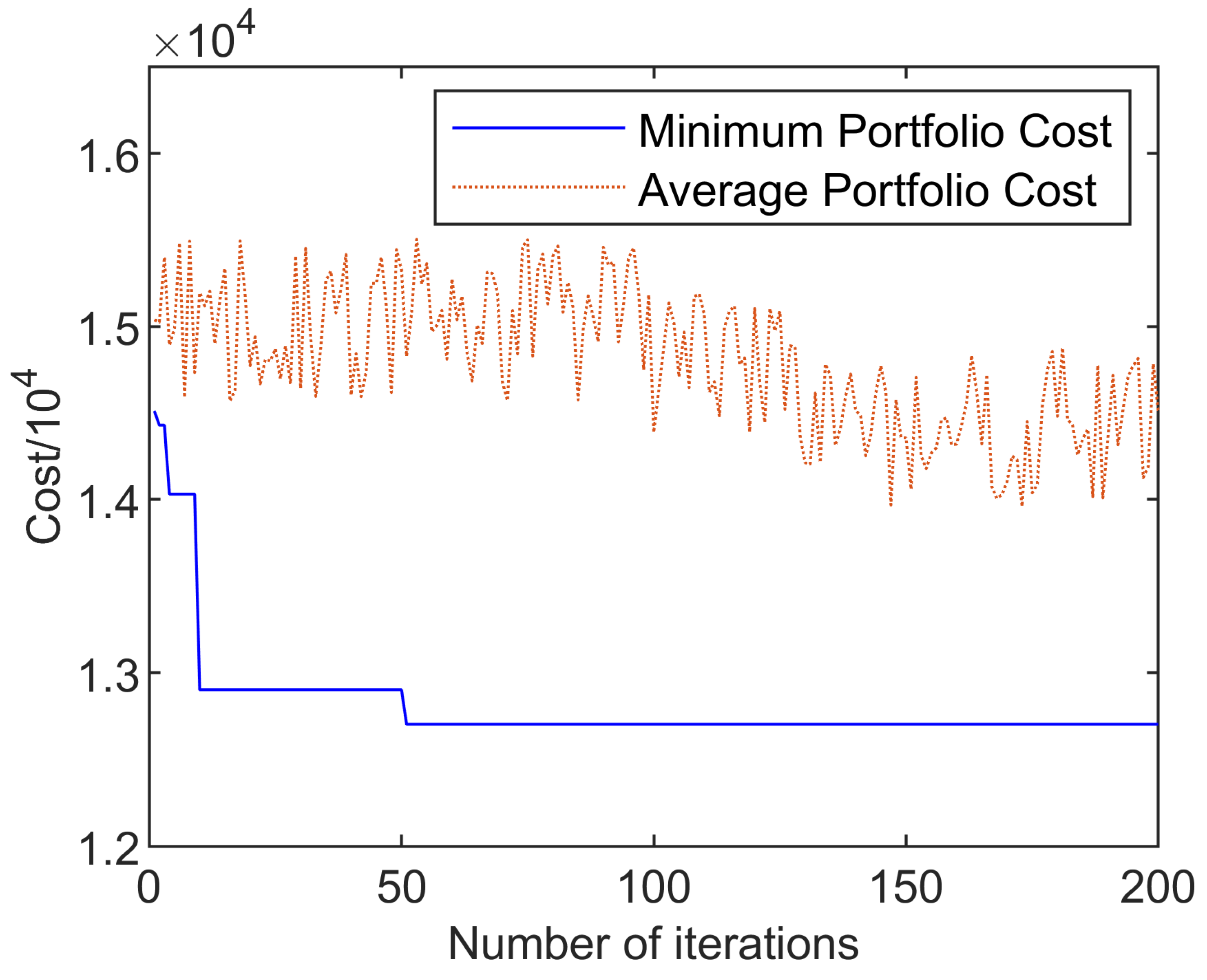
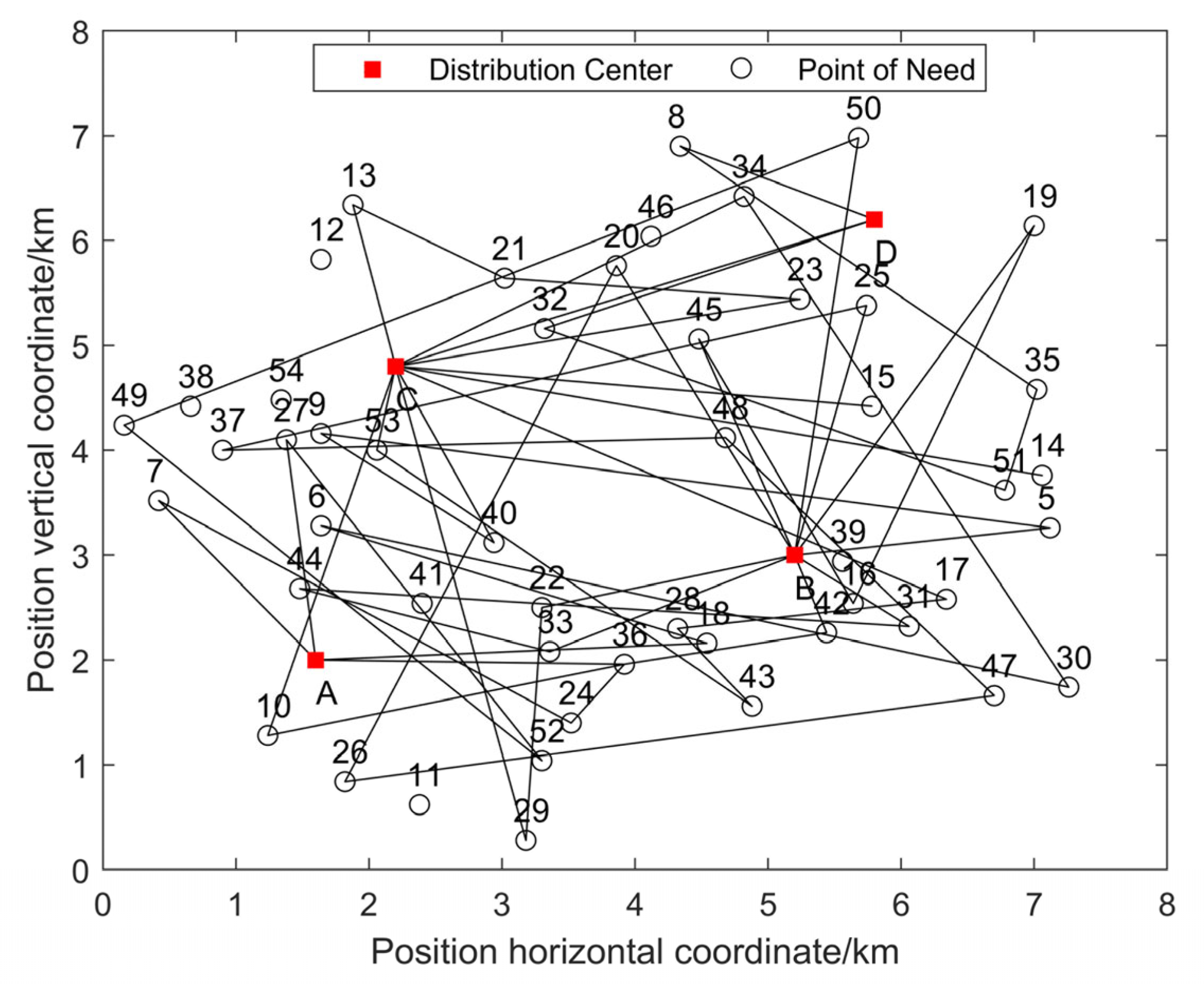
3.4. Example of an Algorithm

A large warehouse logistics case is located in the complete vehicle production base in Baoding City, Hebei Province, China. It produces 400,000 vehicles every year. Therefore, the corresponding workshop production line logistics allocation is a huge problem. This paper explores this issue to some extent, and the following are specific cases.

A warehouse logistics company has four distribution centers with sufficient goods, which are responsible for the distribution service to 50 demand points. Each demand point may generate demand in each cycle (the cycle is a unit of time, and for the convenience of description, the following is used as days), and the demand may be zero. Each distribution center may have two operating conditions: open and idle. The cost of open use is RMB 3000/day, and the cost of idle is RMB 1000/day. The distribution center has 20 light trucks of the same type, the maximum mass of the AMR is 600 kg, each piece of cargo weighs 10 kg, the average speed of the AMR is 10 km/h, the fixed cost of single-use is 200 RMB, and the driving cost is 2 RMB/km. Let the demand point between 8:00 and 13:00 generate the upper boundary of the time window, the lower boundary of the time window in its service time is converted according to the amount of demand, and the conversion standard is 0.15 h/t. If the time window is 10 min earlier or later than that required by the demand point, the corresponding penalty cost is incurred. The location coordinate data of each node are shown in

Table 1. Location Coordinates.

Number	H		C	Number	H	V	C	Number	H	V	C
A	1.6	2	-	15	7.12	2.66	21	33	5.2	3.66	41
B	5.2	3	-	16	7.6	5.56	30	34	1.92	5.68	0
C	2.2	4.8	-	17	4.02	4.88	34	35	5.76	4.48	0
D	5.8	6.2	-	18	5.94	2.6	59	36	2.36	7.26	59
1	6.24	5.28	26	19	4.92	4.64	20	37	7.3	4.3	0
2	0.52	4.42	46	20	1.84	3.32	53	38	2.62	3.48	29
3	1.06	1.94	44	21	4.66	3.9	43	39	3.46	6.48	40
4	1.6	7.18	38	22	7.26	5.84	30	40	7.3	3.84	17
5	2.16	7.48	46	23	2.22	1	21	41	6.12	2.34	56
6	1.7	4.38	44	24	2.4	6.78	32	42	6.06	7.28	0
7	1.66	5.86	0	25	5.38	1.78	35	43	6.08	3.86	51
8	7.26	4.16	0	26	0.14	4.82	18	44	5.74	4.3	25
9	3.38	4.24	60	27	7.78	4.06	40	45	3.3	1.72	41
10	2.34	5.74	20	28	1.26	6.56	23	46	4.5	1.24	13
11	5.16	5.32	14	29	7.28	3.78	31	47	6.22	6.74	32
12	7.38	2.1	39	30	0.68	3.6	40	48	2.24	0.68	27
13	2.08	7.04	55	31	2.38	5.38	24	49	3.42	6	20
14	0.66	4.26	44	32	1.74	3.54	26	50	2.12	4.06	0

H denotes the horizontal coordinate, V denotes the vertical coordinate, and the unit is km.

. The AMR’s main performance parameters are shown in

Table 2. The AMR’s main performance parameters.

Load Capacity	Docking Accuracy	Running Speed	Power Consumption per 100 km	Continuity
200 Kg–700 Kg	10 mm	2.5 m/s	40–50	10 H

.

4. Discussion

The above example is solved by MATLAB 2019b, and the closed multi-distribution center logistics model is solved with the same input parameters, and the optimal paths and costs of the two models are compared and analyzed. Through extensive experimental calculations, the main parameters of the improved ant colony algorithm are set as follows: the numbers A–D denote each distribution center, and the numbers 1–50 denote each demand point. To verify the effectiveness of the improved ant colony algorithm, the improved part of the algorithm in Section 3.2 is calculated using the traditional ant colony algorithm and solves the semi-open model using the ant colony algorithm.

Table 3. Performance comparison of the improved ant colony algorithm.

	Average Convergence Time	Amplitude	Iterative Stability Times	Amplitude	Average Minimum Cost	Amplitude
Traditional ant colony algorithm	2.75 s	-	81	-	1.21 × 104	-
Improved ant colony algorithm	1.27 s	+53.9%	55	+32%	1.14 × 104	+5%

compares the results of the improved ant colony algorithm and the traditional ant colony algorithm for solving the semi-open model.

Table 3 shows that the improved ant colony algorithm has significantly improved the convergence time, which allows for a more satisfactory solution to be obtained in the time allowed for solving the actual problem, and the average cost is guaranteed not to deteriorate. The corresponding iteration diagrams and path diagrams obtained in both semi-open and closed modes are shown in Figure 3, Figure 4, Figure 5 and Figure 6.

By comparing the iteration diagrams of Figure 3 and Figure 5, it can be seen that the closed model is more likely to fall into the local optimal solution, and the number of iterations stops at 50. In addition, the improved ant colony algorithm can still find the optimal solution after the semi-open model falls into the local solution with an increase in the number of iterations, and it tends to be stable. Meanwhile, from the path diagrams of different modes in Figure 4 and Figure 6, there are 10 optimal distribution paths in the semi-open model with the same demand point, demand quantity, and assumptions. The routes are 3→10→36→24→42→2, 2→25→37→48→47→26→20→2, 2→19→16→45→2, 2→50→49→52→27→7→3, 3→18→6→30→34→3, 3→53→43→28→17→3, 3→13→21→23→3 (replenishment)→15→3, 3→40→9→5→2, 2→33→44→31→2, and 2→22→29→3 (replenishment)→14→3, in which two lines are replenishment operations, the comprehensive cost is RMB 11,252.3220, and the path length is 75.76 km. There are also eight optimal distribution paths in the closed mode, which are 4→18→6→30→34→24→36→13→4, 2→53→43→28→40→26→20→2, 4→19→16→45→22→29→4, 4→10→42→21→15→47→4, 4→52→27→7→49→50→4, 4→9→17→14→4, 4→31→44→33→5→4, and 4→23→25→37→48→4. In addition, the integrated cost is RMB 12,499.8842, and the path length is 96.27 km. It can be seen that the integrated cost under the semi-open mode is 10% lower than that under the closed mode, and the distribution path is reduced by 27%.

Table 4. Multiple cycle comparison analysis.

Mode	Number of Cycles	Comprehensive Cost	Transportation Distance	Average Cost	Average Distance
Closed	1	13,350.326	101.2931	86,638.070	686.5428
	2	12,499.884	96.0554
	3	11,361.699	116.908
	4	13,286.472	95.6789
	5	12,198.234	88.6694
	6	12,338.687	95.1275
	7	11,602.765	92.8106
Semi-open	1	11,549.972	69.2789	76,294.338	448.7936
	2	11,252.322	70.1529
	3	10,708.570	66.7828
	4	11,390.421	59.8369
	5	10,411.439	57.1976
	6	10,568.166	64.3066
	7	10,413.447	61.2379

shows the comparative analysis data of multiple cycle paths under the two modes.

The data in the table show that the single cycle cost of the semi-open model is lower than that of the closed model, the average cost of 7 days is reduced by 12%, and the average transportation distance is reduced by 35%. The difference between semi-open and closed models is very large. The semi-open multi-distribution center logistics distribution model takes into account the actual situation of enterprises, so the comprehensive cost is lower and more practical.

According to Table 2 and Table 3, it can be seen that the improved ant colony algorithm saves about 238 km of path and 119 kWh of electricity compared with the traditional ant colony algorithm, which has a non-negligible economic benefit as well as the ability to reduce carbon emissions for a long-term running business.

5. Conclusions

In this paper, a semi-open multi-distribution center logistics network model is proposed for the multi-distribution center AMR path problem, considering the influence of AMR number limitation and time window. An improved ant colony algorithm is proposed, and the optimal AMR path is solved for four distribution centers and 50 demand instances with a cycle number of seven. The results show that the improved ant colony algorithm can effectively prevent the algorithm from falling into the local optimum. The solution results of the semi-open model are more reasonable than those of the closed model, and the cost is lower than that of the closed model, which is in line with the purposes of cost reduction and efficiency improvement. It also effectively proves the superiority of the semi-open multi-distribution center logistics distribution model. At the same time, this model is applicable to any multi-bin distribution solution, which can effectively improve business efficiency from the perspective of economic benefits. From the perspective of environmental sustainability, the improved ant colony algorithm can effectively reduce carbon emissions because, at present, seventy percent of electricity in China needs to be generated by coal. The semi-open model is also widely used in the fields of medical cold chain logistics, take-away delivery, and port logistics and can be applied to other fields by modifying the model parameters.