Information Gap Decision Theory-Based Risk-Averse Scheduling of a Combined Heat and Power Hybrid Energy System

Abstract

This research investigates the optimal management of electric and heat energies in a hybrid energy system (HES). In the studied HES, a pair of photovoltaic and battery storage devices is used to supply the electricity demand, and a boiler system to supply the heat demand directly. In addition, a modified cycle power plant acted as a combined heat and power (CHP) unit to increase the generation capacity and supply reliability. The HES is also able to connect to the electric grid to exchange power according to real-time energy prices. The uncertainty of renewable generation, demand levels, and energy prices challenge the decision-making process. To deal with the uncertainty of these overlapping parameters, a comprehensive information-gap decision theory (IGDT) approach is proposed in this paper that, despite other works, considers the uncertainties in an integrated framework and derives risk-averse and risk seeker strategies in different steps. The problem is modeled as mixed-integer linear programming and solved using the GAMS optimization package. Concerning simulation results, from the viewpoint of a risk-seeking decision maker, the increment of the uncertainty degree by 10.906% results in a reduced operating cost of 8.6%. From the viewpoint of a risk-averse decision maker, the increment of the uncertainty degree by 10.208% results in 8.6% more operating cost.

1. Introduction

Restrictions on the spread of carbon and policies in this respect have pushed the energy section towards a more sustainable and efficient use of energy resources. By decomposing a large power and energy system into several small controllable microgrids (MG) with different energy carriers, it is possible to increase functionality and flexibility. The result is higher functionality, ease of energy conversion, lowered energy losses, increment of supply rate, and more eco-friendly design and operation. The MGs are mainly founded on renewable energy sources (RES), energy storage devices, and co-generation facilities such as combined heat and power technology to cover both electric and heat energy demands sustainably [1]. The MG can be used in an isolated mode and connected to the network depending on requirements. The isolated MGs are mainly used to electrify remote areas, while the grid-connected modes can exchange energy with a local energy market and have a higher reliability rate. The main challenging part of the operation for the MGs is managing enormous sources of uncertainties caused by the intermittent nature of RES output and loads’ behavior (and energy market conditions under the grid-connected operation). This issue is more drastic for small-scale MGs, due to sharp dynamics in power and volatile energy markets. The mismatch of generation and consumption causes damages and economic losses if it has not been addressed well. In addition, the interdependency between electric and heat energy carriers in a combined heat and power MG must be considered during the operation. From here, the hybrid energy system (HES) is used to refer to an MG that covers both electric and heat energy carriers.

The CHP technology includes a wide range of technologies, including hydrogen-based fuel cells, concentrated solar energy, and modified cycle power plants. Biofuels may be offered to the modified cycle power generators to reduce environmental impacts too. The task of making balance and management of electric and heat resources economically is directed by energy management systems that can be designed through an optimization model with risk-hedging approaches to investigate the uncertainties as well. In this paper, a modified cycle power plant acts as a CHP unit, and the energy management system is designed by introducing mixed-integer linear programming, where an information gap decision theory approach is proposed to deal with uncertain values of renewable power generation, load demand, and energy price of the market simultaneously and to schedule different resources according to the decision-making strategy.

Literature Review

The CHP-based HES complicates the energy management problem, since any change in the electric or heat side creates a mismatch on the other side [2]. The uncertainty of RES, load behavior, and energy price cannot be foreseen exactly before the scheduling, thus making the balancing a challenge. To address this issue, various uncertainty modeling and management methods have been developed. These methods are categorized as data-based approaches and mathematical programming tools. For instance, in [3], a multi-objective optimization is proposed to reduce the total operation cost and carbon emission. The uncertainty of electric load is addressed by using a deep-learning approach. In general, for integrating uncertain parameters into an optimization problem, mathematical approaches are popular. In this subject, the known approaches are scenario-based stochastic programming, interval optimization, robust optimization, and information gap decision theory (IGDT).

Stochastic programming requires a historical data set with a known probability distribution function to develop a set of scenarios for an uncertain parameter. Reference [4] propounds stochastic programming for CHP-based energy management in a HES, by considering the uncertainties of load, RES output, and energy price using scenarios. The fundamental drawback of this technique is its reliance on a large amount of data with known probabilities, which increases computing time. Furthermore, stochastic programming generates several solutions for the problem depending on the number of input scenarios.

On the other hand, the interval optimization approach, robust optimization technique, and IGDT rely on defining a boundary for the uncertain parameters. The interval and robust optimization approaches for energy-efficient scheduling of an HES with CHP units are presented in [5,6], respectively. These two approaches require the solution of numerous optimization problems in the bi-level form, which is difficult to solve and time-consuming in general [7]. Furthermore, the accuracy of the selected interval for the uncertain parameter affects the results. The solutions found by the robust optimization approach are very conservative and cannot satisfy an optimistic decision maker.

Similarly, the IGDT is an interval-based approach it does not require precise information about the uncertain parameter. For an electric-only DC MG scheduling problem, the IGDT method is proposed in [8] to deal with the energy price uncertainty. It develops different decision-making strategies in the presence of flexible demand response programs. In [9], for an electric-only MG, the IGDT is proposed to schedule various resources to reduce operating costs and to cope with different uncertainty parameters, including wind and PV generation and load uncertainties. Indeed, it investigates different uncertainty parameters separately, and the concurrent features are missed. Similarly, a risk-averse IGDT-based optimal capacity configuration of an islanded electric MG is investigated in [10]. The uncertainties of wind and PV generation are handled separately by the IGDT. Reference [11] was one of the first studies that used the IGDT for uncertainty management for a HES. The studied HES includes a fuel cell and PV to supply electric and heat demands together. Moreover, an electrical demand response program is considered to fulfill the energy gaps during peak times. In [12], the IGDT is proposed for scheduling problems of HES with combined cooling, heating, and power (CCHP) units to deal with energy price uncertainty. The RESs are included in the model; meanwhile, their uncertain output has not been addressed. This paper derives both risk-averse (RA) and risk seeker (RS) strategies for decision makers and employs a real-time pricing demand response program to reduce the total operation cost. The authors of [13] assessed the optimal energy management problem for a smart apartment in the presence of a CHP unit and boiler, battery, and solar thermal storage to increase flexibility on a residential scale. The IGDT is used to counter energy market price uncertainty, while the load uncertainty is disregarded. By presenting reliability and opportunities functions, the authors provide both RA and RS strategies to the decision makers. Reference [14] optimizes the operation of a CHP-based MG under real-time and time-of-use pricing electricity tariffs. The IGDT is proposed to deal with load uncertainty considering both RA and RS strategies. The study employs power-only and heat-only resources besides the CHP, which obscures the interactions between electricity and heat generation. Although a detailed model of the CHP unit and the heat-only system is presented, the RESs are not involved to ensure sustainability. Reference [15] presents a robust RA strategy for scheduling a CHP-based MG considering demand response program availability, and in the presence of wind and PV power generation systems as the main RESs, boiler systems, and electric/thermal energy storage technology. The uncertainty of RES output is addressed by the IGDT, and the uncertainty of energy price and load demands is not discussed. The studied MG can exchange power with an electric grid, and a demand response program for electric and heat loads helps in holding the energy equilibrium. Moreover, in a recent attempt by [16], the IGDT is used for load uncertainty management in the scheduling problem of a CHP-based MG, which is constructed as multi-objective optimization. The authors of [17] proposed a multi-objective optimization framework coupled with the IGDT method to handle the renewable power uncertainty in a combined heat, hydrogen, and power (CHHP)-based MG with power-to-X conversion technology. Their methodology derives from the risk-averse strategy to reduce the overall cost and environmental issues. For an islanded CHP-based MG, the IGDT method is used to handle the uncertainty of load and renewable wind power to reduce the cost of operation. Based on the robust scheduling of the IGDT, the authors of [18] proposed an optimization framework to schedule a CHP-based MG. The uncertainty related to renewable generation is handled by the IGDT with a risk-averse strategy. In [19], the authors proposed the IGDT to model the uncertainties of wind power and electric load in a CHP-based MG scheduling problem. However, similar to the previous works, they investigated the uncertainties separately, and the overlapping effects of uncertainties are not seen. They presented both risk-averse and risk seeker decision making strategies.

Till here, the reviewed works have used the IGDT to model just one of the existing uncertain parameters, e.g., the energy price, demand variation, or RES output. In the following, certain hybrid approaches are introduced to model multiple uncertainty resources.

Numerous papers presented a hybrid of stochastic, robust, and IGDT approaches to include several uncertain parameters in an integrated optimization. In this regard, the authors of [20] investigated the scheduling problem of the CHP-based MGs with renewable generation in the presence of electric network constraints. The IGDT method is in charge of load behavior uncertainty management, while stochastic programming and robust optimization approaches are used to model the uncertainty of RESs and energy prices, respectively. For scenario-based stochastic programming and robust optimization, the given hybrid technique requires a dataset for the uncertain parameters. With a different perspective, a robust IGDT method is proposed by [21] to consider the uncertainty of component failures in an islanded MG, while conventional uncertainties are modeled by scenario-based stochastic programming. The authors of [22] proposed a hybrid stochastic-IGDT technique for optimal scheduling of CHP units in energy and reserve markets. The feasible operating region for the CHP unit is imposed by mathematical modeling in a network-constrained unit commitment problem in the presence of wind power generation. The IGDT is used to deal with the wind power uncertainty. Scenario-based stochastic programming is used to address the uncertainty of load demands. For different levels of risk-acceptance, the expected operating cost is minimized over demand scenarios. The final results are prepared for both RA and RS decision makers. Similarly, a hybrid stochastic-IGDT optimization method is described in [23] for scheduling a multi-carrier MG with CHP units, a battery, and thermal storage. The use of electric and thermal demand response programs is also proposed to increase the flexibility of operation. The uncertainty associated with wind and solar energy resources, as well as energy prices, is considered. The IGDT is used to address the effects of renewable energy uncertainty. Stochastic programming is also used to address the uncertainty of energy prices. The uncertainty of load is not seen. Moreover, this work disregards the RS strategy while deriving the decisions. The authors of [24] prescribed a hybrid robust-IGDT for energy management of a tri-generation energy system with a CHP unit, gas boiler, power-to-gas facility, and wind turbine. The robust optimization is used to handle the uncertainty of energy prices, while the IGDT is used to control the uncertainty of wind power generation. The proposed hybrid approach considers the worst realization of the wind energy production and energy market price, resulting in a restricted RA strategy. Finally, in [25], a hybrid stochastic-IGDT approach is proposed for scheduling an industrial energy park with various co-generation and energy storage technologies. The proposed hybrid approach can encounter uncertainties of wind output fluctuations, energy price, and electric/heat/cooling demands. From the above-mentioned explanations, these approaches can capture the effects of several uncertain variables, but they are computationally challenging and need precise data for scenario generation and interval specification for robust optimization. Furthermore, these works examine the effects of uncertainties separately, while in reality, the effects of uncertainties are overlapping and should be investigated in an integrated form.

The focus of this research is to extend the IGDT model to link the impacts of several uncertain parameters (i.e., energy price, PV output, and electric/heat load demands) to obtain the best operating strategy in the absence of complete information on the mentioned parameters. Reference [26] prescribed the IGDT for uncertainty modeling of load demand, electricity price, and wind power output that is very similar to the purpose of this paper. However, the authors of [26] neglect the beneficial features of uncertainty and optimistic strategy. They also model the uncertainty margins separately and do not consider them simultaneously during the optimization phase. Actually, the purpose of this study is to reply to two key issues that have arisen:

I.

How we can expand the IGDT method to account for multiple uncertainties with conflicting effects in an integrated optimization model?

II.

In comparison with a risk-neutral strategy, what is the difference between robust and optimistic scheduling strategies?

Previous publications did not give an answer to these concerns.

Table 1. Comparison of the related works.

Ref.	Components Considered in MG	Uncertainties Modeled by IGDT	Decision-Making Strategy
[11]	PV/battery/fuel cell/grid	Electric load	RA/RS
[12]	CCHP/PV/wind/grid	Energy price	RA/RS
[13]	CHP/energy storage/grid	Energy price	RA/RS
[14]	CHP/grid	Electric and heat load	RA/RS
[15]	CHP/fuel-cell/PV/wind/battery/grid	Renewable generation	RA only
[16]	CHP/boiler/wind/energy storage	Electric load/renewable generation	RA/RS
[17]	CHHP/PV/wind/energy storage/P2X	Renewable power generation	RA only
[18]	CHP/boiler/grid/battery	Renewable power generation	RA only
[19]	CHP/boiler/wind/ energy storage/grid	Electric load/wind power generation	RA/RS
[20]	CHP/PV/wind/battery/grid	Electric load	RA/RS
[22]	CHP/wind/grid	Wind power generation	RA/RS
[23]	CHP/boiler/wind/PV/grid	Renewable generation	RA/RS
[24]	CHP/wind/energy storage/grid	Wind power generation	RA/RS
[25]	CCHP/wind/energy storage/grid	Wind power generation	RA only
[26]	CCHP/wind/PV/energy storage/gird	Electric and heat load/renewable generation/energy price	RA only
This paper	CHP/boiler/PV/battery/grid	Electric and heat load/PV generation/energy price	RA/RS

compares relevant works for a better clarification.

To sum up, the contributions of the paper are highlighted in the following:

• Providing a mixed-integer linear problem for scheduling a sustainable hybrid energy system considering the CHP unit;
• Proposing a comprehensive IGDT method for addressing various uncertainty parameters in an integrated form, without a need for a precise data set or known probability distribution function;
• Providing a more flexible decision-making framework that is in favor of both risk-averse and risk seeker decision makers despite the conservative decisions of the robust approach;
• Proposing envelope-bound IGDT with a tractable procedure and efficient solution time.

2. Background Regarding Uncertainty Modeling Using IGDT

The IGDT is a powerful decision-making tool that considers not only the negative effects of uncertainty, but also the probable positive aspects. It is furnished by two performance functions, namely, robustness and opportunity functions. On one hand, the robustness function shows the range of resistance of the system against harmful uncertainty realizations. On the other hand, the opportunity function investigates the benefits that might come through uncertainty reduction. For each function, a predefined criterion is used to immunize the system against uncertainty. In the robustness function, the optimization tries to find the maximum interval bounds for the uncertainty parameter so that the result (i.e., operation cost) is equal to or lower than a predefined criterion. Vice versa, in the opportunity function, the optimization finds the lowest interval bounds in which the operation cost cannot exceed the predefined value. In the following, the robustness function $\widehat{\alpha }$ or the degree of resistance against undesired uncertainty realization, as well as the opportunity function $\widehat{\mathsf{\beta }}$, are expressed, respectively by (1) and (2).

$$\hat{\mathsf{\alpha }}=\underset{\mathsf{\alpha }}{\max }\left\{\mathsf{\alpha }:\mathrm{maximumoperationcostwouldnotbehigherthanapredefinedcriterion}\right\}$$

(1)

$$\hat{\mathsf{\beta }}=\underset{\mathsf{\alpha }}{\min }\left\{\mathsf{\alpha }:\mathrm{minimumoperationcostislessthanapredefinedcriterion}\right\}$$

(2)

To sum up, the IGDT does not require a vast amount of data to model the uncertain parameters’ behavior despite scenario-based approaches. In the absence of complete information, the IGDT provides risk-averse strategies. The results are comprehensive despite the robust optimization approach, which only models the worst-case condition leading to a conservative strategy. Although similar to the robust optimization approach, the IGDT utilizes an uncertainty interval instead of a data set and determines safe operational regions. Furthermore, the IGDT allows making decisions according to specific strategies and priorities. For more information, interested readers are consulted to study reference [27].

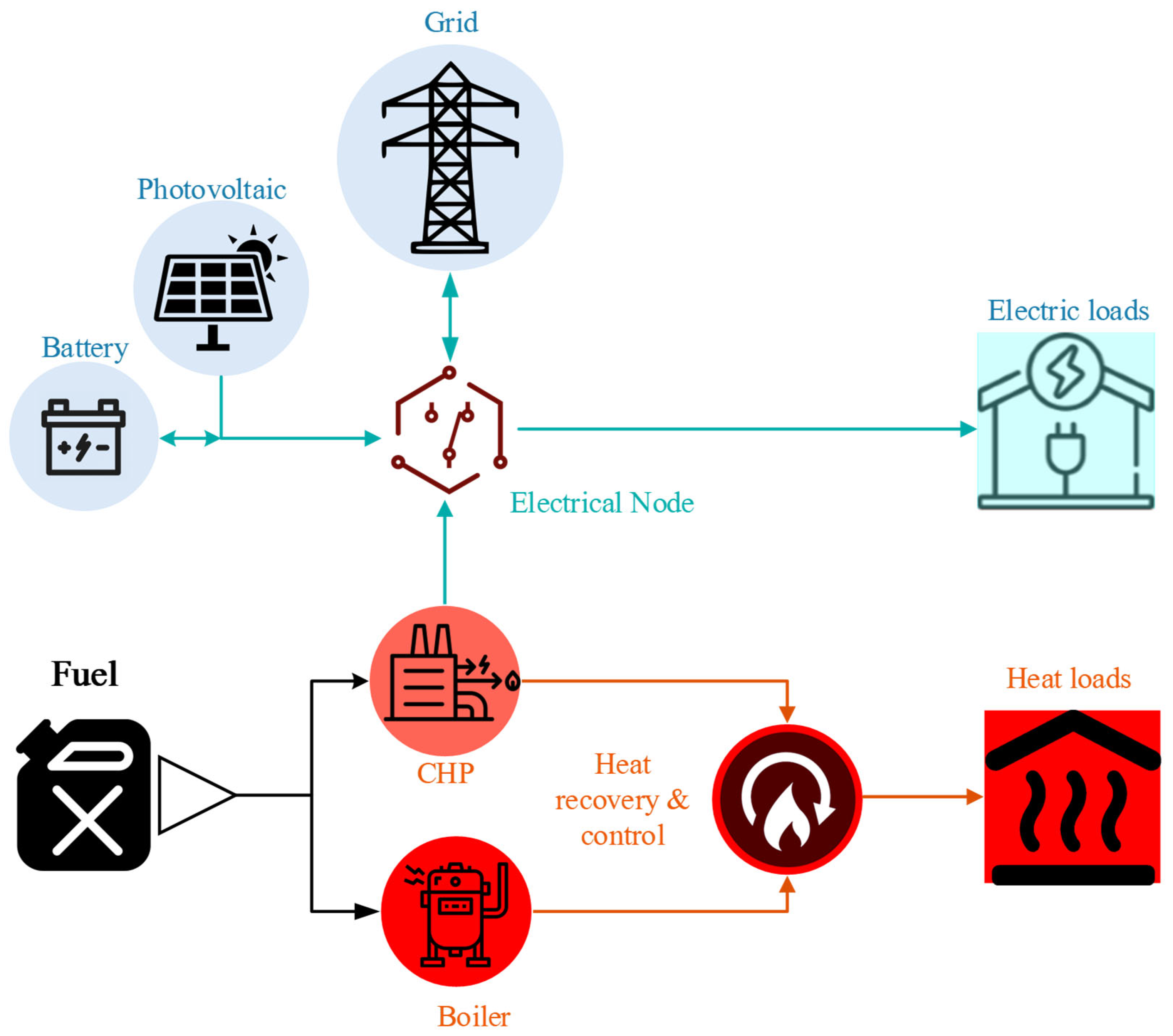
3. Problem Statement

It is increasingly important to use sustainable energy systems to address the greenhouse gas issue. The RES and CHP unit fed by sustainable biofuels are recommended as viable alternatives. CHP units are programmable systems, and consideration should be given to the relationship between generated electricity and heat. While the production of RES is uncontrollable, that is the reason why energy storage devices are being used in MG. In the HES, the integrated form of dispatchable and non-dispatchable generation creates a flexible system to efficiently supply electricity and heat demands. Figure 1 depicts a schematic of the studied HES, highlighting resource connections. Heating loads are served by the CHP unit and a boiler system via a heat exchanger and recovery system, while electric loads are supplied through the grid, PV, and CHP unit. A battery storage system is employed to add flexibility to the operation. The model is based on technical information presented in [28].

The field of optimal energy management will be more interesting when the decision maker is able to plan different reactions against the uncertainties. The IGDT provides various decision-making strategies even with a lack of information. While the uncertainties may have negative effects on the operation, such as the unpredicted rise of load demand, an optimistic decision maker would like to consider the positive aspects, too. For example, the unpredicted growth of renewable generation that can be sold to the grid brings more benefits. The IGDT presented in this paper can cover both perspectives. One of the main attributes of the IGDT is its ability to be included in both positive and pessimistic conditions [29]. In this regard, firstly, the deterministic operation is modeled at the first stage. The results of this stage are used to introduce the predefined criterion for the robustness and opportunity functions of the IGDT in the following.

a.

Deterministic optimal scheduling of the HES

The deterministic optimization presented in this subsection corresponds to a risk-neutral decision-making problem. Similar to any optimization problem, the HES scheduling problem consists of an objective function stated in (3), subject to operational constraints in (4)–(18). Equation (3) defines the objective function trying to minimize the total cost. Equation (4) calculates the cost of power exchange between the HES and grid based on energy prices. According to the amount of power generated by the CHP unit, the fuel cost is calculated as (5). Similarly, the fuel cost of the boiler system is calculated in (6). The amount of heat produced by the CHP and boiler units is delivered to the heat recovery system calculated in (7). The thermal energy balance is assured in (8) considering the efficiency of the heat recovery system. Constraints (9) and (10) limit the power output of the CHP and thermal energy of the boiler, respectively. Constraints (11)–(16) represent the model of the battery storage operation. Using (11) and (12), the stored electrical power in the battery storage is determined based on the initial state of charge and charged/discharged power. Equations (13) and (14) restrict the charged and discharged powers. The simultaneous charging and discharging are forbidden by (15). Finally, the capacity of the battery storage is limited by (16).

$$\mathrm{Min}{\displaystyle \sum }_{\mathrm{t}=1}^{24}({\mathrm{C}}_{\mathrm{grid}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{chp}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{boiler}}\left(\mathrm{t}\right))$$

(3)

$${\mathrm{C}}_{\mathrm{grid}}\left(\mathrm{t}\right)={\mathsf{\lambda }}_{\mathrm{en}}\left(\mathrm{t}\right)\times \left({\mathrm{P}}_{\mathrm{b}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{s}}\left(\mathrm{t}\right)\right)$$

(4)

$${\mathrm{C}}_{\mathrm{chp}}\left(\mathrm{t}\right)={\mathsf{\lambda }}_{\mathrm{f}}\times \left(\frac{{\mathrm{P}}_{\mathrm{chp}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{chp}}}\right)$$

(5)

$${\mathrm{C}}_{\mathrm{boiler}}\left(\mathrm{t}\right)={\mathsf{\lambda }}_{\mathrm{f}}\times \frac{{\mathrm{H}}_{\mathrm{boiler}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{boiler}}}$$

(6)

$${\mathrm{H}}_{\mathrm{he}}\left(\mathrm{t}\right)=\left(\frac{{\mathrm{P}}_{\mathrm{chp}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{chp}}}\left(1-{\mathsf{\eta }}_{\mathrm{chp}}-{\mathsf{\eta }}_{\mathrm{loss}}\right)\right)+{\mathrm{H}}_{\mathrm{boiler}}\left(\mathrm{t}\right)$$

(7)

$${\mathsf{\eta }}_{\mathrm{he}}\times {\mathrm{H}}_{\mathrm{he}}\left(\mathrm{t}\right)={\mathrm{L}}_{\mathrm{h}}\left(\mathrm{t}\right)$$

(8)

$$0\le {\mathrm{P}}_{\mathrm{chp}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{chp}}^{\max }$$

(9)

$$0\le {\mathrm{H}}_{\mathrm{boiler}}\left(\mathrm{t}\right)\le {\mathrm{H}}_{\mathrm{boiler}}^{\max }$$

(10)

$${\mathrm{E}}_{\mathrm{BS}}\left(\mathrm{t}\right)={\mathrm{E}}_{\mathrm{BS}}^{\mathrm{init}}+\left({\mathrm{P}}_{\mathrm{BS}}^{\mathrm{ch}}\left(\mathrm{t}\right)\times {\mathsf{\eta }}_{\mathrm{BS}}^{\mathrm{ch}}-\frac{{\mathrm{P}}_{\mathrm{BS}}^{\mathrm{dis}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{BS}}^{\mathrm{dis}}}\right),\mathrm{t}=1$$

(11)

$${\mathrm{E}}_{\mathrm{BS}}\left(\mathrm{t}\right)={\mathrm{E}}_{\mathrm{BS}}\left(\mathrm{t}-1\right)+\left({\mathrm{P}}_{\mathrm{BS}}^{\mathrm{ch}}\left(\mathrm{t}\right)\times {\mathsf{\eta }}_{\mathrm{BS}}^{\mathrm{ch}}-\frac{{\mathrm{P}}_{\mathrm{BS}}^{\mathrm{dis}}\left(\mathrm{t}\right)}{{\mathsf{\eta }}_{\mathrm{BS}}^{\mathrm{dis}}}\right),\forall \mathrm{t}>1$$

(12)

$${\mathrm{P}}_{\mathrm{ch}}^{\min }{\mathrm{u}}_{\mathrm{ch}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{BS}}^{\mathrm{ch}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{ch}}^{\max }{\mathrm{u}}_{\mathrm{ch}}\left(\mathrm{t}\right)$$

(13)

$${\mathrm{P}}_{\mathrm{dis}}^{\min }{\mathrm{u}}_{\mathrm{dis}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{BS}}^{\mathrm{dis}}\left(\mathrm{t}\right)\le {\mathrm{P}}_{\mathrm{dis}}^{\max }{\mathrm{u}}_{\mathrm{dis}}\left(\mathrm{t}\right)$$

(14)

$${\mathrm{u}}_{\mathrm{ch}}\left(\mathrm{t}\right)+{\mathrm{u}}_{\mathrm{dis}}\left(\mathrm{t}\right)\le 1$$

(15)

$${\mathrm{E}}_{\mathrm{BS}}^{\min }\le {\mathrm{E}}_{\mathrm{BS}}\left(\mathrm{t}\right)\le {\mathrm{E}}_{\mathrm{BS}}^{\max }$$

(16)

The electrical and thermal energy balances are held by (17) and (18), respectively.

$${\mathrm{P}}_{\mathrm{b}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{s}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{chp}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{PV}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{BS}}^{\mathrm{dis}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{BS}}^{\mathrm{ch}}\left(\mathrm{t}\right)={\mathrm{L}}_{\mathrm{E}}\left(\mathrm{t}\right)$$

(17)

$${\mathrm{H}}_{\mathrm{boiler}}\left(\mathrm{t}\right)+{\mathrm{H}}_{\mathrm{chp}}\left(\mathrm{t}\right)=\frac{{\mathrm{L}}_{\mathrm{h}}\left(\mathrm{t}\right)}{{\mathrm{h}}_{\mathrm{he}}}$$

(18)

b.

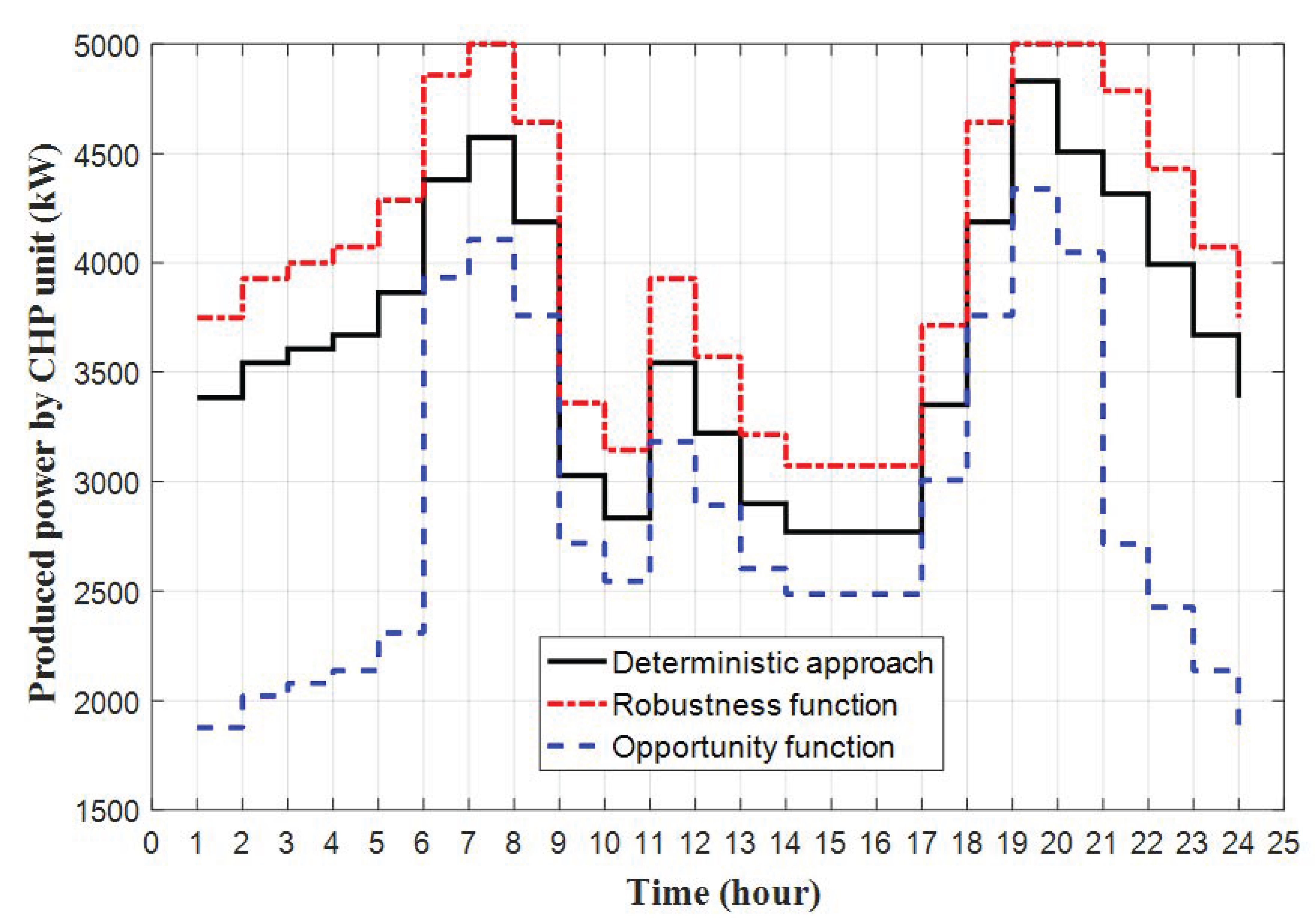
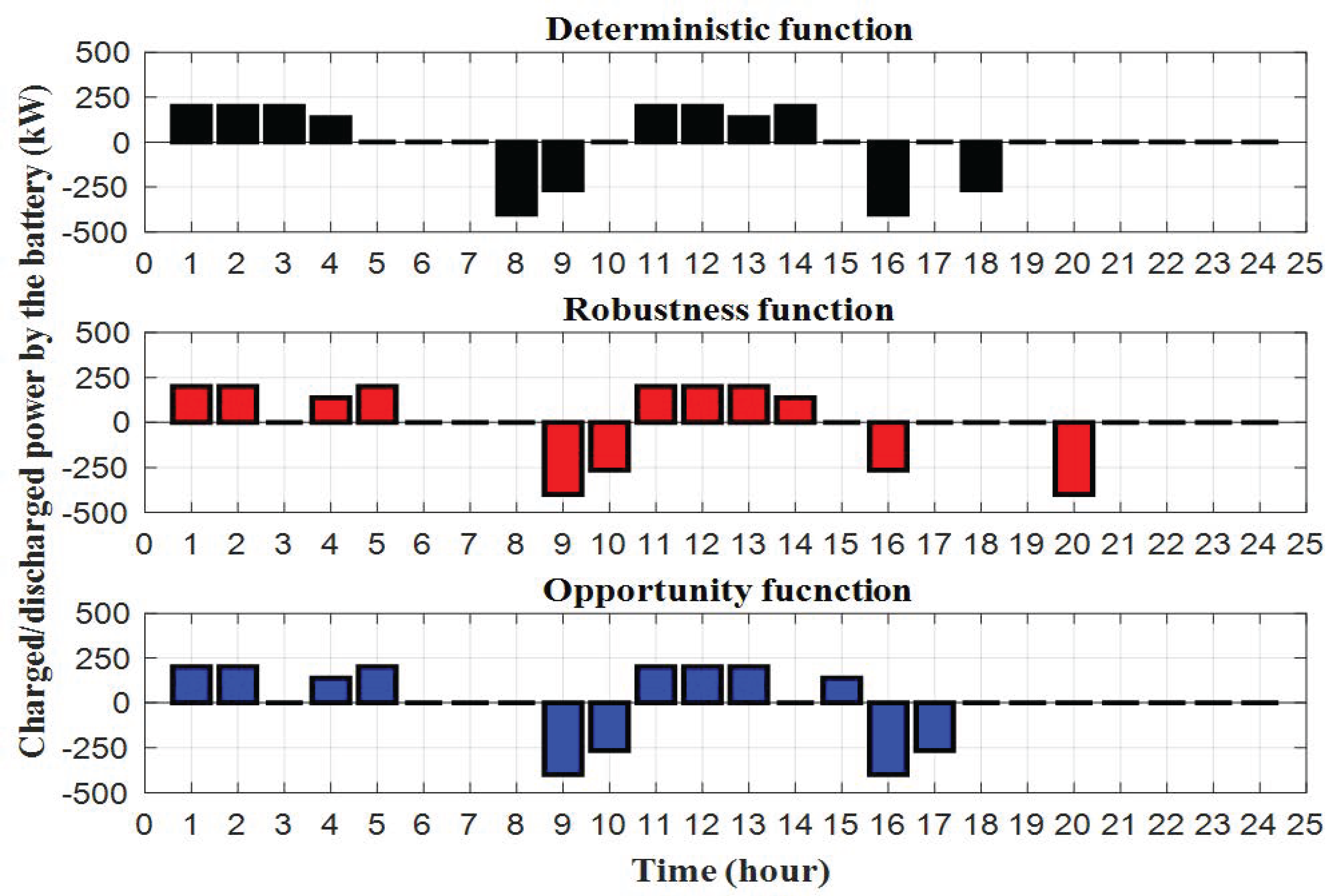
IGDT-based optimal scheduling of the HES

The IGDT is applied to manage the uncertainties of energy price, PV generation, and electric and heat loads simultaneously. The fractional information gap model is presented in (19). If the uncertainty model was represented by $\mathrm{U}(\mathrm{\alpha },{\mathrm{l}}_{\mathrm{i}})$, then ${\mathrm{l}}_{\mathrm{i}}$ would represent the uncertain parameters’ actual values (i.e., energy price, PV generation, electric load, and heat load demands), ${\tilde{\mathrm{l}}}_{\mathrm{i}}$ is the forecasted amounts of the mentioned uncertain parameters, and $\alpha$ indicates horizon of the uncertainty parameter. A greater value of $\alpha$ leads to a greater range of deviation of the uncertain parameters.

$$\mathrm{U}\left(\mathsf{\alpha },{\mathrm{l}}_{\mathrm{i}}\right)=\left\{{\mathrm{l}}_{\mathrm{i}}:\left|{\mathrm{l}}_{\mathrm{i}}-{\tilde{\mathrm{l}}}_{\mathrm{i}}\right|\le \mathsf{\alpha }{\tilde{\mathrm{l}}}_{\mathrm{i}}\right\},\mathsf{\alpha }\ge 0$$

(19)

Based on the definition, the IGDT-based optimal scheduling of the HES can be formulated as follows. For a risk-averse decision maker, the robustness function can be expressed as (20).

$$\hat{\mathsf{\alpha }}\left({\mathrm{C}}_{\mathrm{r}}\right)=\underset{\mathsf{\alpha }}{\max }\{\mathsf{\alpha }:\underset{\mathrm{l}\in \mathrm{U}\left(\mathsf{\alpha },{\tilde{\mathrm{l}}}_{\mathrm{i}}\right)}{\max }(\mathrm{C}\left(\mathrm{q},{\mathrm{l}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{r}}=\left(1+\mathsf{\epsilon }\right){\mathrm{C}}_{\mathrm{b}}\}$$

(20)

where $\mathrm{C}(\mathrm{q},{\mathrm{l}}_{\mathrm{i}})$ models the system cost, q includes decision variables, ${\mathrm{l}}_{\mathrm{i}}$ contains uncertain parameters, and ${\mathrm{C}}_{\mathrm{r}}$ is the maximum or critical operational cost of the HES, which the results should not exceed. In fact, the risk-averse decision maker tries to find the maximum bound of the uncertainty in a way the operation cost is not more than a predefined cost. ${\mathrm{C}}_{\mathrm{b}}$ is the base cost of the system according to forecasted amounts of uncertain parameters. The base cost is the optimal cost of the deterministic problem presented in (3)–(18). $\mathsf{\epsilon }$ is the cost deviation factor, which can adjust the target for the robust problem. The optimization problem (21)–(27) schedules the system operation in a robust condition. From the constraints, it can be deduced that when the maximized degree of uncertainty, $\alpha$, is lesser than the maximum level of uncertainties, $\widehat{\alpha }$, the operational cost will be lower than the critical cost, ${\mathrm{C}}_{\mathrm{r}}$. It should be noted that after several numerical evolutions under the deterministic case, it was found that the total cost is higher when the energy price is targeted to be maximized (i.e., robust cost); for this reason, the effect of price is negative as shown in (23). While the PV generation can reduce the operational cost, the risk-averse decision maker would like to consider the PV output lower than its forecasting amount using robust optimization, as shown in (24). For a robust operation, the decision maker would like to consider more load demands as modeled in (25) and (26) for electrical and heat loads, respectively. Other constraints are the same as the deterministic problem as mentioned in (27).

$$\hat{\mathsf{\alpha }}\left({\mathrm{C}}_{\mathrm{r}}\right)=\max \mathsf{\alpha }$$

(21)

Subject to:

$${\displaystyle \sum }_{\mathrm{t}=1}^{24}({\mathrm{C}}_{\mathrm{grid}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{chp}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{boiler}}\left(\mathrm{t}\right))\le {\mathrm{C}}_{\mathrm{r}}$$

(22)

$${\mathsf{\lambda }}_{\mathrm{en}}\left(\mathrm{t}\right)={\tilde{\mathsf{\lambda }}}_{\mathrm{en}}\left(\mathrm{t}\right)+\mathsf{\alpha }{\tilde{\mathsf{\lambda }}}_{\mathrm{en}}\left(\mathrm{t}\right)$$

(23)

$${\mathrm{P}}_{\mathrm{PV}}\left(\mathrm{t}\right)={\tilde{\mathrm{P}}}_{\mathrm{PV}}\left(\mathrm{t}\right)-\mathsf{\alpha }{\tilde{\mathrm{P}}}_{\mathrm{PV}}\left(\mathrm{t}\right)$$

(24)

$${\mathrm{L}}_{\mathrm{E}}\left(\mathrm{t}\right)={\tilde{\mathrm{L}}}_{\mathrm{E}}\left(\mathrm{t}\right)+\mathsf{\alpha }{\tilde{\mathrm{L}}}_{\mathrm{E}}\left(\mathrm{t}\right)$$

(25)

$${\mathrm{L}}_{\mathrm{H}}\left(\mathrm{t}\right)={\tilde{\mathrm{L}}}_{\mathrm{H}}\left(\mathrm{t}\right)+\mathsf{\alpha }{\tilde{\mathrm{L}}}_{\mathrm{H}}\left(\mathrm{t}\right)$$

(26)

$$\mathrm{Constraints} \mathrm{(5)}–\mathrm{(18)}$$

(27)

On the contrary, for a risk-seeking decision maker, the mathematical model for the opportunity function is expressed in (28).

$$\hat{\mathsf{\beta }}\left({\mathrm{C}}_0\right)=\underset{\mathsf{\alpha }}{\min }\{\mathsf{\alpha }:\underset{{\mathrm{l}}_{\mathrm{i}}\in \mathrm{U}\left(\mathsf{\alpha },{\tilde{\mathrm{l}}}_{\mathrm{i}}\right)}{\min }(\mathrm{C}\left(\mathrm{q},{\mathrm{l}}_{\mathrm{i}}\right)\le {\mathrm{C}}_0=\left(1-\mathsf{\epsilon }\right){\mathrm{C}}_{\mathrm{b}}\}$$

(28)

where ${\mathrm{C}}_0$ is the minimum cost of the system, which the results should not exceed. Thus, $\widehat{\alpha }({\mathrm{C}}_{\mathrm{r}})$ was the largest amount of $\alpha$, and $\widehat{\mathsf{\beta }}({\mathrm{C}}_0)$ is the smallest amount of $\alpha$. $\widehat{\alpha }({\mathrm{C}}_{\mathrm{r}})$ and $\widehat{\mathsf{\beta }}({\mathrm{C}}_0)$, respectively, find the system cost with a high degree of robustness and the smallest cost of the system by considering positive attributes. Obviously, ${\mathrm{C}}_{\mathrm{r}}$ is always greater than ${\mathrm{C}}_0$. Therefore, the opportunity function can be formulated as follows. Despite the RA decision maker, the RS decision maker tries to find the minimum deviation of the uncertainty parameters that push the system operation toward a positive situation. For example, the risk seeker strategy anticipates that uncertainty reduces the energy price, increases the PV generation, and decreases the load consumptions in (31)–(34), respectively.

$$\hat{\mathsf{\beta }}\left({\mathrm{C}}_0\right)=\min \mathsf{\alpha }$$

(29)

Subject to:

$${\displaystyle \sum }_{\mathrm{t}=1}^{24}({\mathrm{C}}_{\mathrm{grid}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{chp}}\left(\mathrm{t}\right)+{\mathrm{C}}_{\mathrm{boiler}}\left(\mathrm{t}\right))\le {\mathrm{C}}_0$$

(30)

$${\mathsf{\lambda }}_{\mathrm{en}}\left(\mathrm{t}\right)={\tilde{\mathsf{\lambda }}}_{\mathrm{en}}\left(\mathrm{t}\right)-\mathsf{\alpha }{\tilde{\mathsf{\lambda }}}_{\mathrm{en}}\left(\mathrm{t}\right)$$

(31)

$${\mathrm{P}}_{\mathrm{PV}}\left(\mathrm{t}\right)={\tilde{\mathrm{P}}}_{\mathrm{PV}}\left(\mathrm{t}\right)+\mathsf{\alpha }{\tilde{\mathrm{P}}}_{\mathrm{PV}}\left(\mathrm{t}\right)$$

(32)

$${\mathrm{L}}_{\mathrm{E}}\left(\mathrm{t}\right)={\tilde{\mathrm{L}}}_{\mathrm{E}}\left(\mathrm{t}\right)-\mathsf{\alpha }{\tilde{\mathrm{L}}}_{\mathrm{E}}\left(\mathrm{t}\right)$$

(33)

$${\mathrm{L}}_{\mathrm{H}}\left(\mathrm{t}\right)={\tilde{\mathrm{L}}}_{\mathrm{H}}\left(\mathrm{t}\right)-\mathsf{\alpha }{\tilde{\mathrm{L}}}_{\mathrm{H}}\left(\mathrm{t}\right)$$

(34)

$$\mathrm{Constraints} \mathrm{(5)}–\mathrm{(18)}$$

(35)

4. Numerical Evolutions

In this section, the results of the proposed scheduling framework are verified on a grid-connected HES including CHP, boiler, PV, and battery storage system, in which the characteristics of them are set based on data of reference [28]. Figure 2 illustrates the electric and heat load demands that all are based on data given by [28]. The problem is modeled in the GAMS software and solved using CPLEX and DICOPT solver. Three optimization problems are solved that are risk-neutral, risk-averse, and risk seeker problems.

Addressing parameter uncertainties will have an impact on the cost of MG operation. The system cost is compared for risk-averse and risk seeker strategies in Figure 3. It should be noted that the operation cost of the system under the risk-neutral strategy is USD 11556.950. Under the risk-averse strategy, modeled by (21)–(27), the decision maker is pessimistic regarding the effects of uncertainty. In other words, he/she thinks that any deviation from uncertain parameters will be harmful. For this reason, he/she takes conservative decisions to reduce the harmful effects, leading to further operating costs. The greater the rate of deviation, the greater the harmful effects. For this reason, more conservative decisions are made, which ultimately leads to higher costs. On the flip side, the risk seeker decision maker, modeled by (29)–(35), anticipates pleasant effects of uncertainty, for example, more PV generation or less load consumption, and for this reason, has different scheduling compared with risk-neutral and risk-averse strategies. In fact, he/she thinks about the optimistic aspects of the uncertain parameters, which ultimately leads to lower costs. The cost steps for both strategies are USD 100 in this paper, and, according to this change at each iteration, the margins for uncertainty deviation are optimized. As an example, USD 1000 is charged for the risk-averse decision maker when the uncertain parameters change by 10.906% from their forecasted values. For the risk-seeking decision maker, USD 1000 decreased when the uncertain parameters changed by 10.208% from their forecasted values. The selection between these strategies depends on the experience of the decision maker and the level of risk acceptance. For various strategies, Figure 3 provides the anticipated operating cost.

The electric power generation of the CHP unit is shown in Figure 4. It should be noted that the amount of heat produced corresponds linearly with the generation of electricity by the CHP unit. From Figure 4, under the risk-averse strategy, the decision maker expects a lower production by PV system, and more electric and heat load demands. Thus, under this strategy, the CHP is committed to generating more power and heat compared to the risk-neutral strategy. With a similar justification and in the opposite direction, the risk seeker decision maker operates the CHP unit at a lower level to save fuel costs. At times before 6 a.m., and after 9 p.m., the differences between risk seeker and risk-averse strategies are remarkable. In these periods, the electric consumption is lesser than in the other periods and PV generation is not available.

The risk seeker decision maker interprets the uncertainty of PV generation and load consumption on the positive side and generates less power by the CHP. This justification is more or less true for heat production and consumption. It should be noted that the presented IGDT method is comprehensive and integrated. In other words, it is possible to separately optimize the decisions with respect to a particular uncertainty parameter and make a multi-objective problem. Thus, when the system operator would like to choose a risk-averse strategy considering several uncertainties simultaneously, it is possible to combine a fuzzy approach to choose the best solution among the Pareto front obtained by the IGDT method. In this regard, by defining a membership function, the decision maker is able to maximize the least satisfaction to achieve a risk-averse decision-making strategy. A description of this approach is presented in [30].

The main source of heating energy is the CHP unit. Under the risk-neutral strategy, the boiler system has not been involved at all. Under the risk-averse strategy, the boiler is committed at hours 7 a.m., 7 p.m., and 8 p.m., with, respectively, total heating power capacity of 124.268 kW, 617.185 kW, and 1.039 kW. For the risk seeker strategy, the boiler system is committed during the hours from 1 a.m. to 5 a.m. and 9 p.m. to 12 p.m., with a full capacity of 2000 kW. In fact, under the risk-averse strategy, the worst realization of PV generation and load consumption required more CHP operation, and consequently the required heating energy from the boiler is reduced significantly. However, the risk seeker strategy schedules the CHP plant with a lower capacity, and the required heating capacity is provided by the boiler system. For the rest of the day, when the CHP has been committed, the boiler is turned off.

The uncertainty of energy prices is very intense in comparison with the uncertainties of PV production and load demand. The HES actively buys and sells power on the market. Thus, the increase or decrease of the price level does not consistently affect the HES energy management strategy. The investigations showed that the HES acts as an energy producer the majority of the time, and Figure 5 shows the hourly sold powers. The purchasing power from the grid is zero under the risk seeker strategy, while, for the risk-neutral strategy, the amount of 260.274 kW is imported from the grid at hour 4 p.m. For the risk-averse strategy, the power-purchasing contracts have been taken into account for hours 4 p.m. and 5 p.m. in the amounts of 38.928 kW and 56.078 kW. From (23) and (31), the energy price is considered higher for the robustness function and lesser for the opportunity function. For this reason, the risk-averse decision maker commits CHP to generate more power to supply electric and heat loads and sell it to the grid; however, the purchased power from the grid is not zero. On the other hand, the risk-seeking decision maker prefers to consume the generated power of the PV and CHP in the daily operation and sells only the surpassing power to the grid. It should be noted that assuming that the price uncertainty effect is reversed in (23) and (31), the overall schedule will change for both strategies.

Battery storage is generally used to offset intermittent renewable electricity generation. However, in this paper, the HES is rich in terms of energy resources, hence, the battery is used to add flexibility and increase the total revenue. The charged/discharged powers by the battery storage are depicted in Figure 6. The positive powers indicate the charging powers and vice versa. Three strategies demonstrate a similar dynamic. Before 6 p.m. when the electric load is low, the battery is charged through power generated by the CHP unit. The battery is discharged before the middle of the day to be ready for recharging by the PV at noon, i.e., between 11 a.m. to 3 p.m. After charging up to maximum capacity, the battery is ready to be discharged for the afternoon. According to the scheduling plan of other resources, the battery is discharged under three strategies.

5. Conclusions

In this paper, an integrated IGDT model is proposed to tackle several uncertainty effects in the optimal energy management problem of a grid-connected HES. The model copes with the uncertainties of energy price, PV solar output, and electric and heat load demands. For RA and RS decision makers, the orientation of the effects of PV output and load uncertainties was expected. According to the results, an RS decision maker expects higher PV generation and lower energy consumption, resulting in lower CHP dispatch. As a result, he/she activates the boiler to meet the heat requirement. The RA decision makers, on the other hand, have committed CHP with a large capacity to meet the amount of pessimistic electric and heat demand and use the boiler at rare times. The underlying cause of this phenomenon is the decision makers’ expectations regarding energy price volatility. While the RS decision maker had an optimistic perspective regarding PV production and load consumptions, the more deviation for the energy price means lesser prices in reality that prevents him/her from generating more power with the CHP unit. On the other hand, because of his or her gloomy assessment of PV and load uncertainty, the RA decision maker has the incentive to use the CHP to generate more power. Furthermore, despite the RS decision maker, the energy price divergence is perceived as higher amounts for the RA decision maker, who can sell the excess power on the market to offset fuel expenses. From the standpoint of a risk-averse decision maker, the system cost will increase by 8.6 percent when the uncertainty increases by 10.906 percent pessimistic. From the standpoint of a risk seeker decision maker, the system cost will reduce by 8.6% when the uncertainty grows by 10.208% optimistically. This shows that uncertainties favor the RS decision maker more than the RA decision maker. Furthermore, it appeared that the RS decision maker scheduled the resources more efficiently and was not reliant on power purchases from the grid. The battery’s role as a flexible resource is also examined, which resulted in a similar scheduling plan for all strategies. In general, the effectiveness of both decision-making approaches should be thoroughly assessed utilizing a bi-level programming approach that takes into account various operational scenarios. Furthermore, combining environmental impacts with multi-objective IGDT-based programming will result in significant improvements in energy management strategy.

The authors are interested in extending the present work to consider a network-constrained HES facing more uncertain resources using hybrid risk-hedging methods for transactive energy management. Peer-to-peer trading within HES in the presence of uncertainty will be another potential future work. Furthermore, the IGDT is a potentially strong tool for decision-making, and, in combination with other decision-making approaches such as the fuzzy method, can be beneficial for decision makers to choose the best solution among a set of strategies provided by IGDT. The idea of optimal IGDT-fuzzy-based energy management of hybrid energy systems is based in this paper, and the investigation of this methodology is left for potential future works.