Effect of a Circular Cylinder on Hydrodynamic Characteristics over a Strongly Curved Channel
Abstract
:1. Introduction
2. Materials and Methods
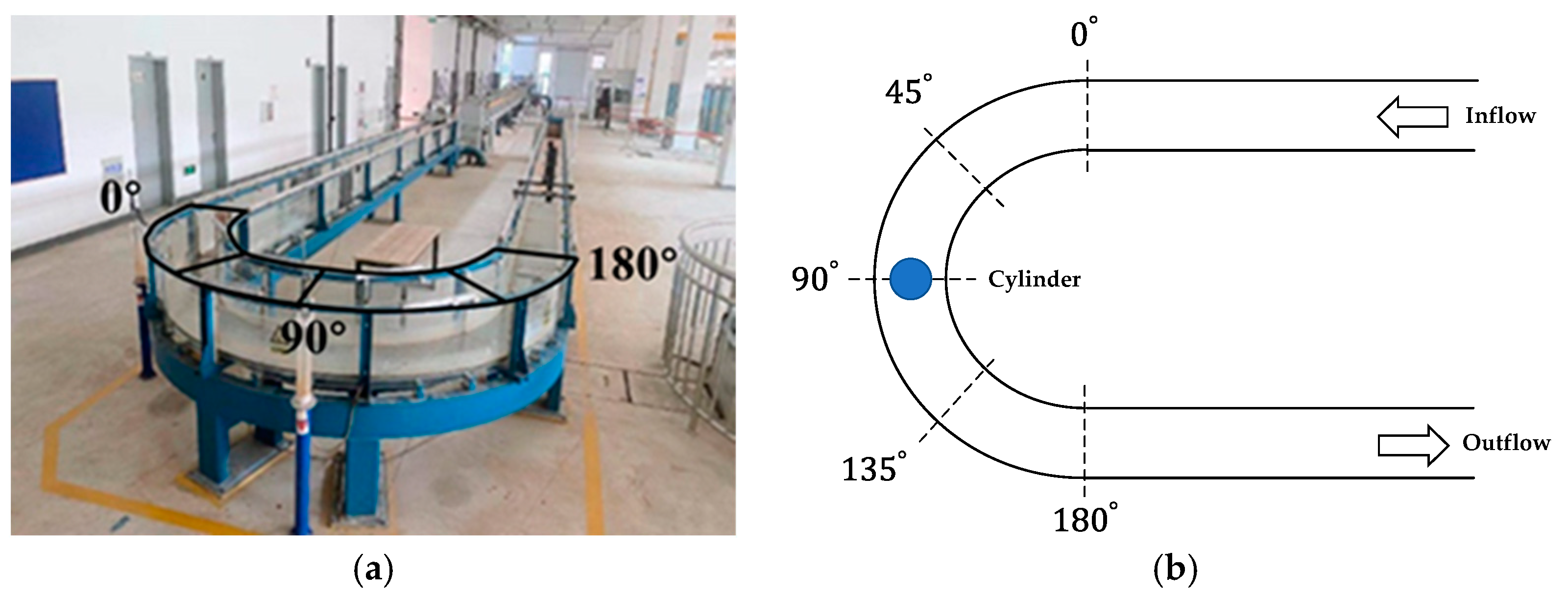
2.1. Experimental Setup
2.2. Numerical Analysis Using FLOW-3D
3. Results and Discussions
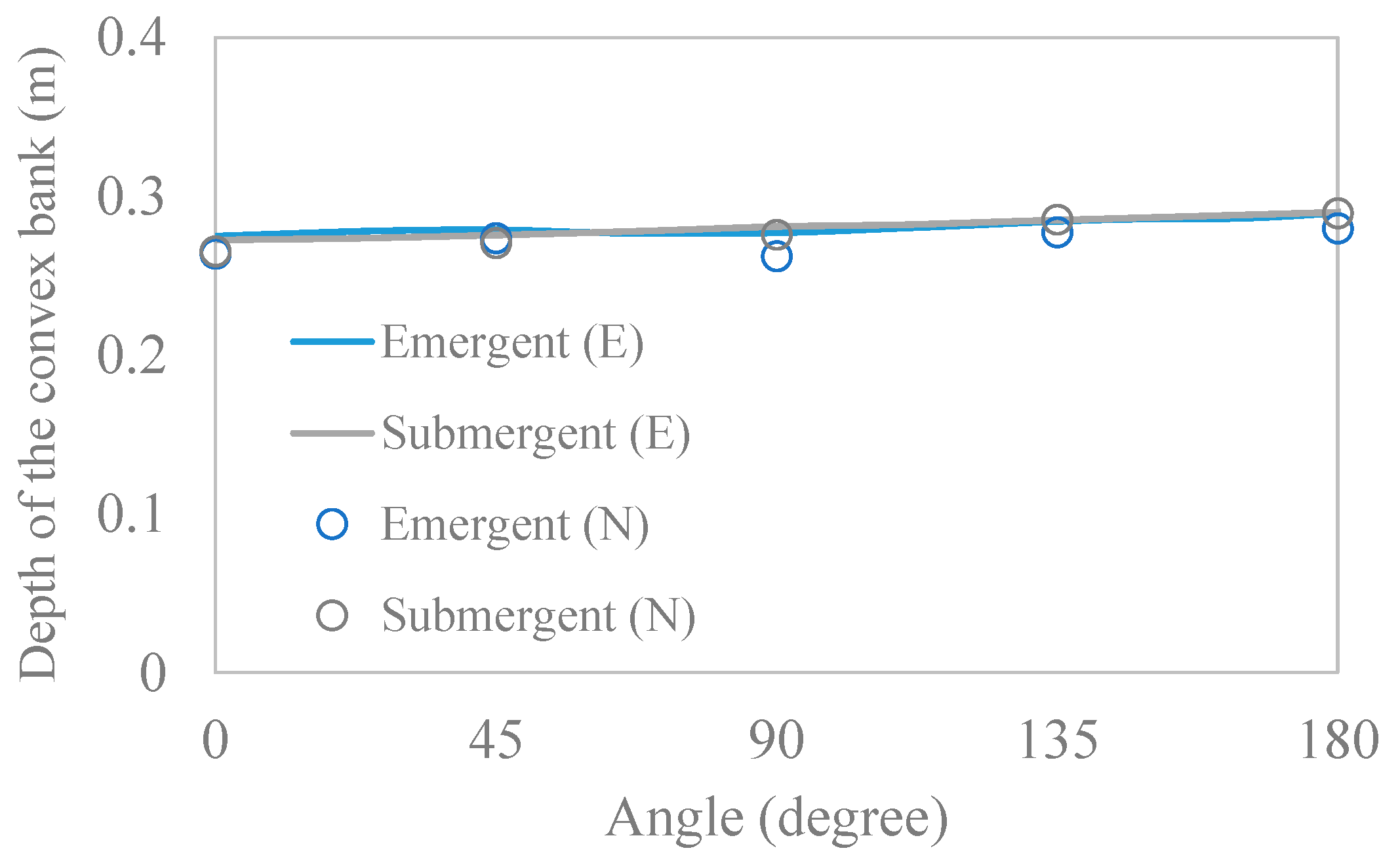
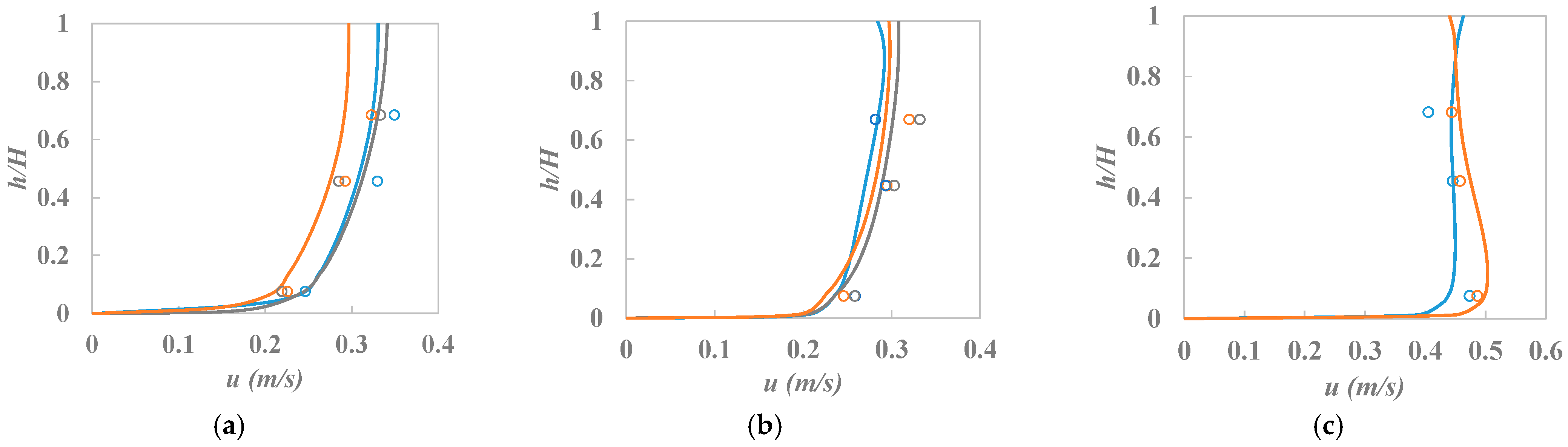
3.1. Model Calibration and Verification
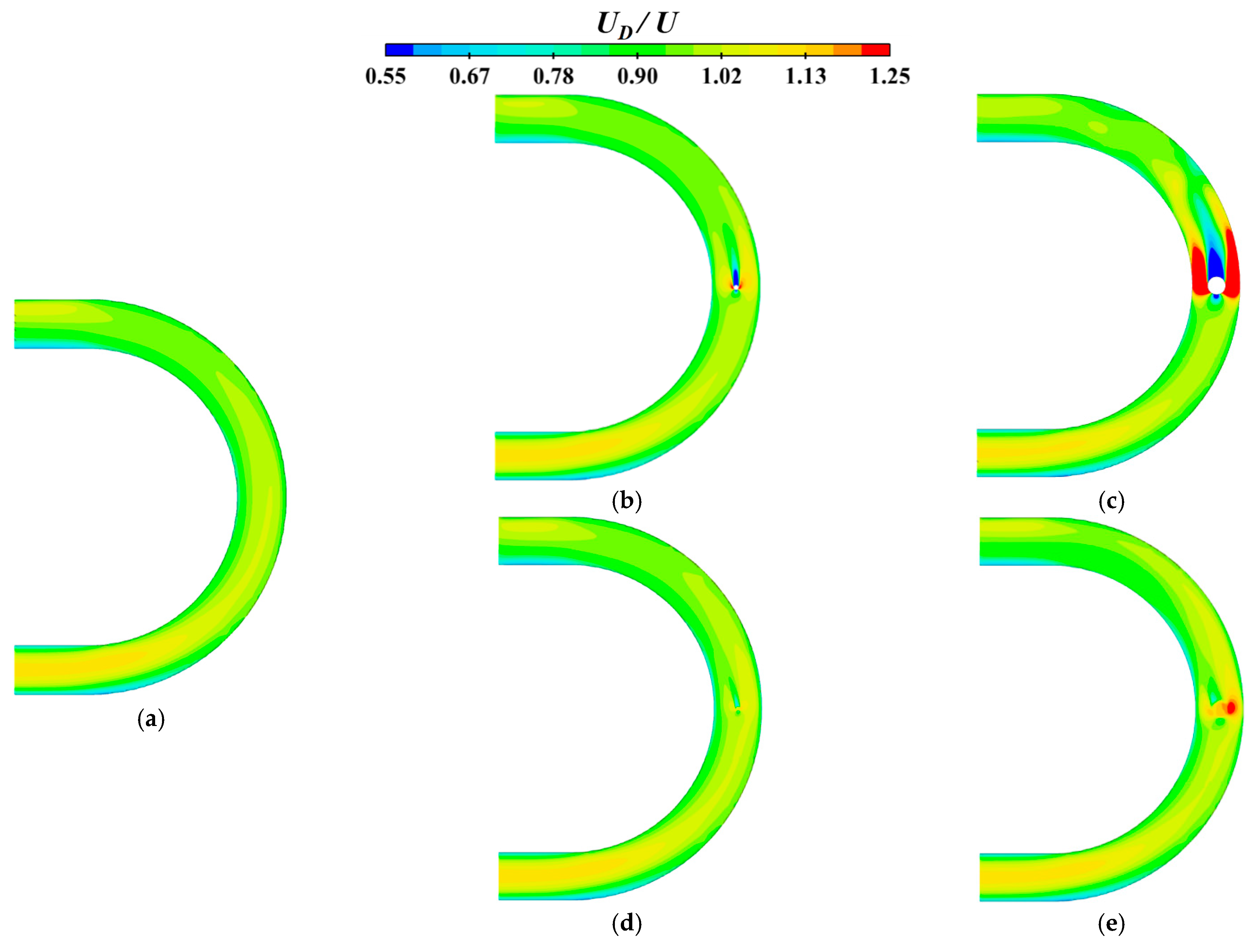
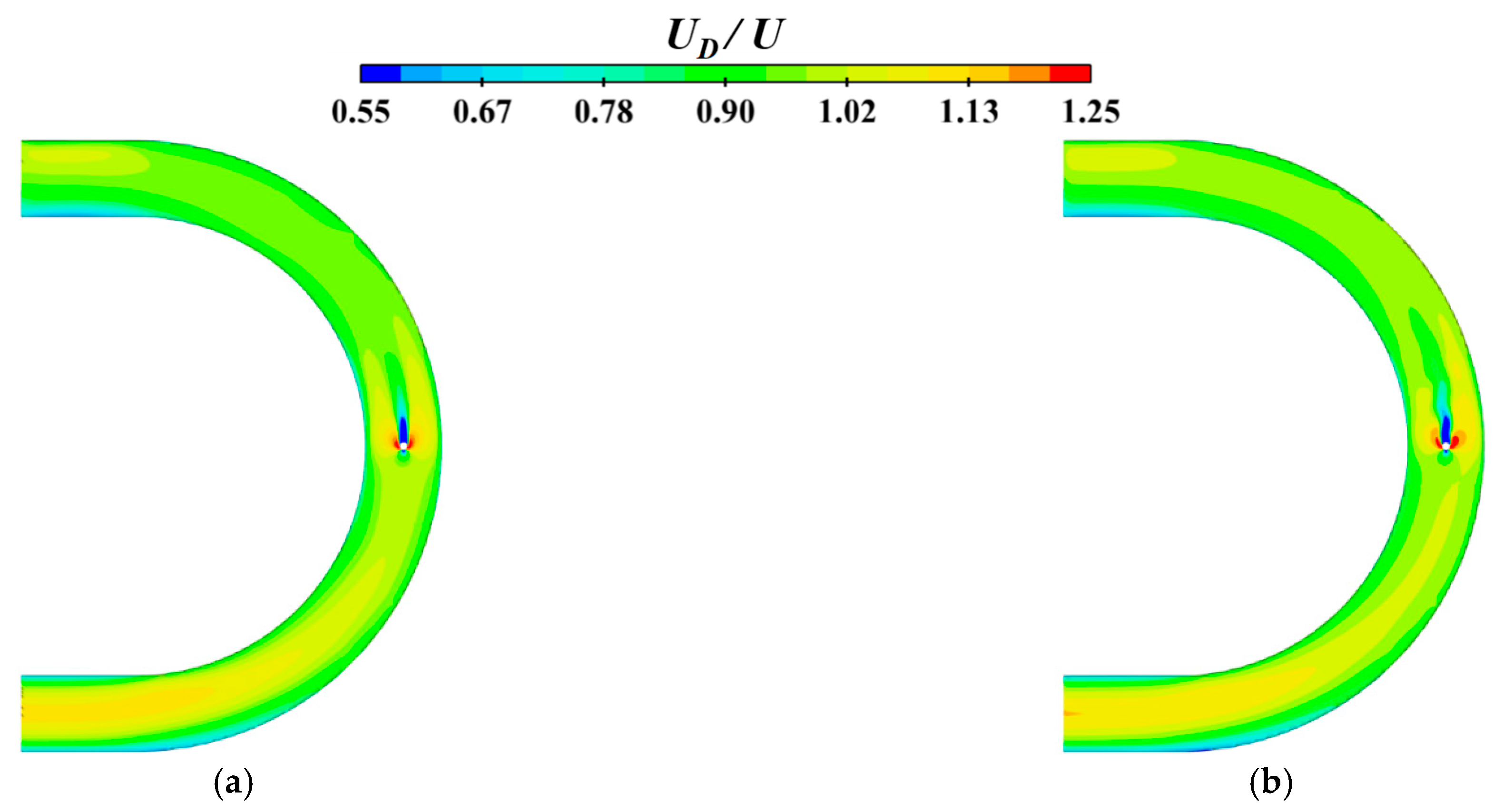
3.2. Distribution of Normalized Depth-Averaged Velocity over a Curved Channel
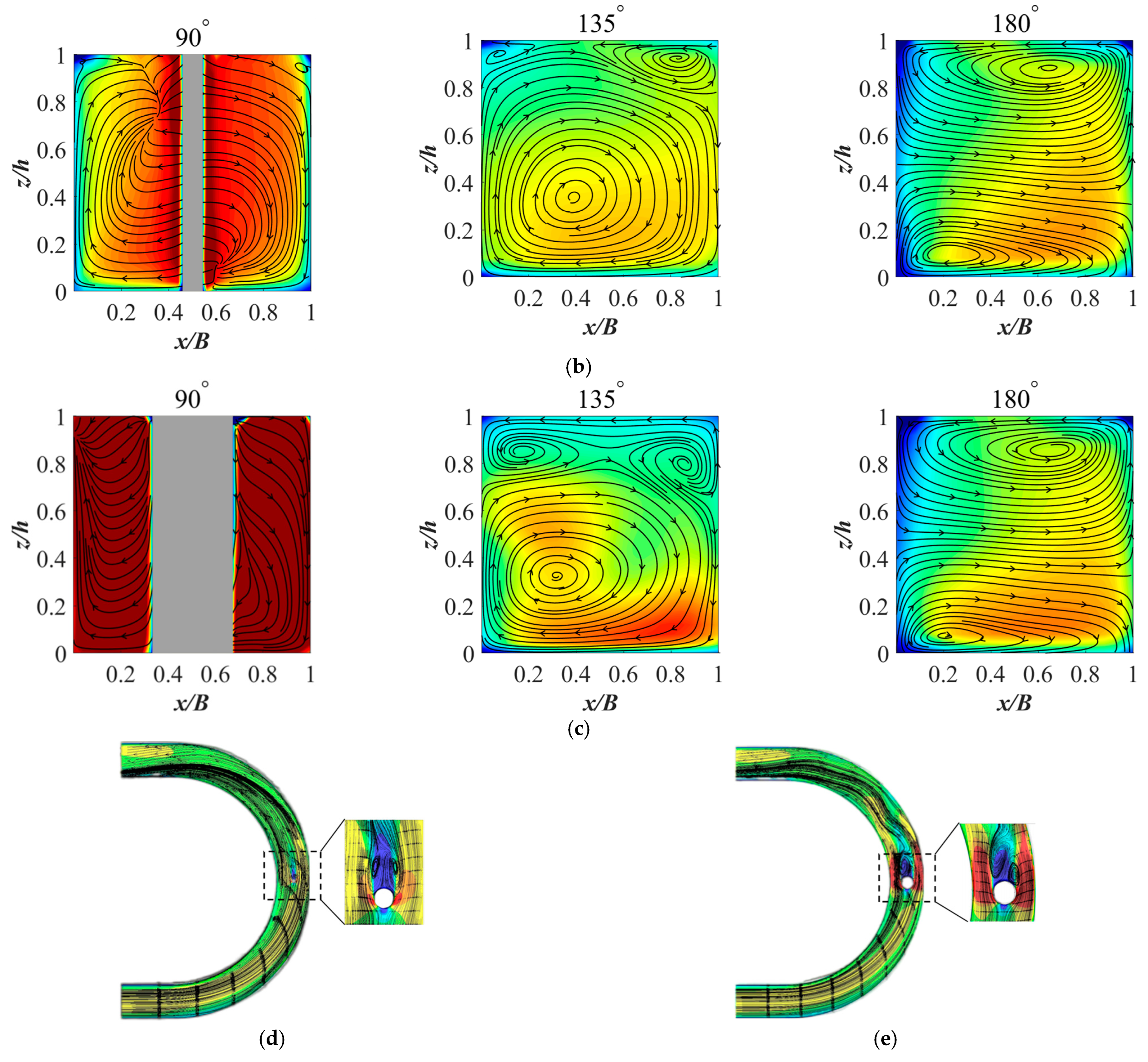
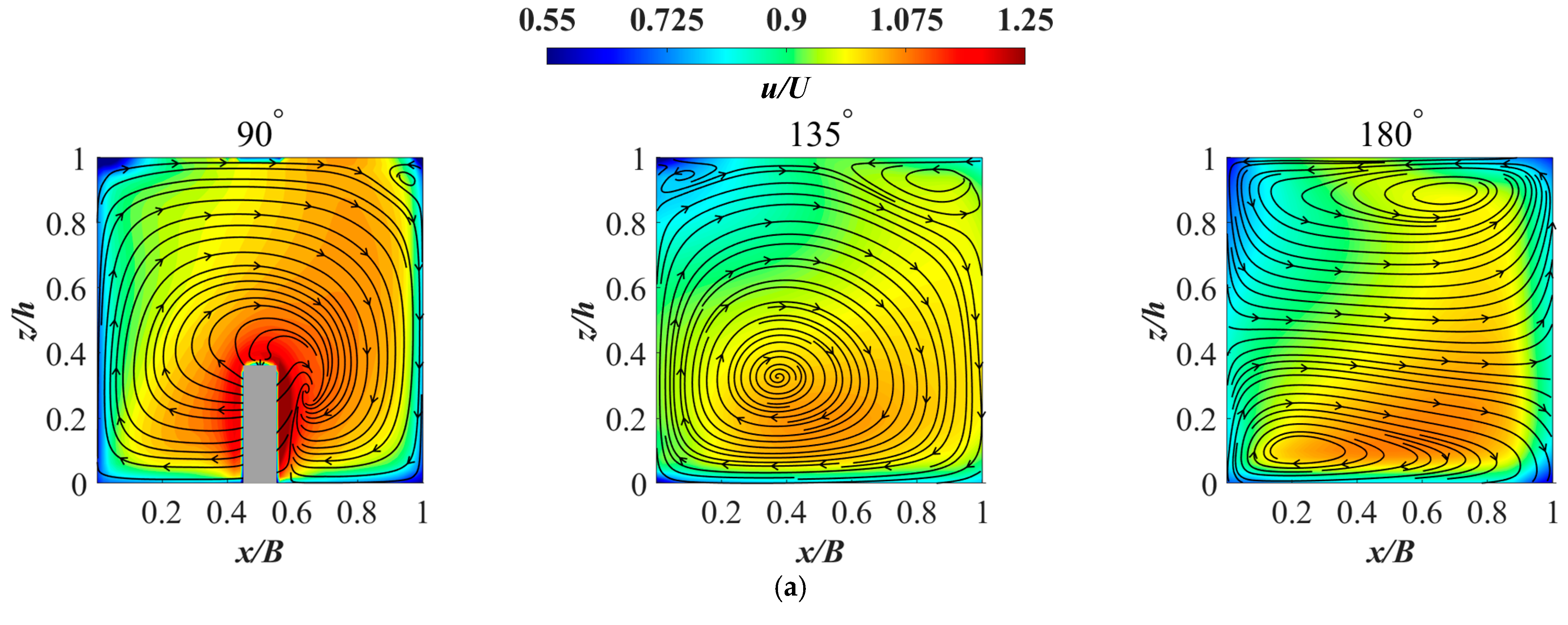
3.3. Streamwise Velocity and Circulation Distribution for Different Diameter of an Emergent Cylinder
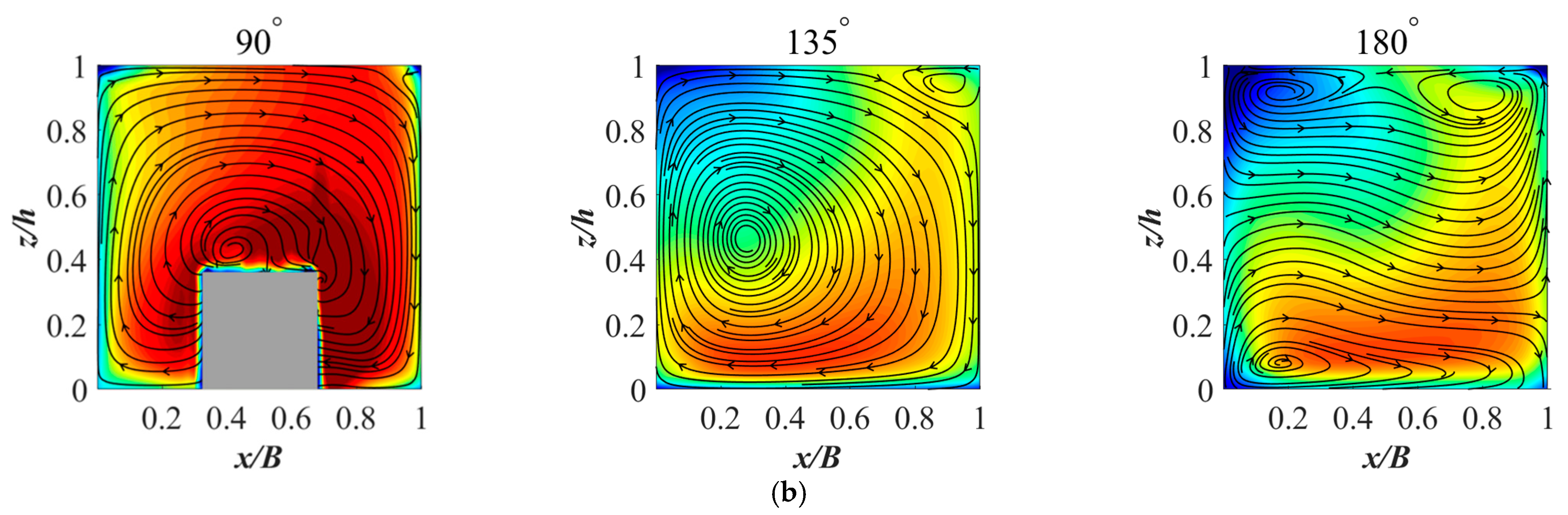
3.4. Streamwise Velocity and Circulation Distribution for Different Diameter of a Submerged Cylinder
3.5. Effect of Flowrate
3.6. Effect of Radius of Curvature
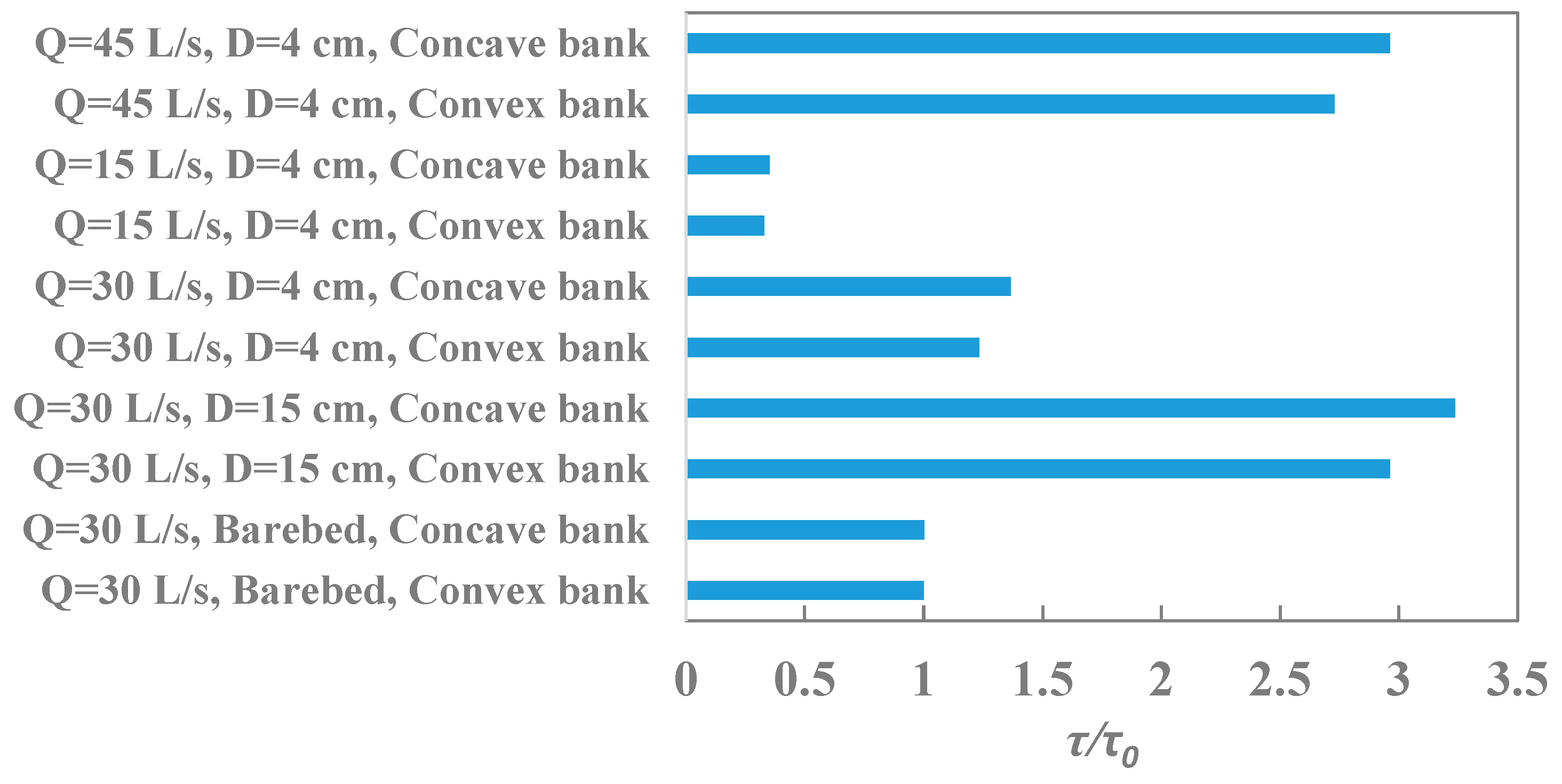
3.7. Shear Stress Acting on the Banks
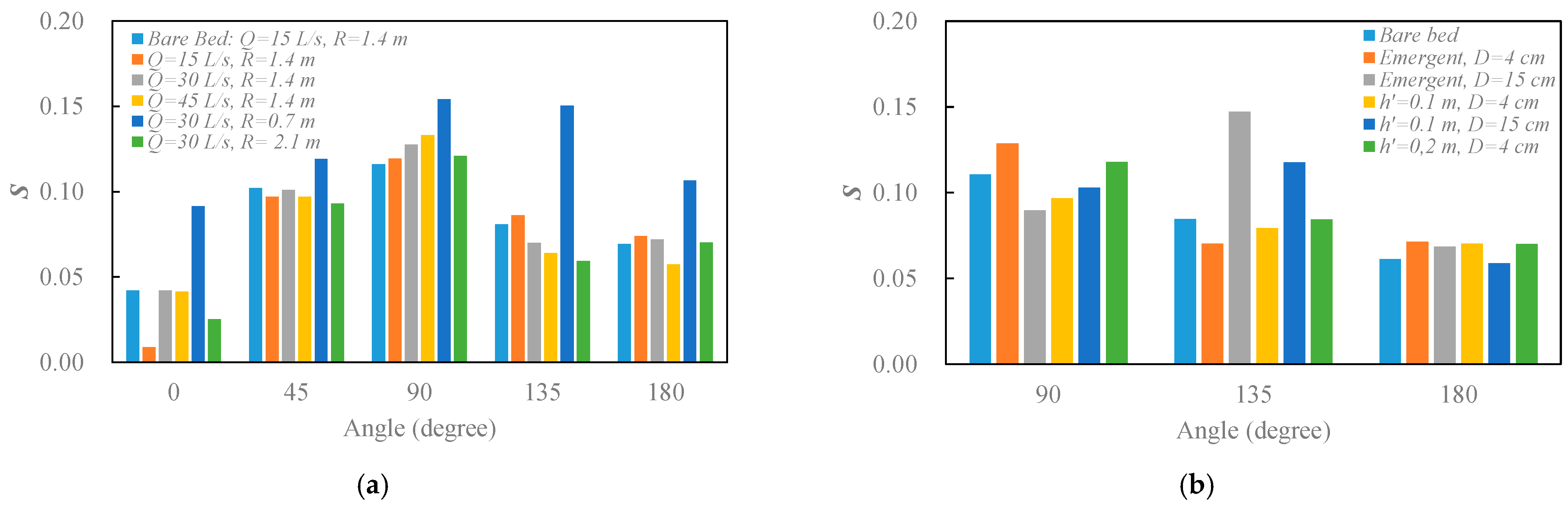
3.8. Strength of Secondary Flow
4. Conclusions
- The presence of a cylinder will change the hydrodynamic characteristics of the curved channel flow, which has a complex relationship with the diameter of the cylinder. A larger cylinder diameter leads to an overall greater streamwise velocity at the section in which the cylinder is placed, and also a greater increase in the streamwise velocity along the concave bank compared to that along the convex bank.
- When the diameter of the cylinder that is placed at the 90° section increases, the two weaker circulations with the same direction are found near the water surface, and for the submerged one, the two weaker circulations appear at the section further downstream than the emergent one.
- As the flowrate increases, the maximum streamwise velocity of the 90° section increases, and the streamwise velocity near the concave bank is also larger. In addition, the low-velocity regions behind the cylinder extend further downstream with an increase in the flowrate.
- The shear stress values on the concave bank are all greater than those on the convex bank for different conditions. The presence of a larger cylinder reduces the flow conveyance area and increases the flow velocity around the cylinder, elevating the shear stress acting on the bank. The degree of variation in the values is larger than that of the flowrate. Therefore, when a cylinder is placed over a curved channel, the changes in the shear stress acting on the banks should also be considered.
- As the flowrate increases or the radius of curvature decreases, the secondary flow intensity correspondingly elevates. When the flowrate is increased by 50%, the maximum secondary flow intensity is increased by 4.3%; on the other hand, when the radius of curvature is decreased by 50%, the maximum secondary flow intensity is elevated by 20.6%. These results reveal that the radius of curvature plays a more important role than the flowrate does. For both emergent and submergent cylinders, the large cylinder produces a greater secondary flow strength, approximately 14.4 to 21.7% for D (=15 cm)/D (=4 cm) at different cylinder submergence levels; however, the emergent one has a greater secondary flow strength than the submergent one by 25~33% depending on the cylinder diameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shaheed, R.; Mohammadian, A.; Yan, X. A review of numerical simulations of secondary flows in river bends. Water 2021, 13, 884. [Google Scholar] [CrossRef]
- Engelund, F. Flow and bed topography in channel bends. J. Hydraul. Div. Am. Soc. Civ. Eng. 1974, 100, 1631–1648. [Google Scholar] [CrossRef]
- Thomson, J. On the origin of windings of rivers in alluvial plains. Proc. Math. Phys. Eng. Sci. 1876, 25, 5–8. [Google Scholar]
- De Vriend, H.J.; Struiksma, N. Flow and bed deformation in river bends. In River Meandering; Elliot, C.M., Ed.; ASCE: New York, NY, USA, 1984; pp. 810–828. [Google Scholar]
- Odgaard, A.J. Meander flow model. I: Development. J. Hydraul. Eng. 1986, 112, 1117–1135. [Google Scholar] [CrossRef]
- Wang, M.; Avital, E.; Korakianitis, T.; Williams, J.; Ai, K. A numerical study on the influence of curvature ratio and vegetation density on a partially vegetated U-bend channel flow. Adv. Water Resour. 2021, 148, 103843. [Google Scholar] [CrossRef]
- Hsieh, T.-Y.; Yang, J.-C. Investigation on the suitability of two-dimensional depth-averaged models for bend-flow simulation. J. Hydraul. Eng. 2003, 129, 597–612. [Google Scholar] [CrossRef]
- Kashyap, S.; Constantinescu, G.; Rennie, C.D.; Post, G.; Townsend, R. Influence of channel aspect ratio and curvature on flow, secondary circulation, and bed shear stress in a rectangular channel bend. J. Hydraul. Eng. 2012, 138, 1045–1059. [Google Scholar] [CrossRef]
- Blanckaert, K.; Graf, W.H. Momentum transport in sharp open-channel bends. J. Hydraul. Eng. 2004, 130, 186–198. [Google Scholar] [CrossRef]
- Zeng, J.; Constantinescu, G.; Blanckaert, K.; Weber, L. Flow and bathymetry in sharp open-channel bends: Experiments and predictions. Water Resour. Res. 2008, 44, W09401. [Google Scholar] [CrossRef]
- van Balen, W.; Uijttewaal, W.S.J.; Blanckaert, K. Large-eddy simulation of a mildly curved open-channel flow. J. Fluid Mech. 2009, 630, 413–442. [Google Scholar] [CrossRef] [Green Version]
- Vaghefi, M.; Akbari, M.; Fiouz, A.R. An experimental study of mean and turbulent flow in a 180 degree sharp open channel bend: Secondary flow and bed shear stress. KSCE J. Civ. Eng. 2016, 20, 1582–1593. [Google Scholar] [CrossRef]
- Masjedi, A.; Bejestan, M.S.; Efsandi, A. Reduction of local scour at a bridge pier fitted with a collar in a 180 degree flume bend. J. Hydrodynam. B 2010, 22, 646–650. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Fazli, M.; Ghodsian, M.; Salehi Neyshabouri, S.A.A. Scour and flow field around a spur dike in a 90° bend. Int. J. Sediment. Res. 2008, 23, 56–68. [Google Scholar] [CrossRef]
- Vaghefi, M.; Ghodsian, M.; Salehi Neyshabouri, S.A.A. Experimental study on scour around a T-shaped spur dike in a channel bend. J. Hydraul. Eng. 2012, 136, 498–509. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, Y.T.; Ji, X.Y. Hydrodynamic characteristics of flow over emergent vegetation in a strongly curved channel. J. Hydraul. Res. 2021, 3, 240–257. [Google Scholar] [CrossRef]
- Sadeque, M.A.; Rajaratnam, N.; Loewen, M.R. Flow around cylinders in open channels. J. Hydraul. Eng. 2008, 134, 60–71. [Google Scholar] [CrossRef]
- Korkmaz, M.; Emiroglu, M.E. Local scour at a bridge abutment along a curved channel. In Institution of Civil Engineers-Bridge Engineering; ICE Publishing: London, UK, 2022. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, B.; Chen, X.; Wang, X.; Liu, J. Modeling and experimental study of a piezoelectric energy harvester from vortex shedding-induced vibration. Energy Convers. Manag. 2018, 162, 145–158. [Google Scholar] [CrossRef]
- Latif, U.; Uddin, E. Experimental investigation of energy harvesting in the wake of a bluff body. J. Renew. Sustain. Ener. 2020, 12, 033301. [Google Scholar] [CrossRef]
- Envelope, I.; Madaro, F.; Rizzi, F.; Vittorio, M.D. Comprehensive experimental study on bluff body shapes for vortex-induced vibration piezoelectric energy harvesting mechanisms. Energy Convers. Manag. X 2022, 13, 100174. [Google Scholar] [CrossRef]
- Moussaed, C.; Salvetti, M.V.; Wornom, S.; Koobus, B.; Dervieux, A. Simulation of the flow past a circular cylinder in the supercritical regime by blending RANS and variational-multiscale LES models. J. Fluids Struc. 2014, 47, 114–123. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Cheng, L. Large-eddy simulation of flow past a circular cylinder for Reynolds numbers 400 to 3900. Phys. Fluids 2021, 33, 034119. [Google Scholar] [CrossRef]
- Catalano, P.; Wang, M.; Iaccarino, G.; Moin, P. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers. Int. J. Heat Fluid Flow 2003, 24, 463–469. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, C. Numerical analysis of the flow around a circular cylinder using RANS and LES. Int. J. Comut. Fluid Dyn. 2006, 20, 301–307. [Google Scholar] [CrossRef]
- Stoesser, T.; Ruether, N.; Reidar, N.; Olsen, B. Calculation of primary and secondary flow and boundary shear stresses in a meandering channel. Adv. Water Resour. 2010, 33, 158–170. [Google Scholar] [CrossRef]
- Kraus, N.C.; Lohrmann, A.; Cabrera, R. New acoustic meter for measuring 3D laboratory flows. J. Hydraul. Eng. 1994, 120, 406–412. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Hirt, C.W. Volume-fraction techniques: Power tools for wind engineering. J. Wind Eng. Ind. Aerodyn. 1993, 46–47, 327–338. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Glatzel, T.; Litterst, C.; Cupelli, C.; Lindemann, T.; Moosmann, C.; Niekrawietz, R.; Streule, W.; Zengerle, R.; Koltay, P. Computational fluid dynamics (CFD) software tools for microfluidic applications—A case study. Comput. Fluids 2008, 37, 218–235. [Google Scholar] [CrossRef]
- Wang, S.; Yang, S.; He, Z.; Li, L.; Xia, Y. Effect of inclination angles on the local scour around a submerged cylinder. Water 2020, 12, 2687. [Google Scholar] [CrossRef]
- Zhou, J.; Venayagamoorthy, S.K. Impact of ambient stable stratification on gravity currents propagating over a submerged canopy. J. Fluid Mech. 2020, 898, A15. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Ye, Y.-Q.; Han, D.-R.; Chiu, Y.-J. Propagation and Separation of Downslope Gravity Currents over Rigid and Emergent Vegetation Patches in Linearly Stratified Environments. J. Mar. Sci. Eng. 2022, 10, 308. [Google Scholar] [CrossRef]
- Zhou, J.; Venayagamoorthy, S.K. Numerical simulations of intrusive gravity currents interacting with a bottom-mounted obstacle in a continuously stratified ambient. Environ. Fluid. Mech. 2017, 17, 191–209. [Google Scholar] [CrossRef]
- Vaghefi, M.; Faraji, B.; Akbari, M.; Eghbalzadeh, A. Numerical investigation of flow pattern around a T-shaped spur dike in the vicinity of attractive and repelling protective structures. J. Braz. Soc. Mech. Sci. 2018, 40, 93. [Google Scholar] [CrossRef]
- Qamar, M.Z.; Verma, M.K.; Meshram, A.P.; Isaac, N. Numerical simulation of desilting chamber using Flow 3D. In River and Coastal Engineering; Water Science and Technology Library; Jha, R., Singh, V.P., Singh, V., Roy, L., Thendiyath, R., Eds.; Springer: Cham, Switzerland, 2022; p. 117. [Google Scholar] [CrossRef]
- Bai, Y.; Song, X.; Gao, S. Efficient investigation on fully developed flow in a mildly curved 180° open-channel. J. Hydroinform. 2014, 16, 1250–1264. [Google Scholar] [CrossRef]
- Gholami, A.; Akhtari, A.A.; Minatour, Y.; Bonakdari, H.; Javadi, A.A. Experimental and numerical study on velocity fields and water surface profile in a strongly-curved 90 degrees open channel bend. Eng. Appl. Comp. Fluid Mech. 2014, 8, 447–461. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-T.; Yang, Y.; Chiu, Y.-J.; Ji, X. Hydrodynamic characteristics of flow in a strongly curved channel with gravel beds. Water 2021, 13, 1519. [Google Scholar] [CrossRef]
- Shukry, A. Flow around bends in an open flume. Trans. Am. Soc. Civil Eng. 1950, 115, 751–788. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Hua, Y.; He, M.; Lin, Y.-T.; Sheng, B. Effect of a Circular Cylinder on Hydrodynamic Characteristics over a Strongly Curved Channel. Sustainability 2023, 15, 4890. https://doi.org/10.3390/su15064890
Jiang S, Hua Y, He M, Lin Y-T, Sheng B. Effect of a Circular Cylinder on Hydrodynamic Characteristics over a Strongly Curved Channel. Sustainability. 2023; 15(6):4890. https://doi.org/10.3390/su15064890
Chicago/Turabian StyleJiang, Shu, Yutong Hua, Mengxing He, Ying-Tien Lin, and Biyun Sheng. 2023. "Effect of a Circular Cylinder on Hydrodynamic Characteristics over a Strongly Curved Channel" Sustainability 15, no. 6: 4890. https://doi.org/10.3390/su15064890
APA StyleJiang, S., Hua, Y., He, M., Lin, Y.-T., & Sheng, B. (2023). Effect of a Circular Cylinder on Hydrodynamic Characteristics over a Strongly Curved Channel. Sustainability, 15(6), 4890. https://doi.org/10.3390/su15064890








