Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost
Abstract
1. Introduction
2. Literature Review
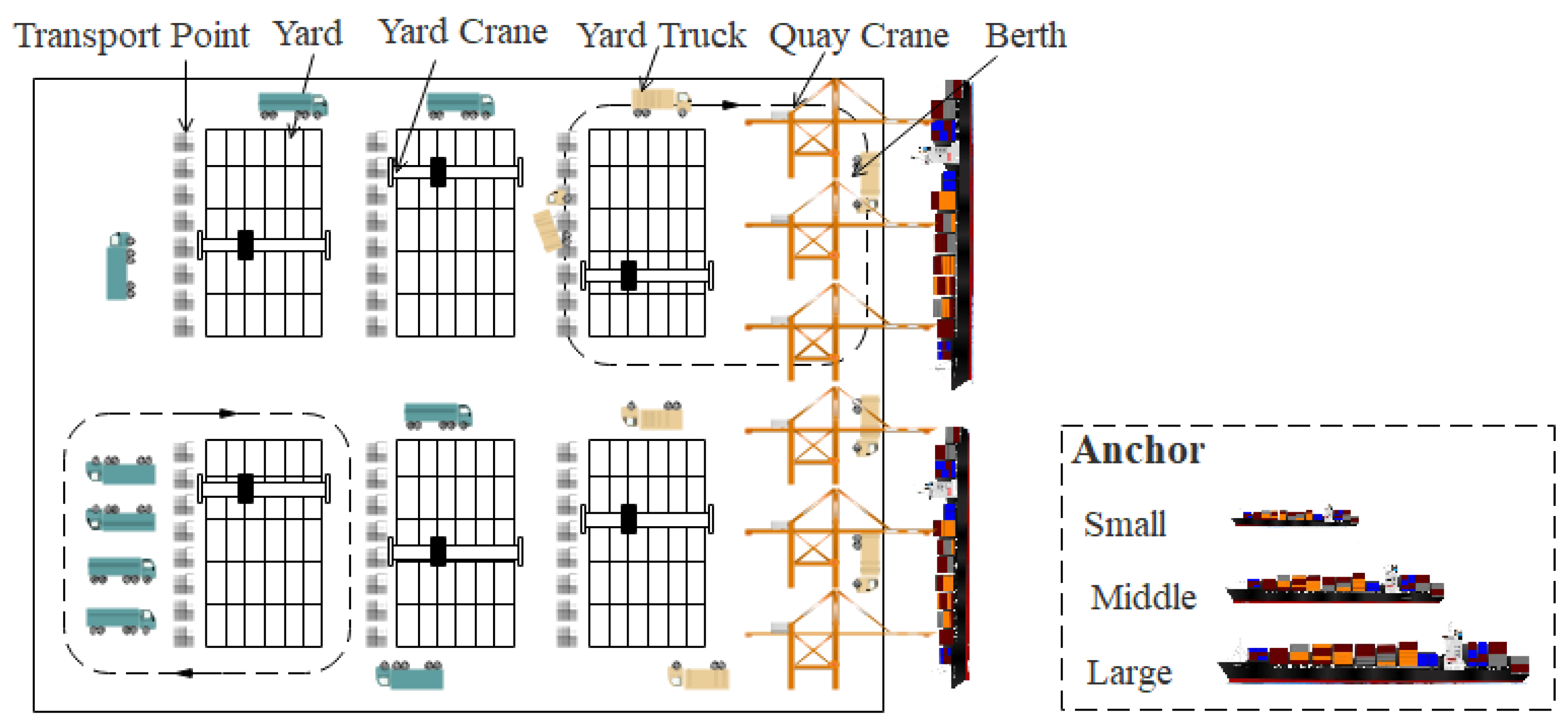
3. Problem Description and Formulation
3.1. Model Assumptions and Notation
- Berths are uninterrupted and vessels may dock at any point along the quay, provided that they meet the necessary requirements;
- Terminals have different water depths, and vessels can only berth at terminals that meet their draft;
- All quay cranes on the same terminal are located on the same track and cannot change or serve across terminals;
- The minimum and maximum number of quay cranes for each vessel are required, and the actual operational efficiency of the quay cranes will decrease when multiple quay cranes are working on the same vessel together.
| Type | Symbol | Definition |
|---|---|---|
| Constants | Set of terminals, | |
| Set of vessels to be scheduled, | ||
| Set of vessels berthed before planning period, | ||
| Set of quay cranes at the terminal , , | ||
| Set of samples; each represents the actual arrival time, the quay crane operational efficiency and the actual departure time, | ||
| Length of quay at the terminal , | ||
| Water depth at the terminal , | ||
| Expected operational efficiency of quay cranes at the terminal , | ||
| Interference factor between quay cranes | ||
| Length of the berthed vessel , including safety distance, | ||
| Berthing position of the berthed vessel , | ||
| If the berthing terminal of the berthed vessel is , ; otherwise, , , | ||
| Number of unfinished containers for the berthed vessel , | ||
| If the quay crane located at terminal serves the berthed vessel , ; otherwise, , , , | ||
| Length of the vessel , including safety distance, | ||
| If the pre-assigned terminal of the vessel is , ; otherwise, , , | ||
| Number of containers exported on the vessel , | ||
| Number of containers imported on the vessel , | ||
| Expected arrival time of the vessel , | ||
| Expected departure time of the vessel , | ||
| Minimum number of quay cranes assigned to the vessel , | ||
| Maximum number of quay cranes assigned to the vessel , | ||
| Draft of the vessel , | ||
| Desired berthing position of the vessel at its pre-assigned terminal, | ||
| Deviation cost per meter between vessel’s berthing position and its desired position | ||
| Operation costs per hour for a quay crane | ||
| Transshipment costs per container from terminal to terminal , | ||
| Penalty cost per hour when the actual departure time of vessel exceeds its expected departure time, | ||
| Waiting cost per hour when actual arrival time earlier than scheduling berthing time | ||
| Penalty cost per hour when actual arrival time later than scheduling berthing time | ||
| A sufficiently large positive number |
| Type | Symbol | Definition |
|---|---|---|
| Decision variables | If the berthing terminal of vessel is , ; otherwise, , , | |
| Berthing position of vessel , | ||
| Berthing time of vessel , | ||
| If the quay crane at terminal serves the vessel , ; otherwise, , , , | ||
| Auxiliary decision variables | Relaxation with arrival times of vessel , | |
| Relaxation with the operational efficiency of quay crane serving vessel , | ||
| Number of quay crane serving vessel , | ||
| Scheduling departure time of vessel | ||
| If the vessel berths after the departure time of vessel , ; otherwise, , , | ||
| If the vessel berths to the right of vessel , ; otherwise, , , | ||
| If the vessel berths after the departure time of berthed vessel , ; otherwise,, , | ||
| If the vessel berths to the right of berthed vessel , ; otherwise, , , | ||
| If the vessel berths to the left of berthed vessel , ; otherwise, , , |
3.2. Cost of Carbon Calculation
3.3. Objective Function
3.4. Constraints
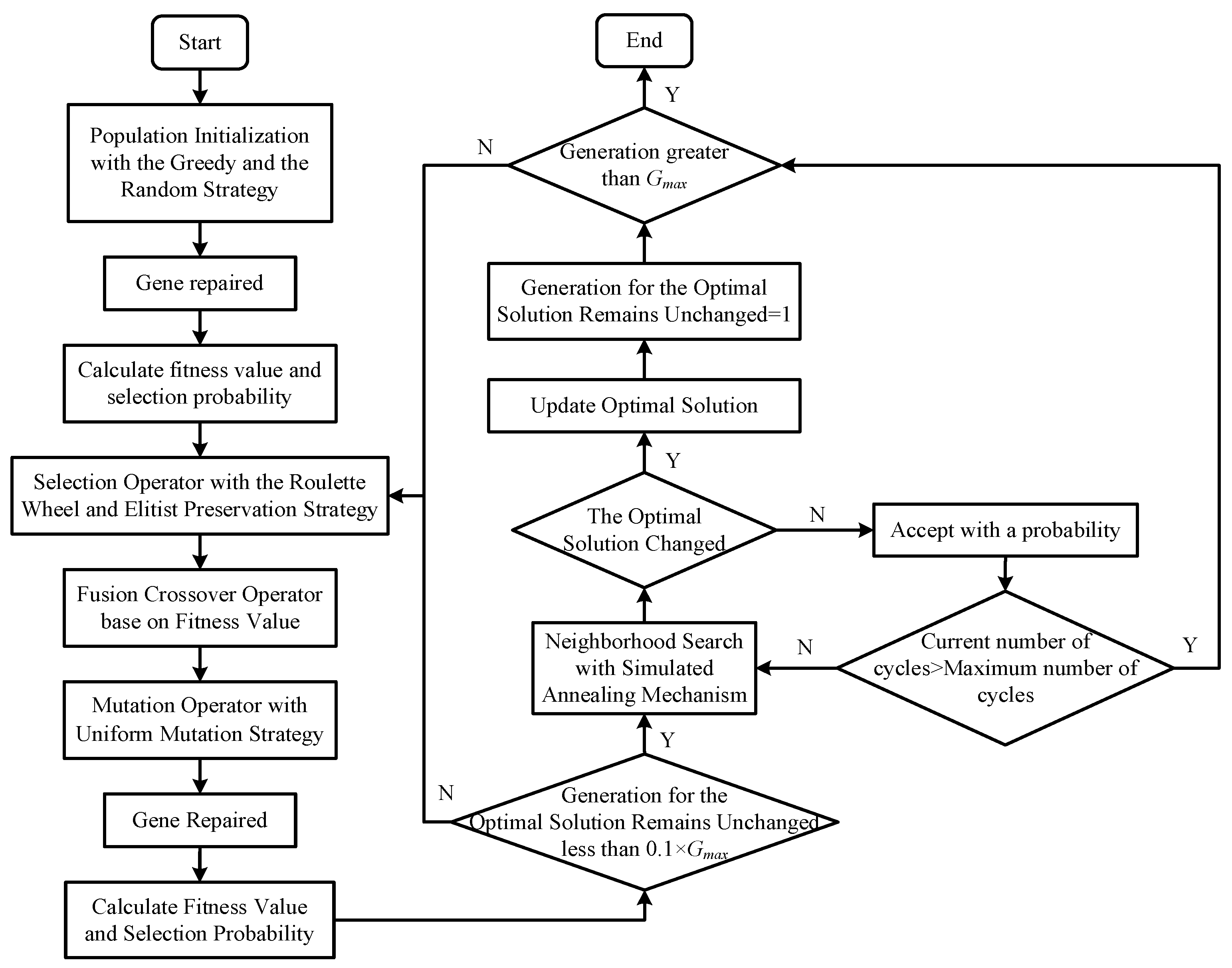
4. Solution Method
4.1. Encoding & Decoding Rules
4.2. Population Initialization
4.3. Gene Repair Method
4.4. Fitness Function and Genetic Operations
4.5. The Simulated Annealing Mechanism
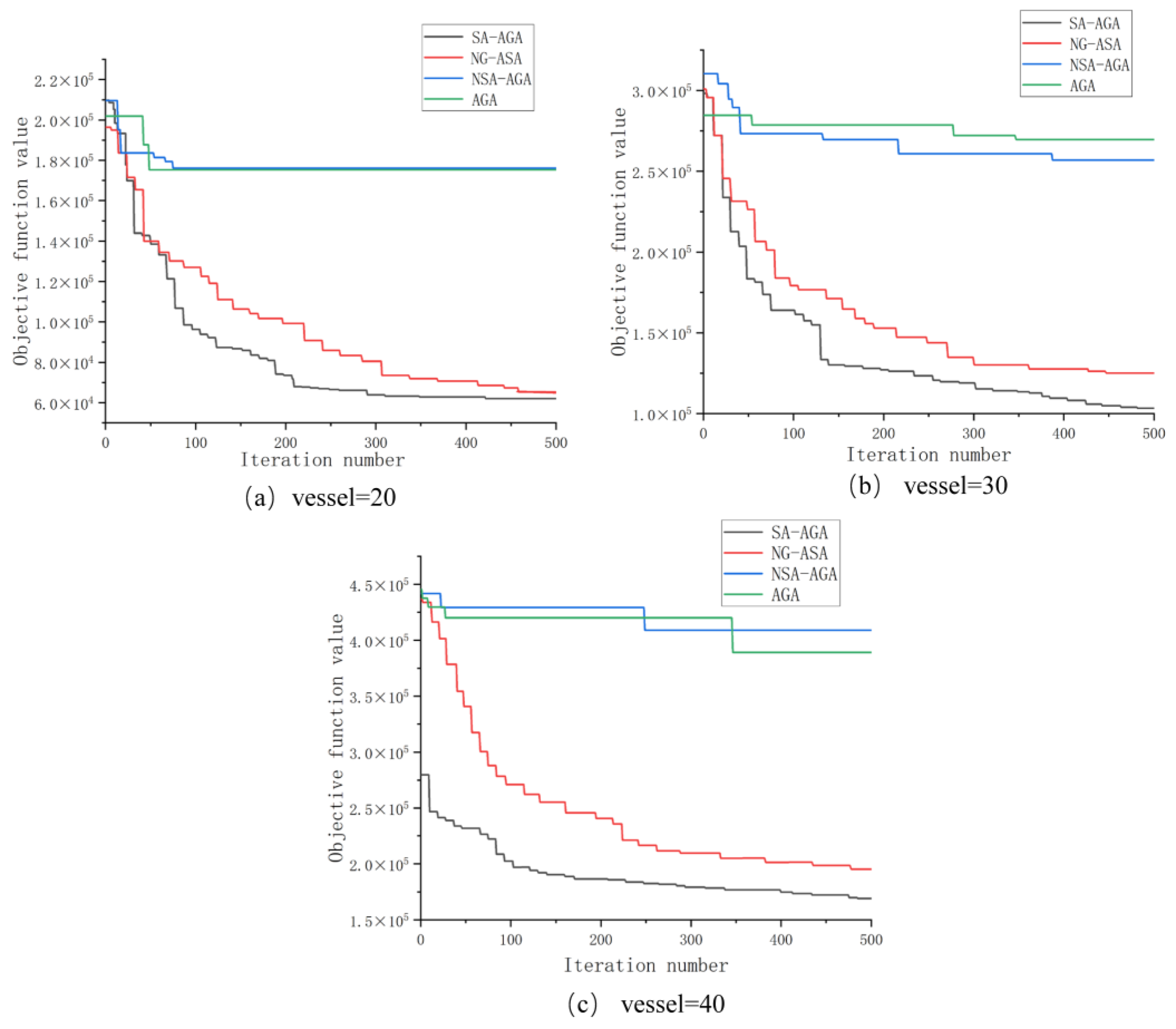
4.6. Analysis of Algorithm Effectiveness
5. Numerical Experiments
5.1. Parameter Design
5.1.1. Terminal Parameters Design
5.1.2. Vessel Parameters Design
5.1.3. Algorithm Parameters Design
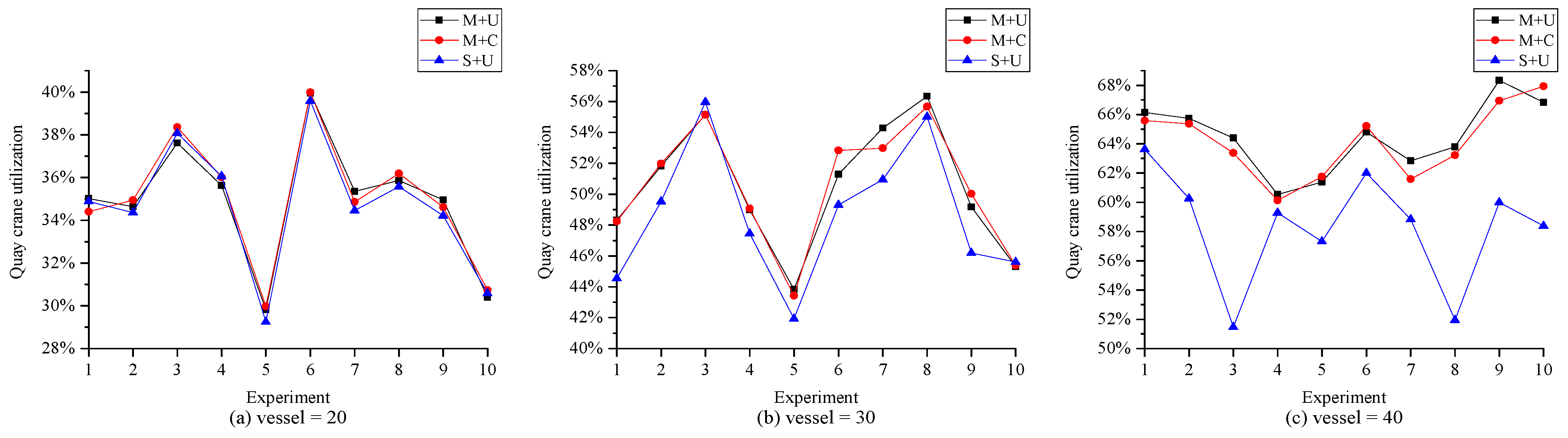
5.2. Results and Analysis
6. Conclusions and Future Work
- (1)
- The quay crane allocation problem studied in this paper is static. However, if the quay crane can be used for other vessels before the vessel it is serving departs (dynamic quay crane allocation problem), the utilization of the quay crane can be greatly improved. Therefore, this restriction can be introduced into the model in subsequent research.
- (2)
- This paper assumes that the quay crane can reach anywhere along the quay. However, in the actual operation of a container port, the quay cranes can only move within a fixed area. Therefore, we need to take it into account in future studies to make the model more realistic and feasible.
- (3)
- The scope of this paper is limited to addressing the berth allocation problem and quay crane allocation problem in container port operations. However, there are many other processes involved, such as container truck scheduling, storage allocation, and yard crane scheduling. These processes are interlinked and interdependent. Therefore, more processes need to be included in the study to obtain a more feasible scheduling solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Frojan, P.; Francisco Correcher, J.; Alvarez-Valdes, R.; Koulouris, G.; Manuel Tamarit, J. The continuous Berth Allocation Problem in a container terminal with multiple quays. Expert Syst. Appl. 2015, 42, 7356–7366. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- De, A.; Pratap, S.; Kumar, A.; Tiwari, M.K. A hybrid dynamic berth allocation planning problem with fuel costs considerations for container terminal port using chemical reaction optimization approach. Ann. Oper. Res. 2020, 290, 783–811. [Google Scholar] [CrossRef]
- Al-Refaie, A.; Abedalqader, H. Optimal berth allocation under regular and emergent vessel arrivals. Proc. Inst. Mech. Eng. Part M-J. Eng. Marit. Environ. 2021, 235, 642–656. [Google Scholar] [CrossRef]
- Wawrzyniak, J.; Drozdowski, M.; Sanlaville, E. Selecting algorithms for large berth allocation problems. Eur. J. Oper. Res. 2020, 283, 844–862. [Google Scholar] [CrossRef]
- Abou Kasm, O.; Diabat, A. Next-generation quay crane scheduling. Transp. Res. Part C-Emerg. Technol. 2020, 114, 694–715. [Google Scholar] [CrossRef]
- Lv, X.; Jin, J.G.; Hu, H. Berth allocation recovery for container transshipment terminals. Marit. Policy Manag. 2020, 47, 558–574. [Google Scholar] [CrossRef]
- Jia, S.; Li, C.-L.; Xu, Z. A simulation optimization method for deep-sea vessel berth planning and feeder arrival scheduling at a container port. Transp. Res. Part B-Methodol. 2020, 142, 174–196. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An expanded robust optimisation approach for the berth allocation problem considering uncertain operation time. Omega-Int. J. Manag. Sci. 2021, 103, 102444. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. Berth allocation and quay crane assignment/scheduling problem under uncertainty: A survey. Eur. J. Oper. Res. 2022, 303, 501–524. [Google Scholar] [CrossRef]
- Cao, J.; Shi, Q.; Der-Horng, L. Integrated Quay Crane and Yard Truck Schedule Problem in Container Terminals. Tsinghua Sci. Technol. 2010, 15, 467–474. [Google Scholar] [CrossRef]
- Safaei, N.; Bazzazi, M.; Assadi, P. An integrated storage space and berth allocation problem in a container terminal. Int. J. Math. Oper. Res. 2010, 2, 674–693. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, N.; de Waal, A.; Negenborn, R.R. Coordinated optimization of equipment operations in a container terminal. Flex. Serv. Manuf. J. 2021, 33, 281–311. [Google Scholar] [CrossRef]
- Agra, A.; Oliveira, M. MIP approaches for the integrated berth allocation and quay crane assignment and scheduling problem. Eur. J. Oper. Res. 2018, 264, 138–148. [Google Scholar] [CrossRef]
- Li, Y.; Chu, F.; Zheng, F.F.; Kacem, I. Integrated berth allocation and quay crane assignment with uncertain maintenance activities. In Proceedings of the International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019; pp. 248–253. [Google Scholar]
- Chargui, K.; Zouadi, T.; El Fallahi, A.; Reghioui, M.; Aouam, T. Berth and quay crane allocation and scheduling with worker performance variability and yard truck deployment in container terminals. Transp. Res. Part E-Logist. Transp. Rev. 2021, 154, 102449. [Google Scholar] [CrossRef]
- Ji, B.; Huang, H.; Samson, S.Y. An Enhanced NSGA-II for Solving Berth Allocation and Quay Crane Assignment Problem with Stochastic Arrival Times. IEEE Trans. Intell. Transp. Syst. 2022, 24, 459–473. [Google Scholar] [CrossRef]
- Tang, M.; Ji, B.; Fang, X.; Yu, S.S. Discretization-Strategy-Based Solution for Berth Allocation and Quay Crane Assignment Problem. J. Mar. Sci. Eng. 2022, 10, 495. [Google Scholar] [CrossRef]
- Zhen, L.; Chang, D.-F. A bi-objective model for robust berth allocation scheduling. Comput. Ind. Eng. 2012, 63, 262–273. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Miao, L. Reactive strategy for discrete berth allocation and quay crane assignment problems under uncertainty. Comput. Ind. Eng. 2018, 126, 196–216. [Google Scholar] [CrossRef]
- Iris, C.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B-Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Rodrigues, F.; Agra, A. An exact robust approach for the integrate d b erth allocation and quay crane scheduling problem under uncertain arrival times. Eur. J. Oper. Res. 2021, 295, 499–516. [Google Scholar] [CrossRef]
- Prayogo, D.N. Carbon emission modelling in container terminal operations planning using a system dynamics approach. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 703, p. 012014. [Google Scholar] [CrossRef]
- Sun, Q.; Zhen, L.; Xiao, L.; Tan, Z. Recoverable Robustness Considering Carbon Tax in Weekly Berth and Quay Crane Planning. In Proceedings of the 6th KES Annual International Conference on Smart Education and e-Learning (KES SEEL)/2nd KES International Symposium on Smart Transportation Systems (KES-STS), St. Julian’s, Malta, 17–19 June 2019; pp. 75–84. [Google Scholar]
- Lin, S.; Zhen, L.; Wang, W.; Tan, Z. Green berth and yard space allocation under carbon tax policy in tidal ports. In Maritime Policy & Management; Taylor & Francis: Abingdon, UK, 2022. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.; Reinau, K.H. Energy-Efficient and Integrated Allocation of Berths, Quay Cranes, and Internal Trucks in Container Terminals. Sustainability 2020, 12, 3202. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S. Berthing ships at a multi-user container terminal with a limited quay capacity. Transp. Res. Part E-Logist. Transp. Rev. 2008, 44, 136–151. [Google Scholar] [CrossRef]
- Krimi, I.; Benmansour, R.; El Cadi, A.A.; Deshayes, L.; Duvivier, D.; Elhachemi, N. A rolling horizon approach for the integrated multi-quays berth allocation and crane assignment problem for bulk ports. Int. J. Ind. Eng. Comput. 2019, 10, 577–591. [Google Scholar] [CrossRef]
- Bouzekri, H.; Alpan, G.; Giard, V. Integrated Laycan and Berth Allocation and time-invariant Quay Crane Assignment Problem in tidal ports with multiple quays. Eur. J. Oper. Res. 2021, 293, 892–909. [Google Scholar] [CrossRef]
- Martin-Iradi, B.; Pacino, D.; Ropke, S. The Multiport Berth Allocation Problem with Speed Optimization: Exact Methods and a Cooperative Game Analysis. Transp. Sci. 2022, 56, 972–999. [Google Scholar] [CrossRef]
- Jiang, M.; Zhou, J.; Feng, J.; Zhou, L.; Ma, F.; Wu, G. Integrated Berth and Crane Scheduling Problem Considering Crane Coverage in Multi-Terminal Tidal Ports under Uncertainty. J. Mar. Sci. Eng. 2022, 10, 506. [Google Scholar] [CrossRef]
- Han, X.-L.; Lu, Z.-Q.; Xi, L.-F. A proactive approach for simultaneous berth and quay crane scheduling problem with stochastic arrival and handling time. Eur. J. Oper. Res. 2010, 207, 1327–1340. [Google Scholar] [CrossRef]
- Beasley, J.E.; Chu, P.C. A genetic algorithm for the set covering problem. Eur. J. Oper. Res. 1996, 94, 392–404. [Google Scholar] [CrossRef]



| The Gene Repair Method: | |
|---|---|
| If the water depth of the terminal where the vessel berths is less than its draft for any vessel , then reselect the its berthing terminal; | |
| Obtain the set of vessels that have already been scheduled and the set of vessels that are planned to schedule for each terminal . Then, sort them according to the increasing order of the vessels’ berthing time; | |
| Let the set of vessels that have already berthed when scheduling be an empty set , and consider the first vessel in the set as the currently scheduled vessel. For any vessel , if its actual departure time is greater than the berthing time of the currently scheduled vessel , add the vessel to the set ; | |
| To schedule , determine the set of unoccupied quay segments based on the berthing position , length , assigned quay cranes , and the serial number of the first assigned quay crane for all vessels in the set ; | |
| Let the set of available idle quay segments when scheduling be an empty set . For each idle quay segment in the set , if its length is greater than the length of the currently scheduled vessel and the number of available quay cranes is greater than the minimum number of quay cranes required for the currently scheduled vessel, then add the idle quay segment to the set ; | |
| If the set of available idle segments is empty, modify the berthing time of the currently scheduled vessel to the minimum departure time for all vessels in set , and turn to ; | |
| If the quay segment occupied by the currently scheduled vessel is within any available idle quay segment in the set , meaning and , where and indicate the start and end of the quay segment respectively, then moor the vessel in the quay segment and go to otherwise, turn to ; | |
| If the set of quay cranes assigned to the vessel is a subset of the set of quay cranes within the quay segment where the vessel moored, i.e., and , where and indicate the serial number of the first and last quay crane of the quay segment respectively, then go to otherwise, turn to ; | |
| Select a random segment from the set . Then, modify the berthing position to a random integer within ; | |
| Let the number of quay cranes assigned be a random integer in the interval and let the serial number of the first quay crane assigned be a random integer in the interval ; | |
| Remove the currently scheduled vessel from the set , and add it to the set ; | |
| If the set in any terminal is empty, then the chromosome has been repaired; otherwise, go back to . | |
| The Crossover Operator: | |
|---|---|
| Randomly select two chromosomes from the parent population, denoted as and their fitness values, represented as and , respectively; | |
| For each gene of the crossed child chromosome , the probability of being is and the probability of being is . | |
| The Neighborhood Search Combined with Simulated Annealing Mechanism: | |
|---|---|
| Initialize the current generation as and the system temperature as ; | |
| If the number of consecutive generations for which the optimal solution remains unchanged, denoted as exceeds 10% of the maximum genetic generation , and the current generation is less than the maximum allowed generations , proceed to ; otherwise, terminate the simulated annealing process; | |
| Search in the neighborhood of the optimal solution of the current population to obtain a new solution ; | |
| Repair the new solution to make it feasible and calculate its fitness value ; | |
| If the fitness value of the new solution is greater than the maximum fitness value , turn to ; otherwise, go to ; | |
| Let , , , and stop the simulated annealing process; | |
| Calculate the acceptance probability , and generate a random number . If , turn to ; otherwise, turn to ; | |
| Modify the worst solution of current population, and set , ; | |
| Modify the system temperature and the current generation , turn to . | |
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 0 | 2.15 | 1.57 |
| 2 | 3.16 | 0 | 2.29 |
| 3 | 1.73 | 1.47 | 0 |
| Symbol | Definition | Range |
|---|---|---|
| Length of scheduled vessels | ||
| Remaining workloads of scheduled vessels | ||
| Berthing terminal of scheduled vessels | ||
| Berthing position of scheduled vessels | ||
| Number of quay cranes allocated to scheduled vessels | ||
| The ordinal number of the first quay crane allocated | ||
| Length of the scheduled vessels | ||
| Pre-assigned terminal for vessels to be scheduled | ||
| The number of containers for export that need to be scheduled for the vessels | ||
| Total count of import containers for scheduled vessels | ||
| Estimated time of arrival for the vessels to be scheduled | ||
| Estimated time of departure for scheduled vessels | ||
| Preferred berth location for scheduled vessels | ||
| Minimum number of quay crane requirement for vessels to be assigned | ||
| Maximum number of quay crane requirement for vessels to be assigned | ||
| Actual arrival time for vessels in sample | ||
| Actual operational efficiency for vessels in sample |
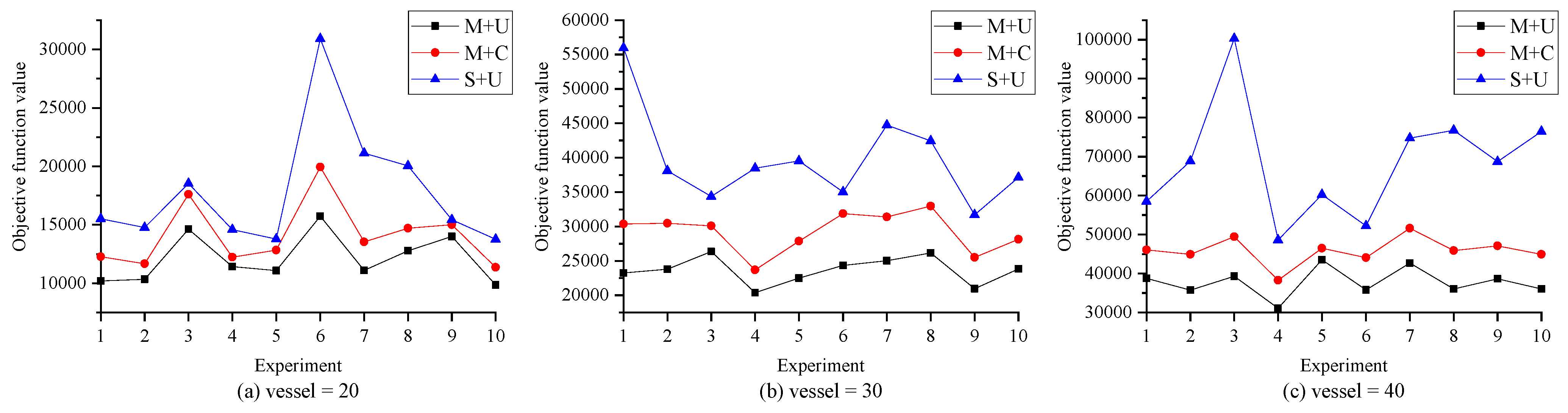
| Scales | 20 | 30 | 40 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment | M + U | S + U | M + U | S + U | M + U | S + U | |||
| 1 | 10,202.8 | 15,512.4 | 52.04 | 23,237.2 | 55,976.0 | 140.89 | 38,769.6 | 58,530.2 | 50.97 |
| 2 | 10,345.4 | 14,766.3 | 42.73 | 23,811.1 | 38,091.5 | 59.97 | 35,757.5 | 68,854.4 | 92.56 |
| 3 | 14,619.8 | 18,524.1 | 26.71 | 26,355.2 | 34,371.8 | 30.42 | 39,283.2 | 100,300.9 | 155.33 |
| 4 | 11,425.8 | 14,579.0 | 27.60 | 20,361.1 | 38,474.0 | 88.96 | 31,072.3 | 48,595.6 | 56.40 |
| 5 | 11,080.7 | 13,781.7 | 24.38 | 22,495.5 | 39,543.8 | 75.79 | 43,519.1 | 60,281.6 | 38.52 |
| 6 | 15,737.0 | 30,911.5 | 96.43 | 24,354.4 | 35,033.4 | 43.85 | 35,796.9 | 52,209.5 | 45.85 |
| 7 | 11,112.4 | 21,132.8 | 90.17 | 25,027.5 | 44,723.5 | 78.70 | 42,684.0 | 74,717.2 | 75.05 |
| 8 | 12,776.6 | 20,041.8 | 56.86 | 26,153.9 | 42,452.0 | 62.32 | 36,026.4 | 76,715.4 | 112.94 |
| 9 | 14,008.9 | 15,429.5 | 10.14 | 20,967.7 | 31,705.4 | 51.21 | 38,618.1 | 68,687.0 | 77.86 |
| 10 | 9849.2 | 13,756.7 | 39.67 | 23,818.3 | 37,136.1 | 55.91 | 36,014.5 | 76,445.6 | 112.26 |
| Expected value | 12,115.9 | 17,843.6 | 46.67 | 23,658.2 | 39,750.8 | 68.80 | 37,754.2 | 68,533.7 | 81.77 |
| Scales | 20 | 30 | 40 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment | M + U | M + C | M + U | M + C | M + U | M + C | |||
| 1 | 10,202.8 | 12,261.5 | 20.18 | 23,237.2 | 30,382.2 | 30.75 | 38,769.6 | 46,054.1 | 18.79 |
| 2 | 10,345.4 | 11,667.4 | 12.78 | 23,811.1 | 30,485.8 | 28.03 | 35,757.5 | 44,915.6 | 25.61 |
| 3 | 14,619.8 | 17,606.2 | 20.43 | 26,355.2 | 30,108.0 | 14.24 | 39,283.2 | 49,423.7 | 25.81 |
| 4 | 11,425.8 | 12,224.4 | 6.99 | 20,361.1 | 23,695.3 | 16.38 | 31,072.3 | 38,300.7 | 23.26 |
| 5 | 11,080.7 | 12,831.8 | 15.80 | 22,495.5 | 27,859.2 | 23.84 | 43,519.1 | 46,477.9 | 6.80 |
| 6 | 15,737.0 | 19,939.8 | 26.71 | 24,354.4 | 31,860.3 | 30.82 | 35,796.9 | 44,082.0 | 23.14 |
| 7 | 11,112.4 | 13,540.2 | 21.85 | 25,027.5 | 31,406.0 | 25.49 | 42,684.0 | 51,590.5 | 20.87 |
| 8 | 12,776.6 | 14,702.6 | 15.07 | 26,153.9 | 32,978.9 | 26.10 | 36,026.4 | 45,905.7 | 27.42 |
| 9 | 14,008.9 | 15,001.4 | 7.08 | 20,967.7 | 25,512.7 | 21.68 | 38,618.1 | 47,116.0 | 22.00 |
| 10 | 9849.2 | 11,373.0 | 15.47 | 23,818.3 | 28,159.0 | 18.22 | 36,014.5 | 44,900.2 | 24.67 |
| Expected value | 12,115.9 | 14,114.8 | 16.24 | 23,658.2 | 29,244.7 | 23.56 | 37,754.2 | 45,876.6 | 21.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Feng, J.; Zhou, J.; Zhou, L.; Ma, F.; Wu, G.; Zhang, Y. Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost. Sustainability 2023, 15, 5018. https://doi.org/10.3390/su15065018
Jiang M, Feng J, Zhou J, Zhou L, Ma F, Wu G, Zhang Y. Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost. Sustainability. 2023; 15(6):5018. https://doi.org/10.3390/su15065018
Chicago/Turabian StyleJiang, Meixian, Jiajia Feng, Jian Zhou, Lin Zhou, Fangzheng Ma, Guanghua Wu, and Yuqiu Zhang. 2023. "Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost" Sustainability 15, no. 6: 5018. https://doi.org/10.3390/su15065018
APA StyleJiang, M., Feng, J., Zhou, J., Zhou, L., Ma, F., Wu, G., & Zhang, Y. (2023). Multi-Terminal Berth and Quay Crane Joint Scheduling in Container Ports Considering Carbon Cost. Sustainability, 15(6), 5018. https://doi.org/10.3390/su15065018





