A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact †
Abstract
1. Introduction
2. Background
- The possibility of expanding the existing capacity of the rail transport network through construction projects;
- Considering demand shortage and time horizon in the problem;
- Considering greenhouse gas emissions as a result of rail transportation operations and minimizing the total emissions in line with the total costs;
- Studying the uncertainty of demand using the robust optimization approach;
- Solving the problem bi-objectively using exact and meta-heuristic approaches.
3. Problem Definition
3.1. Problem Assumptions
3.2. Mathematical Modelling
| Set of directed arcs (rail lines), | |
| Set of new directed arcs (rail lines), | |
| Set of origin–destination (OD) pairs, | |
| Set of capacity improvement projects, | |
| Set of time periods. |
| The available budget for projects, | |
| The capacity of arc , | |
| The added capacity to the arc as a result of project p at period , | |
| Fixed cost of conducting project , | |
| The unit operational cost for arc at period , | |
| The amount of greenhouse emissions on the arc , | |
| The cost of lost demand for each pair of ODs at period , | |
| The demand between each pair of ODs at period , | |
| 1 if arc belongs to the project p, otherwise 0. |
| Lost demand for each pair of ODs at period , | |
| The flow of each OD in arc at period , | |
| 1 if project is conducted, otherwise 0. |
4. Robust Counterpart of the Mathematical Model
5. Solution Method
5.1. Exact Method: ε-Constraint (EC)
5.2. Metaheuristic Approach: NSGA-II
| Algorithm 1. Pseudo-code of proposed NSGA-II. |
| 1. Initialize population 2. Generate N random solutions and insert into population 3. For (i=1 to MaxGen) do 4. Generate Childpop of size N 5. Select Parents from Population 6. Create Childern from Parents 7. Mutate Childern 8. Combine Population and ChildPop into CurrentPop whth size 2N 9. FOR each individual in CurrentPop DO 10. Assign rank based on Pareto non-dominated sort 11. End FOR 12. Generate sets of non-dominated vectors along Pareto Front 13. LOOP by adding solutions to next generation of Population starting from the best front 14. UNTIL N solutions found and determine crowding distance among the points of each front 15. End FOR 16. Print results |
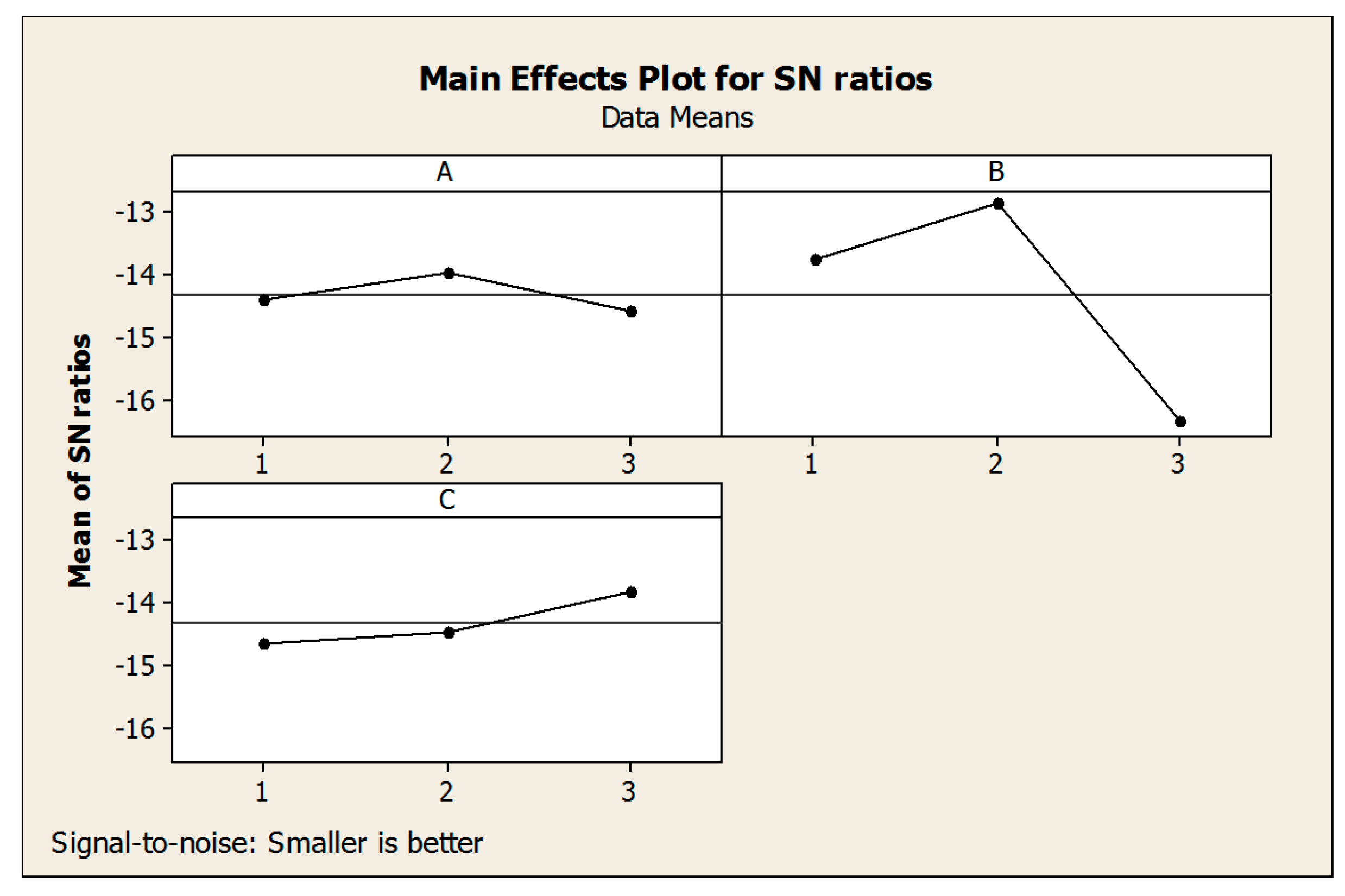
6. Parameter Adjustment: Taguchi Method
7. Computational Results
7.1. Validation of the NSGA-II
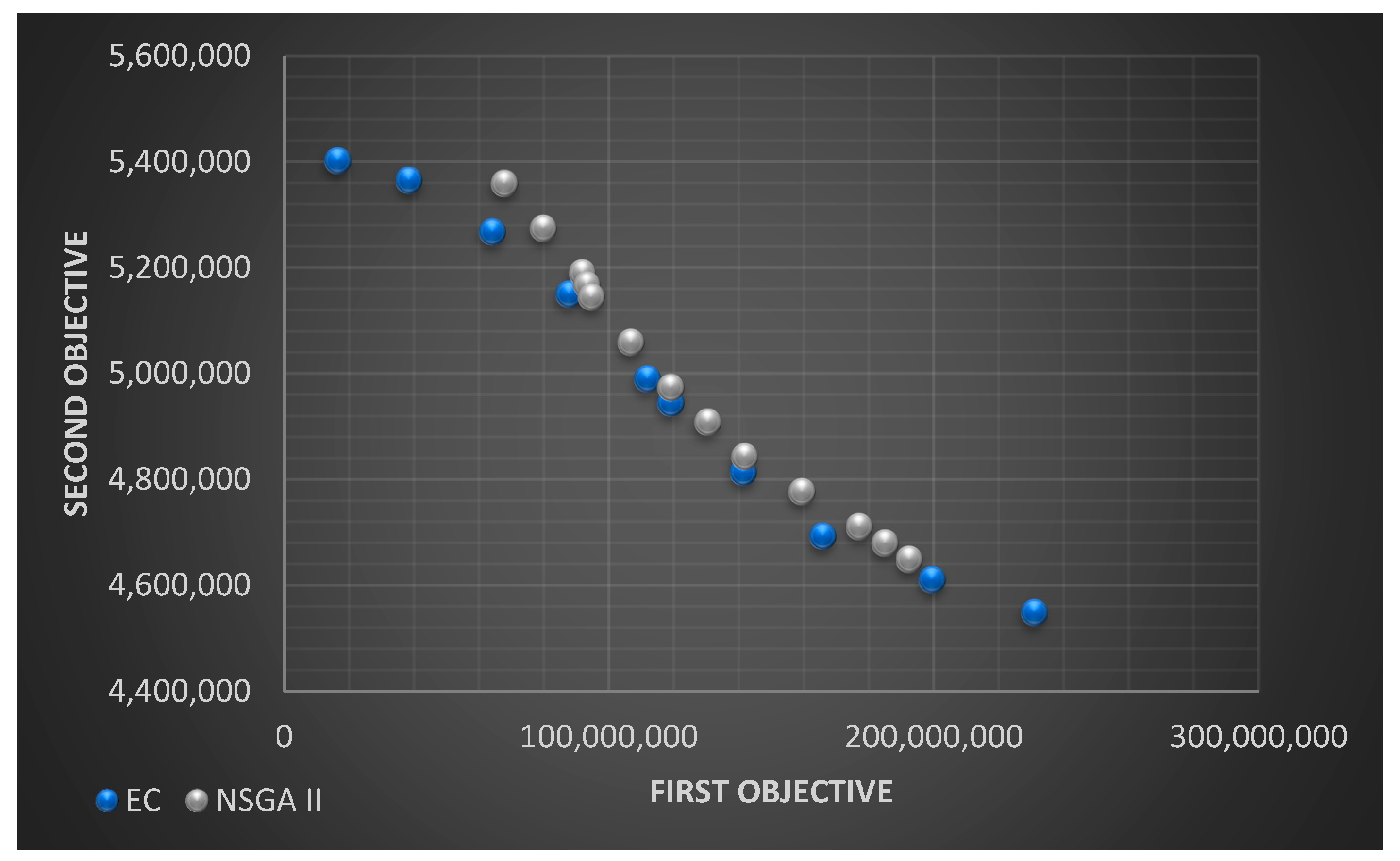
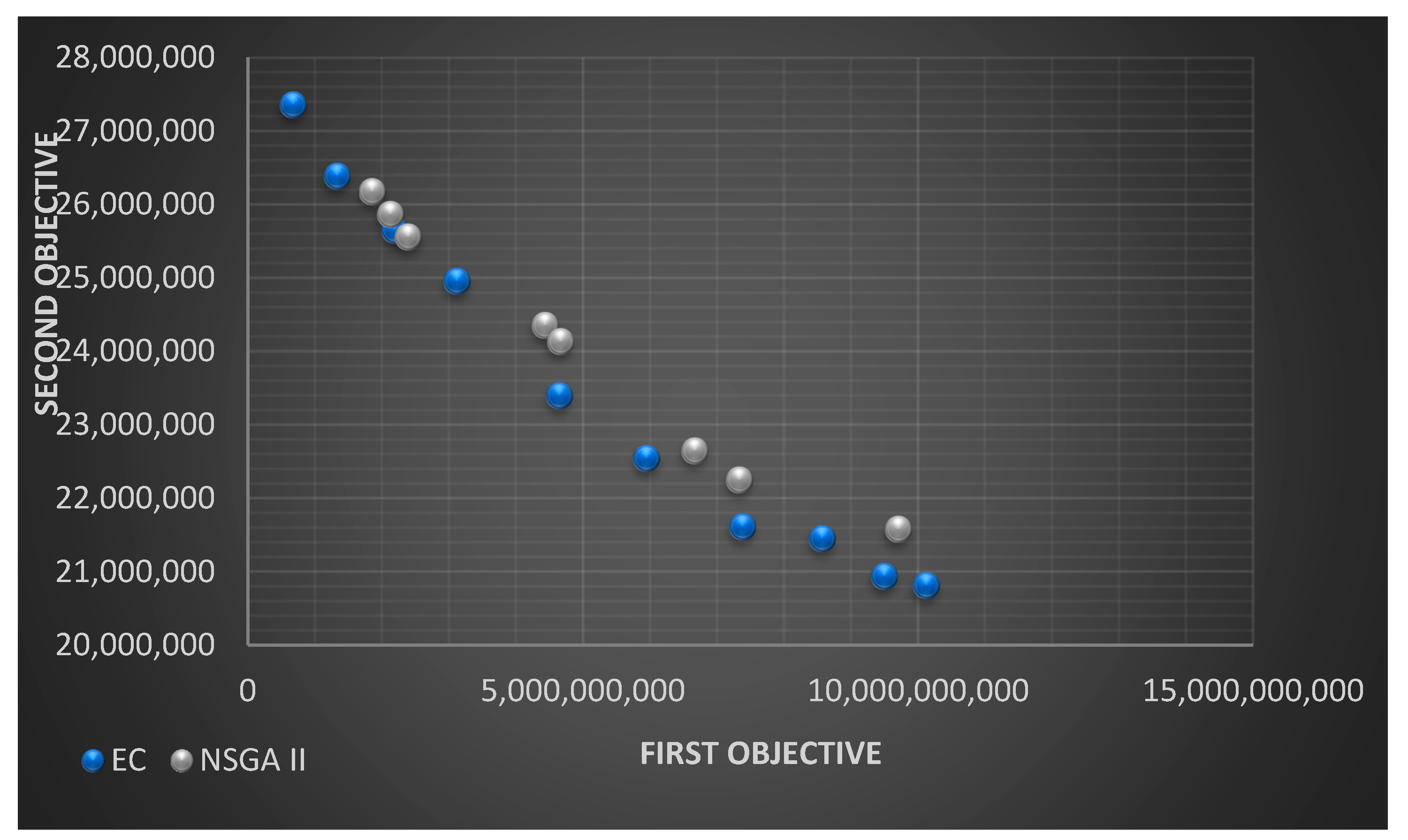
7.2. Measuring the Performance of NSGA-II
8. Conclusions, Managerial Insights, and Future Works
- Developing other uncertainty handling techniques, such as fuzzy programming [32], to be compared to the proposed robust optimization;
- Applying other well-known algorithms, such as the Multi-Objective Grey Wolf Optimization (MOGWO) algorithm [30] and Multi-objective Particle Swarm Optimization (MOPSO) to be compared to the proposed NSGA-II;
- A real case study can be conducted to show the applicability of this model in the real world and provide deeper insights to this problem.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dolinayova, A.; Kanis, J.; Loch, M. Social and economic efficiency of operation dependent and independent traction in rail freight. Procedia Eng. 2016, 134, 187–195. [Google Scholar] [CrossRef]
- Aydin, N.S.; Tirkolaee, E.B. A systematic review of aggregate production planning literature with an outlook for sustainability and circularity. Environ. Dev. Sustain. 2022, 1–42. [Google Scholar] [CrossRef]
- Zhou, W.; You, X.; Fan, W. A mixed integer linear programming method for simultaneous multi-periodic train timetabling and routing on a high-speed rail network. Sustainability 2020, 12, 1131. [Google Scholar] [CrossRef]
- Seyedvakili, S.A.; Nasr Azadani, S.M.; Zakeri, J.A.; Shafahi, Y.; Karimi, M. New model for the railway network design problem. J. Transp. Eng. Part A Syst. 2018, 144, 04018070. [Google Scholar] [CrossRef]
- Zeng, Y.; Ran, B.; Zhang, N.; Yang, X. Estimating the Price Elasticity of Train Travel Demand and Its Variation Rules and Application in Energy Used and CO2 Emissions. Sustainability 2021, 13, 475. [Google Scholar] [CrossRef]
- Dolinayova, A.; Zitricky, V.; Cerna, L. Decision-making process in the case of insufficient rail capacity. Sustainability 2020, 12, 5023. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Kuby, M.; Xu, Z.; Xie, X. Railway network design with multiple project stages and time sequencing. J. Geogr. Syst. 2001, 3, 25–47. [Google Scholar] [CrossRef]
- Lin, B.; Xu, Z.; Huang, M.; Guo, P. An optimization model to railroad network designing. J. China Railw. Soc. 2002, 24, 1–6. [Google Scholar]
- Yan, H.; Lin, B.; Liang, D. An optimization model of railroad network design and investment including multiple projects in several five-year plans. J. China Railw. Soc. 2007, 29, 19–24. [Google Scholar]
- Arnold, P.; Peeters, D.; Thomas, I. Modelling a rail/road intermodal transportation system. Transp. Res. Part E Logist. Transp. Rev. 2004, 40, 255–270. [Google Scholar] [CrossRef]
- Pazour, J.A.; Meller, R.D.; Pohl, L.M. A model to design a national high-speed rail network for freight distribution. Transp. Res. Part A Policy Pract. 2010, 44, 119–135. [Google Scholar] [CrossRef]
- Qiang, S.; Qingyun, W.; Yongling, G. Multi-period bi-level programming model for regional comprehensive transport network design with uncertain demand. J. Transp. Syst. Eng. Inf. Technol. 2011, 11, 111–116. [Google Scholar]
- Laporte, G.; Marin, A.; Mesa, J.A.; Perea, F. Designing robust rapid transit networks with alternative routes. J. Adv. Transp. 2011, 45, 54–65. [Google Scholar] [CrossRef]
- Marín, Á.; García-Ródenas, R. Location of infrastructure in urban railway networks. Comput. Oper. Res. 2009, 36, 1461–1477. [Google Scholar] [CrossRef]
- Marín, Á.; Mesa, J.A.; Perea, F. Integrating robust railway network design and line planning under failures. In Robust and Online Large-Scale Optimization; Models and Techniques for Transportation Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 273–292. [Google Scholar]
- Kermansshahi, S.; Shafahi, M.; Mollanejad, Y.; Zangui, M. Rapid transit network design using simulated annealing. In Proceedings of the 12th World Conference of Transportation Research, Lisbon, Portugal, 11–15 July 2010; pp. 11–15. [Google Scholar]
- García-Archilla, B.; Lozano, A.J.; Mesa, J.A.; Perea, F. GRASP algorithms for the robust railway network design problem. J. Heuristics 2013, 19, 399–422. [Google Scholar] [CrossRef]
- Canca, D.; De-Los-Santos, A.; Laporte, G.; Mesa, J.A. An adaptive neighborhood search metaheuristic for the integrated railway rapid transit network design and line planning problem. Comput. Oper. Res. 2017, 78, 1–14. [Google Scholar] [CrossRef]
- Wang, B.; Huang, J.; Xu, J. Capacity optimization and allocation of an urban rail transit network based on multi-source data. J. Ambient Intell. Humaniz. Comput. 2019, 10, 373–383. [Google Scholar] [CrossRef]
- Alireza Seyedvakili, S.; Zakeri, J.-A.; Nasr Azadani, S.M.; Shafahi, Y. Long-term railway network planning using a multiperiod network design model. J. Transp. Eng. Part A Syst. 2020, 146, 04019054. [Google Scholar] [CrossRef]
- Lin, B.; Liu, C.; Wang, H.; Lin, R. Modeling the railway network design problem: A novel approach to considering carbon emissions reduction. Transp. Res. Part D Transp. Environ. 2017, 56, 95–109. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Weber, G.-W.; Szwedzka, K. A novel formulation for the sustainable periodic waste collection arc-routing problem: A hybrid multi-objective optimization algorithm. In Logistics Operations and Management for Recycling and Reuse; Springer: Berlin/Heidelberg, Germany, 2020; pp. 77–98. [Google Scholar]
- Babaeinesami, A.; Tohidi, H.; Ghasemi, P.; Goodarzian, F.; Tirkolaee, E.B. A closed-loop supply chain configuration considering environmental impacts: A self-adaptive NSGA-II algorithm. Appl. Intell. 2022, 52, 13478–13496. [Google Scholar] [CrossRef]
- Ghasemi, P.; Goodarzian, F.; Abraham, A. A new humanitarian relief logistic network for multi-objective optimization under stochastic programming. Appl. Intell. 2022, 52, 13729–13762. [Google Scholar] [CrossRef] [PubMed]
- Tirkolaee, E.B.; Goli, A.; Weber, G.-W. A robust two-echelon periodic multi-commodity RFID-Based location routing problem to design petroleum logistics networks: A case study. In Logistics and Supply Chain Management: 7th International Conference, LSCM 2020, Tehran, Iran, 23–24 December 2020; Revised Selected Papers 7; Springer: Cham, Switzerland, 2021; pp. 3–23. [Google Scholar]
- Hatefi, S.M.; Jolai, F.; Torabi, S.A.; Tavakkoli-Moghaddam, R. Reliable design of an integrated forward-revere logistics network under uncertainty and facility disruptions: A fuzzy possibilistic programing model. KSCE J. Civ. Eng. 2015, 19, 1117–1128. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in multi-objective mathematical programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Goli, A.; Tirkolaee, E.B.; Weber, G.-W. A perishable product sustainable supply chain network design problem with lead time and customer satisfaction using a hybrid whale-genetic algorithm. In Logistics Operations and Management for Recycling and Reuse; Springer: Berlin/Heidelberg, Germany, 2020; pp. 99–124. [Google Scholar]
- Tirkolaee, E.B.; Goli, A.; Ghasemi, P.; Goodarzian, F. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 2022, 333, 130056. [Google Scholar] [CrossRef]
- Hajibabaie, M.; Lotfi, M.M. Fuzzy bi-objective inventory-routing problem for blood products in a hospital network during disasters: Two multi-objective meta-heuristic approaches. Int. J. Logist. Syst. Manag. 2021, 39, 22–51. [Google Scholar] [CrossRef]
- Kalantari, H.; Badiee, A.; Dezhboro, A.; Mohammadi, H.; Tirkolaee, E.B. A fuzzy profit maximization model using communities viable leaders for information diffusion in dynamic drivers collaboration networks. IEEE Trans. Fuzzy Syst. 2022, 31, 370–379. [Google Scholar] [CrossRef]
- Nguyen, H.; Kieu, L.M.; Wen, T.; Cai, C. Deep learning methods in transportation domain: A review. IET Intell. Transp. Syst. 2018, 12, 998–1004. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Sadeghi, S.; Mooseloo, F.M.; Vandchali, H.R.; Aeini, S. Application of machine learning in supply chain management: A comprehensive overview of the main areas. Math. Probl. Eng. 2021, 2021, 1476043. [Google Scholar] [CrossRef]
- Goli, A.; Tirkolaee, E.B.; Weber, G.-W. An integration of neural network and shuffled frog-leaping algorithm for CNC machining monitoring. Found. Comput. Decis. Sci. 2021, 46, 27–42. [Google Scholar] [CrossRef]

| Parameter | Value in Each Level |
|---|---|
| Crossover rate | 0.6, 0.7, 0.8 |
| Mutation rate | 0.1, 0.15, 0.2 |
| Initial population | 200, 300, 400 |
| Crossover Rate | Mutation Rate | Initial Population | # of Generation |
|---|---|---|---|
| 0.7 | 0.15 | 400 | 50 |
| Problem Size | Problem No. | # of Directed Arcs | # of New Directed Arcs | # of Capacity Improvement Projects | # of Time Periods |
|---|---|---|---|---|---|
| Small | 1 | 5 | 2 | 2 | 1 |
| 2 | 6 | 3 | 2 | 1 | |
| 3 | 7 | 4 | 3 | 1 | |
| 4 | 8 | 5 | 4 | 2 | |
| 5 | 10 | 5 | 4 | 2 | |
| Medium | 6 | 12 | 6 | 5 | 3 |
| 7 | 13 | 7 | 5 | 3 | |
| 8 | 15 | 8 | 6 | 4 | |
| 9 | 17 | 10 | 7 | 4 | |
| 10 | 20 | 12 | 8 | 4 | |
| Large | 11 | 25 | 15 | 9 | 5 |
| 12 | 30 | 17 | 9 | 5 | |
| 13 | 50 | 20 | 10 | 6 | |
| 14 | 75 | 25 | 10 | 6 | |
| 15 | 100 | 30 | 10 | 6 |
| Parameter | Distribution Function | Parameter | Distribution Function |
|---|---|---|---|
| U (1000, 10,000) | U (100, 300) | ||
| U (100, 1000) | U (10, 150) | ||
| U (1000, 5000) | U (0, 1) | ||
| U (200, 500) | U (1,000,000, 10,000,000) | ||
| U (10, 100) | - | - |
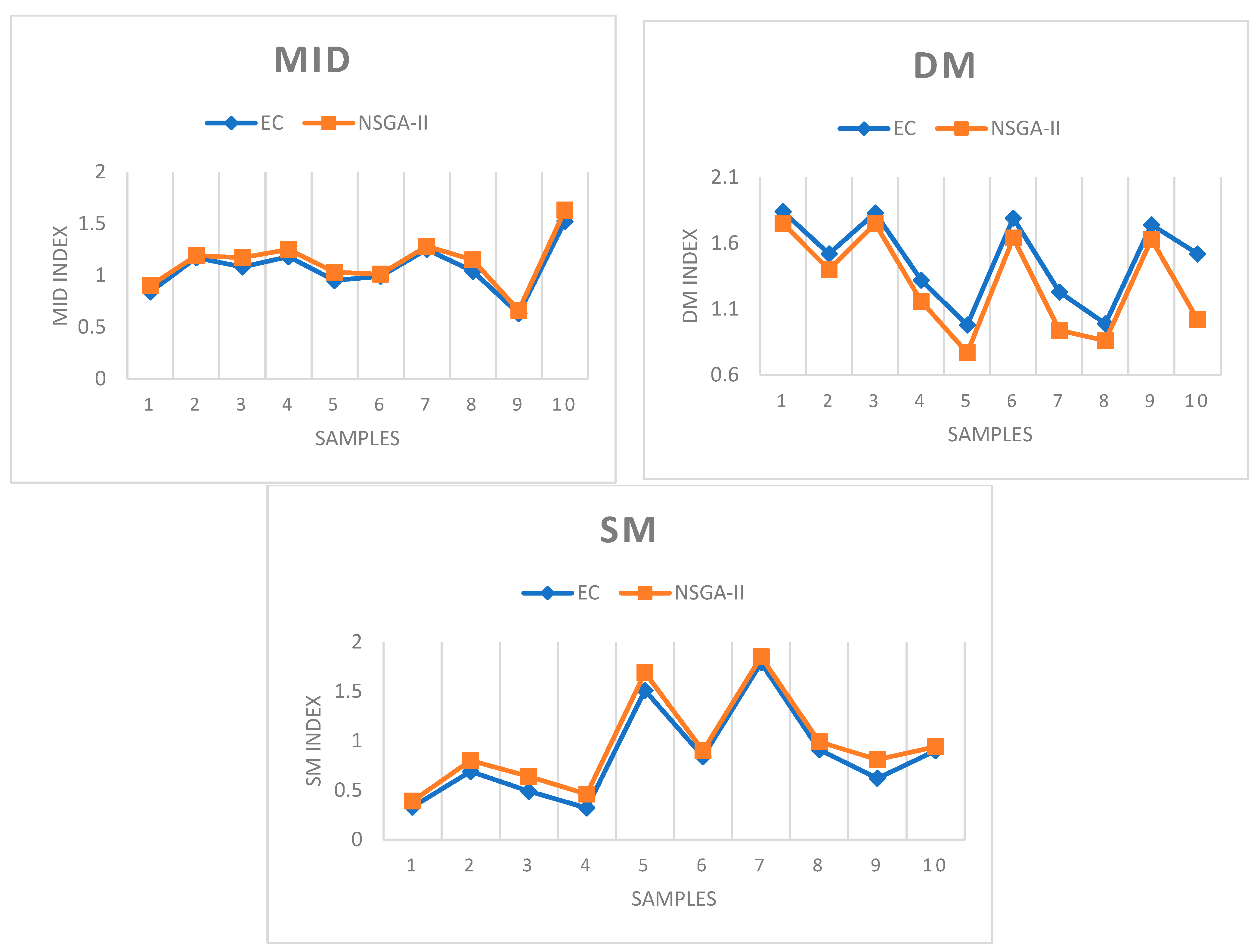
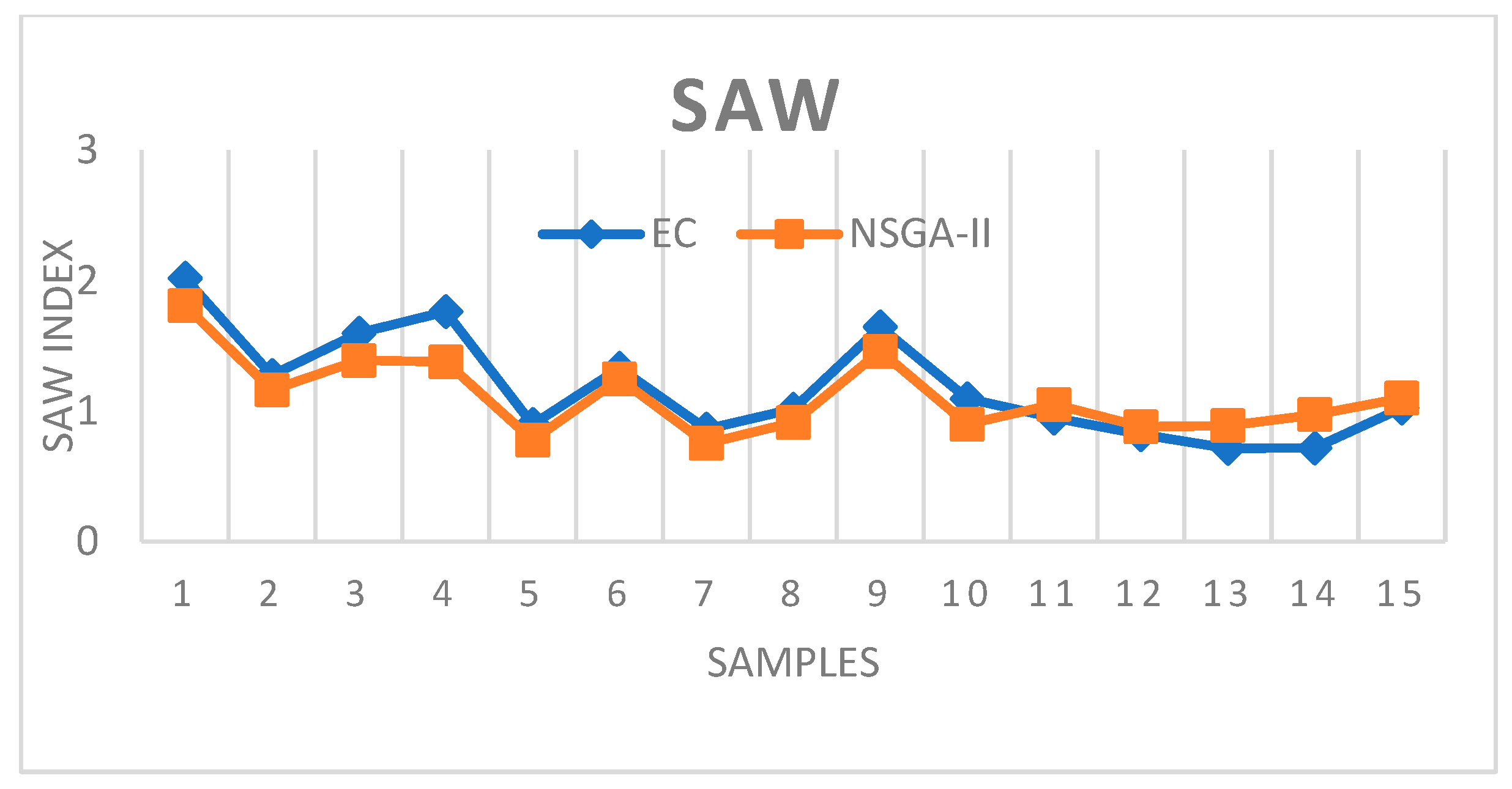
| DM | MID | SM | ||||
|---|---|---|---|---|---|---|
| Problem | EC | NSGA-II | EC | NSGA-II | EC | NSGA-II |
| 1 | 1.84 | 1.75 | 0.84 | 0.9 | 0.33 | 0.39 |
| 2 | 1.52 | 1.4 | 1.17 | 1.19 | 0.69 | 0.8 |
| 3 | 1.83 | 1.75 | 1.08 | 1.17 | 0.49 | 0.64 |
| 4 | 1.32 | 1.16 | 1.18 | 1.25 | 0.32 | 0.46 |
| 5 | 0.98 | 0.77 | 0.95 | 1.03 | 1.51 | 1.69 |
| 6 | 1.79 | 1.64 | 0.99 | 1.01 | 0.84 | 0.9 |
| 7 | 1.23 | 0.94 | 1.25 | 1.28 | 1.79 | 1.85 |
| 8 | 0.99 | 0.86 | 1.04 | 1.15 | 0.91 | 0.99 |
| 9 | 1.74 | 1.63 | 0.63 | 0.66 | 0.62 | 0.81 |
| 10 | 1.52 | 1.02 | 1.52 | 1.63 | 0.9 | 0.94 |
| 11 | 1.44 | 1.72 | 1.45 | 1.4 | 1.4 | 1.39 |
| 12 | 0.69 | 0.73 | 1.56 | 1.48 | 0.88 | 0.81 |
| 13 | 0.85 | 1.06 | 1.44 | 1.11 | 1.66 | 1.42 |
| 14 | 0.98 | 1.57 | 1.98 | 1.57 | 1.49 | 1.4 |
| 15 | 1.39 | 1.48 | 0.88 | 0.79 | 1.83 | 1.81 |
| Average | 1.34 | 1.30 | 1.20 | 1.17 | 1.04 | 1.09 |
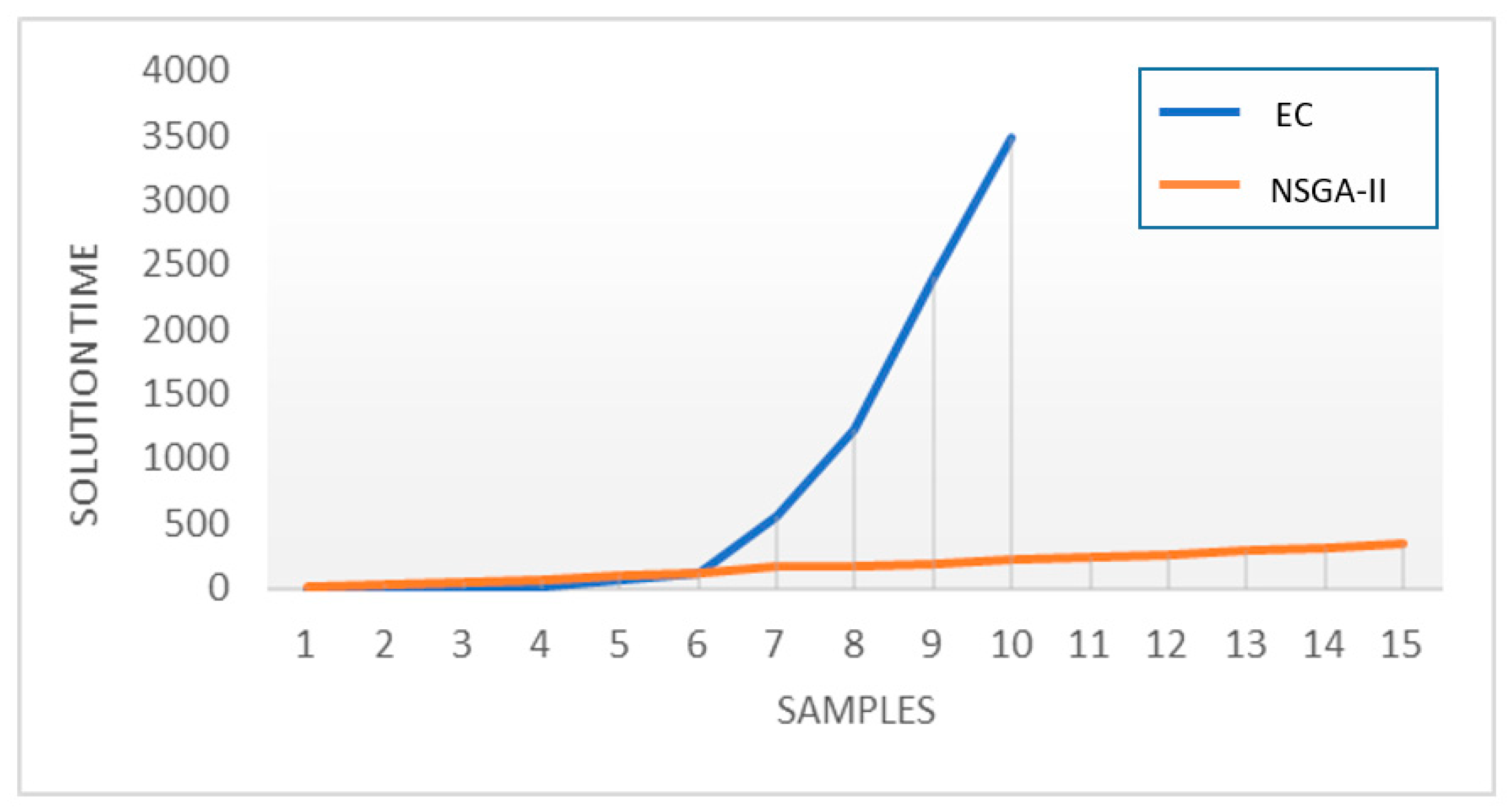
| Problem | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EC | 0.2 | 4.3 | 13.1 | 17.2 | 66.9 | 112.4 | 549.7 | 1233 | 2416 | 3491 | - | - | - | - | - |
| NSGA-II | 13.5 | 29.4 | 44.1 | 60 | 94.5 | 112.9 | 163.2 | 169.2 | 181.7 | 221.5 | 245.7 | 266.3 | 297.6 | 310.7 | 350.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noruzi, M.; Naderan, A.; Zakeri, J.A.; Rahimov, K. A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact. Sustainability 2023, 15, 5022. https://doi.org/10.3390/su15065022
Noruzi M, Naderan A, Zakeri JA, Rahimov K. A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact. Sustainability. 2023; 15(6):5022. https://doi.org/10.3390/su15065022
Chicago/Turabian StyleNoruzi, Morteza, Ali Naderan, Jabbar Ali Zakeri, and Kamran Rahimov. 2023. "A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact" Sustainability 15, no. 6: 5022. https://doi.org/10.3390/su15065022
APA StyleNoruzi, M., Naderan, A., Zakeri, J. A., & Rahimov, K. (2023). A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact. Sustainability, 15(6), 5022. https://doi.org/10.3390/su15065022








