Experimental Investigation of the Parapet Effect on the Wind Load of Roof-Mounted Solar Arrays
Abstract
:1. Introduction
2. Experimental Setups
2.1. Wind Tunnel Facility and Wind Profiles
2.2. Pressure Model Configurations
3. Data Processing
3.1. Pressure Coefficients
3.2. Shape Factors
4. Results and Discussions
4.1. Local Pressure Coefficients
4.1.1. Unfavorable Wind Direction
4.1.2. Effect of Parapet Height
4.2. Area-Averaged Net Pressure Coefficients
4.3. Shape Factors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, S.; Wang, Y.; Yan, X. Analysis of the differences in the structural design of PV supports in Chinese code. Build. Struct. 2020, 50, 699–703. [Google Scholar]
- Velicu, R.; Moldovean, G.; Scaletchi, I.; Butuc, B.R. Wind loads on an azimuthal photovoltaic platform. Experimental study. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’10), Granada, Spain, 2–4 September 2010. [Google Scholar]
- Pfahl, A.; Buselmeier, M.; Zaschke, M. Wind loads on heliostats and photovoltaic trackers of various aspect ratios. Sol. Energy 2011, 85, 2185–2201. [Google Scholar] [CrossRef] [Green Version]
- Abiola-Ogedengbe, A.; Hangan, H.; Siddiqui, K. Experimental investigation of wind effects on a standalone photovoltaic (PV) module. Renew. Energy 2015, 78, 657–665. [Google Scholar] [CrossRef]
- Taylor, Z.J.; Browne, M.T.L. Hybrid pressure integration and buffeting analysis for multi-row wind loading in an array of single-axis trackers. J. Wind. Eng. Ind. Aerodyn. 2020, 197, 104056. [Google Scholar] [CrossRef]
- Pratt, R.N.; Kopp, G.A. Velocity measurements around low-profile, tilted, solar arrays mounted on large flat-roofs, for wall normal wind directions. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 226–238. [Google Scholar] [CrossRef]
- Kopp, G.A.; Farquhar, S.; Morrison, M.J. Aerodynamic mechanisms for wind loads on tilted, roof-mounted, solar arrays. J. Wind. Eng. Ind. Aerodyn. 2012, 111, 40–52. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of the wind tunnel test method for obtaining design wind loads on roof-mounted solar arrays. J. Struct. Eng. 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Kopp, G.A. Wind loads on low-profile, tilted, solar arrays placed on large, flat, low-rise building roofs. J. Struct. Eng. 2014, 140, 04013057. [Google Scholar] [CrossRef]
- Cao, J.; Yoshida, A.; Saha, P.K.; Tamura, Y. Wind loading characteristics of solar arrays mounted on flat roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 214–225. [Google Scholar] [CrossRef]
- Shademan, M.; Barron, R.M.; Balachandar, R.; Hangan, H. Numerical simulation of wind loading on ground-mounted solar panels at different flow configurations. Can. J. Civ. Eng. 2014, 41, 728–738. [Google Scholar] [CrossRef]
- Warsido, W.P.; Bitsuamlak, G.T.; Barata, J.; Chowdhury, A.G. Influence of spacing parameters on the wind loading of solar array. J. Fluids Struct. 2014, 48, 295–315. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Zisis, I.; Xypnitou, E. Local and overall wind pressure and force coefficients for solar panels. J. Wind. Eng. Ind. Aerodyn. 2014, 125, 195–206. [Google Scholar] [CrossRef]
- Estephan, J.; Feng, C.; Chowdhury, A.G.; Chavez, M.; Baskaran, A.; Moravej, M. Characterization of wind-induced pressure on membrane roofs based on full-scale wind tunnel testing. Eng. Struct. 2021, 235, 112101. [Google Scholar] [CrossRef]
- Estephan, J.; Chowdhury, A.G.; Irwin, P. A new experimental-numerical approach to estimate peak wind loads on roof-mounted photovoltaic systems by incorporating inflow turbulence and dynamic effects. Eng. Struct. 2022, 252, 113739. [Google Scholar] [CrossRef]
- ASCE-7-16; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- Peng, H.; Song, S.; Liu, H.; Dai, S.; Zhang, F. Investigation of wind loading characteristics of roof-mounted solar panels on tall buildings. Sustain. Energy Technol. Assess. 2022, 54, 102800. [Google Scholar] [CrossRef]
- NB/T 10115-2018; Code for Design of Photovoltaic Modules Support Structures. China Jihua Press: Beijing, China, 2018.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012.
- JIS C 8955-2018; Design Guide on Structures for Photovoltaic Array . Japanese Industrial Standard: Tokyo, Japan, 2018.
- ASCE-7-22; Standard: Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022.
- Wang, J.; Yang, Q.; Tamura, Y. Effects of building parameters on wind loads on flat-roof-mounted solar arrays. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 210–224. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Hui, Y. Comparisons of design wind pressures on roof-mounted solar arrays between wind tunnel tests and codes and standards. Adv. Struct. Eng. 2021, 24, 653–666. [Google Scholar] [CrossRef]











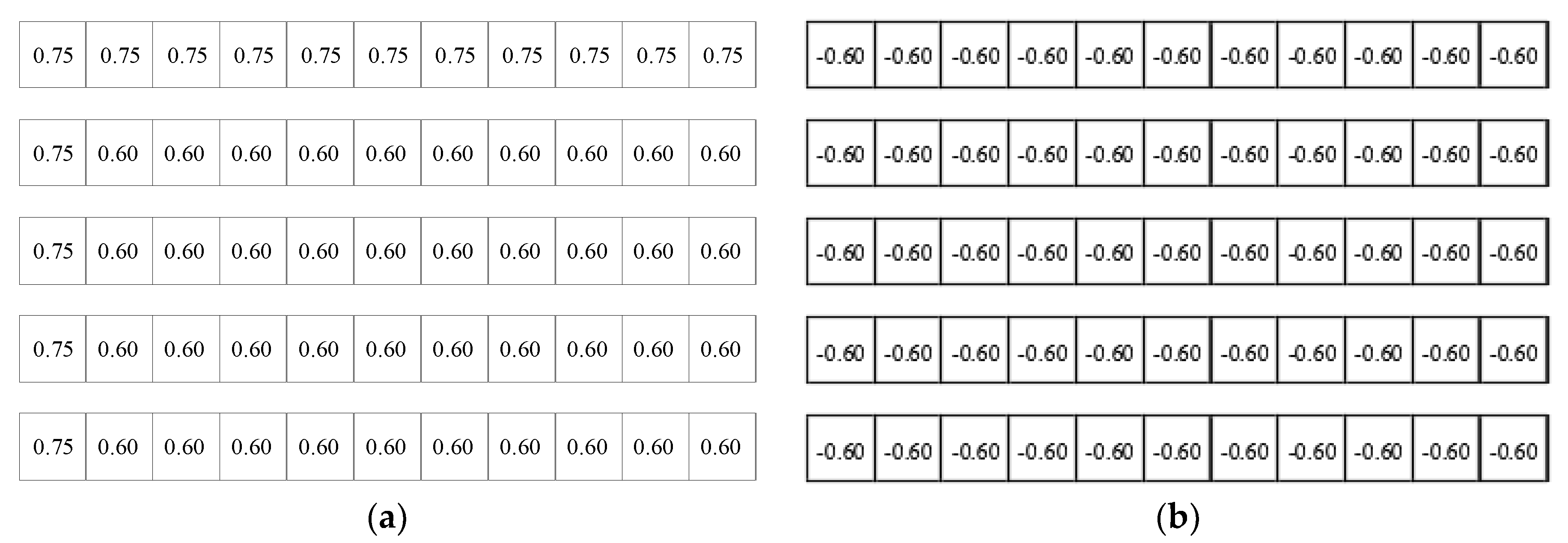
 represents = 0 m,
represents = 0 m,  represents hpt = 1.2 m.
represents hpt = 1.2 m.
 represents = 0 m,
represents = 0 m,  represents hpt = 1.2 m.
represents hpt = 1.2 m.












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Tu, Z.; Wang, D.; Shen, G.; Yu, S.; Lou, W. Experimental Investigation of the Parapet Effect on the Wind Load of Roof-Mounted Solar Arrays. Sustainability 2023, 15, 5052. https://doi.org/10.3390/su15065052
Yao J, Tu Z, Wang D, Shen G, Yu S, Lou W. Experimental Investigation of the Parapet Effect on the Wind Load of Roof-Mounted Solar Arrays. Sustainability. 2023; 15(6):5052. https://doi.org/10.3390/su15065052
Chicago/Turabian StyleYao, Jianfeng, Zhibin Tu, Dong Wang, Guohui Shen, Shice Yu, and Wenjuan Lou. 2023. "Experimental Investigation of the Parapet Effect on the Wind Load of Roof-Mounted Solar Arrays" Sustainability 15, no. 6: 5052. https://doi.org/10.3390/su15065052
APA StyleYao, J., Tu, Z., Wang, D., Shen, G., Yu, S., & Lou, W. (2023). Experimental Investigation of the Parapet Effect on the Wind Load of Roof-Mounted Solar Arrays. Sustainability, 15(6), 5052. https://doi.org/10.3390/su15065052








