A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem
Abstract
:1. Introduction
- 1.
- Handling uncertainty: TSP assumes that the distances between cities are known and fixed. However, in real-world applications, these distances may be uncertain or variable due to factors such as traffic, weather conditions, and road closures. Therefore, there is a need to develop algorithms that can handle uncertainty in TSP.
- •
- Jena et al. [14] proposes a hybrid evolutionary algorithm to solve TSP with stochastic distances.
- 2.
- Dynamic TSP: In dynamic TSP, the set of cities or their distances may change over time. Dynamic TSP is a challenging problem that requires developing efficient algorithms that can adapt to changes in the problem instance.
- •
- Singh et al. provided an overview of dynamic TSP and discusses the challenges and open research questions related to the problem [15].
- 3.
- Multiple criteria: In many real-world applications of TSP, multiple criteria need to be considered, such as the cost of travel, time required to visit cities, and environmental impact. Therefore, there is a need to develop algorithms that can handle multiple criteria in TSP.
- •
- Castellanos et al. proposed a multi-objective approach to TSP with soft time windows [16].
- 4.
- Parallel and distributed algorithms: As the size of TSP instances grows, there is a need to develop parallel and distributed algorithms that can solve the problem in a reasonable amount of time.
- •
- Castro et al. proposed a parallel hybrid genetic algorithm for TSP [17].
2. Related Work
3. Methods
3.1. Traveling Salesman Program Model
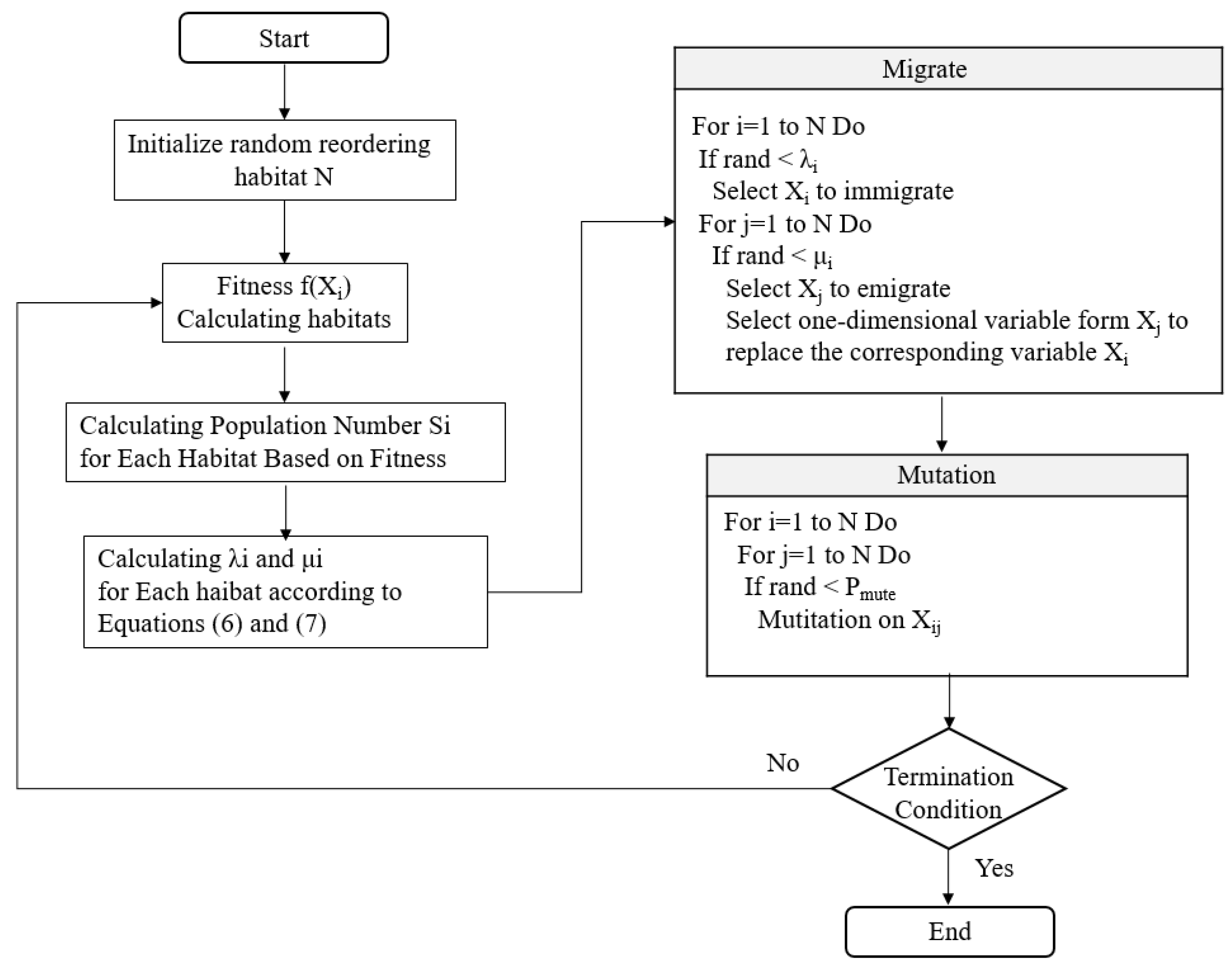
3.2. Biogeography-Based Optimization Algorithm (BBO)
- Step 1.
- Initialization:
- Step 2.
- Migration:
- Step 3.
- Mutation:
3.3. Random Greedy Initialization
3.4. 2-Opt Algorithm
3.5. G2BBO Solving Travel Salesman Problem
4. Experimental Results
4.1. Setting of Experimental Parameters
- Population Size = 10, Iterations = 1000;
- Elite retention number = 2, = 1,Maximum migration probability I = 1;
- Maximum migration probability E = 1;
- Migration rate = 0.7, Mutation rate = 0.07;
- Each method runs independently 10 times to obtain the shortest path solution.
4.2. Analysis of Experimental Results
4.3. Summary
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baranidharan, B.; Meidute-Kavaliauskiene, I.; Mahapatra, G.S.; Činčikaitė, R. Assessing the Sustainability of the Prepandemic Impact on Fuzzy Traveling Sellers Problem with a New Fermatean Fuzzy Scoring Function. Sustainability 2022, 14, 16560. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Exact models for the flying sidekick traveling salesman problem. Int. Trans. Oper. Res. 2022, 29, 1360–1393. [Google Scholar] [CrossRef]
- Huerta, I.I.; Neira, D.A.; Ortega, D.A.; Varas, V.; Godoy, J.; Asín-Achá, R. Improving the state-of-the-art in the traveling salesman problem: An anytime automatic algorithm selection. Expert Syst. Appl. 2022, 187, 115948. [Google Scholar] [CrossRef]
- Salem, I.E.; Mijwil, M.M.; Abdulqader, A.W.; Ismaeel, M.M. Flight-schedule using Dijkstra’s algorithm with comparison of routes findings. Int. J. Electr. Comput. Eng. 2022, 12, 1675. [Google Scholar] [CrossRef]
- Watrous, J. On one-dimensional quantum cellular automata. In Proceedings of the IEEE 36th Annual Foundations of Computer Science, Milwaukee, WI, USA, 23–25 October 1995. [Google Scholar]
- Laporte, G. The traveling salesman problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 231–247. [Google Scholar] [CrossRef]
- Ariani, S.; Santosa, B.; Wiratno, S.E.; Suprianti, R. Analisis Kompleksitas Algoritma Biogeography Based Optimization (BBO) Pada Traveling Salesman Problem (TSP). JASIKA (J. Apl. Sist. Inf. Dan Inform.) 2020, 1, 10–17. [Google Scholar]
- Safayenikoo, H.; Nejati, F.; Nehdi, M.L. Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors. Sustainability 2022, 14, 10373. [Google Scholar] [CrossRef]
- Salehi, A.; Masoumi, B. Solving traveling salesman problem based on biogeography-based optimization and edge assembly cross-over. J. AI Data Min. 2020, 8, 313–329. [Google Scholar]
- Al-Taani, A.T.; Al-Afifi, L.M. Solving the Multiple Traveling Salesman Problem Using Memetic Algorithm. Artif. Intell. Evol. 2022, 3, 27–40. Available online: https://ojs.wiserpub.com/index.php/AIE/article/view/1206 (accessed on 1 May 2022). [CrossRef]
- Mzili, T.; Riffi, M.E.; Mzili, I.; Dhiman, G. A novel discrete Rat swarm optimization (DRSO) algorithm for solving the traveling salesman problem. Decis. Mak. Appl. Manag. Eng. 2022, 8, 287–299. [Google Scholar] [CrossRef]
- Riffi, M.E. Drso: Improved Discrete Rat Swarm Optimization Algorithm (Drso) for Solving the Traveling Salesman Problem. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4154967 (accessed on 1 May 2022).
- Zhang, P.; Wang, J.; Tian, Z.; Sun, S.; Li, J.; Yang, J. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem. Appl. Soft Comput. 2022, 127, 109339. [Google Scholar] [CrossRef]
- Jena, S.S.; Dash, P.K. A Hybrid Evolutionary Algorithm for Traveling Salesman Problem with Stochastic Distances. Evol. Comput. 2019, 12, 241–255. [Google Scholar]
- Singh, P.K.; Dash, P.K. Dynamic Traveling Salesman Problem: An Overview. Math. Model. Eng. Probl. 2019, 6, 309–315. [Google Scholar]
- Castellanos, M.R.; Mezura-Montes, E.; Moreno-Perez, J.A. A multi-objective approach to the traveling salesman problem with soft time windows. Soft. Comput. 2018, 22, 1233–1246. [Google Scholar]
- de Castro, L.A.; Von Zuben, F.J.; Krohling, R.A. A parallel hybrid genetic algorithm for the traveling salesman problem. IEEE Trans. Cybern. 2018, 48, 2838–2849. [Google Scholar]
- Almeida, L.S.; Goerlandt, F.; Pelot, R.; Sörensen, K. A Greedy Randomized Adaptive Search Procedure (GRASP) for the multi-vehicle prize collecting arc routing for connectivity problem. Comput. Oper. Res. 2022, 143, 105804. [Google Scholar] [CrossRef]
- Lakhdar, B.; Yahyaoui, K. Solving the Mixed-model Assembly Line Balancing Problem by using a Hybrid Reactive Greedy Randomized Adaptive Search Procedure. In Optimization and Machine Learning: Optimization for Machine Learning and Machine Learning for Optimization; Wiley-ISTE: Hoboken, NJ, USA, 2022; pp. 91–118. [Google Scholar] [CrossRef]
- Sun, X.; Chou, P.; Koong, C.S.; Wu, C.C.; Chen, L.R. Optimizing 2-opt-based heuristics on GPU for solving the single-row facility layout problem. Future Gener. Comput. Syst. 2022, 126, 91–109. [Google Scholar] [CrossRef]
- Manthey, B.; van Rhijn, J. Improved Smoothed Analysis of 2-Opt for the Euclidean TSP. arXiv 2022, arXiv:2211.16908. [Google Scholar]
- Challaf, O.; Chua, S.L.; Foo, L.K. Trip Itinerary Generation with 2-Opt Algorithm. In Proceedings of the 4th International Conference on Advanced Information Science and System, Sanya, China, 25–27 November 2022; pp. 1–5. [Google Scholar]
- Shayanfar, H.; Gharehchopogh, F.S. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems. Appl. Soft Comput. 2018, 71, 728–746. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Khodadadi, N.; Mirjalili, S. Mountain gazelle optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Adv. Eng. Softw. 2022, 174, 103282. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Soleimanian Gharehchopogh, F.; Mirjalili, S. Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems. Int. J. Intell. Syst. 2021, 36, 5887–5958. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38 (Suppl. 4), 3025–3056. [Google Scholar] [CrossRef]
- Simon, D.; Omran, M.G.; Clerc, M. Linearized biogeography-based optimization with re-initialization and local search. Inf. Sci. 2014, 267, 140–157. [Google Scholar] [CrossRef] [Green Version]
- Baniasadi, P.; Foumani, M.; Smith-Miles, K.; Ejov, V. A transformation technique for the clustered generalized traveling salesman problem with applications to logistics. Eur. J. Oper. Res. 2020, 285, 444–457. [Google Scholar] [CrossRef]
- Keeley, A.T.; Beier, P.; Keeley, B.W.; Fagan, M.E. Habitat suitability is a poor proxy for landscape connectivity during dispersal and mating movements. Landsc. Urban Plan. 2017, 161, 90–102. [Google Scholar] [CrossRef]
- Hadidi, A. A robust approach for optimal design of plate fin heat exchangers using biogeography based optimization (BBO) algorithm. Appl. Energy 2015, 150, 196–210. [Google Scholar] [CrossRef]
- Villacreses, G.; Gaona, G.; Martínez-Gómez, J.; Jijón, D.J. Wind farms suitability location using geographical information system (GIS), based on multi-criteria decision making (MCDM) methods: The case of continental Ecuador. Renew. Energy 2017, 109, 275–286. [Google Scholar] [CrossRef]
- Ma, H.; Simon, D. Evolutionary Computation with Biogeography-Based Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Akhand, M.; Peya, Z.J.; Sultana, T.; Rahman, M.H. Solving capacitated vehicle routing problem using variant sweep and swarm intelligence. J. Appl. Sci. Eng. 2017, 20, 511–524. [Google Scholar]







| Algorithm | Inspiration | Solution |
|---|---|---|
| Farmland Fertility Algorithm [23] | Farmland fertility in nature | Solving a continuous optimization problem |
| The African vulture optimization algorithm [24] | African vultures’ lifestyle | Solving large-scale problems |
| The mountain gazelle optimizer [25] | The social life and hierarchy of wild mountain gazelles | High-dimensional search capabilities |
| The artificial gorilla troops optimizer [26] | Gorilla troops’ social intelligence in nature | Solving onhigh- dimensional problems |
| Artificial rabbits optimization [27] | The survival strategies of rabbits in nature | Solving engineering optimization problems |
| Wild horse optimization [28] | The social behavior of wild horses in nature | Solving problems in various scientific fields |
| G2BBO optimization | Biogeography regarding the migration of species between different habitats, as well as the evolution and extinction of species | Solving large-scale and multiple objectives optimization problems |
| City | X | Y |
|---|---|---|
| City 1 | 225 | 490 |
| City 2 | 425 | 100 |
| City 3 | 425 | 650 |
| City 4 | 650 | 570 |
| City 5 | 675 | 200 |
| City Distance | City 1 | City 2 | City 3 | City 4 | City 5 |
|---|---|---|---|---|---|
| City 1 | 0 | 438 | 256 | 432 | 535 |
| City 2 | 438 | 0 | 550 | 521 | 269 |
| City 3 | 256 | 550 | 0 | 239 | 515 |
| City 4 | 432 | 521 | 239 | 0 | 371 |
| City 5 | 535 | 269 | 515 | 371 | 0 |
| Instance | Optimal | BBO | G2BBO | MA [10] | DRSO [11] | GA-JGHO [13] | BBOEAX [9] |
|---|---|---|---|---|---|---|---|
| eil51 | 426 | 974 | 428 | 501 | 432.57 | 429.93 | 446.43 |
| eil76 | 538 | 1492 | 546 | - | 569.5 | 545.1 | - |
| KroA100 | 21,282 | 99,927 | 21,294 | - | 21,748.4 | 21,522.73 | 22,549.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-H.; Lin, Y.-D.; Yang, C.-H.; Wang, C.-K.; Chiang, L.-C.; Chiang, P.-J. A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem. Sustainability 2023, 15, 5111. https://doi.org/10.3390/su15065111
Tsai C-H, Lin Y-D, Yang C-H, Wang C-K, Chiang L-C, Chiang P-J. A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem. Sustainability. 2023; 15(6):5111. https://doi.org/10.3390/su15065111
Chicago/Turabian StyleTsai, Cheng-Hsiung, Yu-Da Lin, Cheng-Hong Yang, Chien-Kun Wang, Li-Chun Chiang, and Po-Jui Chiang. 2023. "A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem" Sustainability 15, no. 6: 5111. https://doi.org/10.3390/su15065111
APA StyleTsai, C.-H., Lin, Y.-D., Yang, C.-H., Wang, C.-K., Chiang, L.-C., & Chiang, P.-J. (2023). A Biogeography-Based Optimization with a Greedy Randomized Adaptive Search Procedure and the 2-Opt Algorithm for the Traveling Salesman Problem. Sustainability, 15(6), 5111. https://doi.org/10.3390/su15065111









