Ratio of Hysteretic and Input Energy Spectra for Nonlinear Structures under Seismic Sequences
Abstract
:1. Introduction
2. Seismic Sequences
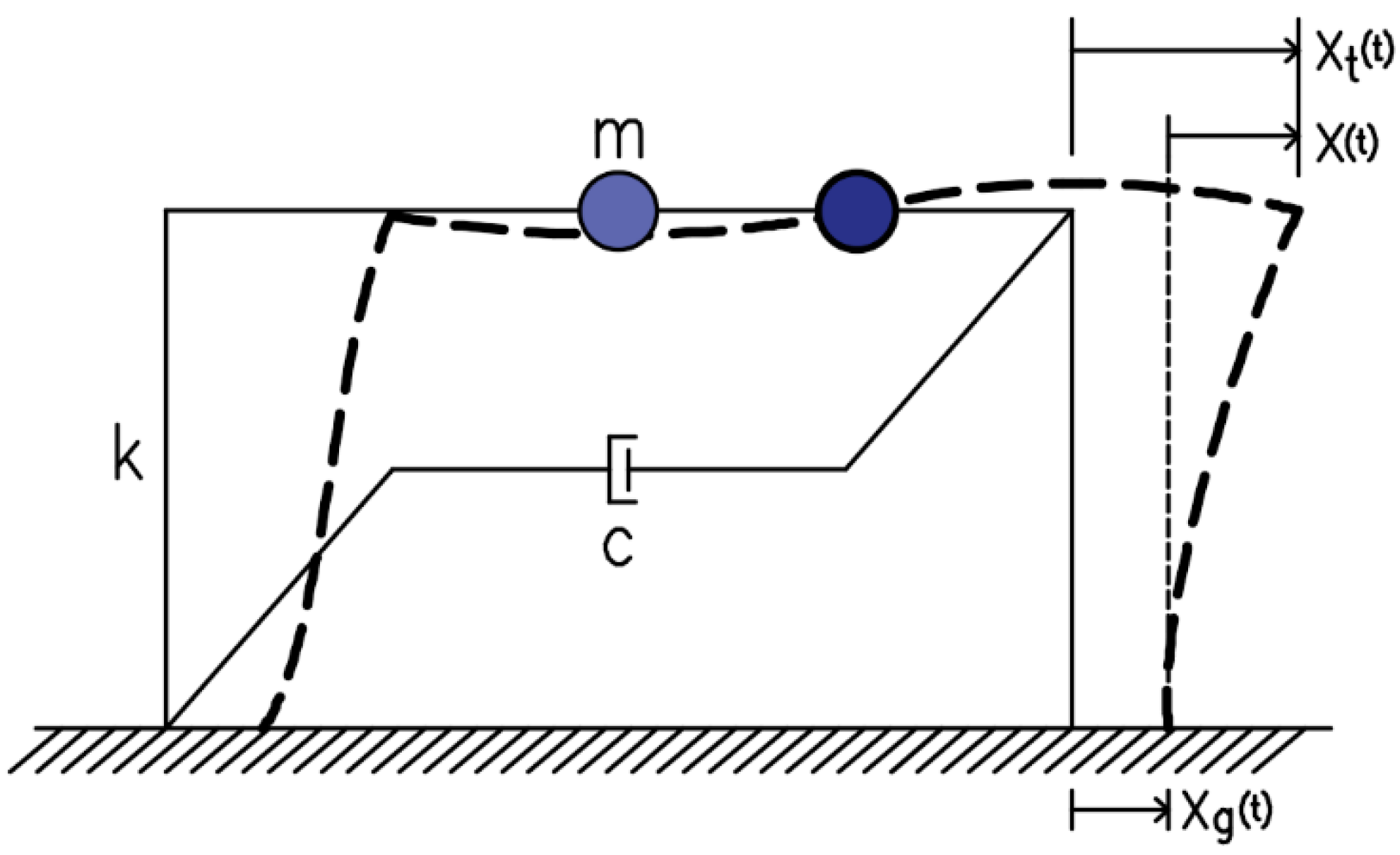
3. Seismic Energy Concepts
4. Ratio EH/EI
5. Selection of the Structural Models
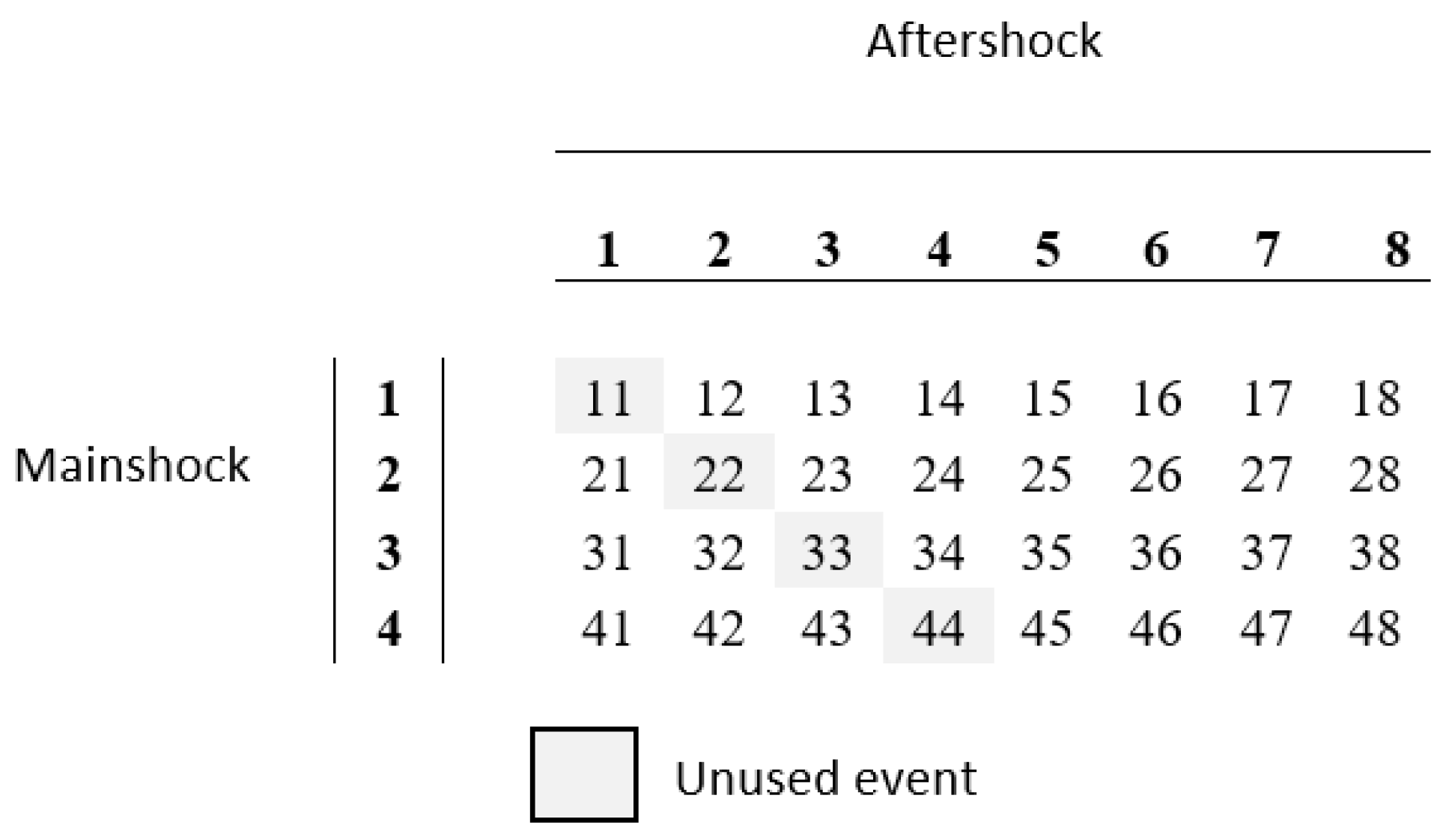
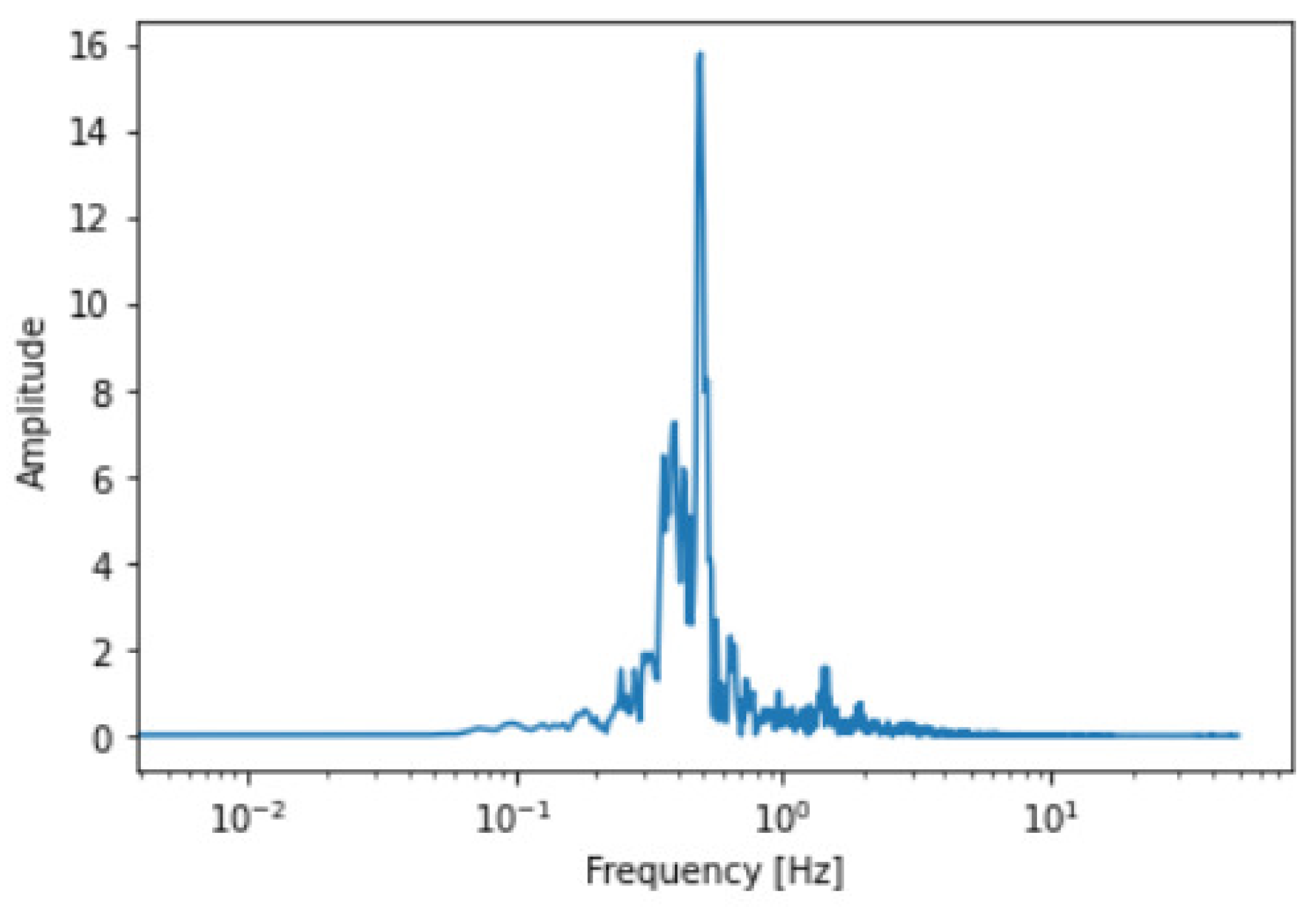
6. Seismic Sequences Used
- First, the eight records were integrated to obtain their velocity history, then the maximum velocity per record was obtained.
- In a similar way, the maximum velocity of the earthquake recorded at the SCT station was obtained and divided by each of the maximum velocities of the records, thus obtaining eight scale factors.
- Velocity histories were multiplied by the corresponding scale factors.
- Velocity histories were derived by the particular scale factors.
- Finally, the velocity histories were derived to obtain an acceleration history, that is, a scaled record.
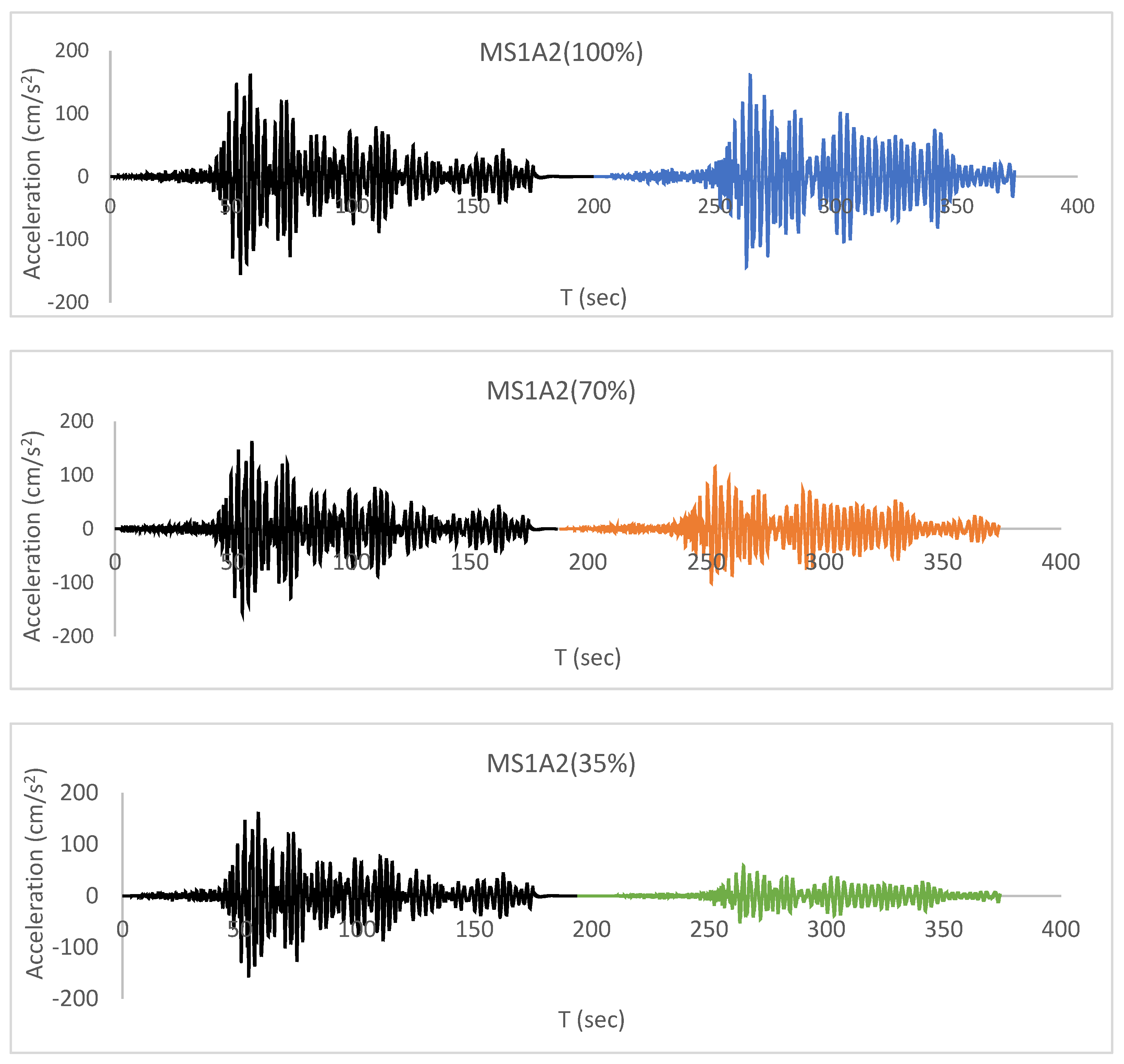
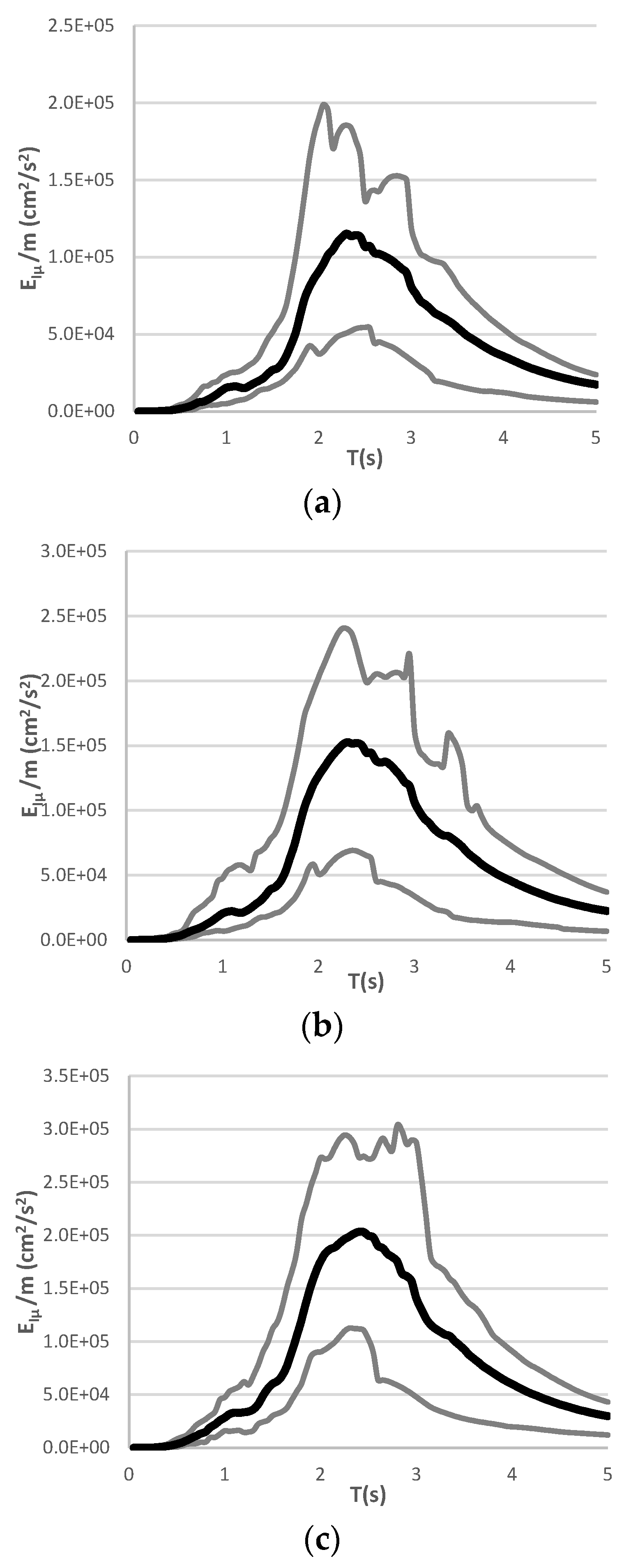
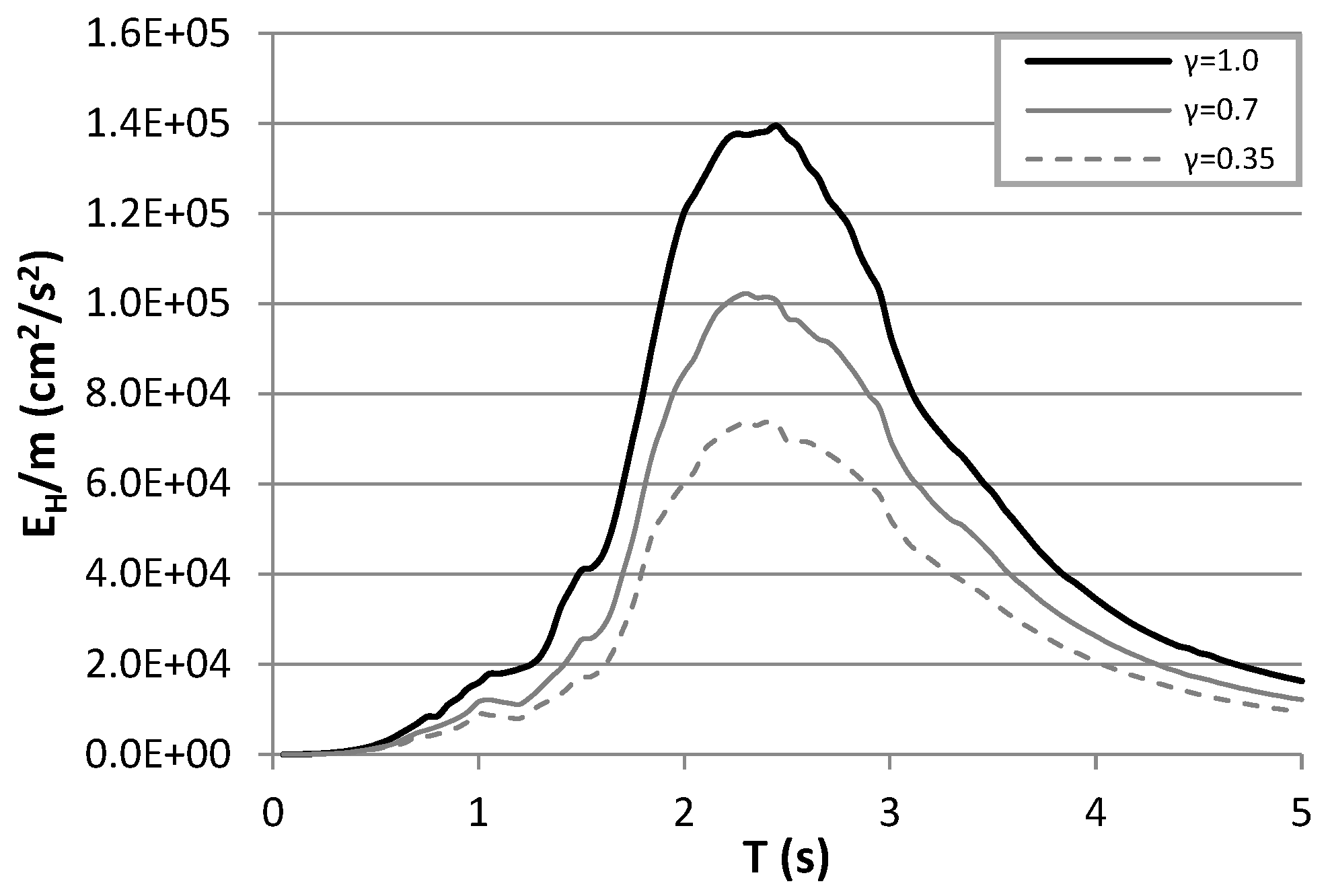
- The sequences of the first group (A) were constituted with mainshocks and aftershocks scaled at 100% (γ = 1.0) of the maximum velocity of the seismic record obtained at the SCT station (61,414 cm/s). Note that γ is defined as the PGVA/PGVM peak ground velocity of the mainshock and peak ground velocity of the aftershock ratio.
- The sequences of the second group (B) were formed with mainshocks scaled at 100% and aftershocks scaled at 70% (γ = 0.7) of the maximum velocity of the seismic record obtained at the SCT station (42.86 cm/s).
- The sequences of the third group (C) were formed with mainshocks scaled at 100% and aftershocks scaled at 35% (γ = 0.35) of the maximum velocity of the seismic record obtained at the SCT station (21.4 cm/s).
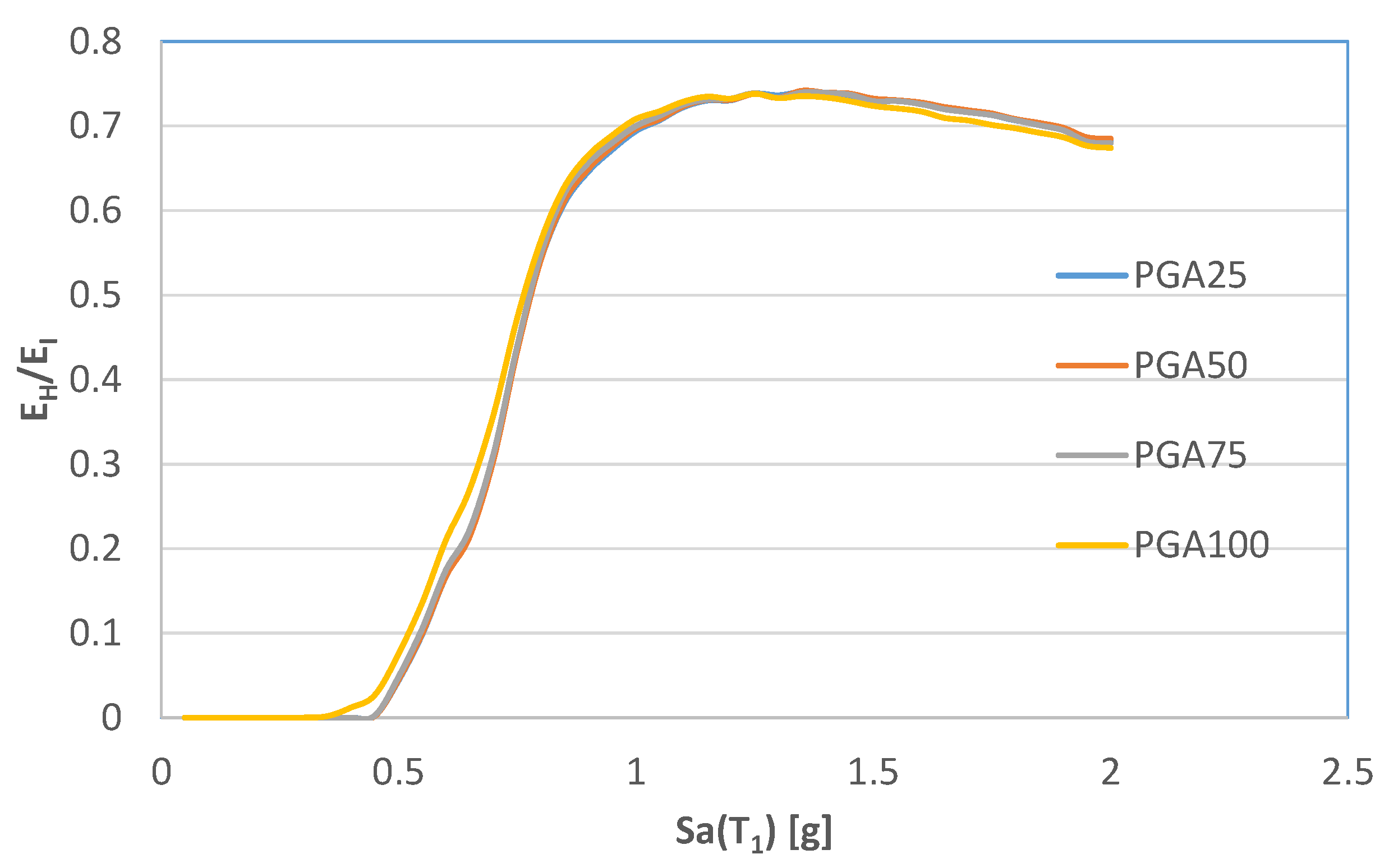
7. Numerical Results
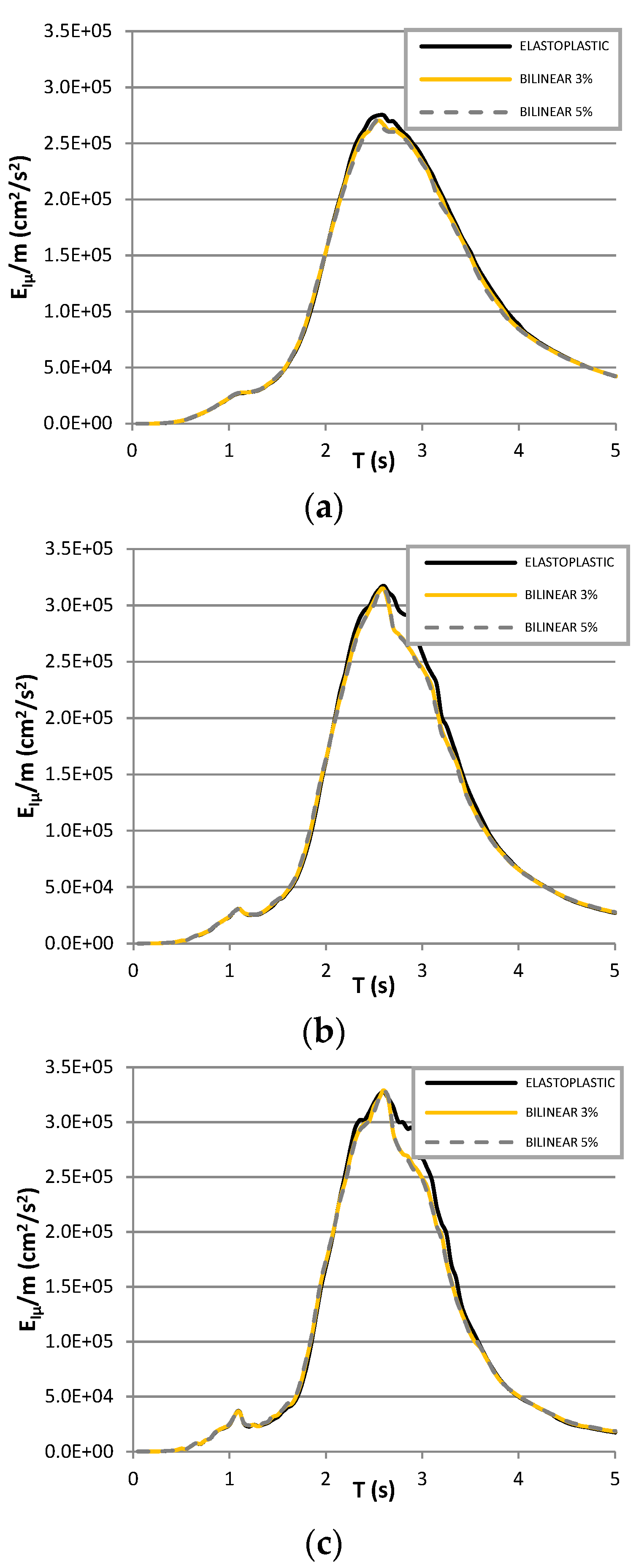
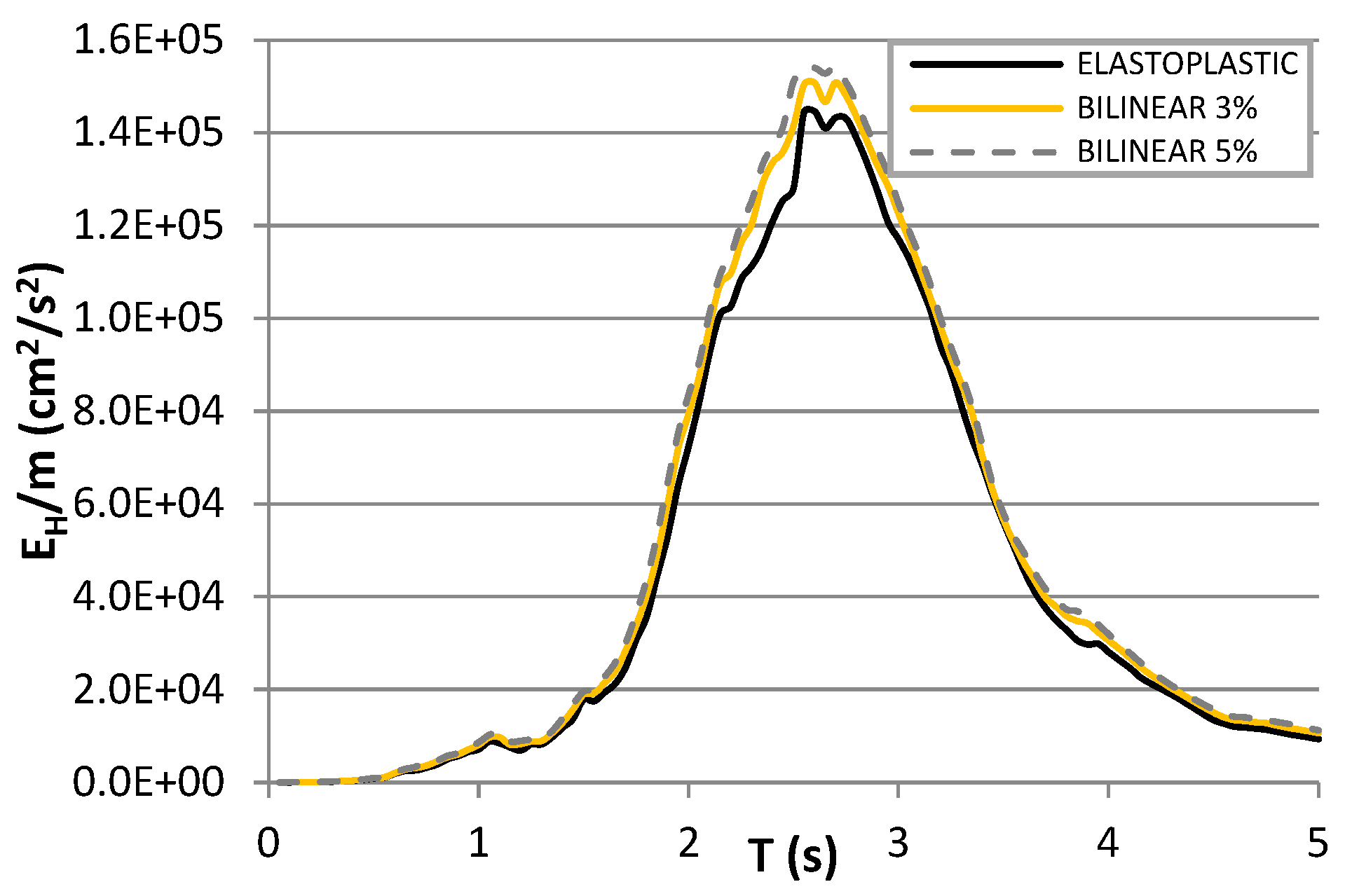
7.1. Elastic Energy Spectra
7.2. Inelastic Energy Spectra
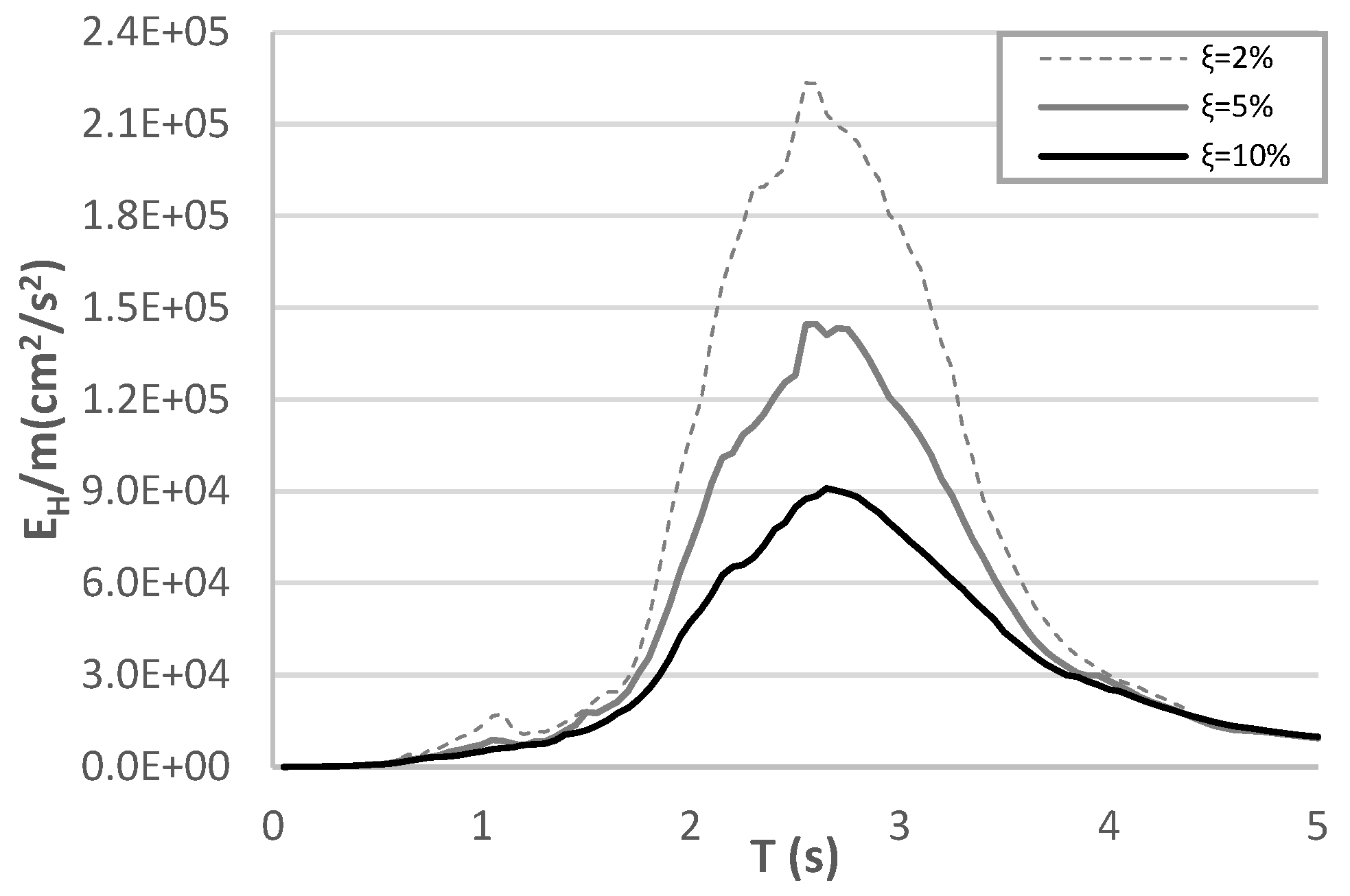
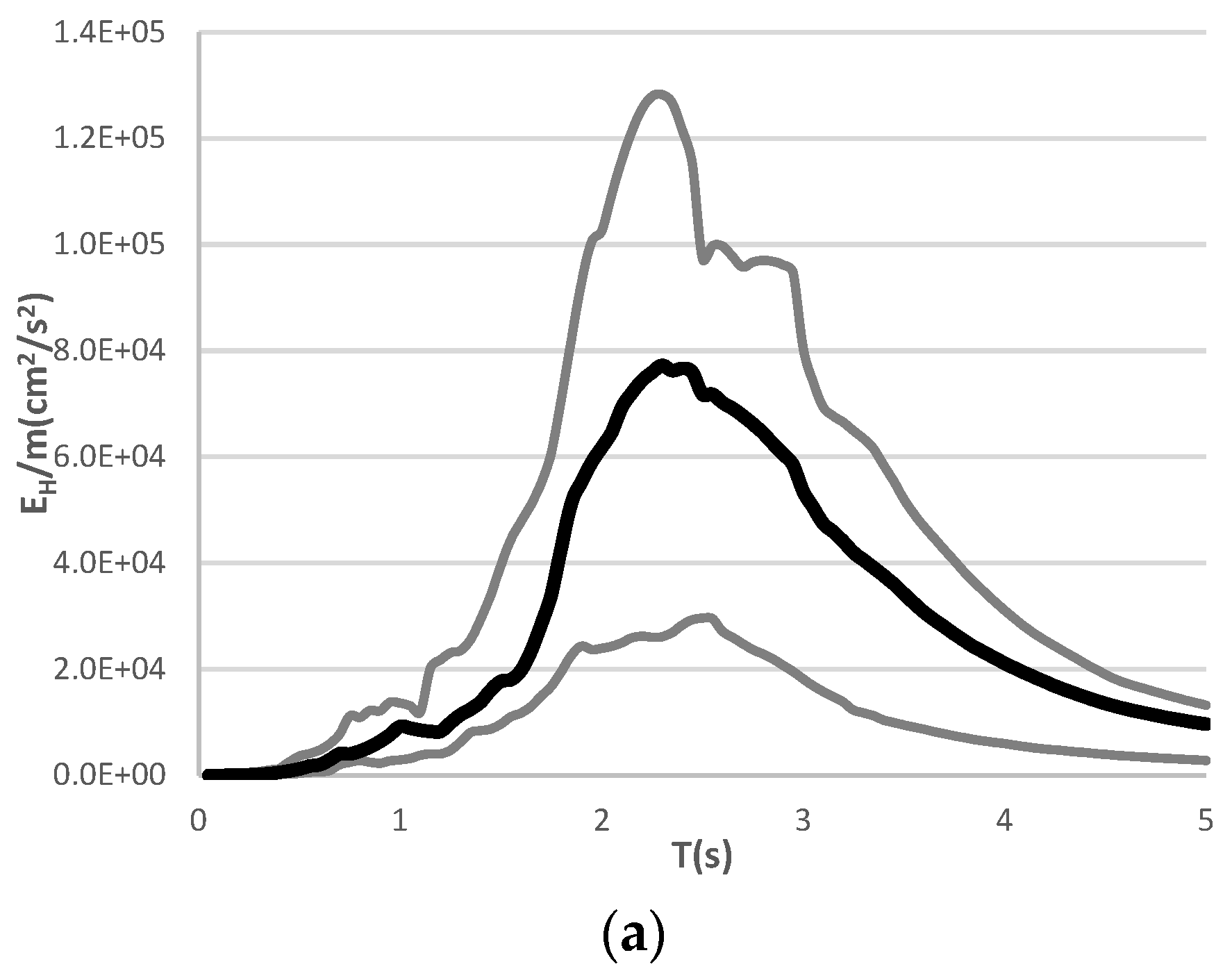
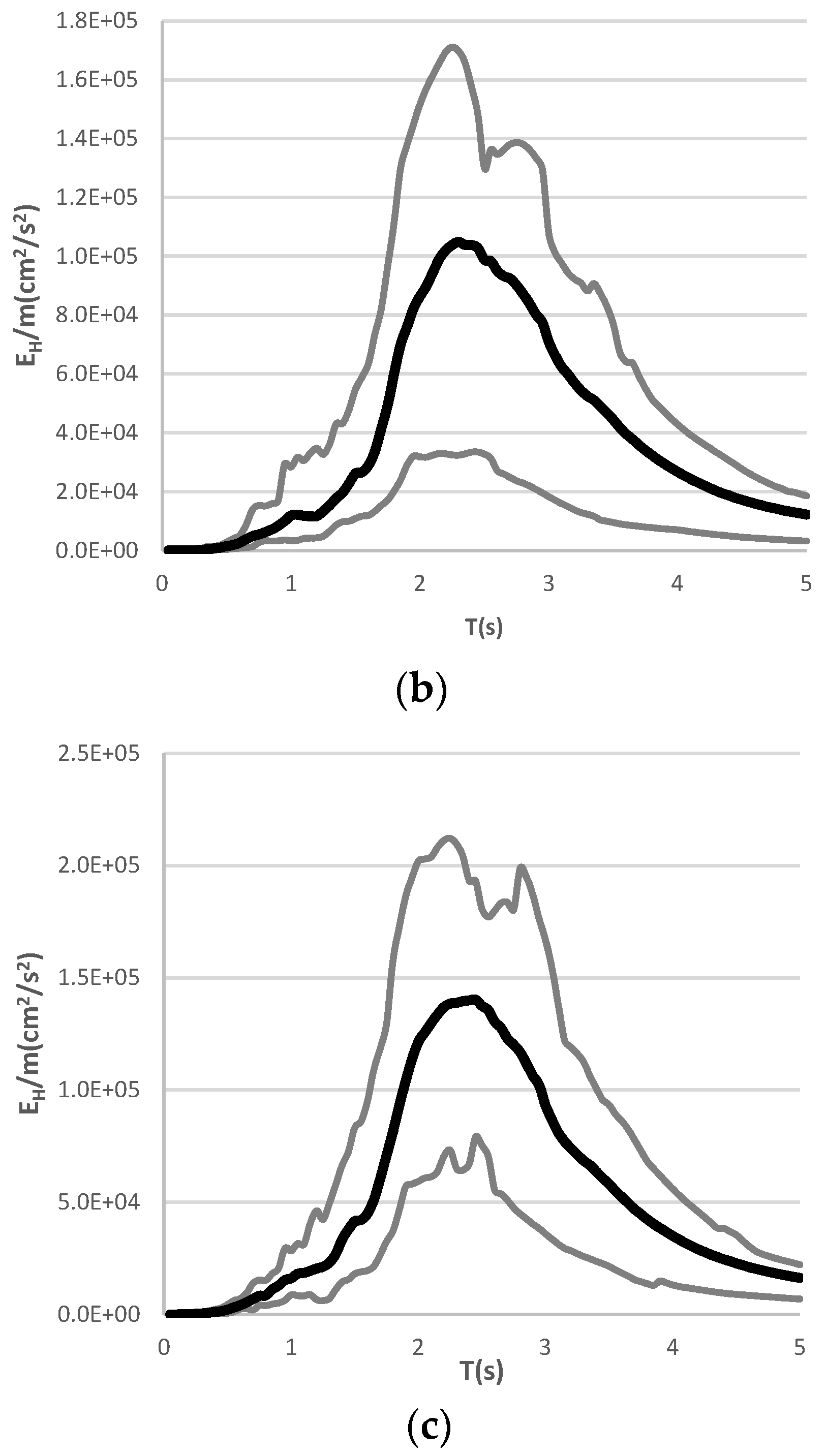
7.3. Hysteretic Energy Spectra
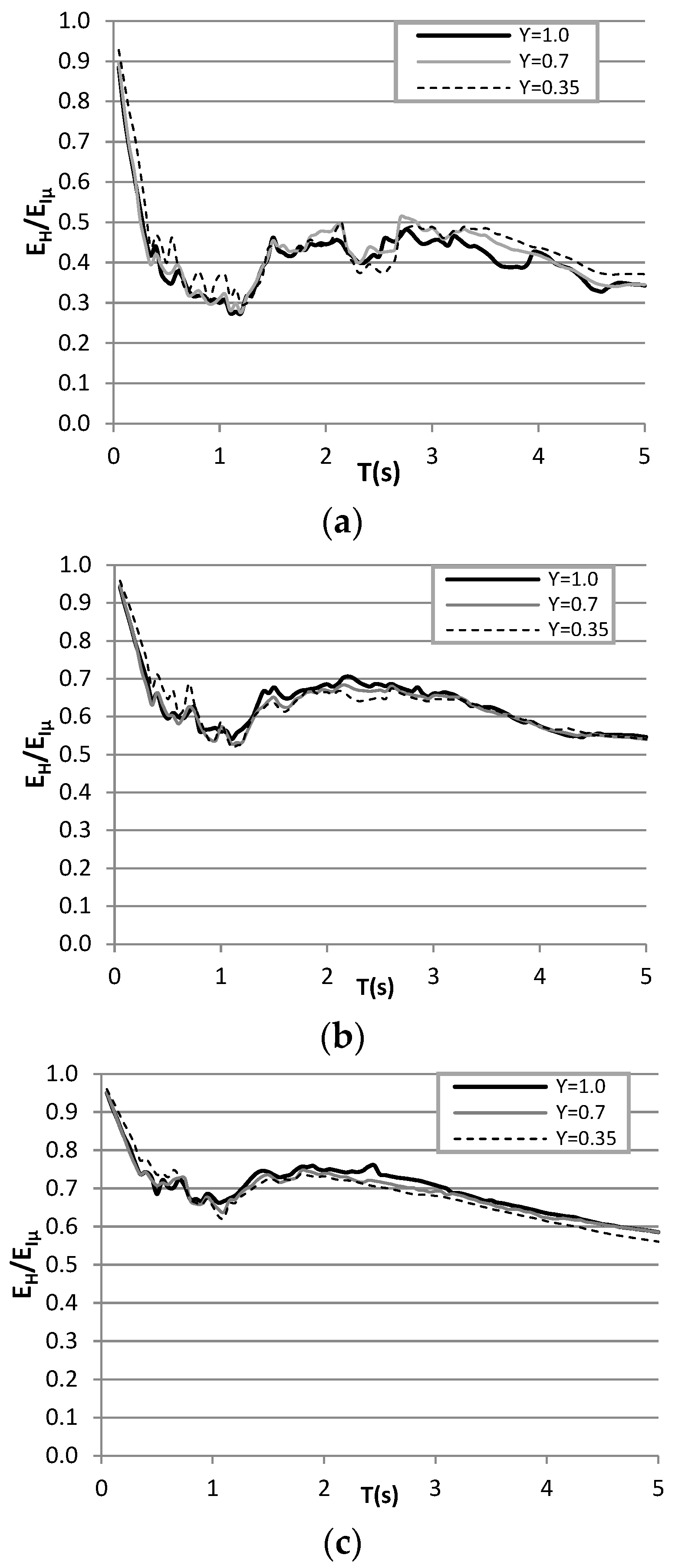
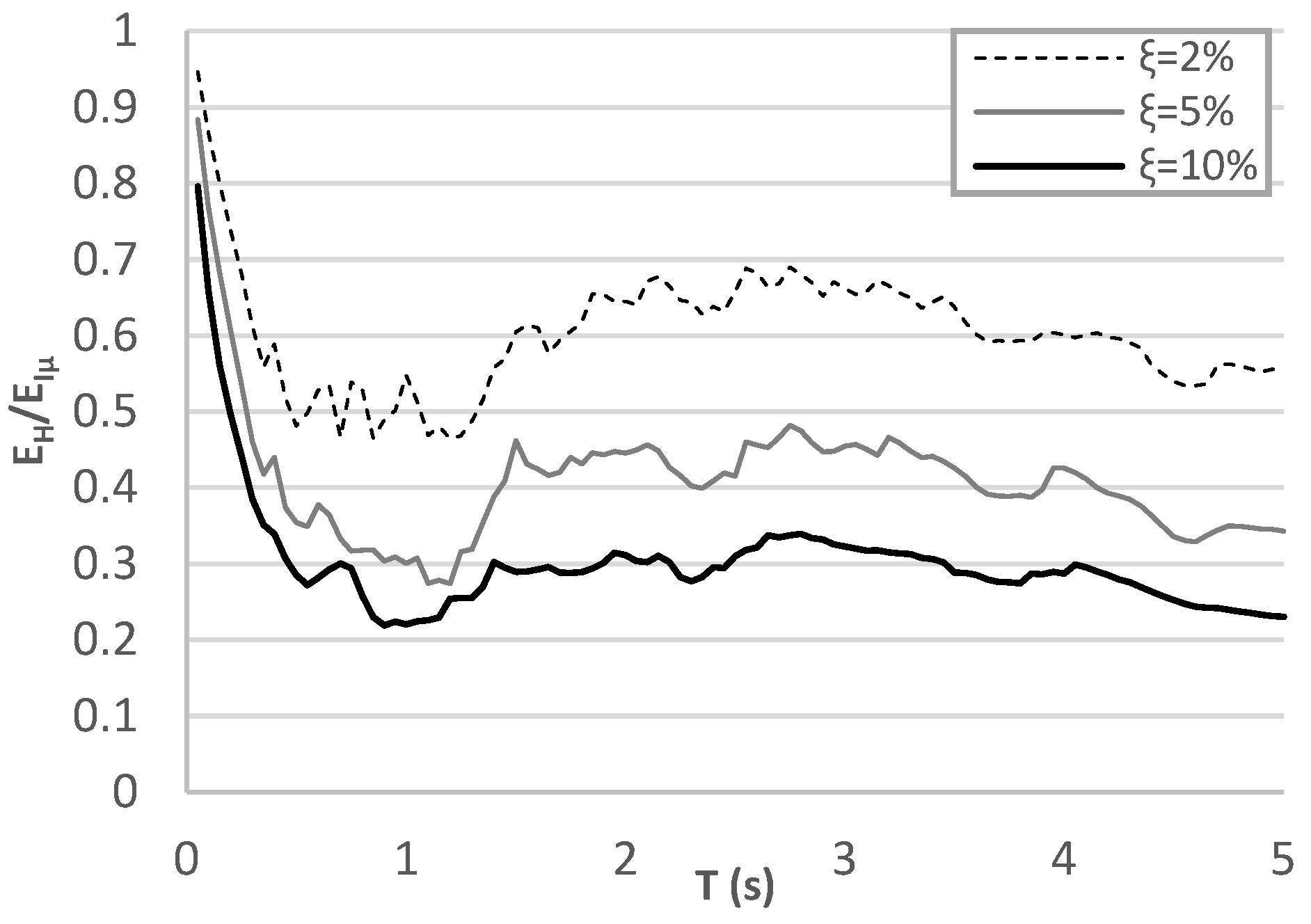
7.4. EH/EIμ Ratio Spectra
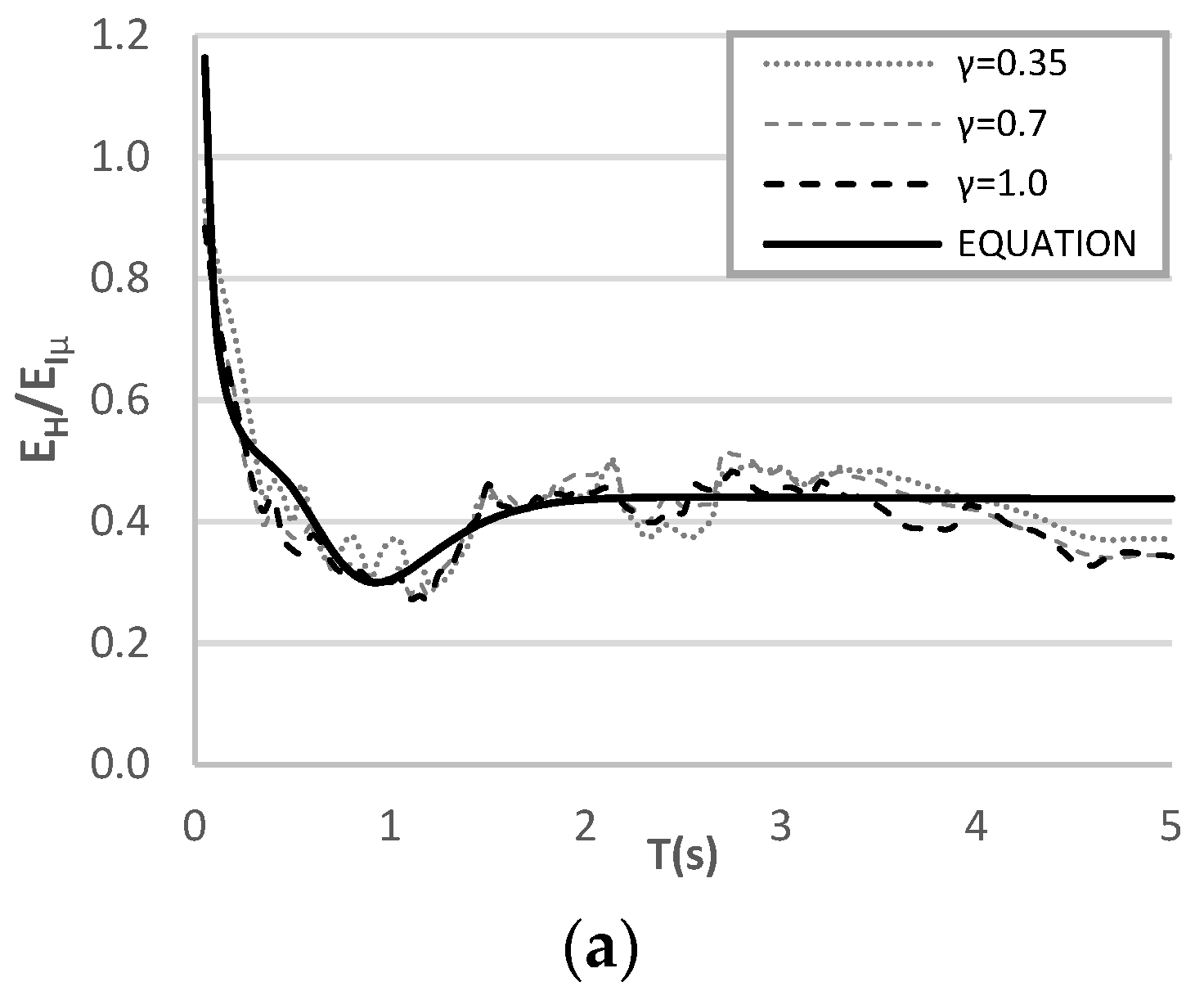
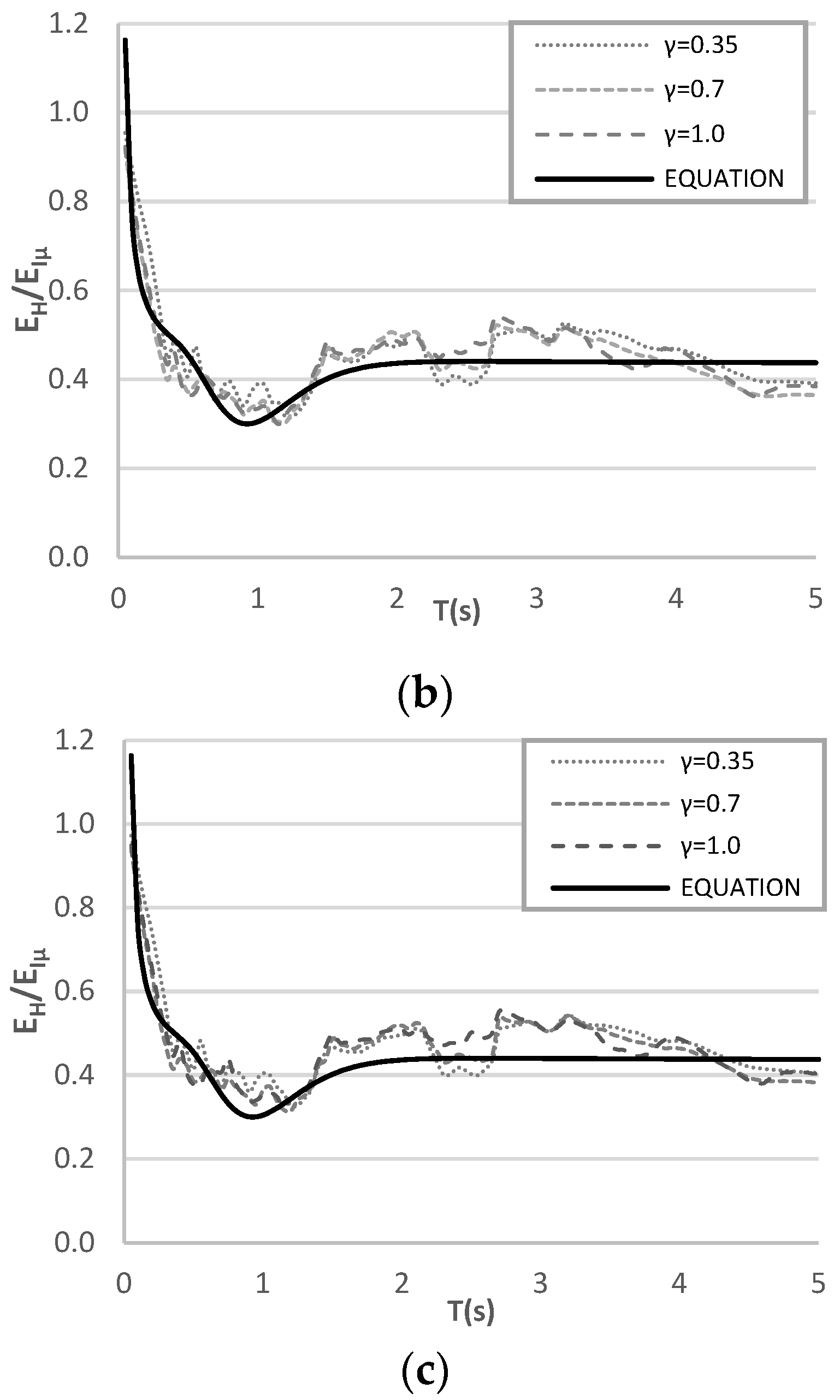
8. Proposed Equation
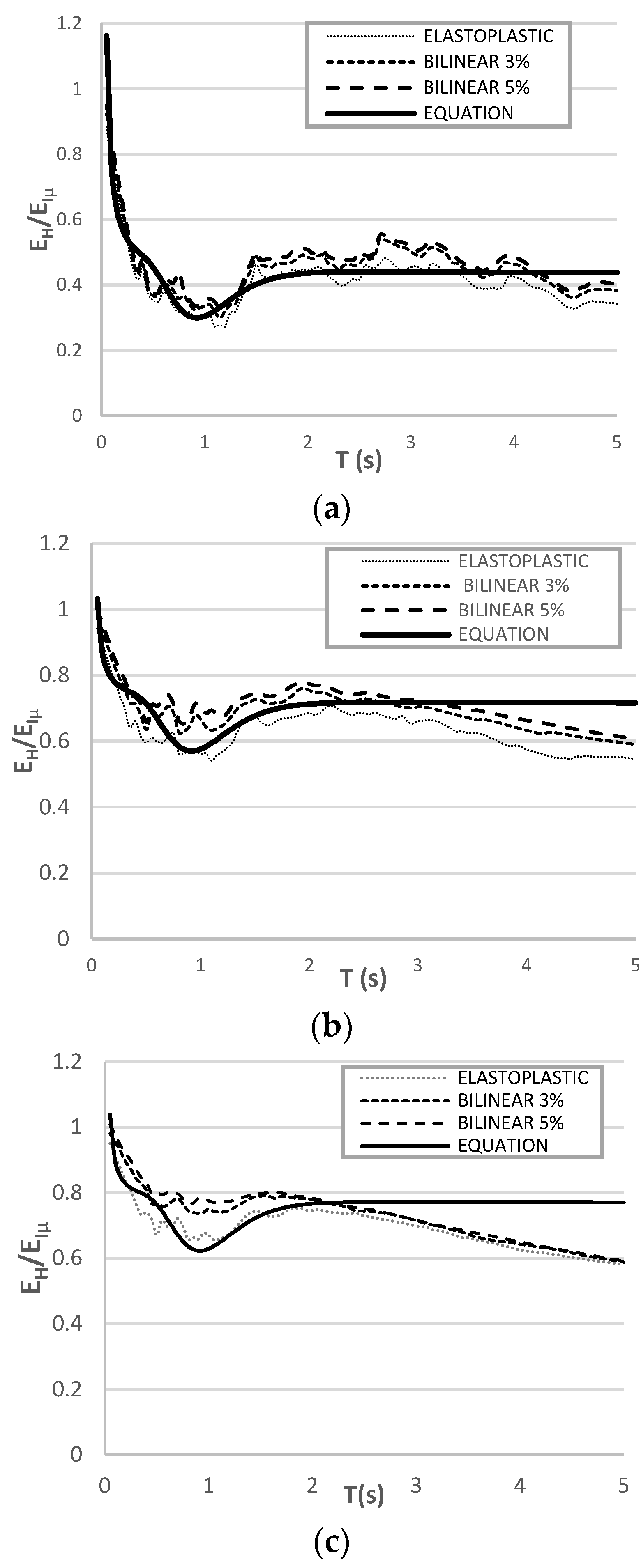
9. Energy Ratio in a Multi-Degree-of-Freedom Reinforced-Concrete Buildings under Seismic Sequences
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Atzori, S.; Tolomei, C.; Antonioli, A.; Boncori, J.M.; Bannister, S.; Trasatti, E.; Pasquali, P.; Salvi, S. The 2010–2011 Canterbury, New Zealand, seismic sequence: Multiple source analysis from InSAR data and modeling. J. Geophys. Res. 2012, 117, B08305. [Google Scholar] [CrossRef]
- Kazuhiko Kasai, M.; Mita, A.; Kitamura, H.; Matsuda, K.; Morgan, T.A.; Taylor, A.W. Performance of Seismic Protection Technologies during the 2011 Tohoku-Oki Earthquake. Earthq. Spectra. 2013, 29, S265–S293. [Google Scholar] [CrossRef]
- Moon, L.; Dizhur, D.; Senaldi, I.; Derakhshan, H.; Griffith, M.; EERI, M.; Magenes, G.; Ingham, J. The Demise of the URM Building Stock in Christchurch during the 2010–2011 Canterbury Earthquake Secuence. Earthq. Spectra. 2014, 30, 253–276. [Google Scholar] [CrossRef] [Green Version]
- Kam, W.Y.; Pampanin, S.; Elwood, K. Seismic Performance of Reinforced Concrete Buildings in the 22 February Christchurch (Lyttelton) earthquake. N. Z. Soc. Earthq. Eng. 2011, 44, 239–278. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Ellingwood, B. Performance evaluation and damage assessment of steel frame buildings under main shock-artershock earthquake sequences. Earthq. Eng. Struct. Dyn. 2007, 36, 405–427. [Google Scholar] [CrossRef]
- Singh, D.K.; Mandal, A.; Karumanchi, S.R.; Murmu, A.; Sivakumar, N. Seismic Behaviour of damaged tunnel during aftershock. Eng. Fail. Anal. 2018, 93, 44–54. [Google Scholar] [CrossRef]
- Lemnitzer, A.; Massone, L.M.; Skolnik, D.; de la Llera Martin, J.C.; Wallace, J.W. Afttershock response of RC buildings in Santiago, Chile, succeeding the magnitude 8.8 Maule earthquake. Eng. Struct. 2014, 76, 324–338. [Google Scholar] [CrossRef]
- Mexico City Building Code. Complementary Technical Norms for Earthquake Resistant Design, Mexico City (RCDF-17); Mexico City Building Code: Mexico City, Mexico, 2017. [Google Scholar]
- MOC-CFE-15; Seismic Design, Design Manual of Civil Works. Federal Commission of Electricity: Mexico City, Mexico, 2015.
- Norma Chilena Oficial. Diseño Sísmico de Edificios; Instituto Nacional de Normalización: Santiago, Chile, 2012. [Google Scholar]
- Gentile, R.; Galasso, C. Hysteretic energy-based state-dependent fragility for ground-motion sequences. Earthq. Eng. Struct. Dyn. 2020, 50, 1187–1203. [Google Scholar] [CrossRef]
- De Risi, R.; Sextos, A.; Zimmaro, P.; Simonelli, A.; Stewart, J. The 2016 Central Italy earthquakes sequence: Observations of incremental building damage. In Proceeding of the 11th U.S. National Conference on Earthquake Engineering, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Aljawhari, K.; Gentile, R.; Freddi, F.; Galasso, C. Effects of ground-motion sequences on fragility and vulnerability of case-study reinforced concrete frames. Bull. Earthq. Eng. 2021, 19, 6329–6359. [Google Scholar] [CrossRef]
- Amiri, S.; Bojórquez, E. Residual displacement ratios of structures under mainshock-aftershock sequences. Soil Dyn. Earthq. Eng. 2019, 121, 179–189. [Google Scholar] [CrossRef]
- Amiri, S.; Garakaninezhad, A.; Bojórquez, E. Normalized residual displacement spectra for post-mainshock assessment of structures subjected to aftershocks. Earthq. Eng. Eng. Vib. 2021, 20, 403–421. [Google Scholar] [CrossRef]
- Lopez-Caballero, F.; Aristizabal, C.; Sanchez-Silva, M. A model to estimate the lifetime of structures located in seismically active regions. Eng. Struct. 2020, 215, 110662. [Google Scholar] [CrossRef]
- Khalil, C.; Lopez-Caballero, F. Survival analysis of a liquefiable embankment subjected to sequential earthquakes. Soil Dyn. Earthq. Eng. 2021, 140, 106436. [Google Scholar] [CrossRef]
- Clark, T.; Bradburn, M.; Love, S.; Altman, D. Survival analysis part i: Basic concepts and first analyses. Br. J. Canc. 2003, 89, 232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schober, P.; Vetter, T.R. Survival analysis and interpretation of time-to-event data: The tortoise and the hare. Anesth. Analg. 2018, 127, 792. [Google Scholar] [CrossRef] [PubMed]
- Diamoutene, A.; Barro, D.; Somda, S.M.A.; Noureddine, F.; Kamsu-Foguem, B. Survival analysis in living and engineering sciences. JP J. Biostat. 2016, 13, 223–238. [Google Scholar]
- EC8-05 EuroCode-8; Design of Structures for Earthquake Resistance. Part 1: General Rules, Seismic Actions and Rules for Buildings. Deutsches Institut für Normung e.V.: Berlin, Germany, 2005.
- ASCE 7-16, ASCE Standard ACE/SEI 7-05; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- Aliakbari, F.; Garivani, S.; Aghakouchak, A. An energy based method for seismic design of frame structures equipped with metallic yielding dampers considering uniform inter-story drift concept. Eng. Struct. 2020, 105, 110114. [Google Scholar] [CrossRef]
- Ma, C. Energy-based seismic design method for EBFs based on hysteretic energy spectra and accumulated ductility ratio spectra. Adv. Civ. Eng. 2019, 2019, 3180596. [Google Scholar] [CrossRef] [Green Version]
- Song, G.; Yang, T.; Zhou, Y. Energy-based seismic design for self-centering concrete frames. Bull. Earthq. Eng. 2021, 19, 5113–5137. [Google Scholar] [CrossRef]
- Bojórquez, E.; Reyes-Salazar, A.; Terán-Gilmore, A.; Ruiz, S.E. Energy-based damage index for Steel Structures. Steel Compos. Struct. 2010, 10, 343–360. [Google Scholar] [CrossRef] [Green Version]
- Bojórquez, E.; Ruiz, S.E.; Terán-Gilmore, A. Reliability-based evaluation of steel structures using energy concepts. Eng. Struct. 2008, 30, 1745–1759. [Google Scholar] [CrossRef]
- Fajfar, P.; Vidic, T. Consistent inelastic design spectra: Hysteretic and input energy. Earthq. Eng. Struct. Dyn. 1994, 23, 523–532. [Google Scholar] [CrossRef]
- Akiyama, H. Earthquake Resistant Limit-State Design for Buildings; University of Tokyo Press: Tokyo, Japan, 1985. [Google Scholar]
- Kuwamura, H.; Galambos, T.V. Earthquake load for structural reliability. J. Struct. Eng. ASCE 1989, 115, 1446–1462. [Google Scholar] [CrossRef]
- Krawinkler, H.; Nassar, A.A. Seismic design based on ductility and cumulative damage demands and capacities. In Nonlinear Seismic Analysis and Design of Reinforced Concrete Buildings; Krawinkler, H., Fajfar, P., Eds.; Elsevier Applied Science: London, UK, 1992; pp. 95–104. [Google Scholar]
- Fajfar, P.; Vidic, T.; Fischinger, M. On energy demand and supply in SDOF systems. In Nonlinear Seismic Analysis and Design of Reinforced Concrete Buildings; CRC Press: Boca Raton, FL, USA, 1992; pp. 48–71. [Google Scholar]
- Decanini, L.; Mollaioli, F. An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 2001, 21, 113–137. [Google Scholar] [CrossRef]
- Akbas, B.; Aksar, B.; Doran, B.; Alacali, S. Hysteretic energy to energy input ratio spectrum in nonlinear systems. Deu Muhendis. Fak. Fen Ve Muhendis. 2016, 18, 239–254. [Google Scholar] [CrossRef]
- Karen, R.F.; Rachel, E.A.; Göran, E. A Common Origin for Aftershocks, and Multiplets. Bull. Seismol. Soc. Am. 2004, 94, 88–98. [Google Scholar]
- Yamashita, T.; Knopoff, L. Models of aftershock occurrence. Geophys. J. Int. 1987, 91, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Henry, C. Spatiel Relation Between main earthquake slip and its aftershock distribution. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef] [Green Version]
- Molchan, G.M.; Dmitrieva, O.E. Aftershock identification: Methods and new approaches. Geophys. J. Int. 1992, 109, 501–516. [Google Scholar] [CrossRef]
- Karen, R.F.; Becker, T.; Abercrombie, R.; Ekstom, G.; Rice, J. Triggering of the 1999 Mw 7.1 Hector Mine earthquake by afthershocks of the 1992 Mw 7.3 Landers earthquake. Journal of Geophysical Research. Solid Earth 2002, 107, 2190. [Google Scholar] [CrossRef]
- Karen, R.F.; Abercrombie, R.; Ekstom, G. Secondary aftershocks and their importance for aftershock forecasting. Bull. Seismol. Soc. Am. 2003, 93, 1433–1448. [Google Scholar] [CrossRef]
- Ogata, Y.; Jones, L.; Toda, S. When and where the aftershock activity was depressed: Contrasting decay patterns of the proximate large earthquakes in southern California. J. Geophys. Res. Solid Earth 2003, 108, 2318. [Google Scholar] [CrossRef]
- Chiarabba, C.; De Gori, P.; Chiaraluce, L.; Bordoni, P.; Cattaneo, M. Mainshocks and Aftershocks of the 2002 Molise Seismic Sequence, Southern Italy. J. Seismol. 2005, 9, 487–494. [Google Scholar] [CrossRef]
- Song, R.; Li, Y.; Van de Lindt, J. Loss estimation of Steel buildings to earthquake mainshocks-aftershock sequences. Struct. Saf. 2016, 61, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Felzer, K. Simulated aftershock sequences for an M 7.8 earthquake on the southern San Andreas fault. Seismol. Res. Lett. 2009, 80, 21–25. [Google Scholar] [CrossRef]
- Milne, J.; Lee, A.W. Earthquakes and Other Earth Movements; Kegan Paul, Trench, Trübner & Co: London, UK, 1939; p. 244. [Google Scholar]
- Omori, F. On the aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–120. [Google Scholar]
- Båth, M. Lateral inhomogeneities of the upper mantle. Tectonophysics 1965, 2, 483–514. [Google Scholar] [CrossRef]
- Helmstetter, A.; Sornette, D. Båth’s law derived from the Gutenberg-Richter law and from aftershock properties. Geophys. Res. Lett. 2003, 30, 2069. [Google Scholar] [CrossRef] [Green Version]
- Vere-Jones, D. A limit theorem with application to Båth’s law in seismology. Appl. Probab. Trust 2008, 40, 882–896. [Google Scholar] [CrossRef] [Green Version]
- Karen, R.F.; Debi, K. A Case Study of Two M ∼5 Mainshocks in Anza, California: Is the Footprint of an Aftershock Sequence Larger Than We Think? Bull. Seismol. Soc. Am. 2009, 99, 2721–2735. [Google Scholar] [CrossRef]
- Felder, K.R.; Brodsky, E.E. Decay of aftershock density with distance indicates triggering by dynamic stress. Nature 2006, 441, 735–738. [Google Scholar] [CrossRef] [Green Version]
- Hough, S.E. Remotely triggered earthquakes following moderate mainshocks (or why California is not falling into the ocean). Seismol. Res. Lett. 2005, 76, 58–66. [Google Scholar] [CrossRef] [Green Version]
- Steacy, S.; Gomberg, J.; Cocco, M. Introduction to special section: Stress transfer, earthquake triggering, and time-dependent seismic hazard. J. Geophys. Res. Solid Earth 2005, 110, B05S01. [Google Scholar] [CrossRef]
- Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Nur, A.; Booker, J.R. Aftershocks caused by pore fluid flow? Science 1972, 175, 885–887. [Google Scholar] [CrossRef]
- Gomberg, J. The failure of earthquake failure models. J. Geophys. Res. Solid Earth. 2001, 106, 16253–16263. [Google Scholar] [CrossRef] [Green Version]
- Housner, G.W. Limit design of structures to resist earthquakes. In Proceedings of the 1st WCEE, Berkeler, CA, USA, 1–13 May 1956. [Google Scholar]
- Zahrah, T.F.; Hall, W.J. Earthquake energy absorption in SDOF structures. J. Struct. Eng. 1984, 110, 1757–1772. [Google Scholar] [CrossRef]
- Zahrah, T.F.; Hall, W.J. Seismic Energy Absorption in Simple Structures; Civil Engineering Studies. Structural Research Series No 501; University of Illinois at Urbana-Champaign: Urbana, IL, USA; Champaign, IL, USA, 1982. [Google Scholar]
- Uang, C.M.; Bertero, V.V. Use of Energy as a Design Criterion in Earthquake Resistant Design; Report No. ºCB/EERC-88/18; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1988. [Google Scholar]
- Uang, C.M.; Bertero, V.V. Evaluation of Seismic Energy in Structures. Earthq. Eng. Struct. Dyn. 1990, 19, 77–90. [Google Scholar] [CrossRef]
- Manfredi, G. Evaluation of seismic energy demand. Earthq. Eng. Struct. Dyn. 2001, 30, 485–499. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Pujades, L.G.; Lopez-Almansa, F. Design energy input spectra for moderate-seismicity regions. Earthq. Eng. Struct. Dyn. 2002, 31, 1151–1172. [Google Scholar] [CrossRef]
- Zhou, Y.; Song, G.G.; Tan, P.P. Hysteretic energy demand for self-centering SDOF systems. Soil Dyn. Earthq. Eng. 2019, 125, 105703. [Google Scholar] [CrossRef]
- Mexican strong earthquake database, Sociedad Mexicana de Ingeniería Sísmica. Available online: https://www.smis.mx (accessed on 21 January 2023).
- Mezgebo, M.G. Estimation of Earthquake Input Energy, Hysteretic Energy and Its Distribution in MDOF Structures. Ph.D. Thesis, Syracuse University, New York, NY, USA, 2015. [Google Scholar]
- Alici, F.S.; Sucuoğlu, H. Elastic and Inelastic Near-Fault Input Energy Spectra. Earthq. Spectra 2018, 34, 611–637. [Google Scholar] [CrossRef]
- Merter, O. An investigation on the maximum earthquake input energy for elastic SDOF systems. Earthq. Struct. 2019, 16, 487–499. [Google Scholar]
- Torres, J.I.; Bojórquez, E.; Reyes, A.; Bojórquez, J. Vector-Valued Intensity Measures to Predict Peak and Hysteretic Energy Demands of 3D R/C Buildings. In Energy-Based Seismic Engineering; IWEBSE Lecture Notes in Civil Engineering; Benavent-Climent, A., Mollaioli, F., Eds.; Springer: Cham, Switzerland, 2021; Volume 155. [Google Scholar] [CrossRef]

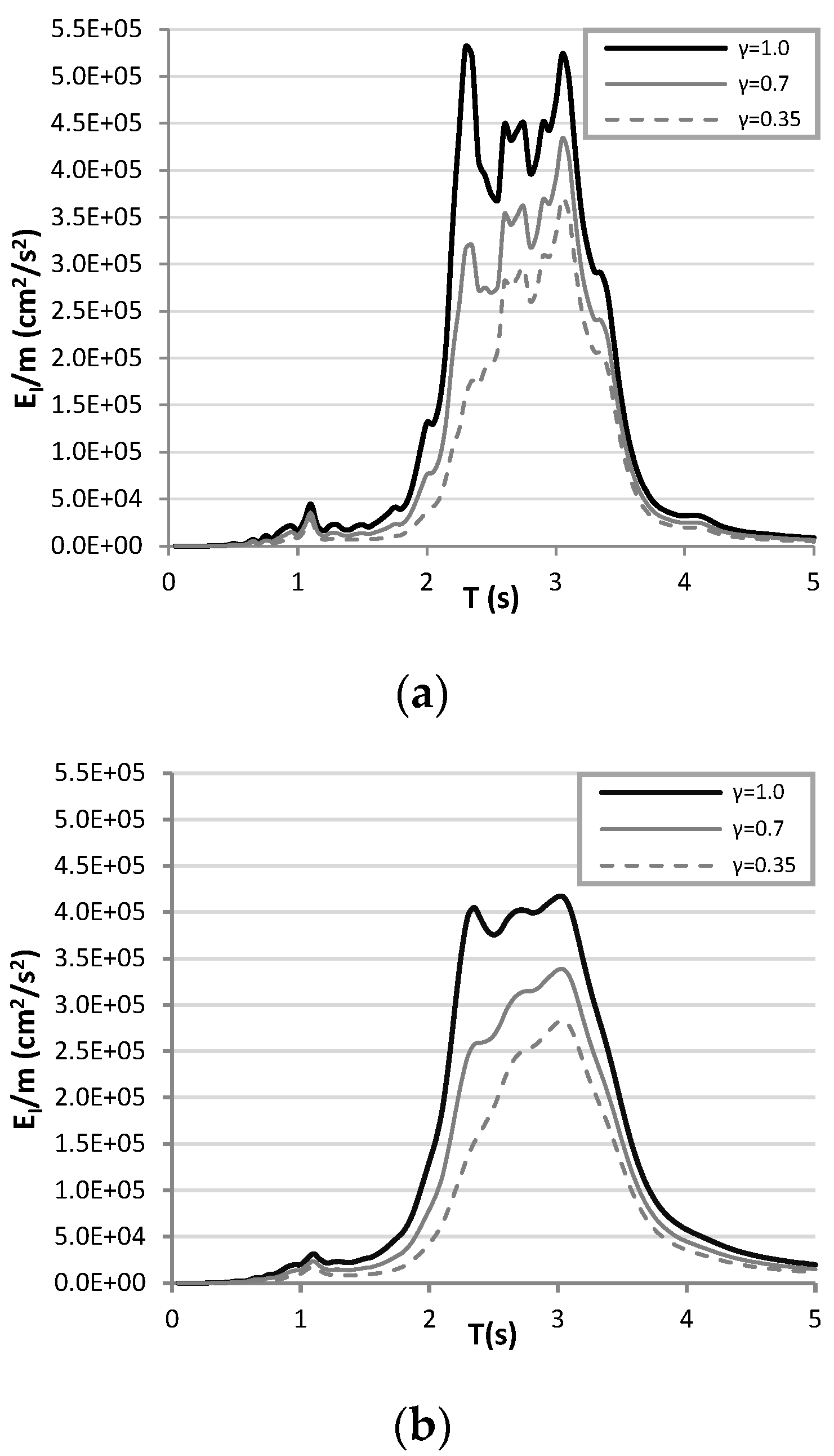
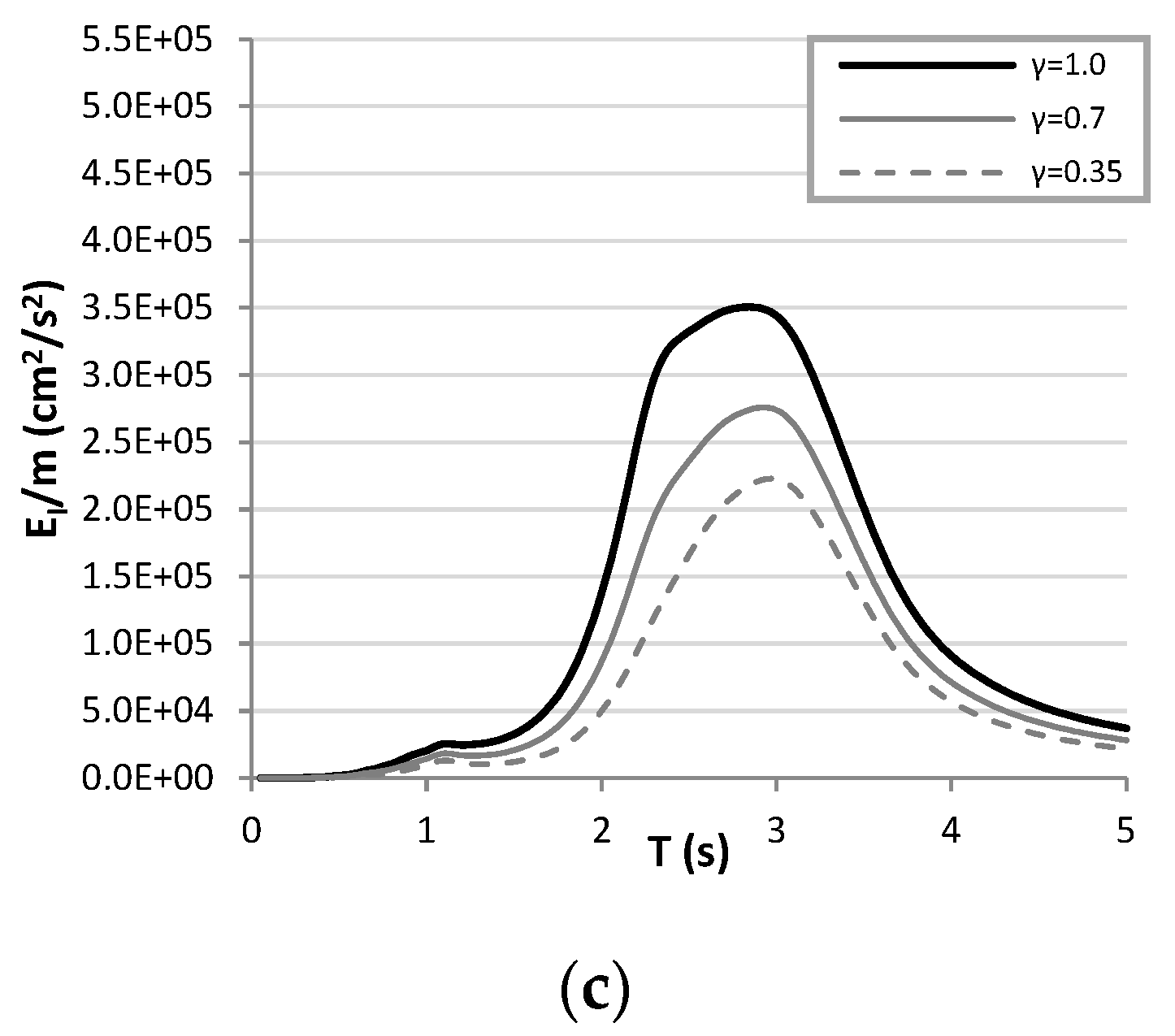
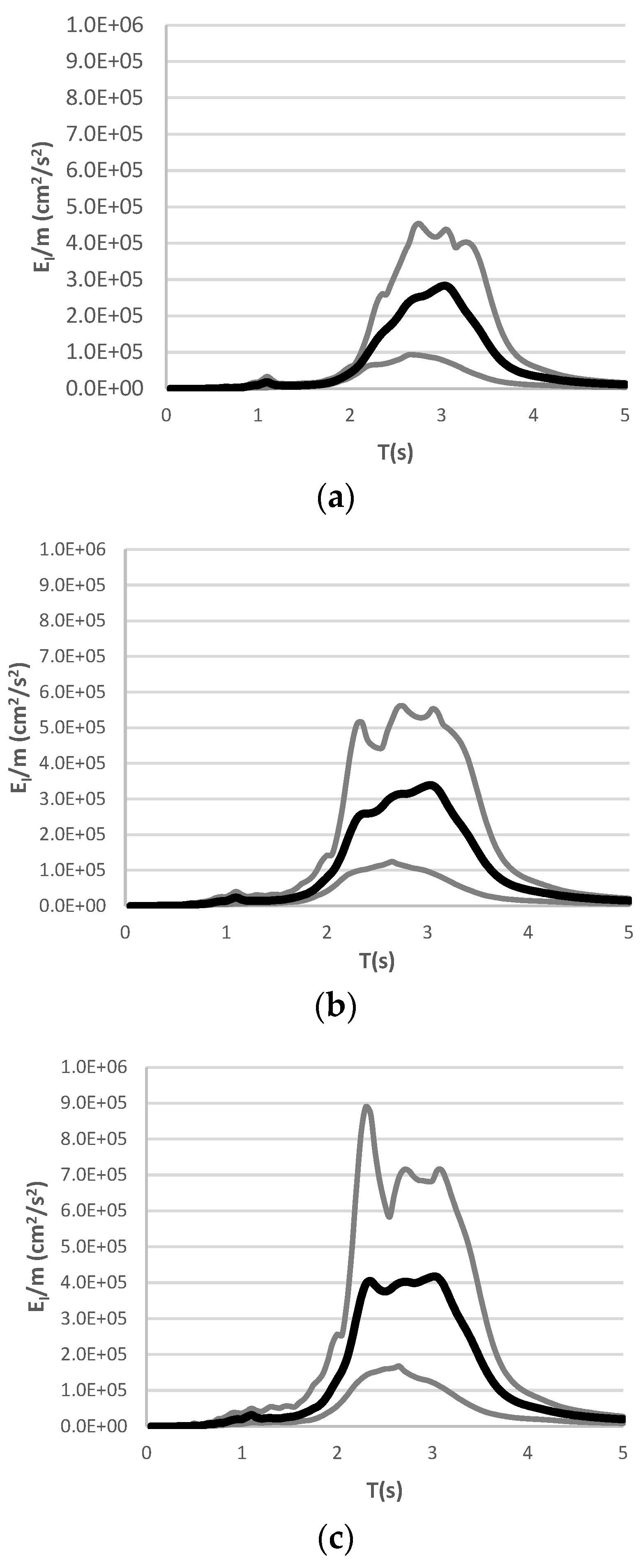
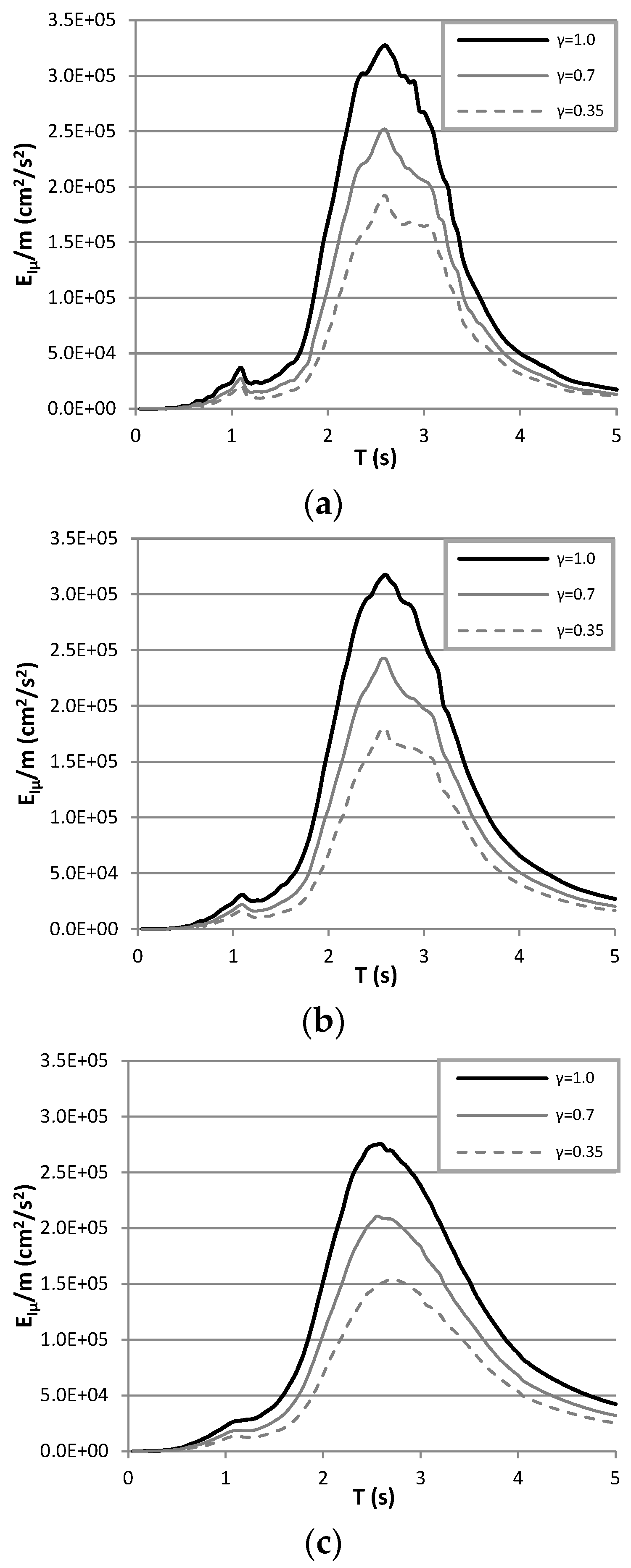






| Events | Date | Country | Mw | Aftershocks |
|---|---|---|---|---|
| 1 | 05/22/1960 | Chile | 9.5 | Six aftershocks. The biggest was 8.75 Mw. |
| 2 | 09/19/1985 | Mexico | 8.1 | Strong aftershocks the next day. The biggest was 7.5 Mw. |
| 3 | 06/28/1992 | Landers, California. | 7.3 | Aftershock of 6.5 Mw in Big Bear City. |
| 4 | 12/26/2004 | Indonesia | 9.1 | A total of 69 aftershocks. The biggest was 7.1 Mw. |
| 5 | 05/13/2005 | Chile | 7.8 | Approximately 2000 aftershocks. |
| 6 | 03/28/2005 | Indonesia | 8.6 | Eight major aftershocks between 5.5 and 6.0 Mw. |
| 7 | 10/08/2005 | Pakistan | 7.6 | A total of 147 aftershocks the next day. The biggest was 6.2 Mw. |
| 8 | 05/12/2008 | China | 8.2 | A total of 46 aftershocks. The biggest was 5.0 Mw. |
| 9 | 02/27/2010 | Chile | 8.8 | A total of 22 aftershocks greater than 6.0 Mw. The biggest was 6.9 Mw. |
| 10 | 02/02/2010 | Haiti | 7.0 | Strong aftershocks between 5.9 and 5.1 Mw were recorded. |
| 11 | 03/11/2011 | Japan | 9 | More than a thousand aftershocks. The strongest were 7.4, 7.9 and 7.7 Mw. |
| 12 | 02/22/2011 | New Zealand | 6.3 | A minute later, a 6.0 Mw aftershock appeared. |
| 13 | 04/11/2012 | Indonesia | 8.6 | A total of 111 aftershocks greater than 4.0 Mw. The biggest was 8.2 Mw. |
| 14 | 09/24/2013 | Pakistan | 7.8 | Hundreds of aftershocks. The biggest was 7.2 Mw. |
| 15 | 04/25/2015 | Nepal | 8.1 | One aftershock reached 6.7 Mw and another was 5 Mw. |
| 16 | 09/19/2017 | Mexico | 7.5 | A total of 9945 aftershocks as of November 6. Two aftershocks were 5.8 and 6.1 Mw. |
| 17 | 02/25/2018 | New Guinea | 7.5 | Aftershocks of 6.0 Mw, 6.7 Mw and 6.3 Mw. |
| 18 | 08/05/2018 | Indonesia | 7.5 | Foreshock of 6.1 Mw, mainshock of 7.5 Mw and 350 aftershocks. |
| 19 | 05/22/2021 | China | 7.3 | Foreshock of 6.4 Mw, after four events greater than magnitude 5 Mw, mainshock of 7.3 Mw and many aftershocks. |
| 20 | 02/06/2023 | Turkey and Syria | 7.8 | Several aftershocks including some with magnitudes larger than 6 Mw. |
| 21 | 02/06/2023 | Turkey and Syria | 7.5 | Mainshock near Kahramanmaraş, several aftershocks, including some with magnitudes larger than 6 Mw. |
| No. | Researchers | Proposals | Description |
|---|---|---|---|
| 1 | Akiyama [29] | = 1 − | ζ is the damping coefficient. |
| 2 | Kuwumura and Galambos [30] | = 1 – | φ is defined as the ratio between the plastic displacement and the creep displacement, and ζ is the damping coefficient. |
| 3 | Fajfar and Vidic [28] | = CE | μ is the ductility. CE and CH are constants that depend on the hysteretic model and the damping. |
| 4 | Manfredi [62] | = 0.72 | μc is the cyclic ductility, equal to 1 + ∆xmax/xy. |
| 5 | Decanini and Molallioli [33] | = Ks | Ks is a coefficient that depends on the type of soil and assumes the values of 0.75, 0.8 and 0.9 for the soil types S1, S2 and S3, respectively, and μ is the ductility. |
| 6 | Benavent-Climent [63] | = | η is a coefficient presenting the level of plastification, and it is estimated by η ≅ 4 (μ − 1); ξ denotes damping ratio; μ is ductility. |
| 7 | B. Akbas, B. Aksar, B. Doran and Alacali [34] | (n)= a + b + cT + d (EH/EI)MDOF = CEH/EI × (EH/EI)SDOF | a, b, c, and d are polynomial constants, and CEH/EI is the modification factor for MDOF. |
| 8 | Zhou, Song GG and Tan PP [64] | )Benchmark = 0.35 () = I1 I2 I3 ()Benchmark | I1, I2, and I3 are theinfluence coefficients. |
| Station | Date | Component | PGA (cm/s2) | Tg (s) | |
|---|---|---|---|---|---|
| MAINSHOCKS | CDAF | 19/09/1985 | N-S | 61.62 | 2.88 |
| E-W | 88.26 | 2.96 | |||
| AFTERSHOCKS | CDAF | 20/09/1985 | N-S | 40.14 | 2.28 |
| E-W | 30.25 | 3.01 |
| # | No. Station | Name | Magnitude (Ms) | PGA (cm/s2) | PGV (cm/s) | Tg (s) |
|---|---|---|---|---|---|---|
| 1 | 29 | Villa del mar | 6.9 | 46.5 | 15.3 | 2.96 |
| 2 | 29 | Villa del mar | 6.9 | 49.4 | 22.0 | 2.96 |
| 3 | 43 | Jamaica | 6.9 | 35.2 | 15.6 | 3.04 |
| 4 | 48 | Rodolfo Menéndez | 6.9 | 47.7 | 18.8 | 2.89 |
| 5 | 25 | P.C.C. Superficie | 6.9 | 42.5 | 15.4 | 2.3 |
| 6 | 56 | Córdova | 7.1 | 19.4 | 11.2 | 2.3 |
| 7 | 58 | Liverpool | 6.9 | 40 | 12.4 | 2.3 |
| 8 | RB | Roma-B | 7.1 | 25 | 4.8 | 2.3 |
| θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | |
|---|---|---|---|---|---|---|
| μ = 2 | 2.3 | 50 | 1.2 | −0.15 | −5 | −0.005 |
| μ = 4 | 1.4 | 85 | 1.1 | −0.15 | −5 | −0.005 |
| μ = 6 | 1.3 | 100 | 1.1 | −0.15 | −5 | −0.005 |
| Ductility | MSE |
|---|---|
| 2 | 0.0030 |
| 4 | 0.0086 |
| 6 | 0.0092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrano, J.A.; Bojórquez, E.; Bojórquez, J.; Reyes-Salazar, A.; Torres, I.; Ruiz-García, J.; Formisano, A.; Fernández, E.; Leyva, H.; Llanes-Tizoc, M.D. Ratio of Hysteretic and Input Energy Spectra for Nonlinear Structures under Seismic Sequences. Sustainability 2023, 15, 5264. https://doi.org/10.3390/su15065264
Serrano JA, Bojórquez E, Bojórquez J, Reyes-Salazar A, Torres I, Ruiz-García J, Formisano A, Fernández E, Leyva H, Llanes-Tizoc MD. Ratio of Hysteretic and Input Energy Spectra for Nonlinear Structures under Seismic Sequences. Sustainability. 2023; 15(6):5264. https://doi.org/10.3390/su15065264
Chicago/Turabian StyleSerrano, Juan A., Edén Bojórquez, Juan Bojórquez, Alfredo Reyes-Salazar, Ignacio Torres, Jorge Ruiz-García, Antonio Formisano, Eduardo Fernández, Herian Leyva, and Mario D. Llanes-Tizoc. 2023. "Ratio of Hysteretic and Input Energy Spectra for Nonlinear Structures under Seismic Sequences" Sustainability 15, no. 6: 5264. https://doi.org/10.3390/su15065264
APA StyleSerrano, J. A., Bojórquez, E., Bojórquez, J., Reyes-Salazar, A., Torres, I., Ruiz-García, J., Formisano, A., Fernández, E., Leyva, H., & Llanes-Tizoc, M. D. (2023). Ratio of Hysteretic and Input Energy Spectra for Nonlinear Structures under Seismic Sequences. Sustainability, 15(6), 5264. https://doi.org/10.3390/su15065264









