Solution Procedure for Fractional Casson Fluid Model Considered with Heat Generation and Chemical Reaction
Abstract
:1. Introduction
2. Preliminaries
3. Fractional Modeling
4. Solutions Procedures for the Constructive Equations
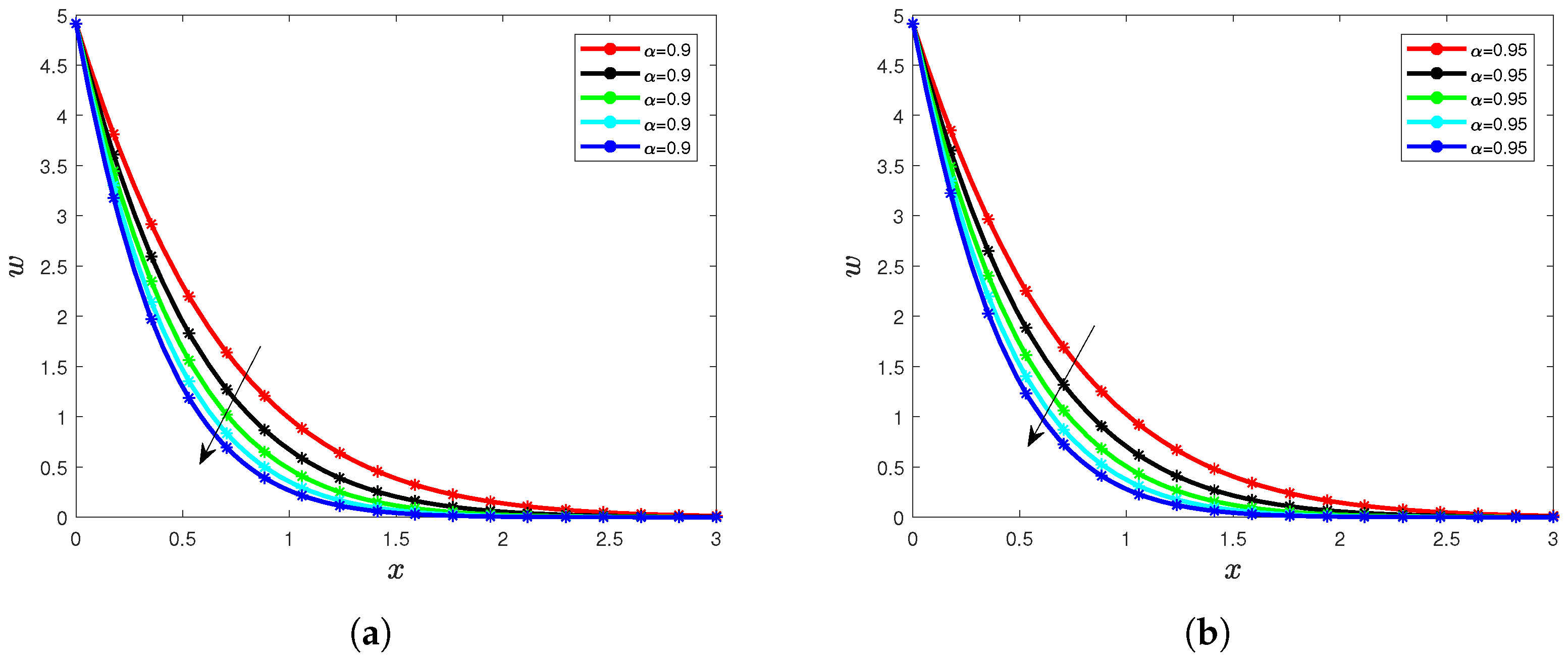
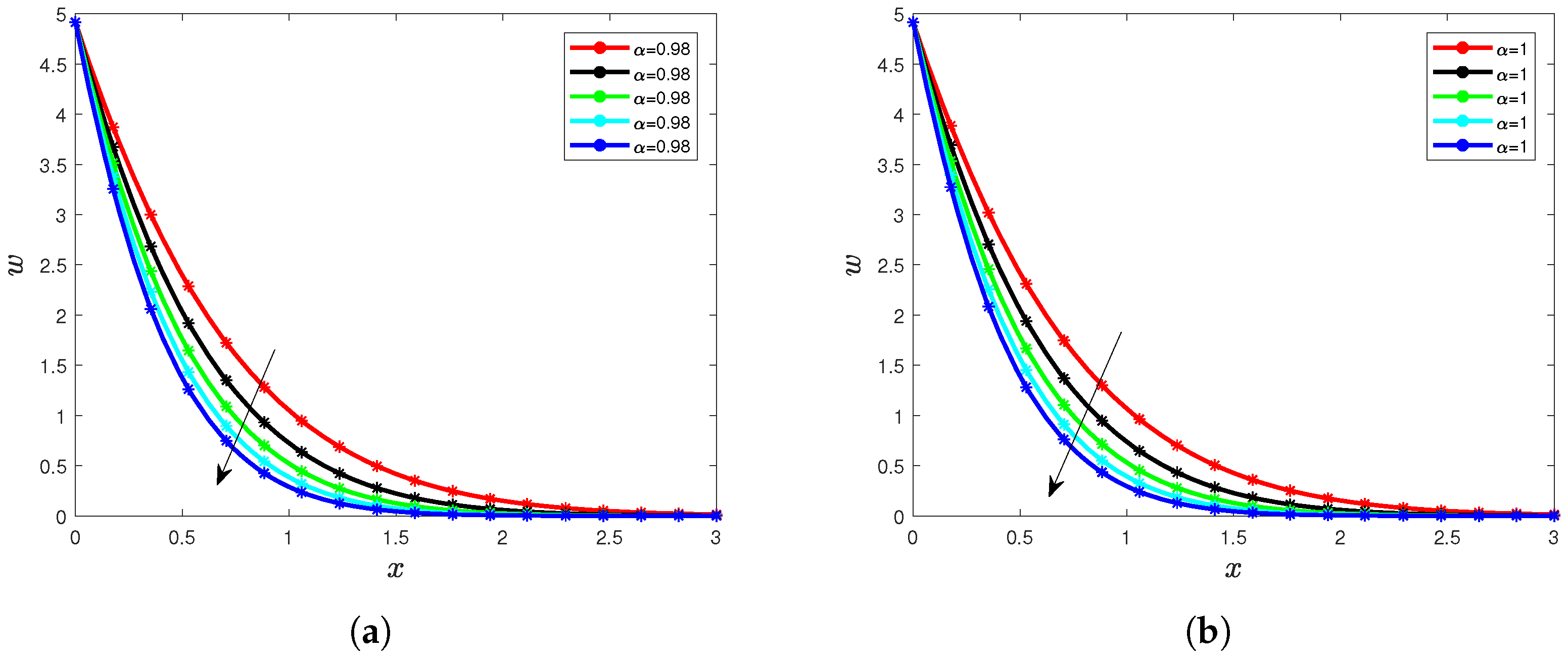
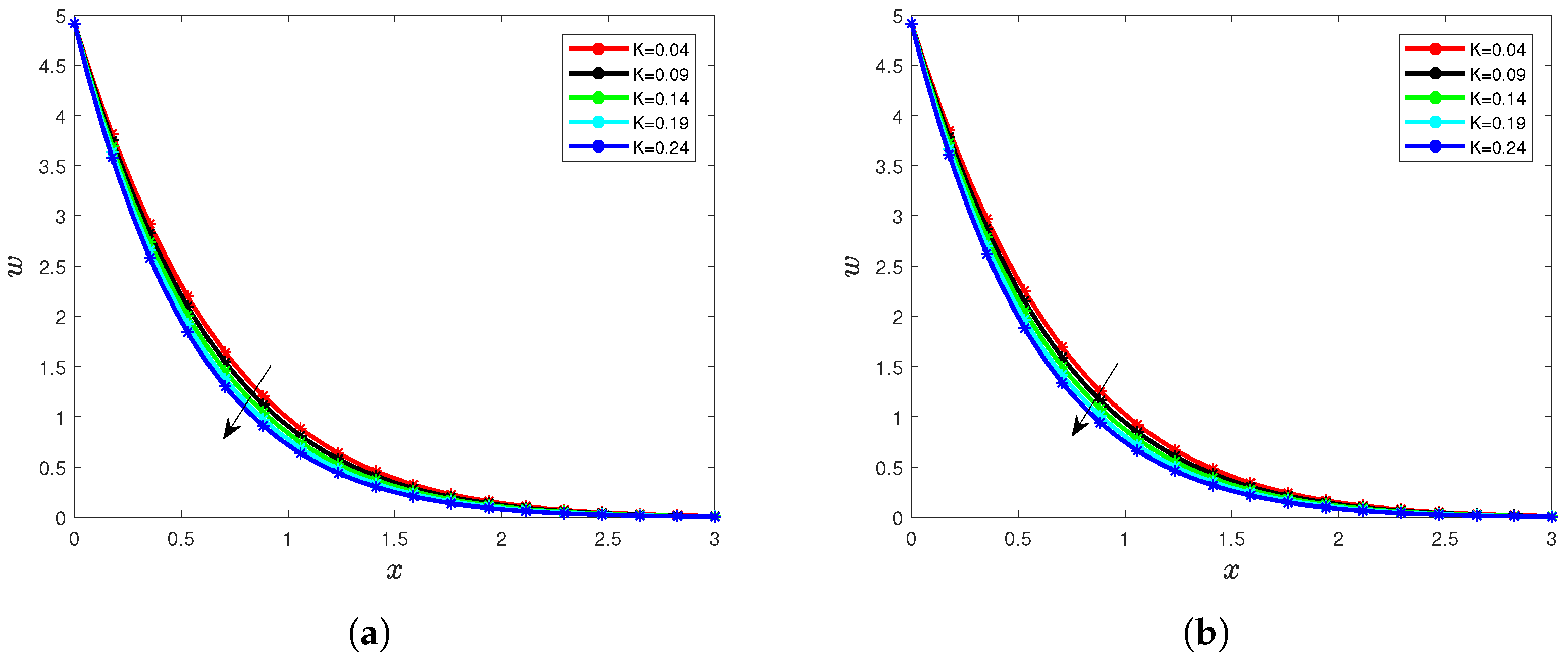
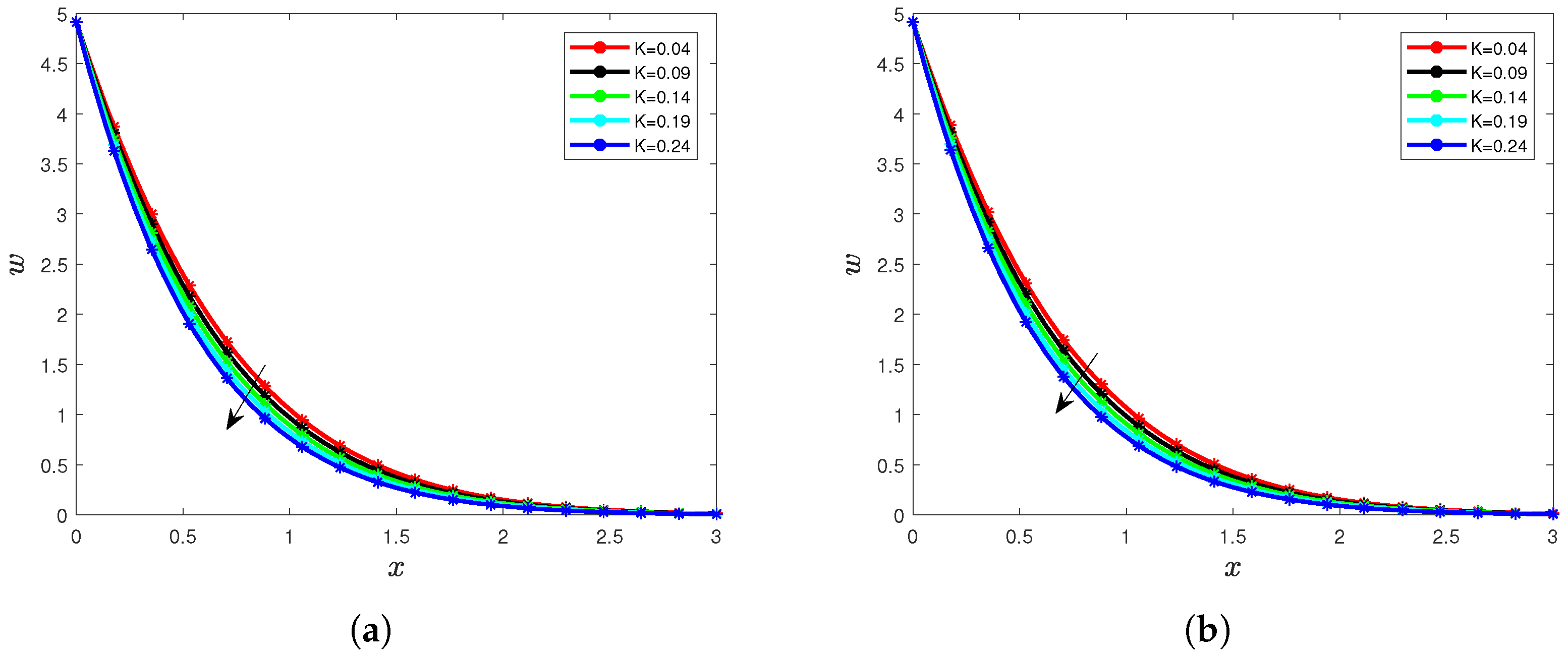
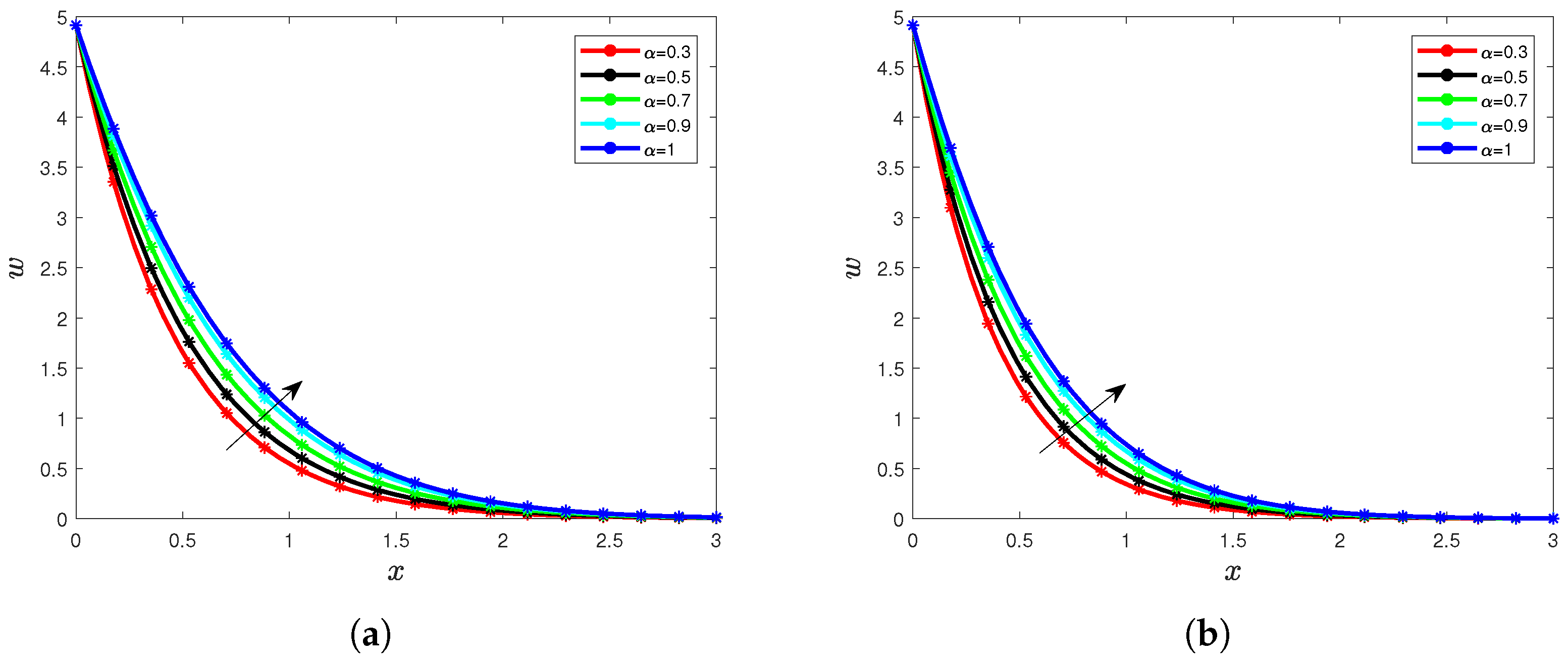
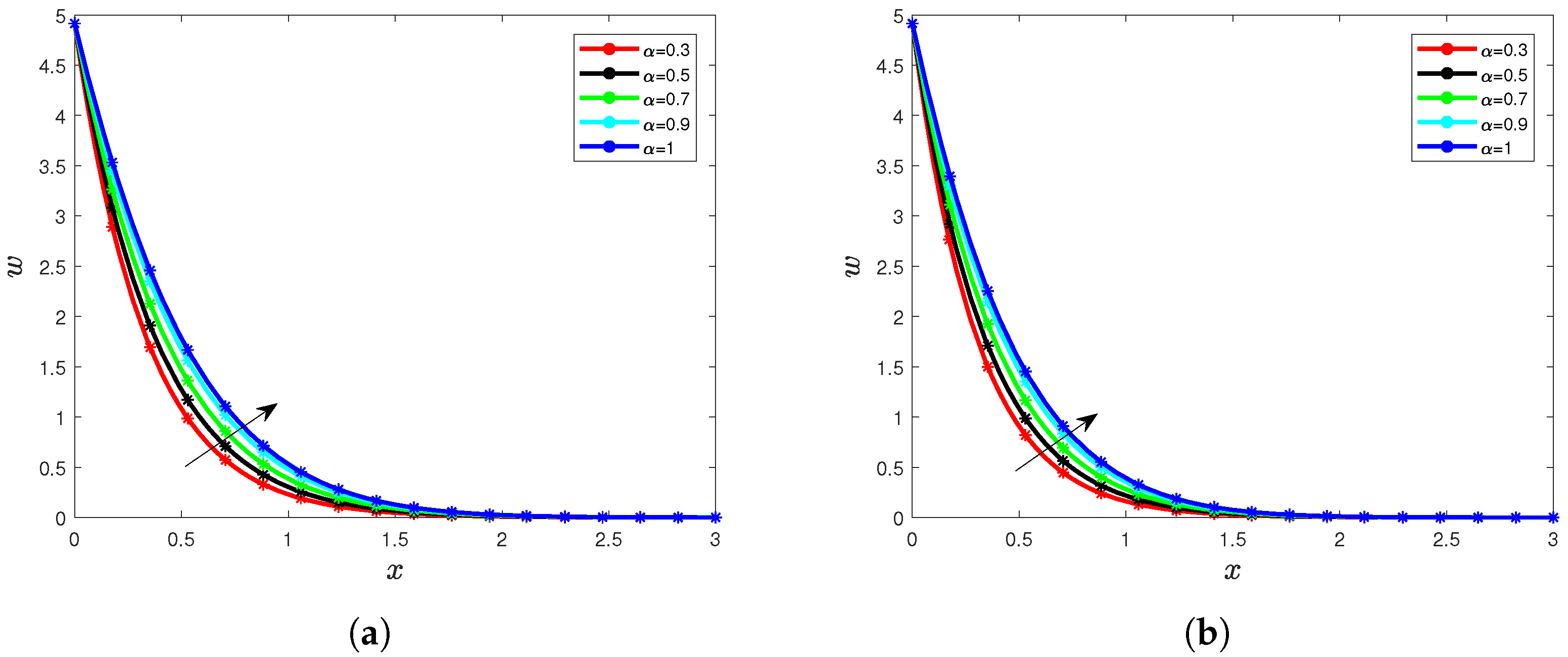
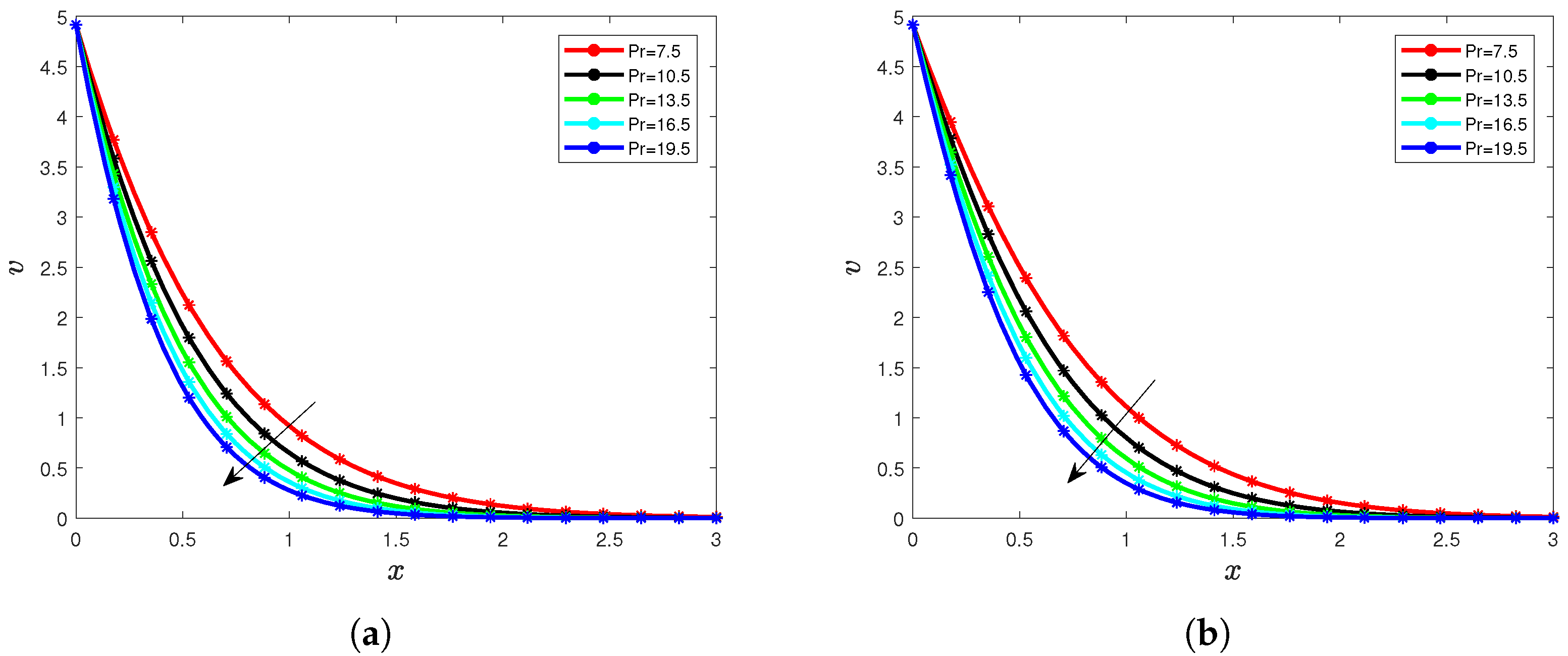
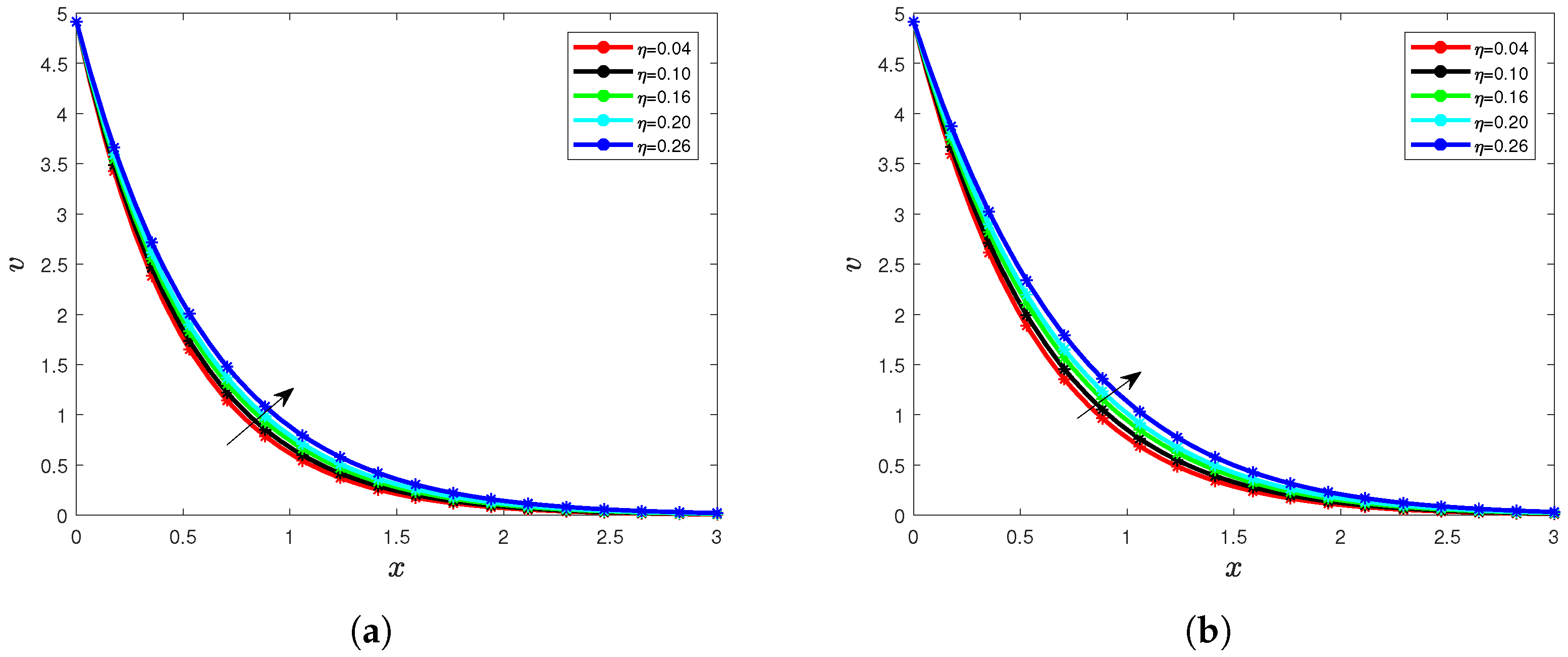
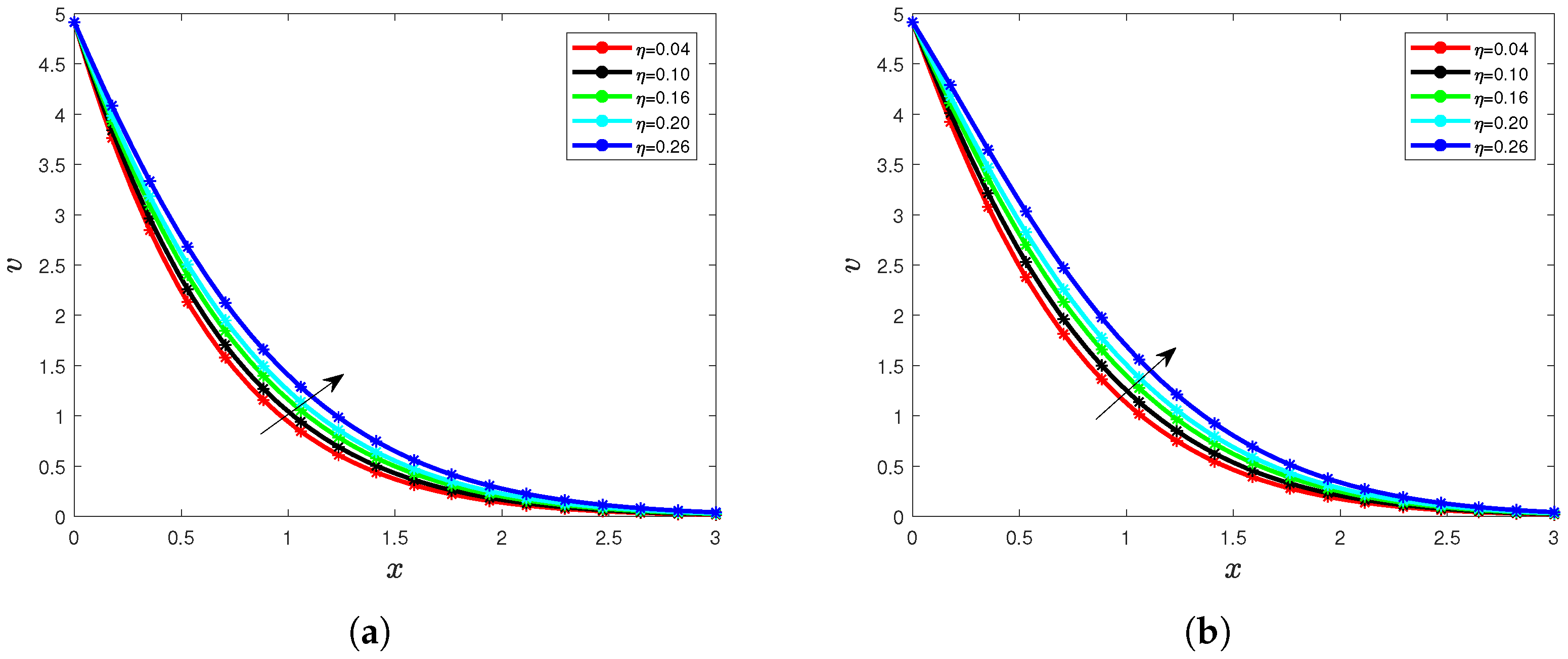
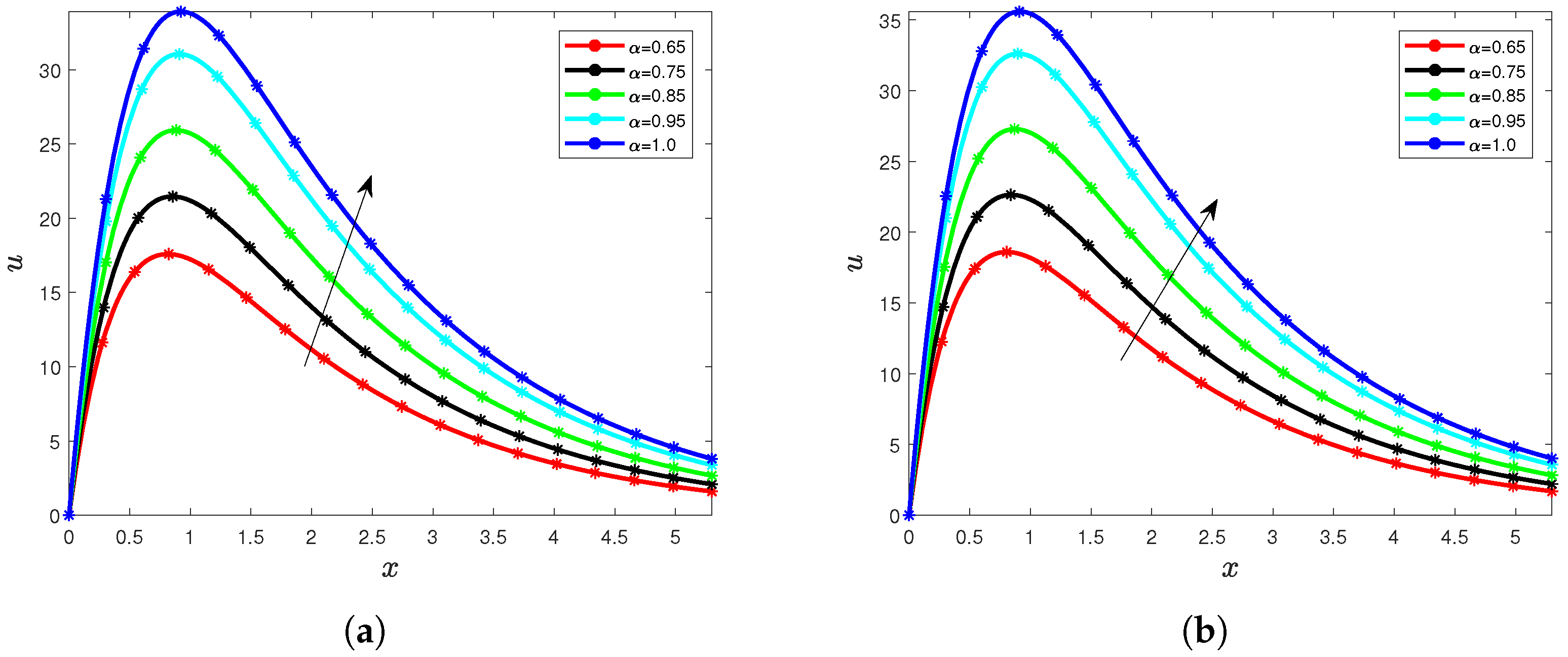
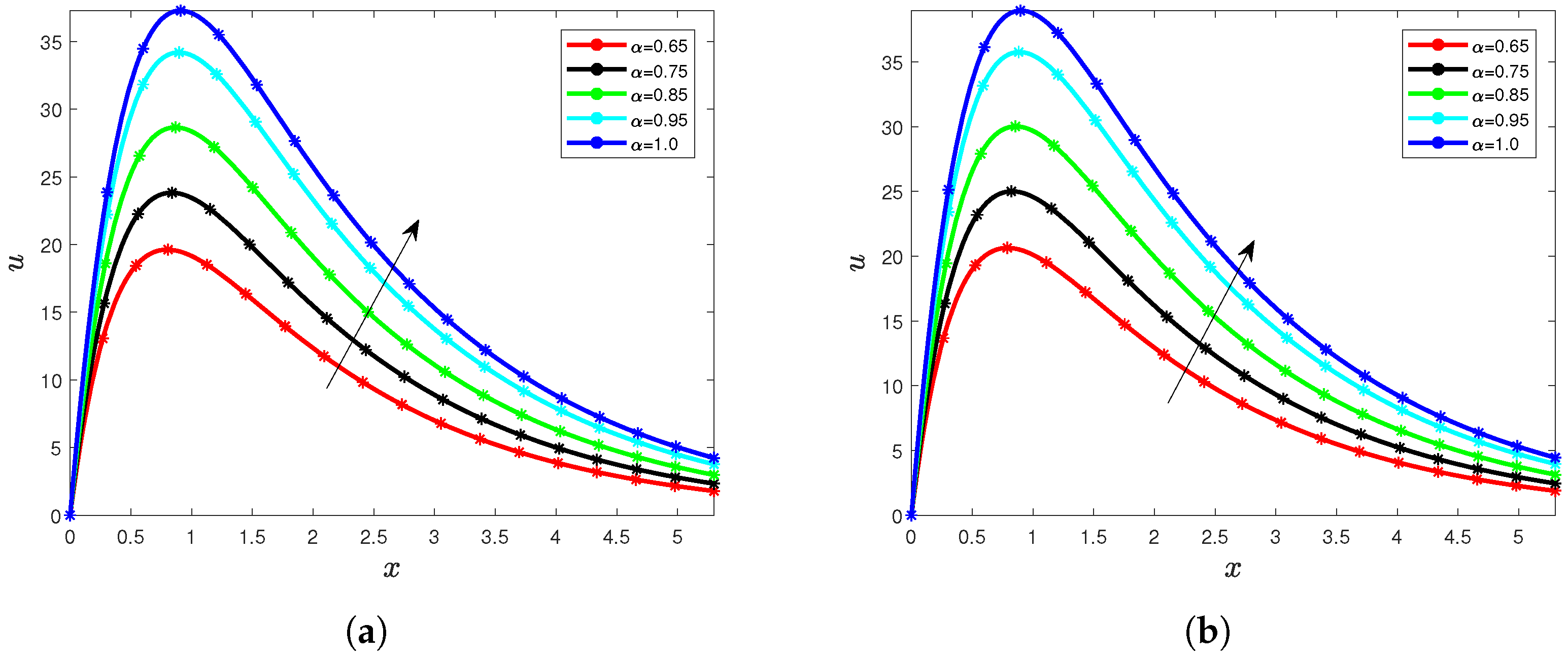
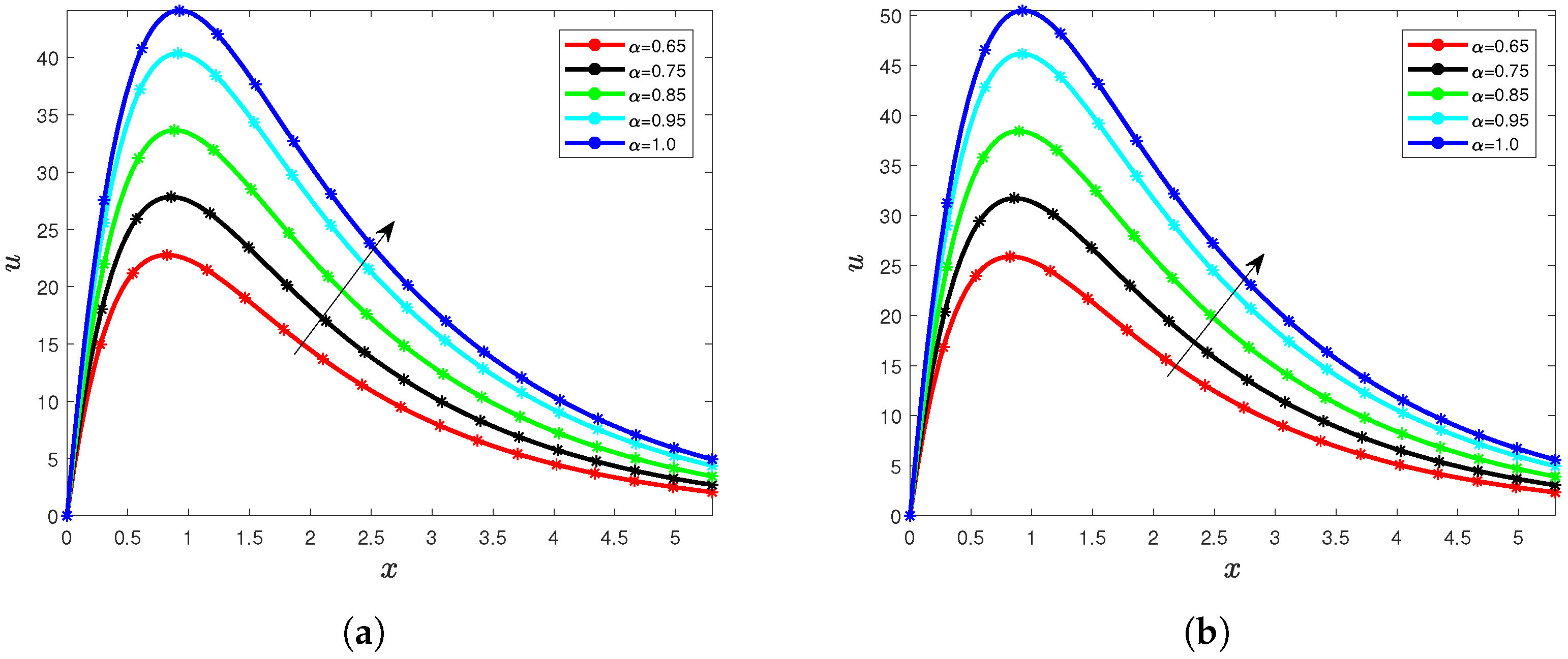
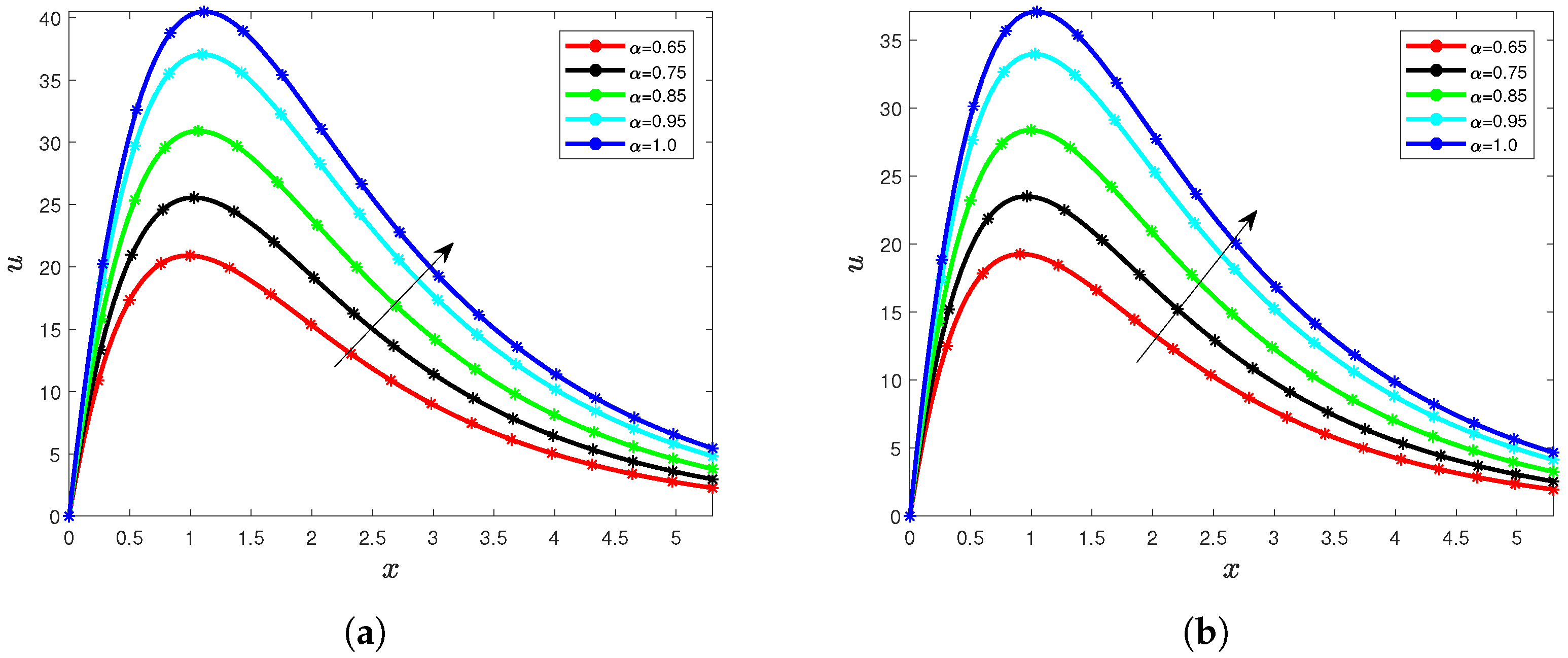
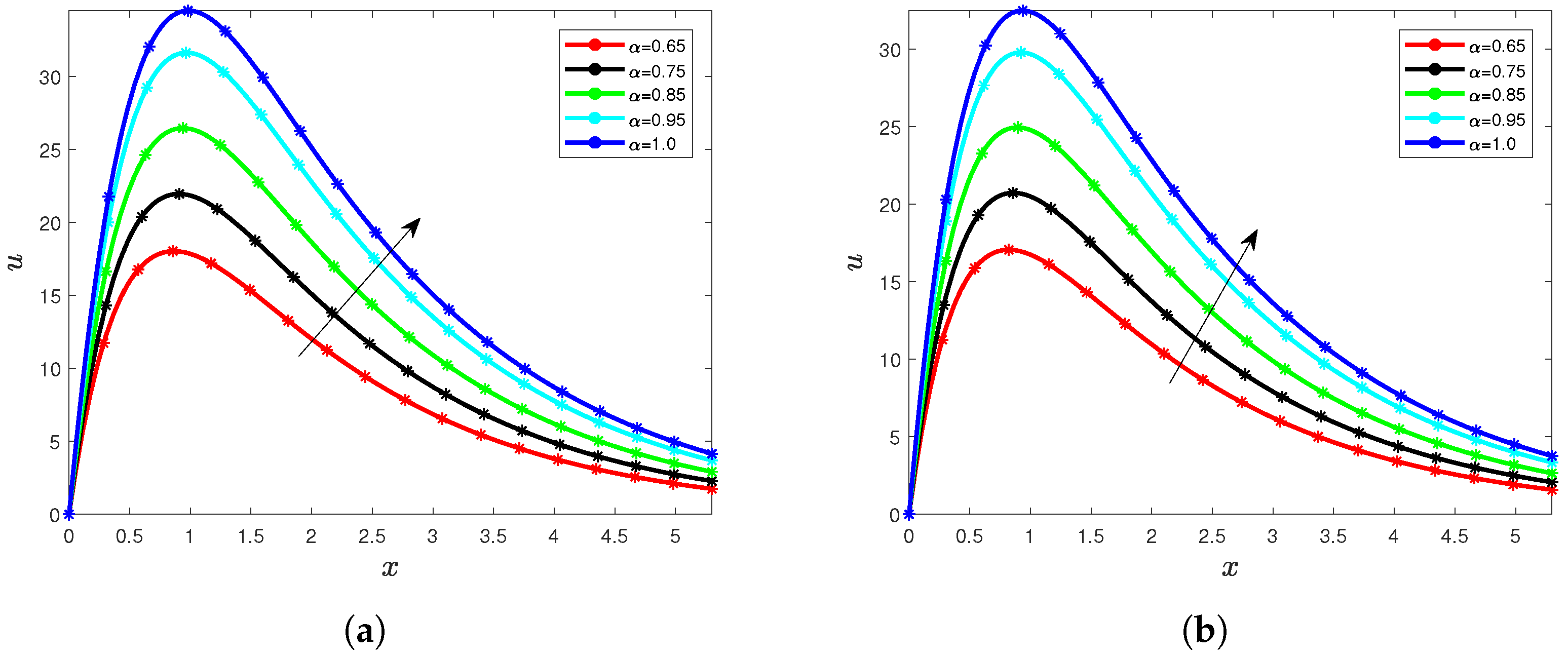
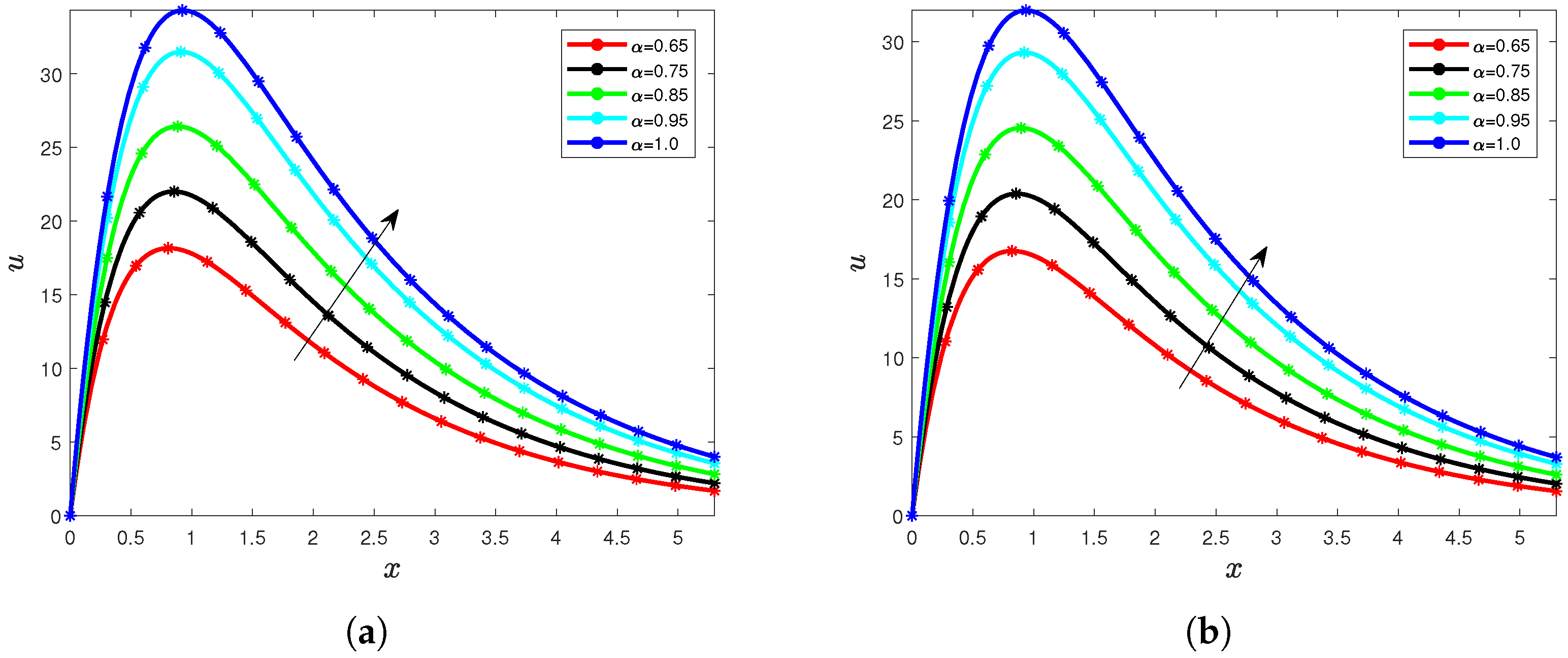
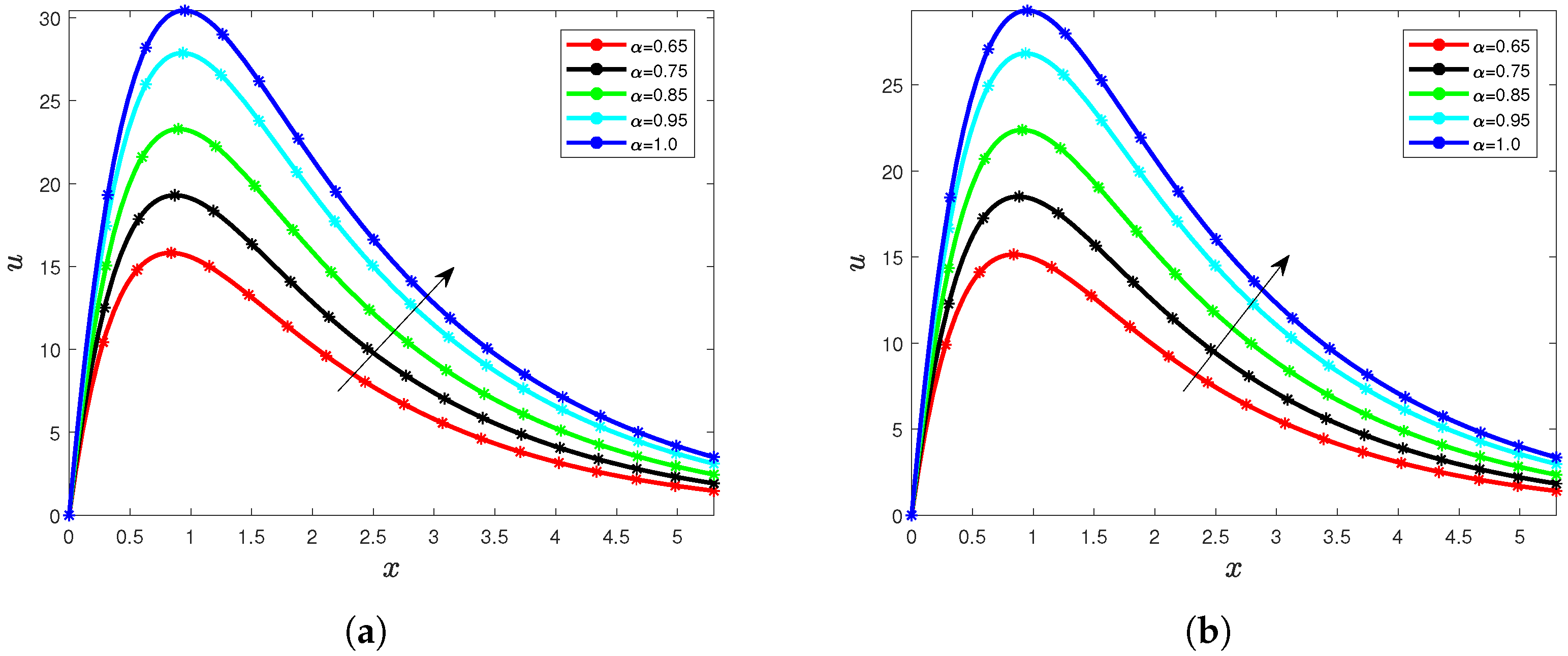
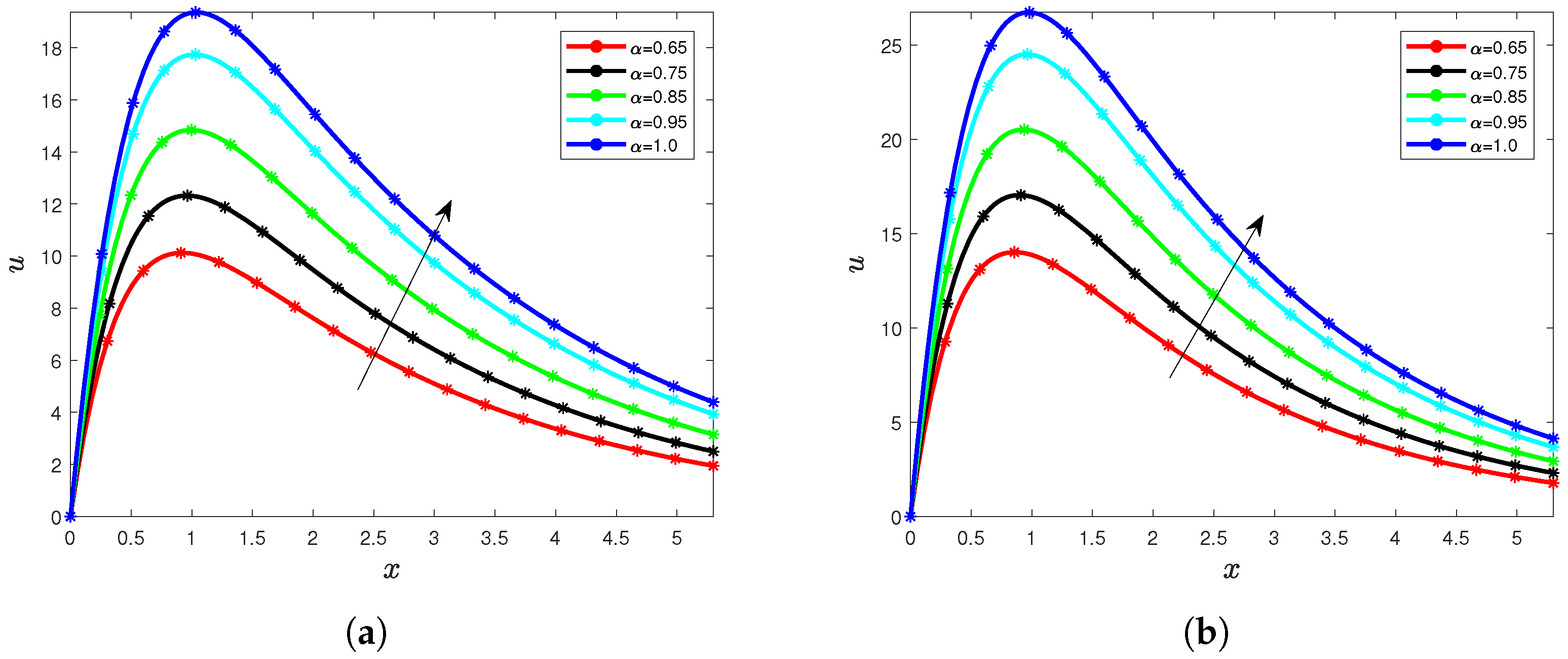
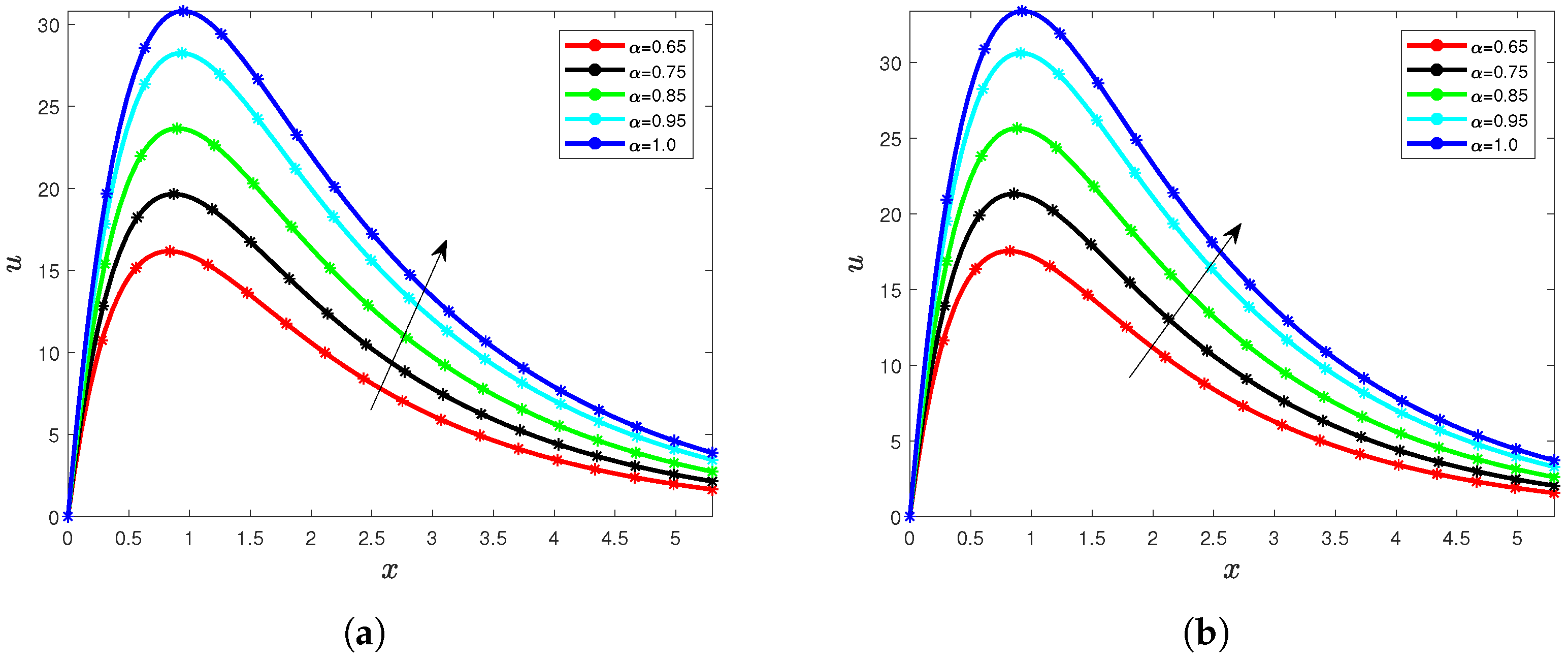
5. Results and Interpretation
6. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Mustafa Inc. Transmission dynamics of varicella zoster virus modeled by classical and novel fractional operators using real statistical data. Phys. A Stat. Mech. Its Appl. 2019, 534, 122149. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z. Dynamic Analysis of a Delayed Fractional-Order SIR Model with Saturated Incidence and Treatment Functio. Int. J. Bifurc. Chaos 2018, 28, 1850180. [Google Scholar] [CrossRef]
- Khan, I.; Shah, N.A.; Vieru, D. Unsteady flow of generalized Casson fluid with fractional derivative due to an infinite plate. Eur. Phys. J. Plus 2016, 131, 181. [Google Scholar] [CrossRef]
- Narahari, M.; Dutta, B.K. Effects of Thermal Radiation and Mass Diffusion on Free Convection Flow Near a Vertical Plate with Newtonian Heating. Chem. Eng. Commun. 2012, 199, 628–643. [Google Scholar] [CrossRef]
- Abro, K.A. A Fractional and Analytic Investigation of Thermo-Diffusion Process on Free Convection Flow: An Application to Surface Modification Technology. Eur. Phys. J. Plus 2019, 135, 31–45. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Application of Caputo-Fabrizio derivatives to MHD free convection flow of generalized Walters’-B fluid model. Eur. Phys. J. Plus 2016, 131, 377. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–15. [Google Scholar]
- Imran, M.A.; Sarwar, S.; Abdullah, M.; Khan, I. An analysis of the semi-analytic solutions of a viscous fluid with old and new definitions of fractional derivatives. Chin. J. Phys. 2018, 56, 1853–1871. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; van Mill, J., Ed.; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999; Volume 198. [Google Scholar]
- Vieru, D.; Fetecau, C.; Fetecau, C. Time-fractional free convection flow near a vertical plate with Newtonian heating and mass diffusion. Therm. Sci. 2015, 19, 85–98. [Google Scholar] [CrossRef]
- Khan, A.; Abro, K.A.; Tassaddiq, A.; Khan, I. Atangana-Baleanu and Caputo Fabrizio Analysis of Fractional Derivatives for Heat and Mass Transfer of Second Grade Fluids over a Vertical Plate: A Comparative Study. Entropy 2017, 19, 279. [Google Scholar] [CrossRef] [Green Version]
- Shah, N.A.; Khan, I.; Aleem, M.; Imran, M.A. Influence of magnetic field on double convection problem of fractional viscous fluid over an exponentially moving vertical plate: New trends of Caputo time-fractional derivative model. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Reyaz, R.; Lim, Y.J.; Mohamad, A.Q.; Saqib, M.; Shafie, S. Caputo Fractional MHD Casson Fluid Flow Over an Oscillating Plate with Thermal Radiation. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 85, 145–158. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A. A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid. Eur. Phys. J. Plus 2017, 132, 54. [Google Scholar] [CrossRef]
- Sene, N. Analytical investigations of the fractional free convection flow of Brinkman type fluid described by the Caputo fractional derivative. Results Phys. 2022, 37, 105555. [Google Scholar] [CrossRef]
- Sene, N. Second-grade fluid with Newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms. Mathematical. Model. Numer. Simul. Appl. 2022, 2, 13–25. [Google Scholar] [CrossRef]
- Sene, N. Analytical Solutions of a Class of Fluids Models with the Caputo Fractional Derivative. Fractal Fract. 2022, 6, 35. [Google Scholar] [CrossRef]
- Sene, N. Fractional Model and Exact Solutions of Convection Flow of an Incompressible Viscous Fluid under the Newtonian Heating and Mass Diffusion. J. Math. 2022, 2022, 8785197. [Google Scholar] [CrossRef]
- Sene, N. Analysis of the Influences of Parameters in the Fractional Second-Grade Fluid Dynamics. Mathematics 2022, 10, 1125. [Google Scholar]
- Alrehili, M.F.; Goud, B.S.; Reddy, Y.D.; Mishra, S.R.; Lashin, M.M.; Govindan, V.; Pimpunchat, B. Numerical computing of Soret and linear radiative effects on MHD Casson fluid flow toward a vertical surface through a porous medium: Finite element analysis. Mod. Phys. Lett. B 2023, 36, 2250170. [Google Scholar] [CrossRef]
- Afikuzzaman, M.; Ferdows, M.; Alam, M.M. Unsteady MHD casson fluid flow through a parallel plate with hall current. Procedia Eng. 2015, 105, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Afikuzzaman, M.; Ferdows, M.; Quadir, R.A.; Alam, M.M. MHD Viscous incompressible Casson fluid flow with hall current. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 60, 270–282. [Google Scholar]
- Jena, S.; Mishra, S.R.; Aghaeiboorkheili, M.; Pattnaik, P.K.; Muduli, K. Impact of Newtonian heating on the conducting Casson fluid flow past a stretching cylinder. J. Interdiscip. Math. 2022, 25, 2401–2416. [Google Scholar] [CrossRef]
- Haque, E.U.; Awan, A.U.; Raza, N.; Abdullah, M.; Chaudhry, M.A. A computational approach for the unsteady flow of maxwell fluid with Caputo fractional derivatives. Alex. Eng. J. 2018, 57, 2601–2608. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo-Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]


| Parameters | Descriptions |
|---|---|
| Density | |
| Constant temperature | |
| Ambient fluid Temperature | |
| Thermal expansion coefficient | |
| Constant concentration level at the plate | |
| Ambient fluid concentration | |
| Kinematic viscosity | |
| Dynamic viscosity of the fluid | |
| k | Thermal conductivity |
| Material parameter of Casson fluid | |
| Coefficient of concentration |
| Parameters | Descriptions |
|---|---|
| Chemical reaction parameter | |
| Density of the fluid | |
| Specific heat capacity of fluids | |
| Heat generation term | |
| d | Mass diffusivity |
| Mass Grashof number | |
| Thermal Grashof number | |
| Prandtl number | |
| Schmidt number | |
| g | Acceleration due to gravity |
| K | The chemical reaction parameter |
| The heat generation parameter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sene, N. Solution Procedure for Fractional Casson Fluid Model Considered with Heat Generation and Chemical Reaction. Sustainability 2023, 15, 5306. https://doi.org/10.3390/su15065306
Sene N. Solution Procedure for Fractional Casson Fluid Model Considered with Heat Generation and Chemical Reaction. Sustainability. 2023; 15(6):5306. https://doi.org/10.3390/su15065306
Chicago/Turabian StyleSene, Ndolane. 2023. "Solution Procedure for Fractional Casson Fluid Model Considered with Heat Generation and Chemical Reaction" Sustainability 15, no. 6: 5306. https://doi.org/10.3390/su15065306
APA StyleSene, N. (2023). Solution Procedure for Fractional Casson Fluid Model Considered with Heat Generation and Chemical Reaction. Sustainability, 15(6), 5306. https://doi.org/10.3390/su15065306







