A Second-Order Cone Programming Model of Controlled Islanding Strategy Considering Frequency Stability Constraints
Abstract
1. Introduction
- (1)
- A frequency constraint for the balanced allocation of synchronous generators to the island is proposed, which takes into account the difference in inertia and the ramping rate of governors. This constraint can reasonably allocate synchronous generators and prevent the islanding strategy from generating islands with too low inertia, which significantly affects the island’s ability to maintain frequency stability after islanding;
- (2)
- Based on the idea of network flow, connectivity constraints are proposed to ensure the connectivity of buses within the island, and there is no connected path between different islands;
- (3)
- A mixed-integer second-order cone programming model of controlled islanding is proposed, which can meet the requirements for a reactive power balance and voltage limit after islanding, and is closer to the actual operation of the power system.
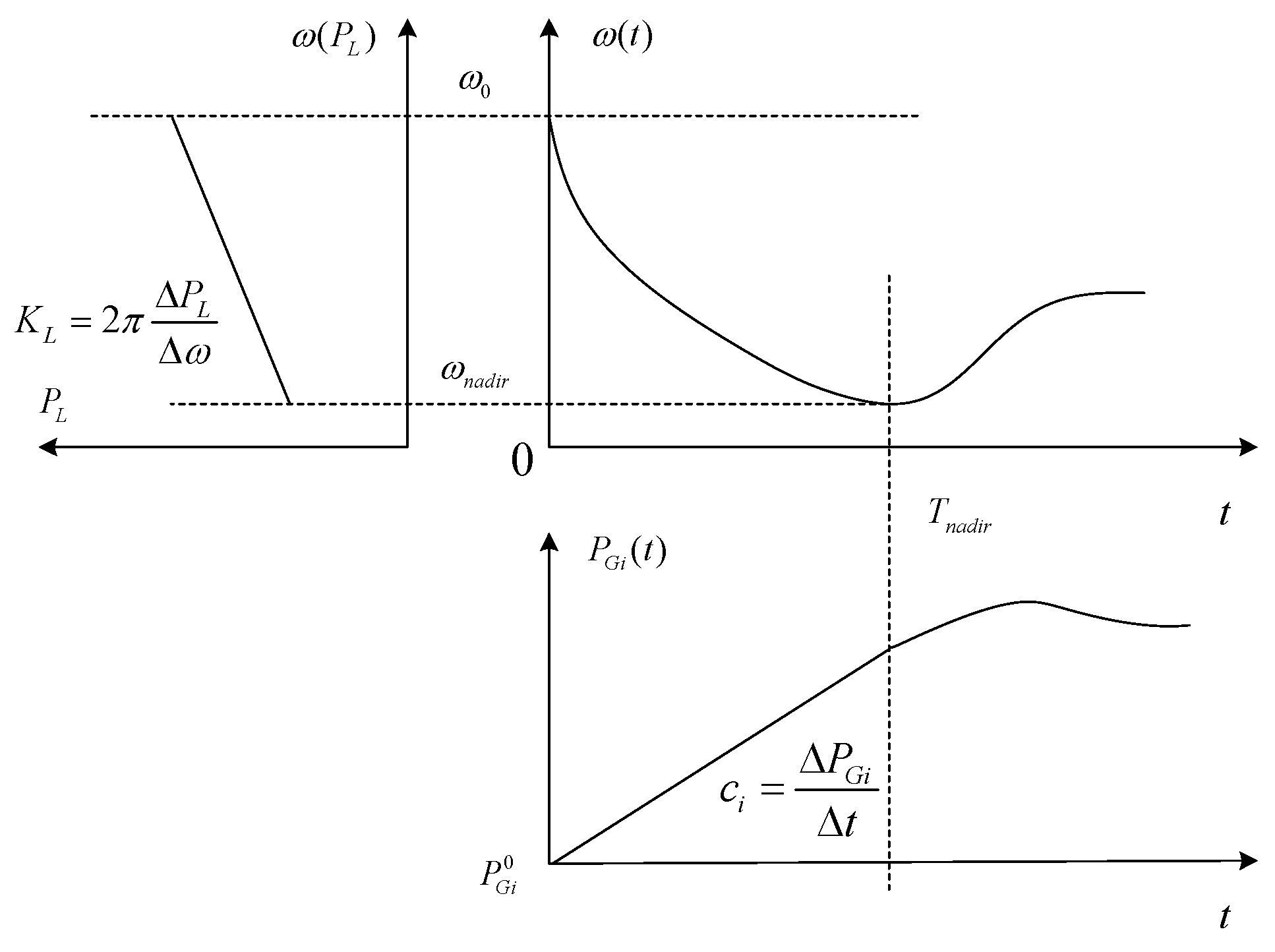
2. Frequency Nadir Constraint
3. Optimization Model for Controlled Islanding
3.1. Objective Function
3.2. Generator Coherency
3.3. Network Connectivity Constraints
3.4. Power System Physical Constraints and Cone Relaxation
3.5. Frequency Nadir Constraint
4. Results
4.1. Validation of the Basic Model for Controlled Islanding
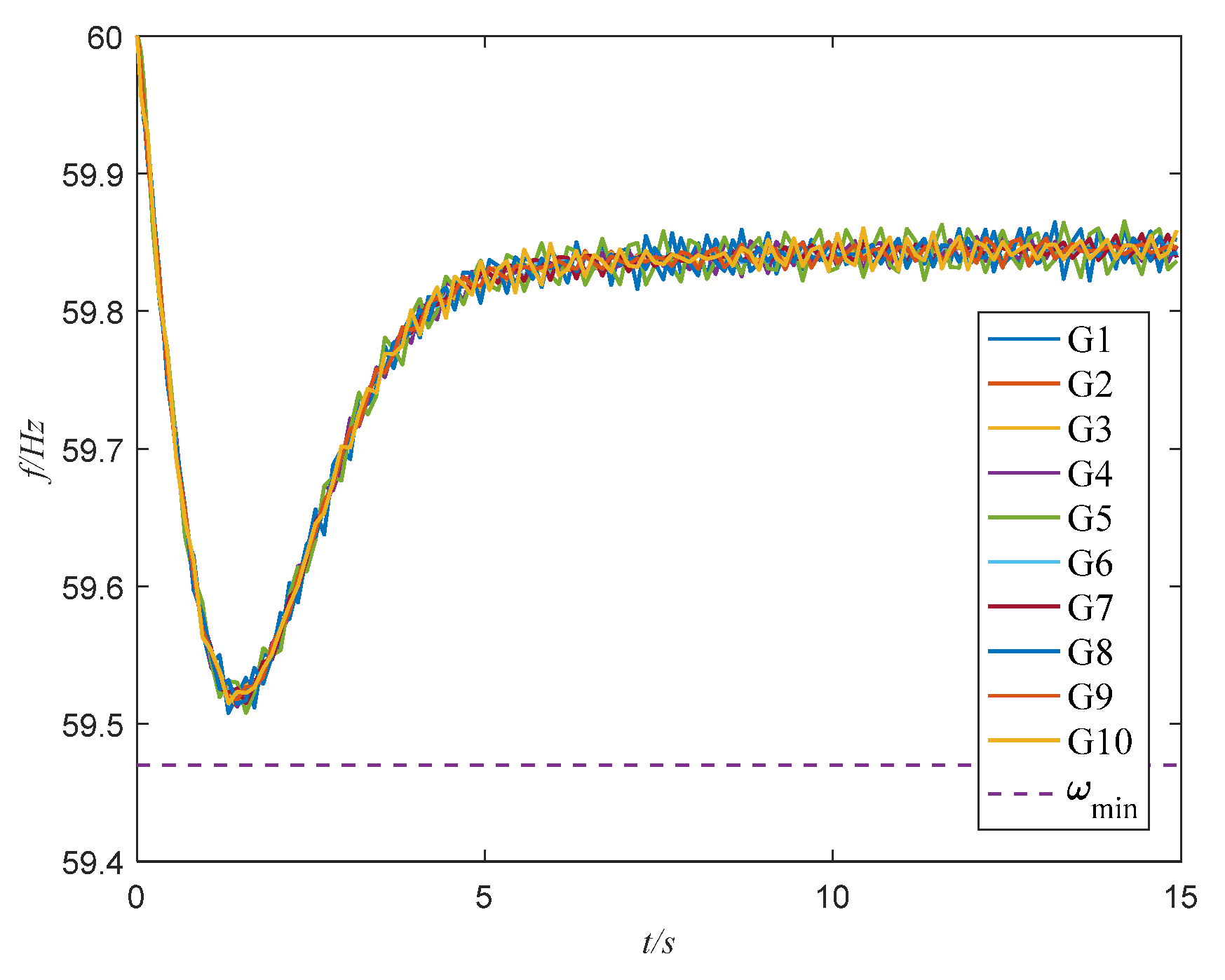
4.2. Verifying the Accuracy of the Frequency Nadir Constraint
4.3. Validation of the Model Considering Frequency Stability Constraints for Controlled Islanding
4.4. Comparison of Different Test Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Panteli, M.; Trakas, D.N.; Mancarella, P.; Hatziargyriou, N.D. Boosting the Power Grid Resilience to Extreme Weather Events Using Defensive Islanding. IEEE Trans. Smart Grid 2016, 7, 2913–2922. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, D.-Z.; Lu, Q. Splitting strategies for islanding operation of large-scale power systems using OBDD-based methods. IEEE Trans. Power Syst. 2003, 18, 912–923. [Google Scholar] [CrossRef]
- Ding, L.; Gonzalez-Longatt, F.M.; Wall, P.; Terzija, V. Two-Step Spectral Clustering Controlled Islanding Algorithm. IEEE Trans. Power Syst. 2012, 28, 75–84. [Google Scholar] [CrossRef]
- Zhao, Q.; Sun, K.; Zheng, D.-Z.; Ma, J.; Lu, Q. A study of system splitting strategies for island operation of power system: A two-phase method based on OBDDs. IEEE Trans. Power Syst. 2003, 18, 1556–1565. [Google Scholar] [CrossRef]
- Senroy, N.; Heydt, G.; Vittal, V. Decision Tree Assisted Controlled Islanding. IEEE Trans. Power Syst. 2006, 21, 1790–1797. [Google Scholar] [CrossRef]
- Aghamohammadi, M.R.; Shahmohammadi, A. Intentional islanding using a new algorithm based on ant search mechanism. Int. J. Electr. Power Energy Syst. 2012, 35, 138–147. [Google Scholar] [CrossRef]
- Ding, L.; Ma, Z.; Wall, P.; Terzija, V. Graph Spectra Based Controlled Islanding for Low Inertia Power Systems. IEEE Trans. Power Deliv. 2016, 32, 302–309. [Google Scholar] [CrossRef]
- Huang, L.; Sun, Y.; Xu, J.; Gao, W.; Zhang, J.; Wu, Z. Optimal PMU Placement Considering Controlled Islanding of Power System. IEEE Trans. Power Syst. 2013, 29, 742–755. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, T.; Lin, Z.; Liu, Y.; Ding, Y.; Yang, L. Controlled Islanding Strategy Considering Uncertainty of Renewable Energy Sources Based on Chance-constrained Model. J. Mod. Power Syst. Clean Energy 2022, 10, 471–481. [Google Scholar] [CrossRef]
- Ding, T.; Sun, K.; Huang, C.; Bie, Z.; Li, F. Mixed-Integer Linear Programming-Based Splitting Strategies for Power System Islanding Operation Considering Network Connectivity. IEEE Syst. J. 2015, 12, 350–359. [Google Scholar] [CrossRef]
- Kyriacou, A.; Demetriou, P.; Panayiotou, C.; Kyriakides, E. Controlled Islanding Solution for Large-Scale Power Systems. IEEE Trans. Power Syst. 2017, 33, 1591–1602. [Google Scholar] [CrossRef]
- Liu, Z.; Clark, A.; Bushnell, L.; Kirschen, D.S.; Poovendran, R. Controlled Islanding via Weak Submodularity. IEEE Trans. Power Syst. 2018, 34, 1858–1868. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Zhao, Y.; Liu, Y.; Ding, Y.; Zhang, B.; Yang, L.; Wang, Q.; White, S.E. Robust System Separation Strategy Considering Online Wide-Area Coherency Identification and Uncertainties of Renewable Energy Sources. IEEE Trans. Power Syst. 2020, 35, 3574–3587. [Google Scholar] [CrossRef]
- Kamali, S.; Amraee, T.; Fotuhi-Firuzabad, M. Controlled Islanding for Enhancing Grid Resilience Against Power System Blackout. IEEE Trans. Power Deliv. 2020, 36, 2386–2396. [Google Scholar] [CrossRef]
- You, H.; Vittal, V.; Wang, X. Slow Coherency-Based Islanding. IEEE Trans. Power Syst. 2004, 19, 483–491. [Google Scholar] [CrossRef]
- Izanloo, M.; Aslani, A.; Zahedi, R. Development of a Machine learning assessment method for renewable energy investment decision making. Appl. Energy 2022, 327, 120096. [Google Scholar] [CrossRef]
- Mehrzad, K.; Rahim, Z.; Reza, F.; Abolfazl, A. Assessment of Renewable Energy Production Capacity of Asian Coun-tries: A Review. New Energy Exploit. Appl. 2022, 1, 25–41. [Google Scholar] [CrossRef]
- Amraee, T.; Saberi, H. Controlled islanding using transmission switching and load shedding for enhancing power grid resilience. Int. J. Electr. Power Energy Syst. 2017, 91, 135–143. [Google Scholar] [CrossRef]
- Teymouri, F.; Amraee, T.; Saberi, H.; Capitanescu, F. Toward Controlled Islanding for Enhancing Power Grid Resilience Considering Frequency Stability Constraints. IEEE Trans. Smart Grid 2017, 10, 1735–1746. [Google Scholar] [CrossRef]
- Yan, R.; Masood, N.-A.; Saha, T.K.; Bai, F.; Gu, H. The Anatomy of the 2016 South Australia Blackout: A Catastrophic Event in a High Renewable Network. IEEE Trans. Power Syst. 2018, 33, 5374–5388. [Google Scholar] [CrossRef]
- Xianzhong, D.; Sheng, S. Self-Organized Criticality in Time Series of Power Systems Fault, Its Mechanism, and Potential Application. IEEE Trans. Power Syst. 2010, 25, 1857–1864. [Google Scholar] [CrossRef]
- Zahedi, R.; Ghodusinejad, M.H.; Aslani, A.; Hachem-Vermette, C. Modelling community-scale renewable energy and electric vehicle management for cold-climate regions using machine learning. Energy Strat. Rev. 2022, 43, 100930. [Google Scholar] [CrossRef]
- Ahmadi, H.; Ghasemi, H. Security-Constrained Unit Commitment With Linearized System Frequency Limit Constraints. IEEE Trans. Power Syst. 2014, 29, 1536–1545. [Google Scholar] [CrossRef]
- Jabr, R. Radial Distribution Load Flow Using Conic Programming. IEEE Trans. Power Syst. 2006, 21, 1458–1459. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M. Power System Dynamics and Stability, 1st ed.; Prentice-Hall: Urbana-Champaign, IL, USA, 1998. [Google Scholar]
- Pai, M.A. Energy Function Analysis for Power System Stability; Kluwer Academic Publishers: Boston, MA, USA, 1989. [Google Scholar]
- Research on Power System Dynamics and Modeling. Available online: https://tweckesser.wordpress.com/power-system-data-and-test-cases/ (accessed on 28 January 2023).
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar] [CrossRef]
- Milano, F. An Open Source Power System Analysis Toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
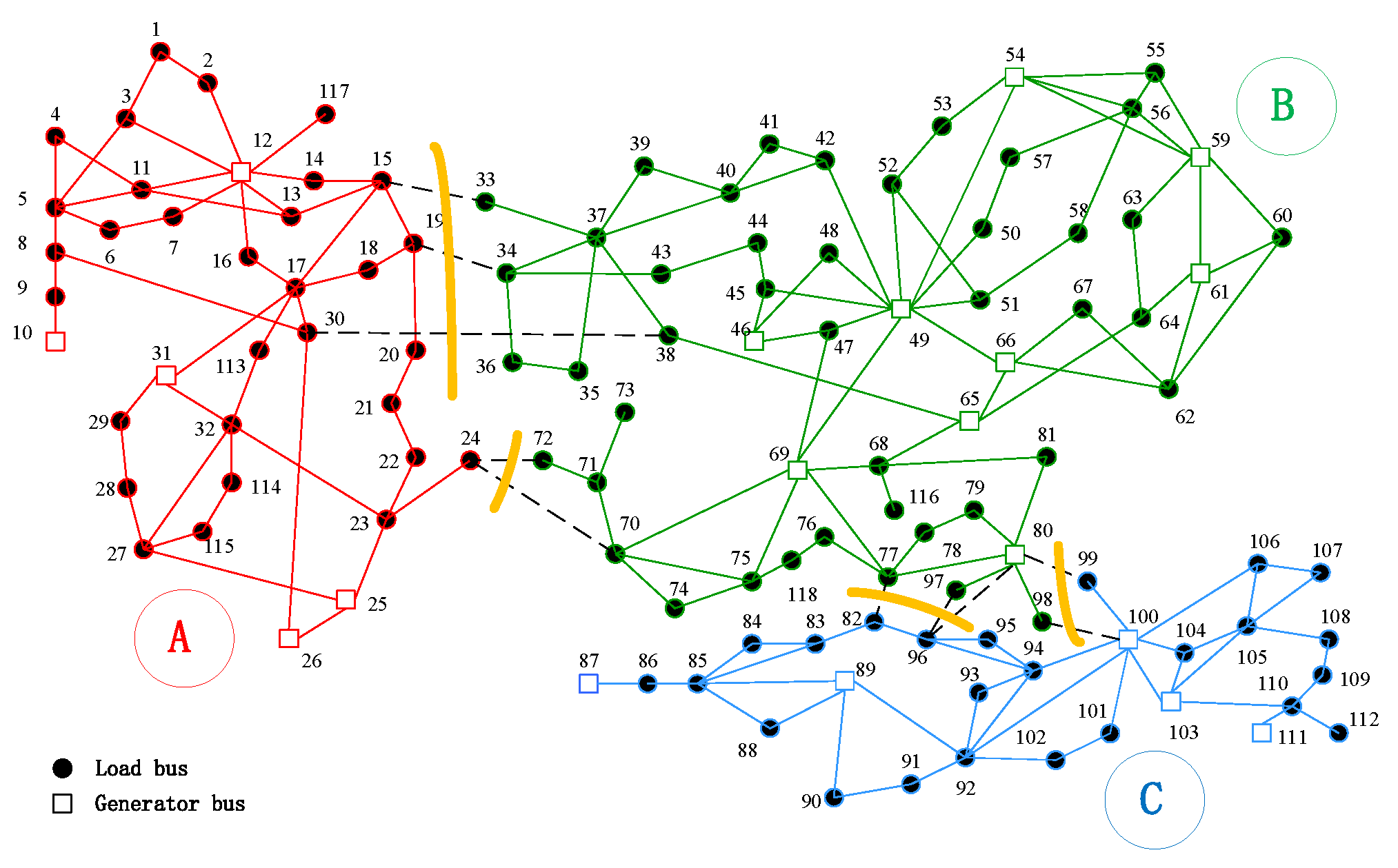

| Coherent Group | Generator Bus |
|---|---|
| 1 | 10, 12, 25, 26, 31 |
| 2 | 46, 49, 54, 59, 61, 65, 66, 69, 80 |
| 3 | 87, 89, 100, 103, 111 |
| Method | Cut Set of Original System | Cut Set of Modified System |
|---|---|---|
| MISOCP | 15–33, 19–34, 30–38, 24–70, 24–72, 77–82, 80–96, 80–99, 96–97, 98–100 | 15–33, 19–34, 30–38, 23–24, 77–82, 80–96, 80–99, 96–97, 98–100 |
| MILP [11] | 15–33, 19–34, 30–38, 24–70, 24–72, 77–82, 80–96, 80–99, 96–97, 98–100 | 15–33, 19–34, 30–38, 24–70, 24–72, 77–82, 80–96, 80–99, 96–97, 98–100 |
| Spectral Clustering Algorithm [3] | 15–33, 19–34, 30–38, 23–24, 77–82, 80–96, 80–99, 96–97, 98–100 | 15–33, 19–34, 30–38, 23–24, 77–82, 80–96, 80–99, 96–97, 98–100 |
| Ploss (MW) | Time-Domain Simulation (Hz) | (Hz) | ||
|---|---|---|---|---|
| Generator 1 | Generator 2 | Generator 3 | ||
| 10 | 59.59 | 59.59 | 59.59 | 59.63 |
| 15 | 59.39 | 59.38 | 59.39 | 59.40 |
| 20 | 59.18 | 59.18 | 59.18 | 59.21 |
| Unit | Bus | c (MW/s) | J (kg·m²) |
|---|---|---|---|
| G1 | 10 | 5.1 | 112,120 |
| G2 | 12 | 1.7 | 10,350 |
| G3 | 26 | 4.5 | 86,480 |
| G4 | 49 | 3.4 | 45,473 |
| G5 | 54 | 4.9 | 6920 |
| G6 | 61 | 2.2 | 31,081 |
| G7 | 65 | 5.6 | 95,793 |
| G8 | 66 | 5.6 | 95,793 |
| G9 | 69 | 3.2 | 112,121 |
| G10 | 80 | 5.15 | 112,121 |
| G11 | 87 | 3.76 | 4830 |
| G12 | 89 | 8.7 | 255,832 |
| G13 | 100 | 3.5 | 45,470 |
| G14 | 111 | 7.6 | 6920 |
| Island | Frequency Nadir Considering Frequency Nadir Constraint (Hz) | Frequency Nadir without Considering Frequency Nadir Constraint (Hz) |
|---|---|---|
| A | 59.40 | 59.12 |
| B | 59.35 | 59.67 |
| C | 59.45 | 59.45 |
| Coherent Group | Generator Bus |
|---|---|
| 1 | 10, 16, 17, 18, 264, 269, 277, 278, 279, 281, 282, 289, 294, 382, 383, 385, 390, 395, 404, 426, 444, 451, 482, 492, 493, 494, 514, 515, 525, 536, 537, 615, 784 |
| 2 | 31, 41, 45, 181, 556, 580, 584, 585, 607, 613, 623, 639, 651, 654, 664, 670, 674, 688, 692, 699, 712, 730, 732, 735, 740, 744, 754, 755, 760, 766, 1359, 1393, 1469 |
| 3 | 67, 83, 84, 85, 86, 93, 95, 97, 103, 104, 105, 109, 110, 180, 184, 185, 196, 790, 795, 798, 814, 834, 878, 884, 892, 895, 901, 910, 911, 912, 914, 917, 919, 920, 929, 959, 968, 993, 994, 995, 996, 997, 1024, 1027, 1028, 1029, 1053, 1054, 1105, 1106, 1107, 1138, 1141, 1175, 1182, 1183, 1184, 1191, 1192, 1201, 1202, 1203, 1232, 1233, 1244, 1247, 1250, 1268, 1316, 1325, 1349, 1356, 1403, 1416, 1417, 1418, 1426, 1429, 1475, 1504, 1514, 1534, 1537, 1538, 1543, 1550, 1566, 1587, 1600, 1620, 1635, 1638, 1710, 1717, 1730, 1734, 1742, 1749, 1793, 1799, 1844, 1871, 1875, 1932, 1947, 1966, 1977 |
| 4 | 131, 132, 139, 140, 1603, 1609, 1617, 1627, 1630, 1664, 1669, 1673, 1674, 1679, 1683, 1685, 1686, 1698, 1700, 1706, 1712, 1719, 1726, 1728, 1735, 1739, 1758, 1760, 1761, 1763, 1764, 1768, 1788 |
| 5 | 176, 2139, 2153, 2159, 2164, 2167, 2168, 2171, 2213, 2268, 2293, 2296, 2307, 2323, 2328, 2330, 2380, 2381 |
| Island | The Model without Considering Frequency Nadir Constraints | The Model Considering Frequency Nadir Constraints | ||
|---|---|---|---|---|
| Amounts of Generators | Synchronous Generator Inertia (kg·m²) | Amounts of Generators | Synchronous Generator Inertia (kg·m²) | |
| 1 | 62 | 4,032,475 | 58 | 3,953,116 |
| 2 | 39 | 821,447 | 40 | 841,879 |
| 3 | 119 | 3,713,401 | 119 | 3,713,401 |
| 4 | 86 | 4,050,519 | 79 | 3,236,963 |
| 5 | 21 | 204,607 | 31 | 1,077,090 |
| Test Systems | NO. of Islands | Power-Flow Disruption (MW) | SOCP Model Times (s) | DC Power Flow Model Times (s) |
|---|---|---|---|---|
| New England 39 bus system | 2 | 222.12 | 0.17 | 0.09 |
| IEEE 118 bus system | 3 | 138.49 | 0.38 | 0.25 |
| Polish 2383 bus system | 5 | 3383.04 | 129.02 | 102.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Xu, D.; Su, H.; Sun, Z. A Second-Order Cone Programming Model of Controlled Islanding Strategy Considering Frequency Stability Constraints. Sustainability 2023, 15, 5386. https://doi.org/10.3390/su15065386
Li P, Xu D, Su H, Sun Z. A Second-Order Cone Programming Model of Controlled Islanding Strategy Considering Frequency Stability Constraints. Sustainability. 2023; 15(6):5386. https://doi.org/10.3390/su15065386
Chicago/Turabian StyleLi, Peijie, Di Xu, Hang Su, and Zhiyuan Sun. 2023. "A Second-Order Cone Programming Model of Controlled Islanding Strategy Considering Frequency Stability Constraints" Sustainability 15, no. 6: 5386. https://doi.org/10.3390/su15065386
APA StyleLi, P., Xu, D., Su, H., & Sun, Z. (2023). A Second-Order Cone Programming Model of Controlled Islanding Strategy Considering Frequency Stability Constraints. Sustainability, 15(6), 5386. https://doi.org/10.3390/su15065386






