Improvement of Autonomy, Efficiency, and Stress of Fuel Cell Hybrid Electric Vehicle System Using Robust Controller
Abstract
:1. Introduction
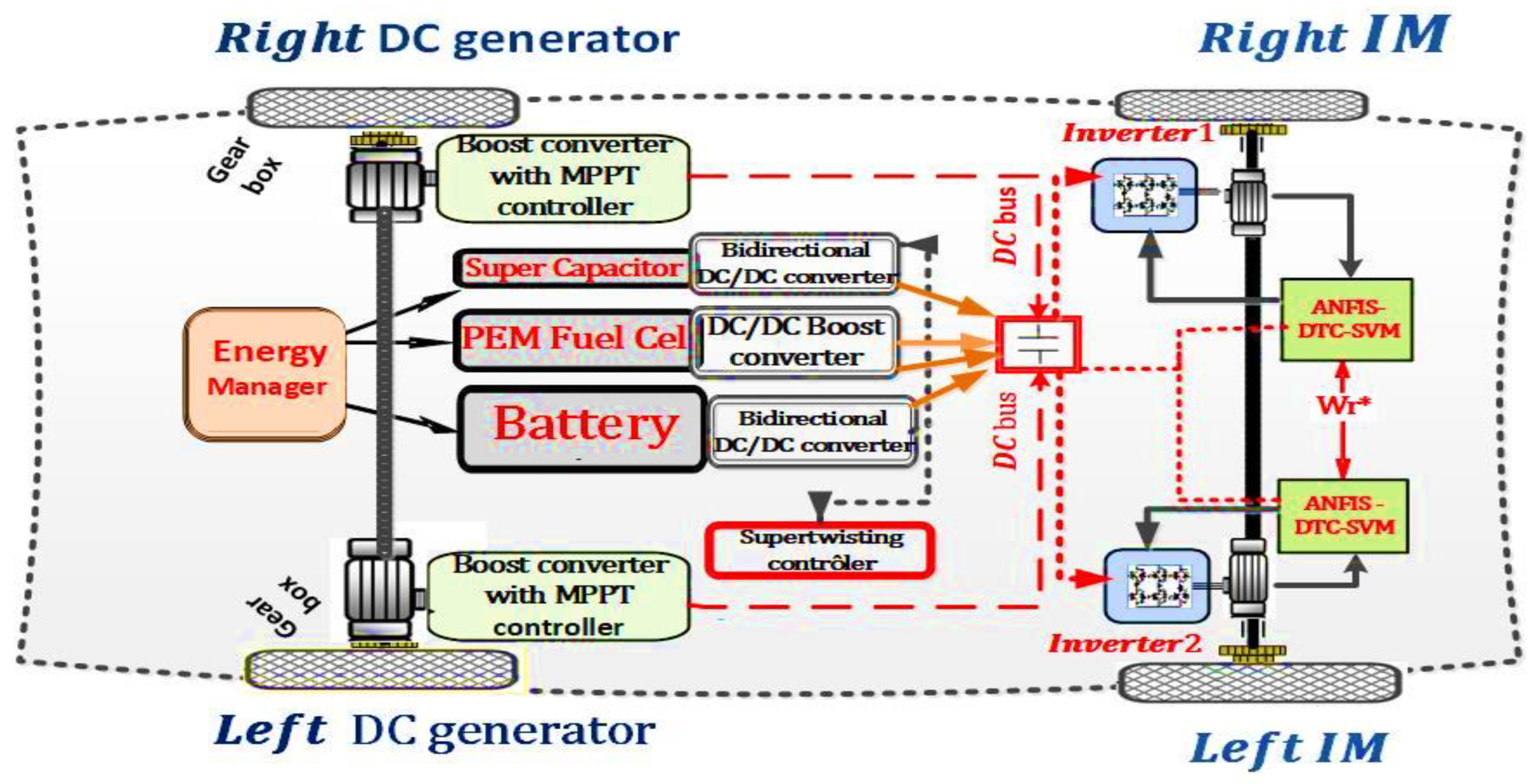
2. Hybrid Electric Vehicle Configuration
3. Modelling of the Proposed HEV
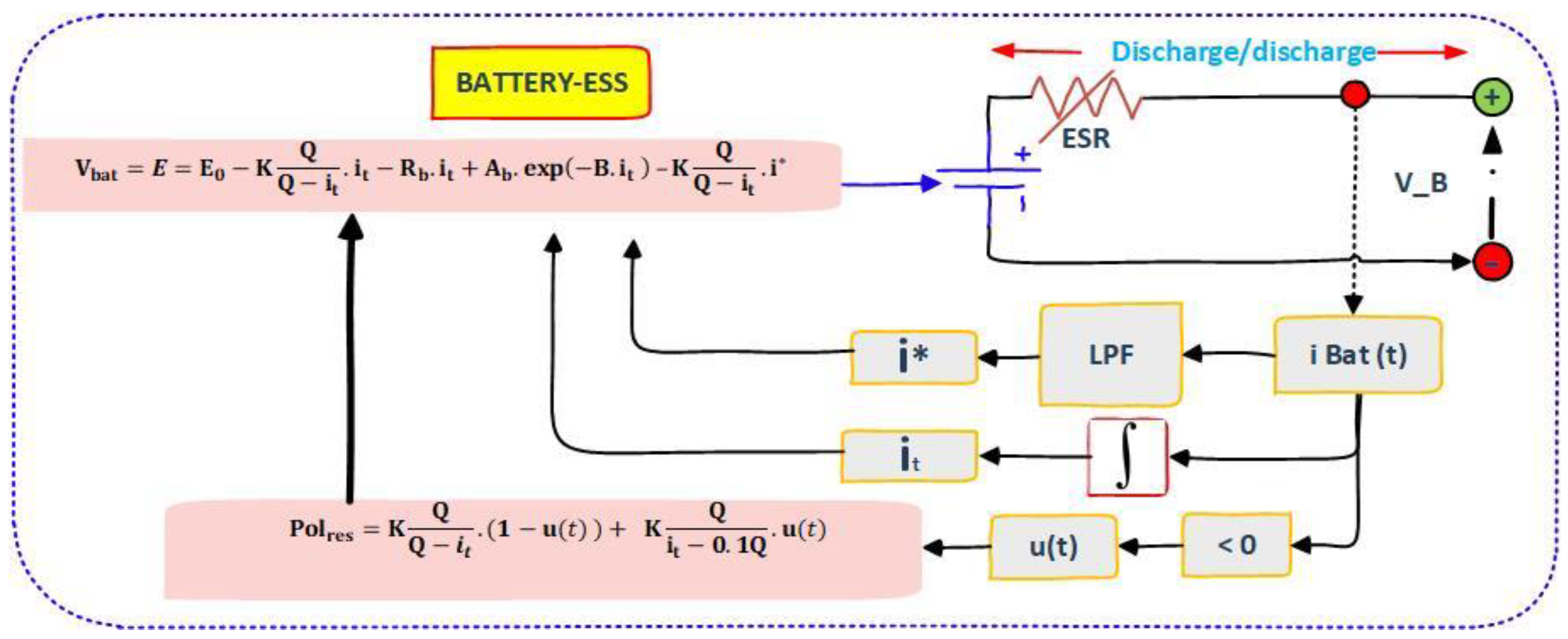
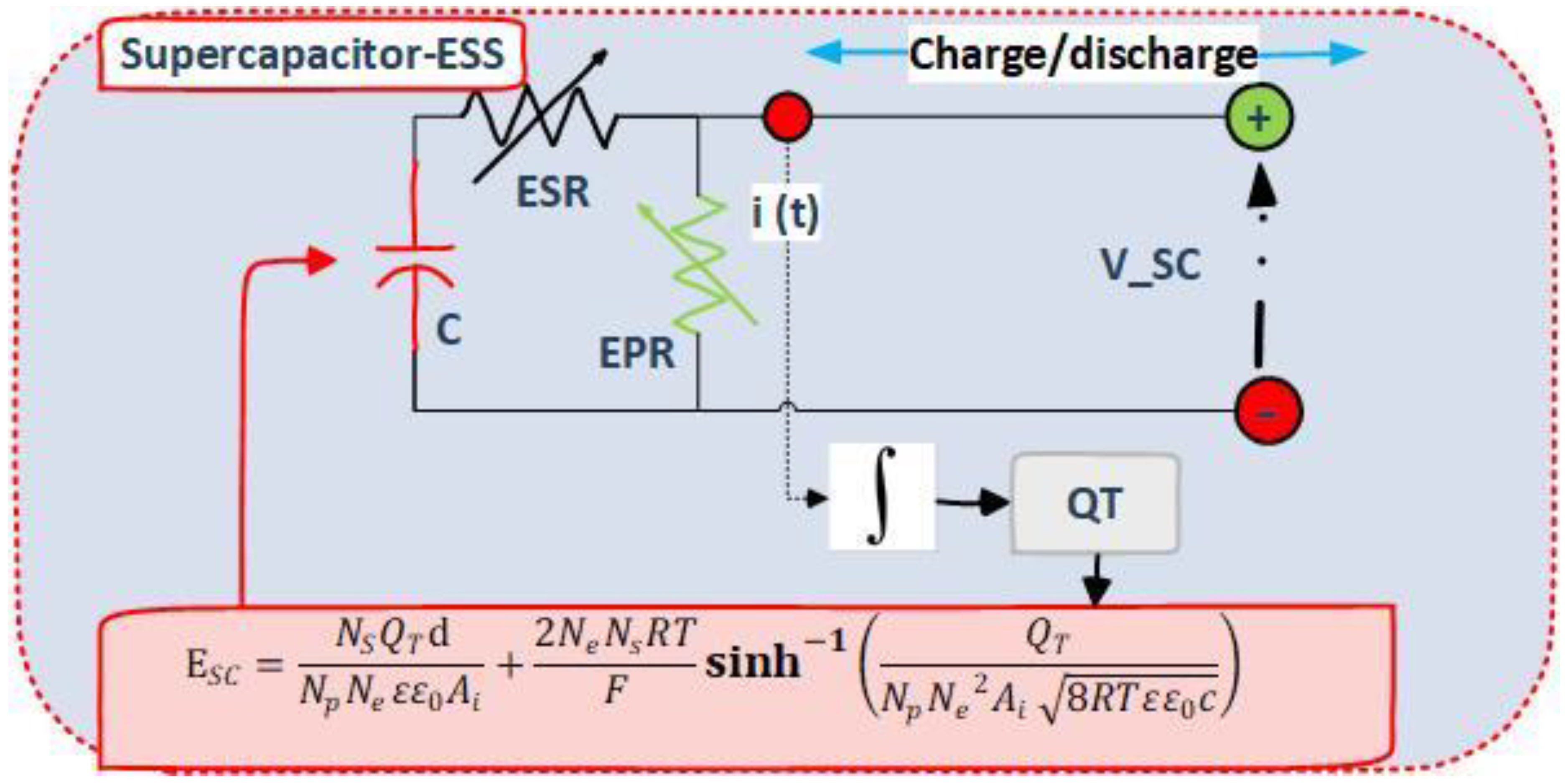
3.1. Modelling of the HESS
3.1.1. Li-Ion Battery Model
3.1.2. Supercapacitor Model
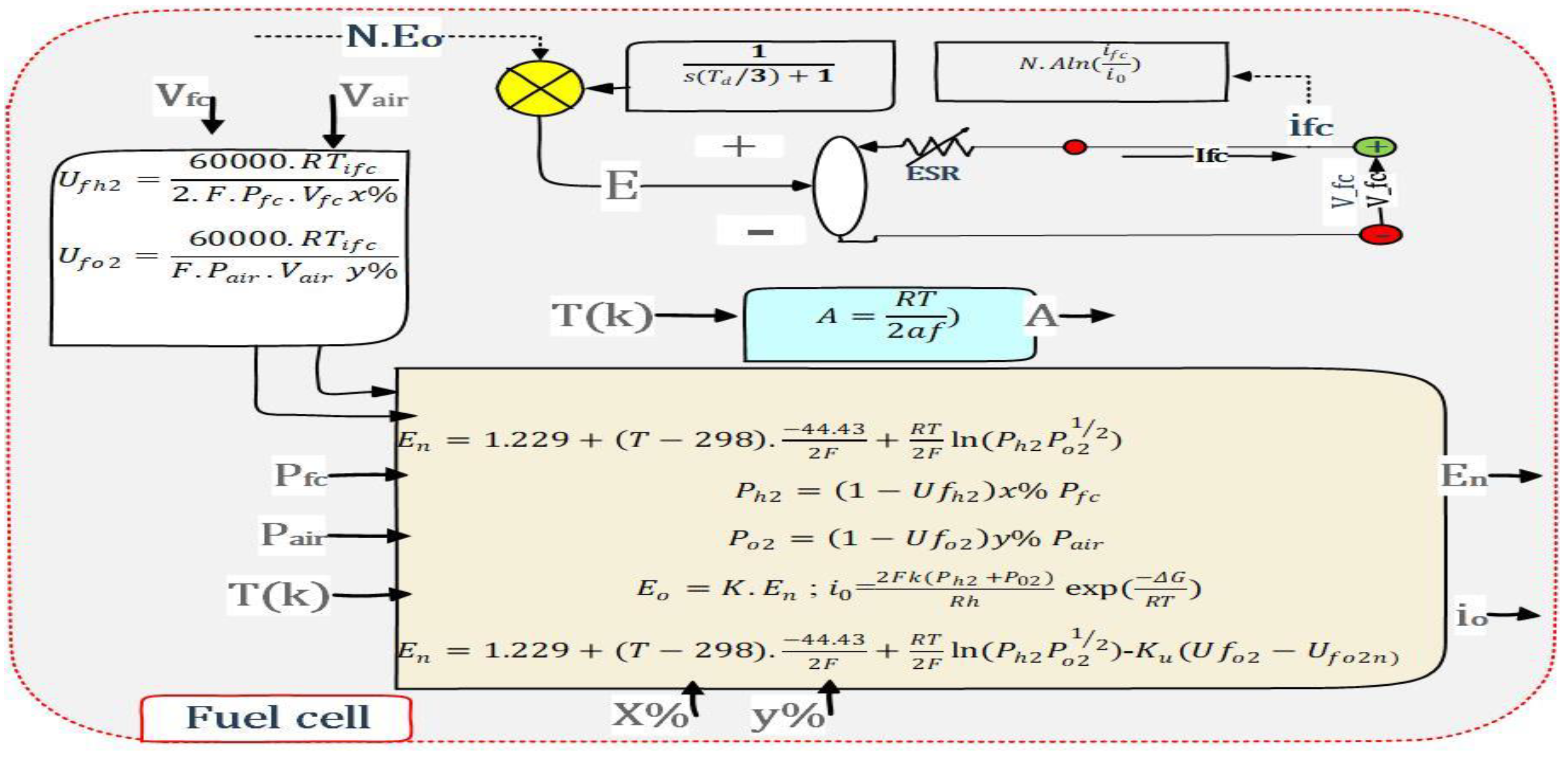
3.2. Modeling of the FC
3.3. Exploiting of EV’s Kinetic Energy
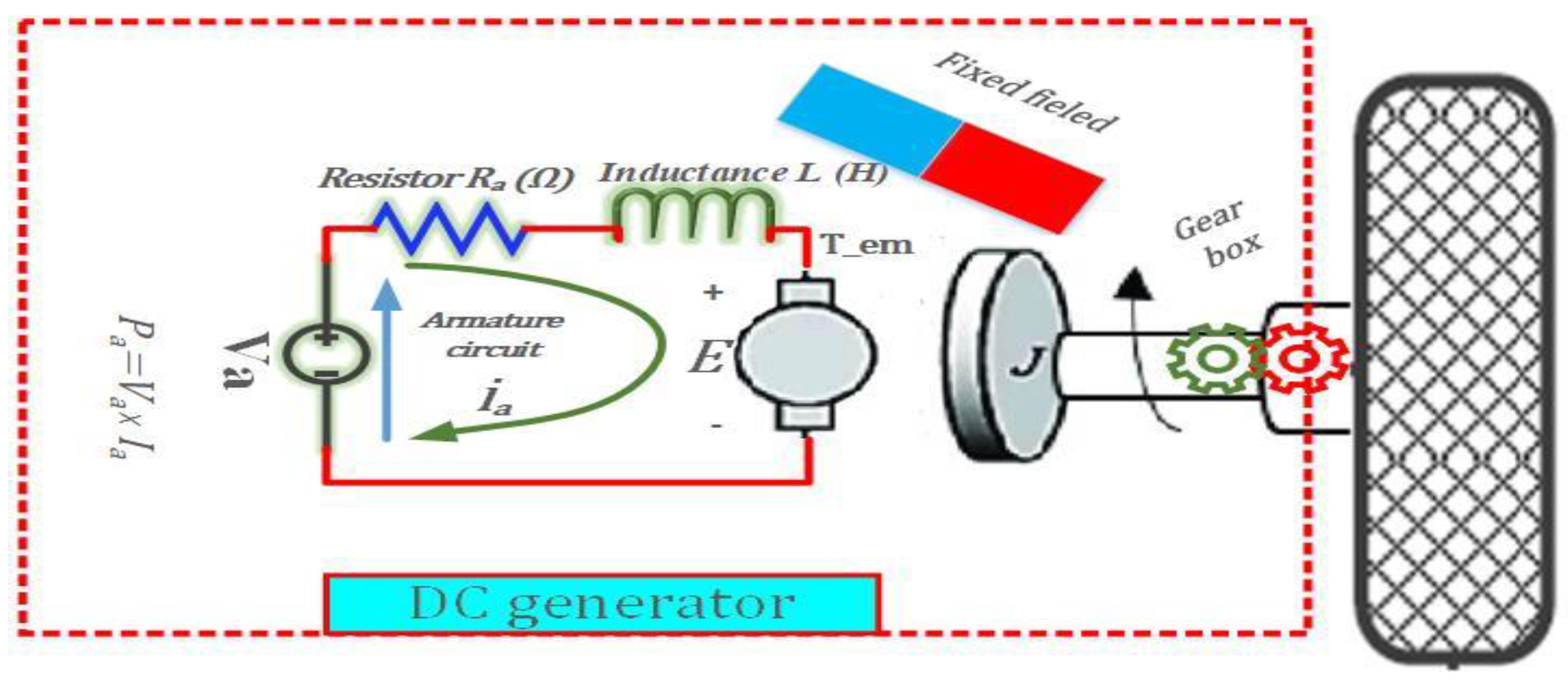
3.3.1. DC Generator
3.3.2. Exploiting of EV’s Kinetic Energy Using DC and AC Generators
3.4. Design and Control of Power Converters
3.4.1. Bi-Directional and Boost DC-DC Converters
3.4.2. LPF Control
3.4.3. The Super-Twisting Controller
- ✓
- Using saturation or sigmoid functions rather than discontinuous switching functions;
- ✓
- Utilizing an adaptive law to change the switching gain dynamically;
- ✓
- Utilizing high-order SMC methods.
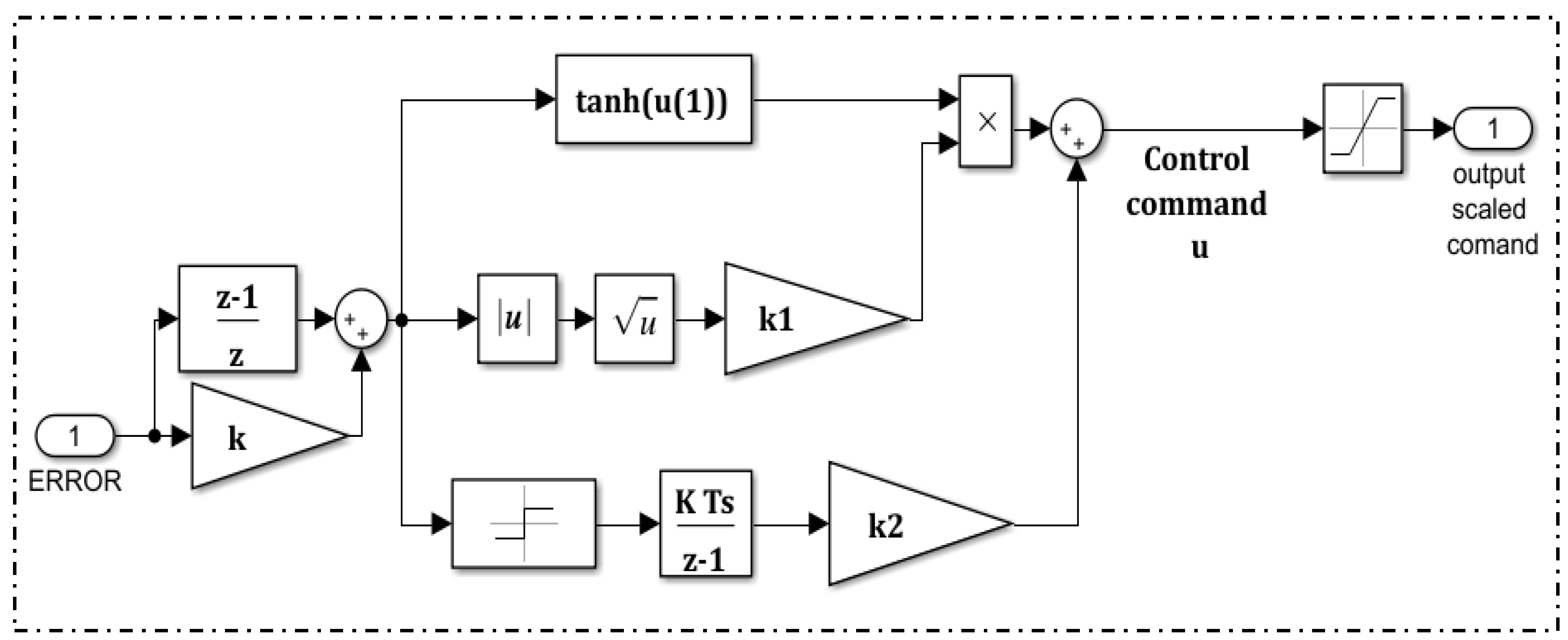
3.5. The ANFIS DTC-SVM Speed Controller
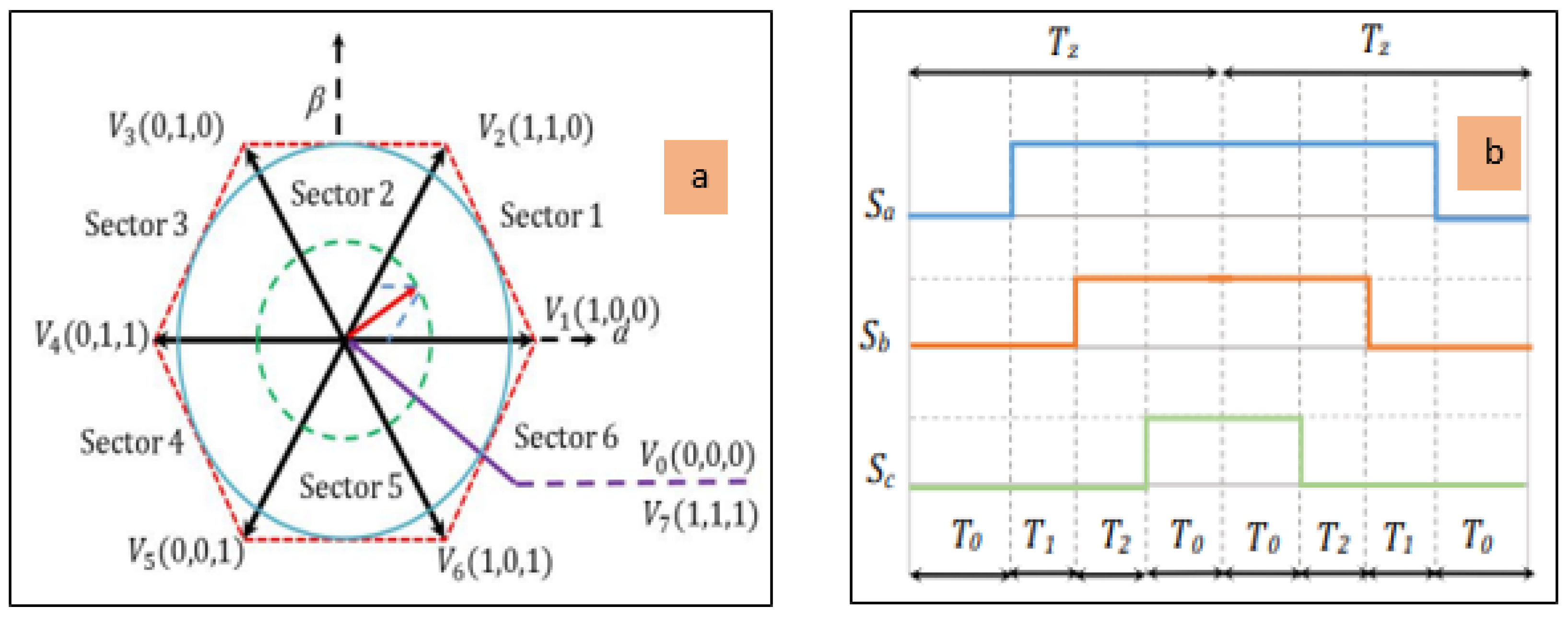
3.5.1. SVM Unit
3.5.2. ANFIS Controller
3.5.3. Flux and Torque Estimators
3.6. The Proposed Energy Management Strategy
3.7. Autonomy and Stress Analyses
3.8. The Supply Efficiency
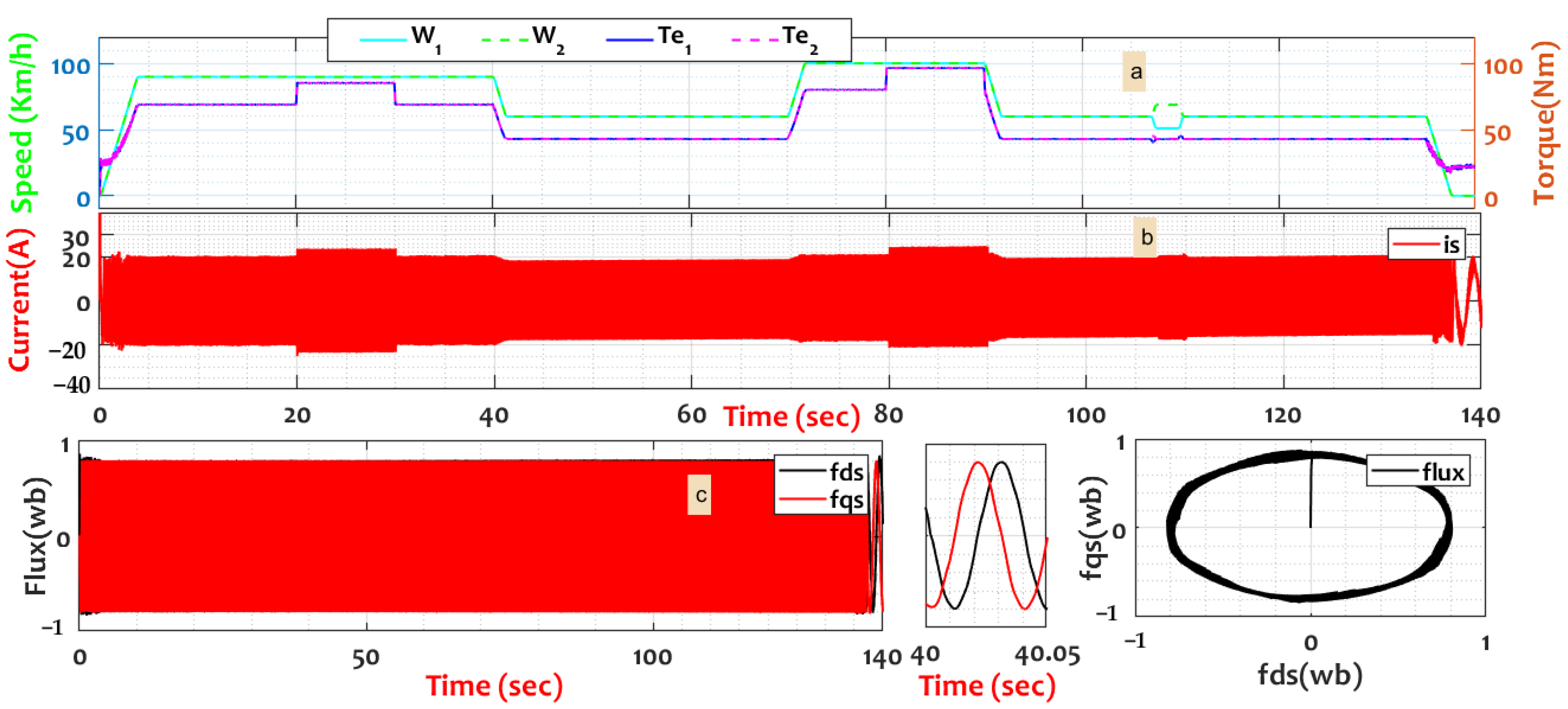
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EMSs | Energy management strategies |
| HEV | Hybrid electric vehicle |
| FC | Fuel cell |
| DC | Direct current |
| AC | Alternative current |
| PI | Proportional-integral |
| SM | State Machine |
| ANFIS | Adaptative neural fuzzy inference system |
| ANN | Artificial neural network |
| SC | Supercapacitor |
| 2WD | Two-wheel drive |
| ESS | Energy storage system technology |
| PMDCG | Permanent magnetic DC generator |
| Kp | Proportional gain |
| Ki | Integral gain |
| DTC | Direct torque control |
| Pev | Electric vehicles power |
| Psc | Supercapacitor power |
| Pbat | Battery power |
| Pfc | Fuel cell power |
| PDCg | DC generators power |
| SVM | Space vector modulation |
| HESS | Hybrid energy storage system |
| HS | Hybrid system |
| BCV | Battery constant voltage |
| DCG | Direct current generator |
| BESS | Battery energy storage system |
| KVL | Kirchhoff voltage law |
| KCL | Kirchhoff current law |
| BDC | Bidirectional converter |
| TF | Transfer function |
| FBC | Filtration-based control |
| HF | High-frequency |
| LF | Low-frequency |
| NOP | Nominal operating point |
| NOP | Nominal operating point |
| BDC | Bidirectional converter |
| SPS | Simulink sim-power systems |
| MPPT | Max power point tracker |
| NIMH | Nickel–metal hydride |
| SOC | State of charge |
| HCC | Hybrid current control |
References
- Song, Z.; Pan, Y.; Chen, H.; Zhang, T. Effects of Temperature on the Performance of Fuel Cell Hybrid Electric Vehicles: A Review. Appl. Energy 2021, 302, 117572. [Google Scholar] [CrossRef]
- Yin, W.; Qin, X.; Huang, Z. Optimal Dispatching of Large-Scale Electric Vehicles into Grid Based on Improved Second-Order Cone. Energy 2022, 254, 124346. [Google Scholar] [CrossRef]
- Hou, R.; Lei, L.; Jin, K.; Lin, X.; Xiao, L. Introducing Electric Vehicles? Impact of Network Effect on Profits and Social Welfare. Energy 2022, 243, 123002. [Google Scholar] [CrossRef]
- Wang, A.; Xu, J.; Zhang, M.; Zhai, Z.; Song, G.; Hatzopoulou, M. Emissions and Fuel Consumption of a Hybrid Electric Vehicle in Real-World Metropolitan Traffic Conditions. Appl. Energy 2022, 306, 118077. [Google Scholar] [CrossRef]
- Tian, X.; Cai, Y.; Sun, X.; Zhu, Z.; Xu, Y. A Novel Energy Management Strategy for Plug-in Hybrid Electric Buses Based on Model Predictive Control and Estimation of Distribution Algorithm. IEEE/ASME Trans. Mechatron. 2022, 27, 4350–4361. [Google Scholar] [CrossRef]
- Dong, H.; Fu, J.; Zhao, Z.; Liu, Q.; Li, Y.; Liu, J. A Comparative Study on the Energy Flow of a Conventional Gasoline-Powered Vehicle and a New Dual Clutch Parallel-Series Plug-in Hybrid Electric Vehicle under NEDC. Energy Convers. Manag. 2020, 218, 113019. [Google Scholar] [CrossRef]
- Soumeur, M.A.; Gasbaoui, B.; Abdelkhalek, O.; Ghouili, J.; Toumi, T.; Chakar, A. Comparative Study of Energy Management Strategies for Hybrid Proton Exchange Membrane Fuel Cell Four Wheel Drive Electric Vehicle. J. Power Sources 2020, 462, 228167. [Google Scholar] [CrossRef]
- Degradation Adaptive Energy Management Strategy Using Fuel Cell State-of-Health for Fuel Economy Improvement of Hybrid Electric Vehicle—ScienceDirect. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0306261920317803 (accessed on 13 September 2022).
- Zhuang, W.; Li, S.; Zhang, X.; Kum, D.; Song, Z.; Yin, G.; Ju, F. A Survey of Powertrain Configuration Studies on Hybrid Electric Vehicles. Appl. Energy 2020, 262, 114553. [Google Scholar] [CrossRef]
- Habib, A.R.R.; Butler, K. Environmental and Economic Comparison of Hydrogen Fuel Cell and Battery Electric Vehicles. Future Technol. 2022, 1, 25–33. [Google Scholar] [CrossRef]
- Tanç, B.; Arat, H.T.; Conker, Ç.; Baltacioğlu, E.; Aydin, K. Energy Distribution Analyses of an Additional Traction Battery on Hydrogen Fuel Cell Hybrid Electric Vehicle. Int. J. Hydrogen Energy 2020, 45, 26344–26356. [Google Scholar] [CrossRef]
- Habib, A.R.R.; Butler, K. Alternatives to Lithium-Ion Batteries in Electric Vehicles. Future Technol. 2022, 1, 33–34. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A Review of Air-Cooling Battery Thermal Management Systems for Electric and Hybrid Electric Vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Muzaffar, A.; Ahamed, M.B.; Deshmukh, K.; Thirumalai, J. A Review on Recent Advances in Hybrid Supercapacitors: Design, Fabrication and Applications. Renew. Sustain. Energy Rev. 2019, 101, 123–145. [Google Scholar] [CrossRef]
- Song, Z.; Liu, C. Electric Machine Design by a Novel Fast Model Predictive Optimization Strategy Treating Dimension-Expensive Problem; IEEE: Piscataway, NJ, USA, 2022; p. 1. [Google Scholar] [CrossRef]
- Tian, X.; Cai, Y.; Sun, X.; Zhu, Z.; Wang, Y.; Xu, Y. Incorporating Driving Style Recognition into MPC for Energy Management of Plug-In Hybrid Electric Buses. IEEE Trans. Transp. Electrif. 2023, 9, 169–181. [Google Scholar] [CrossRef]
- Benhammou, A.; Tedjini, H.; Guettaf, Y.; Soumeur, M.A.; Hartani, M.A.; Hafsi, O.; Benabdelkader, A. Exploitation of Vehicle’s Kinetic Energy in Power Management of Tow—Wheel Drive Electric Vehicles Based on ANFIS DTC-SVM Comparative Study. Int. J. Hydrogen Energy 2021, 46, 27758–27769. [Google Scholar] [CrossRef]
- Amine, H.M.; Mouaz, A.K.; Messaoud, H.; Othmane, A.; Saad, M. The Impacts of Control Systems on Hybrid Energy Storage Systems in Remote DC-Microgrid System: A Comparative Study between PI and Super Twisting Sliding Mode Controllers. J. Energy Storage 2022, 47, 103586. [Google Scholar] [CrossRef]
- Ammar, A.; Kheldoun, A.; Metidji, B.; Ameid, T.; Azzoug, Y. Feedback Linearization Based Sensorless Direct Torque Control Using Stator Flux MRAS-Sliding Mode Observer for Induction Motor Drive. ISA Trans. 2020, 98, 382–392. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A Comprehensive Review of Battery Modeling and State Estimation Approaches for Advanced Battery Management Systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Li, M.; Chen, Z. A Review of Key Issues for Control and Management in Battery and Ultra-Capacitor Hybrid Energy Storage Systems. eTransportation 2020, 4, 100064. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-Ion Battery Modeling and Parameter Identification Based on Fractional Theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Wang, L.; Guo, J.; Xu, C.; Wu, T.; Lin, H. Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge. Energies 2019, 12, 2134. [Google Scholar] [CrossRef] [Green Version]
- Şahin, M.E.; Blaabjerg, F. A Hybrid PV-Battery/Supercapacitor System and a Basic Active Power Control Proposal in MATLAB/Simulink. Electronics 2020, 9, 129. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A Review of Fractional-Order Techniques Applied to Lithium-Ion Batteries, Lead-Acid Batteries, and Supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Blal, M.; Benatiallah, A.; NeÇaibia, A.; Lachtar, S.; Sahouane, N.; Belasri, A. Contribution and Investigation to Compare Models Parameters of (PEMFC), Comprehensives Review of Fuel Cell Models and Their Degradation. Energy 2019, 168, 182–199. [Google Scholar] [CrossRef]
- Yue, M.; Jemei, S.; Gouriveau, R.; Zerhouni, N. Review on Health-Conscious Energy Management Strategies for Fuel Cell Hybrid Electric Vehicles: Degradation Models and Strategies. Int. J. Hydrogen Energy 2019, 44, 6844–6861. [Google Scholar] [CrossRef]
- Nanos, E.M.; Bottasso, C.L.; Campagnolo, F.; Mühle, F.; Letizia, S.; Iungo, G.V.; Rotea, M.A. Design, Steady Performance and Wake Characterization of a Scaled Wind Turbine with Pitch, Torque and Yaw Actuation. Wind. Energy Sci. 2022, 7, 1263–1287. [Google Scholar] [CrossRef]
- Brisset, S.; Radulescu, M. Design of a Brushless DC Permanent-Magnet Generator for Use in Micro-Wind Turbine Applications. Int. J. Appl. Electromagn. Mech. 2018, 56, 3–15. [Google Scholar]
- Laczko, A.A.; Brisset, S.; Radulescu, M. Modeling Approaches to Brushless DC Permanent-Magnet Generator for Use in Micro-Wind Turbine Applications; IEEE: Piscataway, NJ, USA, 2016; pp. 445–451. [Google Scholar]
- O’donnell, R.; Schofield, N.; Smith, A.C.; Cullen, J. Design Concepts for High-Voltage Variable-Capacitance DC Generators. IEEE Trans. Ind. Appl. 2009, 45, 1778–1784. [Google Scholar] [CrossRef]
- Do Dc Generators Offer Fuel Economy Advantages Over Ac Generators? Answers For The Telecom Industry |Cat| Caterpillar. Available online: https://www.cat.com/en_US/by-industry/electric-power/Articles/White-papers/answers-for-the-telecom-industry.html (accessed on 24 February 2023).
- Benchaib, A.; Rachid, A.; Audrezet, E. Sliding Mode Input-Output Linearization and Field Orientation for Real-Time Control of Induction Motors. IEEE Trans. Power Electron. 1999, 14, 3–13. [Google Scholar] [CrossRef]
- Yang, X.; Yao, J.; Deng, W. Output Feedback Adaptive Super-Twisting Sliding Mode Control of Hydraulic Systems with Disturbance Compensation. ISA Trans. 2021, 109, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Ozdemir, S.; Altin, N.; Sefa, I.; Zhang, Z.; Komurcugil, H. Super Twisting Sliding Mode Control of Three-Phase Grid-Tied Neutral Point Clamped Inverters. ISA Trans. 2022, 125, 547–559. [Google Scholar] [CrossRef] [PubMed]
- Sellali, M.; Abdeddaim, S.; Betka, A.; Djerdir, A.; Drid, S.; Tiar, M. Fuzzy-Super Twisting Control Implementation of Battery/Super Capacitor for Electric Vehicles. ISA Trans. 2019, 95, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Chen, Y.; Li, M.; Zhang, P.; Wan, Z. Fractional-Order Sliding Mode Position Tracking Control for Servo System with Disturbance. ISA Trans. 2020, 105, 269–277. [Google Scholar] [CrossRef]
- Suhail, M.; Akhtar, I.; Kirmani, S.; Jameel, M. Development of Progressive Fuzzy Logic and ANFIS Control for Energy Management of Plug-in Hybrid Electric Vehicle. IEEE Access 2021, 9, 62219–62231. [Google Scholar] [CrossRef]
- Elsisi, M.; Tran, M.-Q.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Robust Design of ANFIS-Based Blade Pitch Controller for Wind Energy Conversion Systems against Wind Speed Fluctuations. IEEE Access 2021, 9, 37894–37904. [Google Scholar] [CrossRef]
- Kakodia, S.K.; Giribabu, D.; Ravula, R.K. Torque Ripple Minimization Using an Artificial Neural Network Based Speed Sensor Less Control of SVM-DTC Fed PMSM Drive; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Space Vector Modulated—Direct Torque Controlled (DTC–SVM) Inverter—Fed Induction Motor Drive (Electrical/Electronics Project)|ProjectAbstracts.Com—Projects Ideas and Downloads. Available online: https://projectabstracts.com/6758/space-vector-modulated-direct-torque-controlled-dtc-svm-inverter-fed-induction-motor-drive.html (accessed on 29 August 2022).
- Mahmud, N.; Zahedi, A.; Mahmud, A. A Cooperative Operation of Novel PV Inverter Control Scheme and Storage Energy Management System Based on ANFIS for Voltage Regulation of Grid-Tied PV System. IEEE Trans. Ind. Inf. 2017, 13, 2657–2668. [Google Scholar] [CrossRef]
- Gupta, S.; Garg, R.; Singh, A. ANFIS-Based Control of Multi-Objective Grid Connected Inverter and Energy Management. J. Inst. Eng. India Ser. B 2020, 101, 1–14. [Google Scholar] [CrossRef]
- Song, K.; Li, F.; Hu, X.; He, L.; Niu, W.; Lu, S.; Zhang, T. Multi-Mode Energy Management Strategy for Fuel Cell Electric Vehicles Based on Driving Pattern Identification Using Learning Vector Quantization Neural Network Algorithm. J. Power Sources 2018, 389, 230–239. [Google Scholar] [CrossRef]
- Ammar, A.; Benakcha, A.; Bourek, A. Closed Loop Torque SVM-DTC Based on Robust Super Twisting Speed Controller for Induction Motor Drive with Efficiency Optimization. Int. J. Hydrogen Energy 2017, 42, 17940–17952. [Google Scholar] [CrossRef]
- Ferahtia, S.; Djeroui, A.; Rezk, H.; Houari, A.; Zeghlache, S.; Machmoum, M. Optimal Control and Implementation of Energy Management Strategy for a DC Microgrid. Energy 2022, 238, 121777. [Google Scholar] [CrossRef]
- Kraiem, H.; Flah, A.; Mohamed, N.; Alowaidi, M.; Bajaj, M.; Mishra, S.; Sharma, N.K.; Sharma, S.K. Increasing Electric Vehicle Autonomy Using a Photovoltaic System Controlled by Particle Swarm Optimization. IEEE Access 2021, 9, 72040–72054. [Google Scholar] [CrossRef]
- Yildiz, A.; Özel, M.A. A Comparative Study of Energy Consumption and Recovery of Autonomous Fuel-Cell Hydrogen–Electric Vehicles Using Different Powertrains Based on Regenerative Braking and Electronic Stability Control System. Appl. Sci. 2021, 11, 2515. [Google Scholar] [CrossRef]
- Sorlei, I.-S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel Cell Electric Vehicles—A Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Lee, U.; Jeon, S.; Lee, I. Design for Shared Autonomous Vehicle (SAV) System Employing Electrified Vehicles: Comparison of Battery Electric Vehicles (BEVs) and Fuel Cell Electric Vehicles (FCEVs). Clean. Eng. Technol. 2022, 8, 100505. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Hassan, I.A.; Alhelou, H.H. Robust Control for Techno-economic Efficient Energy Management of Fuel Cell Hybrid Electric Vehicles. IET Renew. Power Gener. 2022, 16, 661–1684. [Google Scholar] [CrossRef]
- Mounica, V.; Obulesu, Y. Hybrid Power Management Strategy with Fuel Cell, Battery, and Supercapacitor for Fuel Economy in Hybrid Electric Vehicle Application. Energies 2022, 15, 4185. [Google Scholar] [CrossRef]
- Salem, M.; Elnaggar, M.; Saad, M.S.; Fattah, H.A.A. Energy Management System for Fuel Cell-Battery Vehicles Using Multi Objective Online Optimization. IEEE Access 2022, 10, 40629–40641. [Google Scholar] [CrossRef]
- Cunanan, C.; Tran, M.-K.; Lee, Y.; Kwok, S.; Leung, V.; Fowler, M. A Review of Heavy-Duty Vehicle Powertrain Technologies: Diesel Engine Vehicles, Battery Electric Vehicles, and Hydrogen Fuel Cell Electric Vehicles. Clean Technol. 2021, 3, 474–489. [Google Scholar] [CrossRef]
- İnci, M.; Büyük, M.; Demir, M.H.; İlbey, G. A Review and Research on Fuel Cell Electric Vehicles: Topologies, Power Electronic Converters, Energy Management Methods, Technical Challenges, Marketing and Future Aspects. Renew. Sustain. Energy Rev. 2021, 137, 110648. [Google Scholar] [CrossRef]
- Carello, M.; de Carvalho Pinheiro, H.; Longega, L.; Di Napoli, L. Design and Modelling of the Powertrain of a Hybrid Fuel Cell Electric Vehicle. SAE Int. J. Adv. Curr. Pract. Mobil 2021, 3, 2878–2892. [Google Scholar]
- Zhou, Y.; Ravey, A.; Péra, M.-C. Real-Time Cost-Minimization Power-Allocating Strategy via Model Predictive Control for Fuel Cell Hybrid Electric Vehicles. Energy Convers. Manag. 2021, 229, 113721. [Google Scholar] [CrossRef]





| Type | Parameters | Value |
|---|---|---|
| Vehicle | fr | 0.0135 |
| rt (m) | 0.31 | |
| cd | 0.32 | |
| ρair (kg/m3) | 1.108 | |
| A (m2) | 2.63 | |
| Motors power (kW) | 30 | |
| Fuel cell | Voltage (v) | 200 |
| MOP and NOP (A, V) | 150,200 and 40,200 | |
| Number of cells | 285 | |
| Supply pressure h2 (bar) | 1.5 | |
| Efficiency (%) | 55 | |
| Composition: H2O, H2, O2 (%) | 1, 99.95, 21 | |
| DC generator | Armature resistance Ra (Ω) | 0.8727 |
| Power (kW) | 3 | |
| La (H) | 0.001882 | |
| Tem (N.m) | 4.2 | |
| Battery pack | Capacity (Ah) | 20 |
| Nominal voltage (V) | 200 | |
| Fully charged (V) | 230 | |
| SC bank | Rated voltage | 200 |
| Internal resistance (Ω) | 2.10−4 | |
| Rated capacitance (F) | 14.6 |
| Sector | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Sa | Tb | Ta | Ta | Tc | Tb | Tc |
| Sb | Ta | Tc | Tb | Tb | Tc | Ta |
| Sc | Tc | Tb | Tc | Ta | Ta | Tb |
| State | Period | Explanation |
|---|---|---|
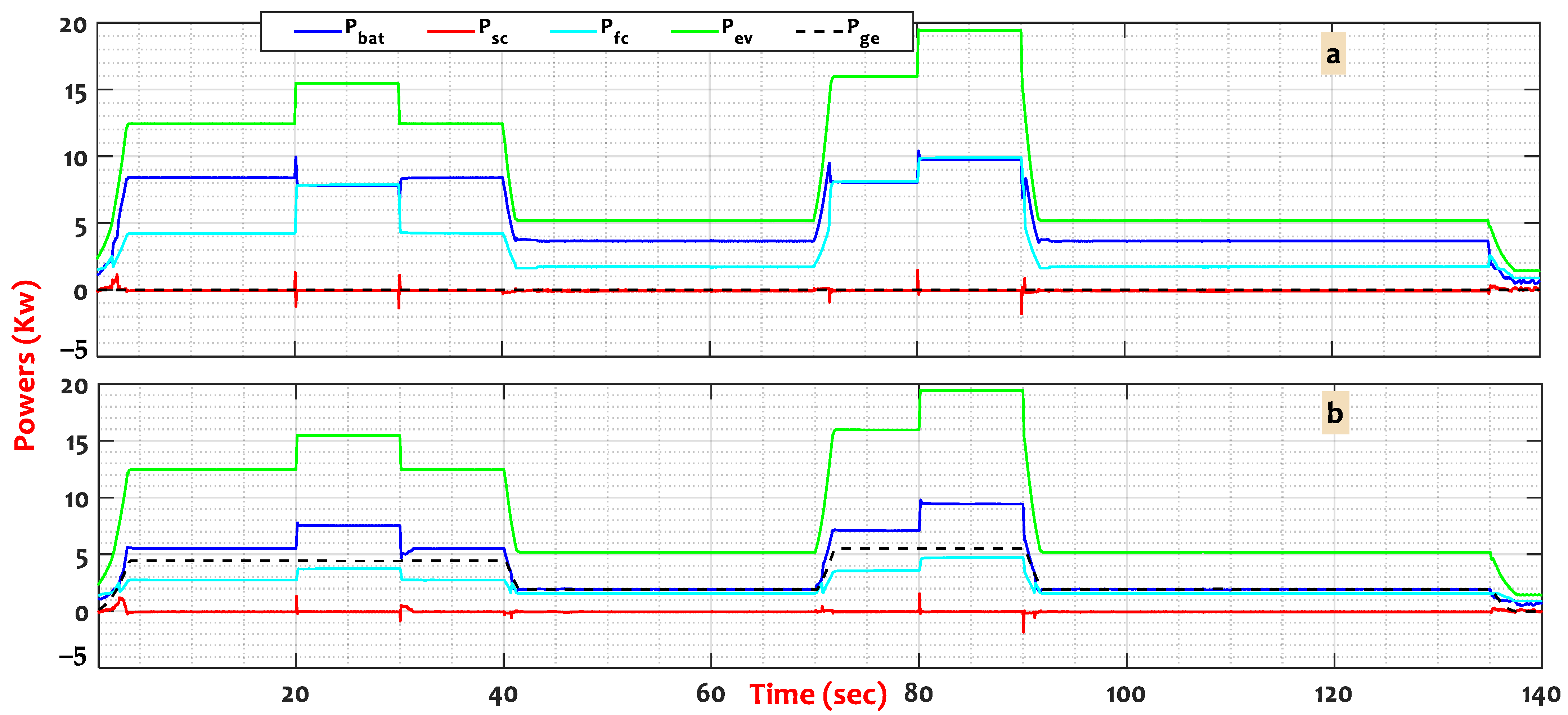
| 1 | [0, 40] | The HEV’s reference speed is 90 km/h using a ramp of (11°) [20–30] (s). |
| 2 | [40, 70] | The HEV’s speed is 60 km/h. |
| 3 | [70, 90] | The HEV runs at 100 km/h, applying the slope of 12° from 80 to 90 (s). |
| 4 | [90, 135] | The HEV’s speed dropped to 60 km/h, detoured 30° on the left. |
| 5 | [135, 140] | The vehicle stopped during this period. |
| HEV Scenarios | with DC Generators | Basic HEV | |
|---|---|---|---|
| Criteria | |||
| Response time (s) | 0.05 | 0.05 | |
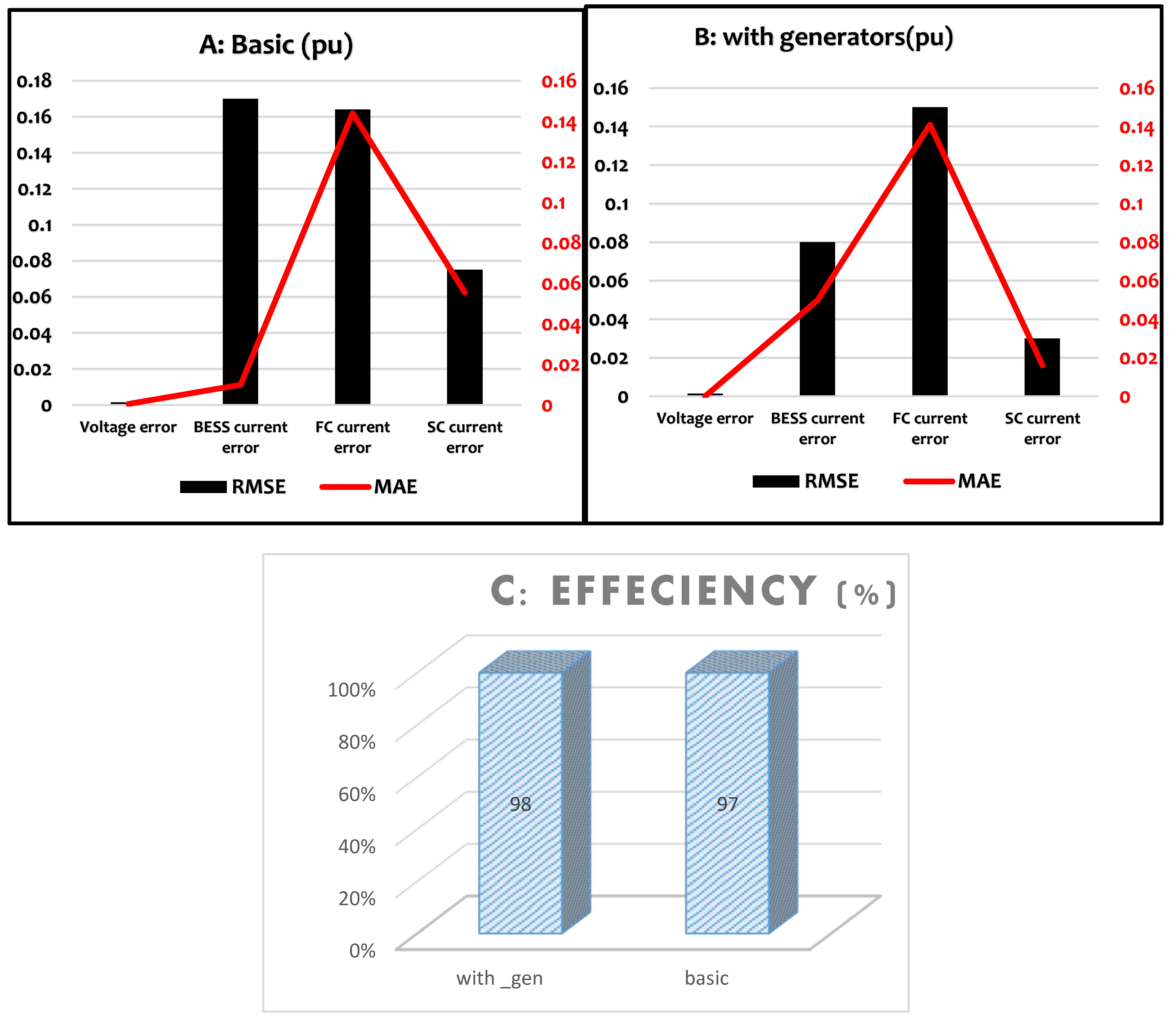
| Efficiency (%) | 98 | 97 | |
| SOC (%) | 60.1–59.7 | 60.1–59.52 | |
| Fuel consumption (SI) | 15.07 | 24.78 | |
| Stress (%) | |||
| BESS | 41 | 62 | |
| FC | 29 | 38 | |
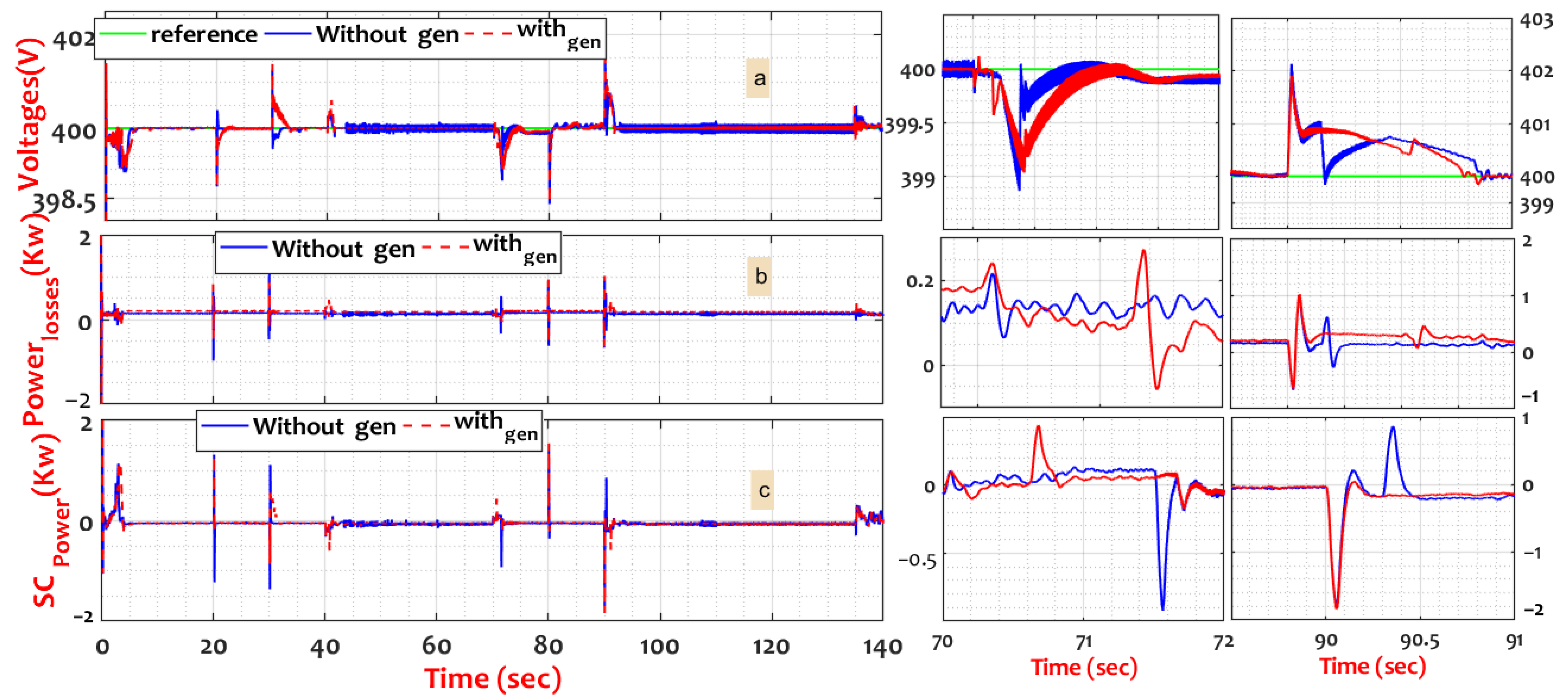
| DC bus voltage (V) | |||
| RMSE (%) | 0.0013 | 0.0014 | |
| MAE (%) | 0.00005 | 0.0047 | |
| Battery current control error (A) | |||
| RMSE (%) | 0.038 | 0.17 | |
| MAE (%) | 0.025 | 0.01 | |
| FC current control error (%) | |||
| RMSE (%) | 0.15 | 0.164 | |
| MAE (%) | 0.141 | 0.144 | |
| SC current control error (A) | |||
| RMSE (%) | 0.004 | 0.075 | |
| MAE (%) | 0.0037 | 0.055 | |
| HEV speed control error (%) | |||
| RMSE (%) | 0.4 | 0.4 | |
| MAE (%) | 0.17 | 0.17 | |
| HEV torque control error (%) | |||
| RMSE (%) | 0.59 | 0.59 | |
| MAE (%) | 0.24 | 0.24 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benhammou, A.; Hartani, M.A.; Tedjini, H.; Rezk, H.; Al-Dhaifallah, M. Improvement of Autonomy, Efficiency, and Stress of Fuel Cell Hybrid Electric Vehicle System Using Robust Controller. Sustainability 2023, 15, 5657. https://doi.org/10.3390/su15075657
Benhammou A, Hartani MA, Tedjini H, Rezk H, Al-Dhaifallah M. Improvement of Autonomy, Efficiency, and Stress of Fuel Cell Hybrid Electric Vehicle System Using Robust Controller. Sustainability. 2023; 15(7):5657. https://doi.org/10.3390/su15075657
Chicago/Turabian StyleBenhammou, Aissa, Mohammed Amine Hartani, Hamza Tedjini, Hegazy Rezk, and Mujahed Al-Dhaifallah. 2023. "Improvement of Autonomy, Efficiency, and Stress of Fuel Cell Hybrid Electric Vehicle System Using Robust Controller" Sustainability 15, no. 7: 5657. https://doi.org/10.3390/su15075657
APA StyleBenhammou, A., Hartani, M. A., Tedjini, H., Rezk, H., & Al-Dhaifallah, M. (2023). Improvement of Autonomy, Efficiency, and Stress of Fuel Cell Hybrid Electric Vehicle System Using Robust Controller. Sustainability, 15(7), 5657. https://doi.org/10.3390/su15075657








