Structural Analysis of Self-Weight Loading Standing Trees to Determine Its Critical Buckling Height

Abstract

A tree may receive compression and flexure combination, and the structural analysis governed by the building code may be capable of estimating the tree’s safety in the built environment. This study proposed to refer to the building code to check the tree dimension adequacy resisting the load. This study simplified the case by focusing only on the self-weight and ignoring the external loads; therefore, the buckling analysis of a slender tapered round column subjected to compression is advocated. Buckling occurs when the tree’s structure can no longer maintain its original shape. Euler and Ylinen’s buckling stress analysis (Method 1) calculated tree safety with a 95% confidence level. This study also applied the Greenhill formula (Method 2) to determine the critical height of a tree receiving the stem weight, then modified it to include the crown weight (Method 3). The three methods calculated the critical height to determine the safety factor (S_f), that is, the ratio of the actual tree height (H) to the 95% confidence level estimated critical height (H_cr). The safety factors were then categorized as unsafe (S_f < 1.00), safe (1.00 < S_f < 1.645), and very safe (1.645 < S_f). This study demonstrated that Method 1 is the most reliable and applicable among other methods. Method 1 resulted in no unsafe trees, 10 safe trees, and 13 very safe trees among the observed excurrent agathis (Agathis dammara). Meanwhile, among the decurrent rain trees (Samanea saman (Jacq.) Merr), 5, 31, and 14 were unsafe, safe, and very safe, respectively.

1. Introduction

Studying the structural behavior of an urban tree planted in a built environment is necessary to calculate its reliability in resisting the self-weight and applied load to ensure the community’s security against the tree’s breaking and falling. The tree’s structural behavior relates to tree architecture, partly controlled by plant phenotype. Several studies have focused on tree stem stability in terms of instantaneous mechanical disturbance and safety, stiffness, breakage, or buckling in response to wind and gravity [1,2,3,4]. The tree stem’s stability is closely related to its stem form and crown characteristics. Several researchers [5,6,7,8] developed a theory whereby a tree’s possible tallest height is consistent with its stability, which can be modeled as a vertical pole. In this model, a compressive load is applied to a straight stem, and eventually, the stem buckles and triggers its instability failure. The load at which this buckling starts to happen is called the critical buckling load (F_cr). In addition to uprooting or steam break because of wind load, buckling is an ecologically relevant biophysical constraint [2,5]. The critical buckling load calculation is necessary for estimating the standing tree’s safety. The buckling load may come from the stem and crown self-weight (gravity) and external compressive load (i.e., the climbing arborist’s weight, snow, and all hanging things). Greenhill [7], in 1881, mathematically demonstrated that a tree could buckle under its self-weight by assuming it resembles a heavy and long slender column. Although the pure buckling failure of a healthy tree planted in a spacely open-grown location rarely occurs because the tree diameter grows following the tree height growth, this theoretical approach is necessary to ensure the community’s convenience against the fear of the tree falling in their environment. This study exemplified the structural instability analysis of a tree to investigate its safety in a built environment. Unlike building construction [9,10,11,12,13,14,15,16,17,18], structural analysis practices of the tree based on engineering mechanics approaches have rarely been conducted before because a tree is not a construction. Dargahi et al. [19] suggested a finite element method to analyze the tree stability to reduce the risk of damage. In addition to general structural analysis software (i.e., SAP 2000, ETABS, STAAD PRO, and Tribby3d), several specific computer numerical simulation programs based on a computer-aided drawing (CAD) (i.e., MECHATREE [20], CAPSIS [21], and AMAPpara [22]) have proven to be satisfyingly reliable and are proposed to conduct the structural analysis of a tree receiving external load and self-weight load. However, drawing every tree for structural analysis during safety assessment is impractical to implement because of the cost ineffectiveness. Pure engineering mechanics formulas for calculating the load-bearing capacity of a tree have been reported [23,24], but the standardization to implement them is still needed. The current building code may be a candidate for developing the standardization of tree safety assessment practices. The standardized and scientific safety justification should doubtlessly advise people to plant some trees in their neighborhood and convince them to avoid casually felling the tree; thus, it may support recent increasing environmental awareness to implement more ecological practices for developing a sustainable and environmentally friendly city. The commitment to sustainability is the primary indicator to appraise a construction company’s performance in the built environment project developments [25].

The risk of instability buckling under self-weight is usually determined by a safety factor that is calculated as the ratio between critical buckling height (H_cr), the maximum height that a tree can reach before buckling occurs, and the actual tree height (H) [2,6,26]. The safety factor is based on the stem’s geometric shapes, density, and mechanical properties. The critical buckling height (H_cr) may be calculated by inputting the actual mechanical properties (strength and elasticity), unbiasedly estimated by its average value, into the structural analysis procedures; thus, the buckling stem shall be visually seen when the actual tree height is taller than the critical buckling height (H > H_cr). However, instead of inputting the average mechanical properties, this study prefers to input the allowable stress for considering the 95% confidence level of safety following the building code specification. The 95% confidence level of safety is necessary because urban trees are planted in the built environment where people’s convenience and security must be prioritized. The allowable stress is the 5% lower exclusion limit of the strength corrected by the corresponding adjustment factors; thus, it represents the reference design values [27]. The adjustment factors accommodate the service environment condition effects on the mechanical properties compared to those resulting in the standardized condition laboratory tests [28,29]. When buckling occurs, a column structure can no longer maintain its original straight shape; the deformed shape resembles an arch curvature-like bending deflection (Figure 1), leading to the tree stem’s instability failure. Buckling is a failure caused by instability within a slender column structure that receives compressive loads. The height and slenderness of a tree create a greater risk of elastic buckling due to the tree’s self-weight [2].

General knowledge about tree growth characteristics, such as the crown shape, apical dominance, and branching, can aid in tree management in terms of pruning and limb manipulation for an aesthetical appearance and in selecting appropriate measurements to monitor tree growth [30]. Tree growth habits may have an excurrent or decurrent form. Trees with an excurrent form have apical dominance, with the main trunk growing throughout the tree’s life, causing a cone-shaped crown [31], such as pines and most other conifers. Trees with a decurrent or deliquescent form have many dominant branches that do not show apical dominance; the trees have a spreading crown shape caused by lateral branches growing at the same level as the main trunk. The tree does not develop one central axis, but many branches spread out [32]. This form is often found in deciduous trees. The tree growth form, including stem and crown architecture characteristics, is a complex factor to which buckling can be attributed in terms of the load that shall be supported by the tree [33]. The stems and crowns produce static self-weight-loading affecting the critical buckling height [34]. This study aimed to analyze the safety factors related to the critical buckling height of decurrent and excurrent trees modeled as slender round columns using three different methods. The structural analysis of a tapered column following the Indonesian Wooden Building Code (SNI 7973:201) [35], which has adopted the National Design Specification for Wood Construction [36] since 2013 [28,29], is Method 1. Euler and Ylinen’s formulas, already familiar to engineers [29,37,38], are required to analyze a column’s buckling as specified by the legally current building code. Although a tree is not a building nor manufactured construction, engineers or arborists shall carefully estimate its structural reliability for carrying loads to ensure its safety when planted in the built environment. Method 2 follows Greenhill’s formula [7], which developed the Euler buckling formula for a tree receiving only its stem weight. Method 3 modifies Greenhill’s formula to add the crown weight to the stem weight as the compressive load. This study promotes the structure’s stability analysis following the standardized methods provided by the building code to answer the question of tree safety planted in a built environment. Although a tree may receive more external loads, this study delimitated its scope to the tree receiving self-weight only and ignoring the external load to simplify the analysis.

2. Methodology

2.1. Target Tree

This study was conducted at the Darmaga Campus–Bogor–West Java (ID) to determine the buckling behavior of trees with decurrent and excurrent growth forms. The selected decurrent tree was the rain tree (Samanea saman (Jacq.) Merr), and the excurrent tree was agathis (Agathis dammara). Both species are widely planted urban tree species with a risk of stem failure due to growth under environmental pressure. The sample size (n) is 73 trees, including 50 rain trees and 23 agathis located in IPB Campus Dramaga (6.54°–6.56° S, 106.71°–106.73° E). The altitude is 145–195 masl. The selected target trees had a single main stem.

2.2. Growth Morphometrical Analysis

This study determines each tree’s morphometrical characteristics by measuring the tip’s diameter (D_tr), crown diameter (D_c), diameter at the breast height (D_bh), lowest crown height (H_ck), branch-free height (H_tbc), and tree height (H) as shown in Figure 2. Except for the tip’s diameter (D_tr), the other parameter measurements follow Pretzsc et al.’s [39] reports. The tip’s diameter (D_tr), diameter at the breast height (D_bh), and tree height (H) are necessary to estimate the stem’s volume. The measurement of the diameter of the tip (D_tr) was carried out using the Spiegel Relaskop Bitterlich (SRB), referring to the Spiegel-Relaskop Metric Standard [40]. The crown diameter of eight sub-cardinal measurements finds the average of the biggest and smallest diameter to determine the mean crown diameter (D_c) parameter. Tree slenderness (S) is the tree height (H) divided by the diameter at breast height (D_bh).

2.3. Determination of the Stem’s Density and Mechanical Properties

The stem’s properties measurement obtained the self-weight of the loading stem. The stem density is the small core sample’s mass/volume ratio. Meanwhile, nondestructive testing based on sonic velocity propagation in the longitudinal direction of the standing tree using the stress wave timer tool of Fakopp Microsecond Timer (Fakopp Bt, Sopron, Hungary) measured the dynamic modulus of elasticity (E_d). Although the E_d values resulting from nondestructive acoustic-based testing were consistently higher than the static bending test results, there was a strong correlation between the values [41,42,43,44,45,46,47,48]; thus, E_d is a common indicating predictor to estimate static mechanical properties of wood. Duong et al. [47] also reported that dynamic modulus of elasticity (E_d) values of small clear wood had a similar trend in radial direction arrangement cutting sawn lumber with the static modulus of elasticity (E_s). He also showed that E_s and E_d have similar patterns among clone variations. This trend paved the way to measure a standing tree’s stress-wave velocity, calculate its E_d, and then estimate the wood’s E_s. Some studies are available concerning the longitudinal stress wave velocity of softwood [44,49,50] and hardwood [47,51,52] standing trees or logs and the correlation with their wood’s static modulus of elasticities. This study converts E_d of standing agathis trees following Wang et al. [44] (Equation (1a)) and stress wave velocity (S_wvT) of standing rain trees following Duong et al. [47] (Equation (1b)) to their wood’s static modulus of elasticity (E_s).

$$E_s=0.352E_d+3691.56$$

(1a)

$$E_s=0.004S_{wvT}-6.127$$

(1b)

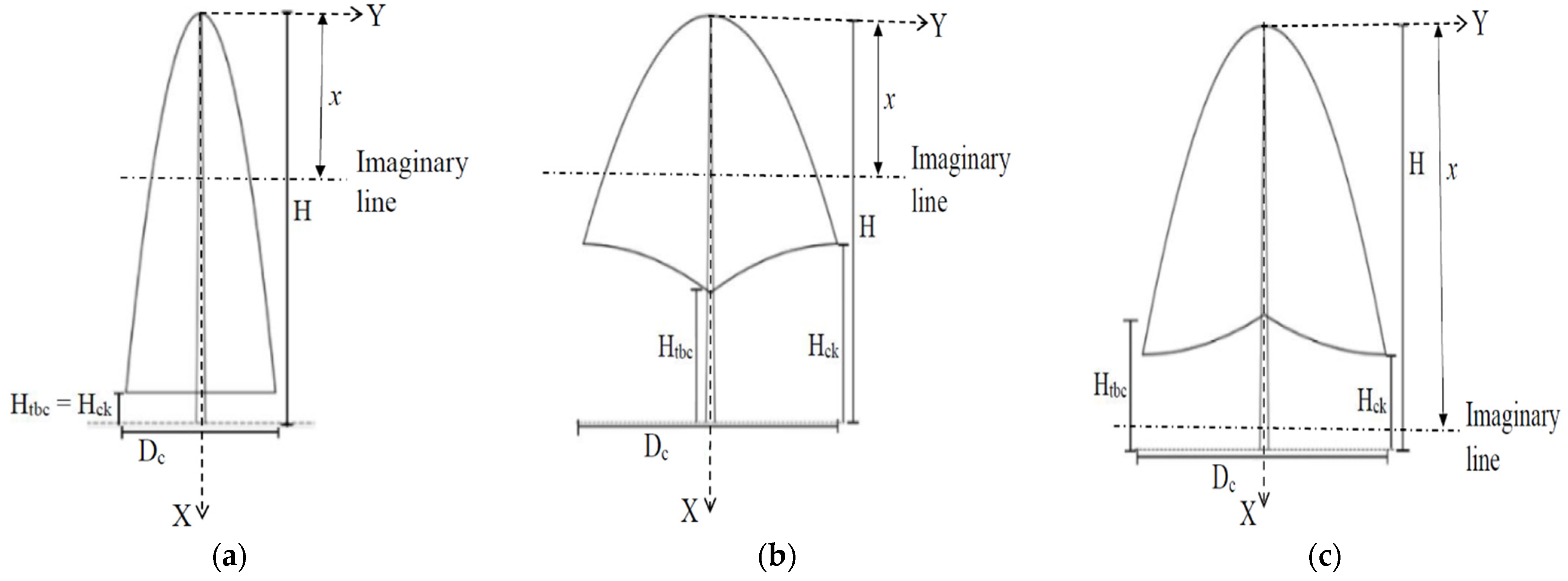
2.4. Determination of Tree Volume

2.4.1. Determination of the Stem Volume

The stem’s volume is mathematically related to the geometric shape, including the taper and cross-sectional area. Three models approach the stem geometry in this study, i.e., the cone, hooked cone, and cylinder (Figure 3). Both excurrent and decurrent tree’s stems are assumed to follow those three models, which was suggested by Greenhill’s statement [7], “Perhaps the best assumption to make our purpose as to the growth of a tree are to assume a uniformly tapering trunk as a central column”. The stem geometric model selection was based on the adjusted tip’s diameter (D_t). The adjusted tip’s diameter (D_t) refers to the tip’s diameter (D_tr) and D_bh values. If D_tr is less than or the same as D_bh, D_t is equal to D_tr; however, if D_tr is greater than D_bh, D_t is D_bh. The cone is chosen when D_t = 0 (Figure 3a), while the hooked cone is chosen when 0 < D_t < D_bh (Figure 3b). Meanwhile, the cylinder is selected when D_t ≥ D_bh (Figure 3c).

The stem’s self-weight load, considered the gravity load applied to a portion of the stem, is the stem’s weight above that particular portion. Suppose an imaginary line is drawn at any x-point perpendicular to the longitudinal direction. In that case, the part below the imaginary line is the structural stem receiving the gravity load generated by the stem’s mass above it. The imaginary line’s x-point origin is the stem’s tip point following Greenhill’s [7] graphs; thus, the x value at the tip is 0 (zero), and at the bottom is H_t. The imaginary line is arbitrary and must slide from the stem’s tip to the bottom (0 ≤ x ≤ H_t) to analyze every possible compressive loading configuration. The stem’s volume above the imaginary line is modeled considering a self-weight loading. The diameter along the x line (D_x) is determined based on the tree tip diameter (D_h), which assumes the tree stem geometry model. D_h and D_x are calculated based on Equations (2) and (3). Equation (4) calculated the tree stem volume above the x-point imaginary line (V_bx).

$$D_h=\frac{\left(H-H_{dbh}\right)D_t-\left(H-H_t\right)D_{bh}}{H_t-H_{dbh}}$$

(2)

$$D_x=D_h+\frac{\left(D_{bh}-D_h\right)x}{(H-H_{dbh})}$$

(3)

$$V_{bx}=\frac{\pi }{12}\left(D_x{}^2+D_h{}^2+D_x{D}_h\right)x$$

(4)

2.4.2. Determination of the Crown Volume

The crown’s height (H−H_c) and diameter (D_c) are critical to determining the tree crown volume. The crown height is the total tree height (H) minus the tree crown or branches‘ lowest height (H_c). The lowest height (H_c) is the lowest value between the crown height (H_ck) and the branch-free height (H_tbc). The determination of the tree crown geometry model (Figure 4) followed the growth habit of the decurrent or excurrent trees. The paraboloid-duo (H_tbc ≠ H_ck) and paraboloid (H_tbc = H_ck) geometry models (Figure 4a) approached the decurrent and excurrent trees, respectively. Two paraboloid duo types could fit the decurrent model: type I (H_tbc ≤ H_ck) (Figure 4b) and type II (H_tbc > H_ck) (Figure 4c).

Similar to the stem’s self-weight loading, the compressive load generated by the crown is limited to the crown’s weight above the imaginary line at the x-point. There are two equations for determining the crown volume for the excurrent tree growth model. The chosen equation depended on the imaginary line location. Equation (5a) calculated the crown’s volume if the imaginary line was above the crown height (H−H_c), while Equation (5b) was employed if the imaginary line was below (H−H_c).

$$V_{cx}=\left\{\begin{array}{c}\frac{\pi }{8}{D}_c^2\left(H-H_c\right) \mathrm{for} x\ge H–H_c \left(a\right)\hfill \\ \frac{\pi }{8}\frac{D_c^2{x}^2}{H-H_c} \mathrm{for} 0\le x<H–H_c \left(b\right)\hfill \end{array}\right.$$

(5)

In the decurrent growth habit model, the crown volumes were calculated using the geometrical crown model. The paraboloid duo type I has three equations for determining the crown volume; the equation used depends on the location of the imaginary line. If the imaginary line was below the crown height with the lowest height, that is, the lowest crown height (H−H_ck), Equation (6a) was used. However, if the imaginary line was located between the crown height with the lowest height, that is, the lowest crown height (H−H_ck) and the crown height with the lowest height, that is, branch-free height (H−H_tbc), Equation (6b) was used. Meanwhile, Equation (6c) was used if the imaginary line was above the crown height with the lowest height, that is, branch-free height (H−H_tbc).

$$V_{cxA}=\{\begin{array}{c}\frac{\pi }{8}\frac{D_c^2{x}^2}{\left(H-H_{ck}\right)} \mathrm{for} 0\le x\le H–H_{ck} \left(a\right)\\ \frac{\pi D_c^2\left(-H+H_{ck}+x\right)\left(8H_{tbc}\sqrt{\frac{-H+H_{ck}+x}{H_{ck}-H_{tbc}}}-8H_{ck}\sqrt{\frac{-H+H_{ck}+x}{H_{ck}-H_{tbc}}}-6H_{tbc}-3H+9H_{ck}+3x\right)}{24 \left(H_{ck}-H_{tbc}\right)}+\frac{\pi }{8}{D}_c^2\left(H-H_{ck}\right) \mathrm{for} H–H_{ck}\le x\le H–H_{tbc}\left(b\right)\\ \frac{\pi }{24}{D}_c^2\left(3H-2H_{ck}-H_{tbc}\right) \mathrm{for} H–H_{tbc}\le x \left(c\right)\end{array}$$

(6)

The determination of the crown volume for paraboloid duo type II in the decurrent model also has three equations referring to the imaginary line. Equation (7a) was used if the imaginary line was below the crown height with the lowest height, that is, branch-free height (H−H_tbc). If the imaginary line was located between the crown height with the lowest height, that is, branch-free height (H−H_tbc), and the crown height with the lowest height, that is, the lowest crown height (H−H_ck), Equation (7b) was used. However, if the imaginary line was above the crown height with the lowest height, that is, the lowest crown height (H−H_ck), Equation (7c) was used. If the imaginary line was located between the crown height with the lowest height, that is, branch-free height (H−H_tbc), and the crown height with the lowest height, that is, the lowest crown height (H−H_ck), Equation (7b) was used. However, if the imaginary line was above the crown height with the lowest height, that is, the lowest crown height (H−H_ck), Equation (7c) was used.

$$V_{cxB}=\{\begin{array}{c}\frac{\pi }{8}\frac{D_c^2{x}^2}{\left(H-H_{ck}\right)} \mathrm{for} 0\le x\le H–H_{tbc} \left(a\right)\\ \frac{\pi D_c^2}{24}\left(\frac{3x^2}{H-H_{tbc}}+\frac{3{(-H+H_{ck}+x)}^2}{\left(H_{tbc}-H_{ck}\right)}-8\left(\frac{{(H-H_{ck}-x)}^{\frac{3}{2}}}{H_{tbc}-H_{ck}{)}^{\frac{1}{2}} }\right)+6H-H_{tbc}-5H_{ck}-6x\right)\mathrm{for} H–H_{tbc}\le x\le H–H_{ck} \left(b\right)\\ \frac{\pi }{24}{D}_c^2\left(3H-2H_{ck}-H_{tbc}\right) \mathrm{for} x>H–H_{ck} \left(c\right)\end{array}$$

(7)

2.5. Determination of the Stem Weight and the Crown Weight

The stem and crown weights calculation can determine the overall self-weight a tree’s stem must support. In calculating stem volume and crown volume, the stem weight and the crown weight measured were above an imaginary line, representing the self-weight loading. Equation (8) calculated the stem weight, in which the wood density ($\rho$) was obtained from the small core sample’s mass-volume ratio previously described in Section 2.3. The g value was gravitational constant (9.806 m/s²). Equation (9) determined the crown weight.

$$P_{bx}=\rho g V_{bx}$$

(8)

$$P_{cx}={\rho }_c g V_{cx}$$

(9)

Since the assumption of the tree crown geometry model used in this study is a paraboloid shape, the crown density used was 1.9 kg/m³, following the previous reports [6,53].

2.6. Stress Analysis of Round Columns due to Self-Weight Loading

Tree stems are usually slender structures; beam-column theory is an appropriate framework for studying their mechanical behavior. This general model is valid for any cross-sectional shape and stem taper [3]. Buckling stress analysis is necessary to determine the critical buckling height of the tree stem due to self-weight loading. This study assumed that the standing trees are round columns to simplify the buckling stress analysis. Two stress analysis methods can approach the round column buckling analysis: the Euler and the Ylinen formula as directed by Indonesian Wooden Building Code SNI 7973:2013 [35], which has adopted the National Design Specification (NDS) [36] since 2013 [28,29].

2.6.1. Euler Buckling Analysis

When a compressive force is applied to a slender column, such as a tree stem, the loads generated by the self-weight may trigger the buckling phenomena. The buckling causes an initially straight stem to bend. Stress due to buckling needs to be calculated to determine the risk of tree stem failure, which its safety factor could indicate. The determination of critical buckling stress (σ_cr) is based on a general formula for Euler buckling, as shown in Equation (10).

$${\sigma }_{cr}=\frac{{\pi }^{2}EI}{\ell A}$$

(10)

where I is a moment of inertia, $\ell$ is the effective length, and A is the cross-sectional area.

The best estimation for critical buckling stress (σ_cr) is determined when the measured actual stem’s modulus of elasticity (E) is inputted into Equation (10). The unbiased estimation shall be the average E. If the average E is inputted into Equation (10), the probability of buckling is 0.5, and the buckling failure may occur in fifty-fifty possibility. This 50% probability of failure is not conventional enough for construction. Building engineers commonly choose 95% confidence in safety. Since urban trees grow in the built environment, a minimum of 95% confidence in safety is necessary to avoid undesirable failure. SNI 7973:2013 [35] and NDS:2018 [54] state that the E reference value shall be the 5% lower exclusion limit adjusted by the safety factor following Equation (11), where static E (E_s) represents the modulus of elasticity (E).

$$E_{min}=\frac{1.03}{1.66}\left(1-1.645C_{ovE}\right)E_s$$

(11)

The coefficient of variation for the modulus of elasticity (C_ovE) is 0.22, referring to Senalik and Farber [55], smaller than the NDS:2018 [54] designated value for visually graded sawn lumber (C_ovE = 0.25). This study prefers to choose C_ovE is equal to 0.22. Meanwhile, the other values: 1.03 is a correction factor to convert E values to a pure bending basis, 1.66 is a safety factor in beam and column stability calculation, and 1.645 represents the normal distribution z-value to approximate 5% lower exclusion limit.

Several adjustment factors shall adjust the critical buckling stress (σ_cr) to consider the environmental service condition according to the building code [35,54]. The adjustment factors include the wet service factor (C_M), temperature factor (C_t), incising factor (C_i), and buckling stiffness factor (C_T). C_M for compression member is 0.8 because the tree moisture content is more than 19%. C_t and C_i values are 1 (one) because the tree grows in a typical environment temperature, and no incising was applied. Meanwhile, Equation (12) calculates the C_T values.

$$C_T=\left\{\begin{array}{l}1+\frac{K_M\left(\frac{{\ell }_{ef}}{0.0254}\right)}{K_T\left(E_s\times 145.038\right)} \mathrm{for} 0<{\ell }_{ef}<96”\times 0.0254\frac{\mathrm{m}}{”} \left(\mathrm{a}\right)\hfill \\ 1+\frac{K_M\left(96\right)}{K_T\left(E_s\times 145.038\right)} \mathrm{for} {\ell }_{ef}\ge 96”\times 0.0254\frac{\mathrm{m}}{”} \left(\mathrm{b}\right)\hfill \end{array}\right.$$

(12)

where the 96” is the ${\ell }_{ef}$, K_M is 1200 for unseasoned wood, K_T is calculated using Equation (13), 0.0254 is the unit conversion of inches to meters, and 145.038 is the conversion of psi to MPa units. Notation of ${\ell }_{ef}$ is the effective length of compression member, K_M is moisture content coefficient, and K_T is truss compression coefficient. The determination of adjusted critical buckling stress (σ_cr’) was then calculated based on Equation (14).

$$K_T=\left(1-1.645C_{ovE}\right)$$

(13)

$${\sigma }_{cr}{}^{’}=\frac{{\pi }^2{I}_{ef}}{{\ell }_{ef}^2{A}_{ef}}{C}_M{C}_t{C}_i{C}_T{E}_{min}{10}^6$$

(14)

In determining the value of the effective moment of inertia (I_ef), effective length (${\ell }_{ef}$), and effective cross-section area (A_ef), it was necessary to determine in advance the diameter of the stem at ground level (D_b) (Equation (15)) and the effective diameter of the stem (D_ef) to resist the stress (Equation (16)). Furthermore, the values of the effective inertial moment (I_ef), effective length (${\ell }_{ef}$), and effective cross-section area (A_ef) were determined using Equations (17)–(19), respectively. In Equation (18), the value of ${\ell }_{ef}$ was adjusted by the coefficient of buckling length (K_e). The correcting coefficient of the actual length with an effective length (K_e) was 2.1, which was used with the consideration of their support as a standing tree column referring to SNI 7973:2013 [35] and NDS:2018 [54].

$$D_b=D_h+\frac{\left(D_{bh}-D_h\right) x}{\left(H-H_{dbh}\right)}$$

(15)

$$D_{ef}=D_x+\frac{\left(D_b-D_x\right)}{3}$$

(16)

$$I_{ef}=\frac{\pi }{64}{D}_{ef}^4$$

(17)

$${\ell }_{ef}=K_e\left(H-x\right)$$

(18)

$$A_{ef}=\frac{\pi }{4}{D}_{ef}^2$$

(19)

The actual compressive stress (σ_a) should be determined by calculating the load the tree may receive. The actual compressive stress was determined using Equation (20), where P is an external load, such as the wind or the weight of a worker who is climbing the tree. Since this study focused on self-weight loading, only the stem weight (P_bx) and the crown weight (P_cx) were calculated as the self-weight loading. For that reason, this study assumed the p-value was 0 (zero), or no external load received by trees

$${\sigma }_a=\frac{P+P_{bx}+P_{cx}}{A_{ef}}$$

(20)

2.6.2. Compression Analysis with Ylinen Formula

Equation (21) (NDS 2018 [54]) calculated the compressive design value parallel to grain (F_c) to consider the 5% exclusion limit and factor of safety. The coefficient of variation for compressive strength parallel to grain (C_oVFc) was obtained from the Wood Handbook [55], which was 0.18. The compressive strengths parallel to the grain, synonym with maximum crushing strength (M_cs), were 22.97 MPa for the rain tree [56] and 28.1 MPa for the agathis tree [57].

$$F_c=\frac{\left(1-1.645C_{ovFc}\right)}{1.9} M_{cs}$$

(21)

The ultimate compressive stress was adjusted by size factor (C_F) (Equation (22)) and a column stability factor (C_p) (Equation (23)). The values of 0.0254 and 100 were the dimension unit conversion from inches to meters and from centimeters to meters, respectively. P_ck was the reference compression design value parallel-to-grain multiplied by all applicable adjustment factors (Equation (24)). P_cE was a critical buckling design value for compressive structure components (Equation (25)), and c for the round column was the constant of 0.85.

$$C_F={(\frac{12\times 0.0254}{D_{ef}\times 100})}^{\frac{1}{9}}$$

(22)

$$C_P=\frac{1+\left(\frac{P_{cE}}{P_{ck}}\right)}{2c}-\sqrt{{\left(\frac{1+\left(\frac{P_{cE}}{P_{ck}}\right)}{2c}\right)}^2-\frac{\left(\frac{P_{cE}}{P_{ck}}\right)}{c}}$$

(23)

$$P_{ck}=C_D{C}_M{C}_t{C}_i{C}_F{F}_c{10}^6{A}_{ef}$$

(24)

$$P_{cE}=\frac{{\pi }^2\left(C_M{C}_t{C}_i{C}_T{E}_{min}{10}^6\right)I_{ef}}{l_{ef}^2}$$

(25)

Except for load duration factor (C_D) of permanent dead load value of 0.9, the other values (C_M, C_t, and C_i) were mentioned in Equation (14), while C_F was determined in Equation (22). Therefore, the ultimate compressive stress (σ_u) based on the Ylinen formula was determined as in Equation (26).

$${\sigma }_u=C_D{C}_M{C}_t{C}_i{C}_F{C}_P{F}_c{10}^6$$

(26)

2.7. Critical Buckling Height (H_cr) Determination

2.7.1. Euler and Ylinen Buckling Stress Methods (Method 1)

The critical buckling height (H_cr) is developed from the safety factor (S_f), which is the ratio of the critical buckling height (H_cr) and the actual height (H) (Equation (27)). This study introduced a simulation using the Euler and Ylinen Buckling Stress Method (Method 1). The Euler and Ylinen Buckling Stress Method used two curves—the curve of the ratio of Euler’s buckling stress to the actual compressive stress ($\frac{{\sigma }_{cr}{}^{’}}{{\sigma }_a}$) and the curve of the ratio of ultimate compressive stress to actual compressive stress ($\frac{{\sigma }_u}{{\sigma }_a}$)—as the Euler Buckling Formula or (K(x)) and Ylinen Buckling Formula or (M(x)), respectively. The analysis used the Desmos graphical calculator and was carried out to simulate the safety condition through those two curves (K(x) and M(x)), which almost overlap (Figure 5).

$$S_f=\frac{H_{cr}}{H}$$

(27)

The value of S_f = 1 is a condition where H_cr and H have the same value, and two curves (K(x) and (M(x)) lie on the dotted line in Figure 5a,d. If the value of S_f is not equal to 1, the critical buckling height of the tree was obtained by sliding the actual height of the tree (H, red bold vertical line in Figure 5) until the curves (K(x) and (M(x)) were on the limit of the safety line. S_f > 1 indicated that the actual tree height (H) was lower than the critical buckling height (H_cr), which meant the tree was in a safe condition (Figure 5b,e). Meanwhile, S_f < 1 indicated that the H was higher than the critical buckling height (H_cr), which meant it was in an unsafe condition (Figure 5c,f).

2.7.2. Greenhill Buckling Method (Method 2)

The previous study by Greenhill [7], derived from Euler’s buckling column formula, was used to determine the critical buckling height of a cylindrical column based on the tree stem characteristics (Method 2). Equation (28) calculated the critical buckling height.

$$H_{cr}={(\frac{9E{k}^2{c}^2}{4\rho g})}^{\frac{1}{3}}$$

(28)

where E = E_min was the modulus of elasticity for column stability calculation, k was the minimum radius gyration ($\frac{D_b}{4}$), c was the Bessel number $J(-\frac{1}{3},x$) of 1.866351, $\rho$ was wood density, and g was the gravitational constant (9.806 m/s²). Greenhill functions dealt with the buckling of columns with the linearly varying inverse of the bending stiffness [15,58]. The critical buckling height (H_cr) was then determined by Equation (29).

$$H_{cr}={(\frac{7.8373E_{min}{10}^6}{16\rho g})}^{\frac{1}{3}}{D}_b^{\frac{2}{3}}$$

(29)

2.7.3. Modification of the Greenhill Buckling Method (Method 3)

This study modified the Greenhill method by calculating the crown weight in addition to the stem weight. Equation (30) determined the modified H_cr.

$$H_{cr}={(\frac{7.8373E_{min}{10}^6{V}_{bx}}{16\left(P_{bx}+P_{cx}\right)})}^{\frac{1}{3}}{D}_b^{\frac{2}{3}}$$

(30)

3. Results and Discussion

3.1. Tree Growth Morphometric and Stem-Crown Characteristics

The growth habit of excurrent and decurrent trees refers to the apical dominance of the trees. The excurrent growth habit has a central stem with lateral branches with a columnar canopy. In contrast, the decurrent growth habit is characterized by a shorter main stem and crown spreading supported by radial branches (Figure 2) [59].

Table 1. Growth morphometric and stem-crown characteristics.

Parameter	Unit	Agathis (n = 23)			Rain Tree (n = 50)
		Average	SD	CV	Average	SD	CV
Total tree height (H)	m	23.89	3.55	0.15	18.84	4.09	0.22
Lowest Crown Height (Hck)	m	2.80	0.60	0.21	6.28	1.92	0.31
Branch-free Height (Htbc)	m	2.80	0.60	0.21	2.50	1.82	0.73
Height when measuring Dtr (Ht)	m	23.89	3.55	0.15	2.50	1.82	0.73
Diameter at breast height (Dbh)	cm	49.96	9.96	0.20	61.48	18.54	0.30
Diameter at the tip of the tree (Dtr)	cm	14.02	2.58	0.18	56.85	18.93	0.33
Corrected diameter at the tip of the tree (Dt)	cm	14.02	2.58	0.18	55.66	18.79	0.34
Calculation Diameter at the tip of the tree (Dh)	cm	14.02	2.58	0.18	22.58	29.32	1.30
Mean crown diameter (Dc)	m	6.93	0.97	0.14	19.86	4.42	0.22
Slenderness (S)	-	48.94	8.67	0.18	32.07	7.74	0.24
Wood Density (ρ)	kg/m3	722.93	73.63	0.10	778.20	64.13	0.08
Dynamic Modulus of Elasticity (Ed)	GPa	8.19	3.99	0.49	4.98	1.52	0.31
Static Modulus of Elasticity (Es)	GPa	6.58	1.40	0.21	3.89	1.51	0.39

lists the growth and stem-crown characteristics of these two tree models. The tapered shape and slenderness of the tree can be calculated based on the diameter at breast height (D_bh), total tree height (H), and the main stem tip’s diameter (D_tr).

Stem taper decreases from D_bh to the tree tip per unit stem length (D_tr). In agathis, the excurrent tree type, the decrease in the shape of the trunk to the tip of the main stem was significantly larger, reaching 3.5 times. Meanwhile, the slenderness value (total tree height - to -D_bh) for the excurrent type is higher than for the decurrent type. In addition to the natural growth characteristics of trees, environmental conditions such as spacing also affect the tree stem shape and slenderness [6]. The differences in the diameter of the tip of the tree among the measured, corrected, and calculated diameters are possible because the adjusted diameter refers to the position of the tree tip diameter and D_bh for the shape of the conical trunk. In the excurrent model tree, with a long central stem as a column system, the measured tip diameter is the same as the corrected and calculated diameter. Meanwhile, in the decurrent model, which has a shorter central stem and radial branches, the diameter of the tree trunk tip measurement is almost the same as the corrected diameter. However, the calculated diameter appears to have a much lower value, indicating the tree stem’s taper condition is more of a conical shape.

Mean crown diameter (D_c, or average diameter of the crown) is essential for assessing related ecosystem services, such as physiological tree functions, carbon sequestration, elimination of air pollution, and rainfall [39,60]. Rain trees in this study had higher mean crown diameter values (19.86 m) than agathis (6.93 m). The rain tree has a decurrent growth habit in which the lateral branches grow faster than or sometimes as fast as the terminal shoot, which gives rise to the tree’s growth habit, whereby the main stem eventually disappears and forms a large crown [32,61].

According to Mattheck et al. [62], a low slenderness coefficient for urban trees typically indicates a larger crown, a lower center of gravity, and a better-developed root system. The higher the S, the more susceptible the tree stability. In our study, rain tree and agathis have slenderness values of 32.07 and 48.94, respectively. For trees growing in urban landscapes, trees with a slenderness value of less than 50 have good resistance to wind and rainstorms [62].

Regarding the green wood density, both trees had almost the same green wood density (about 0.7). Meanwhile, the wood stiffness (E) value of the agathis tree was higher than the rain tree. There was a strong correlation between the stiffness and strength of wood [27], as well as wood products [63] and other biomaterials [64,65,66]. The wood density is also moderately correlated with its strengths [55]. However, wood stiffness depends on the cell wall and the other characteristics of wood anatomy, which were reflected by sonic wave velocity [67,68]. In addition, the excurrent trees, commonly coniferous nonporous wood with homogeneous anatomical characteristics, have a faster acoustic velocity than the heterogeneous ones. The agathis standing trees’ stress wave velocity was 3304 m/s, and that of rain trees was 2503 m/s. Variables of tree stability can be evaluated by predicting E_d based on acoustic wave velocity since this variable had high multi-collinearity in predicting morphometric characteristics [68].

The tree stem’s volume is necessary to determine self-weight loading. Based on the stem’s geometric model, a hooked cone model was found for both excurrent and decurrent tree growth habits, while a cylindrical model was only found in decurrent trees. The crown’s geometry model is paraboloid geometry. Paraboloid was found in all excurrent trees, and Paraboloid Duo type I was dominant in the decurrent growth habit model. This study found that in the excurrent tree growth habit, the tree crown’s volume and weight were a bit higher than the tree stem (

Table 2. Calculation of stem-crown volume and weight.

Tree Growth Habit	Stem					Crown
	Geometry Model	Volume (m3) (Starting at 10 cm above Ground and Upward)		Weight (N)		Geometry Model	Volume (m3) (Starting at Lowest Height Crown and Upward)		Weight (N)
Excurrent	Hooked cone (n = 23)	Av.	2.38	Av.	16,832.58	Paraboloid (n = 23)	Av.	2.58	Av.	18,280.19
		SD	1.07	SD	8021.02		SD	0.90	SD	6775.03
		CV	0.45	CV	0.48		CV	0.35	CV	0.37
Decurrent	Hooked cone (n = 35)	Av.	0.06	Av.	455.01	Paraboloid Duo Type I (n = 34)	Av.	24.96	Av.	187,581.82
		SD	0.13	SD	1010.39		SD	15.60	SD	119,870.71
		CV	2.20	CV	2.22		CV	0.62	CV	0.64
						Paraboloid Duo Type II (n = 1)	Av.	58.18	Av.	467,009.88
							SD	0	SD	0
							CV	0	CV	0
	Cylindrical (n = 15)	Av.	0.57	Av.	4490.90	Paraboloid Duo Type I (n = 15)	Av.	20.41	Av.	158,753.47
		SD	0.42	SD	3404.90		SD	13.46	SD	104,419.83
		CV	0.74	CV	0.76		CV	0.66	CV	0.66

). Meanwhile, the tree crown had significantly higher volume and weight than the tree stem in decurrent trees. In general, for the tree crown, it was in conjunction with the crown’s coverage on the tree height total in which the mean crown diameter of the decurrent tree possessed the wide diameter. In terms of a tree stem, the high value of the excurrent tree relates to higher stiffness, which directly correlates with wood density and stress wave velocity, as well as density-specific stiffness (E/ρ) [34].

3.2. Critical Buckling Height

The critical buckling height indicates the maximum height a vertical stem can attain before it buckles under its self-weight [69]. It is determined by the wood density, modulus of elasticity, and the tree’s height and diameter [70,71]. This study obtained the critical buckling height by using three methods: Euler and Ylinen buckling stresses following SNI 7973:2013 [35] (Method 1), the Greenhill Buckling method [7] (Method 2), and the modified Greenhill Buckling method (Method 3) (Figure 6). The critical buckling values of the excurrent agathis tree were 40.83 m, 36.40 m, and 33.95 m for Methods 1, 2, and 3, respectively. Meanwhile, the critical buckling values for the decurrent rain tree were 27.41 m for Method 1, 33.35 m for Method 2, and 27.44 m for Method 3. The tree with a lower height than these values of critical buckling height (H_cr) will not buckle with a 95% confidence level. The 95% confidence level appeared from the allowable stresses instead of the average strengths, which were inputted into the structural analysis. The adjustment factors corrected the allowable stress to consider the environmental service condition effects on the standardized laboratory mechanical properties test results.

Figure 6 shows that the tree’s actual heights are generally shorter than its critical height, which indicates the trees are reliably receiving their self-weight. All agathis trees’ critical buckling heights are higher than their actual height, exhibiting safety. All rain trees are also safe when ignoring the canopy weight (Method 2). On the contrary, if the canopy weight is also considered the self-weight load (Methods 1 and 3), the error bar of the rain tree’s actual height has a small intersection range with its critical height, indicating some trees may be unsafe, although most of them are safe.

In Methods 1 and 3, the calculation included the tree crown factor, while Method 2 (Greenhill Buckling method) only considered the tree stem characteristics. In the excurrent tree, the critical height buckling (H_cr) value with Method 1 was the largest, followed by Method 2, while H_cr from Method 3 was the smallest. However, the analysis of variance (ANOVA) of those three methods showed no significant difference. In the decurrent tree, the calculation including the tree crown characteristics led to the H_cr value being smaller than in Method 2, which only considered the tree stem’s characteristics. Statistical analysis found that Methods 1 and 3 were not significantly different, while both differed considerably from Method 2. The presence of a crown in plants can affect the critical buckling height. The lower tree’s actual height (H) compared with the critical buckling height (H_cr), the better the tree’s safety against buckling. The greater the crown mass that a tree has, the lower the resulting critical buckling height. In addition, the buckling height was sensitively responsive to decreasing diameter and increasing slenderness [34].

In determining the critical buckling height, we proposed using Euler and Ylinen buckling stresses (Method 1). This method is well-known for column buckling [37,38] and beam stability [29] analysis. It warrants reliability and safety by applying the adjustment factors stipulated by SNI 7973:2013 [35] and NDS:2018 [54] for a slender column subjected to compressive load. The adjustment factors are moisture content, temperature, buckling stiffness, size, and loading duration.

The determination of the limit of the safety factor (S_f = 1) is based on the standardized normal distribution z-value. The S_f values categorize tree conditions more precisely. S_f = 1 indicated that the tree stem is safe and will not buckle with a 95% confidence level. The confidence level will increase if S_f is more than 1 (one). The tree is considered very safe if the S_f is more than 1.645.

Table 3. The category of tree condition based on safety factor (S_f).

Tree Condition	Safety Factor (Sf)	Tree Species
		Rain Tree		Agathis
		Number of Trees	Percentage (%)	Number of Trees	Percentage (%)
Unsafe	Sf ≤ 1.00	5	10	0	0
Safe	1.00 < Sf ≤ 1.645	31	62	10	43
Very Safe	Sf > 1.645	14	28	13	57

shows the result of this categorization.

The safety factor (S_f) is defined as the ratio of critical buckling height (H_cr) and actual height (H) of the trees. The critical buckling height (H_cr) used in this study was based on Euler and Ylinen Buckling Stresses method (Method 1), which has considered the 95% confidence level. Our examples for the simulation in determining safety conditions through the Desmos graphical calculator using two curves (K(x) and M(x)) are shown in Figure 7. The ratios between the actual tree height (H) and the critical buckling height (H_cr) differ between unsafe, safe, and very safe conditions. In Figure 7a, the critical buckling height (H_cr), which is lower than the actual tree height (H > H_cr), will cause the tree to be in an unsafe condition because it has less than 95% confidence level reliability to resist its self-weight. A tree in an unsafe condition will have the probability tree’s weakest point falling within a range along the stem. The risk of falling or breaking the tree stem will occur in the area at the height of the weakest point range. Meanwhile, in safe conditions (Figure 7b for excurrent and Figure 7c for decurrent), the actual tree height is slightly lower than the critical buckling height (H < H_cr). However, in very safe conditions (Figure 7d for excurrent and Figure 7e for decurrent), the actual height (H) of the tree is very low compared with the critical buckling height (H < <H_cr) of the tree. The lower the actual height of the tree compared with its critical buckling height, the safer the tree’s condition.

The results from this study, as presented in Table 3, showed that 10 excurrent agathis trees were safe and 13 were very safe. Meanwhile, 5 unsafe trees were found among the decurrent rain trees, while 31 and 14 trees were safe and very safe trees, respectively. The unsafe trees showed deformation from the straight to the arch curvature form (Figure 1), similar to 15-year-old buckled shape Pinus radiata in New Zealand studied by Dargahi et al. [19]. The safety condition was related to the critical tree height, and this value was affected by the stem’s modulus of elasticity (E). Watt et al. [72] mentioned that an increase in E could increase the critical compressive stress the stem can withstand before buckling occurs. Despite the value of the slenderness excurrent tree being higher, which generally means the tree stem’s stability is low, this tree model is quite good at estimating critical height and safety conditions. Furthermore, Putz et al. [73] reported that trees with stem failure in windstorms usually have lower wood density, strength, and E than uprooted trees. In terms of its crown characteristic effect, the crown weight becomes the dominant influence on the buckling capacity of the column [19]. Further, Watari et al. [74] concluded that critical buckling height increases with crown/stem mass ratio reduction.

This study successfully promotes the safety factor of urban trees growing in a built environment following SNI 7973:2013 [35] by applying the paraboloid geometric model to approach the excurrent tree’s crown characteristics and the paraboloid duo geometric model to approach the decurrent tree’s crown characteristics. The stem geometric may follow a cone, hooked cone, or cylinder depending on the stem’s tip diameter. This study uploaded the tree structural stability analysis based on the paraboloid model at https://www.desmos.com/calculator/hatgnm6q27, (accessed on 9 January 2023) and the paraboloid duo model at https://www.desmos.com/calculator/othn9q0gke, (accessed on 9 January 2023). Engineers or arborists may freely and easily use those uploaded models by inputting the measured parameters during the tree safety assessment and citing this article to recognize it accordingly. This study’s findings were limited to the boundary condition of a tree receiving its self-weight only; thus, more comprehensive models considering the external load shall be further developed. The SNI 7973:2013 [35] also provides the structural analysis of a beam-column subjected to combined bending and axial compression loading.

4. Conclusions

In self-weight loading on the tree, considering the characteristics of tree stems plus the tree crown characteristics is an ideal approach to determining the critical buckling height. In this case, the parameters of height and diameter of the tree’s crown and stem were significantly different between excurrent and decurrent growth habit models. Our study developed cylinder and hooked cone stem geometry models for the stem of both decurrent and excurrent trees. The crown geometry of paraboloid and paraboloid duo types was proposed for excurrent and decurrent growth habit types, respectively. This study assumed a tapered column structure in the stem receiving compressive stress and a paraboloid model for the tree canopy, respectively. This study advocated the Euler and Ylinen buckling stresses method (Method 1) following SNI 7873:2013 Building Code for Wood Construction to determine the tree stem’s critical buckling height rather than the Greenhill method (Method 2) and the modified Greenhill method (Method 3). Method 1 included tree stems and crown characteristics and can be considered relatively simple. The critical buckling height value was inputted into the tree structure stability analysis to determine the tree safety factor (S_f). Every tree can be categorized based on three safety conditions: unsafe, safe, and very safe. The safety condition is affected by the stem’s structural (mechanical) properties (i.e., modulus of elasticity (E) and compressive strength parallel to the grain (F_c)), section properties (i.e., area (A), static moment (Z), and moment of inertia (I)), slenderness ratio (length to diameter ratio), and the self-weight (i.e., stem weight and canopy weight). Based on the determination of safety factors, this study has successfully determined tree safety conditions for both excurrent and decurrent trees.