Research on Home Health Care Scheduling Considering Synchronous Access of Caregivers and Vehicles

Abstract

With the arrival of an aging society, the high shortage of public medical resources leads to the increasingly serious pension problem, which has attracted extensive attention. This has led to a sharp increase in the demand for family doctors. In order to alleviate the shortage of caregivers, this paper considers the scheduling problem of home health care, which includes the synchronous access of caregivers and vehicles, and the flexible marchingmatching between caregivers and patients. First of all, we construct a Mixed Integer Linear Programming (MILP) to characterize the optimization problem. Secondly, an improved non-dominated sorting genetic algorithm with elite strategy (INSGA-II) is designed. The initial solution with high quality is obtained through the simultaneous evolution of two populations. The chromosomes are optimized by using improved crossover and mutation operators, and local search strategies are designed on this basis. Finally, several groups of test examples are used to verify the feasibility and effectiveness of the algorithm, and analyze the impact of different visit modes on objective function. The results show that the synchronous access can effectively reduce the costs, and can provide theoretical support for the medical center to make plans.

1. Introduction

The emergence and development of an aging population is an inevitable product of social progress. In China, the data of the sixth national population census in 2010 showed that the population aged 65 and above accounted for 8.87% of the total. It is predicted that China will enter a “deep aging” society around 2035, when the proportion of the elderly aged 65 and above will exceed 21%. The rapid growth of the elderly population has stimulated the development of the elderly care industry. Among them, home health care is the most popular.

Home health care (HHC) refers to the medical center assigning professional caregivers to the elderly’s homes to provide them with diversified services, such as day care, rehabilitation therapy, chronic disease treatment, and medication guidance. The service objects are the elderly who need long-term or regular medical testing, postoperative recovery, and basic life care. With the improvement of people’s living standards, the requirements for the elderly are also higher. Many developed countries have better pension systems; however, in China, the development of the home health care industry is relatively slow. Most of the institutions charge too much and the system is not perfect, and cannot completely cover all the elderly.

According to the National Health Commission, the pattern of elderly care in China is “9073”. About 90% of the elderly choose to live at home, about 7% choose to rely on communities for elderly care, and 3% choose institutions for elderly care. In order to solve the pension problem, the Chinese government has explored a new home health care model according to the national conditions.

The home health care services can meet the needs of most elderly people, who can receive services without leaving home. Compared with community care and institutional care, home health care can emotionally comfort the elderly, and cost less. In the process of health service, the elderly need to make an appointment for door-to-door service in the system in advance and inform them of their needs. At the same time, the medical center will arrange an appropriate caregiver to provide health services according to their needs. When patients have multiple needs, the medical center will meet the needs of patients by improving the skill level of the caregiver, or arranging multiple caregivers to serve them at the same time. However, there are some basic requirements, such as drug delivery and report delivery, which can be achieved without a senior caregiver. The synchronous access of the caregiver undoubtedly increases the total operating cost. The medical center only needs to arrange personnel without medical certificates to drive to complete the delivery, which also reduces the stay time. However, few studies have considered caregiver and vehicle services separately, but this is very common in actual service systems.

In addition, relevant research shows that the travel time of the caregiver accounts for 18–26% of the total working time; unreasonable route arrangement will lead to an increase in travel time and will increase costs. At the same time, the working time difference between the caregivers directly affects the overall work efficiency. The purpose is to integrate effective resources under the background of scarce medical resources, so as to meet the needs of the elderly home health care service as far as possible, and to improve the quality of life. Therefore, on the basis of considering the work balance of the caregiver, this paper studies the collaboration of vehicle and caregiver; reasonable arrangement of service path is a kind of scientific problem with a strong practical background and important theoretical research value. The new home health care routing and scheduling problem (HHCRSP) model is built to minimize the total operating cost and maximize the work balance of the caregiver, which increases the complexity of the problem. In order to improve the work balance of the caregiver—namely to reduce the working time difference—the dispatch of caregivers and vehicles may increase when the medical center formulates the scheduling plan, thus increasing the total cost and forming a certain degree of inconsistency. That is why we are dealing with a bi-objective model in this work.

Specifically, the contributions of our study are as follows.

First of all, we introduce and model a new home health care routing and scheduling problem with the consideration of synchronous services. To our knowledge, most of the research considers the synchronous access between caregivers; there is little between caregivers and vehicles. In the objective function, the impact of caregiver and vehicle on the total cost is considered, respectively. The arrival time constraint (14) and matching constraint (15–16) are introduced for the synchronous access of caregiver and vehicle.

Second, our mathematical model addresses the diverse needs of patients, and the care center provides multiple visits to patients. We believe that our model better reflects the real situation and solves the actual problem.

Third, to solve this complex problem, we propose an improved non-dominated sorting genetic algorithm with elite strategy (INSGA-II). We improve initialization to improve the quality of the initial solution. New local search operators are embedded to improve the probability of finding the optimal solution. We design new crossover and mutation operators to improve the search space and find a better solution.

Finally, we analyze the sensitivity of synchronous parameters, problem properties, and the performance of the algorithm. Through a large number of experiments, the rationality of the model and the effectiveness of the algorithm are verified.

The remainder of this paper is organized as follows. Section 2 reviews the relevant literature. Section 3 describes and formulates the proposed problem. Section 4 describes the proposed INSGA-II. Section 5 presents the problem properties and the results of the performance of the proposed solution methods. Finally, Section 6 concludes the paper.

2. Literature Review

In recent years, the pension problem has caused continuous hot debate; thus, the home health care routing and scheduling problem (HHCRSP) has attracted a large number of scholars. The HHCRSP is defined as an extension of the vehicle routing problem with time windows (VRPTW). In the home health care scheduling problem, travel time [1] and travel cost [2,3] are regarded as the most common objective functions. Relevant research shows that the travel time of the caregiver accounts for the total working time, and the service path is not properly arranged, which reveals that unreasonable arrangement will lead to an increase in travel time [4]. The classic HHCRSP problem involves patient needs, patient preferences, and the control of service time for special patients, which makes the problem more complicated. For example, medical centers need to consider patient preferences when formulating service plans, such as gender, age, and other factors of the caregiver [5]. Ahmet Kandakoglu et al. [6] studied the factors that affect the emotion of the caregiver, such as the advance or delay of the visit time. Gang Du et al. [7] considered that there are some uncertain special patients who temporarily cancel or increase the emergency service, which affects the service process of other patients on this route.

In home health care, the medical center will assign a matched skill level and experienced caregiver to provide door-to-door service according to the actual situation, such as the patient’s health status or pathological severity. Generally, medical centers will train caregivers according to different standards to save costs. The medical center will match patients with caregivers according to certain criteria, such as the difficulty coefficient of service demand, or the skill level of the caregiver. Caregivers with a high skill level can serve patients with any needs, while caregivers with a low skill level can only serve patients with corresponding needs, which belongs to flexible matching [8]. Some scholars studied the allocation of caregivers with multiple skills, and designed different algorithms to solve the problem [9,10,11,12]. In view of the complexity of nursing procedures during the actual visit, which require the synchronization of multiple caregivers, Patrick Eveborn et al. [13] first proposed the situation of synchronization visits by caregiver. Synchronization access mainly depends on time constraints, including simultaneous access, cross overlap, maximum interval, and minimum interval [14]. S. R. AitHaddadene et al. [15] studied the scheduling problem of home health care with time windows, synchronization constraints, and priority constraints. Wenheng Liu et al. [16] considered the factors that affect the formulation of the final service plan, such as synchronous access, skill demand, lunch break, etc. Most of the above scholars considered the impact of external factors on the final scheduling scheme, while ignoring the importance of caregiver satisfaction. At present, few scholars use the workload difference of caregivers to measure their work balance.

In daily life, in addition to the typical HHC service, the medical center also adds some basic services such as drug delivery and report delivery, which can reduce the unnecessary movement of patients. Because there is a certain service time difference between typical HHC services and new HHC services, it is easy to waste resources if not properly arranged. However, the current research mainly distinguishes different services based on the skill level of the caregiver, which has simplified the difficulty of the problem to a certain extent, but has not fundamentally solved the problem. Shi et al. [17] considered the uncertainty of patients’ demands in the service process of the caregiver, and believed that the amount of drug consumption could only be known after the end of diagnosis and treatment. Fathollahi Fard et al. [18] put forward the green HHC problem for the first time. They considered the carbon emissions generated by different vehicles in the delivery service process, and designed four heuristic algorithms to solve the transportation cost and carbon emissions problems. The above scholars considered that the caregiver would take a vehicle to the patient’s location to provide medical care and delivery services. However, they did not consider collaborative access, nor did they distinguish between HHC services and HDV services. Although this method simplifies the connection between different services, home health care (HHC) takes longer than delivery, which greatly increases the vehicle’s stay time, parking rate, and fixed cost of the caregiver.

So far, scholars have done a lot of research on HHCRSP. If all necessary participants and constraint information are taken into account in the current HHC scheduling decision, the decision will be the optimal one. In other words, this inevitably leads to the vacancy in algorithm solving. Exact methods and heuristic methods are the most commonly used methods for solving combinatorial optimization problems. For small-scale problems, the exact methods can obtain the optimal solutions, but with the gradual expansion of the scale, their computation time is heavily restricted [19]. Therefore, more and more scholars prefer to use heuristic methods to find the best scheme [20,21,22]. The problem of home health care scheduling needs to consider the strong timeliness of patient services and the rationality of the matching of skills; it belongs to the extension of the vehicle routing problem (VRP). Tang et al. [23] showed that the vehicle routing problem belongs to the NP-hard problem. Thus, the home health care scheduling problem also belongs to the NP-hard problem. Therefore, scholars tried to apply heuristic algorithms to the solution of the HHCRSP, and achieved a series of results [24,25]. Mahyar Mirabnejad et al. [26] considered that the time spent in the sample transfer process would have a certain impact on the results, so they built a model aimed at minimizing the sample transfer time, and designed two heuristic algorithms to solve the model. Fariba et al. [27] proposed a green home health care scheduling problem; a novel grey flexible linear programming model is developed to cope with the uncertain nature of costs and capacity parameters, and two heuristic algorithms are designed to solve the problem. However, with the complexity of the model, the difficulty coefficient of the solution gradually increases, and the existing algorithm has difficulty achieving further optimization. Therefore, scholars at home and abroad are trying to find a new, better algorithm to solve HHCRSP. The NSGA-II algorithm is an intelligent optimization algorithm proposed by Deb et al. [28] on the basis of the NSGA algorithm in 2002. It has the characteristics of fast running speed and good convergence. In recent years, the NSGA-II has been widely used to solve the VRP, and has made certain achievements [29,30]. Moreover, the NSGA-II algorithm has been proven to be a relatively mature algorithm for solving multi-objective models [24]. Therefore, according to the characteristics of the HHCRSP, this paper aims to improve the NSGA-II algorithm to achieve an efficient solution for the HHCRSP.

To sum up, most HHCRSP studies usually consider the goal of minimizing cost or distance, ignoring the workload balance and skill matching problems in the actual service process, which results in a large deviation from the actual situation. The existing research distinguishes the home health care service and home delivery service by using the skill level of the caregiver, which simplifies the combination of problems to a certain extent. However, in the actual situation, the home health care service time far exceeds the delivery time, and the delivery vehicles have a large idle time. Therefore, this paper introduces the home delivery route separately, and considers the skills matching problem and the home delivery problem on the basis of the traditional home health care scheduling problem. The HHCRSP model is built to minimize the total operating cost and maximize the work balance of the caregiver, which increases the complexity of the problem. An improved NSGA-II algorithm is designed according to the characteristics of the HHCRSP.

3. Problem Description and Mathematical Model

3.1. Problem Description and Hypothesis

The HHCRSP that considers a synchronous service can be described as follows.

A medical center includes k caregivers, n patients and v vehicles. Each patient has his or her own expected visit time and service needs, and each patient can be visited multiple times by caregivers and delivery vehicles during the specified working hours. Each caregiver or delivery vehicle in the HHCRSP problem has its own access path, and the length of the path depends on the working hours. The optimization goal of the HHCRSP is to minimize the total operating cost and the difference between the working hours of caregivers by assigning caregivers and delivery vehicles, and determining the order of patient visits.

Assumptions are as follows.

• All vehicles in the medical center are homogeneous vehicles, and the speed of the vehicle is constant during driving;
• All drugs come from the medical center;
• Vehicles and caregivers are allowed to be dispatched incompletely;
• The volume of goods transported is small and negligible;
• The patients who need collaborative services are regarded as adding one or more corresponding virtual patients [31];
• The flexible matching method is adopted for the matching between caregivers and patients, but the delivery product must be fully consistent with patients;
• The delivery staff can be ordinary people without medical care certificates.

An example scenario is shown in Figure 1. Patients 8, 9, 10, and 11 are virtual patients corresponding to patients 4, 5, 6, and 7, respectively. The access path of caregiver 14 is 0-6-5-0, and the access path of vehicle 15 is 0-10-9-0.

3.2. Symbol Description

Notations used for the mathematical formulation are shown in

Table 1. Summarizes the notations of the model.

Sets	Definition
$K$	Set of caregivers, $\{\mathrm{1,2},\dots ,k\}$.
$V$	Set of delivery vehicles, $\left\{1,2,\dots ,v\right\}$.
$N$	Set of parents, $\left\{\mathrm{0,1},2,\dots ,n\right\}$, where $h,i,j\in N$.
$S$	The skill set of caregivers, $\left\{\mathrm{1,2},\dots ,s\right\}$.
$Q$	Set of delivery product types, $\left\{\mathrm{1,2},\dots ,q\right\}$.
Parameters
$P$	The unit overtime cost of caregivers.
$L$	The maximum working hours of caregivers.
$D$	The basic working hours of caregivers.
$Length$	Vehicle distance limits.
$C_k^s$	The fixed cost of caregiver $k$ with skill $s$.
$C_v$	The fixed costs of vehicle $v$.
$t_{ik}$	Service duration of caregiver $k$ at patient $i$.
$t_{ij}$	Travel time from patient $i$ to $j$.
($e_i$, $l_i$)	The hard time window at patient $i$ for starting a service.
${wait}_{iv}$	The waiting time of vehicle $v$.
$M$	Big number.
$b$	The unit penalty cost.
$\delta$	The transportation cost per unit distance.
$\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}$	The speed of vehicle.
Δ	A period of time.
$h_k^s$	The skill supply of caregiver $k$ is $s$.
$l_i^s$	The skill requirement of patient $i$ is $s$.
$h_v^q$	The delivered goods type of the vehicle $v$ is $q$.
$l_i^q$	The type of goods required by the patient $i$ is $q$.
Variables
${\lambda }_i$	The patient $i$ satisfaction.
$T_{ik}$	The start time of caregiver $k$ service to patient $i$.
${arrive}_{iv}$	The time when vehicle $v$ arrives at patient $i$.
$X_{ijk}$	1 if caregiver $k$ travels from patient $i$ to $j$, 0 otherwise.
$X_{ijv}$	1 if vehicle $v$ travels from patient $i$ to $j$, 0 otherwise.
$X_{ik}^s$	1 if caregiver $k$ with skill s is assigned to patient $i$, 0 otherwise.
$X_{iv}^q$	1 if vehicle $v$ supplies goods $q$ to patient $i$, 0 otherwise.
$Y_k$	1 if caregiver $k$ is assigned, 0 otherwise.
$Y_v$	1 if vehicle $v$ is assigned, 0 otherwise.

as follows.

3.3. Work Balance Model

The uneven workload distribution of a caregiver is likely to cause a decline in satisfaction of the caregiver, and even directly affect the quality of service. Therefore, in the actual home health service system, the balanced workload distribution of caregivers should be considered. Set the maximum working time difference between different caregivers as $N$; $W_k$ represents the actual working time of the caregiver $k$; $a_k$ represents the time when the caregiver returned to the medical center; and $l_k$ represents the time when the caregiver left the medical center. $N$ is expressed as follows:

$$N=Max\left|W_k-W_r\right|,\forall k,r\in K$$

(1)

where,

$$W_k=a_k-l_k$$

(2)

$$l_k=Min{T}_{ik}-t_{0i}-M\left(X_{0ik}-1\right),\forall i\in N,\forall k\in K$$

(3)

$$a_k=Max{T}_{jk}+t_{jk}+t_{j0}+M\left(X_{j0k}-1\right),\forall j\in N,\forall k\in K$$

(4)

3.4. Satisfaction Model

During the service process, the patient’s satisfaction ${\lambda }_i$ will change with the actual service start time of the caregiver. ${\lambda }_i$ is expressed as follows:

$${\lambda }_i=\{\begin{array}{ll}1-\frac{e_i-T_{ik}}{l_i-e_i},& T_{ik}<e_i\\ 1,& e_i\le T_{ik}\le l_i\\ 1-\frac{T_{ik}-l_i}{l_i-e_i},& T_{ik}>l_i\end{array}$$

(5)

3.5. Mathematical Model

The objective (6) is to minimize the total cost, including five parts: fixed cost of caregiver, overtime cost, maintenance cost, vehicle routing cost, and fixed cost of vehicle dispatching. Objective (7) is to minimize the workload difference of caregivers. Constraint (8) is to ensure that each patient can only be visited once. Constraints (9) and (10) ensure the continuity of caregivers and delivery vehicle services. Constraint (11) means that the caregivers and delivery vehicles depart from the medical center and finally return to it. Constraints (12) and (13) ensure that the service time of caregivers and delivery vehicles meet the constraints. Constraint (14) ensures that the delivery vehicle arrives within the specified time. Constraint (15) ensures that patients can only be served by caregivers with equal or higher skills. Constraint (16) ensures that the delivery vehicle must deliver items consistent with the patient’s needs. Constraints (17) and (18) ensure that working hours of caregivers and the route length of delivery vehicles are within the limits. Constraint (19) represents the decision variable.

$$\begin{array}{c}\mathrm{M}\mathrm{i}\mathrm{n}{Z}_1={\sum }_{i=1}^n{\sum }_{k=1}^k{\sum }_{s=1}^s{C}_k^s\times X_{ik}^s+PC{\sum }_{i,j=1}^n{\sum }_{k=1}^k(t_{ik}+t_{ij}-D)\times X_{ijk}+b\times {\sum }_{i=1}^n(1-\\ {\lambda }_i)+\delta {\sum }_{i,j=1}^n{\sum }_{v=1}^{v}rate\times t_{ij}\times X_{ijv}+{\sum }_{i=1}^n{\sum }_{v=1}^v{C}_v\times \left(1-Y_{iv}\right)\end{array}$$

(6)

$$\mathrm{M}\mathrm{i}\mathrm{n}{Z}_2={\sum }_{k=1}^{k}N$$

(7)

$$\mathrm{S}.\mathrm{T}.{\sum }_{(i,j)\in A}{\sum }_{k\in K}{X}_{ijk}+{\sum }_{(i,j)\in A}{\sum }_{v\in V}{X}_{ijv}=1,\forall i,j\in N$$

(8)

$${\sum }_{(i,h)\in A}{X}_{ihk}-{\sum }_{(h,j)\in A}{X}_{hjk}=0,\forall k\in K,\forall h\in N$$

(9)

$${\sum }_{(i,h)\in A}{X}_{ihv}-{\sum }_{(h,j)\in A}{X}_{hjv}=0,\forall v\in V,\forall h\in N$$

(10)

$${\sum }_{(0,i)\in A}{X}_{0ik}+{\sum }_{(0,j)\in A}{X}_{0iv}={\sum }_{(j,0)\in A}{X}_{j0k}+{\sum }_{(j,0)\in A}{X}_{j0v}=Y_k+Y_v,\forall k\in K,\forall v\in V$$

(11)

$$T_{ik}+\left(t_{ik}+t_{ij}\right)\times X_{ijk}-M\left(1-X_{ijk}\right)\le T_{jk},\forall i,j\in N,\forall k\in K$$

(12)

$${arrive}_{iv}+\left({wait}_{iv}+t_{ij}\right)\times X_{ijv}-\mathrm{M}\times (1-X_{ijv})\le {arrive}_{jv},\forall i,j\in N,\forall v\in V$$

(13)

$$T_{ik}\le {arrive}_{iv}+\mathrm{M}\times \left(1-X_{ijv}\right)\le T_{ik}+∆,\forall i,j\in N,\forall v\in V,\forall k\in K$$

(14)

$$h_k^s\times X_{ik}^s\ge l_i^s,\forall i\in N,\forall k\in K,\forall s\in S$$

(15)

$$h_v^q\times X_{iv}^q=l_i^q,\forall i\in N,\forall v\in V,\forall q\in Q$$

(16)

$$rate\times {\sum }_{i,j\in N}{t}_{ij}\times X_{ijv}\le Length,\forall v\in V$$

(17)

$${\sum }_{i,j\in N}(t_{ik}+t_{ij})\times X_{ijk}\le L,\forall k\in K$$

(18)

$$X_{ijk},X_{ijv},X_{ik}^s,X_{iv}^q,Y_k,Y_v\in \left\{\mathrm{0,1}\right\},\forall i,j\in N,k\in K,v\in V,s\in S,q\in Q$$

(19)

4. Materials and Methods

Combined with the model presented in Section 3, when the scale of the problem becomes larger and larger, it is difficult for the accurate algorithm to obtain the optimal solution in an effective time. The heuristic method has the ability to jump out of the local optimal and search for the global optimal solution. In this paper, the HDV service is introduced on the basis of the traditional home health care scheduling problem, which makes the problem more complex and constrained. Therefore, we select a heuristic algorithm to solve the HHCRSP problem:

The Non-Dominated Sorting Genetic Algorithm (NSGA-II), proposed by Deb et al. in 2002. Considering that the NSGA-II has the advantages of few parameters and good distribution [32], it has been applied by many scholars to solve combinatorial optimization problems. As far as we know, there are few scholars addressing the NSGA-II to solve the multi-objective routing problems in an HHC environment. However, there are some shortcomings. Generally speaking, the initial population of the NSGA-II adopts the strategy of random initialization, which cannot guarantee the quality of the initial population. It is difficult to improve the diversity of solutions in the original genetic operator. In this paper, we improved the initial population and genetic operator, and introduced the population cooperation process, which is described as follows.

4.1. Encoding

Since the model involves the visit order and service type of patients, and the nodes of caregivers and patients are discrete points, we adopt a two-stage non-negative integer coding method; each chromosome represents an individual. The first part of the code represents HHC service and the second part represents HDV service. For a medical center with N patients, k caregiver, and v vehicles, the patient code is $1~N$, the caregiver code is $N+1~N+k$, and the vehicle code is $N+k+1~N+k+v$. 0 indicates the medical center. Each value represents a gene, and the gene order represents the access order of the caregiver. According to the constraints of caregiver working time limit, patient service time window, caregiver-patient skill matching, vehicle distance restriction, and so on. Use 0 to separate the paths into different sets. The first gene of each path represents the number of the caregiver or vehicle, and other genes are patient numbers. A new route will be constructed when caregiver exceeds the required working hours.

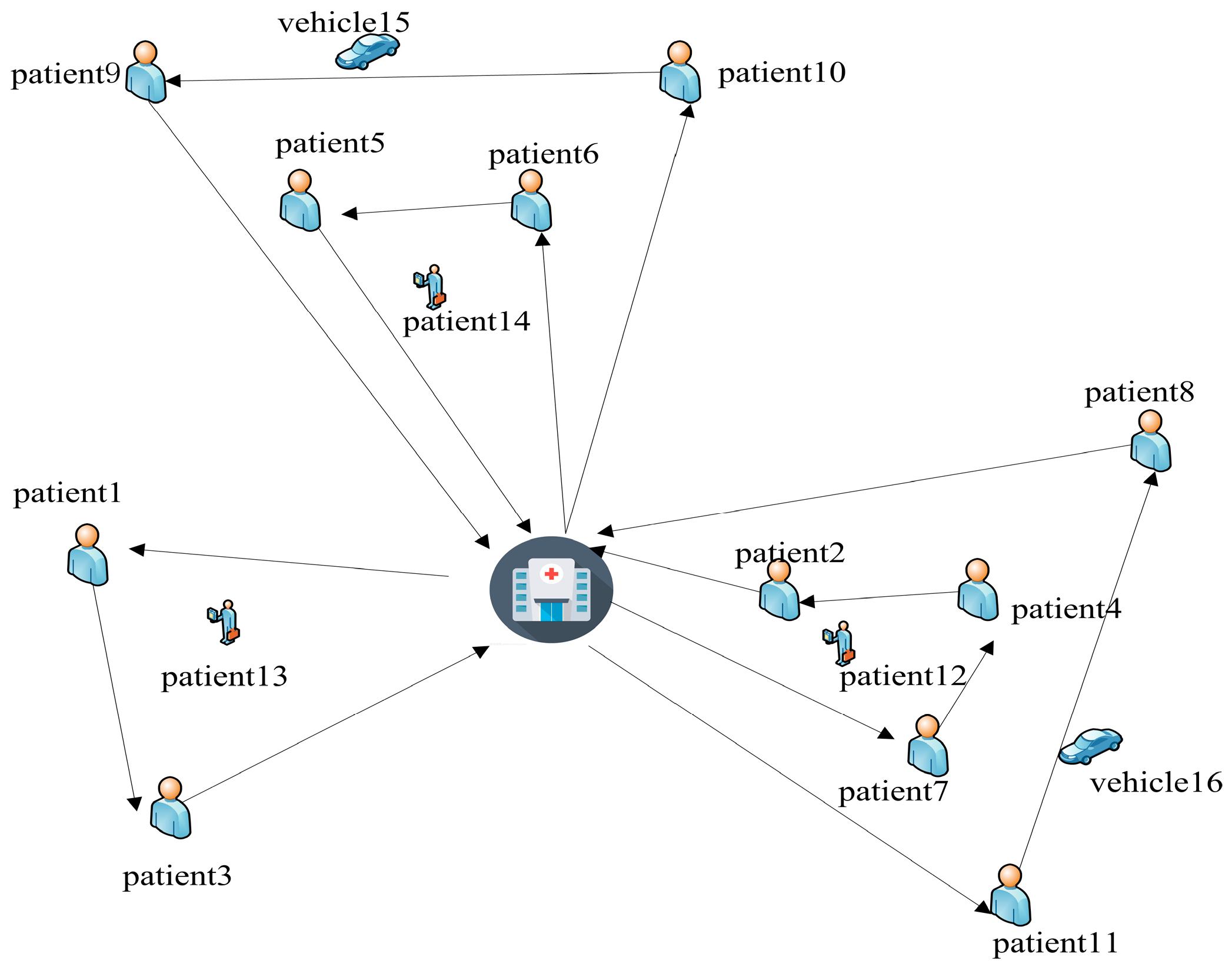
This paper takes a medical center with 7 patients, 3 caregivers and 2 vehicles, as an example, in which patients 1–3 need HHC services and patients 4–7 need synchronous services. Set the patients who need synchronous services to add a virtual patient with codes of 8, 9, 10 and 11; that is, numbers 1–11 represent patients, 12–14 represent caregivers, and 15–16 represent transport vehicles. The codes are shown in Figure 2. There are three HHC service paths and two HDV service paths. (0, 13, 1, 3, 0) indicates that the path of caregiver 12 is 0-1-3-0; (0, 14, 9, 10, 0) means that the path of delivery vehicle 14 is 0-9-10-0, and so on.

4.2. Generation of Initial Solutions

In order to improve the solution of the algorithm, this paper uses heuristic rules to generate the initial solution, and improves it on this basis. In this paper, we designed two populations to evolve simultaneously. Among them, the two populations are recorded as population A and population B, where population A is initialized by heuristic rules and population B is initialized randomly.

The heuristic rules are as follows. For HHC services, first, patients are classified according to skill needs and represented by $S_n$, where n represents the skill type. Select a caregiver $N+k$ from $N+1~N+k$ at random. Then, select a patient i according to the skill level of the caregiver, in which patient i is randomly selected from the corresponding type of patient set as the service object. At this time, the path is represented as $0\to (N+k)\to i\to 0$. Select nearby unserved points and insert them into the current line $0\to (N+k)\to i\to 0$ in time sequence to ensure that the total time and skill type meet the requirements. If the working time of the caregiver exceeds the specified time limit, the next line will be reconstructed until all patients are assigned. For the HDV path, select a vehicle $N+k$ from $N+1~N+k$ at random. Among then, the HDV’s visit order according to the patient’s HHC service time window. When no patient meets the requirements of the current line, or the length of the transportation path reaches the limit, the next line is reconstructed. Based on this initial solution generation method, it can not only meet the needs of matching skills, but also solve problems such as time constraints and synchronous services.

4.3. Genetic Operations

Some of the good individual solutions may disappear during the process of evolution. Therefore, in order to maintain the diversity of the population and avoid falling into the local optimal state, this paper carried out chromosome crossover and mutation operations.

The crossover operations corresponding to population A and population B are recorded as crossover A and crossover B, respectively, and the corresponding mutation operations are recorded as mutation A and mutation B. In this paper, two populations adopt the same crossover mode.

4.3.1. Crossover

Cross operation is prone to the loss and redundancy of gene information. To solve this problem, a new crossover operator is used in this paper. We have comprehensively considered skills matching, patient service order, time window, and distance constraints, which can not only solve a series of constraint problems, but also improve the diversity of solutions on the basis of the original chromosomes. In this paper, the random number (0, 1) is used to determine whether the HHC route or the HDV route should be cross operated. Assuming that the random number is 0, take the HHC path for example, and the crossing steps are as follows.

Step 1: The two parental chromosomes involved in the crossover operation are recorded as $P_1$ and $P_2$, and the crossover probability is recorded as $P_c$.

Step 2: Randomly generate an integer $m,m\in [1,c]$, where c represents the total path number of HHC. We determine the location of chromosome for cross operation based on m.

Step 3: The selected cross area in $P_2$ is placed in the first line in $P_2$, and the remaining patients are reassigned according to the coding rules to generate a new service path. Then, we get the offspring chromosome. Similarly, we can obtain $Q_2$.

When $m=2,c=3$, the specific cross process is shown in Figure 3.

4.3.2. Mutation

In this paper, we consider that the HHCRSP problem has strict constraints on the time window. At the same time, in order to further improve individual performance and increase population diversity, we design a variety of mutation operators. A chromosome was randomly selected and denoted as $P_1$, and the mutation probability was denoted as $P_m$. The HHC or HDV path mutation operation was determined by random number (0, 1). Assume that the random number is 0. Take the HHC service path as an example.

• Mutation A—mutation between lines.

Randomly generate $\theta$, where $\theta \in [0,1]$. If $\theta {\le P}_m$, then select insertion mutation, exchangeable mutation otherwise.

Insertion mutation: generate two numbers x and y randomly, where $x,y\in [1,c]$, c is the number of HHC total paths and $x\ne y$. The position of mutation operation is determined by x and y. Delete the designated gene in path y randomly and insert it into the designated position in path x. If the new path formed meets the time and skill constraints, new chromosomes will be generated. Otherwise, the original chromosome will be retained until the end of the mutation operation. When $x=1,y=2,c=3$, the specific variation process is shown in Figure 4:

Exchangeable mutation: a position is randomly assigned within the selected path x and y for exchange. If the new path meets the time window and skill constraints, a new chromosome $C_1$ will be generated, otherwise the original chromosome will be retained. When $x=1,y=3,c=3$, the specific variation process is shown in Figure 5:

• Mutation B—mutation within the line.

Insertion mutation: select a node randomly and delete it, then reinsert the node into the path. If the new path meets the constraints, the new individual will replace the old.

4.4. Local Search

In the problem, we design three local search operators for HHC and HDV. During a local search, a random search method is selected.

• Randomly delete two or more patients on a line and reassign them to meet the constraints;
• Randomly select two HHC lines to exchange the specified segments;
• For HHC or HDV service, randomly exchange two caregivers with the same skills or vehicles with the same service.

4.5. Population Cooperation

In order to improve the quality of the solution and strengthen the information exchange between populations, some scholars improved the deficiency of the population evolution by exchanging the genetic information carried by excellent individuals [33]. After genetic operation and local search, completed, respectively, by population A and population B, non-dominated sorting is conducted. Exchange the first 50% of the individuals to form a new population A and population B for the next iteration.

4.6. Algorithm Framework

The flowchart of INSGA-II proposed is given in Figure 6.

5. Computational Experiments

In this section, we conducted a lot of experiments to illustrate the nature of the problem and verify the effectiveness of the proposed method. The test environment, experimental parameters, and comparison algorithm are introduced in Section 5.1. Section 5.2 analyzes the effectiveness of the algorithm. Sensitivity analysis is shown in Section 5.3. The codes of all algorithms in this paper are written in MATLAB (2019a) and run on the computer of Windows 10 operating system.

5.1. Test Environment and Parameter Setting

At present, due to the lack of standard calculation examples, the calculation examples in this paper are modified on the basis of Solomon data [34]. The original Solomon standard examples are divided into six categories. In this paper, three examples are randomly selected in each type, and a total of 18 examples are set. In order to distinguish from the classical Solomon example, “HHC” is added before each example as a mark.

In order to verify the effectiveness and superiority of the INSGA-II in solving the HHCRSP, the first 51 nodes in the above 18 examples are modified as the basic data of this experiment. Among them, the node location coordinates are reserved, and the service time window, service duration, and skill demand columns are added. Assuming that the number of patients requiring HHC and HDV collaborative services is 15, and considering the introduction of virtual patients, the total number of patients is 65; the number of disposable caregivers is 25; and the total number of vehicles is 10. Based on the above test examples, the INSGA-II is compared with the multi-objective evolutionary algorithm (MOEAD) [35] and the multi-objective particle swarm optimization (MOPSO) [36]. The population size of the three algorithms is set as $N=40$, and the number of iterations is $iter$ = 200, $P_c$ = 0.8, $P_m$ = 0.1, M = 1000. The specific model parameters are shown in

Table 2. Parameter Settings (according to the research situation).

Symbol	Data Reference Description
$C_k$	set 140, 160 and 180 per day
$C_v$	set 100 per day
$\mathrm{P}\mathrm{C}$	set 25 per hour
$L$	set to 10 h
$D$	set to 8 h
$b$	set to 100 yuan
$\delta$	set to 5 per kilometer
$\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}$	set to 40 km per hour
wait	set to 10 min
Length	set to 160 km
$\Delta$	set to 10 min

. In addition, INSGA-II adopts a dual population initialization strategy, and other algorithms adopt a random initialization strategy.

5.2. Algorithm Performance Analysis

5.2.1. Effectiveness of Population Initialization Strategy

In order to verify the effectiveness of the improved strategy of the initialization method and local search method, compare the INSGA-II with INSGA-II-A and INSGA-II-B. Among them, INSGA-II-A represents the INSGA-II algorithm using a single population random initialization strategy. INSGA-II-B represents the INSGA-II that does not use the local search strategy proposed in Section 4.4. The algorithm performance is evaluated by using the comprehensive evaluation index Hyper Volume (HV) [37] and the diversity evaluation index space (Spacing, SP) [38]. Among them, the larger the HV, the better the convergence of the pareto frontier obtained by the algorithm, and the more uniform the distribution. The smaller the SP, the more uniform the pareto front distribution obtained by the algorithm. Different algorithms are used to run different examples independently for ten times, and then their mean values are compared. The results are shown in

Table 3. Comparison results of INSGA-II and its variant forms.

Instance	INSGA-II		INSGA-II-A		INSGA-II-B
	HV	SP	HV	SP	HV	SP
HHC-R101	3.6795 × 10−1	3.3824 × 10−1	2.4298 × 10−1	3.6592 × 10−1	4.2157 × 10−1	4.0246 × 10−1
HHC-R103	7.8604 × 10−1	1.9761 × 10−1	4.3244 × 10−1	2.1837 × 10−1	4.5269 × 10−1	2.2935 × 10−1
HHC-R107	5.8127 × 10−1	5.7660 × 10−3	2.5699 × 10−1	6.7770 × 10−3	5.2651 × 10−1	1.9615 × 10−2
HHC-R201	5.7159 × 10−1	4.2401 × 10−1	1.6834 × 10−1	2.0574 × 10−1	2.8113 × 10−1	5.1093 × 10−1
HHC-R203	6.0889 × 10−1	9.7553 × 10−2	2.0559 × 10−1	4.5797 × 10−1	4.3653 × 10−1	2.4636 × 10−1
HHC-R207	5.9134 × 10−1	2.0181 × 10−2	6.8510 × 10−1	3.4838 × 10−1	5.6357 × 10−1	3.2479 × 10−1
HHC-C101	7.1139 × 10−1	9.1549 × 10−2	2.8833 × 10−1	6.8497 × 10−3	4.3326 × 10−1	8.3629 × 10−2
HHC-C103	6.7626 × 10−1	8.4326 × 10−2	1.8850 × 10−1	9.6460 × 10−2	3.2562 × 10−1	9.4110 × 10−2
HHC-C107	8.3982 × 10−1	1.2471 × 10−1	8.1256 × 10−1	1.3548 × 10−1	7.3490 × 10−1	2.8173 × 10−1
HHC-C201	6.8752 × 10−1	2.1168 × 10−1	6.3139 × 10−1	2.4446 × 10−1	5.4824 × 10−1	1.9669 × 10−1
HHC-C203	8.6346 × 10−1	5.6131 × 10−2	5.8799 × 10−1	9.6723 × 10−1	5.3525 × 10−1	8.3367 × 10−1
HHC-C207	7.5346 × 10−1	1.3825 × 10−1	5.0568 × 10−1	3.7210 × 10−1	5.5914 × 10−1	3.1185 × 10−1
HHC-RC101	4.4163 × 10−1	2.9896 × 10−1	4.4631 × 10−1	2.9916 × 10−1	5.1636 × 10−1	9.4173 × 10−2
HHC-RC103	6.8478 × 10−1	2.3945 × 10−1	3.2570 × 10−1	3.1499 × 10−1	4.3653 × 10−1	3.7251 × 10−1
HHC-RC107	8.7134 × 10−1	2.1765 × 10−1	4.7852 × 10−1	3.4729 × 10−1	5.3139 × 10−1	2.5318 × 10−1
HHC-RC201	7.9651 × 10−1	1.5689 × 10−1	4.8620 × 10−1	3.7006 × 10−1	4.5480 × 10−1	1.7636 × 10−1
HHC-RC203	7.3978 × 10−1	2.4405 × 10−2	5.7491 × 10−1	2.2250 × 10−2	5.6523 × 10−1	1.1697 × 10−1
HHC-RC207	7.1424 × 10−1	8.8636 × 10−2	4.4963 × 10−1	4.1001 × 10−2	6.6537 × 10−1	2.4986 × 10−1

.

It can be seen from Table 3 that the best results of independent run of each example are shown in bold data. It can be seen from the comparison data that INSGA-II has the best solution result. Among the 18 examples, the HV value of 16 examples can get the best result, and the SP value of 12 examples can get the best result, which is obviously more than other algorithms. Therefore, the dual population evolution and local search strategies can further improve the performance of the algorithm.

5.2.2. Comparison with Existing Algorithms

To verify the effectiveness of INSGA-II in this paper, 18 cases with 65 patients were run independently for 10 times. Evaluate the mean value of the indicators of the Pareto solution; the results are shown in

Table 4. Comparison of algorithm indicators.

Instance	INSGA-II		MOEAD		MOPSO
	HV	SP	HV	SP	HV	SP
HHC-R101	3.6795 × 10−1	3.3824 × 10−1	2.9547 × 10−1	4.5042 × 10−1	1.8885 × 10−1	4.1556 × 10−1
HHC-R103	7.8604 × 10−1	1.9761 × 10−1	2.3374 × 10−2	3.8807 × 10−1	2.9220 × 10−1	8.3471 × 10−1
HHC-R107	5.8127 × 10−1	5.7660 × 10−3	1.6163 × 10−1	1.1993 × 10−1	2.5397 × 10−1	5.8058 × 10−1
HHC-R201	5.7159 × 10−1	4.2401 × 10−1	3.0114 × 10−1	8.1952 × 10−1	1.5324 × 10−1	9.3190 × 10−1
HHC-R203	6.0889 × 10−1	9.7553 × 10−2	4.6331 × 10−1	5.2568 × 10−1	3.1529 × 10−1	3.6847 × 10−1
HHC-R207	5.9134 × 10−1	2.0181 × 10−2	3.8715 × 10−2	2.5083 × 10−1	6.2221 × 10−1	3.0673 × 10−1
HHC-C101	7.1139 × 10−1	9.1549 × 10−2	2.5066 × 10−1	4.5203 × 10−1	2.4560 × 10−1	1.5759 × 10−1
HHC-C103	6.7626 × 10−1	8.4326 × 10−2	3.8858 × 10−1	1.0989 × 10−1	3.0967 × 10−1	3.4256 × 10−1
HHC-C107	8.3982 × 10−1	1.2471 × 10−1	2.7296 × 10−1	6.6591 × 10−1	1.3559 × 10−1	4.3952 × 10−1
HHC-C201	6.8752× 10−1	2.1168 × 10−1	2.6139 × 10−1	3.5487 × 10−1	5.0749 × 10−1	2.9577 × 10−1
HHC-C203	8.6346 × 10−1	5.6131 × 10−2	2.4314 × 10−1	1.9685 × 10−1	6.7469 × 10−1	1.1167 × 10−1
HHC-C207	7.5346 × 10−1	1.3825 × 10−1	5.5504 × 10−1	2.8210 × 10−1	3.7263 × 10−1	1.8966 × 10−1
HHC-RC101	4.4163 × 10−1	2.9896 × 10−1	4.5527 × 10−1	4.8819 × 10−1	4.2433 × 10−1	3.1074 × 10−1
HHC-RC103	6.8478 × 10−1	2.3945 × 10−1	2.9115 × 10−1	5.0238 × 10−1	3.3404 × 10−1	3.4321 × 10−1
HHC-RC107	8.7134 × 10−1	2.1765 × 10−1	4.8029 × 10−1	3.1257 × 10−1	5.6249 × 10−1	6.5327 × 10−1
HHC-RC201	7.9651 × 10−1	1.5689 × 10−1	5.3654 × 10−1	5.3563 × 10−1	4.1489 × 10−1	1.5992 × 10−1
HHC-RC203	7.3978 × 10−1	2.4405 × 10−2	2.6984 × 10−1	8.9892 × 10−2	4.8239 × 10−1	7.0195 × 10−2
HHC-RC207	7.1424 × 10−1	8.8636 × 10−2	8.6272 × 10−1	1.1961 × 10−1	8.6974 × 10−1	2.0029 × 10−1

. The bold part is the optimal result of each example under the comparison of three algorithms.

Table 4 shows the mean values of SP and HV indicators under the three algorithms. It can be seen from the table that 15 of the 18 cases using the INSGA-II have the best HV value, and the remaining 3 cases have slightly lower than the comparison algorithm. This is because the geographical distribution of patients in the examples HHC-R107, HHC-RC101, and HHC-RC207 is more random, and the patient’s time window is wider. The complexity of this problem increases the difficulty of algorithm optimization. Comparing the SP values of different algorithms, the SP values of all examples are optimal under the INSGA-II. In conclusion, the pareto solution set has good convergence and distribution in the INSGA-II, which verifies the effectiveness of the INSGA-II.

In addition, Table 4 can only explain the advantages and disadvantages of the algorithm from a macro perspective. To further verify the statistical advantages of the algorithm performance in this paper, the Wilcoxon sign rank test was conducted, where the confidence level was 0.05. The results are shown in

Table 5. Wilcoxon signed rank test of INSGA-II and other algorithm indicators.

Algorithm	Indicator (p-Value)
	HV	SP
INSGA-II vs. MOEAD	7.38 × 10−4	1.96 × 10−4
INSGA-II vs. MOPSO	5.36 × 10−4	1.96 × 10−4

. The p values in Table 5 are all less than 0.05, which shows that the INSGA-II has better performance, and its solution is significantly better than the comparison algorithm in terms of convergence and diversity.

In order to explain the rationality of the solution more clearly, we randomly select one of the 18 examples for analysis, taking HHC-R207 as an example. Considering the layout limitation, we introduce two solutions for HDV lines, one of which is the solution with the lowest total cost, and the other is the greatest balance, as shown in

Table 6. Pareto solution.

Objective Function Value	HDV Service Path
	Vehicle	Path	Remaining Distance Length
Solution 1:	1	[0-62-61-57-53-59-0]	[160-125.6-115.6-73.6-53.2-21.2]
cost: 3705.61	2	[0-60-51-64-63-65-0]	[160-130.8-108.4-99.6-82-47.6-30.8]
time difference: 16.50	3	[0-55-56-54-58-52-0]	[160-148.8-130.8-112-74-56.8-35.6]
...	...	...	...
Solution 2:	1	[0-60-62-51-64-63-61-0]	[160-130.8-112.8-105.6-96.8-79.2-58.8-23.2]
cost: 4018.19	2	[0-57-58-53-59-52-0]	[160-134.4-125.2-107.2-66.8-56-34.8]
time difference: 9.79	3	[0-55-56-54-65-0]	[160-148.8-130.8-112-74.8-58]

. The distribution of non-dominated solutions of different algorithms is shown in Figure 7.

Table 6 describes the path of each vehicle in the service process, as well as the remaining distance of the vehicle when passing through each patient node. The results meet the model requirements. From the Pareto frontier graph, we can see that the INSGA-II can obtain more Pareto solutions, and the distribution of solutions is more uniform than other algorithms. With regard to the home health care scheduling problem, take the INSGA-II for example—when the medical center pays more attention to economic benefits, they may choose the scheduling plan represented by the leftmost dot in Figure 7. When health care centers are more concerned about caregiver balance, they may choose the scheduling plan represented by the dot on the far right in Figure 7. The medical center needs to choose the appropriate scheduling scheme according to the actual operation situation. Whether the medical center pays attention to the total cost or the work balance, the results of the INSGA-II are optimal. Therefore, we choose the INSGA-II to solve the model effectively.

5.3. Analysis of Model Validity

Taking into account the multiple needs of patients, some health care centers will directly arrange a highly skilled caregiver to provide one-time services to patients, and some others will assign multiple caregivers to provide collaborative services. However, there is a lack of strict division of service needs, and the waste of resources caused by the deviation between basic services and healthcare is not considered. When the caregivers and the vehicles conduct synchronous access, the vehicle can leave after providing services for the current patient, which can reduce the vehicle’s stay time. To verify the effectiveness of the optimization of synchronous access, we analyzed the service schemes under different access forms. The scheme settings are shown in

Table 7. Scheme design.

	Plan A	Plan B
Form of access	HHC and HDV	HHC and HHC

. Among them, Plan A is the caregiver-vehicle synchronous visit mode proposed in this paper, and Plan B is the traditional synchronous visit mode between caregivers. Randomly select HHC-C107 from the above standard examples as the case for analysis, the three algorithms in this paper are used for comparison simulation. Each case is run 10 times respectively, and the average value is taken as shown in Figure 8 and Figure 9.

It can be seen from Figure 8 and Figure 9 that no matter which algorithm is used, Plan A has the best result. Taking the INSGA-II as an example, the cost of Plan A was reduced by 8.4% compared with Plan B, and the work balance of caregiver was improved by 13.1%. The experimental results show that, with the diversified development of service demand, strict classification of patient demand types can effectively reduce the operating cost of the medical center and improve the work balance of caregivers.

6. Conclusions and Future Work

This paper studies the HHCRSP, considering the limitation of caregiver’s skill level, working time, visiting time and vehicle mileage. The problem is formulated as a multi-objective mathematical model to minimize the total cost and maximize the work balance. Then we develop an INSGA-II; the proposed INSGA-II has three main ideals: (1) Two populations are designed to evolve simultaneously, and initial solutions are generated by heuristic rules and random methods, respectively. (2) The optimal individual updating strategy is designed to solve the multi-objective decision model. (3) A variety of local search operators are designed. In order to evaluate the improved performance of the INSGA-II, a large number of calculations and tests were carried out for the problems studied, using 18 examples. The results show that the improved initial generation strategy is effective. In addition, the NSGA-II is compared with the MOEAD and the MOPSO, which also verifies the rationality and effectiveness of the model and algorithm proposed in this paper.

This paper comprehensively considers the benefits and rights of the research subject, and effectively balances the interests of both the medical center and caregiver. It is helpful to the sustainable development of the home health care system, and can provide theoretical guidance for the medical center to formulate plans for caregivers and vehicles, which is of great practical significance. Although this paper has conducted a detailed study on the problem of home health care scheduling, further exploration is still necessary in order to promote the development of the home health care system. A set of new assumptions and innovations can be introduced into the present model for future studies. For example, in order to improve the effectiveness of the optimized route in the real traffic network, Liu et al. [39] considered the differences in vehicle speeds in different road conditions and different time periods—such as morning peak and evening peak—and constructed the speed function. In this paper, we mainly study the synchronous visits of caregivers and vehicles, where the vehicles move at a constant speed. Considering the practical problems of the health service system, we will try to use the real-time network to update vehicle speed and calculate travel time. Additionally, in future research we can develop new algorithms to compare the results of this study, such as hybrid heuristics [40] and metaheuristics [41], and adaptive algorithms [42].