Calibration and Evaluation of the WRF-Hydro Model in Simulating the Streamflow over the Arid Regions of Northwest China: A Case Study in Kaidu River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. WRF-Hydro Model Structure and Configuration
2.3. Experimental Design
2.4. Evaluation Metrics
3. Results
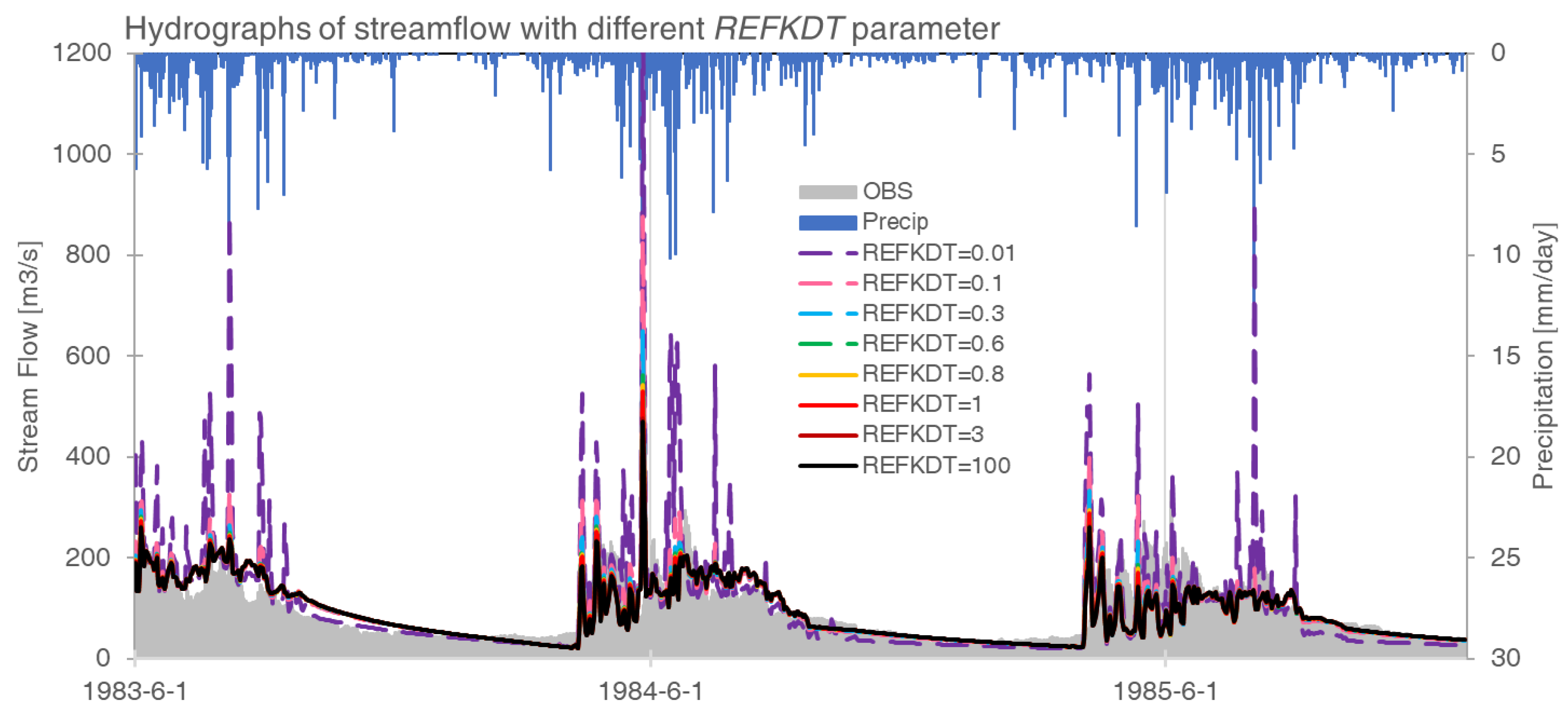
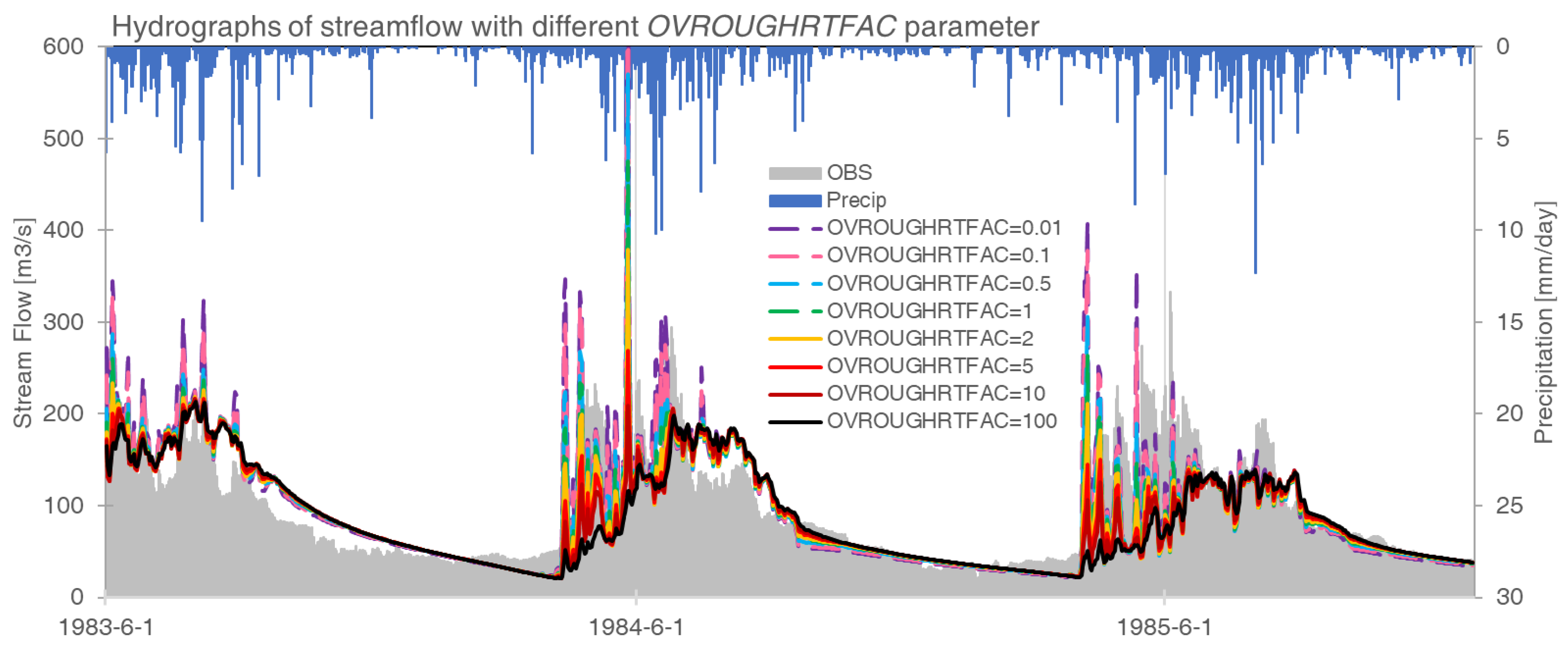
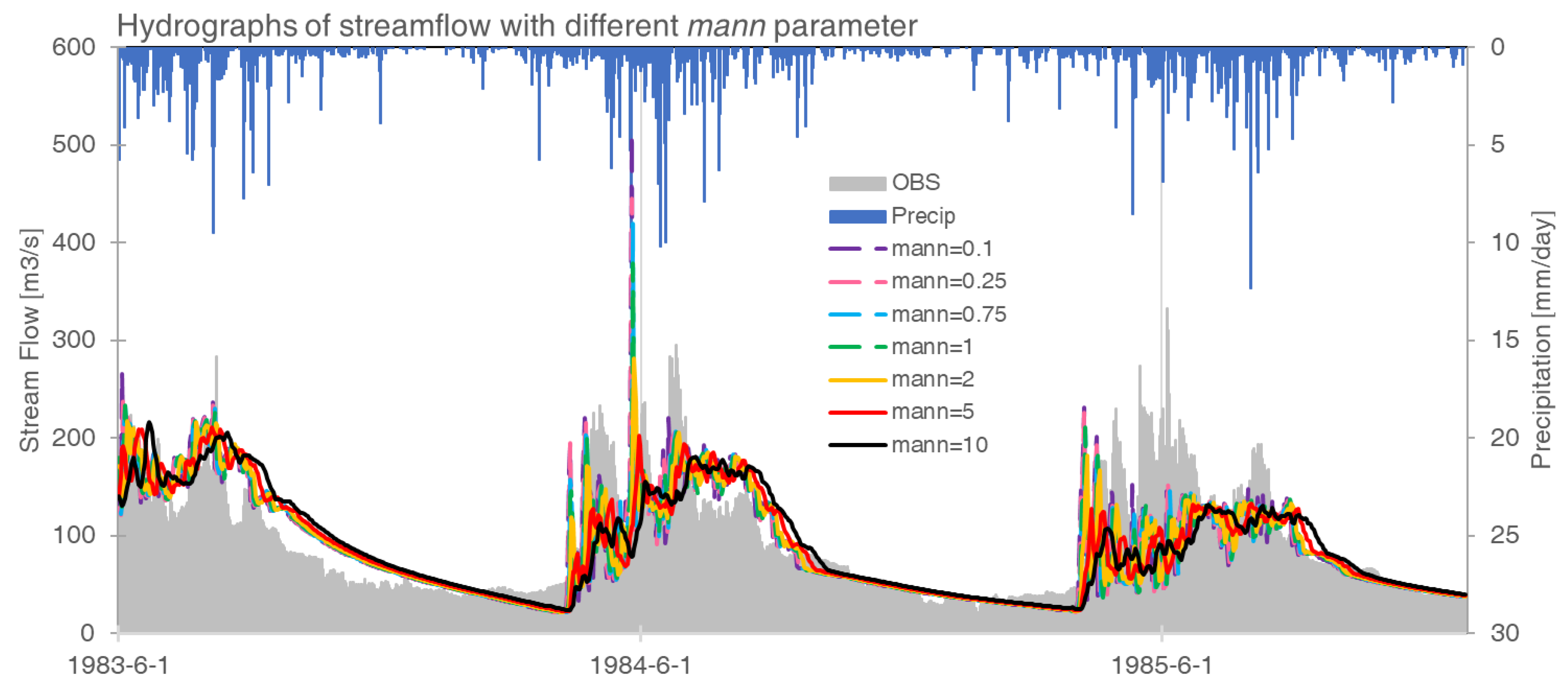
3.1. Model Sensitivity to Key Parameters
3.2. Sensitivity to Noah-MP Options
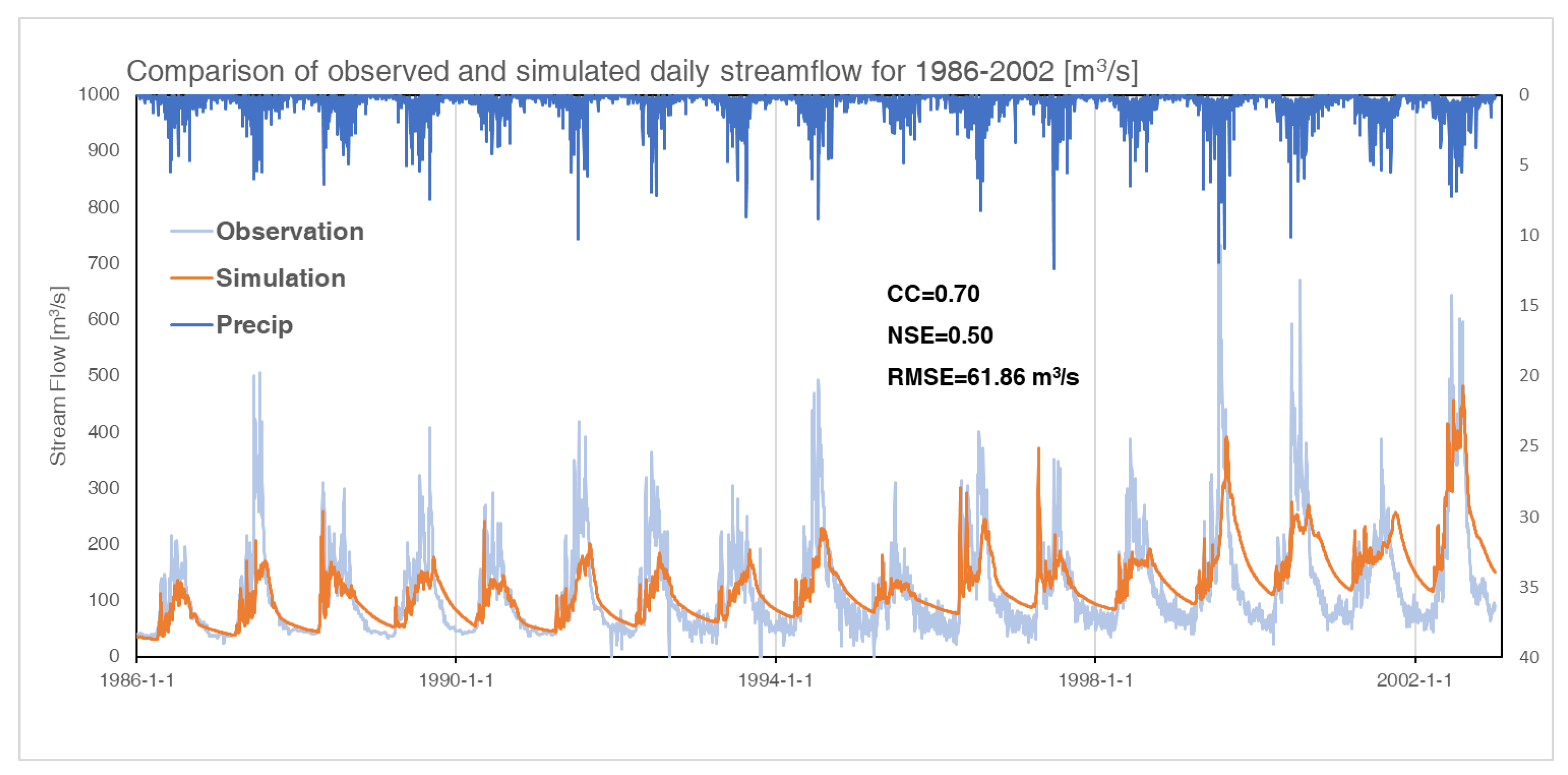
3.3. Model Performance Evaluation
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Li, Z.; Fan, Y.; Wang, H.; Deng, H. Progress and prospects of climate change impacts on hydrology in the arid region of northwest China. Environ. Res. 2015, 139, 11–19. [Google Scholar] [CrossRef]
- Xia, J.; Ning, L.; Wang, Q.; Chen, J.; Wan, L.; Hong, S. Vulnerability of and risk to water resources in arid and semi-arid regions of West China under a scenario of climate change. Clim. Change 2017, 144, 549–563. [Google Scholar] [CrossRef]
- Tao, H.; Gemmer, M.; Bai, Y.; Su, B.; Mao, W. Trends of streamflow in the Tarim River Basin during the past 50years: Human impact or climate change? J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Xue, L.; Wang, J.; Zhang, L.; Wei, G.; Zhu, B. Spatiotemporal analysis of ecological vulnerability and management in the Tarim River Basin, China. Sci. Total Environ. 2019, 649, 876–888. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Wang, Y. The influence of 10 years of water conveyances on groundwater and juvenile Populus euphratica of the lower Tarim River. Env. Earth Sci. 2014, 71, 4091–4096. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Xu, C.; Ye, Z.; Li, Z.; Zhu, C.; Ma, X. Effects of ecological water conveyance on groundwater dynamics and riparian vegetation in the lower reaches of Tarim River, China. Hydrol. Process. 2010, 24, 170–177. [Google Scholar] [CrossRef]
- Wu, J.; Tang, D. The influence of water conveyances on restoration of vegetation to the lower reaches of Tarim River. Env. Earth Sci. 2010, 59, 967–975. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, H.; Yan, D.; Wei, G.; Tuo, Y.; Zhang, W. Quantifying changes and drivers of runoff in the Kaidu River Basin associated with plausible climate scenarios. J. Hydrol. Reg. Stud. 2021, 38, 100968. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J.; Deng, H.; Fang, G.; Tan, J.; He, D.; Chen, Y.; Chen, Y.; Fu, A. Scenario-based runoff prediction for the Kaidu River basin of the Tianshan Mountains, Northwest China. Env. Earth Sci. 2016, 75, 1126. [Google Scholar] [CrossRef]
- Balsamo, G.; Pappenberger, F.; Dutra, E.; Viterbo, P.; van den Hurk, B. A revised land hydrology in the ECMWF model: A step towards daily water flux prediction in a fully-closed water cycle. Hydrol. Process. 2011, 25, 1046–1054. [Google Scholar] [CrossRef]
- Yucel, I.; Onen, A.; Yilmaz, K.K.; Gochis, D.J. Calibration and evaluation of a flood forecasting system: Utility of numerical weather prediction model, data assimilation and satellite-based rainfall. J. Hydrol. 2015, 523, 49–66. [Google Scholar] [CrossRef] [Green Version]
- Senatore, A.; Mendicino, G.; Gochis, D.J.; Yu, W.; Yates, D.N.; Kunstmann, H. Fully coupled atmosphere-hydrology simulations for the central Mediterranean: Impact of enhanced hydrological parameterization for short and long time scales. J. Adv. Model. Earth Syst. 2015, 7, 1693–1715. [Google Scholar] [CrossRef]
- Skamarock, C.; Klemp, B.; Dudhia, J.; Gill, O.; Liu, Z.; Berner, J.; Wang, W.; Powers, G.; Duda, G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4.1. In NCAR Technical Note; National Center for Atmospheric Research: Boulder, CO, USA, 2019. [Google Scholar]
- Yu, E. A Warmer, wetter and less windy China in the twenty-first century as projected by a nested high-resolution simulation using the Weather Research and Forecasting (WRF) model. Asia-Pac. J. Atmos. Sci. 2019, 55, 53–74. [Google Scholar]
- Yu, E.; Ma, J.; Sun, J. Developing a climate prediction system over Southwest China using the 8-km Weather Research and Forecasting (WRF) model: System design, model calibration and performance evaluation. Weather Forecast 2022, 37, 1703–1719. [Google Scholar] [CrossRef]
- Yu, L.; Liu, Y.; Liu, T.; Yu, E.; Bu, K.; Jia, Q.; Shen, L.; Zheng, X.; Zhang, S. Coupling localized Noah-MP-Crop model with the WRF model improved dynamic crop growth simulation across Northeast China. Comput. Electron. Agric. 2022, 201, 107323. [Google Scholar] [CrossRef]
- Gao, S. Dynamical downscaling of surface air temperature and precipitation using RegCM4 and WRF over China. Clim. Dyn. 2020, 55, 1283–1302. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, J.; Zhang, M.; Liu, Z.; Dan, J. Regional climate dynamical downscaling over the Tibetan Plateau—From quarter-degree to kilometer-scale. Sci. China Earth Sci. 2022, 1–11. [Google Scholar] [CrossRef]
- Gochis, J.; Chen, F. Hydrological enhancements to the community Noah land surface model. In NCAR Technical Note; University Corporation for Atmospheric Research: Boulder, CO, USA, 2003. [Google Scholar]
- Gochis, D.; Dugger, A.; Barlage, M.; Fitzgerald, K.; Karsten, L.; Mcallister, M.; McCreight, J.; Mills, J.; Rafieeinasab, A.; Read, L. The NCAR WRF-Hydro Modeling System Technical Description. In NCAR Technical Note; University Corporation for Atmospheric Research: Boulder, CO, USA, 2018. [Google Scholar]
- Givati, A.; Gochis, D.; Rummler, T.; Kunstmann, H. Comparing one-Way and two-way coupled hydrometeorological forecasting systems for flood forecasting in the Mediterranean region. Hydrology 2016, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Liu, J.; Li, C.; Liu, Y.; Yu, F.; Yu, E. An evaluation study of the fully coupled WRF/WRF-Hydro modeling system for simulation of storm events with different rainfall evenness in space and time. Water 2020, 12, 1209. [Google Scholar] [CrossRef]
- Rummler, T.; Arnault, J.; Gochis, D.; Kunstmann, H. Role of lateral terrestrial water flow on the regional water cycle in a complex terrain region: Investigation with a fully coupled model system. J. Geophys. Res. Atmos. 2019, 124, 507–529. [Google Scholar] [CrossRef]
- Zhang, Z.; Arnault, J.; Wagner, S.; Laux, P.; Kunstmann, H. Impact of lateral terrestrial water flow on land-atmosphere interactions in the Heihe River Basin in China: Fully coupled modeling and precipitation recycling analysis. J. Geophys. Res. Atmos. 2019, 124, 8401–8423. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Arnault, J.; Laux, P.; Ma, N.; Wei, J.H.; Shang, S.S.; Kunstmann, H. Convection-permitting fully coupled WRF-Hydro ensemble simulations in high mountain environment: Impact of boundary layer- and lateral flow parameterizations on land-atmosphere interactions. Clim. Dyn. 2022, 59, 1355–1376. [Google Scholar] [CrossRef]
- Wang, J.; Liu, D.; Tian, S.; Ma, J.; Wang, L. Coupling reconstruction of atmospheric hydrological profile and dry-up risk prediction in a typical lake basin in arid area of China. Sci. Rep. 2022, 12, 6535. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Xu, B.; Li, C.; Liu, Y.; Yu, F. A WRF/WRF-Hydro coupling system with an improved structure for rainfall-runoff simulation with mixed runoff generation mechanism. J. Hydrol. 2022, 612, 128049. [Google Scholar] [CrossRef]
- Yan, J.; Jia, S.; Lv, A.; Zhu, W. Water resources assessment of China’s transboundary river basins using a machine learning approach. Water Resour. Res. 2019, 55, 632–655. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Wang, J.; Wei, J.; Wang, H. Hydrological simulation evaluation with WRF-Hydro in a large and highly complicated watershed: The Xijiang River basin. J. Hydrol. Reg. Stud. 2021, 38, 100943. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Li, C.; Yu, F.; Wang, W.; Qiu, Q. Parameter sensitivity analysis of the WRF-Hydro modeling system for streamflow simulation: A case study in semi-humid and semi-arid catchments of Northern China. Asia-Pac. J. Atmos. Sci. 2021, 57, 451–466. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Arnault, J.; Laux, P.; Ma, N.; Wei, J.H.; Kunstmann, H. Diurnal cycle of surface energy fluxes in high mountain terrain: High-resolution fully coupled atmosphere-hydrology modelling and impact of lateral flow. Hydrol. Process. 2021, 35, e14454. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Niu, G.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M. The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116, D12. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Wei, S.; Dai, Y.; Duan, Q.; Liu, B.; Yuan, H. A global soil data set for earth system modeling. J. Adv. Model. Earth Syst. 2014, 6, 249–263. [Google Scholar]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, K.; Kim, Y. Improving streamflow prediction in the WRF-Hydro model with LSTM networks. J. Hydrol. 2022, 605, 127297. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, W01413. [Google Scholar] [CrossRef] [Green Version]
- Sofokleous, I.; Bruggeman, A.; Camera, C.; Eliades, M. Grid-based calibration of the WRF-Hydro with Noah-MP model with improved groundwater and transpiration process equations. J. Hydrol. 2023, 617, 128991. [Google Scholar] [CrossRef]
- Sakaguchi, K.; Zeng, X. Effects of soil wetness, plant litter, and under-canopy atmospheric stability on ground evaporation in the Community Land Model (CLM3.5). J. Geophys. Res. Atmos. 2009, 114, D1. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.; Gitau, M.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Camera, C.; Bruggeman, A.; Zittis, G.; Sofokleous, I.; Arnault, J. Simulation of extreme rainfall and streamflow events in small Mediterranean watersheds with a one-way-coupled atmospheric–hydrologic modelling system. Nat. Hazards Earth Syst. Sci. 2020, 20, 2791–2810. [Google Scholar] [CrossRef]




| Name | Description | Units | Default Value | Calibration Factor |
|---|---|---|---|---|
| bexp | Pore size distribution index | ×1 | multiple | |
| expon | Bucket drainage parameter | 3 | ||
| dksat | Saturated hydraulic conductivity | m/s | ×1 | multiple |
| smcmax | Saturation soil moisture content | fraction | ×1 | multiple |
| REFKDT | Surface runoff parameter | 3 | ||
| slope | Openness of bottom drainage boundary | 0.1 | ||
| RETDEPRTFAC | Multiplier on retention depth limit | 1 | ||
| LKSATFAC | Multiplier on lateral hydraulic conductivity | 1000 | ||
| OVROUGHRTAC | Multiplier on Manning’s roughness | 1 | ||
| mann | Channel Manning roughness | ×1 | multiple | |
| Zmax | Maximum groundwater bucket depth | mm | 50 | |
| mfsno | Melt factor for snow depletion curve | 2.5 |
| Physical Parameterizations | Option | Description |
|---|---|---|
| Runoff options (run) | ||
| 1 | TOPMODEL with groundwater | |
| 2 | TOPMODEL with an equilibrium water table | |
| 3 | original surface and subsurface runoff | |
| 4 | BATS surface and subsurface runoff | |
| Partitioning precipitation into rainfall and snowfall options (pcp) | ||
| 1 | Jordan | |
| 2 | BATS: when SFCTMP < TFRZ + 2.2 | |
| 3 | SFCTMP < TFRZ | |
| Glacier options (gla) | ||
| 1 | include phase change of ice | |
| 2 | ice treatment more like original Noah | |
| Surface resistance option (res) | ||
| 1 | Sakaguchi and Zeng [40] | |
| 2 | Sellers | |
| 3 | Adjusted Sellers to decrease RSURF for wet soil | |
| 4 | Option 1 for non-snow; rsurf = rsurf_snow for snow |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, E.; Liu, X.; Li, J.; Tao, H. Calibration and Evaluation of the WRF-Hydro Model in Simulating the Streamflow over the Arid Regions of Northwest China: A Case Study in Kaidu River Basin. Sustainability 2023, 15, 6175. https://doi.org/10.3390/su15076175
Yu E, Liu X, Li J, Tao H. Calibration and Evaluation of the WRF-Hydro Model in Simulating the Streamflow over the Arid Regions of Northwest China: A Case Study in Kaidu River Basin. Sustainability. 2023; 15(7):6175. https://doi.org/10.3390/su15076175
Chicago/Turabian StyleYu, Entao, Xiaoyan Liu, Jiawei Li, and Hui Tao. 2023. "Calibration and Evaluation of the WRF-Hydro Model in Simulating the Streamflow over the Arid Regions of Northwest China: A Case Study in Kaidu River Basin" Sustainability 15, no. 7: 6175. https://doi.org/10.3390/su15076175
APA StyleYu, E., Liu, X., Li, J., & Tao, H. (2023). Calibration and Evaluation of the WRF-Hydro Model in Simulating the Streamflow over the Arid Regions of Northwest China: A Case Study in Kaidu River Basin. Sustainability, 15(7), 6175. https://doi.org/10.3390/su15076175







