Corrosion Inhibitor Distribution and Injection Cycle Prediction in a High Water-Cut Oil Well: A Numerical Simulation Study
Abstract
:1. Introduction
2. Numerical Models
2.1. Multiphase Flow Model
2.2. Turbulence Modeling
2.3. Numerical Methodology
2.3.1. Computational Geometry
2.3.2. Solution Setup
2.3.3. Grid Independence Verification
3. Results and Discussion
3.1. Effect of Calculation Time
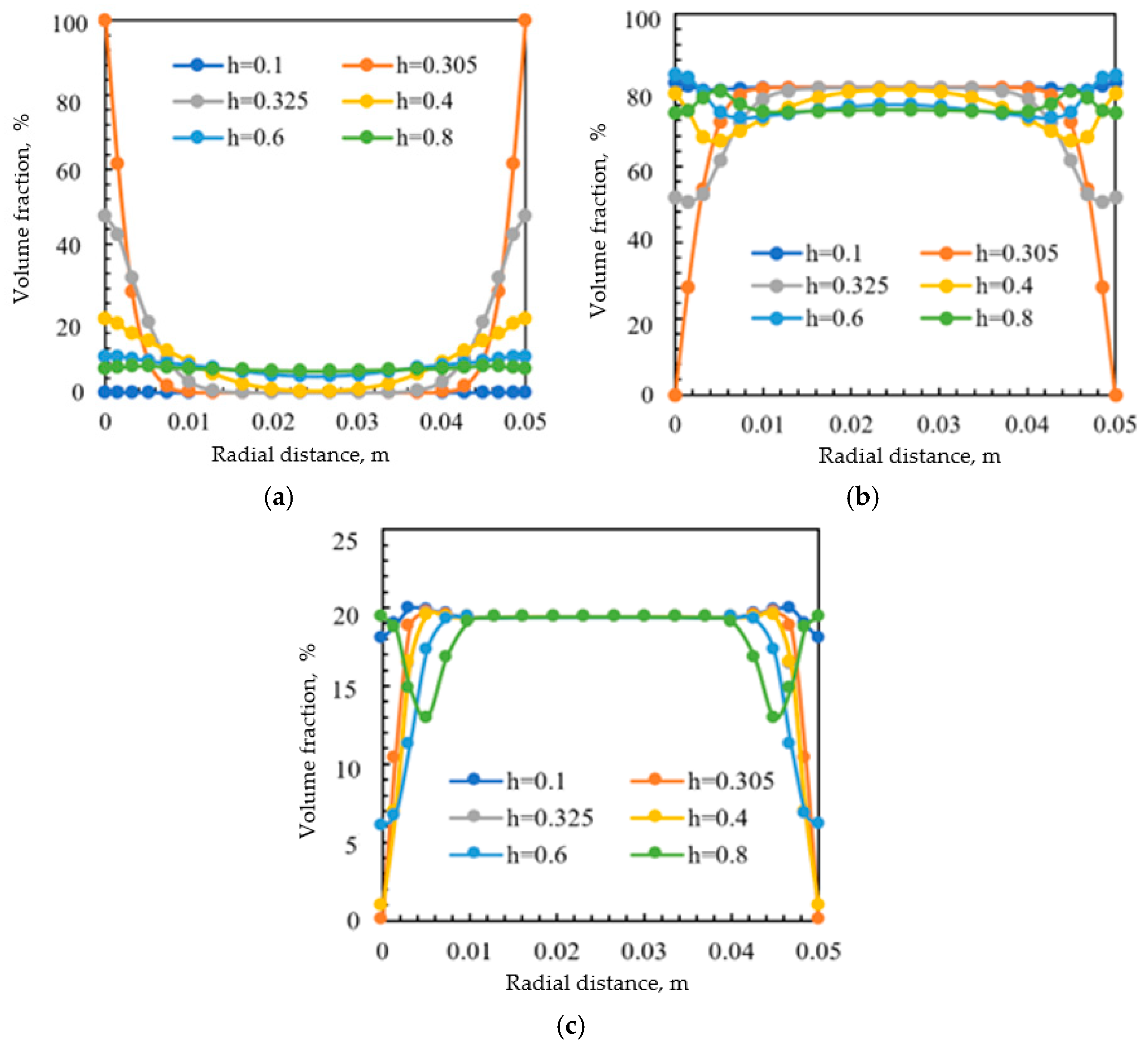
3.2. Effect of Tubing Height
3.3. Effect of Injection Rate of Corrosion Inhibitor
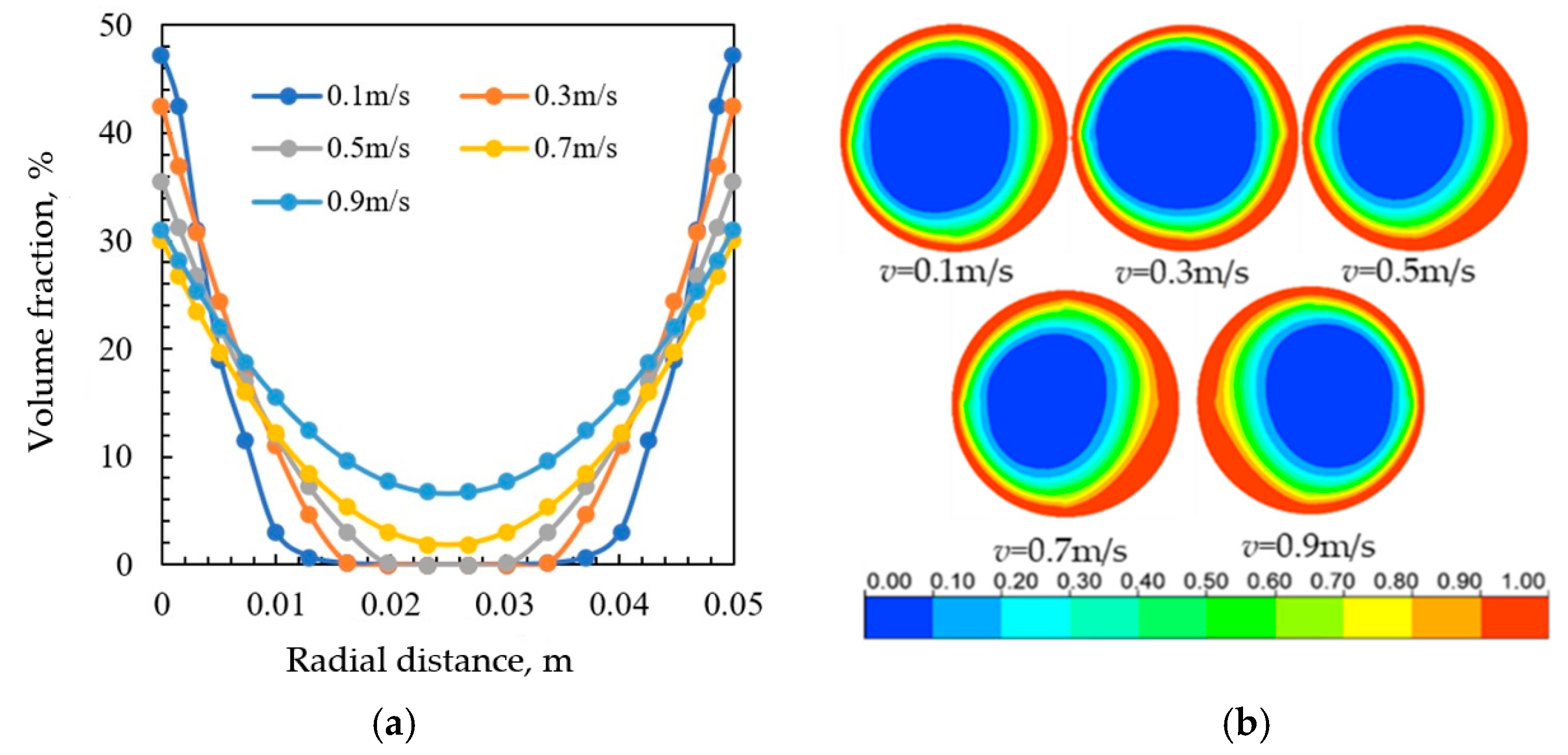
3.4. Effect of Produced Fluid Velocity
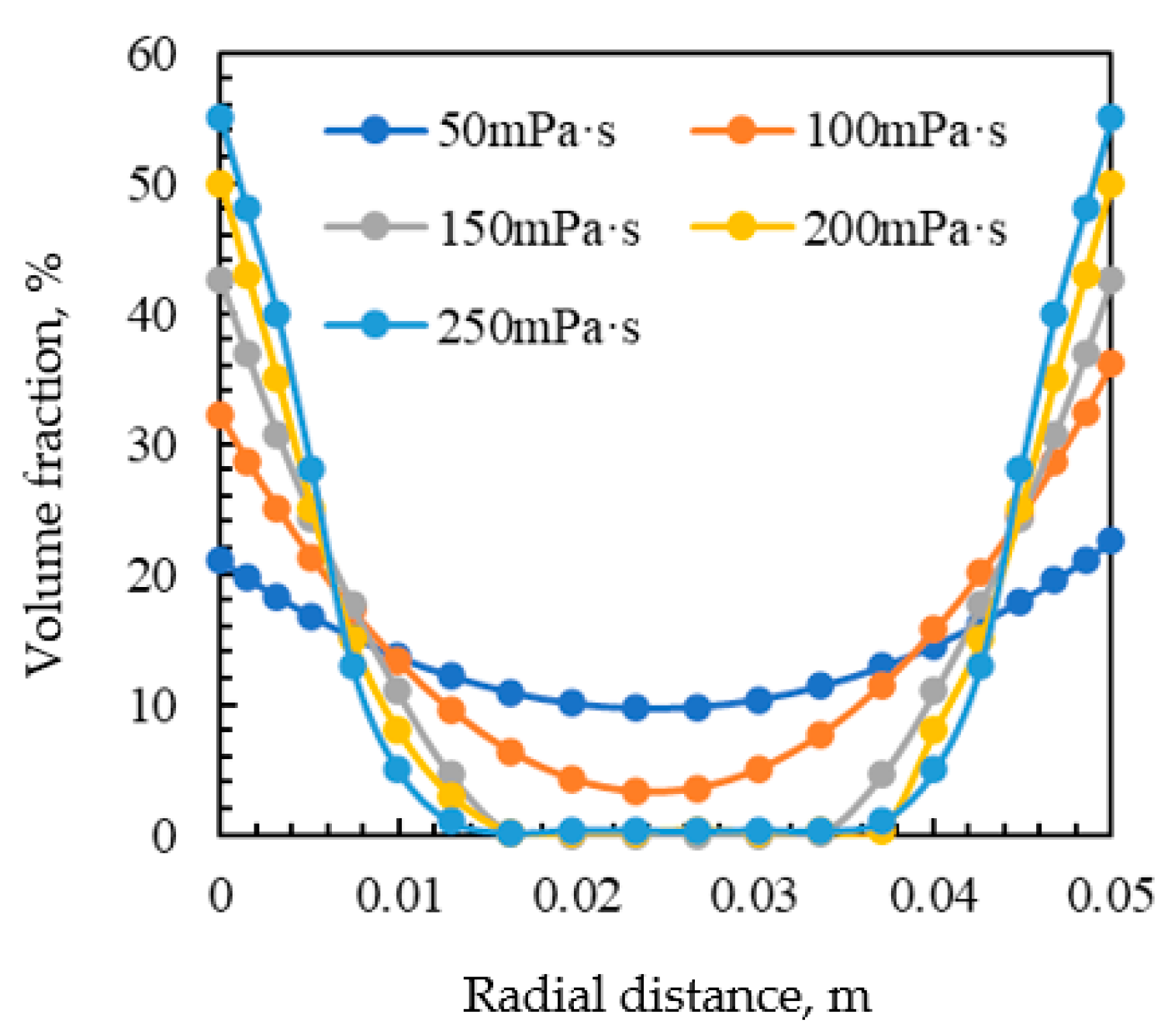
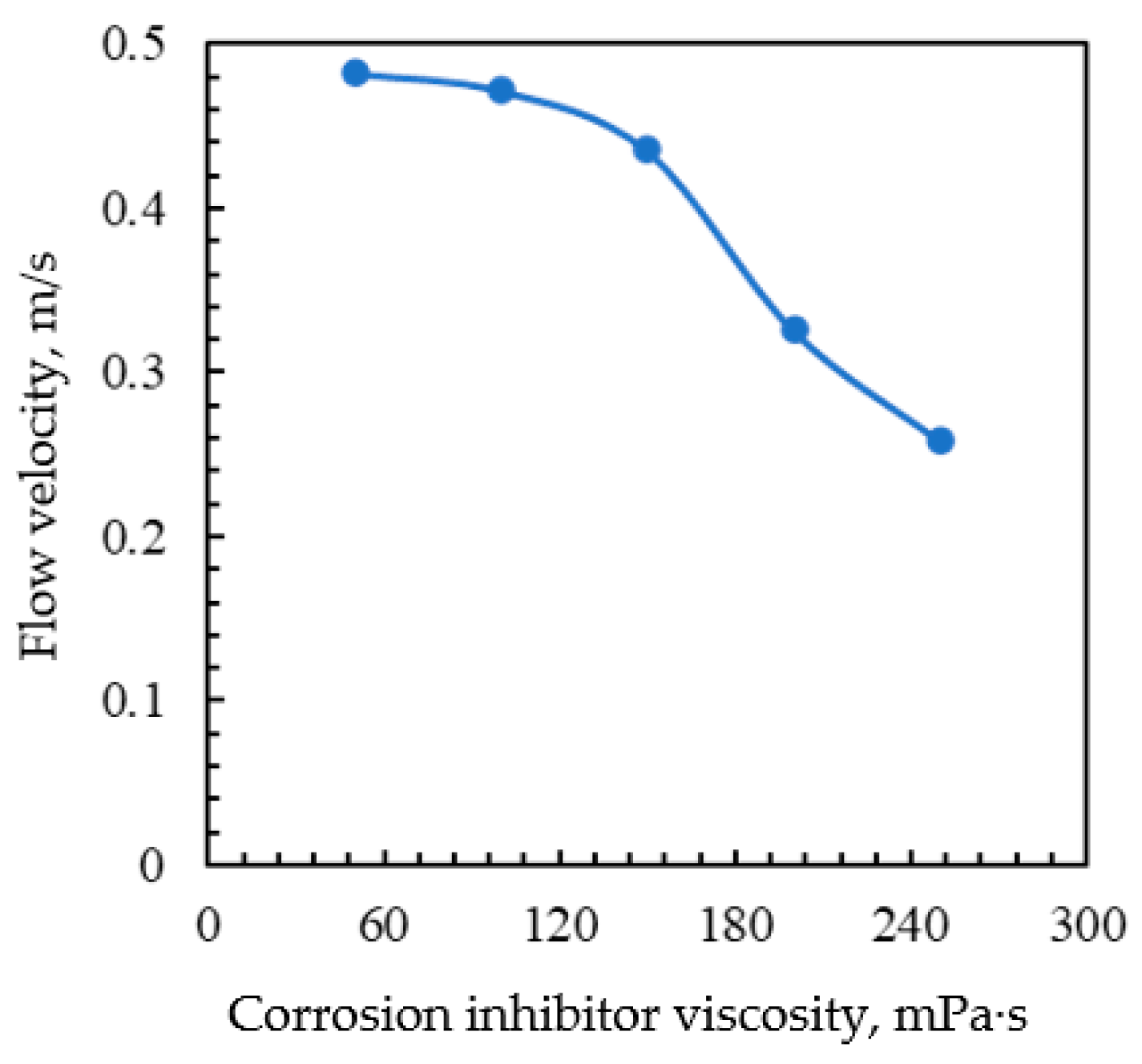
3.5. Effect of Corrosion Inhibitor Viscosity
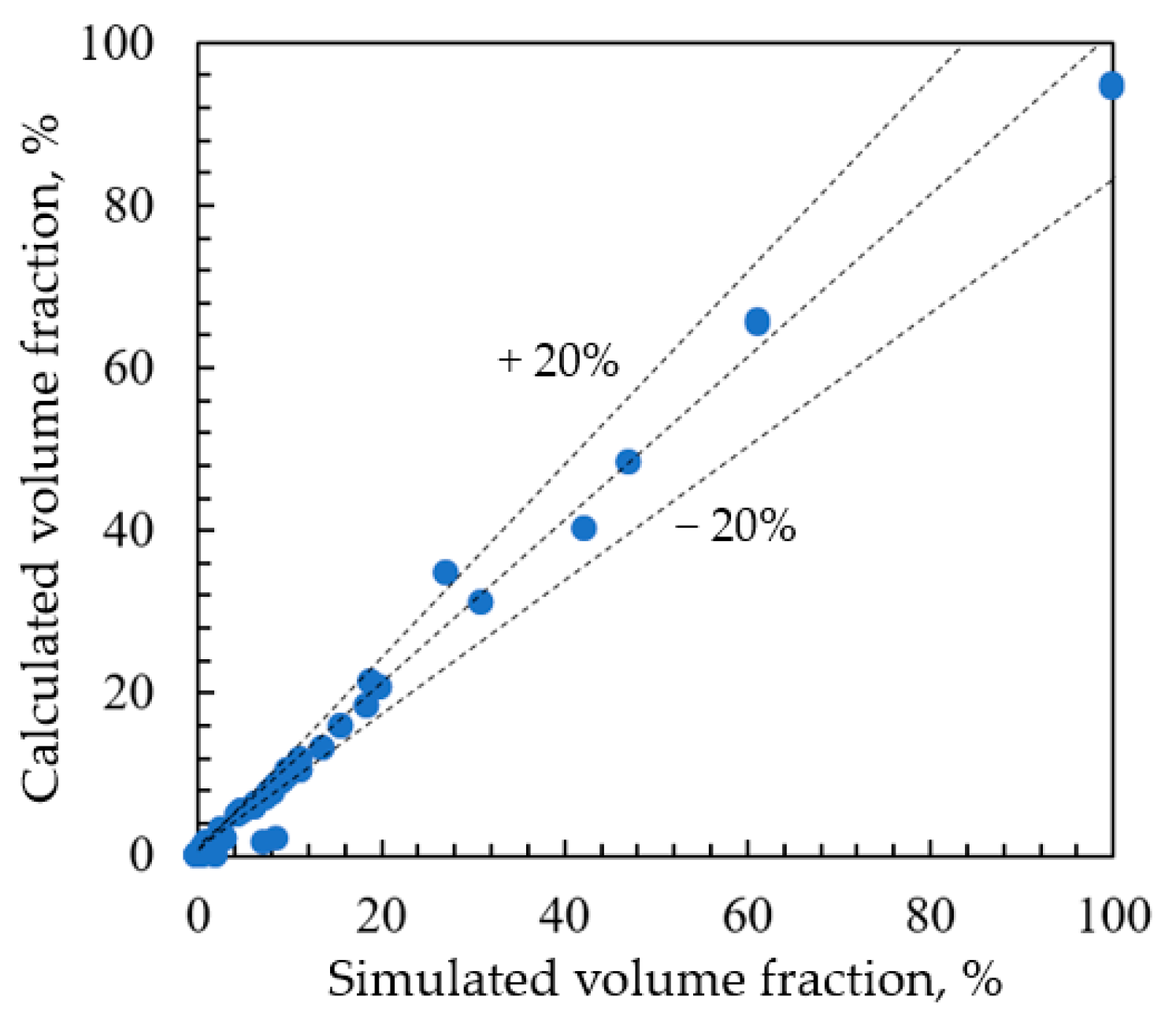
3.6. Injection Cycle of Corrosion Inhibitor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, D.; Dong, B.; Zeng, F.; Yu, Z.; Tao, Y. Analysis of corrosion failure and materials selection for CO2-H2S gas well. J. Nat. Gas Sci. Eng. 2020, 86, 103734. [Google Scholar] [CrossRef]
- Wang, R.; Luo, S. Grooving corrosion of electric-resistance-welded oil well casing of J55 steel. Corros. Sci. 2013, 68, 119–127. [Google Scholar] [CrossRef]
- Abdel Ghany, N.A.; Shehata, M.F.; Saleh, R.M.; El Hosary, A.A. Novel corrosion inhibitor for acidizing oil wells. Mater. Corros. 2016, 68, 355–360. [Google Scholar] [CrossRef]
- Huang, L.; Li, H.; Wu, Y. Comprehensive evaluation of corrosion inhibition performance and ecotoxicological effect of cinchona IIa as a green corrosion inhibitor for pickling of Q235 steel. J. Environ. Manag. 2023, 335, 117531. [Google Scholar] [CrossRef]
- Medupin, R.O.; Ukoba, K.O.; Yoro, K.O.; Jen, T.C. Sustainable approach for corrosion control in mild steel using plant-based inhibitors: A review. Mater. Today Sustain. 2023, 22, 100373. [Google Scholar] [CrossRef]
- Pan, C.; Chen, N.; He, J.; Liu, S.; Xu, P. Effects of corrosion inhibitor and functional components on the electrochemical and mechanical properties of concrete subject to chloride environment. Corros. Sci. 2020, 260, 119–124. [Google Scholar] [CrossRef]
- Shamsa, A.; Barker, R.; Hua, Y.; Barmatov, E.; Hughes, T.; Neville, A. Impact of corrosion products on performance of imidazoline corrosion inhibitor on X65 carbon steel in CO2 environments. Corros. Sci. 2021, 85, 109423. [Google Scholar] [CrossRef]
- Choi, H.; Song, Y.K.; Kim, K.Y.; Park, J.M. Encapsulation of triethanolamine as organic corrosion inhibitor into nanoparticles and its active corrosion protection for steel sheets. Surf. Coat. Technol. 2012, 206, 2354–2362. [Google Scholar] [CrossRef]
- Javidi, M.; Chamanfar, R.; Bekhrad, S. Investigation on the efficiency of corrosion inhibitor in CO2 corrosion of carbon steel in the presence of iron carbonate scale. J. Nat. Gas Sci. Eng. 2019, 61, 1970205. [Google Scholar] [CrossRef]
- Negm, N.A.; Tawfik, S.M.; Badr, E.A.; Abdou, M.I.; Ghuiba, F.M. Evaluation of some nonionic surfactants derived from vanillin as corrosion inhibitors for carbon steel during drilling processes. J. Surfactants Deterg. 2015, 18, 413–420. [Google Scholar] [CrossRef]
- Bacca, K.R.G.; Lopes, N.F.; Marcolino, J.B.; Grasel, F.D.S.; Costa, E.M. Performance of Quebracho extract as eco-friendly corrosion inhibitor for SAE 1010 steel in the oil field environment. Mater. Corros. 2020, 71, 155–165. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, X.; Wang, J. Numerical simulation of corrosion inhibitor behavior. J. Drain. Irrig. Mach. Eng. 2017, 35, 50–55. [Google Scholar]
- Rojas-Figueroa, A.; Fairuzov, Y.V. Numerical simulation of corrosion inhibitor transport in pipelines carrying oil-water mixtures. J. Energy Resour. Technol. 2002, 124, 239–245. [Google Scholar] [CrossRef]
- Quentin, L.; Lamarque, N.; Hélie, J.; Legendre, D. On the spreading of high-pressure spray-generated liquid wall films. Int. J. Multiphas. Flow 2021, 139, 103619. [Google Scholar]
- Liu, E.; Li, D.; Zhao, W.; Peng, S.; Chen, Q. Correlation analysis of pipeline corrosion and liquid accumulation in gas gathering station based on computational fluid dynamics. J. Nat. Gas Sci. Eng. 2022, 102, 104564. [Google Scholar] [CrossRef]
- Liu, E.; Tang, H.; Zhang, Y.; Li, D.; Kou, B.; Liu, N.; Azimi, M. Experiment and numerical simulation of distribution law of water-based corrosion inhibitor in natural gas gathering and transportation pipeline. Petrol. Sci. 2023, in press. [Google Scholar] [CrossRef]
- Jing, J.; Xiao, F.; Yang, L.; Wang, S.; Sun, J. Experimental and simulation study of atomization concentration of corrosion inhibitor in a gas pipe. J. Nat. Gas Sci. Eng. 2018, 49, 8–18. [Google Scholar] [CrossRef]
- Farokhipour, A.; Mansoori, Z.; Saffar-Avval, M.; Ahmadi, G. 3D computational modeling of sand erosion in gas-liquid-particle multiphase annular flows in bends. Wear 2020, 450, 203241. [Google Scholar] [CrossRef]
- Farhadian, A.; Rahimi, A.; Safaei, N.; Shaabani, A.; Alavi, A. A theoretical and experimental study of castor oil-based inhibitor for corrosion inhibition of mild steel in acidic medium at elevated temperatures. Corros. Sci. 2020, 175, 108–113. [Google Scholar] [CrossRef]
- Khan, F.; Sudhakara, S.M.; Puttaigowda, Y.M.; Pushpanjali. Amide substituted zinc centered macrocyclic phthalocyanines for corrosion inhibition of mild steel in hydrochloric acid medium. Surf. Eng. Appl. Electrochem. 2022, 58, 613–624. [Google Scholar] [CrossRef]
- Tarek, G.; Meftah, H.; Shiferaw, R. Experimental investigation of gas–oil–water phase flow in vertical pipes: Influence of gas injection on the total pressure gradient. J. Petrol. Explor. Prod. Technol. 2019, 9, 3071–3078. [Google Scholar]
- Strazza, D.; Grassi, B.; Demori, M.; Ferrari, V.; Poesio, P. Core-annular flow in horizontal and slightly inclined pipes: Existence, pressure drops, and hold-up. Chem. Eng. Sci. 2011, 66, 2853–2863. [Google Scholar] [CrossRef]
- Kouris, C.; Tsamopoulos, J. Concentric core-annular flow in a circular tube of slowly varying cross-section. Chem. Eng. Sci. 2000, 55, 9–30. [Google Scholar] [CrossRef]
- Strazza, D.; Poesio, P. Experimental study on the restart of core-annular flow. Chem. Eng. Res. Des. 2012, 90, 1711–1718. [Google Scholar] [CrossRef]
- Chen, K.P.; Bai, R.; Joseph, D.D. Lubricated pipelining. Part 3. Stability of core annular flow in vertical pipes. J. Fluid Mech. 1990, 214, 251–286. [Google Scholar] [CrossRef]
- Kishan, P.A.; Dash, S.K. Numerical and experimental study of circulation flow rate in a closed circuit due to gas jet impingement. Int. J. Numeri. Method. Heat Fluid Flow. 2006, 16, 890–909. [Google Scholar] [CrossRef]
- Anglart, H.; Nylund, O.; Kurul, N.; Podowski, M.Z. CFD prediction of flow and phase distribution in fuel assemblies with spacers. Nucl. Eng. Des. 1997, 177, 215–228. [Google Scholar] [CrossRef]
- Abubakar, A.; Al, W.Y.; Al, W.T.; Al, H.A.R.; Al, A.A.; Eshrati, M. Effect of pipe diameter on horizontal oil-water flow before and after addition of drag-reducing polymer part I: Flow patterns and pressure gradients. J. Petrol. Sci. Eng. 2017, 153, 12–22. [Google Scholar] [CrossRef]
- Joseph, D.D.; Renardy, M.; Renardy, Y. Instability of the flow of two immiscible liquids with different viscosities in a pipe. J. Fluid Mech. 1984, 141, 309–317. [Google Scholar] [CrossRef] [Green Version]
- Blyth, M.G.; Lug, H.; Pozrikidis, C. Stability of axisymmetric core-annular flow in the presence of an insoluble surfactant. J. Fluid Mech. 2006, 548, 207–235. [Google Scholar] [CrossRef] [Green Version]
- Askari, M.; Aliofkhazraei, M.; Jafari, R.; Hamghalam, P.; Hajizadeh, A. Downhole corrosion inhibitors for oil and gas production—A review. Appl. Surf. Sci. Adv. 2021, 6, 100128. [Google Scholar] [CrossRef]
- Ghosh, S.; Mandal, T.K.; Das, G.; Das, P.K. Review of oil water core annular. Renew. Sust. Energ. Rev. 2009, 13, 1957–1965. [Google Scholar] [CrossRef]
- Al-Aufi, Y.A.; Hewakandamby, B.N. Thin film thickness measurements in two phase annular flows using ultrasonic pulse echo techniques. Flow Meas. Instrum. 2019, 66, 67–78. [Google Scholar] [CrossRef]
- Ooms, G.; Segal, A. A theoretical model for core-annular flow of a very viscous oil core and a water annulus through a horizontal pipe. Int. J. Multiphas. Flow 1983, 10, 41–60. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, W. Molecular simulation study on adsorption and diffusion behaviors of CO2/N2 in lignite. ACS Omega 2020, 5, 29416–29426. [Google Scholar] [CrossRef]
- Zhong, Q.; Jin, M. Zein nanoparticles produced by liquid–liquid dispersion. Food Hydrocolloid. 2009, 23, 2380–2387. [Google Scholar] [CrossRef]
- Jing, J.; Sun, J.; Huang, H.; Zhang, M.; Wang, C.; Xue, X.; Ullmann, A.; Brauner, N. Facilitating the transportation of highly viscous oil by aqueous foam injection. Fuel 2019, 251, 763–778. [Google Scholar] [CrossRef]
- Zhuo, K.; Qiu, Y.; Zhang, Y.; Du, W. Numerical simulation of the distribution of corrosion inhibitors. Petrochem. Technol. 2020, 49, 576–581. [Google Scholar]
- Jovancicevic, V.; Ramachandran, S.; Prince, P. Inhibition of CO2 corrosion of mild steel by imidazolines and their precursors. Corrosion 1999, 55, 449–455. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, F.; Wu, Y.; Dong, Z. Optimization of injection technique of corrosion inhibitor in CO2-flooding oil recovery. J. Southwest Petrol. Univ. (Sci. Technol. Ed.) 2020, 42, 103–109. [Google Scholar]
- Frenier, W.W.; Wint, D.D. Multifaceted approaches for controlling top-of-the-line corrosion in pipelines. Oil Gas Facil. 2014, 3, 65–80. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Du, M.; Yu, H.; Wang, N. Effect of molecular structure of imidazoline inhibitors on growth and decay laws of films formed on Q235 Steel. Acta Phys. Chim. Sin. 2009, 25, 525–531. [Google Scholar]

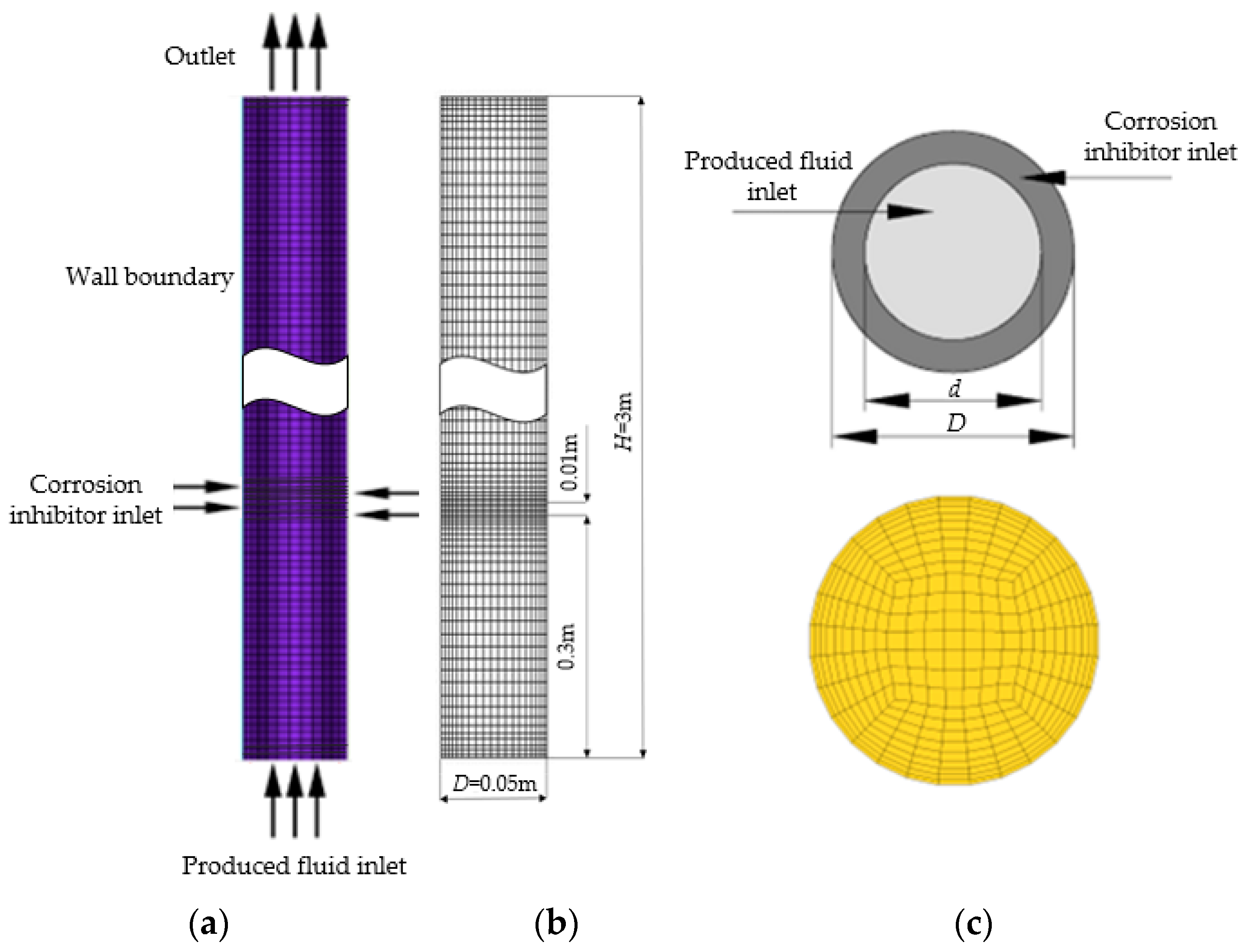




| Well | pH | Density at 20 °C/(g/cm3) | Salinity/(mg/L) | Water-Cut/% | Water Type |
|---|---|---|---|---|---|
| X210 | 8.55 | 1.018 | 25,171 | 96 | CaCl2 |
| X216-2 | 7.53 | 1.019 | 24,015 | 94 | NaHCO3 |
| X275-1 | 7.01 | 1.021 | 27,814 | 94 | CaCl2 |
| H132 | 8.53 | 1.019 | 26,545 | 98 | CaCl2 |
| H131-5 | 8.63 | 1.019 | 26,796 | 93 | CaCl2 |
| X124 | 8.50 | 1.018 | 27,029 | 85 | CaCl2 |
| W214-5 | 7.71 | 1.021 | 25,764 | 81 | CaCl2 |
| W231 | 8.53 | 1.019 | 9205 | 81 | NaHCO3 |
| Density/(g/cm3) | Freezing Point/(°C) | pH | Dosage/(ppm) | Corrosion Rate/(mm/a) | Injection Method |
|---|---|---|---|---|---|
| 20 | −15 | 6–8 | 200 | 0.043 | Continuous injection |
| Simulation Condition | Inlet 1 (Produced Fluid) | Inlet 2 (Corrosion Inhibitor) | |
|---|---|---|---|
| Water | Oil | Polymer Solution | |
| Volume fraction, % | 80 | 20 | 100 |
| Velocity, m/s | 0.05–1.5 | 0.05–1.5 | 0.1–0.9 |
| Volume fraction of corrosion inhibitor, % | 0 | 0 | 100 |
| Viscosity, mPa·s | / | / | 50–250 |
| No. | Elements | Inlet Pressure, MPa | Outlet Flow Velocity, m/s |
|---|---|---|---|
| 1 | 91,000 | 15.37 | 0.84 |
| 2 | 131,096 | 15.93 | 0.76 |
| 3 | 223,215 | 16.07 | 0.73 |
| 4 | 396,354 | 16.03 | 0.77 |
| Tubing Height, m | Fitted Correlations of the Volume Fraction | R2 | Variance | Standard Deviation |
|---|---|---|---|---|
| 0.305 | 0.95 | 0.003295 | 0.0574 | |
| 0.325 | 0.98 | 8.1 × 10−7 | 0.0009 | |
| 0.4 | 0.94 | 0.001867 | 0.04321 | |
| 0.6 | 0.97 | 7.73 × 10−6 | 0.00278 | |
| 0.8 | 0.97 | 7.24 × 10−6 | 0.00269 |
| Parameter | Fitted Parameters | Variance | Standard Deviation | T-Value | t-Test | Independent Distribution | |
|---|---|---|---|---|---|---|---|
| a | t | 30.1262 | 31.48 | 5.61111 | 5.36903 | 0.11723 | 0.99931 |
| m | 0.29645 | 1.0 × 10−6 | 0.001 | 296.2949 | 0.00215 | 0.99822 | |
| n | −1.02911 | 0.004 | 0.06352 | −16.2003 | 0.03925 | 0.99973 | |
| b | t | 1.50629 | 0.0786 | 0.28038 | 5.37228 | 0.11716 | 0.99931 |
| m | 0.29645 | 1.0 × 10−6 | 0.001 | 296.3502 | 0.00215 | 0.99822 | |
| n | −1.02914 | 0.004 | 0.06349 | −16.2093 | 0.03923 | 0.99973 | |
| c | t | 0.0447 | 5.336 × 10−6 | 0.00231 | 19.34401 | 0.03288 | 0.99467 |
| m | 0.29281 | 5.388 × 10−7 | 7.34 × 10−4 | 399.1817 | 0.00159 | 0.98953 | |
| n | −0.69195 | 0.000414 | 0.02034 | −34.0122 | 0.01871 | 0.998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Jing, J.; Sun, J.; Zhang, F.; Huang, W.; Guo, Y. Corrosion Inhibitor Distribution and Injection Cycle Prediction in a High Water-Cut Oil Well: A Numerical Simulation Study. Sustainability 2023, 15, 6289. https://doi.org/10.3390/su15076289
Li W, Jing J, Sun J, Zhang F, Huang W, Guo Y. Corrosion Inhibitor Distribution and Injection Cycle Prediction in a High Water-Cut Oil Well: A Numerical Simulation Study. Sustainability. 2023; 15(7):6289. https://doi.org/10.3390/su15076289
Chicago/Turabian StyleLi, Wangdong, Jiaqiang Jing, Jie Sun, Feng Zhang, Wanni Huang, and Yuying Guo. 2023. "Corrosion Inhibitor Distribution and Injection Cycle Prediction in a High Water-Cut Oil Well: A Numerical Simulation Study" Sustainability 15, no. 7: 6289. https://doi.org/10.3390/su15076289
APA StyleLi, W., Jing, J., Sun, J., Zhang, F., Huang, W., & Guo, Y. (2023). Corrosion Inhibitor Distribution and Injection Cycle Prediction in a High Water-Cut Oil Well: A Numerical Simulation Study. Sustainability, 15(7), 6289. https://doi.org/10.3390/su15076289







