Analysis of Influencing Factors of Gangue Ball Milling Based on Multifractal Theory
Abstract
:1. Introduction
2. Materials and Methods
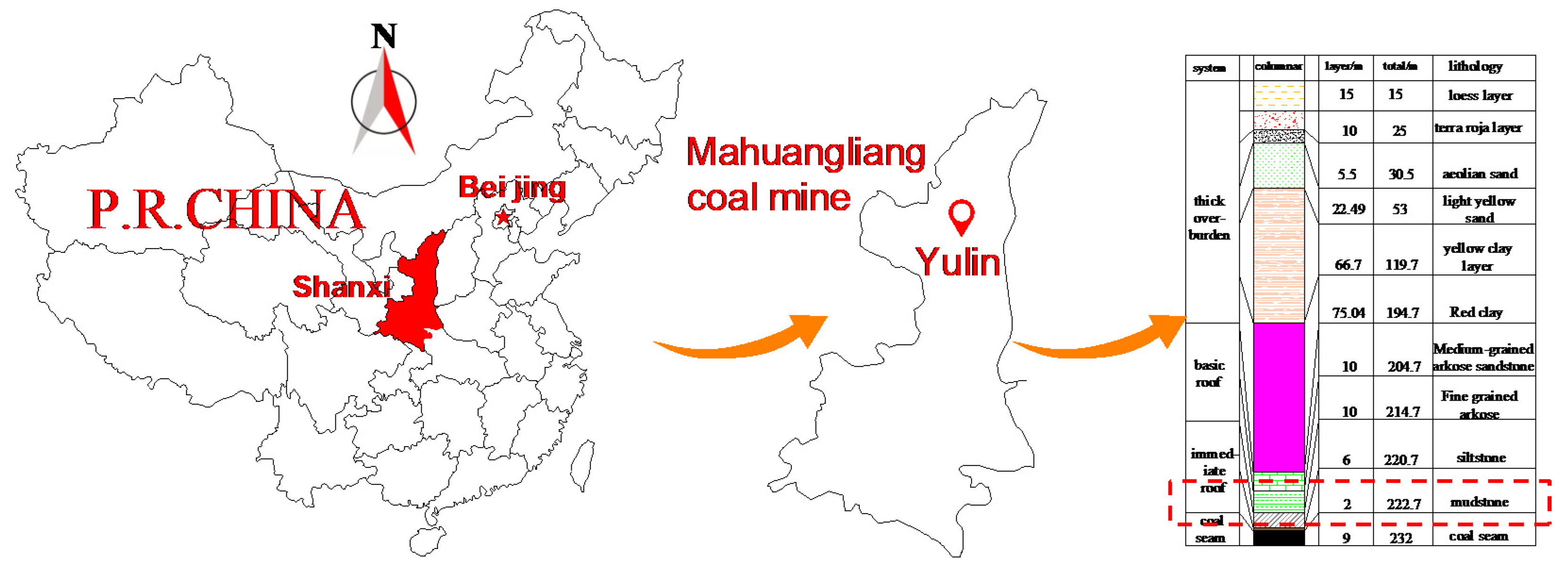
2.1. Preparation of Gangue Samples
2.2. Test Apparatus and Procedure
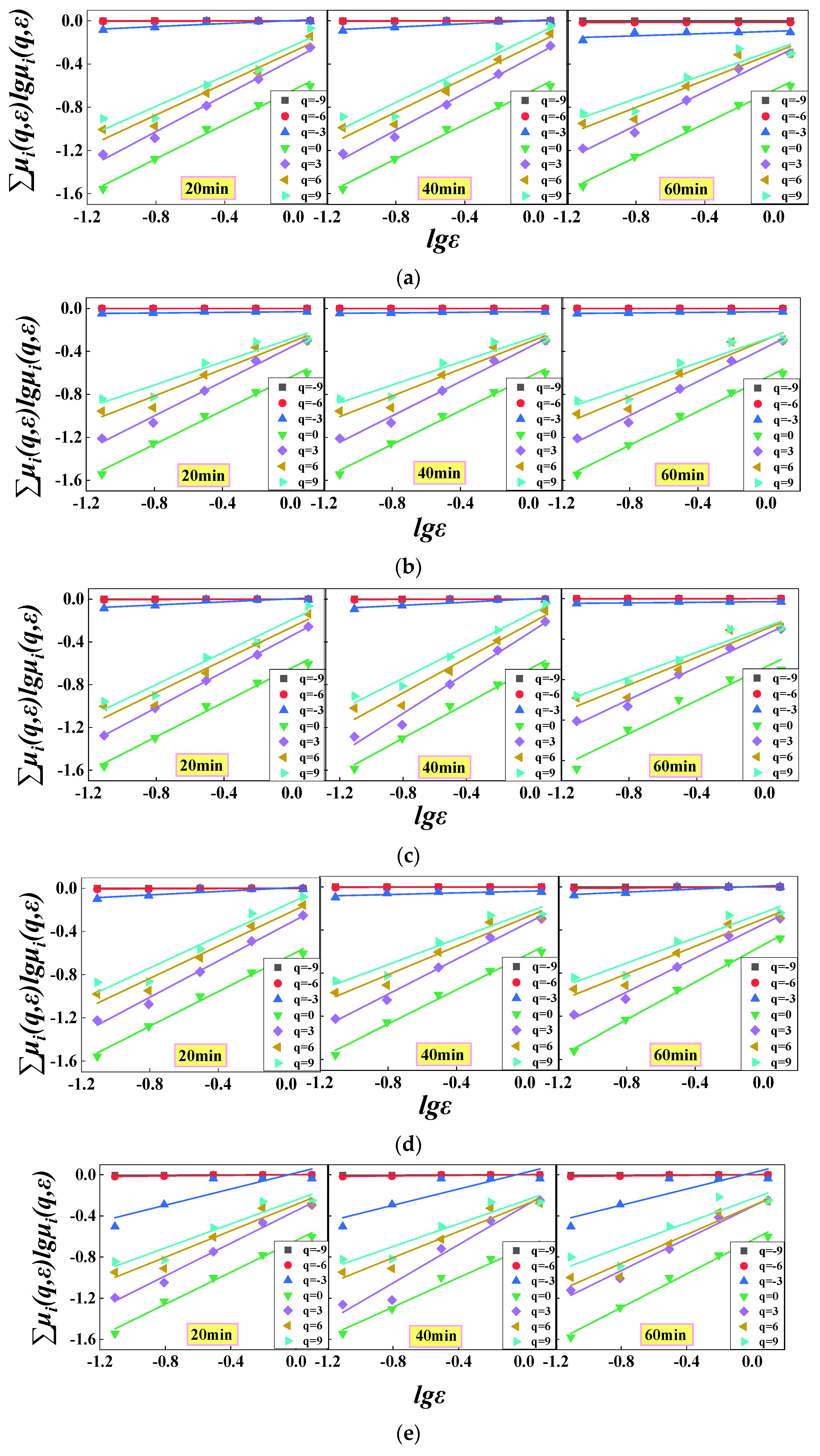
2.3. Multifractal Algorithm for PSD of Gangue Particles
3. Results and Discussion
3.1. PSD Characteristics of Gangue in Ball Milling Process
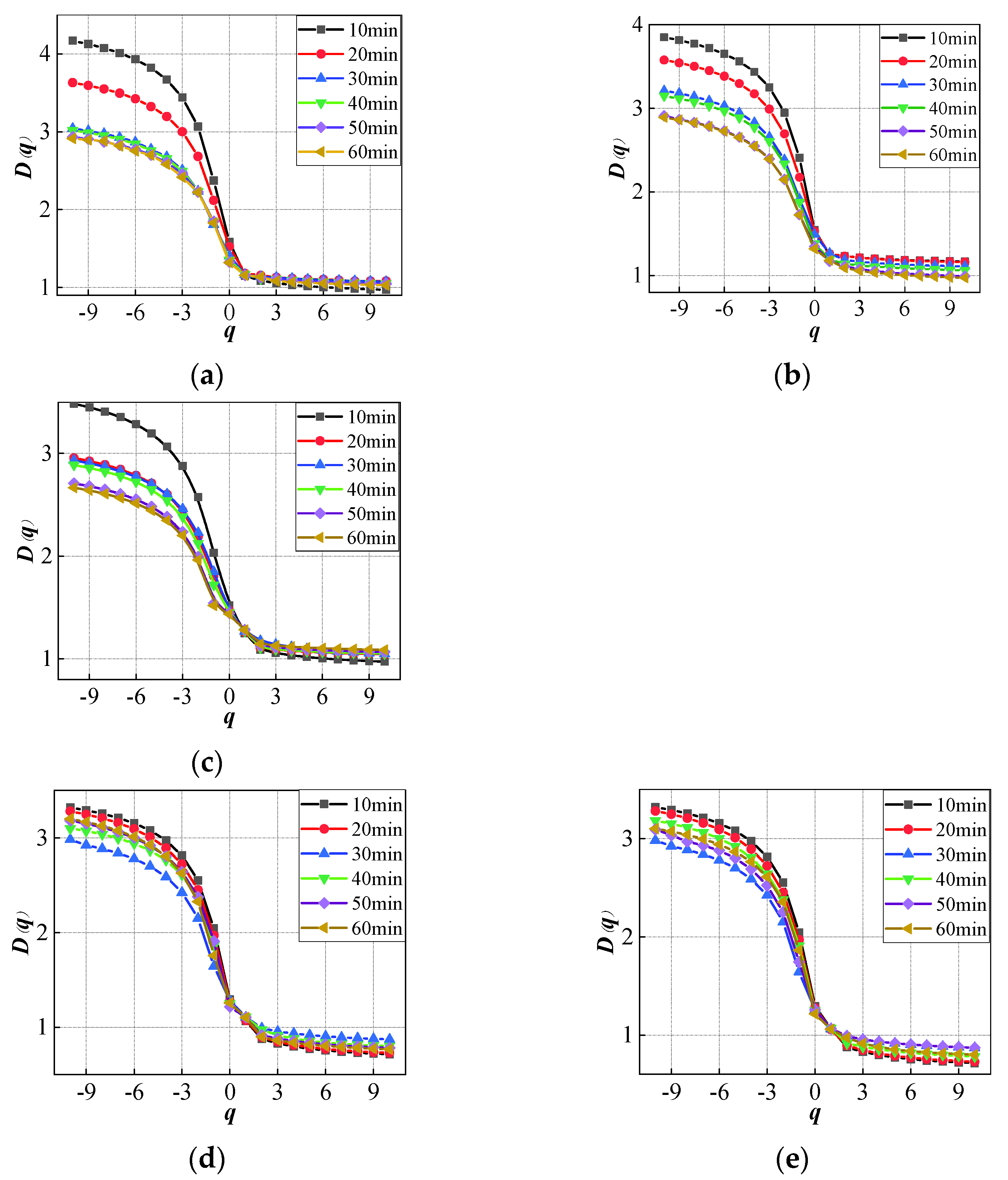
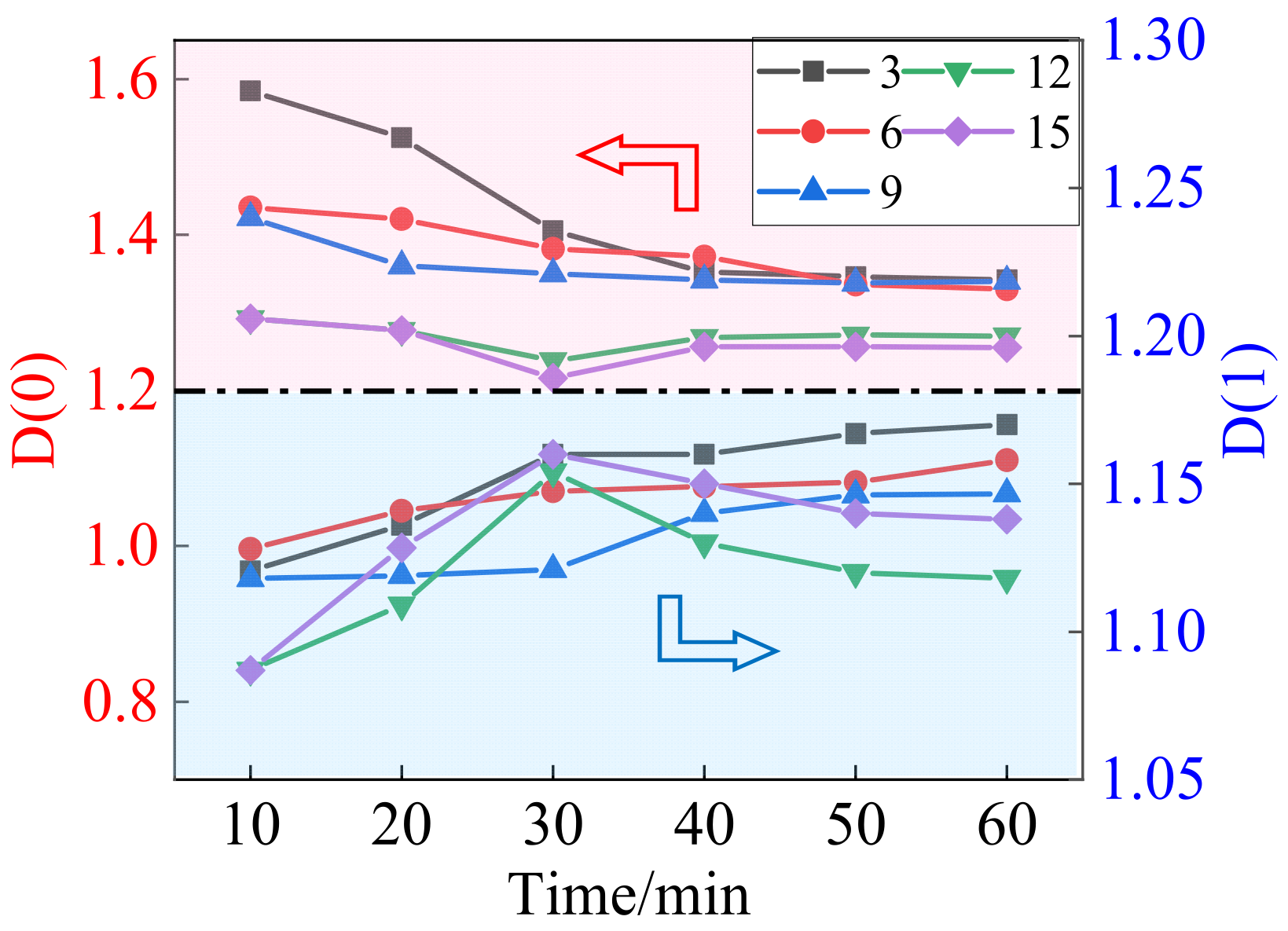
3.2. Multifractal Generalized Dimension Spectrum of Gangue PSD during Ball Milling
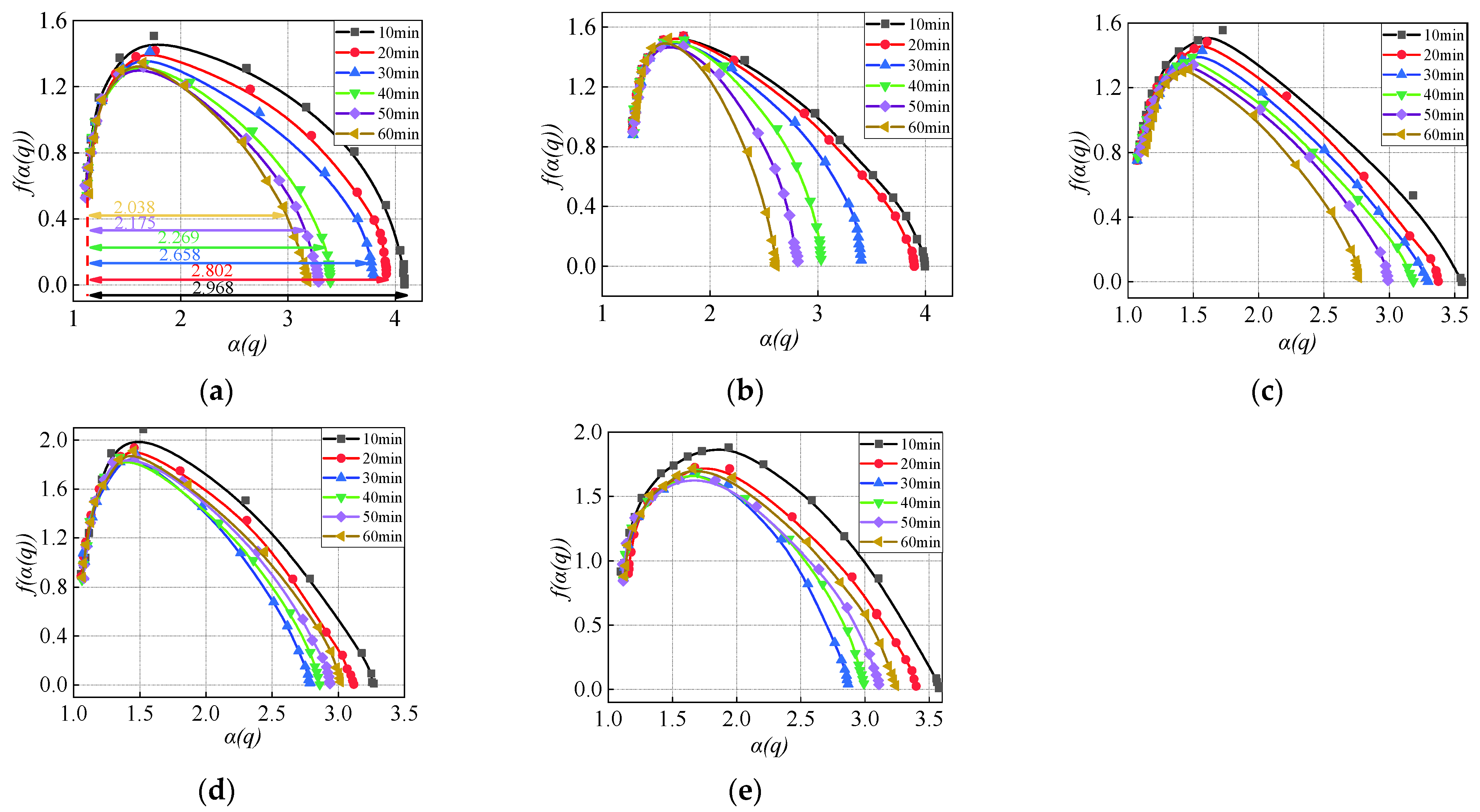
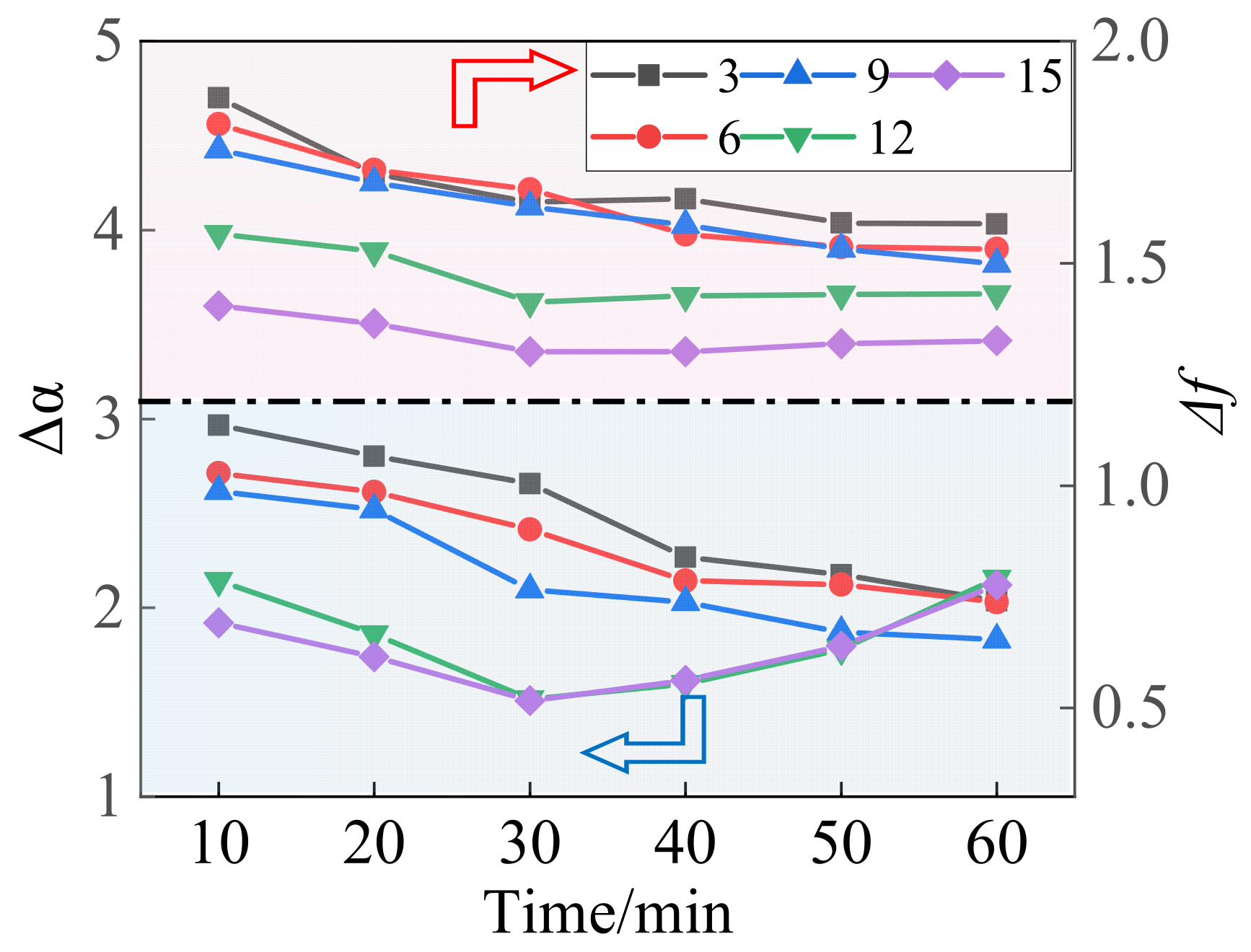
3.3. Multifractal Singular Spectrum of Gangue PSD during Ball Milling
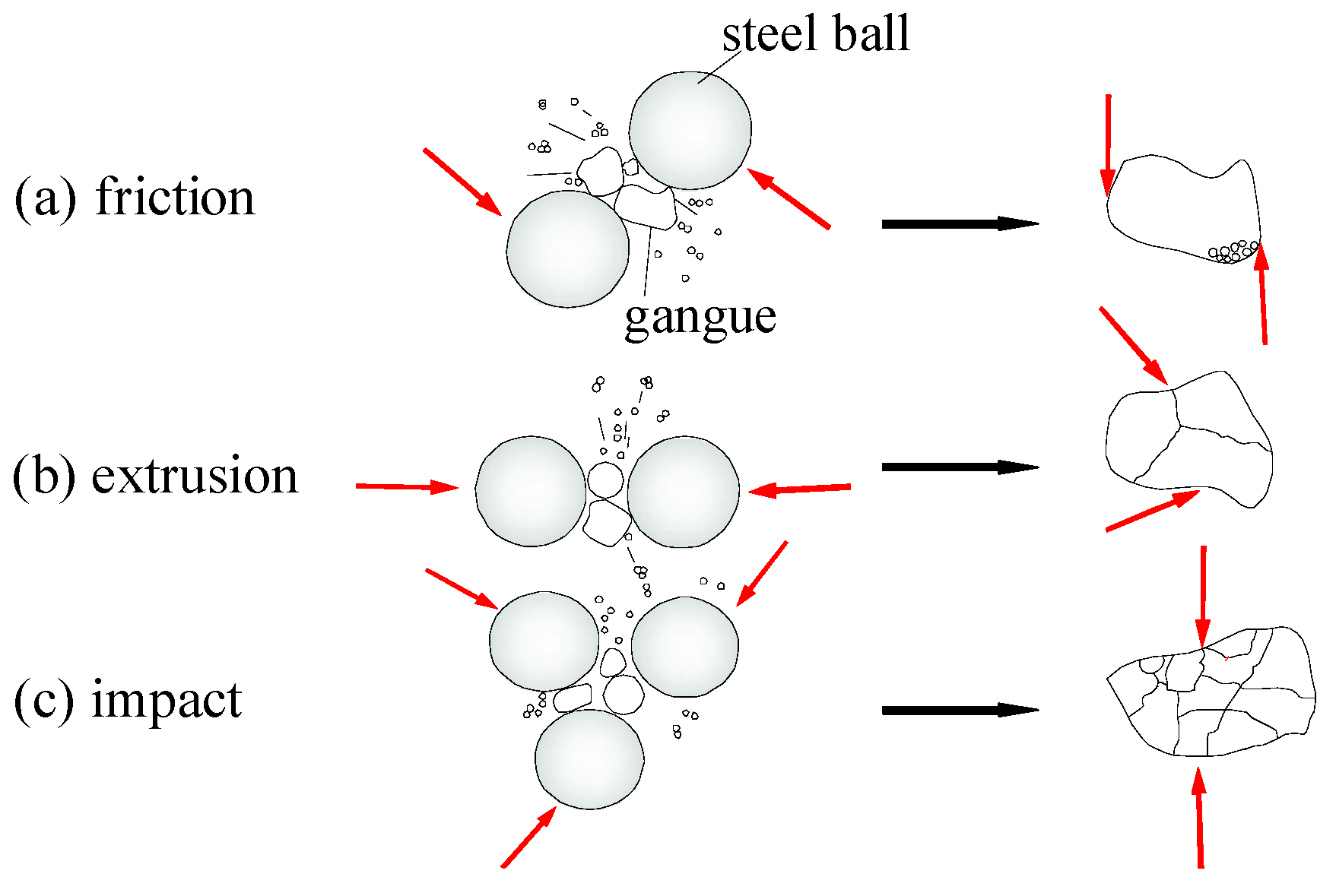
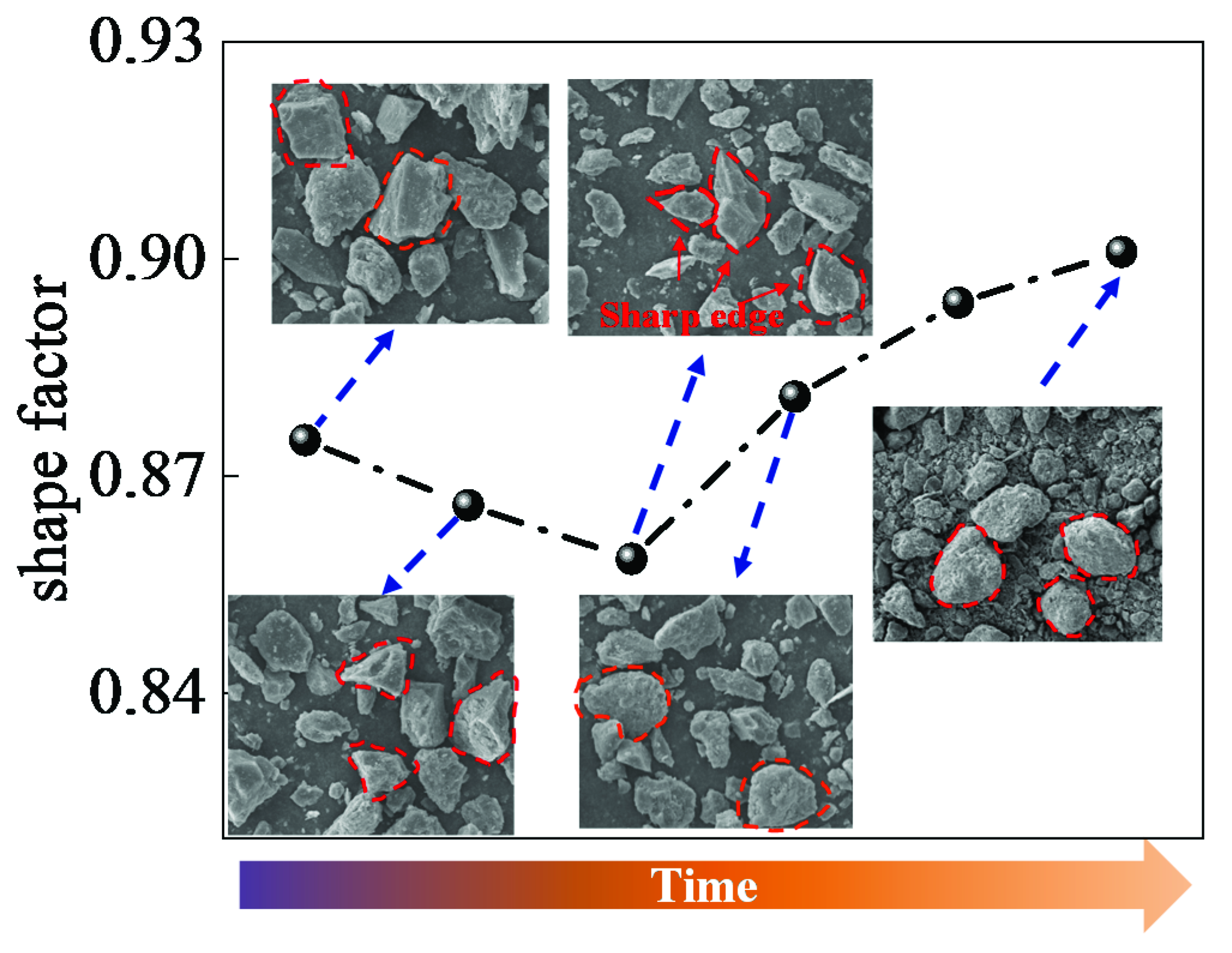
3.4. Correlation Analysis of Particle Morphology and Multifractal Parameters during Ball Milling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chen, Y.; Jiang, Y.; Wang, H. Assessment of ambient air quality in coal mine waste areas—A case study in Fuxin, China. N. Z. J. Agric. Res. 2007, 50, 1187–1194. [Google Scholar] [CrossRef]
- Li, J.; Wang, J. Comprehensive utilization and environmental risks of coal gangue: A review. J. Clean. Prod. 2019, 239, 117946. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, G.; Wu, S.; Lam, P.K.S. The environmental characteristics of usage of coal gangue in bricking-making: A case study at Huainan, China. Chemosphere 2014, 95, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ling, T.C. Reactivity activation of waste coal gangue and its impact on the properties of cement-based materials–a review. Constr. Build. Mater. 2020, 234, 117424. [Google Scholar] [CrossRef]
- Ashfaq, M.; Heeralal, M.; Moghal, A.A.B. Characterization studies on coal gangue for sustainable geotechnics. Innov. Infrastruct. Solut. 2020, 5, 1–12. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Zhang, J.; Zhang, C.; Chen, J.; Liu, C. Effect of particle size and thermal activation on the coal gangue based geopolymer. Mater. Chem. Phys. 2021, 267, 124657. [Google Scholar] [CrossRef]
- Guan, X.; Chen, J.; Zhu, M.; Gao, J. Performance of microwave-activated coal gangue powder as auxiliary cementitious material. J. Mater. Res. Technol. 2021, 14, 2799–2811. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Y.; Duan, X. Study on the factors affecting the deep reduction of coal gangue containing high contents of iron and sulfur. Fuel 2021, 288, 119571. [Google Scholar] [CrossRef]
- Hu, L.; Li, X. Damage and fragmentation of rock under experiencing impact load. J. Cent. South. Univ. Technol. 2006, 13, 432–437. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Zuo, Y.; Liang, H. Fractal characteristics of rock fragmentation at strain rate of 100–102s−1. J. Cent. South. Univ. Technol. 2006, 13, 290–294. [Google Scholar] [CrossRef]
- Feng, G.; Zhao, J.; Wang, H.; Li, Z.; Fang, Z.; Fan, W.; Yang, P.; Yang, X. Study of the internal re-breaking characteristics of broken limestone during compression. Powder Technol. 2022, 396, 449–455. [Google Scholar] [CrossRef]
- Yang, D.; Li, J.; Du, C.; Zheng, K.; Liu, S. Particle size distribution of coal and gangue after impact-crush separation. J. Cent. South. Univ. 2017, 24, 1252–1262. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.D.; Panagouli, O.K.; Mistakidis, E.S. Fractal geometry and fractal material behaviour in solids and structures. Arch. Appl. Mech. 1992, 63, 1–24. [Google Scholar] [CrossRef]
- Wei, X.; Li, X.G.; Wei, N. Fractal features of soil particle size distribution in layered sediments behind two check dams: Implications for the Loess Plateau, China. Geomorphology 2016, 266, 133–145. [Google Scholar] [CrossRef]
- Fernández, E.; Jelinek, H.F. Use of fractal theory in neuroscience: Methods, advantages, and potential problems. Methods 2001, 24, 309–321. [Google Scholar] [CrossRef]
- Perfect, E.; Kay, B.D. Fractal Theory Applied to Soil Aggregation. Soil Sci. Soc. Am. J. 1991, 55, 1552–1558. [Google Scholar] [CrossRef]
- Tsujii, K. Fractal Materials and Their Functional Properties. Polym. J. 2008, 40, 785–799. [Google Scholar] [CrossRef] [Green Version]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef]
- Kravchenko, A.N.; Boast, C.W.; Bullock, D.G. Multifractal analysis of soil spatial variability. Agron. J. 1999, 91, 1033–1041. [Google Scholar] [CrossRef]
- Wang, J.; Lu, X.; Feng, Y.; Yang, R. Integrating multifractal theory and geo-statistics method to characterize the spatial variability of particle size distribution of minesoils. Geoderma 2018, 317, 39–46. [Google Scholar] [CrossRef]
- Martín, M.Á.; Montero, E. Laser diffraction and multifractal analysis for the characterization of dry soil volume-size distributions. Soil Tillage Res. 2002, 64, 113–123. [Google Scholar] [CrossRef]
- Biswas, A.; Cresswell, H.P.; Si, B.C. Application of multifractal and joint multifractal analysis in examining soil spatial variation: A review. In Fractal Analysis and Chaos in Geosciences; InTech: Wellington, New Zealand, 2012; pp. 109–138. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.Y.; Ren, Z.Y.; Liu, Y.S. The causes of land landscape changes in semi-arid area of Northwest China: A case study of Yulin city. J. Geogr. Sci. 2006, 114, 192–198. [Google Scholar] [CrossRef]
- Zhai, X.; Cheng, Z.; Ai, K.; Shang, B. Research on Environmental Sustainability of Coal Cities: A Case Study of Yulin, China. Energies 2020, 13, 2470. [Google Scholar] [CrossRef]
- Bian, X.; Wang, G.; Wang, H.; Wang, S.; Lv, W. Effect of lifters and mill speed on particle behaviour, torque, and power consumption of a tumbling ball mill: Experimental study and DEM simulation. Miner. Eng. 2017, 105, 22–35. [Google Scholar] [CrossRef]
- Zhou, W.X.; Wu, T.; Yu, Z.H. Geometrical characteristics of singularity spectra of multifractals Ⅱ. Partition function definition. J. East. China Univ. Sci. Technol. 2000, 26, 390–395. [Google Scholar]
- Yan, H.; Zhang, J.; Wang, J.; Zhou, N.; Zhang, S. Multifractal characteristics of particle size distribution of granular backfilling materials under different loads. Mater. Test. 2018, 60, 202–208. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Zhou, N.; Guo, Y.; Li, B.; Yan, H.; Deng, X. Investigation of spatial stratified heterogeneity of cemented paste backfill characteristics in construction demolition waste recycled aggregates. J. Clean. Prod. 2020, 249, 119332. [Google Scholar] [CrossRef]
- Cowie, P.A.; Sornette, D.; Vanneste, C. Multifractal scaling properties of a growing fault population. Geophys. J. Int. 1995, 122, 457–469. [Google Scholar] [CrossRef] [Green Version]
- Caniego, F.J.; Espejo, R.; Martın, M.A.; Jose, F.S. Multifractal scaling of soil spatial variability. Ecol. Model. 2005, 182, 291–303. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Zhu, J.; Xia, B. Multifractal fluctuation features of thermal power coal price in China. Energy 2016, 117, 10–18. [Google Scholar] [CrossRef]
- Tang, J.; Zeng, F.; Fan, Q. Multifractal spectrum identification of partial discharge in GIS based on fluorescence optical fiber detection. High. Volt. Eng. 2014, 40, 465–473. [Google Scholar]
- Peitgen, H.O.; Jurgens, H.; Saupe, D. Chaos and Fractals, 2nd ed.; Springer: New York, NY, USA, 1992. [Google Scholar]
- Guzzo, P.L.; Tino, A.A.A.; Santos, J.B. The onset of particle agglomeration during the dry ultrafine grinding of limestone in a planetary ball mill. Powder Technol. 2015, 284, 122–129. [Google Scholar] [CrossRef]
- Fadda, S.; Cincotti, A.; Concas, A.; Pisu, M.; Cao, G. Modelling breakage and reagglomeration during fine dry grinding in ball milling devices. Powder Technol. 2009, 194, 207–216. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Li, B.; Zhou, N.; Xiao, X.; Li, M.; Zhu, C. Environmental behavior of construction and demolition waste as recycled aggregates for backfilling in mines: Leaching toxicity and surface subsidence studies. J. Hazard. Mater. 2020, 389, 121870. [Google Scholar] [CrossRef]
- Sirveiya, A.K.; Thote, N.R. Measurement and Analysis of Blast Fragmentation, 1st ed.; Taylor & Francis Group: London, UK, 2013; pp. 139–144. [Google Scholar]
- Posadas, A.N.D.; Giménez, D.; Bittelli, M.; Vaz, C.M.P.; Flury, M. Multifractal characterization of soil particle-size distributions. Soil Sci. Soc. Am. J. 2001, 65, 1361–1367. [Google Scholar] [CrossRef]
- Zuo, R.G.; Wang, J. Fractal/multifractal modeling of geochemical data: A review. J. Geochem. Explor. 2015, 164, 33–41. [Google Scholar] [CrossRef]
- Gao, M.; Forssberg, E. Prediction of product size distributions for a stirred ball mill. Powder Technol. 1995, 84, 101–106. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, S.; Gao, Z.; Cai, X.; Li, H. Multifractal characterization of gangue particle size distribution structure during ball milling process. Powder Technol. 2022, 412, 117970. [Google Scholar] [CrossRef]
- Olson, E. Particle shape factors and their use in image analysis part 1: Theory. J. GXP Compliance 2011, 15, 85. [Google Scholar]


| Lithology | Elastic Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Compressive Strength (MPa) | Cohesion (MPa) | Internal Friction Angle/° |
|---|---|---|---|---|---|---|
| mudstone | 24.64 | 2630 | 0.27 | 37.66 | 3.01 | 41.94 |
| Gangue Weight/kg | Grinding Medium Weight/kg | Ratios of Ball-to-Gangue | Grinding Time/min |
|---|---|---|---|
| 16.67 | 50 | 3 | 10~60 |
| 8.34 | 50 | 6 | |
| 5.55 | 50 | 9 | |
| 4.16 | 50 | 12 | |
| 3.33 | 50 | 15 |
| Ball-to-Gangue Ratios | Time/min | Percentage/% | |||||
|---|---|---|---|---|---|---|---|
| <2 μm | 2–50 μm | 50–100 μm | 100–250 μm | 250–500 μm | 500–2000 μm | ||
| 3 | 0 | 0.06 | 1.12 | 3.46 | 46.03 | 24.61 | 24.72 |
| 20 | 0.18 | 2.42 | 6.26 | 55.69 | 24.99 | 10.46 | |
| 40 | 0.46 | 6.11 | 8.92 | 64.24 | 17.41 | 2.86 | |
| 60 | 1.79 | 8.48 | 11.14 | 67.6 | 10.84 | 0.15 | |
| 6 | 20 | 0.42 | 4.65 | 9.26 | 56.34 | 21.14 | 8.19 |
| 40 | 0.81 | 10.74 | 12.84 | 57.00 | 12.26 | 6.35 | |
| 60 | 4.98 | 22.18 | 20.57 | 41.58 | 9.49 | 1.20 | |
| 9 | 20 | 0.64 | 6.67 | 22.20 | 51.04 | 18.29 | 1.16 |
| 40 | 8.16 | 27.19 | 29.36 | 31.24 | 4.05 | 0 | |
| 60 | 12.88 | 26.20 | 27.07 | 32.31 | 1.04 | 0 | |
| 12 | 20 | 6.28 | 16.83 | 29.00 | 39.60 | 8.29 | 0 |
| 40 | 14.49 | 28.09 | 33.00 | 20.24 | 4.18 | 0 | |
| 60 | 18.40 | 26.48 | 32.17 | 20.11 | 2.84 | 0 | |
| 15 | 20 | 8.76 | 22.46 | 34.26 | 31.23 | 3.29 | 0 |
| 40 | 16.98 | 24.40 | 39.06 | 19.31 | 0.25 | 0 | |
| 60 | 16.46 | 26.11 | 36.92 | 19.20 | 1.31 | 0 | |
| Ratios of Ball-to-Gangue | D(1)/D(0) | |||||
|---|---|---|---|---|---|---|
| 10 min | 20 min | 30 min | 40 min | 50 min | 60 min | |
| 3 | 0.726 | 0.765 | 0.840 | 0.877 | 0.882 | 0.887 |
| 6 | 0.808 | 0.824 | 0.850 | 0.856 | 0.879 | 0.886 |
| 9 | 0.820 | 0.858 | 0.865 | 0.875 | 0.888 | 0.879 |
| 12 | 0.841 | 0.856 | 0.916 | 0.891 | 0.881 | 0.882 |
| 15 | 0.872 | 0.883 | 0.954 | 0.916 | 0.912 | 0.912 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Gu, W.; Qiu, F.; Zhang, P. Analysis of Influencing Factors of Gangue Ball Milling Based on Multifractal Theory. Sustainability 2023, 15, 6353. https://doi.org/10.3390/su15086353
Zhu L, Gu W, Qiu F, Zhang P. Analysis of Influencing Factors of Gangue Ball Milling Based on Multifractal Theory. Sustainability. 2023; 15(8):6353. https://doi.org/10.3390/su15086353
Chicago/Turabian StyleZhu, Lei, Wenzhe Gu, Fengqi Qiu, and Peng Zhang. 2023. "Analysis of Influencing Factors of Gangue Ball Milling Based on Multifractal Theory" Sustainability 15, no. 8: 6353. https://doi.org/10.3390/su15086353




