Reducing Octane Number Loss in Gasoline Refining Process by Using the Improved Sparrow Search Algorithm
Abstract
:1. Introduction
2. Data Processing
2.1. Processing of Missing Data
2.2. Processing of Anomalous Data
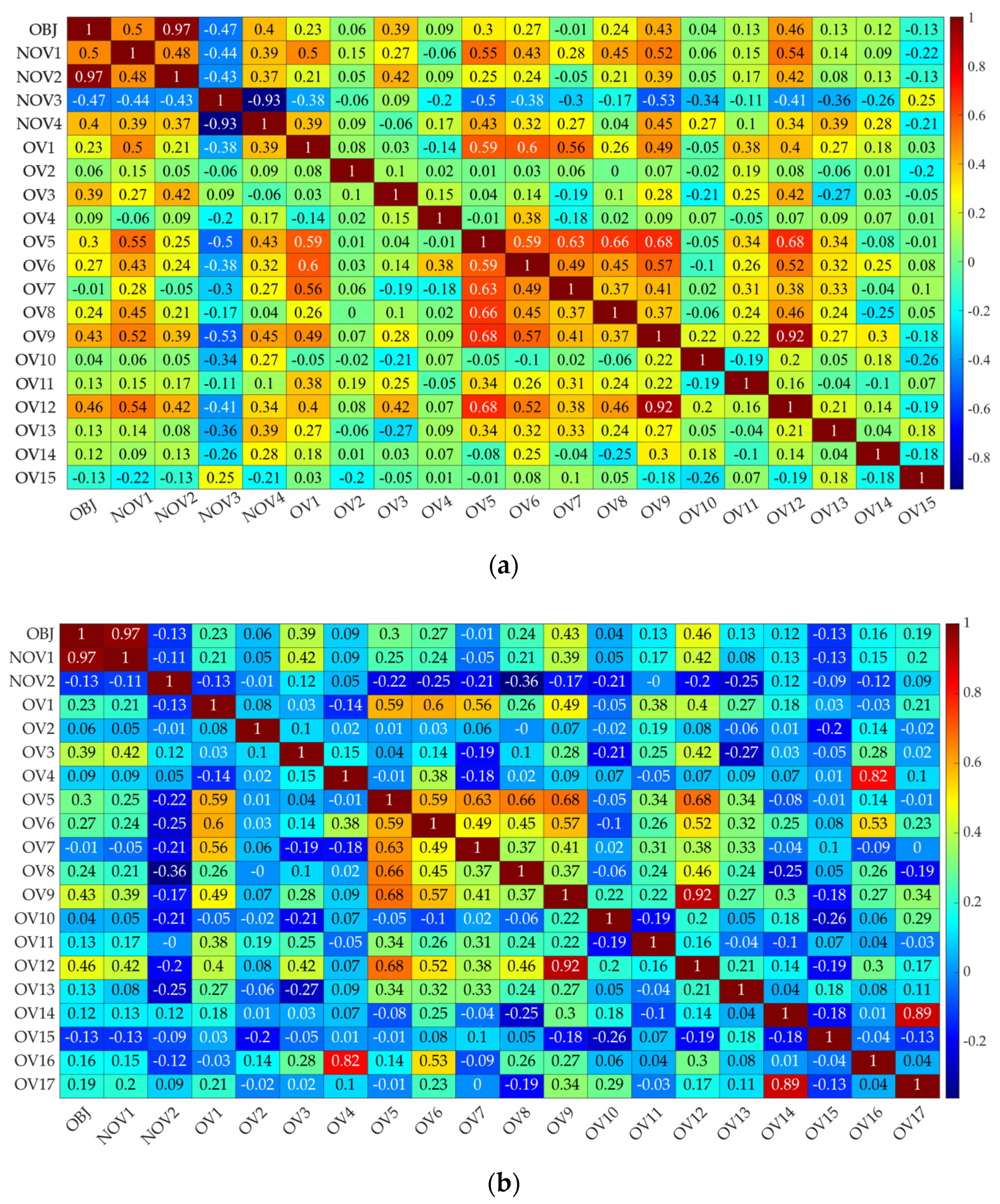
2.3. Data Dimension Reduction
3. Method
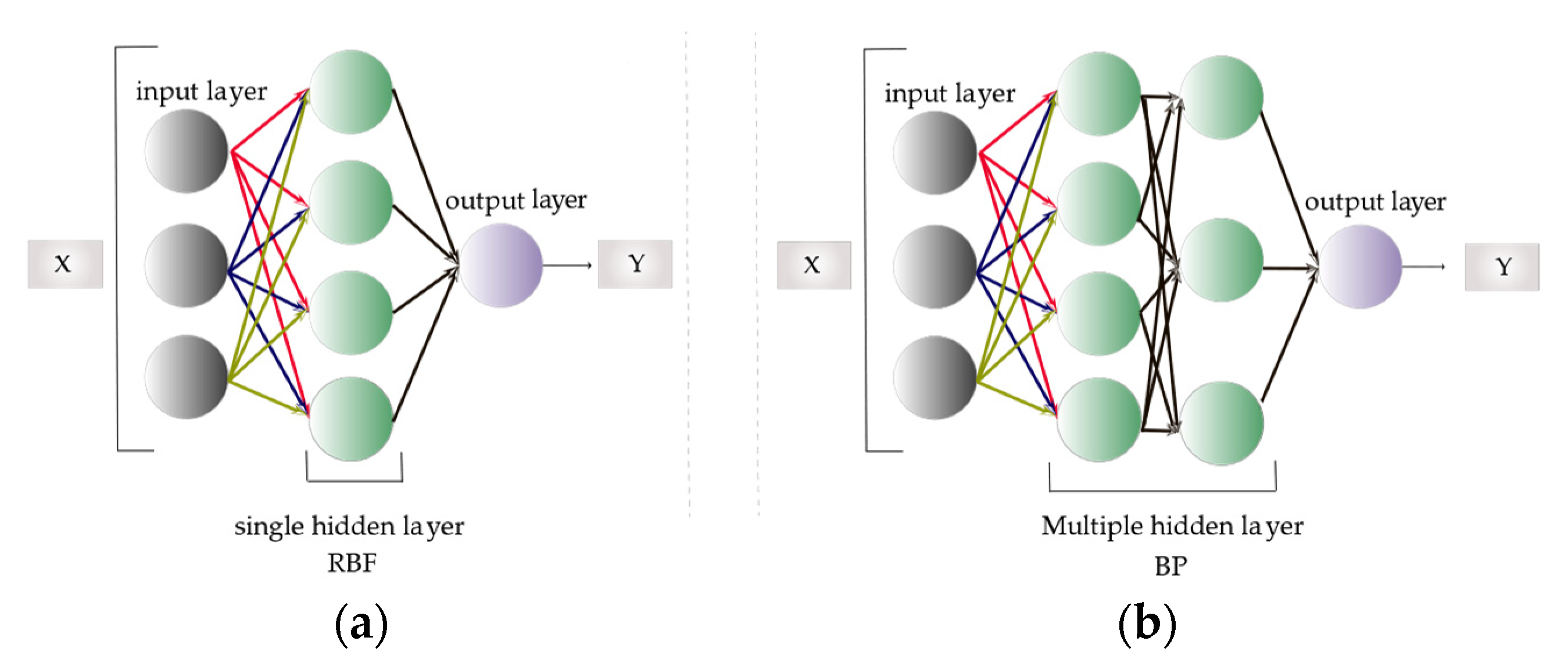
3.1. Development of Octane Number Prediction Model
3.2. Establishment of Octane Number Loss Optimization Model
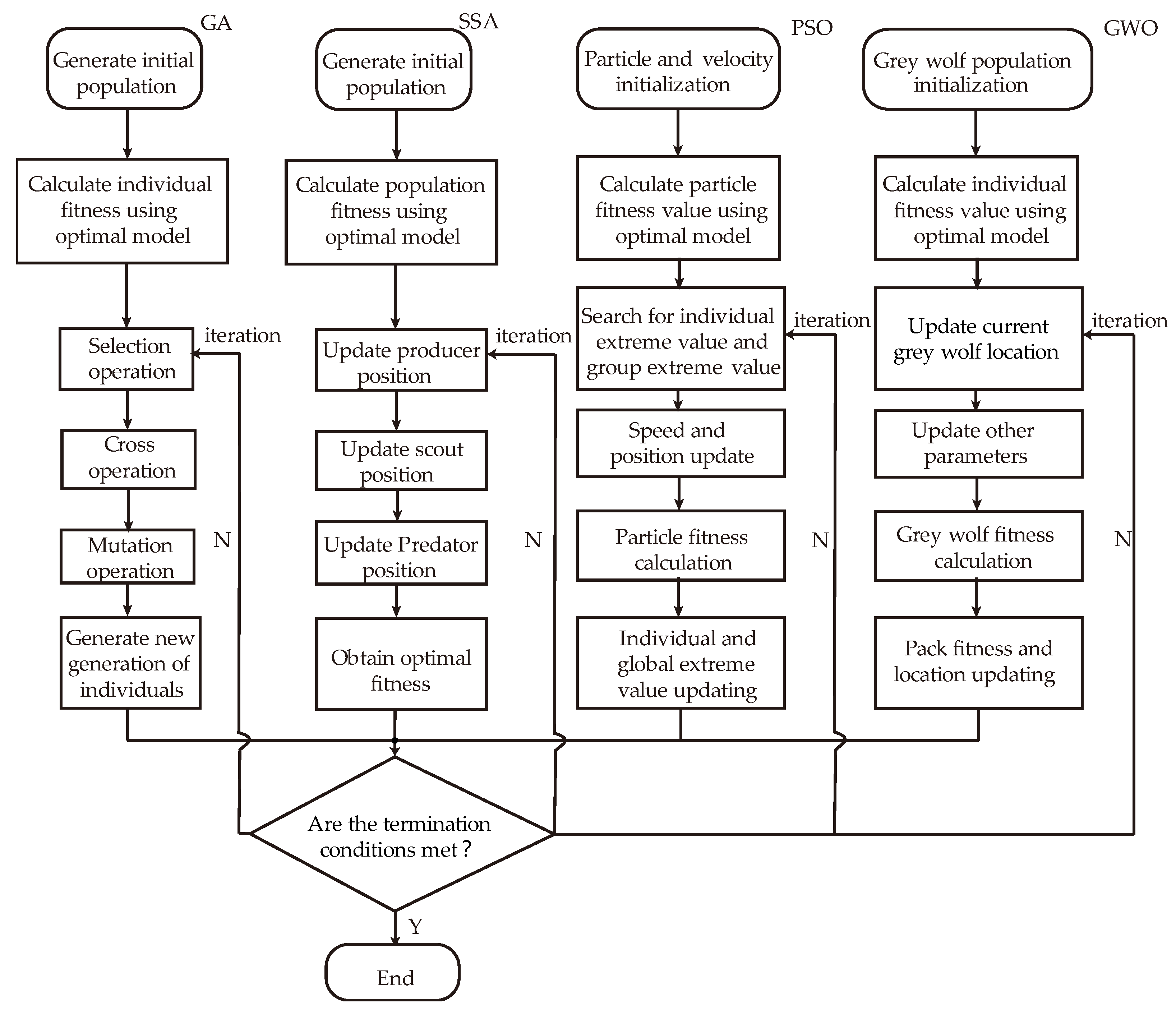
3.3. Improvement and Selection of the Optimization Algorithm
4. Results
4.1. Results of the Feature Parameter Selection
4.2. Results of the Prediction and Optimization
4.2.1. Prediction Result of Gasoline Octane Number
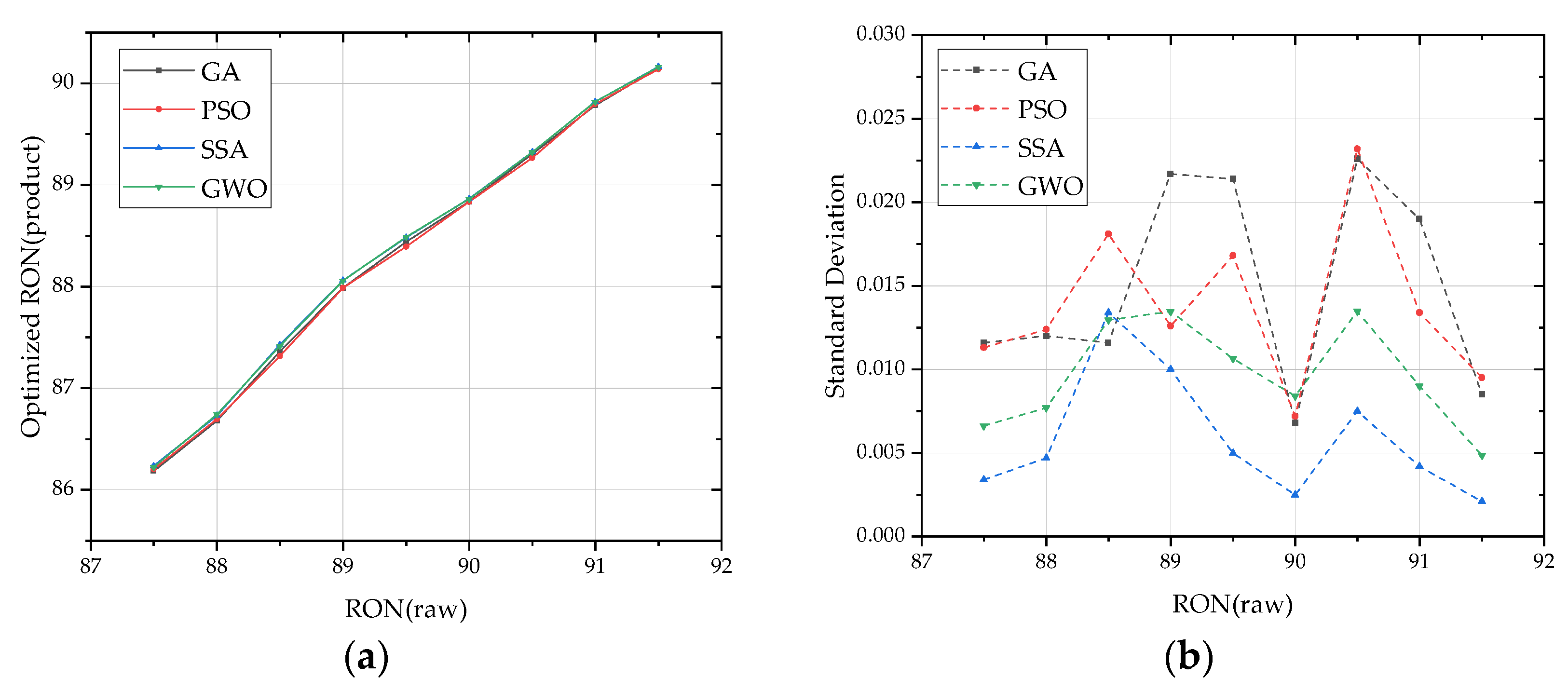
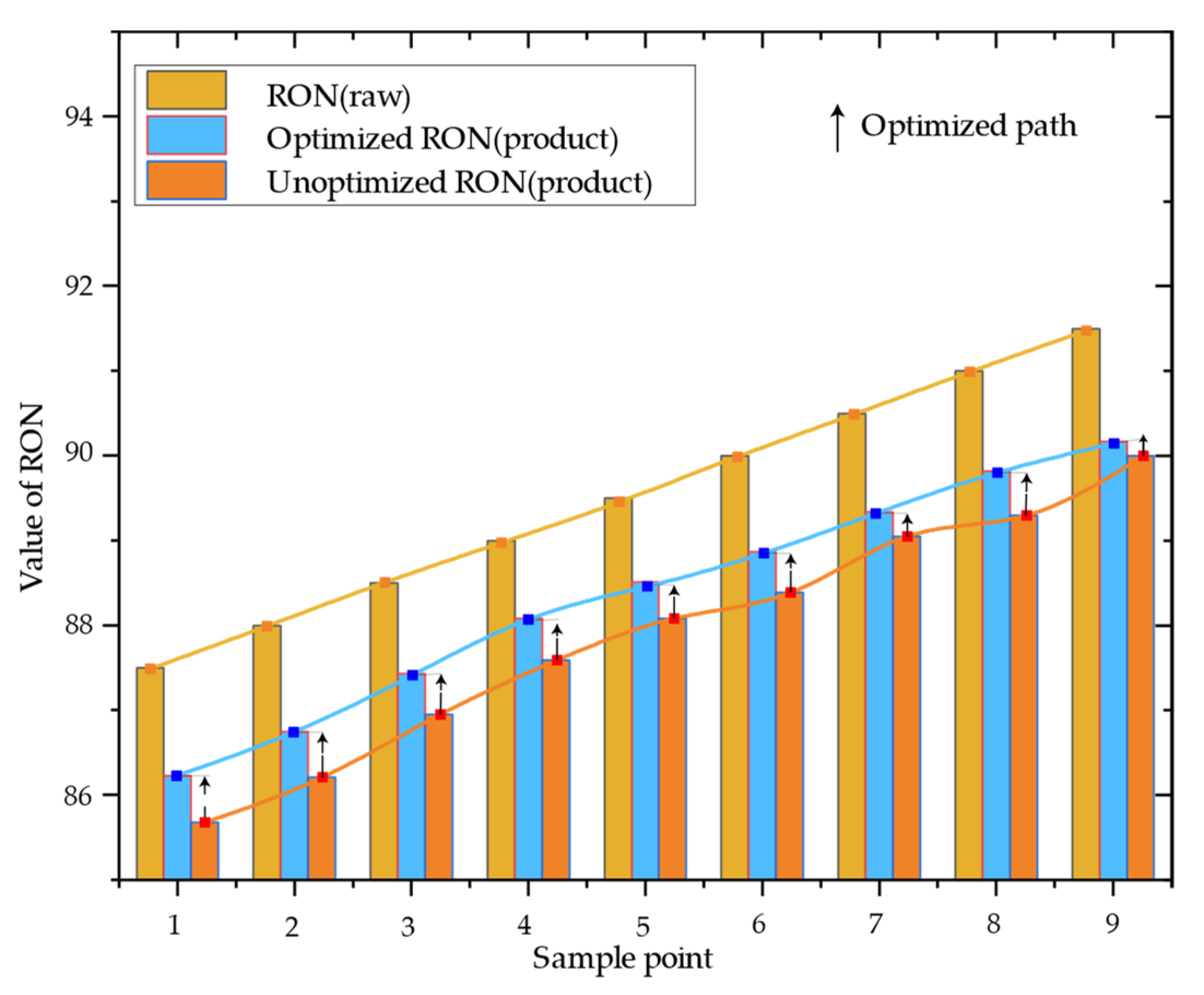
4.2.2. Optimization Results of the Gasoline Octane Number
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pasadakis, N.; Gaganis, V.; Foteinopoulos, C. Octane Number Prediction for Gasoline Blends. Fuel Process. Technol. 2006, 87, 505–509. [Google Scholar] [CrossRef]
- Song, C. An Overview of New Approaches to Deep Desulfurization for Ultra-clean Gasoline, Diesel Fuel and Jet Fuel. Catal. Today 2003, 86, 211–263. [Google Scholar] [CrossRef]
- Orazbayev, B.; Zhumadillayeva, A.; Orazbayeva, K.; Iskakova, S.; Utenova, B.; Gazizov, F.; Ilyashenko, S.; Afanaseva, O. The System of Models and Optimization of Operating Modes of a Catalytic Reforming Unit Using Initial Fuzzy Information. Energies 2022, 15, 1573. [Google Scholar] [CrossRef]
- Ospanov, Y.A.; Orazbayev, B.B.; Orazbayeva, K.N.; Mukataev, N.S.; Demyanenko, A.I. Mathematical modeling and decision-making on controlling modes of technological objects in the fuzzy environment. In Proceedings of the 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; pp. 103–108. [Google Scholar]
- Pasadakis, N.; Kardamakis, A.A. Identifying Constituents in Commercial Gasoline Using Fourier Transform-infrared Spectroscopy and Independent Component Analysis. Anal. Chim. Acta 2006, 578, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, Y.; He, X.; Xiao, M.; Jiang, T. Multi-objective Nonlinear Programming Model for Reducing Octane Number Loss in Gasoline Refining Process based on Data Mining Technology. Processes 2021, 9, 721. [Google Scholar] [CrossRef]
- Wang, H.; Chu, X.; Chen, P.; Li, J.; Liu, D.; Xu, Y. Partial Least Squares Regression Residual Extreme Learning Machine (PLSRR-ELM) Calibration Algorithm Applied in Fast Determination of Gasoline Octane Number with Near-infrared Spectroscopy. Fuel 2022, 309, 122224. [Google Scholar]
- Li, B.; Qin, C. Predictive Analytics for Octane Number: A Novel Hybrid Approach of KPCA and GS-PSO-SVR Model. IEEE Access 2021, 9, 66531–66541. [Google Scholar] [CrossRef]
- Fu, N.; Lai, Z.; Zhang, Y.; Ma, Y. An Effective Method based on Multi-model Fusion for Research Octane Number Prediction. New J. Chem. 2021, 45, 9668–9676. [Google Scholar] [CrossRef]
- Sun, F.; Xue, N.; Liu, M.; Li, X. Application of an improved partial least squares algorithm for predicting octane losses in gasoline refining process. In Proceedings of the 9th IEEE Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 1573–1581. [Google Scholar]
- Xia, Q.; Zang, H.; Liu, L.; Jiang, X.; Wei, Z. Research on Solar Radiation Estimation based on Singular Spectrum Analysis-Deep Belief Network. In Proceedings of the 2021 IEEE 11th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Jiaxing, China, 27–31 July 2021; pp. 472–477. [Google Scholar]
- Tao, X.; Liu, Y.; Li, H.; Xie, Y.; Peng, L.; Li, C.; Guo, L.; Zhang, Y. Applying Machine Learning to Chemical Industry: A Self-Adaptive GA-BP Neural Network-Based Predictor of Gasoline Octane Number. Mob. Inf. Syst. 2022, 2022, 8546576. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, W.; Liang, W.; Yang, B.; Law, C.K. Predicting Octane Number from Species Profiles: A Deep Learning Model. Proc. Combust. Inst. 2022, 16, 1–9. [Google Scholar]
- Li, R.; Herreros, J.M.; Tsolakis, A.; Yang, W. Machine Learning Regression based Group Contribution Method for Cetane and Octane Numbers Prediction of Pure Fuel Compounds and Mixtures. Fuel 2020, 280, 118589. [Google Scholar] [CrossRef]
- Yao, X.; Zhao, Q.; Gong, D.; Zhu, S. Solution of Large-scale Many-objective Optimization Problems based on Dimension Reduction and Solving Knowledge Guided Evolutionary Algorithm. IEEE Trans. Evol. Comput. 2021. [Google Scholar] [CrossRef]
- Chen, C.; Lu, N.; Wang, L.; Xing, Y. Intelligent Selection and Optimization Method of Feature Variables in Fluid Catalytic Cracking Gasoline Refining Process. Comput. Chem. Eng. 2021, 150, 107336. [Google Scholar] [CrossRef]
- Cui, S.; Qiu, H.; Wang, S.; Wang, Y. Two-stage stacking heterogeneous ensemble learning method for gasoline octane number loss prediction. Appl. Soft Comput. 2021, 113, 107989. [Google Scholar] [CrossRef]
- Zhang, F.; Su, X.; Tan, A.; Yao, J.; Li, H. Prediction of Research Octane Number Loss and Sulfur Content in Gasoline Refining Using Machine Learning. Energy 2022, 261, 124823. [Google Scholar] [CrossRef]
- Guo, J.; Lou, Y.; Wang, W.; Wu, X. Optimization Modeling and Empirical Research on Gasoline Octane Loss Based on Data Analysis. J. Adv. Transp. 2021, 2021, 5553069. [Google Scholar] [CrossRef]
- Xu, X.; Peng, L.; Ji, Z.; Zheng, S.; Tian, Z.; Geng, S. Research on Substation Project Cost Prediction Based on Sparrow Search Algorithm Optimized BP Neural Network. Sustainability 2021, 13, 13746. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, H.; Wang, Q.; Zheng, Z.; Wang, H.; Yue, Z.; Ming, Z.; Wen, M.; Feng, L.; Yao, M. Investigation on the ignition delay prediction model of multi-component surrogates based on back propagation (BP) neural network. Combust. Flame 2021, 237, 111852. [Google Scholar] [CrossRef]
- Giordano, P.C.; Goicoechea, H.C.; Olivieri, A.C. SRO_ANN: An Integrated MatLab Toolbox for Multiple Surface Response Optimization Using Radial Basis Functions. Chemom. Intell. Lab. Syst. 2017, 171, 198–206. [Google Scholar] [CrossRef]
- Mohammadi, M.-R.; Hadavimoghaddam, F.; Pourmahdi, M.; Atashrouz, S.; Munir, M.T.; Hemmati-Sarapardeh, A.; Mosavi, A.H.; Mohaddespour, A. Modeling hydrogen solubility in hydrocarbons using extreme gradient boosting and equations of state. Sci. Rep. 2021, 11, 17911. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Yang, S. Load Demand Forecasting of Residential Buildings Using a Deep Learning Model. Electr. Power Syst. Res. 2020, 179, 106073. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, X. Design of Intelligent Control System for Agricultural Greenhouses based on Adaptive Improved Genetic Algorithm for Multi-energy Supply System. Energy Rep. 2022, 8, 12126–12138. [Google Scholar] [CrossRef]
- Elbes, M.; Alzubi, S.; Kanan, T.; Al-Fuqaha, A.; Hawashin, B. A survey on particle swarm optimization with emphasis on engineering and network applications. Evol. Intell. 2019, 12, 113–129. [Google Scholar] [CrossRef]
- Sharma, J.; Singhal, R.S. Comparative Research on Genetic Algorithm, Particle Swarm Optimization and Hybrid GA-PSO. In Proceedings of the 2nd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 11–13 March 2015; pp. 110–114. [Google Scholar]
- Hou, Y.; Gao, H.; Wang, Z.; Du, C. Improved Grey Wolf Optimization Algorithm and Application. Sensors 2022, 22, 3810. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Shen, B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- China Post-Graduate Mathematical Contest in Modeling. [11 October 2020]. Available online: https://cpipc.acge.org.cn//cw/detail/4/2c9088a674924b7f01749981b29502e9 (accessed on 10 February 2023).
- Saharian, A.A. The Generalized Abel-Plana Formula with Applications to Bessel Functions and Casimir Effect. arXiv 2007, arXiv:0708.1187. [Google Scholar]
- Ren, Q.; Cheng, H.; Han, H. Research on machine learning framework based on random forest algorithm. In Proceedings of the AIP Conference; AIP Publishing LLC: Melville, NY, USA, 2017; Volume 1820, p. 080020. [Google Scholar]
- Fang, S.; Yao, X.; Zhang, J.; Han, M. Grey Correlation Analysis on Travel Modes and their Influence Factors. Procedia Eng. 2017, 174, 347–352. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Wagenmakers, E.J. Analytic Posteriors for Pearson’s Correlation Coefficient. Stat. Neerl. 2018, 72, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Sugiartawan, P.; Pulungan, R.; Sari, A.K. Prediction by a Hybrid of Wavelet Transform and Long-short-term-memory Neural Network. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 326–332. [Google Scholar] [CrossRef]
- Zhou, H.; Deng, Z.; Xia, Y.; Fu, M. A new sampling method in particle filter based on Pearson correlation coefficient. Neurocomputing 2016, 216, 208–215. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, P.; Fu, X.; Zhang, J.; Yang, H.; Gao, H.; Li, Y. Comparative analysis of BP neural network and RBF neural network in seismic performance evaluation of pier columns. Mech. Syst. Signal Process. 2020, 141, 106707. [Google Scholar] [CrossRef]
- Das, K.; Behera, R. A survey on Machine Learning: Concept, Algorithms and Applications. Int. J. Innov. Res. Comput. Commun. Eng. 2017, 5, 1301–1309. [Google Scholar]
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Fu, Z.H.; Wang, Z.J. Prediction of Financial Economic Time Series based on Group Intelligence Algorithm based on Machine Learning. Int. J. Early Child. Spec. Educ. 2021, 30, 938. [Google Scholar]
- Sun, W.; Huang, C. A Carbon Price Prediction Model based on Secondary Decomposition Algorithm and Optimized Back Propagation Neural Network. J. Clean. Prod. 2020, 243, 118671. [Google Scholar] [CrossRef]
- Liu, G.; Shu, C.; Liang, Z.; Peng, B.; Cheng, L. A Modified Sparrow Search Algorithm with Application in 3d Route Planning for UAV. Sensors 2021, 21, 1224. [Google Scholar] [CrossRef]
- Gao, B.; Shen, W.; Guan, H.; Zheng, L.; Zhang, W. Research on Multistrategy Improved Evolutionary Sparrow Search Algorithm and its Application. IEEE Access 2022, 10, 62520–62534. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Wang, F. A Learning Sparrow Search Algorithm. Comput. Intell. Neurosci. 2021, 2021. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A Stochastic Configuration Network based on Chaotic Sparrow Search Algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Singh, P.; Mittal, N.; Salgotra, R. Comparison of Range-based Versus Range-free WSNs Localization Using Adaptive SSA Algorithm. Wirel. Netw. 2022, 28, 1625–1647. [Google Scholar] [CrossRef]



| pRON | SC(µg/g) | rRON | Saturated Hydrocarbon(v%) | … | S-ZORB.FT_1504.DACA.PV | S-ZORB.FT_1504.TOTALIZERA.PV | S-ZORB.PC_1001A.PV | |
|---|---|---|---|---|---|---|---|---|
| 1 | 89.22 | 188.00 | 90.60 | 53.23 | … | 1840.14 | 39,608,757 | 0.35 |
| 2 | 89.32 | 169.00 | 90.50 | 52.30 | … | 1641.73 | 39,389,299 | 0.35 |
| 3 | 89.32 | 177.00 | 90.70 | 52.30 | … | 1600.68 | 39,312,616.5 | 0.35 |
| … | … | … | … | … | … | … | … | … |
| 324 | 88.05 | 271.43 | 89.40 | 47.19 | … | −10,846.1 | 693,676.8 | −119.53 |
| 325 | 88.12 | 266.00 | 89.40 | 46.72 | … | −12,373.3 | 569,836.8 | −120.05 |
| 326 | 88.65 | 266.00 | 89.90 | 46.72 | … | −13,900.5 | 445,996.8 | −120.56 |
| Reference Designator | Variable Types | Relevancy | Reference Designator | Variable Types | Relevancy |
|---|---|---|---|---|---|
| pRON | NOV | 0.894 | S-ZORB.TE_1105.PV | OV | 0.768 |
| S-ZORB.FT_9403.PV | OV | 0.796 | S-ZORB.TE_5006.DACA | OV | 0.767 |
| S-ZORB.LC_1201.PV | OV | 0.789 | S-ZORB.TE_1601.PV | OV | 0.766 |
| S-ZORB.FC_1203.PV | OV | 0.784 | S-ZORB.TE_5002.DACA | OV | 0.762 |
| S-ZORB.FC_1201.PV | OV | 0.783 | S-ZORB.FT_1003.PV | OV | 0.762 |
| S-ZORB.TE_2603.DACA | OV | 0.778 | S-ZORB.TE_5003.DACA | OV | 0.761 |
| S-ZORB.FC_5202.PV | OV | 0.775 | S-ZORB.PT_9401.PV | OV | 0.760 |
| S-ZORB.FT_2433.DACA | OV | 0.774 | S-ZORB.FC_1005.PV | OV | 0.760 |
| S-ZORB.TC_3102.DACA | OV | 0.768 | Bromine value | NOV | 0.759 |
| S-ZORB.TE_1105.PV | OV | 0.768 | S-ZORB.TE_5004.DACA | OV | 0.759 |
| S-ZORB.TE_5006.DACA | OV | 0.767 | / | / | / |
| Reference Designator | Minimum | Maximum | Variable Types |
|---|---|---|---|
| SC (µg/g) | 57.0 | 392.0 | NOV |
| pRON | 87.2 | 91.7 | NOV |
| Saturated hydrocarbon (v%) | 43.2 | 63.4 | NOV |
| Olefins (v%) | 14.6 | 34.7 | NOV |
| S-ZORB.LC_1201.PV | 49.38 | 50.29 | OV |
| S-ZORB.LC_1202.PV | 49.70 | 50.86 | OV |
| S-ZORB.LT_1501.DACA | −1.265 | −1.248 | OV |
| S-ZORB.TE_2005.PV | 412.26 | 428.20 | OV |
| S-ZORB.PT_9403.PV | 0.9866 | 0.9985 | OV |
| S-ZORB.TE_2004.DACA | 411.85 | 427.67 | OV |
| S-ZORB.RXL_0001.AUXCALCA.PV | 92.08 | 97.30 | OV |
| S-ZORB.TE_2003.DACA | 411.85 | 427.67 | OV |
| S-ZORB.TE_2002.DACA | 413.08 | 429.49 | OV |
| S-ZORB.TE_1604.DACA | 407.04 | 421.58 | OV |
| S-ZORB.TE_1102.DACA | 417.53 | 432.74 | OV |
| S-ZORB.TE_1602.DACA | 404.67 | 417.88 | OV |
| S-ZORB.TC_1606.PV | 403.25 | 416.71 | OV |
| S-ZORB.TE_2103.PV | 415.82 | 431.20 | OV |
| S-ZORB.TE_1603.DACA | 403.39 | 419.55 | OV |
| Method | Data Partition | RMSE | R2 |
|---|---|---|---|
| BP | Training set | 0.0566 | 0.9645 |
| Testing set | 0.3321 | 0.9221 | |
| RBF | Training set | 0.0631 | 0.8911 |
| Testing set | 0.8457 | 0.7039 | |
| XGboost | Training set | 0.0192 | 0.9996 |
| Testing set | 0.2175 | 0.9475 | |
| SVR | Training set | 0.0973 | 0.9898 |
| Testing set | 0.2534 | 0.9390 |
| Model | Parameter Name | Parameter Value | Model | Parameter Name | Parameter Value |
|---|---|---|---|---|---|
| XGboost | Base learner | Decision Tree | RBF | Input layer elements | 19 |
| Number of base learners M | 75 | Hide Layer elements | 227 | ||
| Learning Rate η | 0.1 | Output layer elements | 1 | ||
| L1 Regular Terms λ | 0 | Expansion speed of RBF | 100 | ||
| L2 Regular Terms γ | 1 | BP | Input layer elements | 19 | |
| Maximum depth of tree | 10 | Hide Layer elements | 10 | ||
| SVR | Loss-function P | 0.1 | Output layer elements | 1 | |
| Kernel function type | RBF | Training algorithm | Levenberg-Marquardt | ||
| Penalty factor | 4 | Learn Rate | 0.01 | ||
| Radial basis function parameters | 0.8 | MERT | 0.00001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhu, J.; Qin, X.; Xie, W. Reducing Octane Number Loss in Gasoline Refining Process by Using the Improved Sparrow Search Algorithm. Sustainability 2023, 15, 6571. https://doi.org/10.3390/su15086571
Chen J, Zhu J, Qin X, Xie W. Reducing Octane Number Loss in Gasoline Refining Process by Using the Improved Sparrow Search Algorithm. Sustainability. 2023; 15(8):6571. https://doi.org/10.3390/su15086571
Chicago/Turabian StyleChen, Jian, Jiajun Zhu, Xu Qin, and Wenxiang Xie. 2023. "Reducing Octane Number Loss in Gasoline Refining Process by Using the Improved Sparrow Search Algorithm" Sustainability 15, no. 8: 6571. https://doi.org/10.3390/su15086571
APA StyleChen, J., Zhu, J., Qin, X., & Xie, W. (2023). Reducing Octane Number Loss in Gasoline Refining Process by Using the Improved Sparrow Search Algorithm. Sustainability, 15(8), 6571. https://doi.org/10.3390/su15086571






