Spatial Distribution of Soil Water and Salt in a Slightly Salinized Farmland
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Experimental Design and Soil Sample Measurements
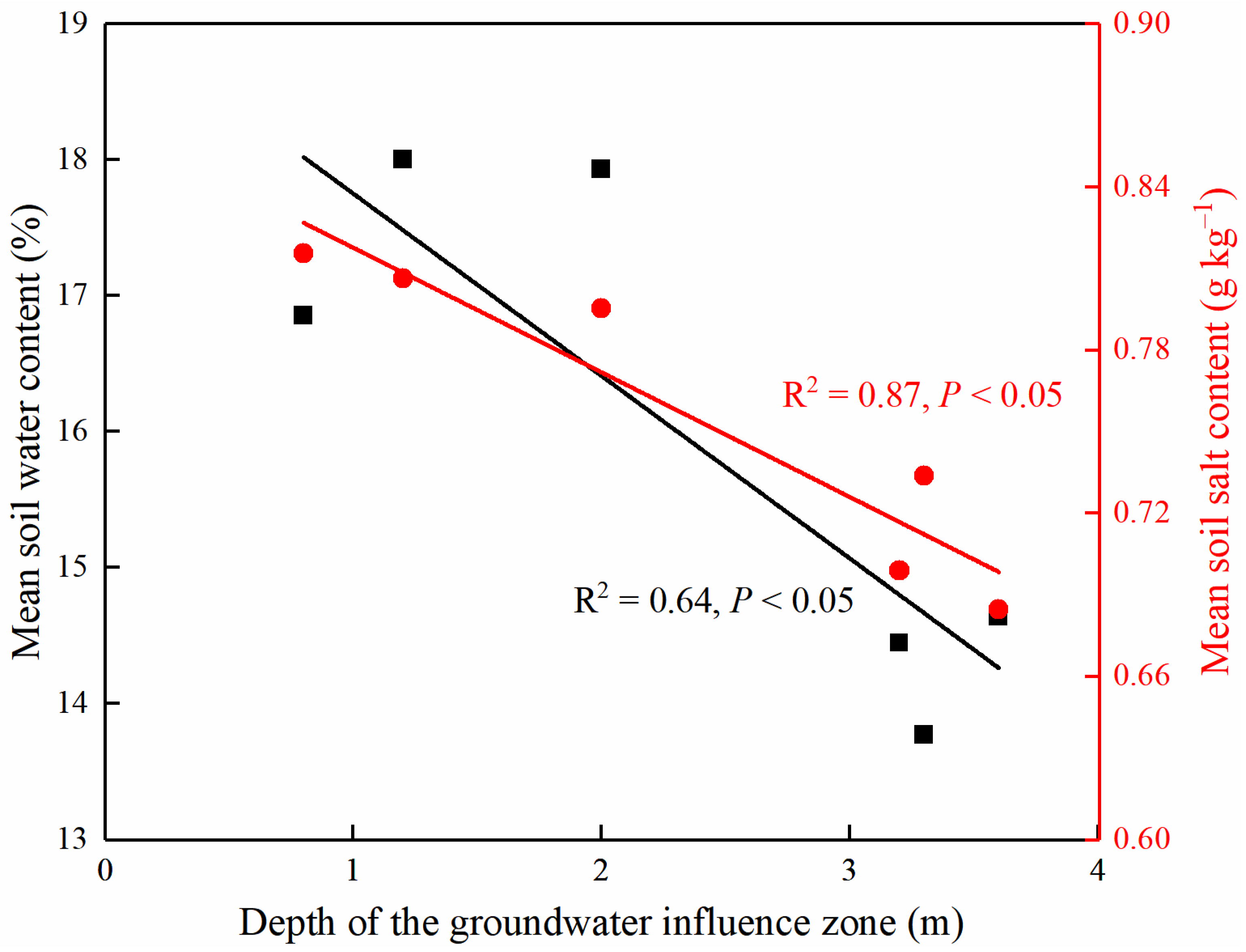
2.3. Depth of the Groundwater Influence Zone
2.4. Fractal Methods
2.4.1. Multifractal Analysis
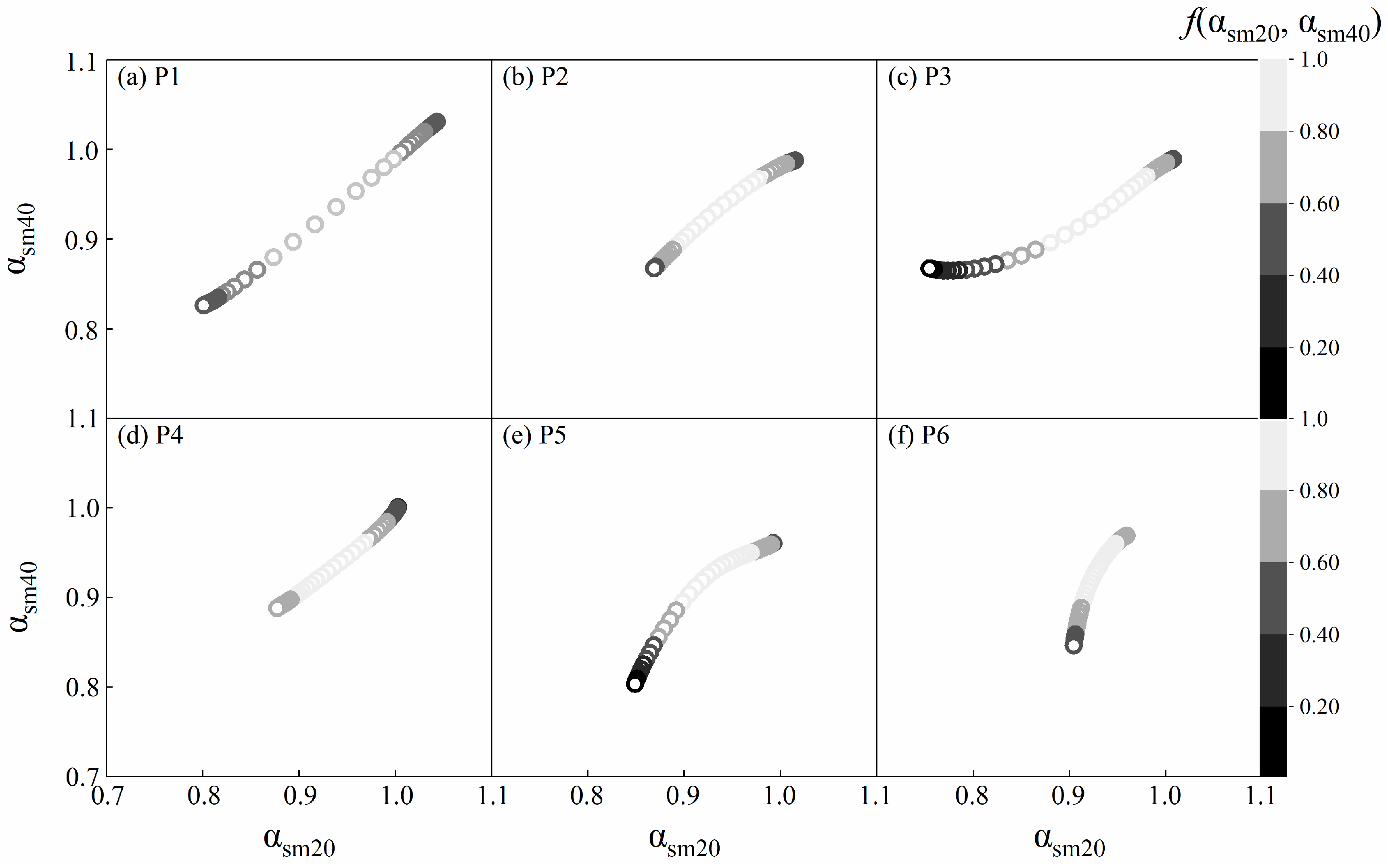
2.4.2. Joint Multifractal Analysis
2.5. Statistical Analysis
3. Results
3.1. Descriptive Statistics for Soil Water and Salt
3.2. Spatial Distribution of Soil Water and Salt
3.3. Correlations between Soil Water and Salt in the Same Layer
3.4. Correlations between Soil Water and Salt in the 0–20 cm and 20–40 cm Soil Layers
4. Discussion
4.1. Spatial Variability of Soil Water and Salt
4.2. Correlations between the Spatial Variability of Soil Water and Salt
4.3. Optimization of Soil Water and Salt Sampling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Butcher, K.; Wick, A.F.; Desutter, T.; Chatterjee, A.; Harmon, J. Soil Salinity: A Threat to Global Food Security. Agron. J. 2016, 108, 2189. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, Y.; Zhang, T.; Zhou, L.; He, J.; Chau, H.W.; Zou, Y.; Feng, H. Impacts of ridge with plastic mulch-furrow irrigation on soil salinity, spring maize yield and water use efficiency in an arid saline area. Agric. Water Manag. 2018, 201, 268–277. [Google Scholar] [CrossRef]
- Akça, E.; Aydin, M.; Kapur, S.; Kume, T.; Nagano, T.; Watanabe, T.; Çilek, A.; Zorlu, K. Long-term monitoring of soil salinity in a semi-arid environment of Turkey. CATENA 2020, 193, 104614. [Google Scholar] [CrossRef]
- Litalien, A.; Zeeb, B. Curing the earth: A review of anthropogenic soil salinization and plant-based strategies for sustainable mitigation. Sci. Total Environ. 2020, 698, 134235. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Deng, C.; Liu, Y.; Niu, Z.; Li, Y. Identifying change in spatial accumulation of soil salinity in an inland river watershed, China. Sci. Total Environ. 2018, 621, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Ma, Y.; Li, G.; Huang, W.; Zhao, H.; Cao, G.; Wang, A. Spatial Distribution Characteristics of Soil Salt Ions in Tumushuke City, Xinjiang. Sustainability 2022, 14, 16486. [Google Scholar] [CrossRef]
- Liu, W.Q.; Lu, F.; Xu, X.; Chen, G.; Fu, T.; Su, Q. Spatial and Temporal Variation of Soil Salinity during Dry and Wet Seasons in the Southern Coastal Area of Laizhou Bay, China. Indian J. Geo-Mar. Sci. 2020, 49, 260–270. [Google Scholar]
- Tan, X.; Wu, M.; Huang, J.; Wu, J.; Chen, J. Similarity of soil freezing characteristic and soil water characteristic: Application in saline frozen soil hydraulic properties prediction. Cold Reg. Sci. Technol. 2020, 173, 102876. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, Y.; Li, J.; Zhao, Y. Study on the influence of hydro-thermal-salt-mechanical interaction in saturated frozen sulfate saline soil based on crystallization kinetics. Int. J. Heat Mass Transf. 2020, 146, 118868. [Google Scholar] [CrossRef]
- Mainuddin, M.; Maniruzzaman, M.; Gaydon, D.; Sarkar, S.; Rahman, M.; Sarangi, S.; Sarker, K.; Kirby, J. A water and salt balance model for the polders and islands in the Ganges delta. J. Hydrol. 2020, 587, 125008. [Google Scholar] [CrossRef]
- Wu, M.; Zhao, Q.; Jansson, P.E.; Wu, J.; Tan, X.; Duan, Z.; Wang, K.; Chen, P.; Zheng, M.; Huang, J. Improved soil hydrological modeling with the implementation of salt-induced freezing point depression in CoupModel: Model calibration and validation. J. Hydrol. 2020, 596, 125693. [Google Scholar] [CrossRef]
- Zhu, X.; Fu, S.; Wu, Q.; Wang, A. Soil detachment capacity of shallow overland flow in Earth-Rocky Mountain Area of Southwest China. Geoderma. 2020, 361, 114021. [Google Scholar] [CrossRef]
- Luo, Y.X.; Li, H.; Ding, W.Q.; Hu, F.N.; Li, S. Effects of DLVO, hydration and osmotic forces among soil particles on water infiltration. Eur. J. Soil Sci. 2018, 69, 710–718. [Google Scholar] [CrossRef]
- Wen, W.; Lai, Y.; You, Z. Numerical modeling of water–heat–vapor–salt transport in unsaturated soil under evaporation. Int. J. Heat Mass Transf. 2020, 159, 120114. [Google Scholar] [CrossRef]
- Yuan, S.; Zhanbin, L.I.; Zhang, Y.; Dong, Q.; Wang, D. Impact of Layered Deposition on Temporal and Spatial Distribution Characteristic of Soil Moisture of Check Dam Land. Res. Soil Water Conserv. 2018, 25, 29–34. [Google Scholar]
- Benslama, A.; Khanchoul, K.; Benbrahim, F.; Boubehziz, S.; Chikhi, F.; Navarro-Pedreno, J. Monitoring the Variations of Soil Salinity in a Palm Grove in Southern Algeria. Sustainability 2020, 12, 19. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Hanati, G.; Danierhan, S.; Liu, G.M.; Zhang, Y.; Zhang, Z.P. Identifying Seasonal Accumulation of Soil Salinity with Three-Dimensional Mapping-A Case Study in Cold and Semiarid Irrigated Fields. Sustainability 2020, 12, 14. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, J.; Zhao, X.; Triantafilis, J. Clay content mapping and uncertainty estimation using weighted model averaging. CATENA 2022, 209, 105791. [Google Scholar] [CrossRef]
- Wang, F.; Wang, J.; Wang, Y. Using multi-fractal and joint multi-fractal methods to characterize spatial variability of reconstructed soil properties in an opencast coal-mine dump in the Loess area of China. CATENA 2019, 182, 104111. [Google Scholar] [CrossRef]
- Liao, K.; Lai, X.; Zhou, Z.; Zhu, Q. Applying fractal analysis to detect spatio-temporal variability of soil moisture content on two contrasting land use hillslopes. CATENA 2017, 157, 163–172. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Kravchenko, A. Soil Variability Assessment with Fractal Techniques. In Soil-Water-Solute Process Characterization; CRC Press: Boca Raton, FL, USA, 2004; pp. 617–638. [Google Scholar]
- Wang, J.; Zhang, J.; Feng, Y. Characterizing the spatial variability of soil particle size distribution in an underground coal mining area: An approach combining multi-fractal theory and geostatistics. CATENA 2019, 176, 94–103. [Google Scholar] [CrossRef]
- Xia, J.; Ren, R.; Chen, Y.; Sun, J.; Zhao, X.; Zhang, S. Multifractal characteristics of soil particle distribution under different vegetation types in the Yellow River Delta chenier of China. Geoderma 2020, 368, 114311. [Google Scholar] [CrossRef]
- Triantafilis, J.; Odeh, I.O.A.; McBratney, A.B. Five geostatistical models to predict soil salinity from electromagnetic induction data across irrigated cotton. Soil Sci. Soc. Am. J. 2001, 65, 869–878. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Shao, M.A. Spatial variability of soil physical preoperties in a region of the Loess Plateau of pr China subject to wind and water erosion. Land Degrad. Dev. 2013, 24, 296–304. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B.; Huang, J.; An, Z.; Jiang, P.; Chen, Y.; Liu, Y. Estimating soil organic carbon density in plains using landscape metric-based regression Kriging model. Soil Tillage Res. 2019, 195, 104381. [Google Scholar] [CrossRef]
- Zhao, D.; Arshad, M.; Li, N.; Triantafilis, J. Predicting soil physical and chemical properties using vis-NIR in Australian cotton areas. Catena. 2021, 196, 104938. [Google Scholar] [CrossRef]
- Bertol, I.; Schick, J.; Bandeira, D.H.; Paz-Ferreiro, J.; Vázquez, E.V. Multifractal and joint multifractal analysis of water and soil losses from erosion plots: A case study under subtropical conditions in Santa Catarina highlands, Brazil. Geoderma 2017, 287, 116–125. [Google Scholar] [CrossRef]
- Jin, Z.; Guo, L.; Wang, Y.; Yu, Y.; Lin, H.; Chen, Y.; Chu, G.; Zhang, J.; Zhang, N. Valley reshaping and damming induce water table rise and soil salinization on the Chinese Loess Plateau. Geoderma 2019, 339, 115–125. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, X.; Ma, L.; Feng, Z.; Tu, W.; Dong, Q.G.; Jiao, F.; Wang, Z. Rainstorm events increase risk of soil salinization in a loess hilly region of China. Agric. Water Manag. 2021, 256, 107081. [Google Scholar] [CrossRef]
- Ke, Z.; Ma, L.; Jiao, F.; Liu, X.; Liu, Z.; Wang, Z. Multifractal parameters of soil particle size as key indicators of the soil moisture distribution. J. Hydrol. 2021, 595, 125988. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, X.; Ma, L.; Dong, Q.; Jiao, F.; Wang, Z. Excavated farmland treated with plastic mulching as a strategy for groundwater conservation and the control of soil salinization. Land Degrad. Dev. 2022, 33, 3036–3048. [Google Scholar] [CrossRef]
- Walter, J.; Lück, E.; Bauriegel, A.; Facklam, M.; Zeitz, J. Seasonal dynamics of soil salinity in peatlands: A geophysical approach. Geoderma 2018, 310, 1–11. [Google Scholar] [CrossRef]
- Wang, J.Y.; Yang, R.; Bai, Z. Spatial distribution of soil salinity and potential implications for soil management in the Manas River watershed, China. Soil Use Manag. 2020, 36, 93–103. [Google Scholar] [CrossRef]
- Mirzavand, M.; Ghasemieh, H.; Javad Sadatinejad, S.; Bagheri, R. Delineating the source and mechanism of groundwater salinization in crucial declining aquifer using multi-chemo-isotopes approaches. J. Hydrol. 2020, 586, 124877. [Google Scholar] [CrossRef]
- Wang, Q.; Huo, Z.; Zhang, L.; Wang, J.; Zhao, Y. Impact of saline water irrigation on water use efficiency and soil salt accumulation for spring maize in arid regions of China. Agric. Water Manag. 2016, 163, 125–138. [Google Scholar] [CrossRef]
- Bao, S.D. Soil Analysis in Agricultural Chemistry; China Agricultural Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Jing, Z.; Wang, J.; Wang, R.; Wang, P. Using multi-fractal analysis to characterize the variability of soil physical properties in subsided land in coal-mined area. Geoderma 2019, 361, 114054. [Google Scholar] [CrossRef]
- Caniego, F.J.; Espejo, R.; Martín, M.A.; José, F.S. Multifractal scaling of soil spatial variability. Ecol. Model. 2005, 182, 291–303. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Horton, R. Single and Joint Multifractal Analysis of Soil Particle Size Distributions. Pedosphere 2011, 21, 75–83. [Google Scholar] [CrossRef]
- Zhou, H.; Li, B.; Lv, Y.; Liu, W. Multifractal characteristics of soil porestructure under different tillage systems. Acta Pedol. Sin. 2010, 47, 1094–1100. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, X.; Ma, L.; Tu, W.; Feng, Z.; Jiao, F.; Wang, Z. Effects of restoration modes on the spatial distribution of soil physical properties after land consolidation: A multifractal analysis. J. Arid Land 2021, 13, 1201–1214. [Google Scholar] [CrossRef]
- Jiménez-Hornero, F.J.; Gutiérrez de Ravé, E.; Ariza-Villarverde, A.B.; Giráldez, J.V. Description of the seasonal pattern in ozone concentration time series by using the strange attractor multifractal formalism. Environ. Monit. Assess. 2010, 160, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, E.V.; Miranda, J.G.V.; Paz-Ferreiro, J. A multifractal approach to characterize cumulative rainfall and tillage effects on soil surface micro-topography and to predict depression storage. Biogeosciences 2010, 7, 2989–3004. [Google Scholar] [CrossRef]
- Perri, S.; Viola, F.; Noto, L.V.; Molini, A. Salinity and periodic inundation controls on the soil-plant-atmosphere continuum of gray mangroves. Hydrol. Process. 2017, 31, 1271–1282. [Google Scholar] [CrossRef]
- Fang, K.; Li, H.; Wang, Z.; Du, Y.; Wang, J. Comparative analysis on spatial variability of soil moisture under different land use types in orchard. Sci. Hortic. 2016, 207, 65–72. [Google Scholar] [CrossRef]
- Cao, Q.; Yang, B.; Li, J.; Wang, R.; Liu, T.; Xiao, H. Characteristics of soil water and salt associated with Tamarix ramosissima communities during normal and dry periods in a semi-arid saline environment. CATENA 2020, 193, 104661. [Google Scholar] [CrossRef]
- Sun, M.; Ren, A.X.; Gao, Z.Q.; Wang, P.R.; Mo, F.; Xue, L.Z.; Lei, M.M. Long-term evaluation of tillage methods in fallow season for soil water storage, wheat yield and water use efficiency in semiarid southeast of the Loess Plateau. Field Crops Res. 2018, 218, 24–32. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Huo, Z.; Adeloye, A.J. A sustainable irrigation water management framework coupling water-salt processes simulation and uncertain optimization in an arid area. Agric. Water Manag. 2020, 231, 105994. [Google Scholar] [CrossRef]
- Taylor, M.; Krüger, N. Changes in salinity of a clay soil after a short-term salt water flood event. Geoderma Reg. 2019, 19, e00239. [Google Scholar] [CrossRef]
- Orr, C.H.; Predick, K.I.; Stanley, E.H.; Rogers, K.L. Spatial Autocorrelation of Denitrification in a Restored and a Natural Floodplain. Wetlands 2014, 34, 89–100. [Google Scholar] [CrossRef]
- Wang, J.; Yang, R.; Bai, Z. Spatial variability and sampling optimization of soil organic carbon and total nitrogen for Minesoils of the Loess Plateau using geostatistics. Ecol. Eng. 2015, 82, 159–164. [Google Scholar] [CrossRef]
- Domenech, M.B.; Castro-Franco, M.; Costa, J.L.; Amiotti, N.M. Sampling scheme optimization to map soil depth to petrocalcic horizon at field scale. Geoderma 2017, 290, 75–82. [Google Scholar] [CrossRef]








| Soil Layers (cm) | Bulk Density (g cm−3) | Field Capacity (%) | Saturated Hydraulic Conductivity (cm min−1) | Clay (0~0.002 mm) % | Silt (0.002~0.02 mm) % | Sand (0.02~2 mm) % | Soil Texture |
|---|---|---|---|---|---|---|---|
| 0–20 | 1.17 | 24.80 | 0.57 | 9.85 | 39.20 | 50.96 | Loam |
| 20–40 | 1.26 | 25.00 | 0.36 | 9.99 | 40.04 | 49.97 | Loam |
| Soil Properties | Soil Layers (cm) | Upstream | Downstream | ||||
|---|---|---|---|---|---|---|---|
| Plot 1 | Plot 2 | Plot 3 | Plot 4 | Plot 5 | Plot 6 | ||
| Soil water | 0–20 | 15.80 | 17.07 | 16.85 | 12.62 | 13.63 | 13.24 |
| content (%) | 20–40 | 17.79 | 18.94 | 19.01 | 14.91 | 15.27 | 16.04 |
| Mean | 16.79 | 18.00 | 17.93 | 13.77 | 14.45 | 14.64 | |
| Soil salt | 0–20 | 0.90 | 0.84 | 0.81 | 0.75 | 0.73 | 0.72 |
| content (g kg−1) | 20–40 | 0.74 | 0.77 | 0.78 | 0.72 | 0.67 | 0.65 |
| Mean | 0.82 | 0.81 | 0.80 | 0.73 | 0.70 | 0.68 |
| Soil Properties | Soil Layers (cm) | Multifractal Parameters | Upstream Farmland | Downstream Farmland | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Plot 1 | Plot 2 | Plot 3 | Mean | Plot 4 | Plot 5 | Plot 6 | Mean | |||
| Soil water | 0–20 | D1 | 1.9694 | 1.9610 | 1.9579 | 1.9628 | 1.9772 | 1.9740 | 1.9846 | 1.9786 |
| ΔD | 0.1929 | 0.4208 | 0.5421 | 0.3853 | 0.1969 | 0.2440 | 0.0774 | 0.1728 | ||
| 20–40 | D1 | 1.9791 | 1.9789 | 1.9743 | 1.9774 | 1.9800 | 1.9768 | 1.9754 | 1.9774 | |
| ΔD | 0.1051 | 0.1594 | 0.2214 | 0.1620 | 0.1601 | 0.2523 | 0.2366 | 0.2163 | ||
| Soil salt | 0–20 | D1 | 1.9817 | 1.9796 | 1.9842 | 1.9818 | 1.9852 | 1.9848 | 1.9857 | 1.9852 |
| ΔD | 0.1655 | 0.1593 | 0.0927 | 0.1392 | 0.0689 | 0.0620 | 0.0711 | 0.0673 | ||
| 20–40 | D1 | 1.9849 | 1.9811 | 1.9829 | 1.9830 | 1.9839 | 1.9855 | 1.9849 | 1.9848 | |
| ΔD | 0.1300 | 0.1397 | 0.1499 | 0.1399 | 0.0829 | 0.0540 | 0.0659 | 0.0676 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, Z.; Liu, X.; Ma, L.; Jiao, F.; Wang, Z. Spatial Distribution of Soil Water and Salt in a Slightly Salinized Farmland. Sustainability 2023, 15, 6872. https://doi.org/10.3390/su15086872
Ke Z, Liu X, Ma L, Jiao F, Wang Z. Spatial Distribution of Soil Water and Salt in a Slightly Salinized Farmland. Sustainability. 2023; 15(8):6872. https://doi.org/10.3390/su15086872
Chicago/Turabian StyleKe, Zengming, Xiaoli Liu, Lihui Ma, Feng Jiao, and Zhanli Wang. 2023. "Spatial Distribution of Soil Water and Salt in a Slightly Salinized Farmland" Sustainability 15, no. 8: 6872. https://doi.org/10.3390/su15086872




