Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance
Abstract
:1. Introduction
2. Literature Review
3. Hypothesis Formulation and Model-Building
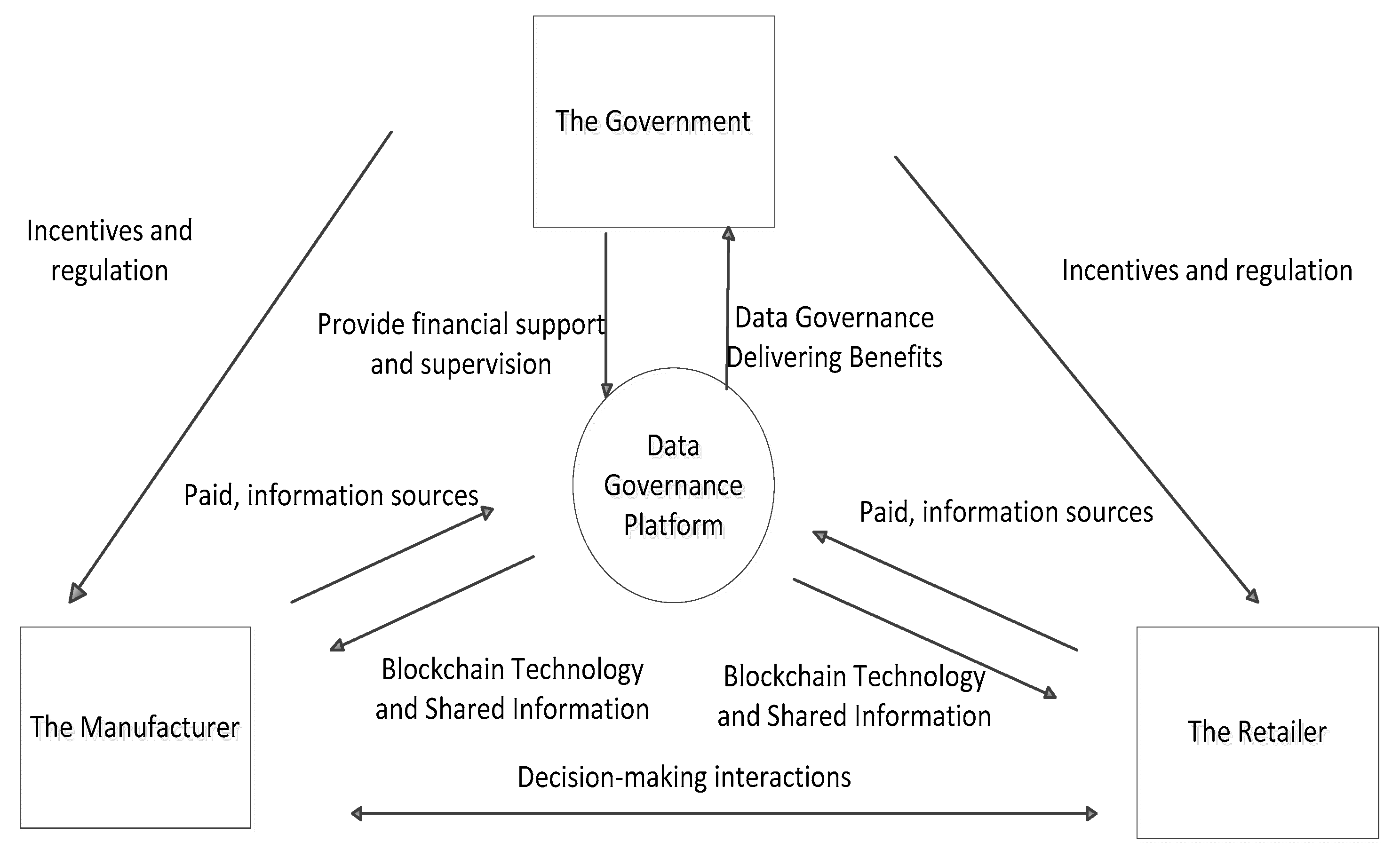
3.1. Problem Hypothesis
3.2. Model Hypothesis
3.3. Model Construction
4. Analysis of the Evolutionary Game Mode and Numerical Study
4.1. Analysis of Evolutionarily Optimal Stabilization Strategies
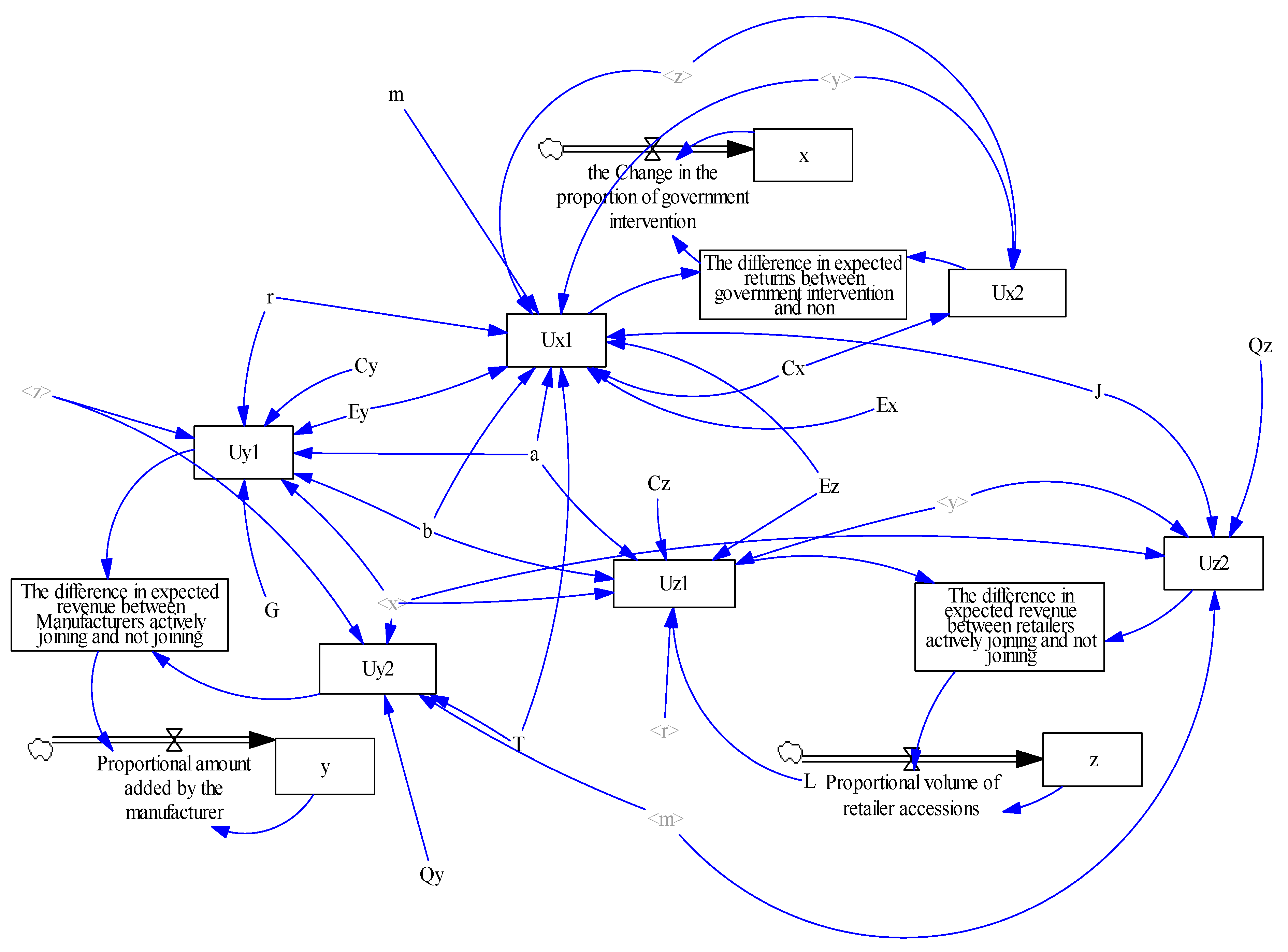
4.2. Model of System Dynamics
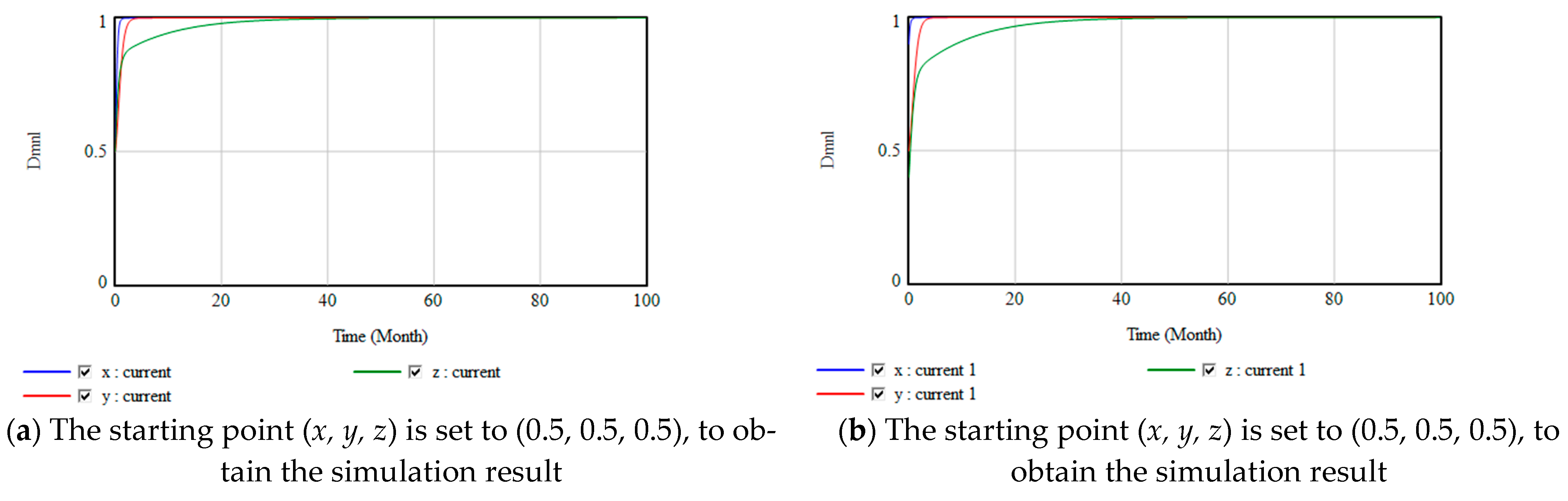
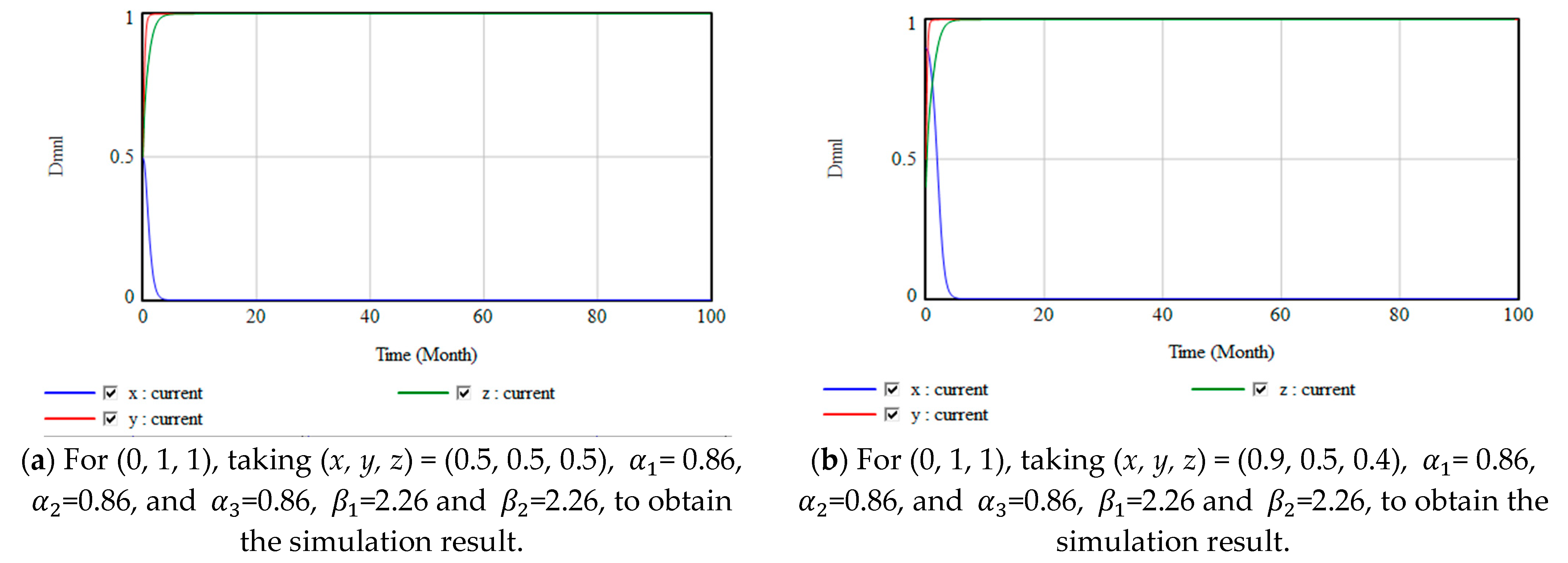
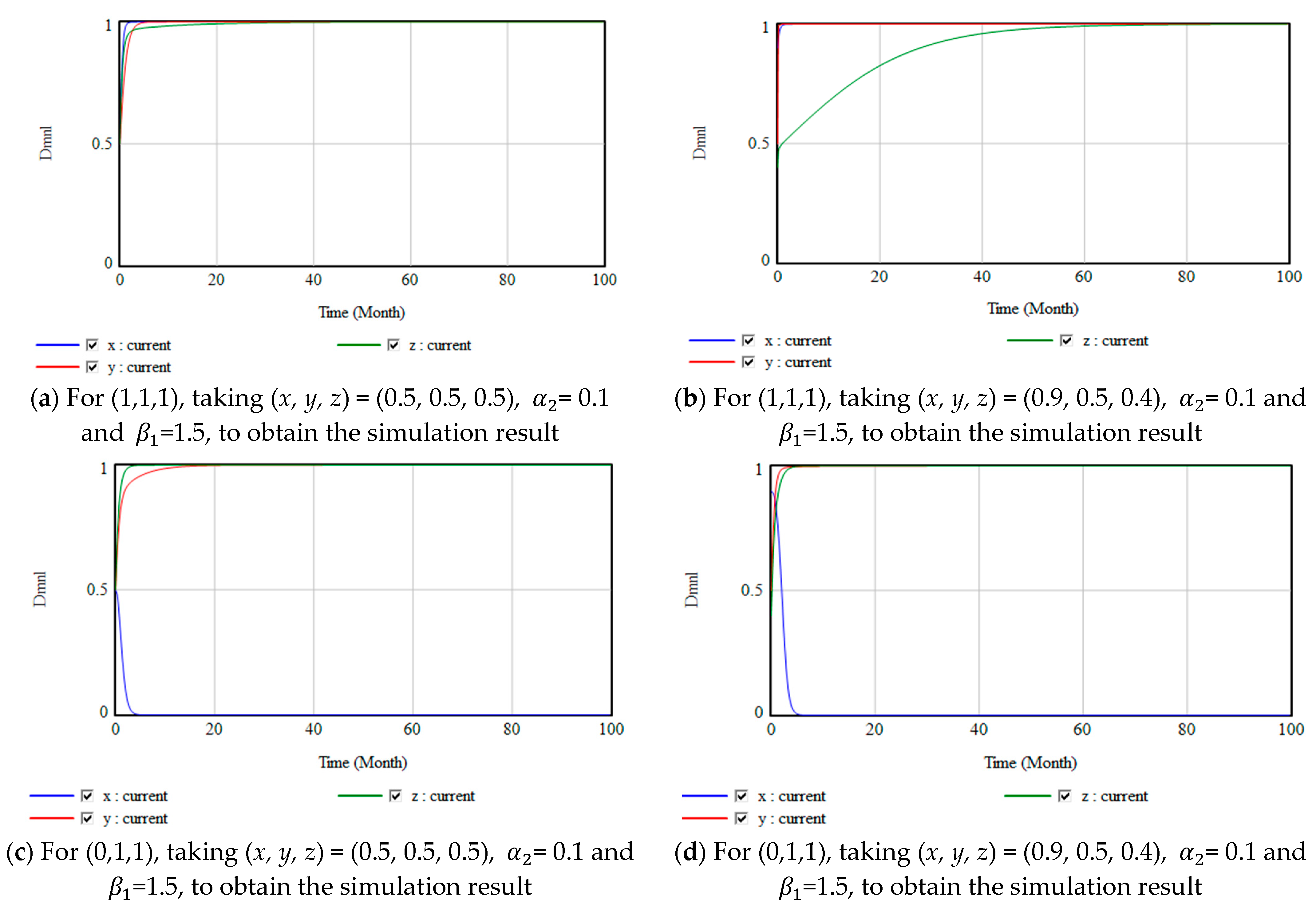
4.3. Simulations
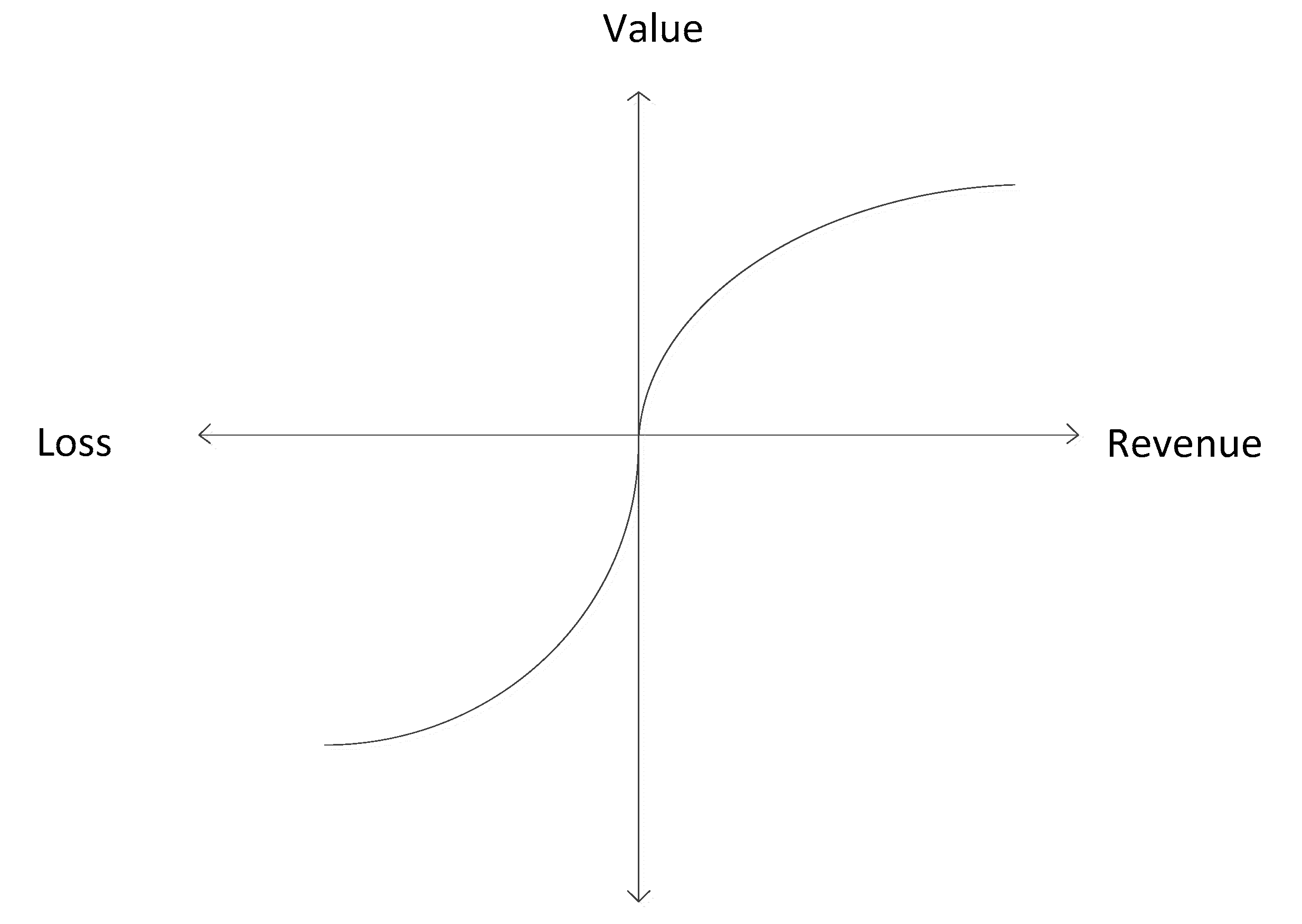
5. Prospect Theory Model Optimization
5.1. Analysis of Evolutionary Game Models under Prospect Theory
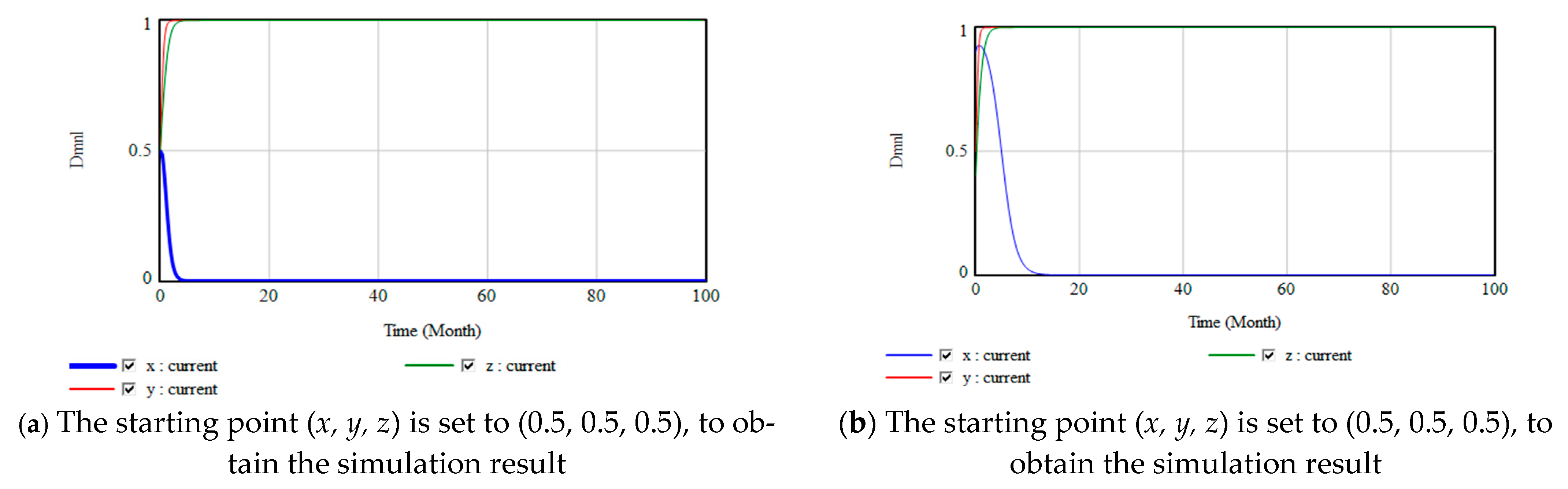
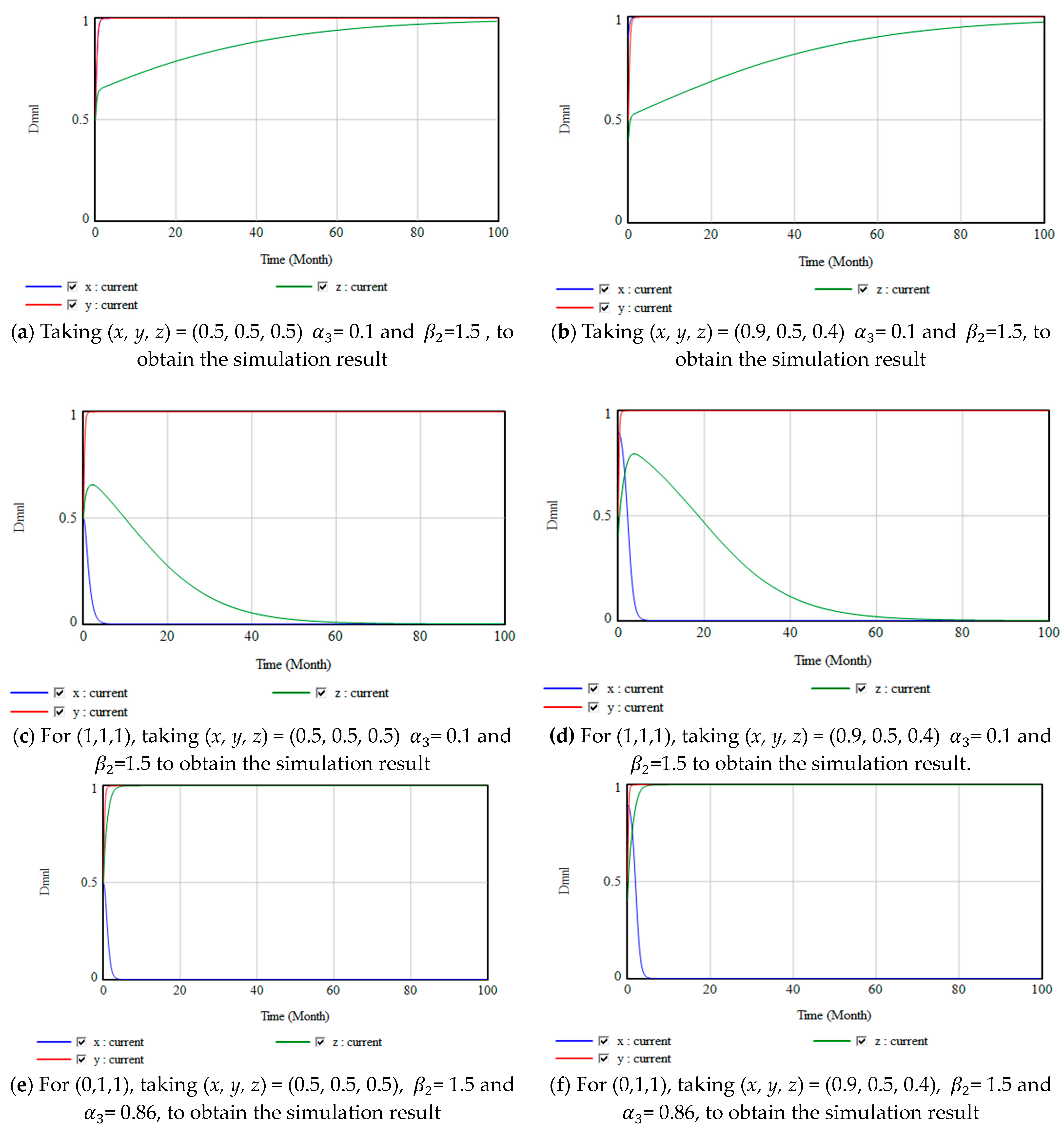
5.2. Simulation Analysis after Optimization
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Addo-Tenkorang, R.; Helo, P.T. Big data applications in operations/supply-chain management: A literature review. Comput. Ind. Eng. 2016, 101, 528–543. [Google Scholar] [CrossRef]
- Baihaqi, I.; Sohal, A.S. The impact of information sharing in supply chains on organisational performance: An empirical study. Prod. Plan. Control. 2013, 24, 743–758. [Google Scholar] [CrossRef]
- Sanders, N.R.; Ganeshan, R. Big Data in Supply Chain Management. Prod. Oper. Manag. 2018, 27, 1745–1748. [Google Scholar] [CrossRef]
- Müller, J.M.; Veile, J.W.; Voigt, K.-I. Prerequisites and incentives for digital information sharing in Industry 4.0—An international comparison across data types. Comput. Ind. Eng. 2020, 148, 106733. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Sun, H.Y. Research on Blockchain Technology Based Manufacturing Supply Chain Management. West. Financ. Account. 2022, 733, 77–79. [Google Scholar] [CrossRef]
- Farooq, M.U.; Hussain, A.; Masood, T.; Habib, M.S. Supply Chain Operations Management in Pandemics: A State-of-the-Art Review Inspired by COVID-19. Sustainability 2021, 13, 2504. [Google Scholar] [CrossRef]
- Xu, X.Y.; Sethi, S.P.; Chung, S.H.; Choi, T.M. Reforming global supply chain management under pandemics: The GREAT-3Rs framework. Prod. Oper. Manag. 2023, 32, 524–546. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, G.C. A Novel Hybrid Methodology to Study the Risk Management of Prefabricated Building Supply Chains: An Outlook for Sustainability. Sustainability 2023, 15, 361. [Google Scholar] [CrossRef]
- Wang, S.L.; Ji, Y.; Wahab, M.I.M.; Xu, D.; Zhou, C.B. A New Decision Framework of Online Multi-Attribute Reverse Auctions for Green Supplier Selection under Mixed Uncertainty. Sustainability 2022, 14, 16879. [Google Scholar] [CrossRef]
- Al-Ruithe, M.; Benkhelifa, E.; Hameed, K. A systematic literature review of data governance and cloud data governance. Pers. Ubiquitous Comput. 2019, 23, 839–859. [Google Scholar] [CrossRef]
- Liu, X.Z.; Sun, S.X.; Huang, G. Decentralized Services Computing Paradigm for Blockchain-Based Data Governance: Programmability, Interoperability, and Intelligence. IEEE Trans. Serv. Comput. 2020, 13, 343–355. [Google Scholar] [CrossRef]
- Yang, X.T.; Li, M.Q.; Yu, H.J.; Wang, M.T.; Xu, D.M.; Sun, C.H. A Trusted Blockchain-Based Traceability System for Fruit and Vegetable Agricultural Products. IEEE Access 2021, 9, 36282–36293. [Google Scholar] [CrossRef]
- Urovi, V.; Jaiman, V.; Angerer, A.; Dumontier, M. LUCE: A blockchain-based data sharing platform for monitoring data license accoUntability and CompliancE. Blockchain Res. Appl. 2022, 3, 100102. [Google Scholar] [CrossRef]
- Sheng, S.Y. Information Sharing Model Construction of Supply Chain Based on Blockchain Technology. Inf. Sci. 2021, 39, 162–168. [Google Scholar] [CrossRef]
- Li, B.; Guo, H.; Peng, S. Impacts of production, transportation and demand uncertainties in the vaccine supply chain considering different government subsidies. Comput. Ind. Eng. 2022, 169, 108169. [Google Scholar] [CrossRef]
- Yu, J.J.; Tang, C.S.; Li, M.K.; Shen, Z.J.M. Coordinating Installation of Electric Vehicle Charging Stations between Governments and Automakers. Prod. Oper. Manag. 2022, 31, 681–696. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, L.; Wang, J.; Wu, D.; Tang, Y. Diffusion of new energy vehicles under incentive policies of China: Moderating role of market characteristic. J. Clean. Prod. 2022, 353, 131660. [Google Scholar] [CrossRef]
- Kumi, S.; Lomotey, R.K.; Deters, R. A Blockchain-based platform for data management and sharing. Procedia Comput. Sci. 2022, 203, 95–102. [Google Scholar] [CrossRef]
- Shen, L.; Yang, Q.; Hou, Y.; Lin, J. Research on information sharing incentive mechanism of China’s port cold chain logistics enterprises based on blockchain. Ocean Coast. Manag. 2022, 225, 106229. [Google Scholar] [CrossRef]
- Luo, X.G.; Zhang, Z.L.; He, J.H.; Hu, S.N. Strategic Analysis of the Parameter Servers and Participants in Federated Learning: An Evolutionary Game Perspective. IEEE Trans. Comput. Soc. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, K.; Dong, F. Government strategy for banning gasoline vehicles: Evidence from tripartite evolutionary game. Energy 2022, 254, 124158. [Google Scholar] [CrossRef]
- Yuan, S.J.; Li, J.; Su, X. Impact of Government Subsidy Strategies on Supply Chains Considering Carbon Emission Reduction and Marketing Efforts. Sustainability 2022, 14, 3111. [Google Scholar] [CrossRef]
- Zhang, M.; Kong, Z. A tripartite evolutionary game model of emergency supplies joint reserve among the government, enterprise and society. Comput. Ind. Eng. 2022, 169, 108132. [Google Scholar] [CrossRef]
- Yang, Z.; Shi, Y.; Li, Y. Analysis of intellectual property cooperation behavior and its simulation under two types of scenarios using evolutionary game theory. Comput. Ind. Eng. 2018, 125, 739–750. [Google Scholar] [CrossRef]
- Göksu, A.; Kocamaz, U.E.; Uyaroğlu, Y. Synchronization and control of chaos in supply chain management. Comput. Ind. Eng. 2015, 86, 107–115. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, W.; Xie, L. Dynamic competitive game study of a green supply chain with R&D level. Comput. Ind. Eng. 2022, 163, 107785. [Google Scholar] [CrossRef]
- Wang, T.; Li, C.; Yuan, Y.; Liu, J.; Adeleke, I.B. An evolutionary game approach for manufacturing service allocation management in cloud manufacturing. Comput. Ind. Eng. 2019, 133, 231–240. [Google Scholar] [CrossRef]
- He, S.-F.; Wang, Y.-M.; Martínez, L. Gaussian IT2FSs-based prospect theory method with application to the evaluation of renewable energy sources. Comput. Ind. Eng. 2022, 169, 108266. [Google Scholar] [CrossRef]
- Xue, W.; Xu, Z.; Mi, X. Solving hesitant fuzzy linguistic matrix game problems for multiple attribute decision making with prospect theory. Comput. Ind. Eng. 2021, 161, 107619. [Google Scholar] [CrossRef]
- Liang, W.; Goh, M.; Wang, Y.-M. Multi-attribute group decision making method based on prospect theory under hesitant probabilistic fuzzy environment. Comput. Ind. Eng. 2020, 149, 106804. [Google Scholar] [CrossRef]




| Parameters | Description |
|---|---|
| The revenue to the government from the platform when the government intervenes in the platform. | |
| The government’s monetary support factor for the manufacturer and the retailer. | |
| The government tax credit factor for the manufacturer and the retailer. | |
| The government tax factor for the manufacturer and the retailer. | |
| The cost of the government regulation of the platform. | |
| The revenue gained by the manufacturer using the platform. | |
| The revenue gained by the manufacturer using the information gap when the manufacturer does not join the platform. | |
| The amount of government penalty for non-compliance with data governance when the manufacturer does not join. | |
| The loss to the manufacturer caused by the lack of data from the retailer when the manufacturer joins the platform. | |
| The fee the manufacturer has to pay to join the platform. | |
| The revenue gained by the retailer using the platform. | |
| The revenue gained by the retailer using the information gap when the retailer does not join the platform. | |
| The amount of government penalty for non-compliance with data governance when the retailer does not join | |
| The loss to the retailer caused by the lack of data from the manufacturer when the retailer joins the platform. | |
| The fee the retailer has to pay to join the platform. | |
| The probability of data governance non-compliance for the manufacturer and the retailer. | |
| The government’s probability of adopting the “intervention” tactic. | |
| The government’s probability of adopting the “non-intervention”tactic. | |
| The manufacturer’s probability of adopting the “joining”tactic. | |
| The manufacturer’s probability of adopting the “not joining”tactic. | |
| The retailer’s probability of adopting the “joining” tactic. | |
| The retailer’s probability of adopting the “not joining” tactic. |
| The Manufacturer | |||
|---|---|---|---|
| The retailer | “joining” (z) | ||
| “not joining” (1 − z) | |||
| The Manufacturer | |||
|---|---|---|---|
| The retailer | “joining” (z) | ||
| “not joining” (1 − z) | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Yi, X.; Yang, X.; Liu, Y. Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance. Sustainability 2023, 15, 6968. https://doi.org/10.3390/su15086968
Wei J, Yi X, Yang X, Liu Y. Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance. Sustainability. 2023; 15(8):6968. https://doi.org/10.3390/su15086968
Chicago/Turabian StyleWei, Jinyu, Xiuping Yi, Xin Yang, and Yaoxi Liu. 2023. "Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance" Sustainability 15, no. 8: 6968. https://doi.org/10.3390/su15086968
APA StyleWei, J., Yi, X., Yang, X., & Liu, Y. (2023). Blockchain-Based Design of a Government Incentive Mechanism for Manufacturing Supply Chain Data Governance. Sustainability, 15(8), 6968. https://doi.org/10.3390/su15086968




