Optimal Planning Approaches under Various Seasonal Variations across an Active Distribution Grid Encapsulating Large-Scale Electrical Vehicle Fleets and Renewable Generation
Abstract
:1. Introduction
- In this paper, three metaheuristic techniques (GWO, WOA, and DO algorithms) for optimal RE-DG allocation, placement of EVCSs, and optimal allocation of hybrid RE-DGs and EVCSs for both single-objective optimization problems (SOOPs) and multi-objective optimization problems (MOOPs) were used. The contributions of this paper are as follows:
- Three metaheuristic techniques were used: GWO, WOA, DO.
- The optimal allocation of REG (solar and WTG) was determined considering uncertainties with four seasonal impacts: spring, summer, autumn, and winter.
- The impact of optimal EVCS placements in RDNs was analyzed.
- The techniques focused on optimal RE-DG allocation problems for MOOPs, with the aim of optimizing four objectives: RPL, QPL, and TVD minimization and VSI maximization.
- The attained objectives were evaluated with related optimization methods.
- The proficiency of the algorithms was assessed across IEEE 33-bus RDNs.
2. Literature Review
3. Problem Formulations
3.1. Objective Functions
3.1.1. Real Power Loss (RPL)
3.1.2. Reactive Power Loss (QPL)
3.1.3. Total Voltage Deviation Minimization (TVD)
3.1.4. Voltage Stability Index Maximization (VSI)
3.2. Formulation of Multi-Objective Function
3.3. System Constraints
3.3.1. Equality Constraints
3.3.2. Inequality Constraints
Voltage Limits
DG Capacity Limits
DG Power Factor Limit
4. Uncertainty Modeling
4.1. Solar Modeling
Solar Irradiance Modeling
4.2. Wind Modeling
4.3. Electrical Vehicle Modeling
4.3.1. EVCS Model, EV Population Estimation, and Study Area
- i.
- Ordinary loads that absorb continuous power while charging, known as the grid to a vehicle (G2V).
- ii.
- Storage devices such as batteries are charged (G2V) and then discharged (V2G) based on the system requirement.
4.3.2. EVCS Characteristics
4.4. Load Modeling
5. Methodology
5.1. Grey Wolf Optimization (GWO)
5.1.1. Encircling
5.1.2. Chasing the Prey
5.1.3. Attacking
5.1.4. Searching for Prey
5.2. Whale Optimization Algorithm (WOA)
5.2.1. Inspiration
5.2.2. Encircling Prey
5.2.3. Rising Bubble Method
5.2.4. Seeking Prey
5.3. Dandelion Optimizer (DO)
5.3.1. Inspiration
5.3.2. Rising Stage
5.3.3. Descending Stage
5.3.4. Landing Stage
6. Simulation Results and Discussions
6.1. IEEE 33-Bus Test System
6.1.1. Multi-Objective Assessment of the 33-Bus RDN
6.1.2. RE-DGs and EVCSs Allocation for the 33-Bus RDN
6.1.3. Scenario 1: Only SPV
Loss Profiles of SPV DGs
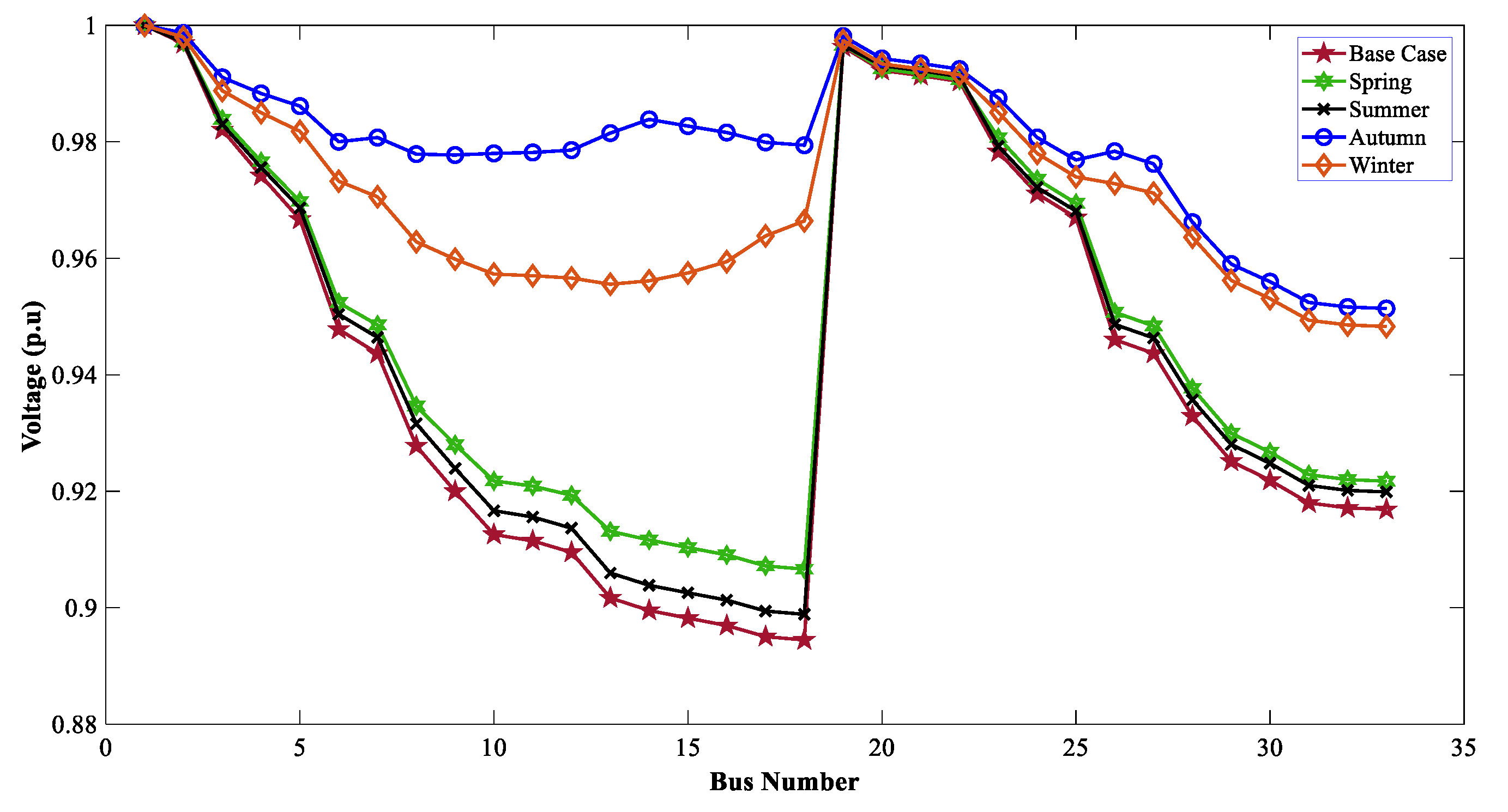
Voltage Profiles of 33-Bus RDN for SPV DGs
6.1.4. Scenario 2: Only WTG
Voltage Profiles of 33-Bus RDN for WTG DGs
6.1.5. Scenario 3: Only EVCSs
6.1.6. Scenario 4: SPV-DGs and EVCSs
Voltage Profiles of the 33-Bus RDN with SPV-DGs and EVCSs
6.1.7. Scenario 5: WTG-DGs and EVCSs
Voltage Profiles of the 33-Bus RDN for WTG, DGs, and EVCSs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akbar, M.I.; Kazmi, S.A.A.; Alrumayh, O.; Khan, Z.A.; Altamimi, A.; Malik, M.M. A Novel Hybrid Optimization-Based Algorithm for the Single and Multi-Objective Achievement with Optimal DG Allocations in Distribution Networks. IEEE Access 2022, 10, 25669–25687. [Google Scholar] [CrossRef]
- Haider, W.; Ul Hassan, S.J.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.H. Voltage profile enhancement and loss minimization using optimal placement and sizing of distributed generation in reconfigured network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. The optimal placement and sizing of distributed generation in an active distribution network with several soft open points. Energies 2021, 14, 1084. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, C.H.; Mehdi, A. A Comprehensive Review of Intelligent Islanding Schemes and Feature Selection Techniques for Distributed Generation System. IEEE Access 2021, 9, 146603–146624. [Google Scholar] [CrossRef]
- Nezhadpashaki, M.A.; Karbalaei, F.; Abbasi, S. Optimal placement and sizing of distributed generation with small signal stability constraint. Sustain. Energy Grids Netw. 2020, 23, 100380. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. A Quasi-Oppositional-Chaotic Symbiotic Organisms Search algorithm for optimal allocation of DG in radial distribution networks. Appl. Soft Comput. J. 2020, 88, 106067. [Google Scholar] [CrossRef]
- Yao, M.; Molzahn, D.K.; Mathieu, J.L. An optimal power-flow approach to improve power system voltage stability using demand response. IEEE Trans. Control Netw. Syst. 2019, 6, 1015–1025. [Google Scholar] [CrossRef]
- Arasteh, A.; Alemi, P.; Beiraghi, M. Optimal allocation of photovoltaic/wind energy system in distribution network using meta-heuristic algorithm. Appl. Soft Comput. 2021, 109, 107594. [Google Scholar] [CrossRef]
- Taha, H.A.; Alham, M.H.; Youssef, H.K.M. Multi-Objective Optimization for Optimal Allocation and Coordination of Wind and Solar DGs, BESSs and Capacitors in Presence of Demand Response. IEEE Access 2022, 10, 16225–16241. [Google Scholar] [CrossRef]
- Hassan, A.S.; Othman, E.A.; Bendary, F.M.; Ebrahim, M.A. Distribution systems techno-economic performance optimization through renewable energy resources integration. Array 2021, 9, 100050. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, C.H.; Jabbar, M.S. An Intelligent Deep Convolutional Neural Networks-Based Islanding Detection for Multi-DG Systems. IEEE Access 2022, 10, 131920–131931. [Google Scholar] [CrossRef]
- Senthil kumar, J.; Charles Raja, S.; Srinivasan, D.; Venkatesh, P. Hybrid renewable energy-based distribution system for seasonal load variations. Int. J. Energy Res. 2018, 42, 1066–1087. [Google Scholar] [CrossRef]
- Zeb, M.Z.; Imran, K.; Khattak, A.; Janjua, A.K.; Pal, A.; Nadeem, M.; Zhang, J.; Khan, S. Optimal Placement of Electric Vehicle Charging Stations in the Active Distribution Network. IEEE Access 2020, 8, 68124–68134. [Google Scholar] [CrossRef]
- Khatibi, M.; Jalilzadeh, S.; Hussain, A.; Haider, W. A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems. Electronics 2022, 11, 3980. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M.; Alsaidan, I.; Almasoudi, F.M. AI-Based Approach for Optimal Placement of EVCS and DG with Reliability Analysis. IEEE Access 2021, 9, 154204–154224. [Google Scholar] [CrossRef]
- Pratap, A.; Tiwari, P.; Maurya, R.; Singh, B. Minimisation of electric vehicle charging stations impact on radial distribution networks by optimal allocation of DSTATCOM and DG using African vulture optimisation algorithm. Int. J. Ambient Energy 2022, 43, 8653–8672. [Google Scholar] [CrossRef]
- Fachrizal, R.; Shepero, M.; Åberg, M.; Munkhammar, J. Optimal PV-EV sizing at solar powered workplace charging stations with smart charging schemes considering self-consumption and self-sufficiency balance. Appl. Energy 2022, 307, 118139. [Google Scholar] [CrossRef]
- Ahmed, A.; Nadeem, M.F.; Sajjad, I.A.; Bo, R.; Khan, I.A.; Raza, A. Probabilistic generation model for optimal allocation of wind DG in distribution systems with time varying load models. Sustain. Energy Grids Netw. 2020, 22, 100358. [Google Scholar] [CrossRef]
- Yenchamchalit, K.; Kongjeen, Y.; Prabpal, P.; Bhumkittipich, K. Optimal placement of distributed photovoltaic systems and electric vehicle charging stations using metaheuristic optimization techniques. Symmetry 2021, 13, 2378. [Google Scholar] [CrossRef]
- Gampa, S.R.; Jasthi, K.; Goli, P.; Das, D.; Bansal, R.C. Grasshopper optimization algorithm based two stage fuzzy multiobjective approach for optimum sizing and placement of distributed generations, shunt capacitors and electric vehicle charging stations. J. Energy Storage 2020, 27, 101117. [Google Scholar] [CrossRef]
- Barik, S.; Das, D. Determining the sizes of renewable DGs considering seasonal variation of generation and load and their impact on system load growth. IET Renew. Power Gener. 2018, 12, 1101–1110. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Adeagbo, A.P.; Adebayo, I.G.; Howlader, H.O.R.; Sun, Y. Modified analytical approach for pv-dgs integration into a radial distribution network considering loss sensitivity and voltage stability. Energies 2021, 14, 7775. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Integrated operation of electric vehicles and renewable generation in a smart distribution system. Energy Convers. Manag. 2015, 89, 99–110. [Google Scholar] [CrossRef]
- Kabir, M.E.; Assi, C.; Tushar, M.H.K.; Yan, J. Optimal Scheduling of EV Charging at a Solar Power-Based Charging Station. IEEE Syst. J. 2020, 14, 4221–4231. [Google Scholar] [CrossRef]
- Kayal, P.; Chanda, S.; Chanda, C.K. An analytical approach for allocation and sizing of distributed generations in radial distribution network. Int. Trans. Electr. Energy Syst. 2017, 27, e2322. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Jalilian, A. Optimal sizing and location of renewable energy based DG units in distribution systems considering load growth. Int. J. Electr. Power Energy Syst. 2018, 101, 356–370. [Google Scholar] [CrossRef]
- Hadidian-Moghaddam, M.J.; Arabi-Nowdeh, S.; Bigdeli, M.; Azizian, D. A multi-objective optimal sizing and siting of distributed generation using ant lion optimization technique. Ain Shams Eng. J. 2018, 9, 2101–2109. [Google Scholar] [CrossRef]
- Elkadeem, M.R.; Abd Elaziz, M.; Ullah, Z.; Wang, S.; Sharshir, S.W. Optimal Planning of Renewable Energy-Integrated Distribution System Considering Uncertainties. IEEE Access 2019, 7, 164887–164907. [Google Scholar] [CrossRef]
- Fathy, A.; Kaaniche, K.; Alanazi, T.M. Recent Approach Based Social Spider Optimizer for Optimal Sizing of Hybrid PV/Wind/Battery/Diesel Integrated Microgrid in Aljouf Region. IEEE Access 2020, 8, 57630–57645. [Google Scholar] [CrossRef]
- Maya, K.N.; Jasmin, E.A. Optimal integration of distributed generation (DG) resources in unbalanced distribution system considering uncertainty modelling. Int. Trans. Electr. Energy Syst. 2017, 27, e2248. [Google Scholar] [CrossRef]
- Wu, F.; Sioshansi, R. A stochastic flow-capturing model to optimize the location of fast-charging stations with uncertain electric vehicle flows. Transp. Res. Part D Transp. Environ. 2017, 53, 354–376. [Google Scholar] [CrossRef]
- De Quevedo, P.M.; Munoz-Delgado, G.; Contreras, J. Impact of Electric Vehicles on the Expansion Planning of Distribution Systems Considering Renewable Energy, Storage, and Charging Stations. IEEE Trans. Smart Grid 2019, 10, 794–804. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, H.; Hu, R.; Qiu, Y. Location of electric vehicle charging stations: A perspective using the grey decision-making model. Energy 2019, 173, 548–553. [Google Scholar] [CrossRef]
- Dixon, J.; Bukhsh, W.; Edmunds, C.; Bell, K. Scheduling electric vehicle charging to minimise carbon emissions and wind curtailment. Renew. Energy 2020, 161, 1072–1091. [Google Scholar] [CrossRef]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2020, 210, 44–59. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Electrical Power and Energy Systems Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. Electrical Power and Energy Systems A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Ranjan, R.; Das, D. Electric Power Components and Systems Voltage Stability Analysis of Radial Distribution Networks. Electr. Power Compon. Syst. 2010, 31, 501–511. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Elazim, S.M.A.; Abdelaziz, A.Y.; Ali, E.S.; Elazim, S.M.A. Electric Power Components and Systems Flower Pollination Algorithm for Optimal Capacitor Placement and Sizing in Distribution Systems Flower Pollination Algorithm for Optimal Capacitor Placement and Sizing in Distribution Systems. Electr. Power Compon. Syst. 2016, 44, 544–555. [Google Scholar] [CrossRef]
- Abd Elazim, S.M.; Ali, E.S. Optimal network restructure via improved whale optimization approach. Int. J. Commun. Syst. 2021, 34, e4617. [Google Scholar] [CrossRef]
- Meena, N.K.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Multi-objective Taguchi approach for optimal DG integration in distribution systems. IET Gener. Transm. Distrib. 2017, 11, 2418–2428. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd Elazim, S.M. Mine blast algorithm for environmental economic load dispatch with valve loading effect. Neural Comput. Appl. 2018, 30, 261–270. [Google Scholar] [CrossRef]
- Sanjay, R.; Jayabarathi, T.; Raghunathan, T.; Ramesh, V.; Mithulananthan, N. Optimal allocation of distributed generation using hybrid grey Wolf optimizer. IEEE Access 2017, 5, 14807–14818. [Google Scholar] [CrossRef]
- Abu-Mouti, F.S.; El-Hawary, M.E. Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm. IEEE Trans. Power Deliv. 2011, 26, 2090–2101. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.H.; Kim, M.K.; Nebhen, J. A novel multiobjective hybrid technique for siting and sizing of distributed generation and capacitor banks in radial distribution systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Oda, E.S.; El Hamed, A.M.A.; Ali, A.; Elbaset, A.A.; El Sattar, M.A.; Ebeed, M. Stochastic optimal planning of distribution system considering integrated photovoltaic-based dg and dstatcom under uncertainties of loads and solar irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Grosan, C. Feature selection via chaotic antlion optimization. PLoS ONE 2016, 11, e0150652. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Han, R.; Zhang, H.; Zhou, J.; Guerrero, J.M. A Multiagent-Based Consensus Algorithm for Distributed Coordinated Control of Distributed Generators in the Energy Internet. IEEE Trans. Smart Grid 2015, 6, 3006–3019. [Google Scholar] [CrossRef]
- Ebeed, M.; Ali, A.; Mosaad, M.I.; Kamel, S. An improved lightning attachment procedure optimizer for optimal reactive power dispatch with uncertainty in renewable energy resources. IEEE Access 2020, 8, 168721–168731. [Google Scholar] [CrossRef]
- Zubo, R.H.A.; Mokryani, G.; Abd-Alhameed, R. Optimal operation of distribution networks with high penetration of wind and solar power within a joint active and reactive distribution market environment. Appl. Energy 2018, 220, 713–722. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Fu, Q.; Yu, D.C.; Zhang, L. Economic allocation for energy storage system considering wind power distribution. IEEE Trans. Power Syst. 2015, 30, 644–652. [Google Scholar] [CrossRef]
- John Hetzer, D.C.Y.K.B. An Economic Dispatch Model Incorporating Wind Power. IEEE Trans. Energy Convers. 2012, 23, 56. [Google Scholar] [CrossRef]
- Battapothula, G.; Yammani, C.; Maheswarapu, S. Multi-objective simultaneous optimal planning of electrical vehicle fast charging stations and DGs in distribution system. J. Mod. Power Syst. Clean Energy 2019, 7, 923–934. [Google Scholar] [CrossRef]
- Tounsi Fokui, W.S.; Saulo, M.J.; Ngoo, L. Optimal Placement of Electric Vehicle Charging Stations in a Distribution Network with Randomly Distributed Rooftop Photovoltaic Systems. IEEE Access 2021, 9, 132397–132411. [Google Scholar] [CrossRef]
- Basics of Charging. City of Phoenix. 2022. Available online: https://www.phoenix.gov/sustainabilitysite/Pages/Basics-of-Charging.aspx (accessed on 8 January 2023).
- Taha, I.B.M.; Elattar, E.E. Optimal reactive power resources sizing for power system operations enhancement based on improved grey wolf optimiser. IET Gener. Transm. Distrib. 2018, 12, 3421–3434. [Google Scholar] [CrossRef]
- Muro, C.; Escobedo, R.; Spector, L.; Coppinger, R.P. Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 88, 192–197. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]



























| Ref. | Optimization Methods | Objectives | Seasonal Variations | Uncertainty Modeling of RER | |||
|---|---|---|---|---|---|---|---|
| APL | QPL | TVD | VSI | ||||
| [35] | Hybrid PV-WT system | X | X | X | X | X | ✓ |
| [20] | GOA | ✓ | X | ✓ | X | X | X |
| [13] | PSO | ✓ | ✓ | ✓ | X | X | ✓ |
| [27] | ALO | ✓ | X | ✓ | X | X | X |
| [32] | MILP | ✓ | X | X | X | X | X |
| [10] | WOA, SCA, MVOA | ✓ | X | X | ✓ | X | X |
| [9] | GAMS Theory | ✓ | X | ✓ | X | X | ✓ |
| [31] | SFCLM | ✓ | X | X | X | X | ✓ |
| [28] | HHO and PSO | ✓ | X | ✓ | ✓ | X | ✓ |
| [15] | HGWOPSO | ✓ | X | ✓ | ✓ | X | ✓ |
| [29] | SSO | X | X | X | X | X | ✓ |
| [16] | AVOA | ✓ | X | ✓ | ✓ | X | X |
| [12] | HNM-PSO | ✓ | ✓ | X | ✓ | ✓ | ✓ |
| [21] | SOA | ✓ | X | ✓ | X | ✓ | ✓ |
| [8] | IWOA | ✓ | X | X | ✓ | ✓ | ✓ |
| [P] | GWO, WOA, DO | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Power Demand | Active Power (kW) | Reactive Power (kVAR) | Apparent Power (kVA) |
|---|---|---|---|
| IEEE 33 node network | 3715 | 2300 | 4369.35 |
| Institutional Load (EV) | 3231.19 | 2289.56 | 3960.133 |
| EV Model | EV Specifications | Charging Type | |||
|---|---|---|---|---|---|
| Level 2 (19.2 kW) | Level 3 (50 kW) | ||||
| Charging Time | No. of EVs | Charging Time | No. of EVs | ||
| Nissan Leaf 2018 | 40 kWh, 220 km | 2 h 5 m | 16 | 48 m | 34 |
| MG ZS EV | 44.5 kWh, 220 km | 2 h 19 m | 18 | 53 m | 32 |
| Total number of EVs | 34 | 66 | |||
| Charger | Rating of CP (kW) | No CP per EVCS | Rating of EVCS (kW) | No of EVCS | Total Rating (kW) |
|---|---|---|---|---|---|
| Level 2 | 19.2 | 15 | 288 | 2 | 576 |
| Level 3 | 50 | 10 | 500 | 3 | 1500 |
| Total no of EVCSs and power demand | 5 | 2076 | |||
| Algorithms | Parameters |
|---|---|
| GWO | Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000 |
| WOA | Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000 |
| DO | Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000 |
| Scenarios | SPV | WTG | EVCSs |
|---|---|---|---|
| Scenario 1 | ✓ | X | X |
| Scenario 2 | X | ✓ | X |
| Scenario 3 | X | X | ✓ |
| Scenario 4 | ✓ | X | ✓ |
| Scenario 5 | X | ✓ | ✓ |
| Methods | Location | P (MW) | Q (MVAR) | RPL (kW) (%) | QPL (kVAR) (%) | TVD (p.u) | VSI (p.u) |
|---|---|---|---|---|---|---|---|
| Base case | - | - | - | 210.05 | 142.44 | 0.1328 | 0.6697 |
| GWO [P] | 14, 25, 32 | 0.688, 0.793, 1.306 | 0.246, 0.334, 0.503 | 65.5066 (68.813%) | 45.8701 (67.797%) | 0.003824 | 0.92513 |
| WOA [P] | 12, 24, 31 | 0.816, 0.952, 1.085 | 0.297 0.303, 0.398 | 56.8897 (72.913%) | 38.7945 (72.764%) | 0.002839 | 0.94655 |
| DO [P] | 14, 24, 30 | 0.809, 0.833, 1.072 | 0.213, 0.253, 0.477 | 61.5987 (70.674%) | 45.1846 (68.278%) | 0.004336 | 0.92127 |
| Methods | Location | P (MW) | Q (MVAR) | RPL (kW) (%) | QPL (kVAR) (%) | TVD (p.u) | VSI (p.u) |
|---|---|---|---|---|---|---|---|
| Base Case | - | - | - | 210.05 | 142.44 | 0.1328 | 0.6697 |
| GWO [P] | 13, 24, 30 | 0.772, 0.922, 1.348 | 0.258, 0.324, 0.584 | 49.4825 (76.44%) | 34.7879 (75.577%) | 0.004624 | 0.89905 |
| WOA [P] | 13, 24, 30 | 0.765, 0.880, 1.452 | 0.372, 0.381, 0.643 | 54.0478 (74.269%) | 40.4329 (71.614%) | 0.009322 | 0.84611 |
| DO [P] | 13, 24, 30 | 0.853, 1.006, 1.266 | 0.425, 0.457, 0.510 | 54.083 (74.252%) | 36.823 (74.148%) | 0.005671 | 0.97896 |
| Methods | Location | P (MW) | Q (MVAR) | RPL (kW) (%) | QPL (kVAR) (%) | TVD (p.u) | VSI (p.u) |
|---|---|---|---|---|---|---|---|
| Base Case | - | - | - | 210.05 | 142.44 | 0.1328 | 0.6697 |
| GWO [P] | 4, 12, 13, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | 267.1758 (27.187%) | 181.1311 (27.166%) | - | - |
| WOA [P] | 2, 3, 4, 9, 13 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | 262.1438 (24.792%) | 177.1492 (24.371%) | - | - |
| DO [P] | 6, 12, 17, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | 280.4705 (33.516%) | 189.8264 (33.271%) | - | - |
| Methods | SPV and EVCSs | Location | P (MW) | Q (MVAR) | RPL (kW) (%) | QPL (kVAR) (%) | TVD (p.u) | VSI (p.u) |
|---|---|---|---|---|---|---|---|---|
| Base Case | - | - | - | 210.05 | 142.44 | 0.1328 | 0.6697 | |
| GWO [P] | SPV | 9, 23, 29 | 0.725, 0.939, 1.159 | 0.281, 0.292, 0.491 | 79.4624 (62.170%) | 62.3089 (56.256%) | 0.005726 | 0.94724 |
| EVCSs | 4, 12, 13, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | |||||
| WOA [P] | SPV | 8, 22, 29 | 0.690, 0.973, 1.099 | 0.231, 0.392, 0.495 | 54.0478 (74.269%) | 40.4329 (71.614%) | 0.009322 | 0.84611 |
| EVCSs | 2, 3, 4, 9, 13 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | |||||
| DO [P] | SPV | 13, 22, 29 | 0.768, 0.977, 1.330 | 0.331, 0.391, 0.571 | 63.8158 (69.619%) | 45.4183 (68.114%) | 0.005419 | 0.94821 |
| EVCSs | 6, 12, 17, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 |
| Methods | SPV and EVCSs | Location | P (MW) | Q (MVAR) | RPL (kW) (%) | QPL (kVAR) (%) | TVD (p.u) | VSI (p.u) |
|---|---|---|---|---|---|---|---|---|
| Base Case | - | - | - | 210.05 | 142.44 | 0.1328 | 0.6697 | |
| GWO [P] | WTG | 6, 14, 28 | 0.604, 1.015, 1.324 | 0.235, 0.344, 0.507 | 76.4404 (63.608%) | 57.8867 (59.361%) | 0.009827 | 0.92341 |
| EVCSs | 4, 12, 13, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | |||||
| WOA [P] | WTG | 11, 18, 29 | 0.577, 1.167, 1.173 | 0.166, 0.248, 0.543 | 89.6694 (57.310%) | 69.5078 (51.202%) | 0.005515 | 0.92139 |
| EVCSs | 2, 3, 4, 9, 13 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 | |||||
| DO [P] | WTG | 9, 20, 28 | 0.746, 0.912, 0.951 | 0.228, 0.418, 0.426 | 90.207 (57.055%) | 65.3175 (54.144%) | 0.02631 | 0.79254 |
| EVCSs | 6, 12, 17, 22, 25 | 1.332, 0.546, 1.497, 0.546, 1.299 | 0.841, 0.345, 0.945, 0.345, 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huzaifa, M.; Hussain, A.; Haider, W.; Kazmi, S.A.A.; Ahmad, U.; Rehman, H.U. Optimal Planning Approaches under Various Seasonal Variations across an Active Distribution Grid Encapsulating Large-Scale Electrical Vehicle Fleets and Renewable Generation. Sustainability 2023, 15, 7499. https://doi.org/10.3390/su15097499
Huzaifa M, Hussain A, Haider W, Kazmi SAA, Ahmad U, Rehman HU. Optimal Planning Approaches under Various Seasonal Variations across an Active Distribution Grid Encapsulating Large-Scale Electrical Vehicle Fleets and Renewable Generation. Sustainability. 2023; 15(9):7499. https://doi.org/10.3390/su15097499
Chicago/Turabian StyleHuzaifa, Muhammad, Arif Hussain, Waseem Haider, Syed Ali Abbas Kazmi, Usman Ahmad, and Habib Ur Rehman. 2023. "Optimal Planning Approaches under Various Seasonal Variations across an Active Distribution Grid Encapsulating Large-Scale Electrical Vehicle Fleets and Renewable Generation" Sustainability 15, no. 9: 7499. https://doi.org/10.3390/su15097499







