Abstract
Optimizing traffic control systems at traffic intersections can reduce network-wide fuel consumption as well as improve traffic flow. While traffic signals have conventionally been controlled based on predetermined schedules, various adaptive control systems have been developed recently using advanced sensors such as cameras, radars, and LiDARs. By utilizing rich traffic information enabled by the advanced sensors, more efficient or optimal traffic signal control is possible in response to varying traffic conditions. This paper proposes an optimal traffic signal control method to minimize network-wide fuel consumption utilizing real-time traffic information provided by advanced sensors. This new method employs a priority metric calculated by a weighted sum of various factors, including the total number of vehicles, total vehicle speed, vehicle waiting time, and road preference. Genetic Algorithm (GA) is used as a global optimization method to determine the optimal weights in the priority metric. In order to evaluate the effectiveness of the proposed method, a traffic simulation model is developed in a high-fidelity traffic simulation environment called SUMO, based on a real-world traffic network. The traffic flow within this model is simulated using actual measured traffic data from the traffic network, enabling a comprehensive assessment of the novel optimal traffic signal control method in realistic conditions. The simulation results show that the proposed priority metric-based real-time traffic signal control algorithm can significantly reduce network-wide fuel consumption compared to the conventional fixed-time control and coordinated actuated control methods that are currently used in the modeled network. Additionally, incorporating truck priority in the priority metric leads to further improvements in fuel consumption reduction.
1. Introduction
As the transportation sector accounts for 67% of the United States’ petroleum consumption, reducing transportation fuel consumption is crucial to overall petroleum consumption reduction in the country [1]. Among various factors contributing to transportation fuel consumption, traffic congestion has a significant impact on network-wide fuel consumption by causing frequent stops of vehicles and extending their travel times in the traffic network. Due to this fact, efficient or optimal traffic signal control is gaining increased attention as an effective means to reduce network-wide fuel consumption and alleviate traffic congestion within the traffic network.
Traditional traffic signal control methods, characterized by fixed signal phase and timing, are inefficient, leading to increased travel times for vehicles and elevated network-wide fuel consumption. With the advent of vehicle-detecting sensors, actuated traffic control methods have been implemented at real-world traffic intersections. However, the currently utilized actuated control methods employing proximity sensors still exhibit room for improvement. Recent advancements in traffic monitoring technologies using advanced sensors, such as cameras and radars, have opened the door to the development of new traffic control methods.
In order to further improve the network-wide energy efficiency of the vehicles, a new traffic signal control method is proposed in this paper. By utilizing real-time traffic data from advanced sensors, such as roadside cameras and radars, it is possible to obtain rich and diverse traffic information, including the number of vehicles, total vehicle speed, and total vehicle waiting time in each traffic phase. The proposed novel control method employs various combinations of this diverse traffic information to control traffic signals at multiple intersections optimally. Simulation results based on a real-world traffic network with actual traffic data reveal significant improvements in the network-wide energy efficiency compared to a conventional fixed-time method and a sensor-based actuated coordinated control method. It is also shown that incorporating additional information on vehicle type further improves network-wide fuel efficiency. Optimal control of traffic signals at multiple intersections using diverse traffic information is novel and will pave the way for similar research as more efficient and cost-effective advanced sensors are developed.
The remainder of this paper is organized as follows. Section 2 provides a literature review of traffic data collection technologies and control methods. Section 3 presents the simulation environment, including the network model, traffic volume model, and vehicle models. Section 4 describes the conventional fixed-time control method for comparison purposes. Section 5 introduces the proposed optimal control method. In Section 6, the performance of the methods is compared in terms of network-wide fuel consumption. Lastly, Section 7 concludes the paper and suggests directions for future research.
2. Related Works
To design a new traffic control method, related studies are investigated. Traffic data collection technologies and traffic signal control with optimization methods are presented from traditional ways to recent feasible ways.
2.1. Traffic Data Collection Technologies
The development of proximity sensors that can detect the presence of vehicles in an intersection enabled adaptive traffic signal control based on real-time traffic conditions. For example, inductive loop sensors [2] and wireless magnetometer sensors [3] have been used to control traffic signals based on changing traffic conditions. As opposed to the conventional fixed-time traffic signal control systems, these adaptive traffic signal control systems can respond to real-time traffic changes by utilizing basic information provided by proximity sensors. Although proximity sensors can provide basic traffic information, such as the presence of a vehicle at a stop line, it has been difficult to develop optimal traffic signal control systems based on this simple limited information. The recent advancement in vehicle detection technologies using roadside cameras and radars has enabled the collection of more diverse traffic information, including the type, size, and speed of multiple vehicles approaching the traffic intersection.
With the assistance of machine learning algorithms, cameras have been used to detect and track vehicles within a traffic network. For example, one study utilized various deep-learning methods and a novel data association algorithm to estimate and monitor traffic flow on a highway in real-time [4]. By providing accurate and reliable traffic flow estimations, this system can be used for effective traffic management and help alleviate congestion on highways. Another study combined stereo vision and deep learning to reconstruct precise vehicle locations in a traffic scene [5]. This system used multiple cameras to capture video footage of a traffic scene and then processed the video frames with a deep neural network to construct 3D bounding boxes around detected vehicles, yielding vehicle location and speed data. The system could also classify vehicle types based on the size of the 3D bounding box. The results showed an average vehicle localization error of 1.81 m using differential GPS as a reference and 1.68 m using a drone as a reference. Additionally, other studies have applied computer vision algorithms to estimate and monitor traffic flow using multiple cameras, potentially enhancing traffic safety and efficiency in a cost-effective manner [6,7]. A simple and effective approach was also reported to compensate for errors in localizing vehicle centers detected by a single traffic camera and processed by YOLO. The error was corrected using regression models trained with rectangular prism images. When tested with stationary vehicles in a parking lot and a moving vehicle at a traffic intersection, the results showed average vehicle localization errors of 0.43 m and 1.52 m, respectively [8].
Radar-based object detection methods have also shown great promise, achieving accuracy rates of 99% or higher in classifying vehicle types using confusion matrices in both parallel and serial input convolutional neural network (CNN) structures [9]. While cameras exhibit a detection range of 80 m [8], fusing camera detection with radar detection has the potential to extend the range of vehicle detection. Recent research has suggested that radar-based object identification is particularly suited for real-time scenarios, boasting a detection range of up to 300 m [10]. These advanced traffic information collection technologies enable more sophisticated control of traffic signals based on real-time information on the total number of vehicles, their collective speed, and the type of vehicles approaching an intersection.
2.2. Traffic Control and Optimization Methods
Conventionally, traffic signals have been controlled by a fixed-time method where predetermined signal phase and timing for different phases are used to change traffic signals [11]. Both fixed-time and adaptive traffic signal control systems have been applied to coordinated control of neighboring intersections as well as single intersections. For example, MAXBAND [12] and TRAffic Network StudY Tool (TRANSYT) [13] were developed for fixed-time coordinated control of neighboring intersections. MAXBAND program was used to define offsets between intersections to maximize traffic throughput without stops at the intersections based on the speed limit. TRANSYT program determines offset time by decreasing average vehicle travel time. However, signal phase and timing in these fixed-time coordinated control methods were determined based on historical traffic data and could be used only for undersaturated traffic areas [14]. As an adaptive coordinated control method responsive to changing traffic conditions, the split, cycle, and offset optimization technique (SCOOT) [15] was developed. Furthermore, optimization policies for adaptive control (OPAC) [16] and PRODYN [17] were developed as model-based optimization methods. These methods collect real-time traffic data and calculate appropriate control parameters to optimally control neighboring traffic signals [14]. A recent study employed a fuzzy controller with a multi-objective differential evolution algorithm to implement coordinated control in an urban traffic network model, aiming to reduce the average vehicle delay [18]. Another study proposed a coordinated control optimization method based on an asymmetrical multiband model, incorporating phase optimization to minimize vehicle delays and exhaust gas emissions [19]. For the optimization of traffic signal control parameters, several different optimization methods have been utilized. A study utilized the generalized reduced gradient (GRG) nonlinear method built in MS Excel to optimize the phase length and cycle of two isolated traffic signals [20]. Genetic Algorithm (GA) has been widely applied in many different traffic signal optimization problems [21,22,23,24]. Particle swarm optimization (PSO) has also been used as an effective optimization algorithm for traffic signal systems to reduce emissions and fuel consumption [25,26,27].
Assuming that rich and diverse traffic information is available through the use of advanced sensors, emissions of different vehicle types were considered in a simulation study [28]. However, this study was based on a simplified traffic grid model without considering actual road or real traffic data. Other studies based on actual road and traffic data distinguished vehicle types and evaluated their control methods [29,30]. Yet, these studies did not provide vehicle specifications, and the proposed method was not compared to any other adaptive traffic signal control systems. Another study investigated an adaptive traffic signal control system that utilized vehicle speed information received from a vehicle-to-infrastructure (V2I) communication system [31]. However, this research was limited to a simplified intersection without a left-turn lane, and the vehicle speeds were randomly generated rather than based on real-world data.
To overcome these deficiencies, a new real-time optimal traffic signal control method based on advanced traffic information is proposed and presented for a real road using real traffic data in this paper. The proposed control method is simulated under real road conditions, and the results are compared to those of a fixed-time coordinated method and an actuated coordinated method based on the NEMA configuration [32].
3. Traffic Simulation Environment
In this study, the performances of conventional traffic signal controllers are evaluated together with the proposed algorithm over a traffic corridor, including three intersections in a simulation environment called Simulation of Urban MObility (SUMO) [33]. The target traffic corridor is recreated in the SUMO simulation environment, and real-world historical data are used to build the traffic volume model and then calibrate the microsimulation model.
3.1. Traffic Network Model
In SUMO, the network file contains the definition of road geometry, lane layout, intersection type, and traffic signal parameters. Figure 1 shows the completed network model overlaid on an aerial image, with three intersections labeled TL1, TL2, and TL3, from west to east. Detailed configurations of the three intersections are also shown in Figure 2. This traffic network lies to the north of Tuscaloosa, Alabama, and represents a portion of US82, which connects Tuscaloosa to smaller towns to the west. TL1 serves the aptly named Airport Rd., which in addition to the Airport, also connects to an industrial district. This industrial district, in combination with the truck traffic entering and leaving Tuscaloosa on US82, contributes to heavy truck traffic in the network. Per the Alabama Department of Transportation data, the average annual daily traffic (AADT) of the main road was 23,888 in 2021, and the average annual daily truck traffic (AADTT) was 11% at TL2, which is higher than the Tuscaloosa average [34]. Additionally, the speed limit of the main road is 50 mph (80 km/h), while the side roads have limits ranging from 35 to 45 mph (56.3–72.4 km/h). Pedestrians and bikes are not allowed on the main road.
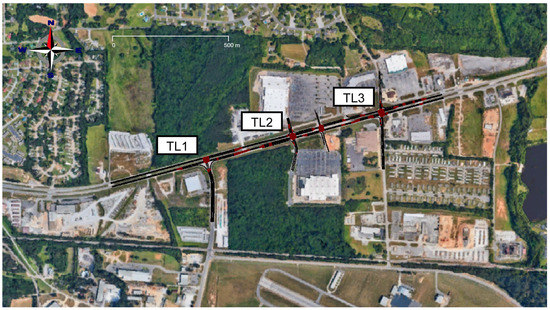
Figure 1.
SUMO network model for the road network of interest overlaid on an aerial image obtained from Google Earth.
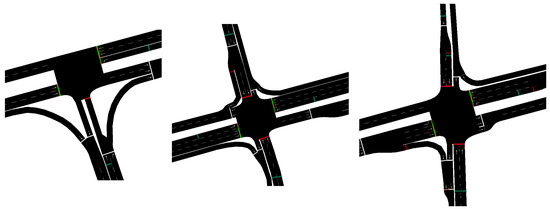
Figure 2.
Detailed configurations of three intersections, TL1, TL2, and TL3, from left to right with green and red lines indicating green and red traffic lights, respectively.
In the dimensionally accurate model, induction-loop vehicle detectors are added in locations based on documentation from the transportation authority. As the primary means of calibration, the simulation detectors are placed to match the real locations to enable a fair comparison between simulation and real-world detector data. Each real-world intersection in the study area has additional “hockey-puck” detectors. Although not used for traffic signal control, these single-lane detectors are used for augmenting traffic volume data in the eastbound and westbound directions. In addition to the “hockey-puck” detectors, all intersections have left turns and side-street detectors at the stop bar, each being 50 feet long. The network file also contains information on the intersection layout, including valid turn movements and the signal layout. Google Street View, Google Maps, and the local transportation authority are used to determine the turning movements and signal layouts.
3.2. Traffic Volume Model
All three traffic signals in the real-world network of interest are equipped with high-resolution data loggers, which store detector events as well as traffic signal states at a resolution of 100 milliseconds. The recorded traffic volume vs. location information is processed using a SUMO tool called “routeSampler”. This tool uses integer linear programming (ILP) to generate vehicle trips (trip defines the route and the departure probability inside of a time window) that satisfy the traffic counts at each location. It takes a pool of possible routes to select from as input, which is defined by the user. To create the pool of trips, the SUMO tool “randomTrips” is used to generate a list of possible routes in the network layout. It is weighted towards a preference for routes that utilize multi-lane roads. Owing to the layout of the network of interest, only routes that start and end at the network’s boundaries can be considered realistic, and thus all routes not meeting this condition are removed from the routeSampler input pool. The output of the routeSampler is then fed to the simulation as an input. The corresponding simulated traffic volumes pass USDOT calibration [35].
3.3. Vehicle Model
Several vehicle emissions and fuel consumption models are included in SUMO, as reviewed in previous literature [36,37]. For this study, TU Graz’s PHEMLight model, which approximates EU standard vehicles, is selected due to its superior performance compared to other SUMO models [37]. Although the network of interest is in the U.S. and not Europe, the PHEMLight model is still considered appropriate to assess the relative performance of traffic signal controllers. To account for the fact that traffic in the real network is not comprised of a homogeneous fleet, two vehicle classes are used to approximate the fuel consumption. The first class is a standard car (PC_D_EU4 in PHEMLight), while the second class is a class 8 truck with a trailer (HDV_TT_D_EU6 in PHEMLight), which is commonly used for freight transportation. This approach allows for a more accurate assessment of the fuel consumption of the network, as well as separate treatment in the control scheme since heavy-duty trucks consume considerably more fuel. The Intelligent Driver Model (IDM) car-following model [38] is employed for all simulated vehicles, and each vehicle is sampled from a distribution of model parameters to capture the variability in driving behaviors among different drivers. The simulation assumes a weight of 1285 kg for passenger cars and 29,945 kg for trucks.
4. Conventional Traffic Control System
Conventional traffic control systems have been based on either fixed-time or simple adaptive algorithms using proximity sensors. In both cases, the traffic signal sequence is predetermined with small variations based on the time of the day or binary detection of vehicles using proximity sensors. A typical design of a traffic control system begins with the definition of the traffic signal phases.
4.1. Traffic Signal Phases
In this study, traffic signal phases are defined based on the Traffic Signal Design Guide and Timing Manual [39] published by the Alabama Department of Transportation (ALDOT). In Figure 3, a standard phase numbering convention is shown for all traffic movements except the right turns. This standardized representation of traffic movements allows convenience in programming, modeling, and calculation of signal control parameters. In the ALDOT manual, standard two-phase, four-phase, and eight-phase operations are described based on traffic demands at a four-way intersection. Eight possible phase combinations of the standard eight-phase directions can be utilized, as shown in Figure 4, for four-way intersections, as the eight-phase operation allows efficient traffic signal control for a given traffic demand. For three-way intersections, three different phase combinations can be utilized, as shown in Figure 5. For each intersection, phase combinations are classified into two types, primary and secondary, as shown in Figure 4 and Figure 5. The combination of 2 + 6 phases is designated as primary, and all the other phase combinations are considered as secondary. The purpose of this classification is to assign a higher priority to the main road than the other side roads since traffic on the main road is responsible for the majority of traffic volume.

Figure 3.
Standard ALDOT phase numbering convention.

Figure 4.
Eight phase combinations for four-way intersection.

Figure 5.
Three phase combinations for three-way intersection.
In Figure 6 and Figure 7, aerial images of four-way and three-way intersections in the traffic corridor used in the research are shown with phase combinations. In the figures, the primary phase combination of 2 + 6 phases is clearly identified as the main road serving the majority of the traffic volume in the state route 82, while all side roads constitute secondary phase combinations.

Figure 6.
Four-way intersection with phase numbering.

Figure 7.
Three-way intersection with phase numbering.
4.2. Conventional Traffic Control Logics
Phase operations suggested by the ALDOT traffic manual are used to design conventional control logic. As a baseline control algorithm for the comparison study, a fixed-time four-phase logic is used for the four-way intersections, and a fixed-time three-phase logic is used for the three-way intersection. Moreover, for the actuated and coordinated control, eight-phase dual-ring control logic based on the NEMA configuration is used in this research. The four-phase operation sequence starts from 1 + 6 and ends at 4 + 8 phase combinations, as shown in Figure 8. After the 4 + 8 phase combination, the sequence repeats itself. The three-phase operation also repeats the sequence from 1 + 5 to 4 phase combinations, as shown in Figure 9. The conventional eight-phase dual-ring control logic based on the ALDOT traffic manual is shown in Figure 10, where two groups of four-phase combinations are separated by a barrier based on the involvement of the main road. All four phase combinations in the left group include at least one main road, while none in the right group includes a main road. The eight-phase dual-ring operation is used for the actuated coordinated control with proximity sensors.

Figure 8.
Four-phase control logic for four-way intersection.

Figure 9.
Three-phase control logic for three-way intersection.

Figure 10.
Conventional eight-phase dual-ring control logic.
4.3. Fixed-Time Signal Timing Design
To calculate the optimal cycle length for the conventional control logic, Webster’s method is used in this research [39]. According to Webster’s method, the cycle length, , can be calculated as
where is the lost time per cycle in seconds and is the ratio of the critical lane volume to the saturation flow rate. The lost time per cycle can be calculated as the sum of the yellow interval and all red clearance intervals over one cycle. Critical lane volume can be obtained from the highest volume lane among all possible phases, and the saturation flow rate is assumed to be 1800 (vehicles per hour) following the ALDOT manual.
The green interval time can be calculated once the cycle length has been established. To accomplish this, it is necessary to have data on the yellow interval, all red clearance intervals, and the critical lane volume for each phase combination. Using this information, the green light time for each phase, , can be calculated by
where is the critical lane volume for phase in vehicles per hour, is the yellow interval for phase in seconds, and is all red clearance intervals for phase in seconds. The yellow interval and red clearance interval are chosen to be the values currently used in the studied network. Green interval time is calculated by Equation (2), and the minimum green interval is considered based on the ALDOT manual. Table 1 and Table 2 show yellow, red, and green interval times for four-way intersections and three-way intersections, respectively.

Table 1.
Green, yellow, and red interval times in seconds for four-way intersections.

Table 2.
Green, yellow, and red interval times in seconds for three-way intersections.
5. Priority-Based Traffic Control Algorithm
For the optimal control of the traffic signal, a priority-based algorithm is proposed in this research. In this section, the details of the priority metric as well as the optimization of the involved parameters, are described.
5.1. Priority Metric
In the proposed traffic signal control method, a priority metric is calculated for each phase combination, and the one with the maximum value is given priority and receives the next green light. This approach is based on the assumption that advanced traffic measurement sensors such as cameras, radars, or LiDARs are available to detect and track all vehicles in the approaching lanes at a traffic intersection. As a result, the traffic control system can measure the speed and location of all vehicles in each approaching lane at a traffic intersection. Furthermore, if the vehicles are stopped at a red light, the combined waiting time of all stopped vehicles is calculated. Based on these directly measured and indirectly calculated traffic information, different priority metrics can be formed. In order to study the effectiveness of various traffic information in the priority metric, three priority metrics with different combinations of variables are applied in this research.
The first priority metric, , for the i-th intersection and j-th phase combination at time instant, , is defined as
where is the total vehicle count, is the total vehicle waiting time, is the weight for the total vehicle count, is the weight for the total waiting time, and is the road priority. The second priority metric, , for the i-th intersection and j-th phase combination can be written as
where is the total vehicle speed, is the weight for the total vehicle speed. The total vehicle speed is the sum of the individual speeds of all vehicles in the corresponding phase combination. Although the same notation, is used in different metrics, and , it is understood that represents weights for different variables depending on which priority metric it is used for. The third priority metric, , considers the vehicle type and assigns a higher priority to heavy trucks as heavy trucks require more energy to stop and start at a traffic light. is based on the second priority metric, , but when a heavy truck is detected, the speed of the truck and the waiting time of the truck are multiplied by amplification factors, , and , respectively, before added to the total vehicle speed and the total vehicle waiting time.
The weights in the priority metrics should be optimized to minimize the network-wide fuel consumption of all vehicles over a given period of time. Considering the fact that the traffic volume for the primary phase combination is much higher than those for the secondary phase combinations, the three weights, , , and , are simplified into two groups such that one group is for the primary phase combinations and the other group is for all secondary phase combinations regardless of the intersection. In this manner, the number of parameters to be optimized is greatly reduced to only 6, as shown in the following equations.
If the decision on the next green light is based solely on the priority metric, an undesirable situation may occur. For example, even if one of the secondary phase combinations receives a green light due to a high-priority metric, it will quickly return the green light to the primary phase combination if a wave of vehicles is approaching the intersection in the primary phase combination. After the wave of vehicles in the primary phase combination has passed through the intersection, the secondary phase may receive the next green light again due to the long waiting vehicles in that phase combination. Because of the overhead time during signal switching, this type of frequent alternation of traffic signals will negatively affect network-wide energy efficiency. Therefore, in order to prevent frequent signal switching, once a green light has been assigned to a secondary phase combination, it will maintain the green light until all vehicles that have arrived in the phase combination pass through the intersection.
5.2. Weight Optimization
In this study, a genetic algorithm (GA) is used to find the optimal weights to minimize network-wide fuel consumption. As explained in Section 5.1, two parameter values (primary and secondary) exist for each of the three weights. Therefore, a total of six weights are used and optimized for each priority metric. Since the priority metric is calculated for each phase combination and compared to determine which phase combination will get the next green light, only relative magnitude is important for the weights. For this reason, the most important and largest weight, , which is for the total vehicle count or total vehicle speed in the primary phase combination, is set to 1, and only the other five weights are optimized. Additionally, since vehicle count, vehicle speed, waiting time, and road preference have different units, their values are normalized so that their corresponding weights are ranged between 0 and 1. A chromosome used in the GA is depicted in Figure 11, where it can be seen that five out of six parameters are optimized within the range of [0, 1] while is fixed at 1.
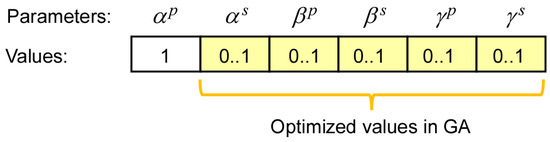
Figure 11.
Chromosome used in genetic algorithm for weight optimization.
The overall structure of the weight optimization process is shown in Figure 12. The GA optimizer runs multiple traffic simulations in SUMO by changing the weights based on a predefined scheme and selects the values that minimize the network-wide fuel consumption. The optimization code is written in Python (version 3.9.6), and the TraCI interface is used to communicate with the SUMO simulation model. For parallel optimization, a workstation equipped with an AMD EPYC 7452 32-core processor, operating at 2.35 GHz, was utilized on the Windows 10 operating system.

Figure 12.
Optimization process.
Inspired by natural selection in organismic evolution, GA consists of a fitness function and three operators, including reproduction, crossover, and mutation, to change chromosomes. The fitness function is a measure of the superiority of each solution, which is a set of weights. From the biological point of view, fitness is a creature’s ability to survive in a given environment. The fitness values of the solutions are used for the reproduction of new offspring solutions from previous generation solutions. After offspring is copied from the parent generation, a promising area in the solution space is searched by the stochastic selection, crossover, and mutation [40]. In this research, weight optimization is performed with an initial population of 60 solutions to maximize the fitness function defined as the negative network-wide fuel consumption. This GA search uses a random mutation whose probability is set to 0.4 within a range from −0.01 to 0.01. Also, the number of parent mating is set to 4. These parameters, summarized in Table 3, are all based on heuristic tuning.

Table 3.
Genetic algorithm parameters selected for weight optimization.
6. Simulation Results and Comparison
The SUMO traffic model was simulated over 6 h from 6 AM to 12 PM using different traffic signal controllers. The traffic data were recreated based on measured traffic information. Vehicle detection was simulated in SUMO using multi-entry/exit detectors, with the aim of replicating the behavior of radar sensors at three intersections. Based on the performance of real radars, the radar detection range was limited to 140 m in the simulation. Due to the network geometry, it was not possible to differentiate the intended movement of vehicles until they were closer to each intersection, at which point lanes for individual movements began. In cases such as the northbound approach at TL2, it is assumed that the radar cannot differentiate whether the vehicle intends to continue through the intersection or turn right. If there is a separate lane for the desired movement, the vehicle is first categorized in the straight approach until it moves into the left-turn lane. The resulting network-wide fuel consumption obtained by each traffic signal controller was compared with that of the baseline controller.
For the baseline controller, the fixed-time four-phase traffic signal controller is used in coordination mode. In this case, the coordination mode means that the signal switching at the three intersections is coordinated such that when a wave of vehicles has passed through an intersection, the next intersection in the downstream changes its signal to green so that the vehicles can pass through without stopping. The coordination of the switching time is determined based on the distance and the average vehicle speed between the adjacent intersections. This method has been proven to be effective in improving the network-wide fuel economy without any sophisticated control scheme.
In addition to the conventional fixed-time coordinated traffic controller, another conventional traffic signal controller based on actuation and coordination is applied to study the effectiveness of this scheme compared to other methods. In this case, it is assumed that proximity sensors such as induction-loop sensors are installed in all intersections such that the sensors can detect the presence of vehicles at the stop line without providing any advanced traffic information. The method is based on the eight-phase dual-ring control logic with the coordination of controllers at multiple intersections.
The optimized parameters for the three different priority metrics are shown in Table 4. As explained in Section 4, the first parameter, , was set to 1 since only relative magnitudes of the parameters are meaningful in this approach. In the table, it is shown that parameter values for the secondary phase combinations are smaller than those for the primary phase combinations. This is due to the fact that it is more energy efficient to assign a higher priority to the main road than the side roads, as a larger volume of vehicles is moving at higher speeds on the main road. Additionally, for the amplification factors, , and , for TSP, the optimal values were found to be 8 and 3. Since the three priority metrics use different combinations of variables and those variables are normalized, the absolute magnitudes of the optimized parameters do not hold any special meaning.

Table 4.
Optimized parameters for three different priority metrics.
Table 5 presents the network-wide fuel consumption of the vehicles in the SUMO simulation model operated by five different traffic signal control algorithms. For all simulations, the total number of vehicles that were generated by SUMO was about 12,758. In the four-phase fixed-time control, the system does not respond to dynamically varying traffic conditions, operating based on a predetermined schedule. Therefore, the fuel consumption is the largest among all control algorithms. In the adaptive control method actuated by proximity sensors, the system can detect vehicles near the traffic stop line. Based on the information on whether there are vehicles near the stop lines or not, the system can actively respond to the changing traffic condition and thus improve the overall fuel consumption. When more information is available on the surrounding traffic conditions near a traffic intersection using advanced sensors, the control system can make a better decision using priority metrics to improve the network-wide fuel efficiency further. Among the three priority metrics, it was observed that the VSP based on the total vehicle speed shows better fuel economy than VCP based on the total vehicle count. This can be attributed to the fact that the total vehicle speed implicitly includes the number of vehicles with the additional speed factor. Since it requires more energy to stop and start a vehicle moving at a higher speed, this metric leads to more efficient control of the traffic signal. Finally, it is observed that considering heavy trucks with larger weights in TSP results in even further improvement in network-wide fuel consumption. This is also due to the fact that it requires more energy to stop and start heavy trucks than light passenger vehicles. Thus, assigning higher priority to heavy trucks improves fuel economy. In the priority metric-based approaches, the average time that vehicles spent within the sensor detection zone across all secondary phase combinations was approximately 85.6 s. This indicates that while the priority metric-based approaches improve network-wide fuel efficiency by favoring the primary phase combination, the waiting time for vehicles in secondary phase combinations does not experience a significant increase.

Table 5.
Comparison of fuel consumption by different traffic control algorithms.
Table 6 shows the average fuel consumption per vehicle for two vehicle types (passenger cars and trucks) by the five different traffic signal control methods. Classification of the vehicle data shows that the number of trucks accounts for 8% of the total vehicles measured during the 6-h time frame used in this research. Similar to the combined fuel consumption shown in Table 5, both vehicle types show improved fuel consumption as the traffic signal controller becomes more sophisticated with additional traffic information. One notable observation is that when heavy trucks are separately considered with amplification factors in TSP, it improves not only the fuel consumption of trucks but also that of passenger cars. This may be explained by the fact that improving the traffic flow of the trucks also helps improve the flow of passenger cars.

Table 6.
Comparison of fuel consumption per vehicle for passenger cars and trucks separately.
Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show time–space diagrams for different controllers. In Figure 13, it can be seen that FFC has regularly spaced signal intervals due to its fixed-time schedule. As a result, a large number of vehicles in both directions are stopped, although the three traffic signals are coordinated to facilitate continuous traffic flow. The traffic flow is greatly improved when proximity sensors are used in ACE to detect vehicles at stop lines to allow actuated coordinated operation of the traffic signals, as shown in Figure 14. When the priority metrics are used to control the traffic signals, the traffic flow is even further improved with few vehicles stopped at the intersections, as shown in Figure 15, Figure 16 and Figure 17. The time–space diagrams for the VCP, VSP, and TSP visually confirm the numerical results shown in Table 5 and Table 6.

Figure 13.
Time–space diagram for fixed-time four-phase coordinated (FFC).

Figure 14.
Time–space diagram for actuated coordinate NEMA eight-phase (ACE).
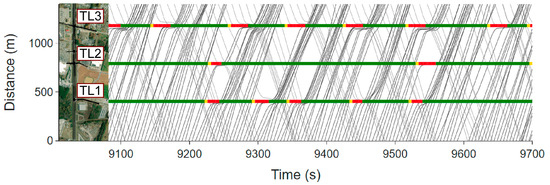
Figure 15.
Time–space diagram for priority metric with vehicle count (VCP).

Figure 16.
Time–space diagram for priority metric with vehicle speed (VSP).

Figure 17.
Time–space diagram for priority metric with truck speed (TSP).
7. Conclusions and Future Works
The goal of this study is to develop an optimal traffic signal control algorithm to minimize the total fuel consumption in a traffic network. For this purpose, a priority metric-based traffic signal control algorithm was developed with optimized weighting factors, and the algorithm was evaluated in a traffic simulation environment called SUMO. In SUMO, three signaled intersections were implemented based on a real road, and the traffic flow was simulated based on measured traffic data on the road. For the priority metric for each phase combination, different combinations of total vehicle speed, the total number of vehicles, total vehicle waiting time, and road preference were used and later expanded with an additional truck priority. The optimal weights multiplied by the terms in the priority metric were found by utilizing the genetic algorithm. Once optimized, the priority values were calculated for all phase combinations based on real-time dynamic traffic information, and the lane with the largest value received the next green light. The simulation results showed that the priority metric based on the total vehicle speed, total vehicle waiting time, and road preference performed best with a reduction in the network-wide fuel consumption by 14.3% compared to the baseline fixed-time four-phase coordinated controller and 3.6% compared to the actuated coordinated NEMA-based eight-phase controller. Moreover, adding truck priority to the priority metric further improved the fuel consumption by 14.8% and 4.1% compared to the baseline fixed-time four-phase coordinated controller and the actuated coordinated NEMA-based eight-phase controller, respectively. It was also found that considering truck priority was not only effective in reducing the total fuel consumption of trucks but also that of passenger cars.
This study will be extended in the future in four different aspects. First, vehicle mass will be considered as an additional factor in the priority metrics to distinguish heavy trucks from light trucks for a higher priority. It is expected that the vehicle types and the associated vehicle mass can be estimated with good accuracy using camera and radar sensors. Second, optimization of the weights in the priority metrics for varying traffic volumes across the network can further reduce the total fuel consumption. Although it will require a substantial amount of optimization, this gain scheduling will further improve the network-wide energy efficiency without requiring much computational load during operation. Third, an extended priority metric will be developed to consider multiple adjacent intersections simultaneously. The priority metric-based algorithm presented in this paper is a local method without cooperating with other traffic controllers. Considering traffic signal controllers in multiple adjacent intersections simultaneously will further improve the traffic control performance by optimally planning for upcoming traffic conditions in advance using information from adjacent traffic controllers. Finally, the benefits of other global optimization algorithms in optimizing the weights of priority metrics will be examined. For instance, the particle swarm optimization method [25,26,27] and the Nelder–Mead method [41,42] have been employed in traffic control optimization problems previously, and we plan to consider them in our future research.
Author Contributions
Conceptualization, H.-S.Y. and M.K.; methodology, H.-S.Y. and M.K.; software, M.S. and M.K.; validation, M.K. and H.-S.Y.; formal analysis, M.K.; investigation, M.K.; resources, H.-S.Y. and J.A.B.; data curation, M.K.; writing—original draft preparation, M.K. and M.S.; writing—review and editing, H.-S.Y.; visualization, M.K.; supervision, H.-S.Y.; project administration, J.A.B.; funding acquisition, J.A.B. and H.-S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U.S. Department of Energy, grant number DE-EE0009210.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- U.S. Energy Information Administration. Oil and Petroleum Products Explained. Available online: https://www.eia.gov/energyexplained/oil-and-petroleum-products/use-of-oil.php (accessed on 1 July 2022).
- Branke, J.; Goldate, P.; Prothmann, H. Actuated traffic signal optimization using evolutionary algorithms. In Proceedings of the 6th European Congress and Exhibition on Intelligent Transport Systems and Services, Aalborg, Denmark, 18–20 June 2007; pp. 203–225. [Google Scholar]
- Tubaishat, M.; Shang, Y.; Shi, H. Adaptive traffic light control with wireless sensor networks. In Proceedings of the 2007 4th IEEE Consumer Communications and Networking Conference, Washington, DC, USA, 1–13 January 2007; pp. 187–191. [Google Scholar]
- Azimjonov, J.; Özmen, A. A real-time vehicle detection and a novel vehicle tracking systems for estimating and monitoring traffic flow on highways. Adv. Eng. Inform. 2021, 50, 101393. [Google Scholar] [CrossRef]
- Lu, D.; Jammula, V.C.; Como, S.; Wishart, J.; Chen, Y.; Yang, Y. CAROM-Vehicle Localization and Traffic Scene Reconstruction from Monocular Cameras on Road Infrastructures. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 11725–11731. [Google Scholar]
- Ge, L.; Dan, D.; Li, H. An accurate and robust monitoring method of full-bridge traffic load distribution based on YOLO-v3 machine vision. Struct. Control Health Monit. 2020, 27, e2636. [Google Scholar] [CrossRef]
- Mandal, V.; Mussah, A.R.; Jin, P.; Adu-Gyamfi, Y. Artificial intelligence-enabled traffic monitoring system. Sustainability 2020, 12, 9177. [Google Scholar] [CrossRef]
- Li, S.; Yoon, H.-S. Vehicle Localization in 3D World Coordinates Using Single Camera at Traffic Intersection. Sensors 2023, 23, 3661. [Google Scholar] [CrossRef] [PubMed]
- Kwak, S.; Kim, H.; Kim, G.; Lee, S. Multi-view convolutional neural network-based target classification in high-resolution automotive radar sensor. IET Radar Sonar Navig. 2023, 17, 15–26. [Google Scholar] [CrossRef]
- Lim, H.-S.; Lee, J.-E.; Park, H.-M.; Lee, S. Stationary Target Identification in a Traffic Monitoring Radar System. Appl. Sci. 2020, 10, 5838. [Google Scholar] [CrossRef]
- Webster, F.V. Traffic Signal Settings; Road Research Technique Paper No. 39; Road Reserch Lab: London, UK, 1958. [Google Scholar]
- Little, J.D. The synchronization of traffic signals by mixed-integer linear programming. Oper. Res. 1966, 14, 568–594. [Google Scholar] [CrossRef]
- Robertson, D.I. ‘Tansyt’ method for Area Traffic Control. Traffic Eng. Control 1969, 11, 276–281. [Google Scholar]
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Hunt, P.; Robertson, D.; Bretherton, R.; Royle, M.C. The SCOOT on-line traffic signal optimisation technique. Traffic Eng. Control. 1982, 23, 190–192. [Google Scholar]
- Gartner, N.H. OPAC: A demand-responsive strategy for traffic signal control. In Proceedings of the 62nd Annual Meeting of the Transportation Research Board, Washington, DC, USA, 17–21 January 1983. [Google Scholar]
- Henry, J.-J.; Farges, J.L.; Tuffal, J. The PRODYN real time traffic algorithm. In Control in Transportation Systems; Elsevier: Amsterdam, The Netherlands, 1984; pp. 305–310. [Google Scholar]
- Lin, H.; Han, Y.; Cai, W.; Jin, B. Traffic signal optimization based on fuzzy control and differential evolution algorithm. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, M.; Luo, D.; Liu, B.; Zhang, X.; Liu, Z.; Li, M. Arterial coordination control optimization based on AM–BAND–PBAND model. Sustainability 2022, 14, 10065. [Google Scholar] [CrossRef]
- Dimitrov, S. Optimal control of traffic lights in urban area. In Proceedings of the 2020 International Conference Automatics and Informatics (ICAI), Varna, Bulgaria, 1–3 October 2020; pp. 1–6. [Google Scholar]
- “Brian” Park, B.; Yun, I.; Ahn, K. Stochastic optimization for sustainable traffic signal control. Int. J. Sustain. Transp. 2009, 3, 263–284. [Google Scholar] [CrossRef]
- Stevanovic, A.; Stevanovic, J.; Zhang, K.; Batterman, S. Optimizing traffic control to reduce fuel consumption and vehicular emissions: Integrated approach with VISSIM, CMEM, and VISGAOST. Transp. Res. Rec. 2009, 2128, 105–113. [Google Scholar] [CrossRef]
- Kwak, J.; Park, B.; Lee, J. Evaluating the impacts of urban corridor traffic signal optimization on vehicle emissions and fuel consumption. Transp. Plan. Technol. 2012, 35, 145–160. [Google Scholar] [CrossRef]
- Al-Turki, M.; Jamal, A.; Al-Ahmadi, H.M.; Al-Sughaiyer, M.A.; Zahid, M. On the potential impacts of smart traffic control for delay, fuel energy consumption, and emissions: An NSGA-II-based optimization case study from Dhahran, Saudi Arabia. Sustainability 2020, 12, 7394. [Google Scholar] [CrossRef]
- Olivera, A.C.; García-Nieto, J.M.; Alba, E. Reducing vehicle emissions and fuel consumption in the city by using particle swarm optimization. Appl. Intell. 2015, 42, 389–405. [Google Scholar] [CrossRef]
- Garcia-Nieto, J.; Olivera, A.C.; Alba, E. Optimal cycle program of traffic lights with particle swarm optimization. IEEE Trans. Evol. Comput. 2013, 17, 823–839. [Google Scholar] [CrossRef]
- Celtek, S.A.; Durdu, A.; Alı, M.E.M. Real-time traffic signal control with swarm optimization methods. Measurement 2020, 166, 108206. [Google Scholar] [CrossRef]
- Zhao, J.; Li, W.; Wang, J.; Ban, X. Dynamic traffic signal timing optimization strategy incorporating various vehicle fuel consumption characteristics. IEEE Trans. Veh. Technol. 2015, 65, 3874–3887. [Google Scholar] [CrossRef]
- Zhao, Y.; Ioannou, P. A traffic light signal control system with truck priority. IFAC-PapersOnLine 2016, 49, 377–382. [Google Scholar]
- Zhao, Y.; Ioannou, P. A co-simulation, optimization, control approach for traffic light control with truck priority. Annu. Rev. Control. 2019, 48, 283–291. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Chen, Y. A self-adaptive traffic light control system based on speed of vehicles. In Proceedings of the 2016 IEEE International Conference on Software Quality, Reliability and Security Companion (QRS-C), Vienna, Austria, 1–3 August 2016; pp. 382–388. [Google Scholar]
- Schrader, M.; Wang, Q.; Bittle, J. Extension and Validation of NEMA-Style Dual-Ring Controller in SUMO. In Proceedings of the SUMO Conference Proceedings, Virtual Event, 9–11 May 2022; pp. 1–13. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.-P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic traffic simulation using sumo. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar]
- Alabama Department of Transportation. TDM Public. Available online: https://aldotgis.dot.state.al.us/TDMPublic/ (accessed on 20 October 2020).
- Wunderlich, K.E.; Vasudevan, M.; Wang, P. TAT Volume III: Guidelines for Applying Traffic Microsimulation Modeling Software 2019 Update to the 2004 Version; Federal Highway Administration: Washington, DC, USA, 2019. [Google Scholar]
- Krajzewicz, D.; Behrisch, M.; Wagner, P.; Luz, R.; Krumnow, M. Second generation of pollutant emission models for SUMO. In Proceedings of the Modeling Mobility with Open Data: 2nd SUMO User Conference 2014, Berlin, Germany, 15–16 May 2014; pp. 203–221. [Google Scholar]
- Hausberger, S.; Krajzewicz, D. COLOMBO Deliverable 4.2: Extended Simulation Tool PHEM Coupled to SUMO with User Guide; Institute of Transportation Systems: Berlin, Germany, 2014. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef] [PubMed]
- Andrew Sullivan, S.L.J.; Tedla, E.; Doustmohammadi, E. Traffic signal Design Guide & Timing Manual; Alabama Department of Transportation: Montgomery, AL, USA, 2015; p. 240. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning, 13th ed.; Addison-Wesley: Reading, MA, USA, 1989; p. 432. [Google Scholar]
- Spiliopoulou, A.; Papamichail, I.; Papageorgiou, M.; Tyrinopoulos, Y.; Chrysoulakis, J. Macroscopic traffic flow model calibration using different optimization algorithms. Oper. Res. 2017, 17, 145–164. [Google Scholar] [CrossRef]
- Maripini, H.; Vanajakshi, L.D.; Chilukuri, B.R. Simulation-Based Optimization for Heterogeneous Traffic Control. In Proceedings of the Fifth International Conference of Transportation Research Group of India: 5th CTRG Volume 2, Bhopal, India, 18–21 December 2019; pp. 135–149. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).