A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs
Abstract
:1. Introduction
2. Problem Setting and Literature Review
2.1. Problem Setting
- Cluster-level route planning. In CVRP, the visiting order of each group of customers is usually further specified after grouping customers. However, in the case of customer cluster distribution, only the visiting order of the cluster corresponding to each group of customers is specified, and the visiting order of customers within each cluster can be decided by the driver experience.
- Split delivery at the cluster level. Since the size relationship between cluster demand and vehicle capacity is uncertain, the cluster demand can be split among multiple vehicles. Therefore, a vehicle does not need to visit all customers within a cluster without exceeding the capacity limit. As considered in the Split Delivery Vehicle Routing Problem (SDVRP, see Archetti et al. [34]), this allows a customer to be visited by multiple vehicles, resulting in significant savings in the total distance traveled and the number of vehicles used.
- Soft cluster conflicts. The long transportation distances between clusters are much greater than the distances between customers within the cluster. The carrier’s preference for the direct shipment of a single cluster rather than consolidated transportation between clusters can be regarded as a conflict between clusters. In this scenario, the subsidy costs associated with inter-cluster transportation act as penalty costs for violating the conflict relationship between clusters.
- Customer-related costs. The cost-calculating model avoids the impact of the order of customer visits on the transportation cost, making the cost of each vehicle dependent on the direct shipment costs and quantities of the customers visited. Additionally, penalty costs are further related to the clusters corresponding to the customers visited.
2.2. Literature Review
3. Problem Statement and Model Formulation
3.1. Problem Statement
3.2. Model Formulation
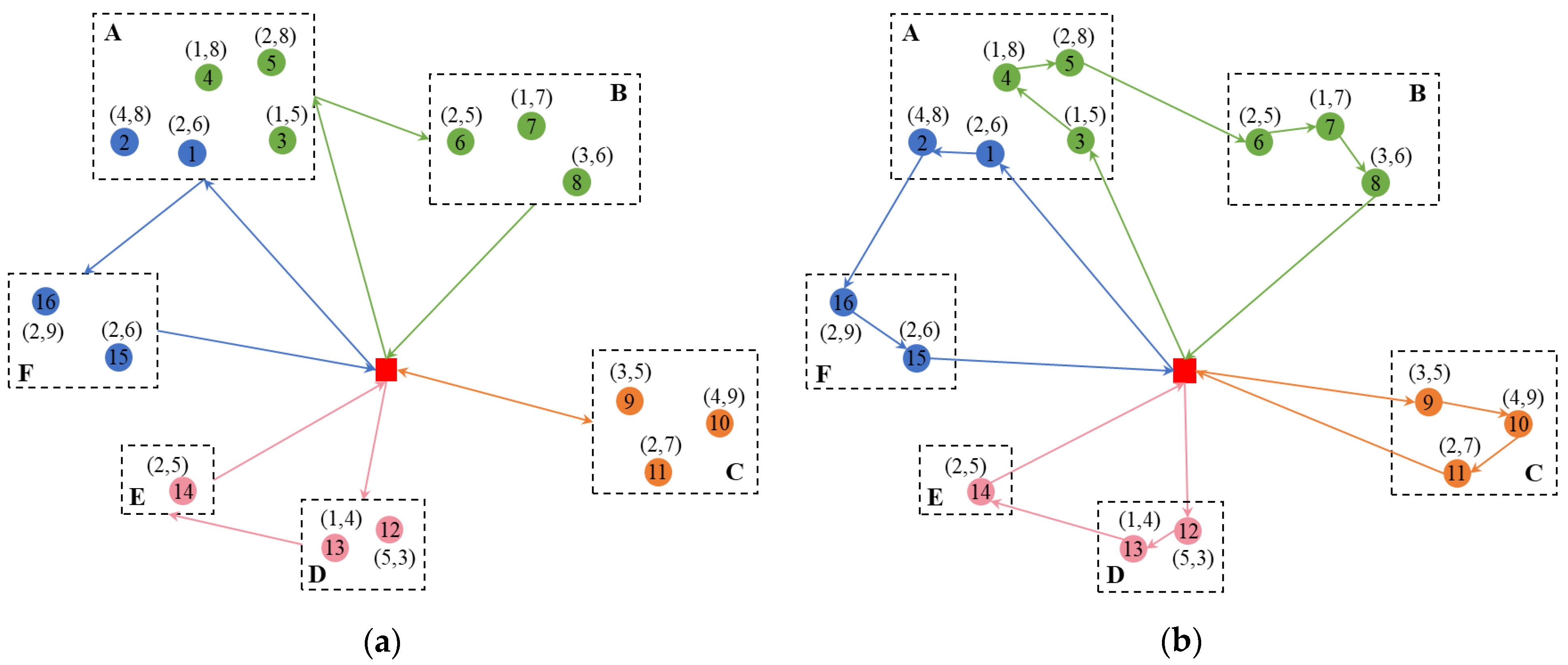
3.3. Numerical Example
4. Solution Methodology
4.1. Overview
| Algorithm 1 Outline of Two-level Variable Neighborhood Descent |
| Input: Output: 1: 2: 3: 4: ▷Construction 5: While do ▷Intensification 6: VND- 7: 8: While do 9: 10: if then 11: 12: 13: else 14: 15: if then 16: 17: break 18: end if 19: end if 20: ) ▷Diversification 21: random number in [0, 1] 22: if then 23: 24: else 25: 26: end if 27: end while 28: 29: if then 30: 31: break 32: end if 33: end while |
4.2. Construction Phase
| Algorithm 2 Two-stage Heuristic |
| Input: Output: 1: ▷First-stage 2: Solve the CAP instance by BFDCC 3: 4: for ) do ▷Second-stage 5: 6: and a virtual point 7: Solve the CSP instance by LKH 8: Solution 9: end 10: ▷Combination |
4.2.1. Customer Assignment Problem
4.2.2. Cluster Sequence Problem
4.3. Intensification Phase
4.3.1. Intensification at the Cluster Level
4.3.2. Intensification at the Customer Level
4.4. Diversification Phase
4.5. Adapted Heuristics
4.5.1. First Fit Decreasing in Demand and Cost with LKH
- Step 1:
- Calculate the total demand of each cluster, i.e., the sum of the demand of all customers in the cluster.
- Step 2:
- Sort the clusters in descending order according to the total demand, and then sort all customers in each cluster first according to the direct shipment cost and then the demand in descending order.
- Step 3:
- Assign each sorted customer in turn to the first vehicle with sufficient remaining capacity.
- Step 4:
- For each vehicle, the LKH is used to determine the visiting order of clusters.
4.5.2. Adapted CluVRP Solution Approach
5. Results and Discussion
5.1. Benchmark Instances Description
5.2. Parameter Setting
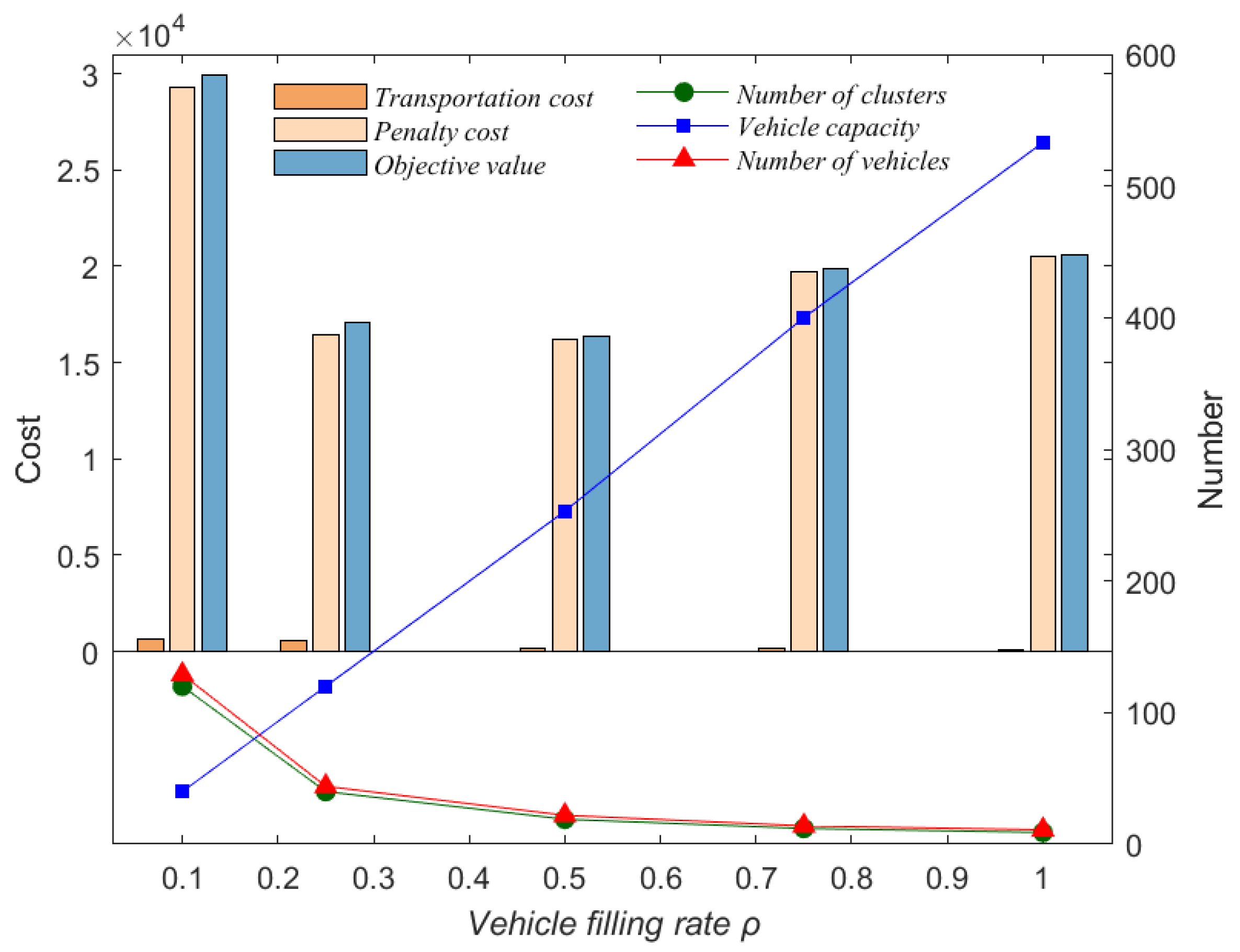
5.3. Characteristic Analysis of SDCVRPSC
5.4. Performance Evaluations
5.5. Real Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Svensson, G. The Impact of Outsourcing on Inbound Logistics Flows. Int. J. Logist. Manag. 2001, 12, 21–35. [Google Scholar] [CrossRef]
- Boysen, N.; Emde, S.; Hoeck, M.; Kauderer, M. Part logistics in the automotive industry: Decision problems, literature review and research agenda. Eur. J. Oper. Res. 2015, 242, 107–120. [Google Scholar] [CrossRef]
- Harrison, A. Perestroika in automotive inbound. Manuf. Eng. 2001, 80, 247–251. [Google Scholar] [CrossRef]
- Hosseini, S.D.; Shirazi, M.A.; Karimi, B. Cross-docking and milk run logistics in a consolidation network: A hybrid of harmony search and simulated annealing approach. J. Manuf. Syst. 2014, 33, 567–577. [Google Scholar] [CrossRef]
- Mao, Z.; Huang, D.; Fang, K.; Wang, C.; Lu, D. Milk-run routing problem with progress-lane in the collection of automobile parts. Ann. Oper. Res. 2019, 291, 657–684. [Google Scholar] [CrossRef]
- Meyer, A.; Amberg, B. Transport concept selection considering supplier milk runs—An integrated model and a case study from the automotive industry. Transp. Res. Part E Logist. Transp. Rev. 2018, 113, 147–169. [Google Scholar] [CrossRef]
- Ranjbaran, F.; Kashan, A.H.; Kazemi, A. Mathematical formulation and heuristic algorithms for optimisation of auto-part milk-run logistics network considering forward and reverse flow of pallets. Int. J. Prod. Res. 2019, 58, 1741–1775. [Google Scholar] [CrossRef]
- Sadjadi, S.J.; Jafari, M.; Amini, T. A new mathematical modeling and a genetic algorithm search for milk run problem (an auto industry supply chain case study). Int. J. Adv. Manuf. Technol. 2008, 44, 194–200. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; He, Y.; Xuan, J.; He, W. A robust hybrid heuristic algorithm to solve multi-plant milk-run pickup problem with uncertain demand in automobile parts industry. Adv. Prod. Eng. Manag. 2018, 13, 169–178. [Google Scholar] [CrossRef]
- Barthélemy, T.; Rossi, A.; Sevaux, M.; Sörensen, K. Metaheuristic approach for the clustered vrp. In Proceedings of the EU/MEeting: 10th Anniversary of the Metaheuristics Community-Université de Bretagne Sud, Lorient, France, 3 June 2010. [Google Scholar]
- Pop, P.C.; Kara, I.; Marc, A.H. New mathematical models of the generalized vehicle routing problem and extensions. Appl. Math. Model. 2012, 36, 97–107. [Google Scholar] [CrossRef]
- Battarra, M.; Erdoğan, G.; Vigo, D. Exact algorithms for the clustered vehicle routing problem. Oper. Res. 2014, 62, 58–71. [Google Scholar] [CrossRef]
- Marc, A.H.; Fuksz, L.; Pop, P.C.; Dănciulescu, D. A novel hybrid algorithm for solving the clustered vehicle routing problem. In International Conference on Hybrid Artificial Intelligence Systems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Vidal, T.; Battarra, M.; Subramanian, A.; Erdogˇan, G. Hybrid metaheuristics for the Clustered Vehicle Routing Problem. Comput. Oper. Res. 2015, 58, 87–99. [Google Scholar] [CrossRef]
- Expósito-Izquierdo, C.; Rossi, A.; Sevaux, M. A Two-Level solution approach to solve the Clustered Capacitated Vehicle Routing Problem. Comput. Ind. Eng. 2016, 91, 274–289. [Google Scholar] [CrossRef]
- Defryn, C.; Sörensen, K. A fast two-level variable neighborhood search for the clustered vehicle routing problem. Comput. Oper. Res. 2017, 83, 78–94. [Google Scholar] [CrossRef]
- Hintsch, T.; Irnich, S. Large multiple neighborhood search for the clustered vehicle-routing problem. Eur. J. Oper. Res. 2018, 270, 118–131. [Google Scholar] [CrossRef]
- Horvat-Marc, A.; Fuksz, L.; Pop, P.C.; Dănciulescu, D. A decomposition-based method for solving the clustered vehicle routing problem. Log. J. IGPL 2017, 26, 83–95. [Google Scholar] [CrossRef]
- Pop, P.C.; Fuksz, L.; Marc, A.H.; Sabo, C. A novel two-level optimization approach for clustered vehicle routing problem. Comput. Ind. Eng. 2018, 115, 304–318. [Google Scholar] [CrossRef]
- Xu, R.; Guo, R.; Jia, Q. A Novel Hybrid Metaheuristic for Solving Automobile Part Delivery Logistics with Clustering Customer Distribution. IEEE Access 2019, 7, 106075–106091. [Google Scholar] [CrossRef]
- Hintsch, T.; Irnich, S. Exact solution of the soft-clustered vehicle-routing problem. Eur. J. Oper. Res. 2019, 280, 164–178. [Google Scholar] [CrossRef]
- Aerts, B.; Cornelissens, T.; Sörensen, K. The joint order batching and picker routing problem: Modelled and solved as a clustered vehicle routing problem. Comput. Oper. Res. 2020, 129, 105168. [Google Scholar] [CrossRef]
- Hintsch, T. Large multiple neighborhood search for the soft-clustered vehicle-routing problem. Comput. Oper. Res. 2020, 129, 105132. [Google Scholar] [CrossRef]
- Islam, A.; Gajpal, Y.; ElMekkawy, T.Y. Hybrid particle swarm optimization algorithm for solving the clustered vehicle routing problem. Appl. Soft Comput. 2021, 110, 107655. [Google Scholar] [CrossRef]
- Li, S.; Wu, W.; Ma, X.; Zhong, M.; Safdar, M. Modelling medium- and long-term purchasing plans for environment-orientated container trucks: A case study of Yangtze River port. Transp. Saf. Environ. 2022, 5. [Google Scholar] [CrossRef]
- Hussain, I.; Wang, H.; Safdar, M.; Ho, Q.B.; Wemegah, T.D.; Noor, S. Estimation of Shipping Emissions in Developing Country: A Case Study of Mohammad Bin Qasim Port, Pakistan. Int. J. Environ. Res. Public Health 2022, 19, 11868. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Chen, Y.; Langevin, A. An inverse optimization approach for a capacitated vehicle routing problem. Eur. J. Oper. Res. 2021, 295, 1087–1098. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Reichhart, A.; Holweg, M. Co-located supplier clusters: Forms, functions and theoretical perspectives. Int. J. Oper. Prod. Manag. 2008, 28, 53–78. [Google Scholar] [CrossRef]
- Dror, M.; Trudeau, P. Savings by Split Delivery Routing. Transp. Sci. 1989, 23, 141–145. [Google Scholar] [CrossRef]
- Dror, M.; Trudeau, P. Split delivery routing. Nav. Res. Logist. 1990, 37, 383–402. [Google Scholar] [CrossRef]
- Archetti, C.; Savelsbergh, M.W.P.; Speranza, M.G. Worst-Case Analysis for Split Delivery Vehicle Routing Problems. Transp. Sci. 2006, 40, 226–234. [Google Scholar] [CrossRef]
- Fu, L.-L.; Aloulou, M.A.; Triki, C. Integrated production scheduling and vehicle routing problem with job splitting and delivery time windows. Int. J. Prod. Res. 2017, 55, 5942–5957. [Google Scholar] [CrossRef]
- Archetti, C.; Speranza, M.G.; Savelsbergh, M.W.P. An Optimization-Based Heuristic for the Split Delivery Vehicle Routing Problem. Transp. Sci. 2008, 42, 22–31. [Google Scholar] [CrossRef]
- Sevaux, M.; Sörensen, K. Hamiltonian paths in large clustered routing problems. In Proceedings of the EU/MEeting 2008 Workshop on Metaheuristics for Logistics and Vehicle Routing, EU/ME, Athens, Greece, 1 October 2008. [Google Scholar]
- Ghiani, G.; Improta, G. An efficient transformation of the generalized vehicle routing problem. Eur. J. Oper. Res. 2000, 122, 11–17. [Google Scholar] [CrossRef]
- Lin, S.; Kernighan, B.W. An Effective Heuristic Algorithm for the Traveling-Salesman Problem. Oper. Res. 1973, 21, 498–516. [Google Scholar] [CrossRef]
- Helsgaun, K. An effective implementation of the Lin–Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Johnson, D.S. Near-Optimal Bin Packing Algorithms; Massachusetts Institute of Technology: Cambridge, MA, USA, 1973. [Google Scholar]
- Christofides, N. The Shortest Hamiltonian Chain of a Graph. SIAM J. Appl. Math. 1970, 19, 689–696. [Google Scholar] [CrossRef]
- Vidal, T. Hybrid genetic search for the CVRP: Open-source implementation and SWAP* neighborhood. Comput. Oper. Res. 2021, 140, 105643. [Google Scholar] [CrossRef]



| Source | Problem | Heu/Ex | Solution Approach(es) |
|---|---|---|---|
| Sevaux and Sörensen [35] | CluVRP | - | Introduction of CluVRP |
| Barthélemy et al. [10] | CluVRP | Heu | Transformation into CVRP, simulated-annealing |
| Pop et al. [11] | CluVRP | Ex | Two compact integer programming formulations |
| Battarra et al. [12] | CluVRP | Ex | Branch-and-cut, branch-and-cut-and-price |
| Vidal et al. [14] | CluVRP | Heu | Iterated local search, unified hybrid genetic search |
| Expósito-Izquierdo et al. [15] | CluVRP | Heu | Two-level approach: record-to-record algorithm (high-level) and mixed integer linear programming model, Christofides heuristic, and Lin-kernighan heuristic (low-level) |
| Defryn and Sorensen [16] | CluVRP (+SoftCluVRP) | Heu | Two-level variable neighborhood search (cluster-level and customer-level) (in addition adapted to soft-cluster constraints by simple modifications) |
| Horvat-Marc et al. [18] | CluVRP | Heu | Two-level approach: genetic algorithm (high-level) and simulated annealing (low-level) |
| Pop et al. [19] | CluVRP | Heu | Two-level approach: genetic algorithm (high-level) and transformation to TSP solved by Concorde TSP solver (low-level) |
| Hintsch and Irnich [17] | CluVRP | Heu | Large multiple neighborhood search |
| Xu et al. [20] | CluVRP | Heu | Two-level approach: variable neighborhood search (high-level) and Lin-kernighan heuristic (low-level) |
| Hintsch and Irnich [21] | SoftCluVRP | Ex | Branch-and-price |
| Aerts et al. [22] | CluVRP | Heu | Adaption of two-level variable neighborhood search developed by Defryn and Sorensen [16] |
| Islam et al. [24] | CluVRP | Heu | Particle swarm optimization and variable neighborhood search |
| Hintsch [23] | SoftCluVRP (+CluVRP) | Heu | Large multiple neighborhood search tailored to soft-cluster constraints (in addition, adapted to hard-cluster constraints by simple modifications) |
| Sets | |
| set of clusters, , indexed by . | |
| set of edges connecting clusters and . | |
| set of available vehicles, indexed by . | |
| set of customers, , indexed by . | |
| set of customers in cluster . | |
| Parameters | |
| maximum vehicle capacity. | |
| demand of customer . | |
| total demand of cluster . | |
| drop cost per customer visit. | |
| direct shipment cost of customer . | |
| penalty cost from cluster to cluster . | |
| Decision variables | |
| Binary: 1 if vehicle travels from cluster to cluster ; 0 otherwise. | |
| Binary: 1 if vehicle is used; 0 otherwise. | |
| Binary: 1 if customer is visited by vehicle ; 0 otherwise. | |
| Binary: 1 if cluster is visited by vehicle ; 0 otherwise. | |
| Auxiliary variables | |
| maximum direct shipment cost of customers visited by vehicle . | |
| drop costs of customers visited by vehicle . | |
| penalty cost between clusters visited by vehicle . | |
| Cluster | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 0 | 9 | 15 | 12 | 10 | 7 |
| B | 0 | 8 | 11 | 12 | 12 | |
| C | 0 | 9 | 13 | 15 | ||
| D | 0 | 5 | 9 | |||
| E | 0 | 4 | ||||
| F | 0 |
| Inter-Route Operators at the Cluster Level | |
|---|---|
| Relocate | Reassign one subcluster in another route. |
| Swap | Exchange the position of two subclusters in two routes. |
| Swap2vs1 | Exchange the position of a pair of subclusters and one subcluster in two routes. |
| Inter-Route Operators at the Customer Level | |
|---|---|
| Relocate | Reassign one customer to another route and assign it to the corresponding subcluster. |
| Swap | Exchange the routes of two customers and assign them to the corresponding subclusters. |
| Swap2vs1 | Exchange the routes of a pair of customers and one customer and assign them to the corresponding subclusters. |
| Parameter | Definition | Tested Values | Best |
|---|---|---|---|
| Percentage of the solution that is randomly destroyed by the perturbation operator. | 0.1, …, 0.5 | 0.1 | |
| Probability that the new solution after the diversification phase enters the local search at the cluster level first. | 0.5, …, 1 | 1 |
| Instance Scale | No. of Customers | Gurobi | TLVND | (%) | ||||
|---|---|---|---|---|---|---|---|---|
| (%) | ||||||||
| 5% (small) | 19 | 276.65 | 344.80 | 21.93 | 3 | 347.00 | 5.18 | 0.24 |
| 10% (middle) | 37 | 336.20 | 702.89(1) | 55.91(1) | 0 | 719.00 | 13.19 | −0.43(1) |
| 20% (large) | 74.5 | 437.87 | /(10) | /(10) | 0 | 1195.30 | 25.33 | /(10) |
| Avg. (rounding) | 43 | 350.24 | 514.42(4) | 38.03(4) | 1 | 753.77 | 14.57 | −0.08(4) |
| FFDDC_LKH | Two-Level VNS | TLVND | |||||
|---|---|---|---|---|---|---|---|
| (%) | (s) | (%) | (s) | (%) | (s) | ||
| 10% | 20,671.25 | 35.57 | 10.09 | 6.37 | 68.23 | 0.00 | 178.95 |
| 25% | 15,909.05 | 33.59 | 7.50 | 6.64 | 54.62 | 0.00 | 213.28 |
| 50% | 16,245.35 | 28.07 | 5.39 | 9.08 | 13.76 | 0.00 | 290.89 |
| 75% | 17,817.50 | 19.06 | 3.46 | 5.92 | 5.76 | 0.00 | 385.17 |
| 100% | 18,928.65 | 14.95 | 2.59 | 4.76 | 3.34 | 0.00 | 457.24 |
| Avg. | 17,914.36 | 26.25 | 5.80 | 6.55 | 29.14 | 0.00 | 305.11 |
| No. of Case | No. of Customers | TPL (Yuan) | TLVND (Yuan) | (%) |
|---|---|---|---|---|
| Case 1 | 64 | 14,660 | 11,066 | 24.52 |
| Case 2 | 161 | 26,888 | 18,973 | 29.44 |
| Case 3 | 242 | 22,622 | 16,817 | 25.66 |
| Avg. (rounding) | 156 | 21,390 | 15,619 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Huang, Y.; Xiao, W. A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs. Sustainability 2023, 15, 7639. https://doi.org/10.3390/su15097639
Xu R, Huang Y, Xiao W. A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs. Sustainability. 2023; 15(9):7639. https://doi.org/10.3390/su15097639
Chicago/Turabian StyleXu, Rui, Yumiao Huang, and Wei Xiao. 2023. "A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs" Sustainability 15, no. 9: 7639. https://doi.org/10.3390/su15097639
APA StyleXu, R., Huang, Y., & Xiao, W. (2023). A Two-Level Variable Neighborhood Descent for a Split Delivery Clustered Vehicle Routing Problem with Soft Cluster Conflicts and Customer-Related Costs. Sustainability, 15(9), 7639. https://doi.org/10.3390/su15097639





