Hydraulic Effect of Vegetation Zones in Open Channels: An Experimental Study of the Distribution of Turbulence
Abstract
:1. Introduction
- v′x, v′y, v′z—velocity fluctuation components [m/s], vm,x, vm,y, vm,z—average velocity components [m/s].
2. Materials and Methods
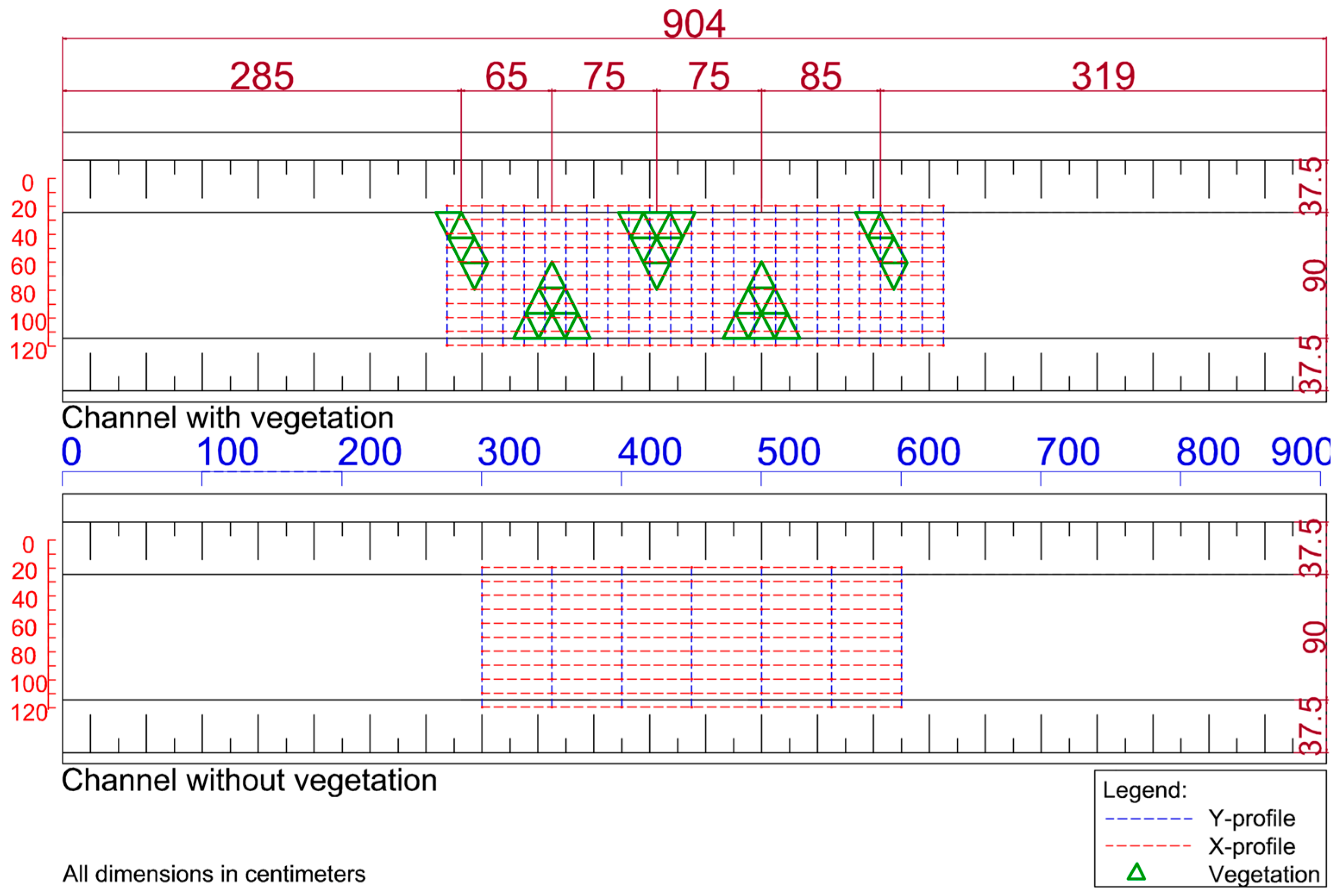
2.1. Modelling Research
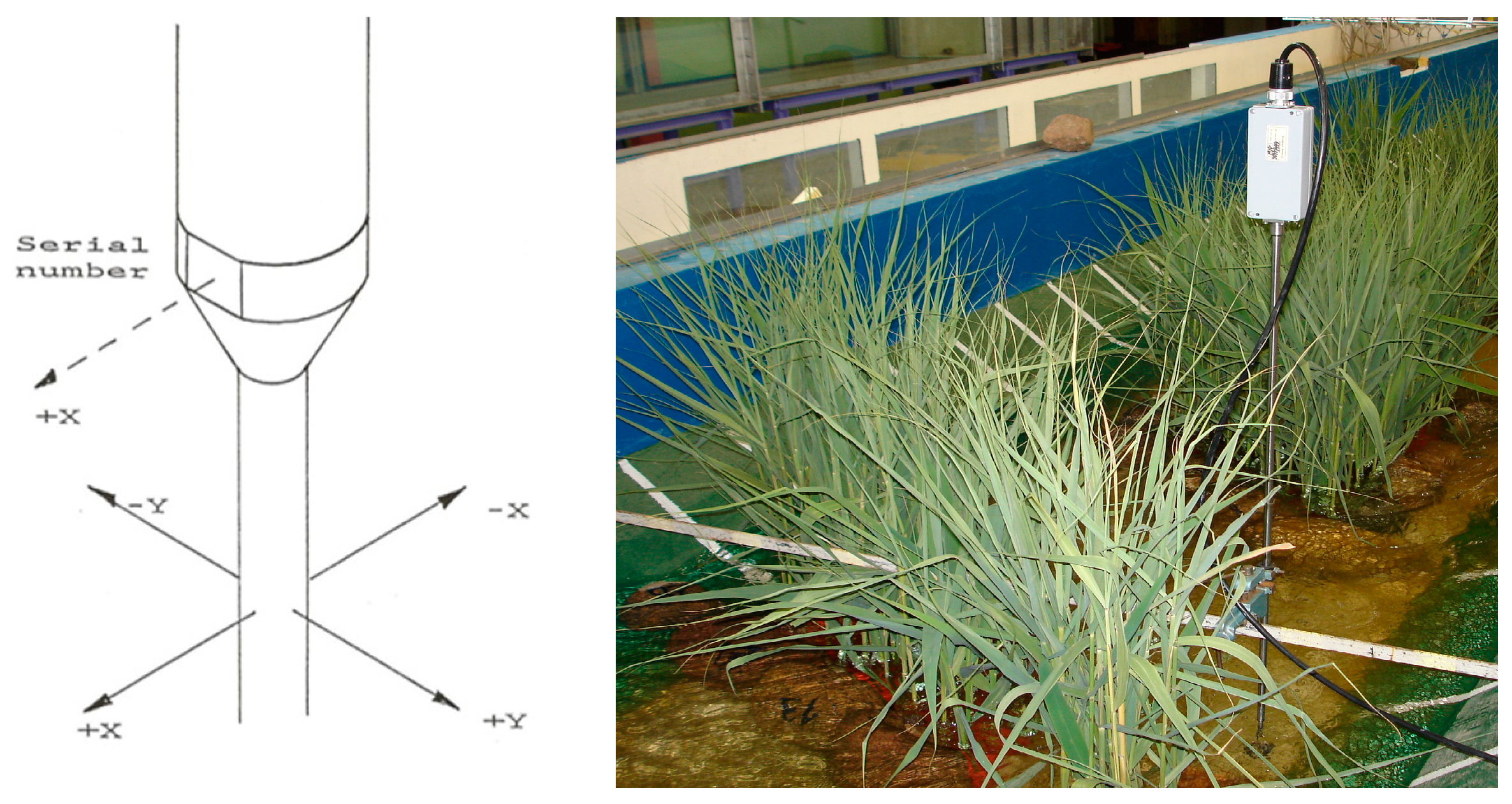
2.2. Methods and Scope of Research
3. Results and Discussion
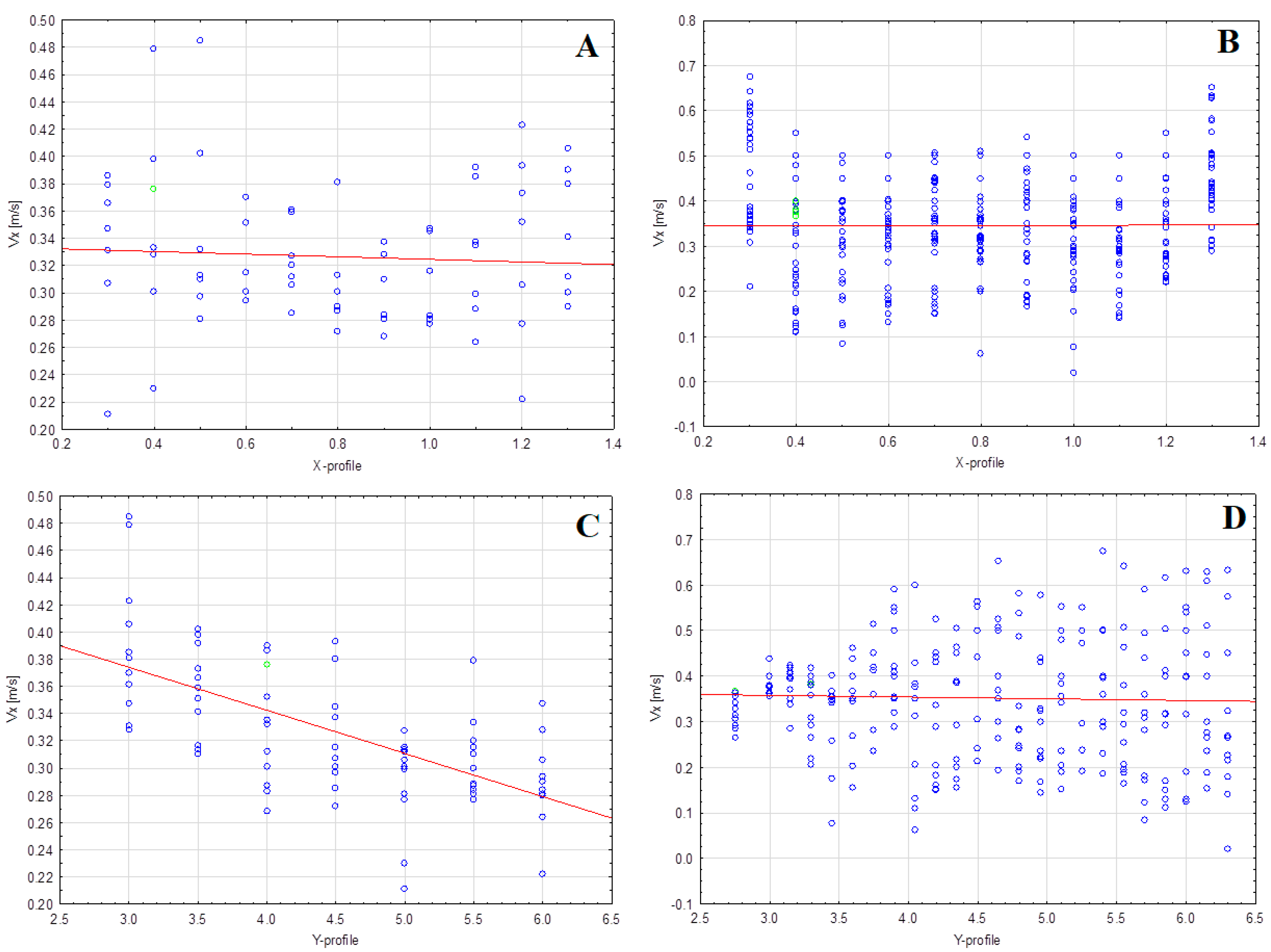
3.1. Spatial Distribution of the vx Velocity (the Longitudinal Component of Flow Velocity)
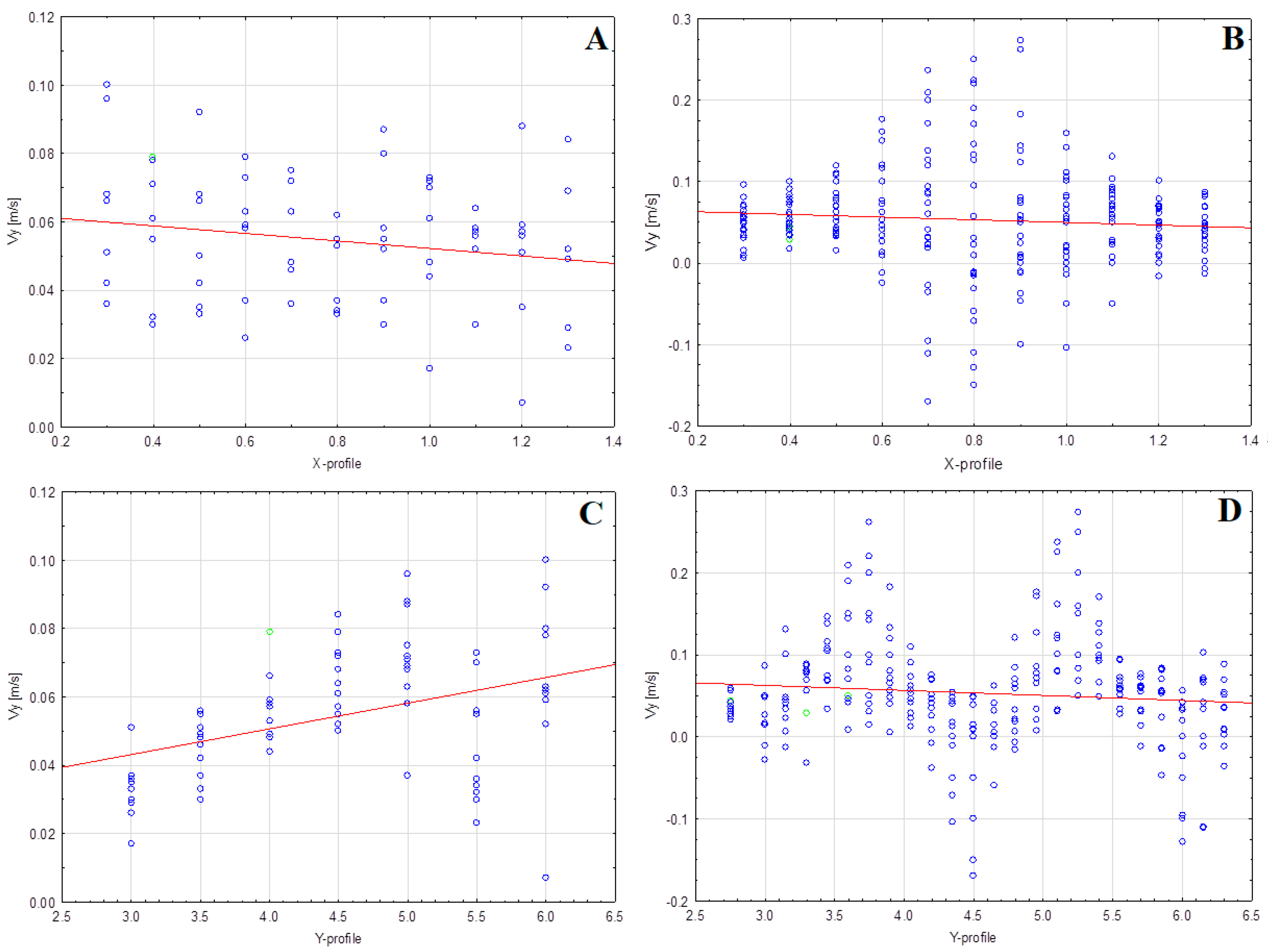
3.2. Spatial Distribution of the vy Velocity (the Lateral Component of Flow Velocity)
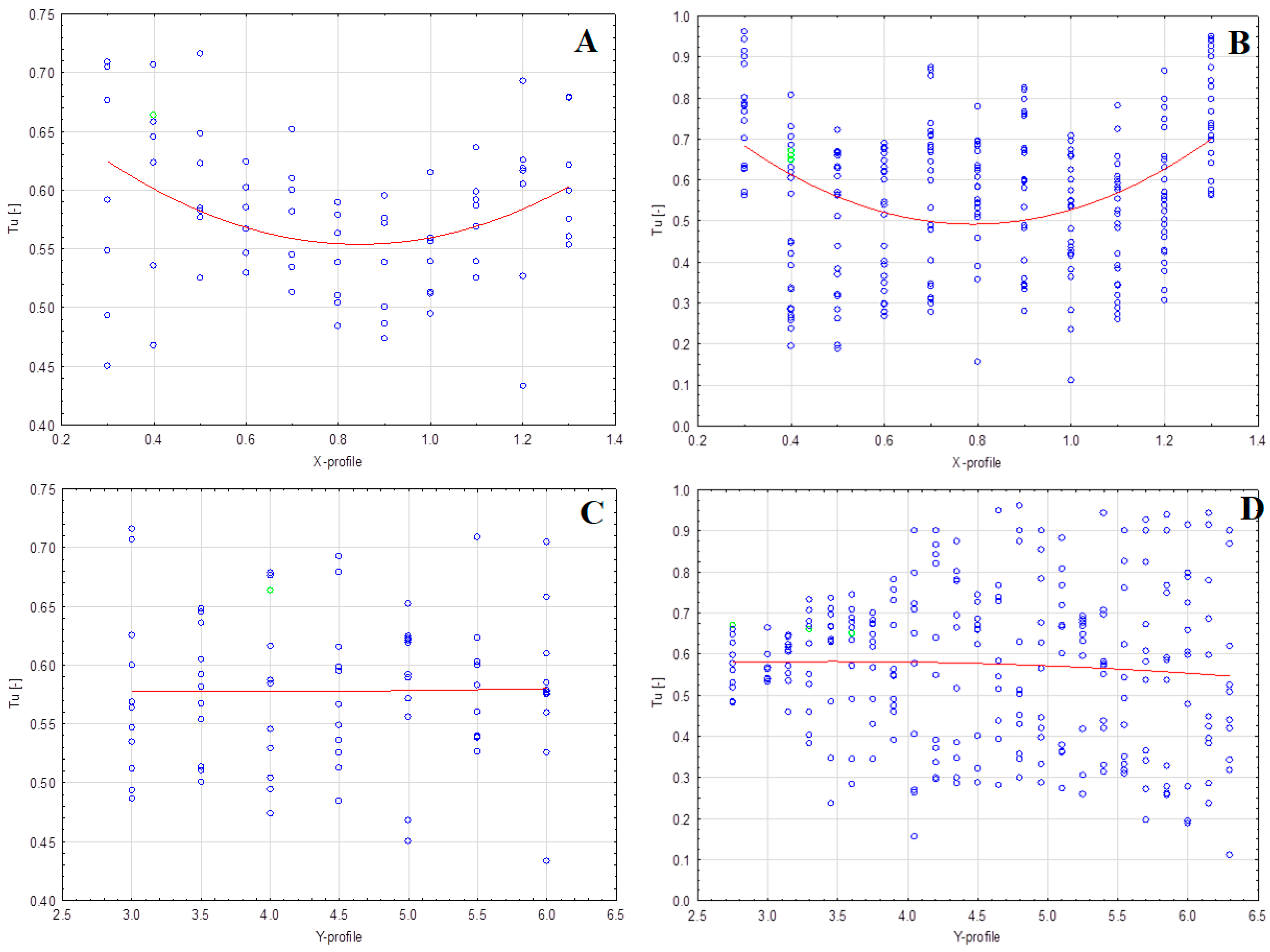
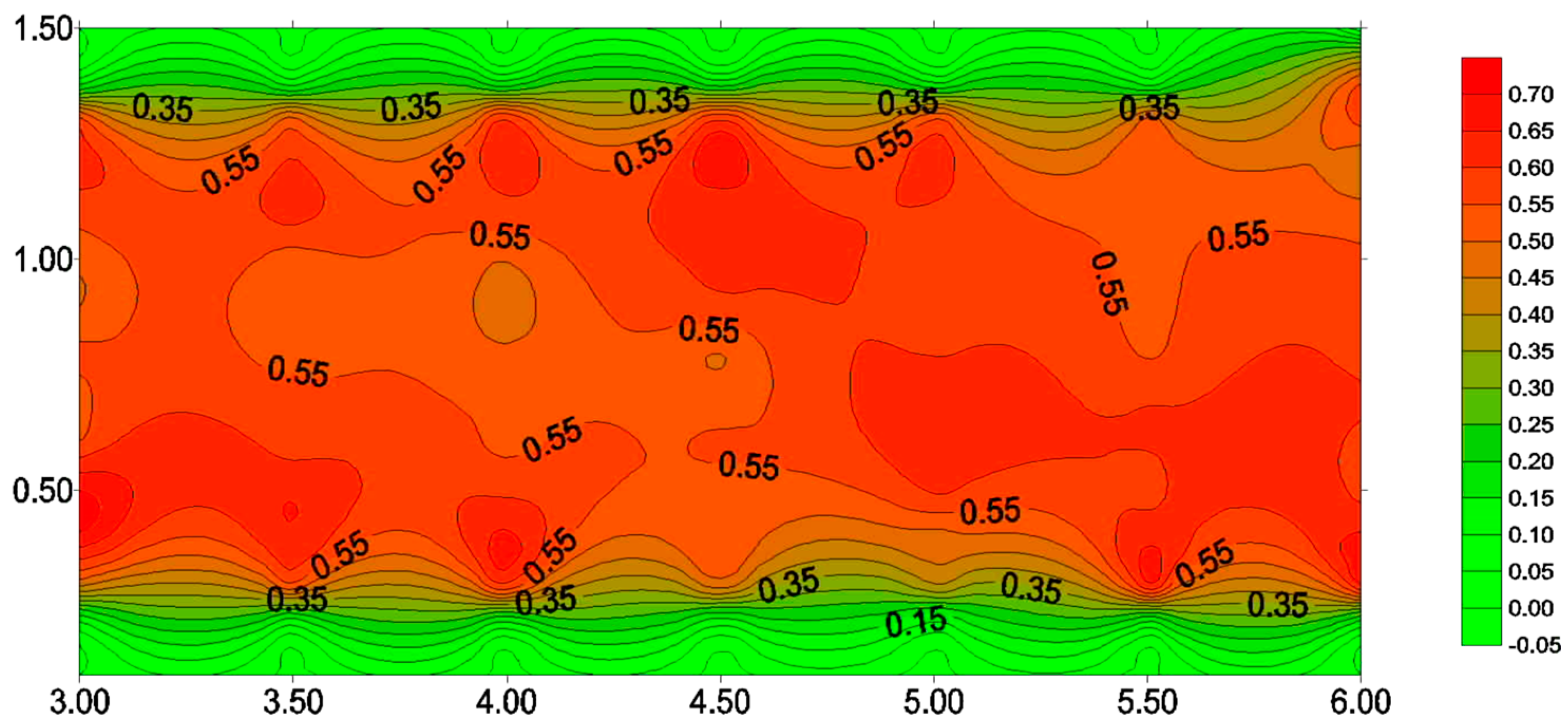
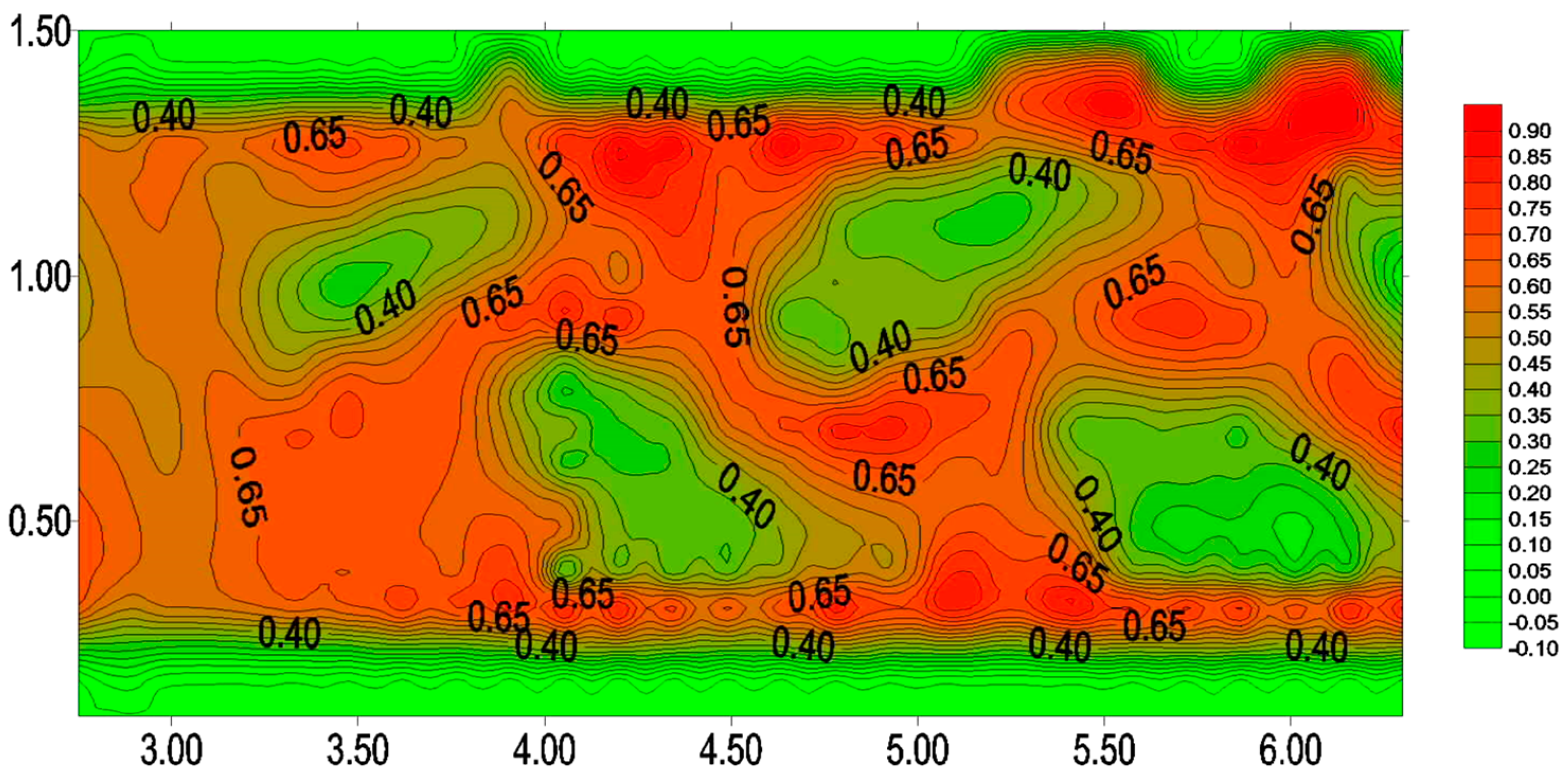
3.3. Intensity of Turbulence
4. Final Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Järvelä, J. Flow Resistance of Flexible and Stiff Vegetation: A Flume Study with Natural Plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Järvelä, J. Flow Resistance in Environmental Channels: Focus on Vegetation; Helsinki University of Technology Water Resources Publications: Espoo, Finland, 2004; ISBN 978-951-22-7074-3. [Google Scholar]
- Kałuża, T. Resistance in Floodwater Flow Caused by Floodplain Vegetation. Ph.D. Thesis, Agricultural University Poznan, Poznan, Poland, 2000. (In Polish). [Google Scholar]
- Wolski, K.; Tymiński, T. Studies on the Threshold Density of Phragmites Australis Plant Concentration as a Factor of Hydraulic Interactions in the Riverbed. Ecol. Eng. 2020, 151, 105822. [Google Scholar] [CrossRef]
- Tymiński, T.; Kałuża, T. Investigation of Mechanical Properties and Flow Resistance of Flexible Riverbank Vegetation. Pol. J. Environ. Stud. 2012, 21, 201–207. [Google Scholar]
- Tymiński, T.; Kałuża, T.; Hämmerling, M. Verification of methods for determining flow resistance coefficients for floodplains with flexible vegetation. Sustainability 2022, 14, 16170. [Google Scholar] [CrossRef]
- Walczak, N.; Walczak, Z.; Ficner, T. Determination of the Variation of the Geometric and Dynamic Parameters of the Floodplain Vegetation. Water 2022, 14, 1274. [Google Scholar] [CrossRef]
- Walczak, N.; Walczak, Z.; Kałuża, T.; Hämmerling, M.; Stachowski, P. The Impact of Shrubby Floodplain Vegetation Growth on the Discharge Capacity of River Valleys. Water 2018, 10, 556. [Google Scholar] [CrossRef]
- Kubrak, J.; Żelazo, J.; Kozioł, A.; Kubrak, E.; Kiczko, A. On removing vegetation from river floodplains. Gospod. Wodna 2014, 74, 95–102. (In Polish) [Google Scholar]
- Västilä, K.; Järvelä, J. Characterizing natural riparian vegetation for modeling of flow and suspended sediment transport. J. Soils Sediments 2017, 18, 3114–3130. [Google Scholar] [CrossRef]
- Finnemore, E.J.; Franzini, J.B. Fluid Mechanics with Engineering Applications, 10th ed.; The McGraw-Hill Series in Civil and Environmental Engineering; McGraw-Hill: Boston, MA, USA, 2002; ISBN 978-0-07-243202-2. [Google Scholar]
- Garde, R.J. Turbulent Flow; Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Puzyrewski, R.; Sawicki, J. Basic Fluid Mechanics and Hydraulics; Wyd. Nauk. PWN: Warsaw, Poland, 2000; p. 335. (In Polish) [Google Scholar]
- Jeżowiecka-Kabsch, K.; Szewczyk, H. Fluid Mechanics; OficynaWyd. PWR: Wroclaw, Poland, 2001; p. 386. (In Polish) [Google Scholar]
- Mazurczyk, A.K. Turbulent Velocity Fields in Complex Cross-Section Channels with Wooded Floodplains. Ph.D. Thesis, Institute of Geophysics Polish Academy of Sciences, Warsaw, Poland, 2007. (In Polish). [Google Scholar]
- Sigloch, H. Technical Fluidmechanics; VDI-Verlag: Duesseldorf, Germany, 1991; Volume 351. (In German) [Google Scholar]
- Carollo, F.G.; Ferro, V.; Termini, D. Analyzing Turbulence Intensity in Gravel Bed Channels. J. Hydraul. Engin. ASCE 2005, 131, 1050–1061. [Google Scholar] [CrossRef]
- Pasche, E. Turbulence Mechanism in Natural Streams and the Possibility of Its Mechanical Representation. In Mitteilungen des Instituts Fürwasserbau Und Wasserwirtschaft; TU Aachen: Aachen, Germany, 1984; Volume 52. (In German) [Google Scholar]
- Kozioł, A.P. Laboratory Studies of the Effect of Trees in Lowland River Channels on Turbulent Stream Flow Characteristics; Monograph, SGGW-University: Warsaw, Poland, 2019. (In Polish) [Google Scholar]
- Kozioł, A.P. Turbulent kinetic energy of water in a compound channel. Ann. Wars. Univ. Life Sci.-SGGW Land Reclam. 2011, 43, 193–205. [Google Scholar] [CrossRef]
- Nezu, I.; Onitsuka, K. Turbulent structures in partly vegetated open-channel flows with LDA and PIV measurements. J. Hydraul. Res. 2001, 39, 629–642. [Google Scholar] [CrossRef]
- Neary, V.; Constantinescu, S.; Bennett, S.; Diplas, P. Effects of Vegetation on Turbulence, Sediment Transport and Stream Morphology. J. Hydraul. Eng. 2012, 138, 765–776. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.; Nepf, H. Mean and turbulent velocity fields near rigid and flexible plants and the implications for deposition. J. Geophys. Res. Earth Surf. 2013, 118, 2585–2599. [Google Scholar] [CrossRef]
- Tsujimoto, T.; Kitamura, T. Flow over Flexible Vegetation and Formation of Honami Motion; Monograph of 9th APD-IAHR: Singapore, 1994. [Google Scholar]
- Mazurczyk, A.K. Scales of Turbulence in Compound Channels with Trees on Floodplains; Publications of the Institute of Geophysics Polish Academy of Sciences: Warsaw, Poland, 2007; Volume 401, pp. 169–176. [Google Scholar]
- Yalin, M.S. Large-scale turbulence and river morphology. In Proceedings of the 3rd International Conference on Fluvial Hydraulics, Lisbon, Portugal, 6–8 September 2006; pp. 6–8. [Google Scholar]
- Franca, M.J.; Brocchini, M. Turbulence in Rivers. In Rivers—Physical, Fluvial and Environmental Processes; Rowinski, P., Radecki-Pawlik, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 51–78. [Google Scholar]
- Książek, L.; Bartnik, W.; Rumian, J.; Zagórowski, P. Turbulent water flow over rough bed. 13th European Turbulence Conference in Warsaw 2011. J. Phys. Conf. Ser. 2011, 318, 022021. [Google Scholar] [CrossRef]
- Tang, X.; Lin, P.; Liu, P.L.F.; Zhang, X. Numerical and experimental studies of turbulence in vegetated open-channel flows. Environ. Fluid Mech. 2021, 21, 1137–1163. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed Roughness Effects on the Turbulence Characteristics of Flows through Emergent Rigid Vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Valyrakis, M.; Liu, D.; Turker, U.; Yagci, O. The role of increasing riverbank vegetation density on flow dynamics across an asymmetrical channel. Environ. Fluid Mech. 2021, 21, 643–666. [Google Scholar] [CrossRef]
- Woś, A.; Książek, L. Hydrodynamics of the Instream Flow Environment of a Gravel-Bed River. Sustainability 2022, 14, 15330. [Google Scholar] [CrossRef]
- Soltani, N.; Afzalimehr, H.; Singh, V.P. Influence of Vegetated Banks on Turbulent Characteristics of Non-uniform Flow in Gravel Bed River. Int. J. Hydraul. Eng. 2020, 9, 15–23. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Maddahi, M.R.; Sui, J.; Rahimpour, M. Flow characteristics in gravel-bed rivers. J. Hydrodyn. 2019, 31, 986–998. [Google Scholar] [CrossRef]
- Tymiński, T.; Kałuża, T. Effect of Vegetation on Flow Conditions in the “nature-like“ Fishways. Ann. Set Environ. Protect. 2013, 15, 348–360. [Google Scholar]
- Wałęga, A.; Kędzior, R.; Książek, L.; Młyński, D.; Strużyński, A.; Grela, J.; Madej, P.; Skalski, T. Flow predictability indicates the ecological quality of the river: A case of invertebrates in Central Europe. Ecol. Indic. 2022, 143, 109308. [Google Scholar] [CrossRef]
- Liu, D.; Valyrakis, M.; Williams, R. Flow Hydrodynamics across Open Channel Flows with Riparian Zones: Implications for Riverbank Stability. Water 2017, 9, 720. [Google Scholar] [CrossRef]
- Babaeyan-Koopaei, K.; Ervine, D.A.; Carling, P.A.; Cao, Z. Velocity and Turbulence Measurements for Two Overbank Flow Events in River Severn. J. Hydraul. Engin. ASCE 2002, 128, 891–900. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Rowiński, P.M. Vertical Velocity Distributions through and above Submerged, Flexible Vegetation. Hydrol. Sci. J. 2008, 53, 905–920. [Google Scholar] [CrossRef]
- Laks, I.; Szoszkiewicz, K.; Kałuża, T. Analysis of in situ water velocity distributions in the lowland river floodplain covered by grassland and reed marsh habitats—A case study of the bypass channel of Warta River (Western Poland). J. Hydrol. Hydromech. 2017, 65, 325–332. [Google Scholar] [CrossRef]
- Wolski, K.; Tymiński, T.; Chrobak, G. Numerical modeling of the hydraulic impact of riparian vegetation. In Proceedings of the 10th Conference on Interdisciplinary Problems in Environmental Protection and Engineering EKO-DOK 2018, Polanica-Zdrój, Poland, 16–18 April 2018. [Google Scholar]
- Zhang, J.; Zhong, Y.; Huai, W. Transverse distribution of streamwise velocity in open-channel flow with artificial emergent vegetation. Ecol. Eng. 2018, 110, 78–86. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, C.; Huang, H.; Nanson, G.C.; Chen, Z.; Yao, W. Analytical models for velocity distributions in compound channels with emerged and submerged vegetated floodplains. Chin. Geogr. Sci. 2017, 27, 577–588. [Google Scholar] [CrossRef]
- Kałuża, T.; Radecki-Pawlik, A.; Szoszkiewicz, K.; Plesiński, K.; Radecki-Pawlik, B.; Laks, I. Plant basket hydraulic structures (PBHS) as a new river restoration measure. Sci. Total Environ. 2018, 627, 245–255. [Google Scholar] [CrossRef]
- Mera, I.; Franca, M.J.; Anta, J.; Pena, E. Turbulence anisotropy in a compound meandering channel with different submergence conditions. Adv. Water Resour. 2015, 81, 142–151. [Google Scholar] [CrossRef]
- Sukhodolov, A.N. Structure of turbulent flow in a meander bend of a lowland river. Water Resour. Res. 2012, 48, 1–21. [Google Scholar] [CrossRef]
- Szałkiewicz, E.; Dysarz, T.; Kałuża, T.; Malinger, A.; Radecki-Pawlik, A. Analysis of in-stream restoration structures impact on hydraulic condition and sedimentation in the Flinta river, Poland. Carpath. J. Earth Environ. Sci. 2019, 14, 275–286. [Google Scholar] [CrossRef]
- Zaborowski, S.; Kałuża, T.; Rybacki, M.; Radecki-Pawlik, A. Influence of river channel deflector hydraulic structures on lowland river roughness coefficient values: The Flinta river, Wielkopolska Province, Poland. Ecohydrol. Hydrobiol. 2022, 11, 79–97. [Google Scholar] [CrossRef]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Lee, C.; Ji, U.; Kim, H.S.; Kim, S. Flow and Wake Characteristics Associated with Riparian Vegetation Patches: Results from Field-scale Experiments. Hydrol. Process. 2022, 36, e14506. [Google Scholar] [CrossRef]
- Ghani, U.; Anjum, N.; Pasha, G.A.; Ahmad, M. Investigating the turbulent flow characteristics in an open channel with staggered vegetation patches. River Res. Appl. 2019, 35, 966–978. [Google Scholar] [CrossRef]
- Kubrak, E.; Kubrak, J.; Kiczko, A. Experimental Investigation of Kinetic Energy and Momentum Coefficients in Regular Channels with Stiff and Flexible Elements Simulating Submerged Vegetation. Acta Geophys. 2015, 63, 1405–1422. [Google Scholar] [CrossRef]
- Hawryło, A.; Książek, L.; Leja, M. Turbulence intensity in different morphological units using the Skawa River as an example. In Interdisciplinary Issues in Environmental Engineering and Protection; Traczewska, T., Ed.; Wroclaw University of Science and Technology: Wrocław, Poland, 2013; pp. 195–202. (In Polish) [Google Scholar]
- Velasco, D.; Bateman, A.; Redondo, J.M.; Demedina, V. An Open Channel Flow Experimental and Theoretical Study of Resistance and Turbulent Characterization over Flexible Vegetated Linings Flow. In Turbulence and Combustion; Kluwer Academic Publishers: London, UK, 2003; Volume 70, pp. 69–88. [Google Scholar]
- Kałuża, T.; Sojka, M.; Wróżyński, R.; Jaskuła, J.; Zaborowski, S.; Hämmerling, M. Modeling of River Channel Shading as a Factor for Changes in Hydromorphological Conditions of Small Lowland Rivers. Water 2020, 12, 527. [Google Scholar] [CrossRef]
- Kałuża, T.; Sojka, M.; Strzeliński, P.; Wróżyński, R. Application of Terrestrial Laser Scanning to Tree Trunk Bark Structure Characteristics Evaluation and Analysis of Their Effect on the Flow Resistance Coefficient. Water 2018, 10, 753. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tymiński, T.; Wolski, K. Hydraulic Effect of Vegetation Zones in Open Channels: An Experimental Study of the Distribution of Turbulence. Sustainability 2024, 16, 337. https://doi.org/10.3390/su16010337
Tymiński T, Wolski K. Hydraulic Effect of Vegetation Zones in Open Channels: An Experimental Study of the Distribution of Turbulence. Sustainability. 2024; 16(1):337. https://doi.org/10.3390/su16010337
Chicago/Turabian StyleTymiński, Tomasz, and Krzysztof Wolski. 2024. "Hydraulic Effect of Vegetation Zones in Open Channels: An Experimental Study of the Distribution of Turbulence" Sustainability 16, no. 1: 337. https://doi.org/10.3390/su16010337
APA StyleTymiński, T., & Wolski, K. (2024). Hydraulic Effect of Vegetation Zones in Open Channels: An Experimental Study of the Distribution of Turbulence. Sustainability, 16(1), 337. https://doi.org/10.3390/su16010337





