Mitigating Supply Disruption: The Interplay between Responsive Pricing and Information Sharing under Dual Sourcing
Abstract
:1. Introduction
2. Literature Review
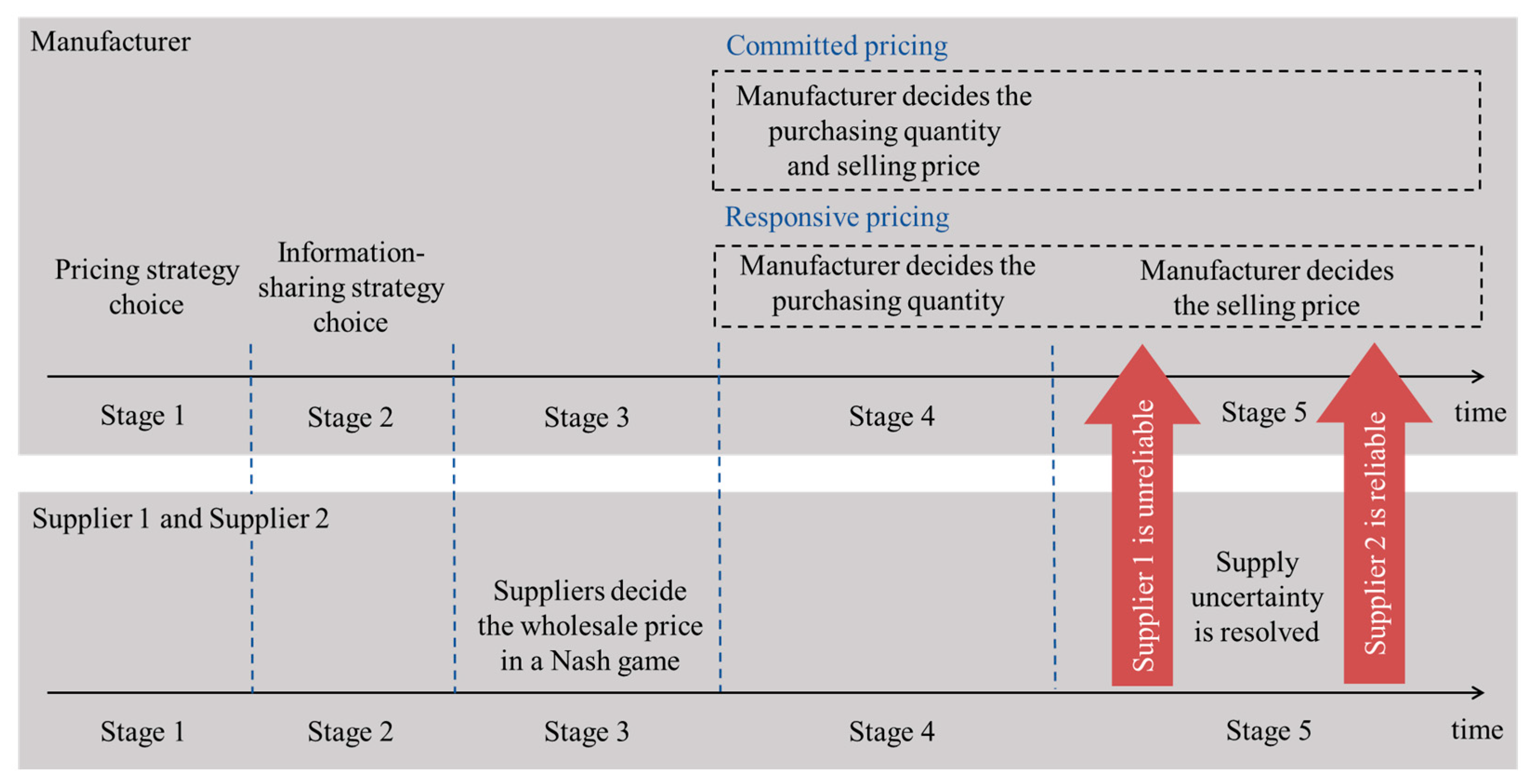
3. Model Descriptions, Notations, and Assumptions
4. Equilibrium Analysis
4.1. Equilibrium Decision Making with the Responsive Pricing Strategy
4.1.1. Optimal Selling Price Decision
4.1.2. Optimal Sourcing Quantity Decisions
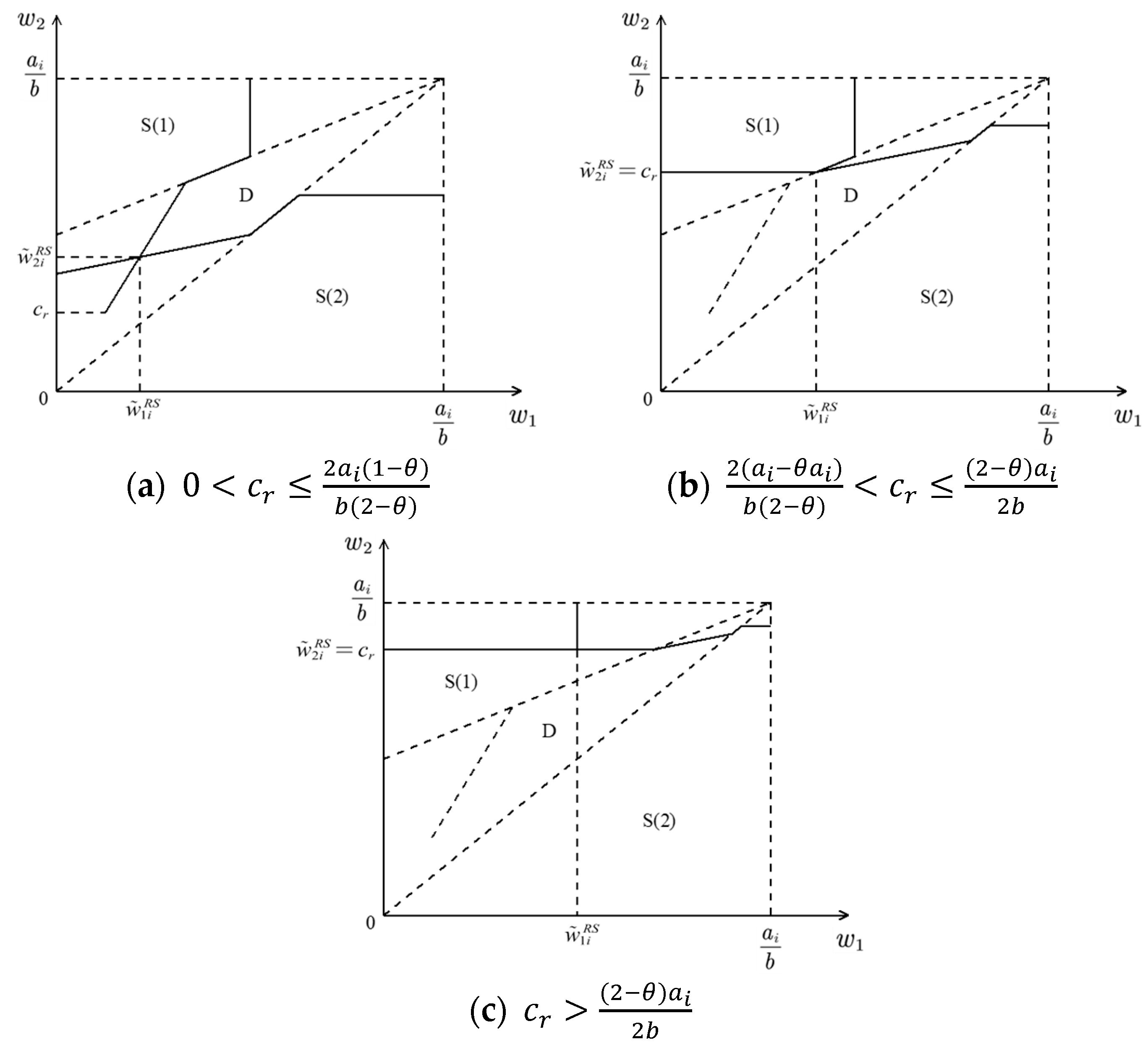
4.1.3. Equilibrium Wholesale Price Decisions
- (1)
- When , , ;
- (2)
- When , , ;
- (3)
- When , , .where , .
- (1)
- When , , ;
- (2)
- When , , ;
- (3)
- When , , ;where , .
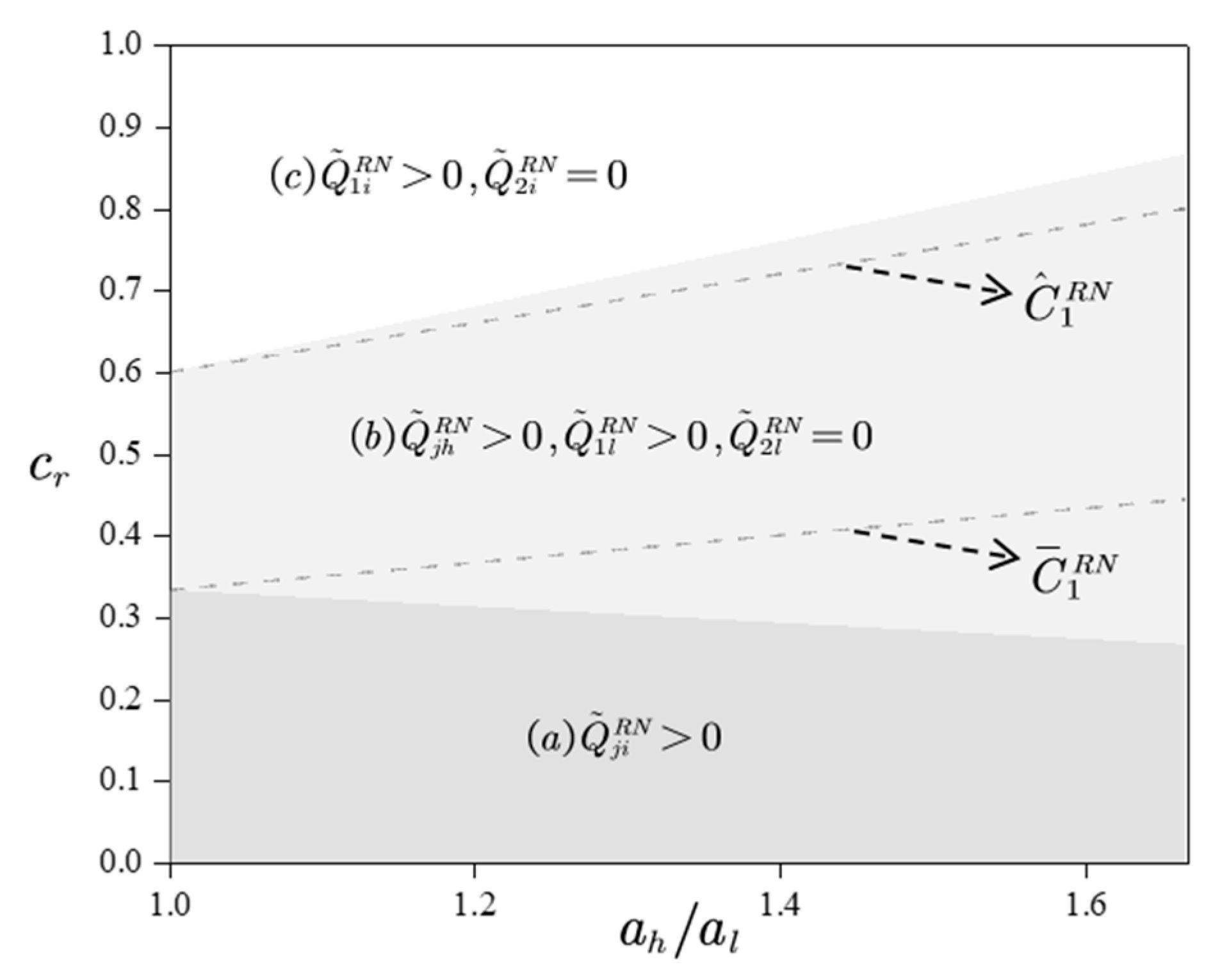
- (1)
- When , , , ;
- (2)
- When , , , , ;
- (3)
- When , , , , ;
- (4)
- When , , , , ;
- (5)
- When , , , , .
4.2. Equilibrium Decision Making with the Committed Pricing Strategy
4.2.1. Optimal Selling Price and Sourcing Quantity Decisions
- (1)
- When , , ;
- (2)
- When ,where .
4.2.2. Equilibrium Wholesale Price Decisions
- (1)
- When , , ;
- (2)
- When , , .
- (1)
- When , , ;
- (2)
- When , , .
- (1)
- When :For , , , , , ;For , , or , , , , , ;For , or , , , , .
- (2)
- When :For , , , , ;For , , , , .
5. Comparison and Discussion
5.1. Demand-Information-Sharing Strategy Options
5.2. Value Analysis of Responsive Pricing
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Liu, X.; Hu, D. Assessment of Sustainable Development: A Case Study of Wuhan as a Pilot City in China. Ecol. Indic. 2015, 50, 206–214. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, X.; Xiao, X.; Zhou, Z. Institutional Pressures, Sustainable Supply Chain Management, and Circular Economy Capability: Empirical Evidence from Chinese Eco-Industrial Park Firms. J. Clean. Prod. 2017, 155, 54–65. [Google Scholar] [CrossRef]
- Khalili-Fard, A.; Parsaee, S.; Bakhshi, A.; Yazdani, M.; Aghsami, A.; Rabbani, M. Multi-Objective Optimization of Closed-Loop Supply Chains to Achieve Sustainable Development Goals in Uncertain Environments. Eng. Appl. Artif. Intell. 2024, 133, 108052. [Google Scholar] [CrossRef]
- Bashir, M.F.; Shahbaz, M.; Malik, M.N.; Ma, B.; Wang, J. Energy Transition, Natural Resource Consumption and Environmental Degradation: The Role of Geopolitical Risk in Sustainable Development. Resour. Policy 2023, 85, 103985. [Google Scholar] [CrossRef]
- Chen, Z.-S.; Chen, J.-Y.; Chen, Y.-H.; Yang, Y.; Jin, L.; Herrera-Viedma, E.; Pedrycz, W. Large-Group Failure Mode and Effects Analysis for Risk Management of Angle Grinders in the Construction Industry. Inf. Fusion 2023, 97, 101803. [Google Scholar] [CrossRef]
- Khalili-Fard, A.; Hashemi, M.; Bakhshi, A.; Yazdani, M.; Jolai, F.; Aghsami, A. Integrated Relief Pre-Positioning and Procurement Planning Considering Non-Governmental Organizations Support and Perishable Relief Items in a Humanitarian Supply Chain Network. Omega 2024, 127, 103111. [Google Scholar] [CrossRef]
- Tang, C.S. Perspectives in Supply Chain Risk Management. Int. J. Prod. Econ. 2006, 103, 451–488. [Google Scholar] [CrossRef]
- Park, Y.; Hong, P.; Roh, J.J. Supply Chain Lessons from the Catastrophic Natural Disaster in Japan. Bus. Horiz. 2013, 56, 75–85. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, L.; Chen, M.; Qiu, C. The Impact of SIPOC on Process Reengineering and Sustainability of Enterprise Procurement Management in E-Commerce Environments Using Deep Learning. J. Organ. End User Comput. 2022, 34, 70. [Google Scholar] [CrossRef]
- Merzifonluoglu, Y. Risk Averse Supply Portfolio Selection with Supply, Demand and Spot Market Volatility. Omega-Int. J. Manag. Sci. 2015, 57, 40–53. [Google Scholar] [CrossRef]
- Dada, M.; Petruzzi, N.C.; Schwarz, L.B. A Newsvendor’s Procurement Problem When Suppliers Are Unreliable. Manuf. Serv. Oper. Manag. 2007, 9, 9–32. [Google Scholar] [CrossRef]
- Babich, V.; Burnetas, A.N.; Ritchken, P.H. Competition and Diversification Effects in Supply Chains with Supplier Default Risk. Manuf. Serv. Oper. Manag. 2007, 9, 123–146. [Google Scholar] [CrossRef]
- Wu, Z.H.; Choi, T.Y. Supplier-Supplier Relationships in the Buyer-Supplier Triad: Building Theories from Eight Case Studies. J. Oper. Manag. 2005, 24, 27–52. [Google Scholar] [CrossRef]
- Etienne, X.L.; Mallory, M.L.; Irwin, S.H. Estimating the Cost of Pre-harvest Forward Contracting Corn and Soybeans in Illinois before and after 2007. Agribusiness 2017, 33, 358–377. [Google Scholar] [CrossRef]
- Tomlin, B. On the Value of Mitigation and Contingency Strategies for Managing Supply Chain Disruption Risks. Manag. Sci. 2006, 52, 639–657. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, P.; Wang, J.; Chen, X. A Neutrosophic Normal Cloud and Its Application in Decision-Making. Cogn. Comput. 2016, 8, 649–669. [Google Scholar] [CrossRef]
- Hu, B.; Kostamis, D. Managing Supply Disruptions When Sourcing from Reliable and Unreliable Suppliers. Prod. Oper. Manag. 2015, 24, 808–820. [Google Scholar] [CrossRef]
- Gümüş, M.; Ray, S.; Gurnani, H. Supply-Side Story: Risks, Guarantees, Competition, and Information Asymmetry. Manag. Sci. 2012, 58, 1694–1714. [Google Scholar] [CrossRef]
- Shan, X.; Li, T.; Sethi, S.P. A Responsive-Pricing Retailer Sourcing from Competing Suppliers Facing Disruptions. Manuf. Serv. Oper. Manag. 2022, 24, 196–213. [Google Scholar] [CrossRef]
- Kraemer, K.L.; Dedrick, J.; Yamashiro, S. Refining and Extending the Business Model With Information Technology: Dell Computer Corporation. Inf. Soc. 2000, 16, 5–21. [Google Scholar] [CrossRef]
- Snyder, L.V.; Atan, Z.; Peng, P.; Rong, Y.; Schmitt, A.J.; Sinsoysal, B. OR/MS Models for Supply Chain Disruptions: A Review. IIE Trans. 2016, 48, 89–109. [Google Scholar] [CrossRef]
- Shekarian, M.; Mellat Parast, M. An Integrative Approach to Supply Chain Disruption Risk and Resilience Management: A Literature Review. Int. J. Logist. Res. Appl. 2021, 24, 427–455. [Google Scholar] [CrossRef]
- Chen, J.; Sohal, A.S.; Prajogo, D.I. Supply Chain Operational Risk Mitigation: A Collaborative Approach. Int. J. Prod. Res. 2013, 51, 2186–2199. [Google Scholar] [CrossRef]
- Golmohammadi, A.; Hassini, E. Review of Supplier Diversification and Pricing Strategies under Random Supply and Demand. Int. J. Prod. Res. 2020, 58, 3455–3487. [Google Scholar] [CrossRef]
- Goldschmidt, K.; Kremer, M.; Thomas, D.J.; Craighead, C.W. Strategic Sourcing Under Severe Disruption Risk: Learning Failures and Under-Diversification Bias. Manuf. Serv. Oper. Manag. 2021, 23, 761–780. [Google Scholar] [CrossRef]
- Yan, R.; Kou, D.; Lu, B. Optimal Order Policies for Dual-Sourcing Supply Chains under Random Supply Disruption. Sustainability 2019, 11, 698. [Google Scholar] [CrossRef]
- Shan, X.; Xiong, S.; Zhang, C. Mitigating Supply Disruption Risks by Diversifying Competing Suppliers and Using Sales Effort. Int. J. Prod. Econ. 2023, 255, 108637. [Google Scholar] [CrossRef]
- Lv, F.; Yin, Z. Mitigating Risky Sourcing with a Responsible Supplier in a Competitive Environment: The Implication of Product Line Design and Sourcing Diversification. Int. J. Prod. Res. 2024, 1–21. [Google Scholar] [CrossRef]
- Pan, W.; So, K.C.; Xiao, G. Benefits of Backup Sourcing for Components in Assembly Systems under Supply Uncertainty. Eur. J. Oper. Res. 2022, 302, 158–171. [Google Scholar] [CrossRef]
- Tang, C.S.; Yin, R. Responsive Pricing under Supply Uncertainty. Eur. J. Oper. Res. 2007, 182, 239–255. [Google Scholar] [CrossRef]
- Feng, Q. Integrating Dynamic Pricing and Replenishment Decisions Under Supply Capacity Uncertainty. Manag. Sci. 2010, 56, 2154–2172. [Google Scholar] [CrossRef]
- Li, T.; Sethi, S.P.; Zhang, J. Supply Diversification with Responsive Pricing. Prod. Oper. Manag. 2013, 22, 447–458. [Google Scholar] [CrossRef]
- Li, T.; Sethi, S.P.; Zhang, J. Mitigating Supply Uncertainty: The Interplay Between Diversification and Pricing. Prod. Oper. Manag. 2017, 26, 369–388. [Google Scholar] [CrossRef]
- Geng, X.; Guo, X.; Xiao, G.; Yang, N. Supply Risk Mitigation in a Decentralized Supply Chain: Pricing Postponement or Payment Postponement? Manuf. Serv. Oper. Manag. 2023, 26, 646–663. [Google Scholar] [CrossRef]
- Dominguez, R.; Ponte, B.; Cannella, S.; Framinan, J.M. Building Resilience in Closed-Loop Supply Chains through Information-Sharing Mechanisms. Sustainability 2019, 11, 6746. [Google Scholar] [CrossRef]
- Yang, Z.; Aydın, G.; Babich, V.; Beil, D.R. Supply Disruptions, Asymmetric Information, and a Backup Production Option. Manag. Sci. 2009, 55, 192–209. [Google Scholar] [CrossRef]
- Yang, Z.; Aydın, G.; Babich, V.; Beil, D.R. Using a Dual-Sourcing Option in the Presence of Asymmetric Information About Supplier Reliability: Competition vs. Diversification. Manuf. Serv. Oper. Manag. 2012, 14, 202–217. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Shang, J. Multi-Sourcing and Information Sharing under Competition and Supply Uncertainty. Eur. J. Oper. Res. 2019, 278, 658–671. [Google Scholar] [CrossRef]
- Yoon, J.; Talluri, S.; Rosales, C. Procurement Decisions and Information Sharing under Multi-Tier Disruption Risk in a Supply Chain. Int. J. Prod. Res. 2020, 58, 1362–1383. [Google Scholar] [CrossRef]
- Li, G.; Liu, M.; Zheng, H. Subsidization or Diversification? Mitigating Supply Disruption with Manufacturer Information Sharing. Omega 2022, 112, 102670. [Google Scholar] [CrossRef]
- Xu, H.; Liu, X.; Huang, H. Information Sharing and Order Allocation Rule in Dual-Sourcing. Omega 2023, 114, 102741. [Google Scholar] [CrossRef]
- Li, G.; Li, X.; Liu, M. Inducing Supplier Backup via Manufacturer Information Sharing under Supply Disruption Risk. Comput. Ind. Eng. 2023, 176, 108914. [Google Scholar] [CrossRef]
- Jiang, B.; Tian, L.; Xu, Y.; Zhang, F. To Share or Not to Share: Demand Forecast Sharing in a Distribution Channel. Mark. Sci. 2016, 35, 800–809. [Google Scholar] [CrossRef]
- Jung, S.H.; Kouvelis, P. On Co-Opetitive Supply Partnerships with End-Product Rivals: Information Asymmetry, Dual Sourcing and Supply Market Efficiency. Manuf. Serv. Oper. Manag. 2022, 24, 1040–1055. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, H.; Zhao, X. The Role of Supply Chain Diversification in Mitigating the Negative Effects of Supply Chain Disruptions in COVID-19. Int. J. Oper. Prod. Manag. 2024, 44, 99–132. [Google Scholar] [CrossRef]


| Decision Variables | |
| Parameters | |
| High-type demand potential | |
| Low-type demand potential | |
| Price sensitivity factor | |
| Unit production costs for Supplier 2 | |
| Reliability of Supplier 1 | |
| Total actual deliveries by suppliers |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, X. Mitigating Supply Disruption: The Interplay between Responsive Pricing and Information Sharing under Dual Sourcing. Sustainability 2024, 16, 5691. https://doi.org/10.3390/su16135691
Chen X, Liu X. Mitigating Supply Disruption: The Interplay between Responsive Pricing and Information Sharing under Dual Sourcing. Sustainability. 2024; 16(13):5691. https://doi.org/10.3390/su16135691
Chicago/Turabian StyleChen, Xiaohong, and Xiaoyang Liu. 2024. "Mitigating Supply Disruption: The Interplay between Responsive Pricing and Information Sharing under Dual Sourcing" Sustainability 16, no. 13: 5691. https://doi.org/10.3390/su16135691
APA StyleChen, X., & Liu, X. (2024). Mitigating Supply Disruption: The Interplay between Responsive Pricing and Information Sharing under Dual Sourcing. Sustainability, 16(13), 5691. https://doi.org/10.3390/su16135691






