Hydrologic Model Prediction Improvement in Karst Watersheds through Available Reservoir Capacity of Karst
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Methodology
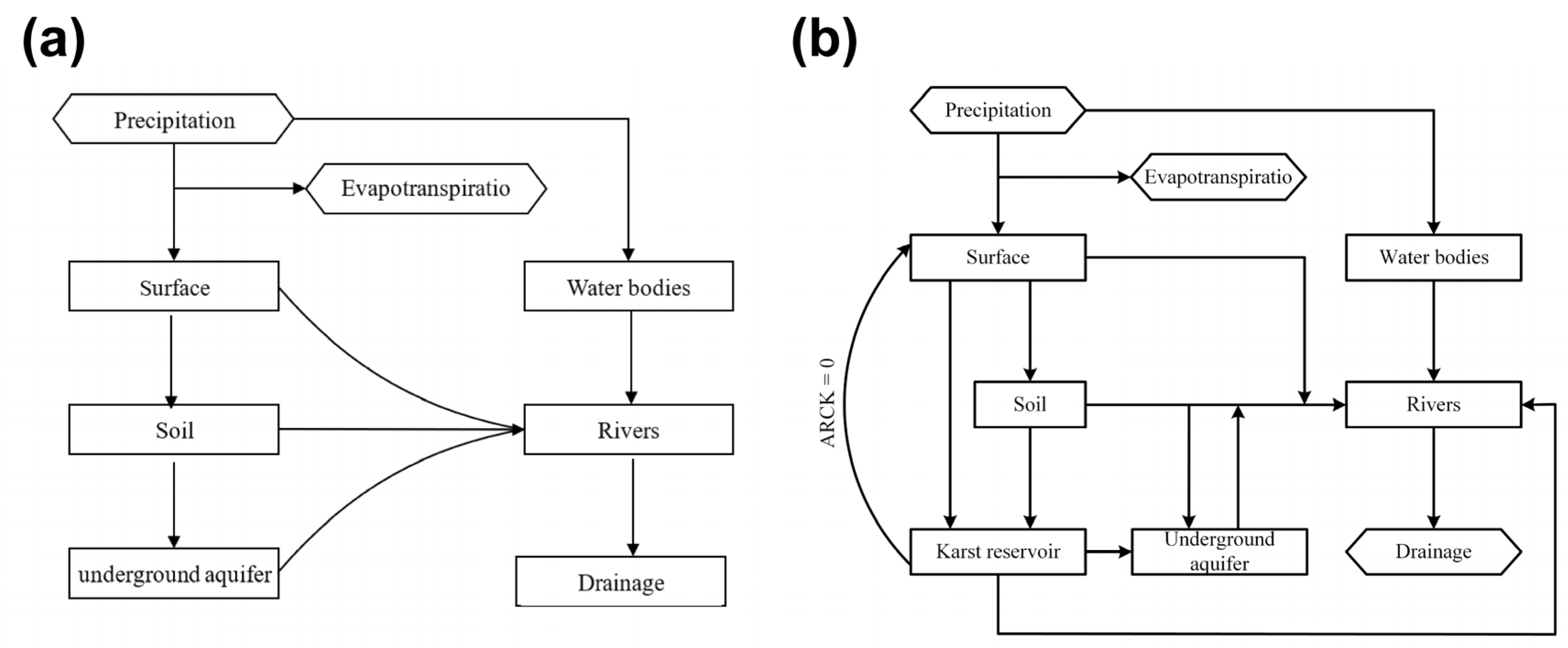
2.2.1. HEC-HMS Model Establishment and Its Extensions
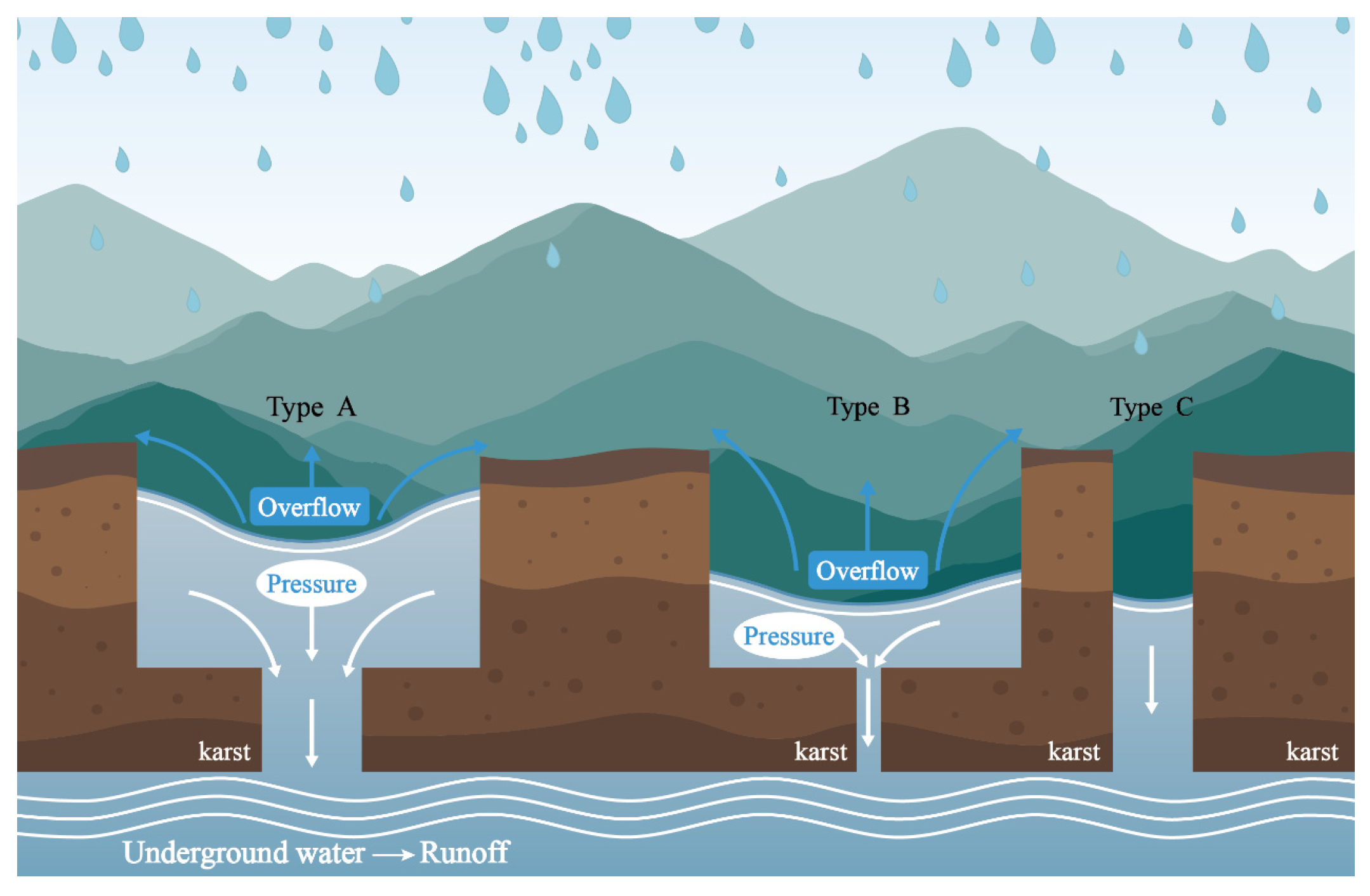
2.2.2. ARCK Inclusion
3. Results and Analyses
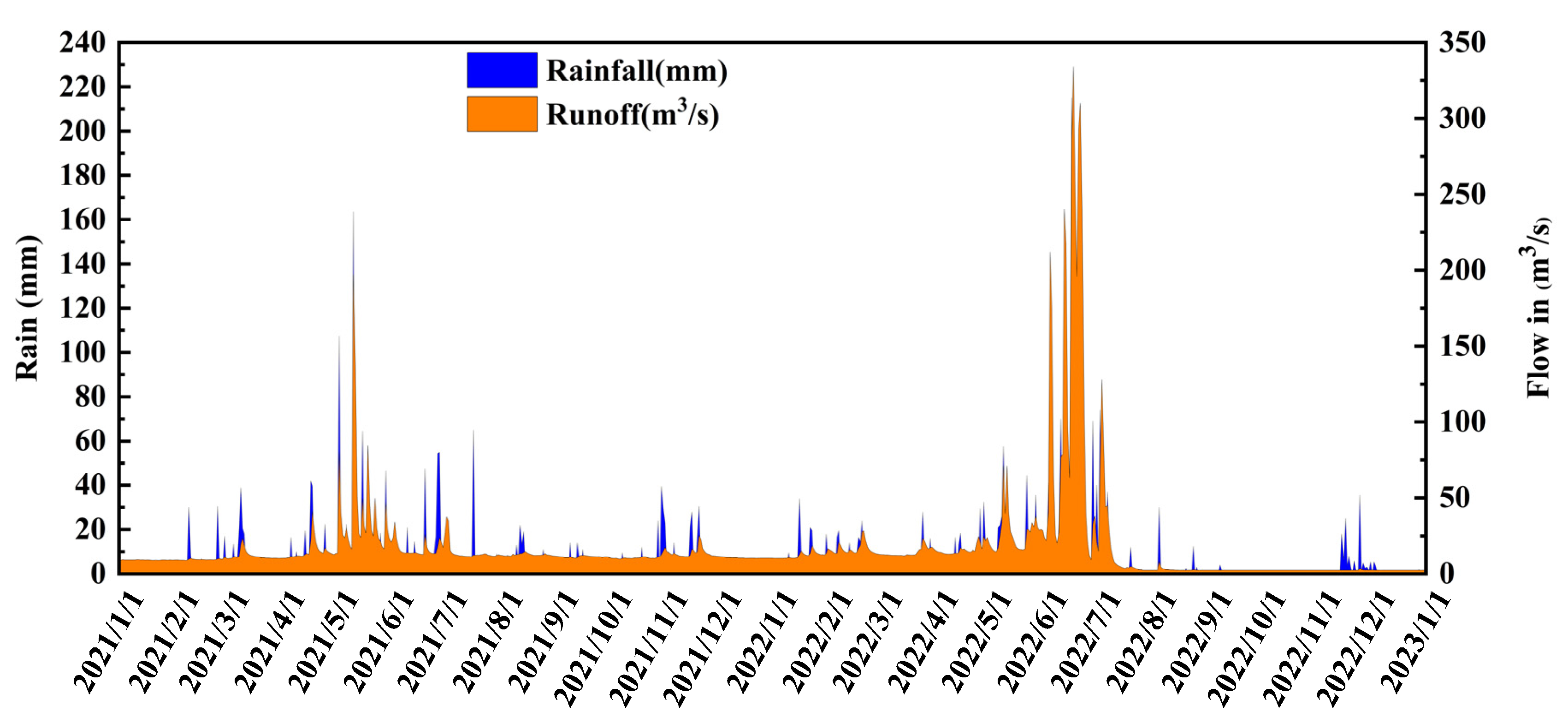
3.1. Initial Model
3.2. Modified Model
3.3. Uncertainties and Explanations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, L.; Zhao, Y.; Zhu, C.; Shi, C. Route Selection for Scenic Byways in Karst Areas Based on the Minimum Cumulative Resistance Model: A Case Study of the Nanpan–Beipan River Basin, China. Ecol. Indic. 2024, 163, 112093. [Google Scholar] [CrossRef]
- Chen, S.; Wei, X.; Cai, Y.; Li, H.; Li, L.; Pu, J. Spatiotemporal Evolution of Rocky Desertification and Soil Erosion in Karst Area of Chongqing and Its Driving Factors. Catena 2024, 242, 108108. [Google Scholar] [CrossRef]
- Fushan, L.; Guilin, H.; Yang, T. C-N Isotope Coupling along the Vertical Profiles under Different Land Use in a Typical Karst Area, Guizhou, Southwest China. Procedia Earth Planet. Sci. 2014, 10, 194–199. [Google Scholar] [CrossRef]
- Iacobellis, V.; Castorani, A.; Di Santo, A.R.; Gioia, A. Rationale for Flood Prediction in Karst Endorheic Areas. J. Arid Environ. 2015, 112, 98–108. [Google Scholar] [CrossRef]
- Zhang, W.; Duan, L.; Liu, T.; Shi, Z.; Shi, X.; Chang, Y.; Qu, S.; Wang, G. A Hybrid Framework Based on LSTM for Predicting Karst Spring Discharge Using Historical Data. J. Hydrol. 2024, 633, 130946. [Google Scholar] [CrossRef]
- Guan, N.; Cheng, J.; Bi, H.; Shi, X. Laboratory and Field Characterization of Preferential Flow under Consideration of Geometric Fracture Features in a Karst Region in Southwest China. J. Hydrol. 2024, 631, 130851. [Google Scholar] [CrossRef]
- Xu, X.; Yan, Y.; Dai, Q.; Yi, X.; Hu, Z.; Cen, L. Spatial and Temporal Dynamics of Rainfall Erosivity in the Karst Region of Southwest China: Interannual and Seasonal Changes. Catena 2023, 221, 106763. [Google Scholar] [CrossRef]
- Baraza, T.; Hasenmueller, E.A. Floods Enhance the Abundance and Diversity of Anthropogenic Microparticles (Including Microplastics and Treated Cellulose) Transported through Karst Systems. Water Res. 2023, 242, 120204. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Zhao, X.; Yu, M. Exploring the Multiple Disturbances of Karst Landscape in Guilin World Heritage Site, China. Catena 2021, 203, 105349. [Google Scholar] [CrossRef]
- Husic, A.; Al-Aamery, N.; Fox, J.F. Simulating Hydrologic Pathway Contributions in Fluvial and Karst Settings: An Evaluation of Conceptual, Physically Based, and Deep Learning Modeling Approaches. J. Hydrol. X 2022, 17, 100134. [Google Scholar] [CrossRef]
- Yan, Y.; Dai, Q.; Yuan, Y.; Peng, X.; Zhao, L.; Yang, J. Effects of Rainfall Intensity on Runoff and Sediment Yields on Bare Slopes in a Karst Area, SW China. Geoderma 2018, 330, 30–40. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Y.; Peng, L. Exploring Social-Ecological System Resilience in South China Karst: Quantification, Interaction and Policy Implication. Geogr. Sustain. 2024, 5, 289–301. [Google Scholar] [CrossRef]
- Siou, L.K.A.; Johannet, A.; Borrell, V.; Pistre, S. Complexity Selection of a Neural Network Model for Karst Flood Forecasting: The Case of the Lez Basin (Southern France). J. Hydrol. 2011, 403, 367–380. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, F.; Chi, F.; Zhang, N.; Ma, J.; Miao, Y.; Chen, F. Hydrogeological Structures of Karst Features Using Hydrographs in an Underground River Basin Formed in a Peak Cluster Depression, Southwest China. J. Hydrol. 2024, 634, 131085. [Google Scholar] [CrossRef]
- Chen, L.; Deng, J.; Yang, W.; Chen, H. Hydrological Modelling of Large-Scale Karst-Dominated Basin Using a Grid-Based Distributed Karst Hydrological Model. J. Hydrol. 2024, 628, 130459. [Google Scholar] [CrossRef]
- Chen, S.; Xiong, L.; Zeng, L.; Kim, J.-S.; Zhang, Q.; Jiang, C. Distributed Rainfall-Runoff Simulation for a Large-Scale Karst Catchment by Incorporating Landform and Topography into the DDRM Model Parameters. J. Hydrol. 2022, 610, 127853. [Google Scholar] [CrossRef]
- Duran, L.; Gill, L. Modeling Spring Flow of an Irish Karst Catchment Using Modflow-USG with CLN. J. Hydrol. 2021, 597, 125971. [Google Scholar] [CrossRef]
- Li, J.; Yuan, D.; Jiang, Y.; Liu, J. Elaborate Simulations of Floods in a Karst Trough Valley Basin with the Simplified Karst-Liuxihe Model. J. Hydrol. 2022, 614, 128504. [Google Scholar] [CrossRef]
- Li, J.; Yuan, D.; Liu, J.; Ma, M.; Li, Y. Evaluating the Effects of Water Exchange between Surface Rivers and Karst Aquifers on Surface Flood Simulations at Different Watershed Scales. J. Hydrol. 2023, 623, 129851. [Google Scholar] [CrossRef]
- Lin, Q.; Lin, B.; Zhang, D.; Wu, J. Web-Based Prototype System for Flood Simulation and Forecasting Based on the HEC-HMS Model. Environ. Model. Softw. 2022, 158, 105541. [Google Scholar] [CrossRef]
- Ren-Jun, Z. The Xinanjiang Model Applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, L.; Singh, V.P.; Zhou, J.; Chen, X.; Xiong, L. Rainfall-Runoff Simulation in Karst Dominated Areas Based on a Coupled Conceptual Hydrological Model. J. Hydrol. 2019, 573, 524–533. [Google Scholar] [CrossRef]
- Mo, C.; Wang, Y.; Ruan, Y.; Qin, J.; Zhang, M.; Sun, G.; Jin, J. The Effect of Karst System Occurrence on Flood Peaks in Small Watersheds, Southwest China. Hydrol. Res. 2021, 52, 305–322. [Google Scholar] [CrossRef]
- Arabi, M.; Govindaraju, R.S.; Hantush, M.M. A Probabilistic Approach for Analysis of Uncertainty in the Evaluation of Watershed Management Practices. J. Hydrol. 2007, 333, 459–471. [Google Scholar] [CrossRef]
- Oleyiblo, J.O. Application of HEC-HMS for Flood Forecasting in Misai and Wan’an Catchments in China. Water Sci. Eng. 2010, 3, 1. [Google Scholar]
- Palacios-Cabrera, T.; Valdes-Abellan, J.; Jodar-Abellan, A.; Rodrigo-Comino, J. Land-Use Changes and Precipitation Cycles to Understand Hydrodynamic Responses in Semiarid Mediterranean Karstic Watersheds. Sci. Total Environ. 2022, 819, 153182. [Google Scholar] [CrossRef] [PubMed]
- Guduru, J.U.; Jilo, N.B.; Rabba, Z.A.; Namara, W.G. Rainfall-Runoff Modeling Using HEC-HMS Model for Meki River Watershed, Rift Valley Basin, Ethiopia. J. Afr. Earth Sci. 2023, 197, 104743. [Google Scholar] [CrossRef]
- Alemu, G.T.; Ayalew, M.M.; Geremew, B.S.; Bihonegn, B.G.; Tareke, K.A. Evaluation of Semi-Distributed Hydrological Models Performance in Borkena Watershed; Upper Awash Basin, Ethiopia. Heliyon 2023, 9, e18030. [Google Scholar] [CrossRef] [PubMed]
- Mauri, L.; Tarolli, P. Modeling Windthrow Effects on Water Runoff and Hillslope Stability in a Mountain Catchment Affected by the VAIA Storm. Sci. Total Environ. 2023, 895, 164831. [Google Scholar] [CrossRef]
- Ju, Q.; Liu, X.; Zhang, D.; Shen, T.; Wang, Y.; Jiang, P.; Gu, H.; Yu, Z.; Fu, X. Application of Distributed Xin’anjiang Model of Melting Ice and Snow in Bahe River Basin. J. Hydrol. Reg. Stud. 2024, 51, 101638. [Google Scholar] [CrossRef]
- Dai, J.; Rad, S.; Xu, J.; Wan, Z.; Li, Z.; Pan, L.; Shahab, A. Influence of Karst Reservoir Capacity on Flood in Lijiang Basin Based on Modified HEC-HMS through Soil Moisture Accounting Loss. Atmosphere 2022, 13, 1544. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Z.; Lei, Q.; Yao, J.; Gong, L.; Sun, S.; Li, Y. Connectivity, Permeability and Flow Channelization in Fractured Karst Reservoirs: A Numerical Investigation Based on a Two-Dimensional Discrete Fracture-Cave Network Model. Adv. Water Resour. 2022, 161, 104142. [Google Scholar] [CrossRef]
- Amatya, D.M.; Walega, A.; Callahan, T.J.; Morrison, A.; Vulava, V.; Hitchcock, D.R.; Williams, T.M.; Epps, T. Storm Event Analysis of Four Forested Catchments on the Atlantic Coastal Plain Using a Modified SCS-CN Rainfall-Runoff Model. J. Hydrol. 2022, 608, 127772. [Google Scholar] [CrossRef]
- Liu, W.; Feng, Q.; Wang, R.; Chen, W. Effects of Initial Abstraction Ratios in SCS-CN Method on Runoff Prediction of Green Roofs in a Semi-Arid Region. Urban For. Urban Green. 2021, 65, 127331. [Google Scholar] [CrossRef]
- Jia, M.; He, D.; Huo, X.; Zhang, H.; Jia, S.; Zhang, J. Exploring the Impact of Climate Change on Flood Risk at Cultural Heritage Sites Using a GIS-Based SCS-CN Method: A Case Study of Shanxi Province, China. Int. J. Disaster Risk Reduct. 2023, 96, 103968. [Google Scholar] [CrossRef]
- Rad, S.; Junfeng, D.; Jingxuan, X.; Zitao, L.; Linyan, P.; Wan, Z.; Lin, L. Flood Characteristics and Implication of Karst Storage through Muskingum Flood Routing via HEC-HMS, S. China. Hydrol. Res. 2022, 53, 1480–1493. [Google Scholar] [CrossRef]
- Li, R.; Fan, J.; Zhao, W.; Jia, Y.; Xi, N.; Li, J.; Zhang, T.; Pu, J. High-Frequency Dynamics of CO2 Emission Flux and Its Influencing Factors in a Subtropical Karst Groundwater-Fed Reservoir, South China. Environ. Res. 2024, 251, 118552. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Yan, Y.; Yu, K.; Xin, X.; Guzman, S.M.; Lu, J.; He, Z. Baseflow Estimation Based on a Self-Adaptive Non-Linear Reservoir Algorithm in a Rainy Watershed of Eastern China. J. Environ. Manag. 2023, 332, 117379. [Google Scholar] [CrossRef] [PubMed]
- Tu, T.; Li, Y.; Duan, K.; Zhao, T. Enhancing Physically Based Hydrological Modeling with an Ensemble of Machine-Learning Reservoir Operation Modules under Heavy Human Regulation Using Easily Accessible Data. J. Environ. Manag. 2024, 359, 121044. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. HEC-5: Simulation of Flood Control and Conservation Systems User’s Manual; Hydrologic Engineering Center: Davis, CA, USA, 1998.
- U.S. Army Corps of Engineers. Hydraulic Design of Spillways, EM 1110-2-1603; Office of Chief of Engineers: Washington, DC, USA, 1965.
- Plunge, S.; Schürz, C.; Čerkasova, N.; Strauch, M.; Piniewski, M. SWAT+ Model Setup Verification Tool: SWATdoctR. Environ. Model. Softw. 2024, 171, 105878. [Google Scholar] [CrossRef]
- Braswell, A.S.; Winston, R.J.; Dorsey, J.D.; Youssef, M.A.; Hunt, W.F. Calibration and Validation of DRAINMOD to Predict Long-Term Permeable Pavement Hydrology. J. Hydrol. 2024, 637, 131373. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Zhang, P. A Skillful Method for Precipitation Prediction over Eastern China. Atmos. Ocean. Sci. Lett. 2022, 15, 100133. [Google Scholar] [CrossRef]
- Lin, G.; Lan, H.; Li, P.; Li, L.; Liu, S.; Sun, W. Role of Rainfall Temporal Distribution on Effective Infiltration in the Loess Slope and Prediction Model. Eng. Geol. 2024, 335, 107541. [Google Scholar] [CrossRef]
- Shukla, S.; Shukla, A.; Knowles, J.M.; Harris, W.G. Shifting Nutrient Sink and Source Functions of Stormwater Detention Areas in Sub-Tropics. Ecol. Eng. 2017, 102, 178–187. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Gao, H.; Huang, J.; Shen, C.; Li, Q.; Qi, H.; Zheng, L.; Liu, M. Comparison of Deep Learning Models and a Typical Process-Based Model in Glacio-Hydrology Simulation. J. Hydrol. 2022, 615, 128562. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, Q.; Xu, Y.; Luo, S.; Zhou, C.; Yu, Z.; Xu, C.-Y. Soil Moisture Dynamics and Associated Rainfall-Runoff Processes under Different Land Uses and Land Covers in a Humid Mountainous Watershed. J. Hydrol. 2024, 636, 131249. [Google Scholar] [CrossRef]
- Al Khoury, I.; Boithias, L.; Bailey, R.T.; Ollivier, C.; Sivelle, V.; Labat, D. Impact of Land-Use Change on Karst Spring Response by Integration of Surface Processes in Karst Hydrology: The ISPEEKH Model. J. Hydrol. 2023, 626, 130300. [Google Scholar] [CrossRef]
- Thomas, N.W.; Ayalew, T.B.; Arenas, A.A.; Schilling, K.E.; Weber, L.J.; Krajewski, W.F. Characterizing the Effects of Dry Antecedent Soil Moisture Conditions, Channel Transmission Losses, and Variable Precipitation on Peak Flow Scaling. Adv. Water Resour. 2021, 158, 104061. [Google Scholar] [CrossRef]
- He, C.; Chen, Z.; Qiu, K.-Y.; Chen, J.-S.; Bohoussou, Y.N.; Dang, Y.P.; Zhang, H.-L. Effects of Conservation Agriculture on Carbon Mineralization: A Global Meta-Analysis. Soil Tillage Res. 2023, 229, 105685. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Zhang, T.; Kang, Y.; Zhang, B. How Does High Resolution Topography Affect Flood Simulation at Watershed Scale: A Case Study in a Small Watershed Based on Tilt Photography. Phys. Chem. Earth Parts A/B/C 2023, 131, 103443. [Google Scholar] [CrossRef]
- Workneh, H.T.; Chen, X.; Ma, Y.; Bayable, E.; Dash, A. Comparison of IDW, Kriging and Orographic Based Linear Interpolations of Rainfall in Six Rainfall Regimes of Ethiopia. J. Hydrol. Reg. Stud. 2024, 52, 101696. [Google Scholar] [CrossRef]
- Innocente dos Santos, C.; Carlotto, T.; Steiner, L.V.; Chaffe, P.L.B. Development of the Synthetic Unit Hydrograph Tool—SUnHyT. Appl. Comput. Geosci. 2023, 20, 100138. [Google Scholar] [CrossRef]
- Hao, Z.; Gao, Y.; Zhang, Q.; Wen, W. Isotopic Insights on Quantitative Assessments of Interaction of Eco-Hydrological Processes in Multi-Scale Karst Watersheds. Int. Soil Water Conserv. Res. 2024, 12, 156–170. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, L.; Rad, S.; Dai, J.; Shahab, A.; Xu, J.; Xia, R. Hydrologic Model Prediction Improvement in Karst Watersheds through Available Reservoir Capacity of Karst. Sustainability 2024, 16, 6557. https://doi.org/10.3390/su16156557
Liao L, Rad S, Dai J, Shahab A, Xu J, Xia R. Hydrologic Model Prediction Improvement in Karst Watersheds through Available Reservoir Capacity of Karst. Sustainability. 2024; 16(15):6557. https://doi.org/10.3390/su16156557
Chicago/Turabian StyleLiao, Lin, Saeed Rad, Junfeng Dai, Asfandyar Shahab, Jingxuan Xu, and Rui Xia. 2024. "Hydrologic Model Prediction Improvement in Karst Watersheds through Available Reservoir Capacity of Karst" Sustainability 16, no. 15: 6557. https://doi.org/10.3390/su16156557
APA StyleLiao, L., Rad, S., Dai, J., Shahab, A., Xu, J., & Xia, R. (2024). Hydrologic Model Prediction Improvement in Karst Watersheds through Available Reservoir Capacity of Karst. Sustainability, 16(15), 6557. https://doi.org/10.3390/su16156557








